Prerpints.org logo
Preprint
Article

Impact Assessment of Coupling Mode of Hy-Drological Model and Machine Learning Model on Runoff Simulation

This version is not peer-reviewed.

Submitted:

08 November 2024

Posted:

08 November 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

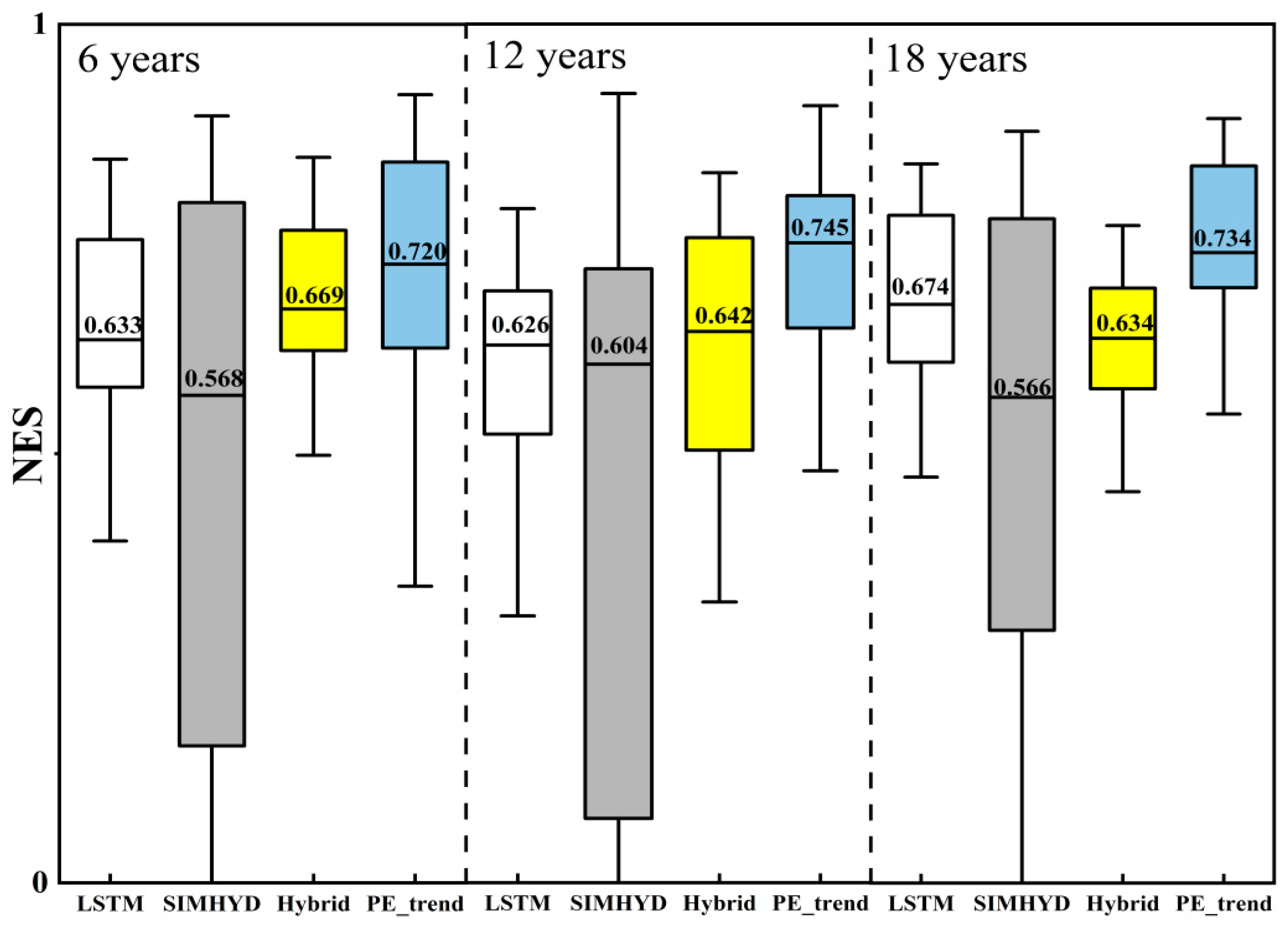
The inherent uncertainties in traditional hydrological models present significant chal-lenges for accurately simulating runoff. Combining machine learning models with tradi-tional hydrological models is an essential approach to enhancing the runoff modeling capabilities of hydrological models. However, research on the impact of mixed models on runoff simulation capability is limited. Therefore, this study uses the traditional hy-drological model SIMHYD and the machine learning model LSTM (Long Short-Term Memory) to construct two coupled models: a direct coupling model and a dynamically improved predictive validity hybrid model. These models were evaluated using the US CAMELS dataset to assess the impact of the two model combination methods on runoff modeling capabilities. The results indicate that the runoff modeling capabilities of both model combination methods were improved compared to individual models, with the dynamically improved predictive validity hybrid model demonstrating the optimal mod-eling capability. Compared to LSTM, this hybrid model showed a 12.8% increase in the Nash-Sutcliffe efficiency (NSE) median value for daily runoff during the validation pe-riod, a 28.4% increase in the NSE median value for high flows compared to SIMHYD, this hybrid model showed a 12.5% increase in the NSE median value for daily runoff during the validation period, a 23.6% increase in the NSE median value for high flows, and a significant improvement in the stability of low-flow runoff simulations. In per-formance testing involving varying training period lengths, the PE_trend model trained for 12 years exhibited the best performance, showing a 3.5% and 1.5% increase in the median NES compared to training periods of 6 years and 18 years, respectively.

Keywords: 
Subject: 
Environmental and Earth Sciences  -   Water Science and Technology

1. Introduction

In recent years, global climate change has led to a significant increase in the frequency of droughts and floods worldwide, resulting in severe economic losses [1]. The issue of drought and flood early warning has garnered widespread attention from various coun-tries and sectors of society [2]. Hydrological models provide a mathematical abstraction of the complex hydrological processes[3] in nature. They are widely used for water re-sources management, flood and drought forecasting, and the assessment of eco-hydrological effects [4]. However, accurate streamflow prediction faces numerous challenges due to spatial variations in climate and land surface characteristics[5] and the inherent uncertainty of hydrological models[6]. Notably, in the context of significant climate and land surface changes, the predictive capability of hydrological models based on historical data calibration becomes unstable [7]. Therefore, enhancing the streamflow prediction capability of hydrological models is crucial in the current context.
With the advancement of computational capabilities and the widespread application of big data, many scholars are exploring using data-driven models for streamflow predic-tion [8]. Compared to hydrological models, data-driven models do not require an under-standing of the physical transformation process of precipitation-runoff[9]; they can di-rectly analyze and learn from data, fitting them to the target and offer the advantages of higher simulation accuracy and lower computational complexity. Machine learning (ML) models are a type of data-driven model, and employing machine learning for hydrolog-ical simulation is a current research focus[10], with widespread applications in stream-flow prediction [11]. Standard machine learning models include support vector ma-chines[12], random forests[13], and recurrent neural networks (RNNs)[14]. As hydro-logical events exhibit lag effects[15], most hydrological variables change over time. However, specific machine-learning models are unsuitable for considering the lag ef-fects between hydrological drivers and outputs in streamflow prediction [16]. Some machine learning models incorporating time series data structures, such as RNN mod-els[17], have demonstrated exemplary performance in time series prediction[18]. How-ever, their unique structure also leads to the problem of gradient explosion or disap-pearance [19]. Therefore, to overcome this issue, Hochreiter [20] developed the Long Short-Term Memory (LSTM) neural network based on the RNN structure in 1997. Compared to traditional hydrological models, the LSTM model can better learn the nonlinear relationships in the streamflow process and effectively capture and utilize long-term dependencies in time series[21], thereby improving streamflow prediction capability. However, the LSTM model has multiple parameters, including learning rate and regularization parameters, which must be adjusted according to different watersheds and hydrological conditions. Therefore, selecting appropriate parameters for the LSTM model is crucial in improving its performance. Some scholars have attempted to blend machine learning models with optimization algorithms and achieved promising results. For instance, Yuan et al. [22] combined the LSTM model with Ant Lion Optimizer (LSTM-ALO) for monthly runoff prediction. Adnan et al. [23,24] integrated Relevance Vector Machine (RVM) with Improved Moth-Flame Optimization (IMRFO) model for evaporation forecasting and also applied Firefly Algorithm Particle Swarm Optimization (FFAPSO) to Support Vector Machine (SVM) model for predicting dissolved oxygen concentration in rivers, all yielding favorable outcomes.
Coupling machine learning models in traditional hydrological models can enhance the hydrological model's ability to capture the nonlinear relationship between precipitation and runoff [25], and the hydrological model can provide data input for the machine learning model, thereby improving the runoff modeling capability [26]. Many scholars have researched different aspects of the coupling methods of hydrological and machine learning models. Yang et al. [27] combined a distributed hydrological model with an artificial neural network (ANN) to develop an ML-based hydrological model, finding that this combined model provided satisfactory accuracy for long-term daily runoff sim-ulation. Liu et al. [28] integrated traditional hydrological models with meteorological forecasts and machine learning, reducing the error in runoff prediction. Yu et al.[29], using the Loess Plateau semiarid region as an example, combined the HBV hydrologi-cal model with the LSTM model, proposing two different coupling methods, tight and loose, and found that the hybrid model significantly improved the accuracy and stability of runoff simulation. While many scholars have proposed different model combination methods, there needs to be more research evaluating the performance of different hybrid models and studying the performance of hybrid models in simulating extreme flows, which can confirm whether hybrid models can genuinely contribute to flood and drought early warning. Therefore, our study utilized data from 30 basins in the US CAMELS dataset to construct and evaluate two coupling methods of the hydrological model SIMHYD and the LSTM model. We also compared these two combined models with independent LSTM and SIMHYD models, validating the performance improve-ment of the hybrid models in simulating extreme flows, aiming to analyze whether the combined models enhance the runoff modeling capabilities compared to individual models. The research findings can provide new insights for improving the runoff mod-eling capabilities of traditional hydrological models.

2. Materials and Methods

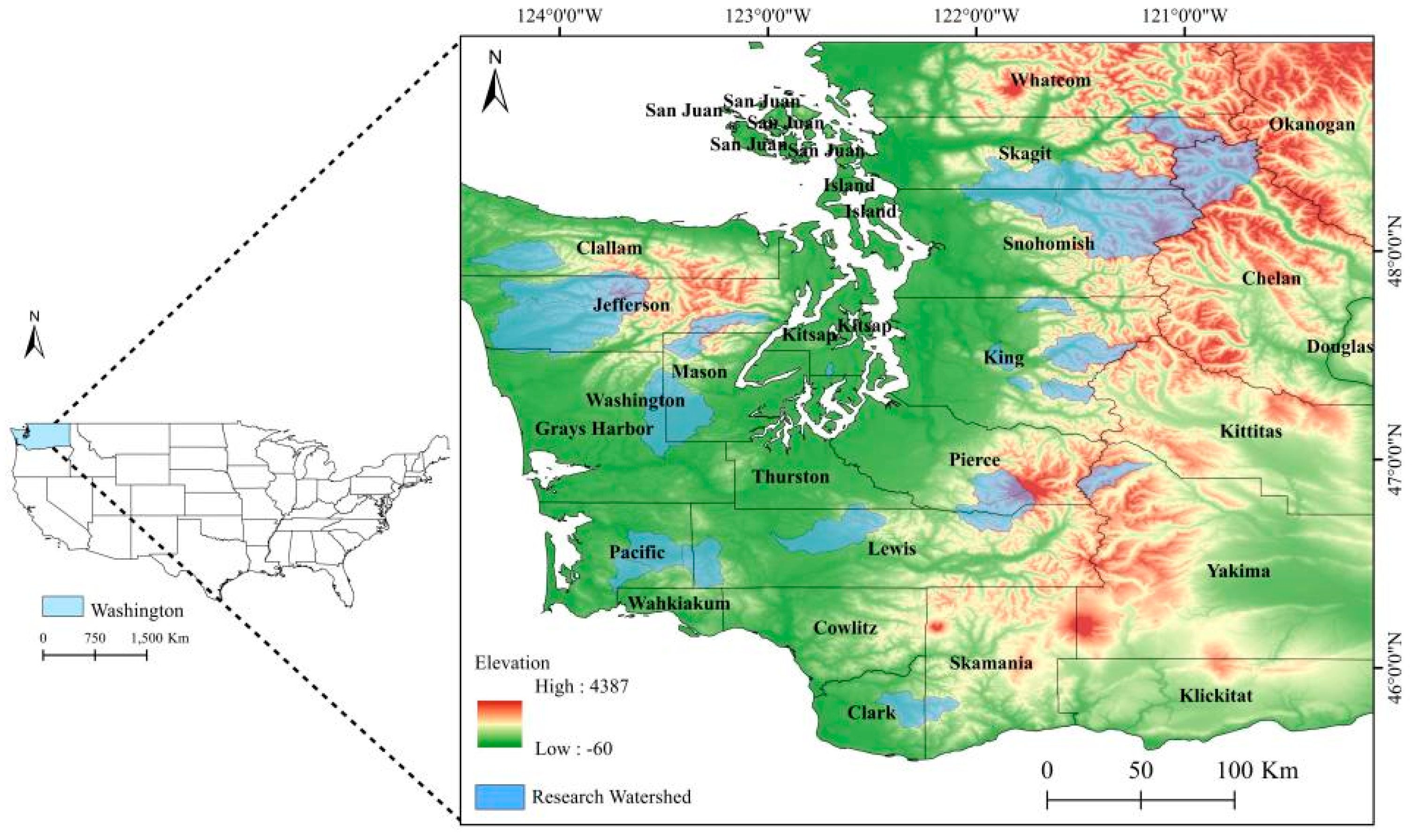
2.1. Research Area and Data

This study evaluates the predictive capability of hydrological models in 30 watersheds in Washington, USA (Figure 1). Washington is located on the continent's west coast between latitudes 40 and 60 degrees. The western coastal region has a temperate marine climate with moderate temperatures and high precipitation, with an annual average rainfall of over 1000 millimeters. The eastern inland region has a semiarid climate with lower precipitation, with an annual average rainfall of around 250-500 millimeters. Due to the mountainous areas in Washington, winter precipitation often occurs in the form of snow, which melts in spring and becomes a critical water resource for irrigation, urban water supply, and hydropower.
Each watershed includes 25 years (1980-2004) of hydrometeorological data, which are divided into a model training period (1980-1999) and a validation period (2000-2004). The data are sourced from the US CAMLES dataset (https://gdex.ucar.edu/dataset/camels.html), which includes daily sunshine duration, daily precipitation, daily streamflow, daily maximum and minimum temperatures, as well as the elevation, latitude, and atmospheric pressure of the watersheds. Potential evapotranspiration (PET) is an essential input for hydrological models[30], but various methods exist to calculate it. In this study, the FAO-56 Penman-Monteith method is used as a reference, and daily reference crop evapotranspiration is calculated based on data such as daily sunshine duration, daily maximum and minimum temperatures, at-mospheric pressure, elevation, and latitude.

2.2. Models and Methods

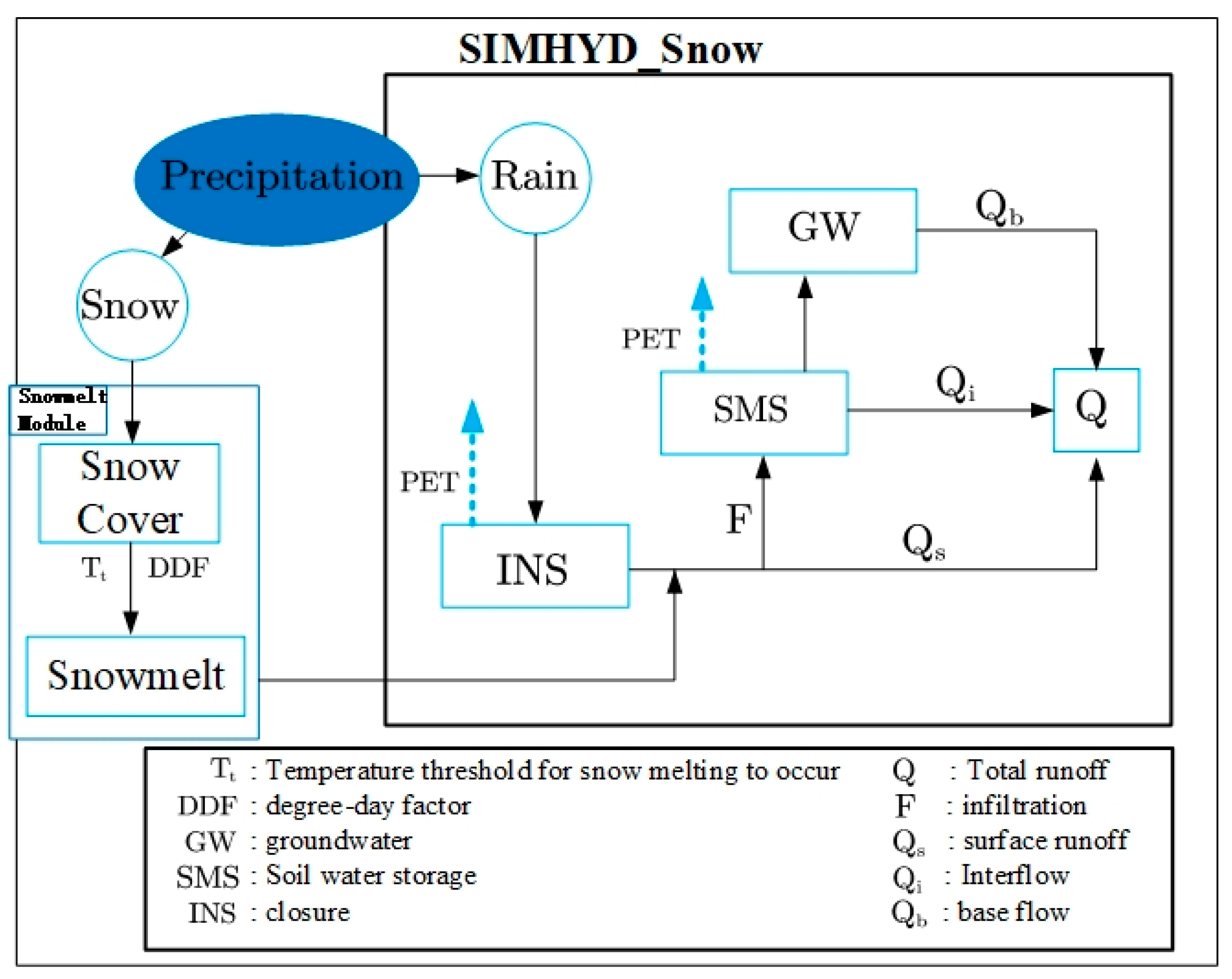
2.2.1. Introduction to Hydrological Models

Chiew simplified the HYDROLOG and MODHYDROLOG models and proposed the daily conceptual hydrological model SIMHYD[31]. The advantages of this model are its few input parameters, simple principles and structure, and good accuracy and ap-plicability. The original SIMHYD model does not include a snowmelt module, which may lead to significant errors in simulating snowmelt-dominated watershed models.
The SIMHYD_Snow model incorporates a snowmelt module, Snowmelt[32], into the SIMHYD model (Figure 2). This module divides daily precipitation into rainfall and snowfall based on maximum and minimum temperatures and then calculates daily snowmelt using the degree-day factor method. The SIMHYD_Snow model has 11 pa-rameters, including maximum infiltration capacity, maximum soil moisture content, ac-tual evapotranspiration parameters, and groundwater recharge parameters. This study used a genetic algorithm for parameter calibration to achieve the best fit between the model and observed data, with the root mean square error (RMSE) set as the objective function.

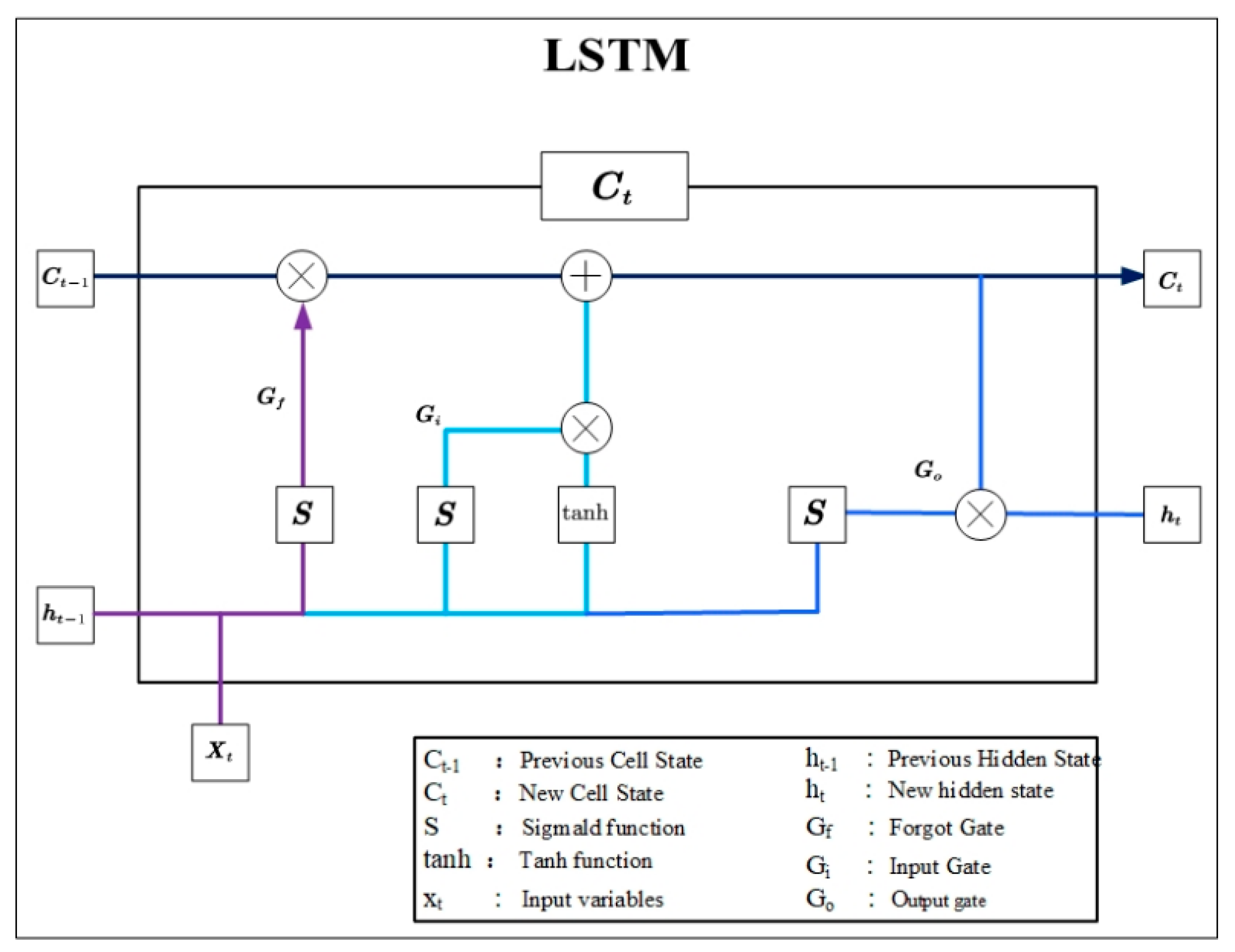
2.2.2. Introduction to LSTM Model

LSTM is a recurrent neural network (RNN) model widely used to classify, process, and predict time series data. In terms of long-term memory, LSTM outperforms RNN due to its unique architecture, which overcomes the limited memory capacity issue in RNN.
The LSTM model consists of recursively connected memory cells, each equipped with a cell state, forget gate, input gate, output gate, and hidden state (Figure 3). The cell state stores and transmits information, while the forget gate is responsible for discarding certain information from the previous time step's cell state. The input gate updates and stores important information in the cell state. The output gate extracts information into the hidden state at the current time step, which serves as the model's output at each time step.
In this study, the LSTM model was constructed using the Deep Learning Toolbox in MATLAB. In order to optimize the structure and performance of the model and obtain the best prediction results, the model parameters were set as shown in Table 1 (The se-lected parameter set demonstrates exemplary performance in terms of computational efficiency and model stability, facilitating practical training and optimization of the model.).

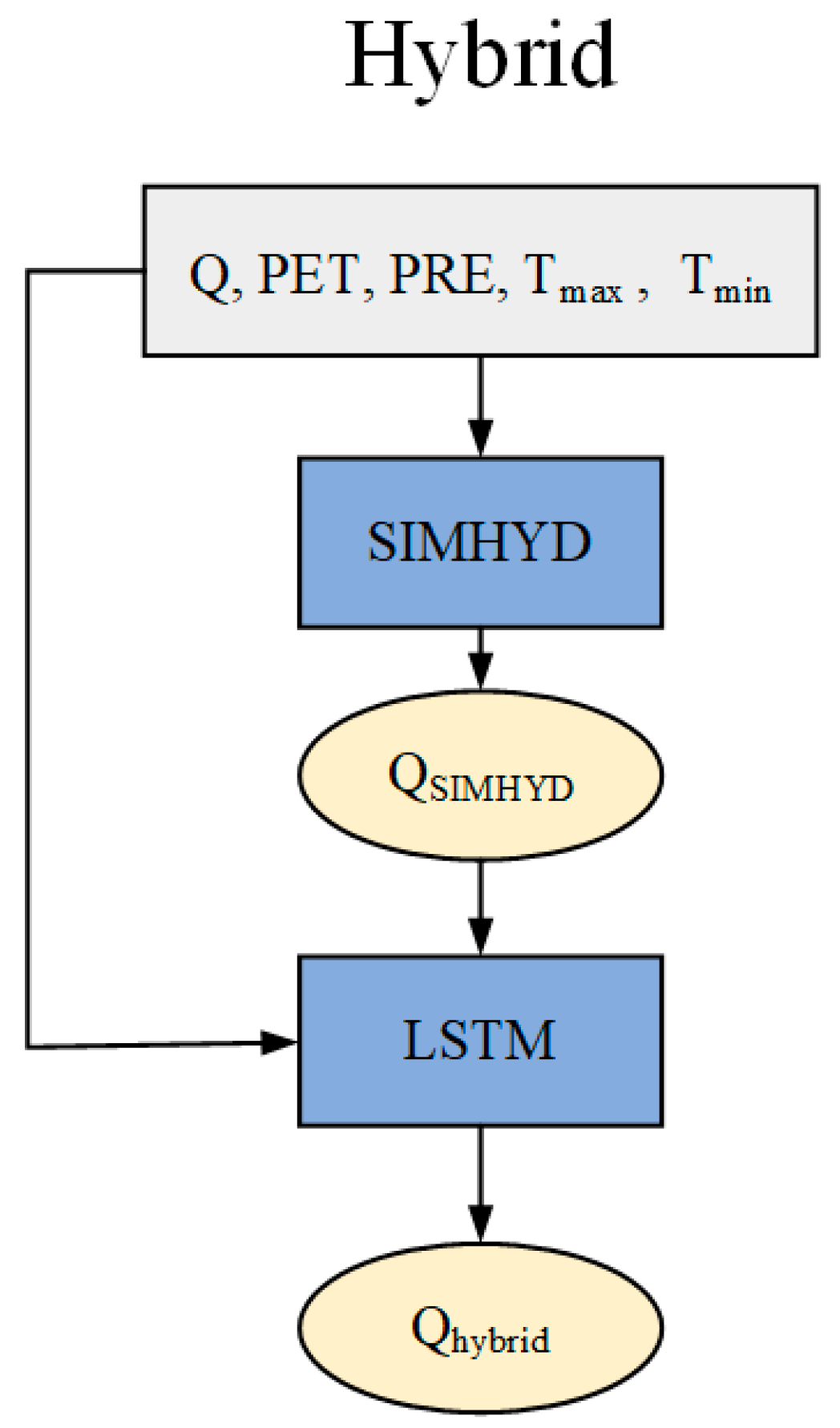
2.2.3. Combined Model Hybrid

In this study, a novel approach is proposed to utilize the output of the SIMHYD model as input for the LSTM model to simulate streamflow. Figure 4 shows primary meteoro-logical data (including potential evapotranspiration PET, precipitation PRE, maximum temperature Tmax, and minimum temperature Tmin) that are input into the SIMHYD model to calculate the runoff. Then, the output of the SIMHYD model is used as input for the LSTM model to obtain the simulated streamflow of the combined model. De-tailed information on the variables is provided in Table 2.

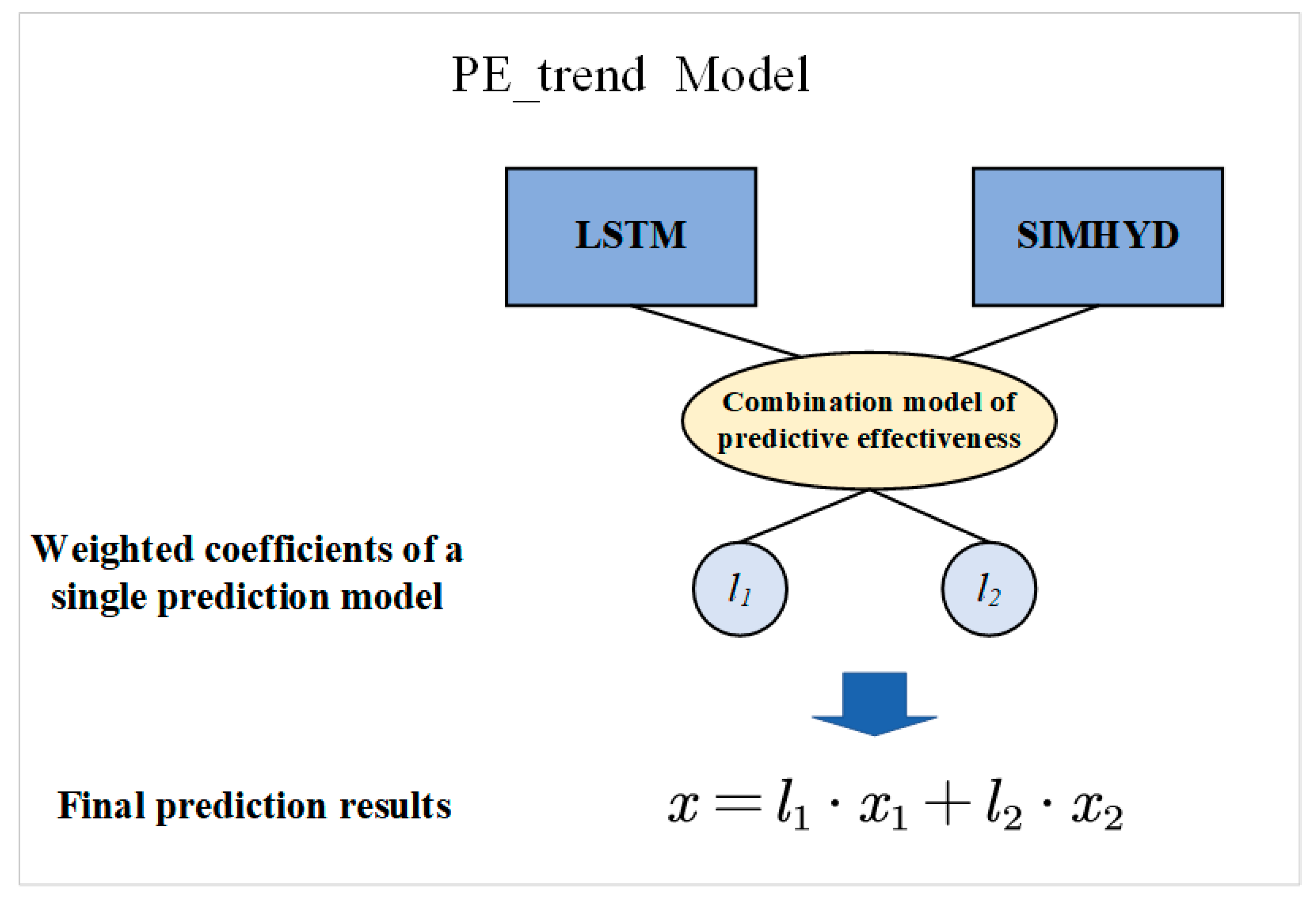
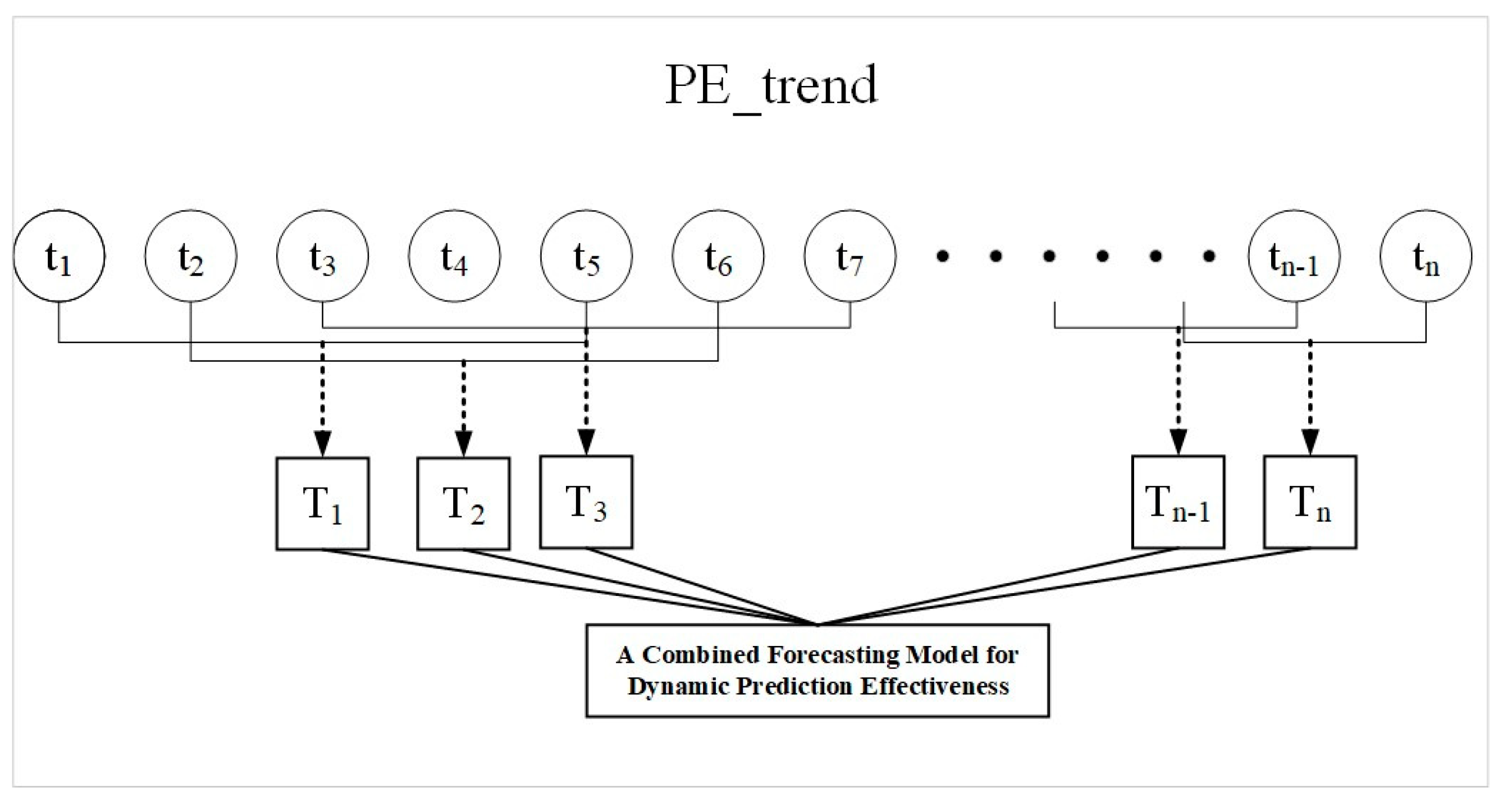
2.2.4. Hybrid Model PE_Trend Based on Dynamic Prediction Effectiveness

2.2.4.1. Modeling Mechanism of Combination Prediction Model Based on Prediction Effectiveness
The combination forecasting model based on predictive validity utilizes the practical information provided by various forecasting methods, calculated in an appropriate weighted average form to obtain the combined model. In order to improve the accuracy of the combined forecasting model, this study focuses on two aspects: firstly, the deter-mination of the weighted average coefficients for each individual forecasting model in the combined forecasting model, and secondly, the examination of whether the com-bined forecasting results are superior to those of the individual forecasting models. The Predictive Validity-based Combined Forecasting Model (PE) selected in this study uti-lizes the mean of predictive accuracy and the mean square deviation reflecting the de-gree of dispersion to construct an optimal calculation model for weighted coefficients through linear programming (Figure 5). It overcomes the influence of the deviation in forecasting results due to the different dimensions of the indicator sequences in the or-dinary combined forecasting model, thereby improving the forecasting accuracy. Moreover, the model is intuitive, computationally concise, and possesses practical ap-plication value.
The measured runoff sequence is {xt, t=1,2,3…N}, and there are m individual prediction models predicting it. xit is the water quality prediction value of the i-th single-item prediction method at time t, where i ranges from 1 to N. eit is the relative error between the measured runoff and the predicted runoff by the i-th prediction method at time t, i.e., eit=（xi-xit）/xi. Let Ait=e-|eit|, and 0≤eit≤1, then Ait is the prediction accuracy of the i-th runoff prediction model at time t, obviously 0≤Ait≤1.
Let t be the combined prediction value of xt, then we have:
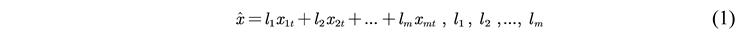
Preprints 138922 i001
ln is the weighted coefficient of a single prediction model and has:
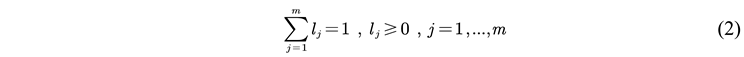
Preprints 138922 i002
If At and et are the combined prediction accuracy and relative error at time t, then there are:
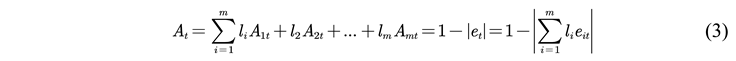
Preprints 138922 i003
The effectiveness of the i-th prediction model is:
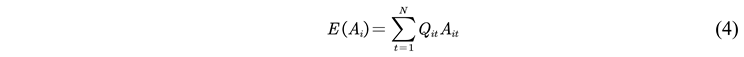
Preprints 138922 i004
Where Qit represents the weight coefficient of the accuracy Ait of the i-th prediction method at time t on the sample interval and has:
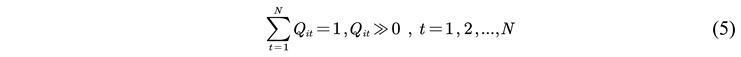
Preprints 138922 i005
Because prior information is not clear, Q is taken as 1/N. So there are:
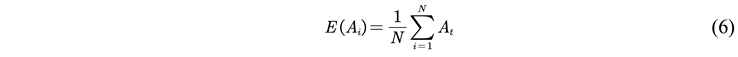
Preprints 138922 i006
The prediction validity sequence values for each individual model. The prediction accuracy sequence of the combined prediction model satisfies:
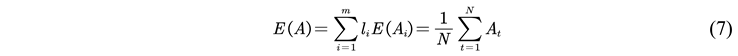
Preprints 138922 i007
Variance σ The solution formula for σ2(A) is:
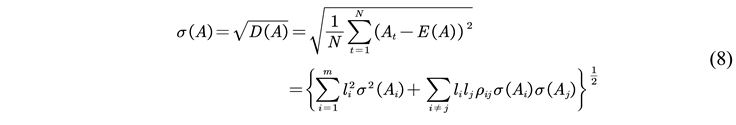
Preprints 138922 i008
Among ρij is the correlation coefficient between the prediction accuracy of the i-th runoff prediction model and the prediction accuracy of the j-th runoff prediction model, namely:
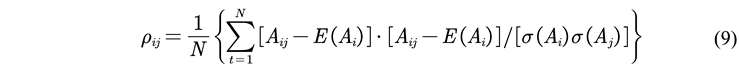
Preprints 138922 i009
E(A) represents the average prediction accuracy of the combination prediction method at different times, with larger values leading to higher accuracy: σ (A) The prediction accuracy sequence of the combination prediction model is unstable, and the smaller the numerical value, the better the model.
The effectiveness index of the combination prediction model is defined as:
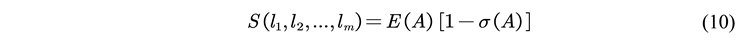
Preprints 138922 i010
In the equation, S represents the fitting between the predicted model and the measured runoff. The larger S, the better the linear fitting between the two, and the higher the effectiveness of the predicted results.
The combination prediction model based on prediction effectiveness is:
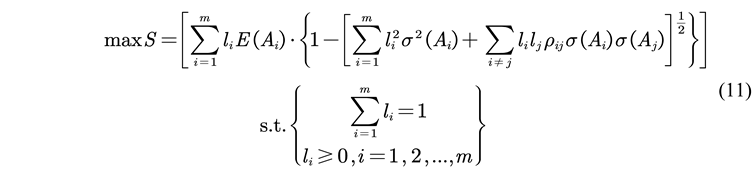
Preprints 138922 i011
In this system of equations, as long as the predicted values xit of m prediction methods at different times are calculated, the definition equation can be used to calculate (E)Ai, (σ)Ai, (σ)2Ai and then to calculate ρij. Using the Lagrange multiplier method, the calculated values of (E)Ai, (σ)Ai, (σ)2Ai, ρij are used to calculate the weighting coefficients l1, l2,... for various prediction models, The functions of lm and ln are used to find l1, l2,... that meet the maximum value requirements of the formula maxS, The weight values of lm and ln.
2.2.4.2. A Combined Forecasting Model for Dynamic Prediction Effectiveness
In order to further enhance the prediction accuracy of the combination prediction model based on predictive validity, this study proposes an improved dynamic Predictive Effec-tiveness Trend hybrid model (PE_trend). As shown in Figure 6, we set 5 unit times as one-time step T and input T into the predictive validity hybrid model to calculate the individual model weight values corresponding to this time segment, which are then used to compute the combined model simulation results for the time point after T. (The short-er the set time interval, the higher the accuracy of the model, although it comes at the cost of increased computational time. In our testing, it was observed that setting the time interval to 5 units yielded more favorable simulation results while requiring less compu-tational time.) Subsequently, the initial and final values of period T are incremented by 1, and the combination prediction model is re-input for the calculation to obtain the weighted coefficients of the individual models for the time point after T. This process is iterated until the last time point, thus computing the individual model weight values corresponding to all time points.

2.2.5. Model Evaluation Indicators

This study selects the Nash-Sutcliffe Efficiency (NES) to evaluate model performance. The Nash-Sutcliffe Efficiency is a commonly used index proposed by hydrologist J.R. Nash in 1970. It measures the fit between model simulation results and actual observed values, assessing model simulation performance[33]. A value of NES closer to 1 indicates a better fit of the model to the observed values. NES is calculated using the following formula:
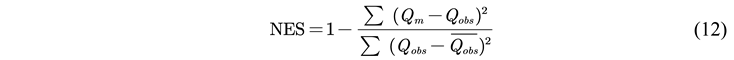
Preprints 138922 i012
In the equation, Qm represents the modeled runoff (m3/s), and Qobs represents the observed runoff (m3/s).
The Taylor diagram is a graphical representation method used to compare the correlation, bias, and standard deviation between model outputs and observed data. It shows the performance of different model predictions in terms of correlation, variance, and standard deviation compared to observed data, helping to evaluate the accuracy and bias of the models. The Taylor diagram is typically presented in a polar plot, with the standard deviation and correlation coefficient of the observed values as axes and the standard deviation and correlation coefficient of the model predictions plotted as points, visually comparing the differences between the models and observed data. A Taylor diagram typically displays three evaluation metrics: Correlation Coefficient, Standard Deviation, and Root Mean Square Error (RMSE).
The Correlation Coefficient measures the strength and direction of the linear relationship between model predictions and observed values. It is calculated as:
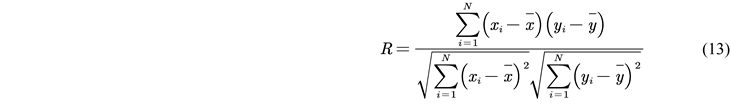
Preprints 138922 i013
In the equation, N is the total number of data points, xi and yi are individual data points for the two variables, x and y are the means of the two variables.
The Standard Deviation measures the variability or spread of data points around the mean. In the Taylor diagram, it represents the dispersion of model predictions and observed values. It is calculated as:
Preprints 138922 i014
In the equation, N is the total number of data points, xi represents each data point, x is the mean value of the data points.
The Root Mean Square Error is a measure of the differences between values predicted by a model and the observed values. It is calculated as:
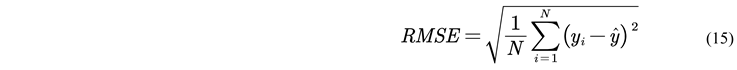
Preprints 138922 i015
In the equation, N is the total number of data points, yi represents the observed values, yi represents the model-predicted values.

3. Results

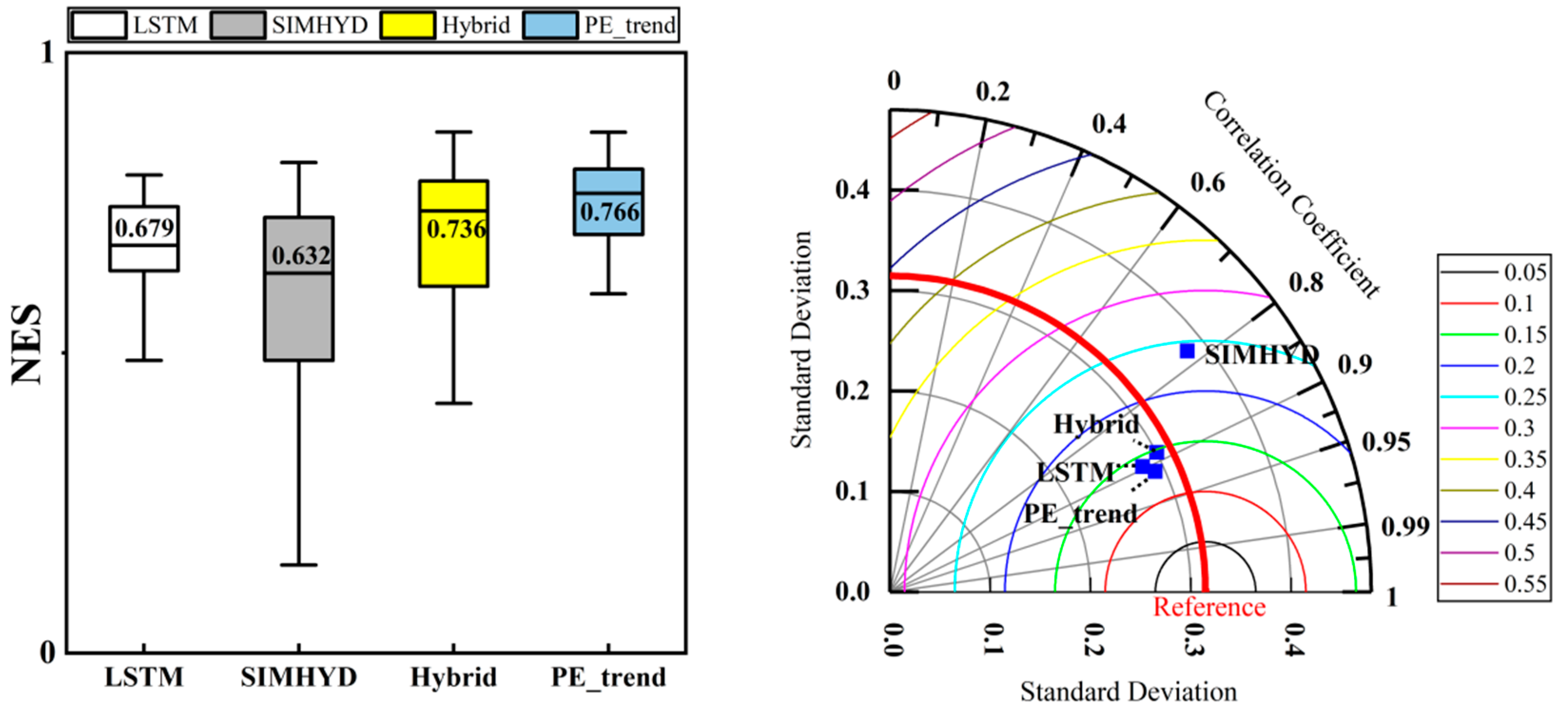
3.1. Model Runoff Simulation Capability

Figure 7 presents the boxplots of evaluation metrics for the simulated runoff results from the individual models and two hybrid models. The results indicate that, compared to the independent SIMHYD model, the median NES of the validation period for the Hybrid model and the PE_trend model have improved by 16.5% and 21.2%, respectively. That demonstrates a significant enhancement in the runoff modeling capabilities of the two hybrid models, with the PE_trend model exhibiting more robust runoff modeling capabilities. Additionally, the runoff simulation stability of the two hybrid models has significantly improved compared to the SIMHYD model. Furthermore, the Taylor diagrams of the models reveal that the hybrid models and the PE_trend model exhibit higher correlation coefficients, lower root mean square errors, and more minor standard deviations than the SIMHYD model.

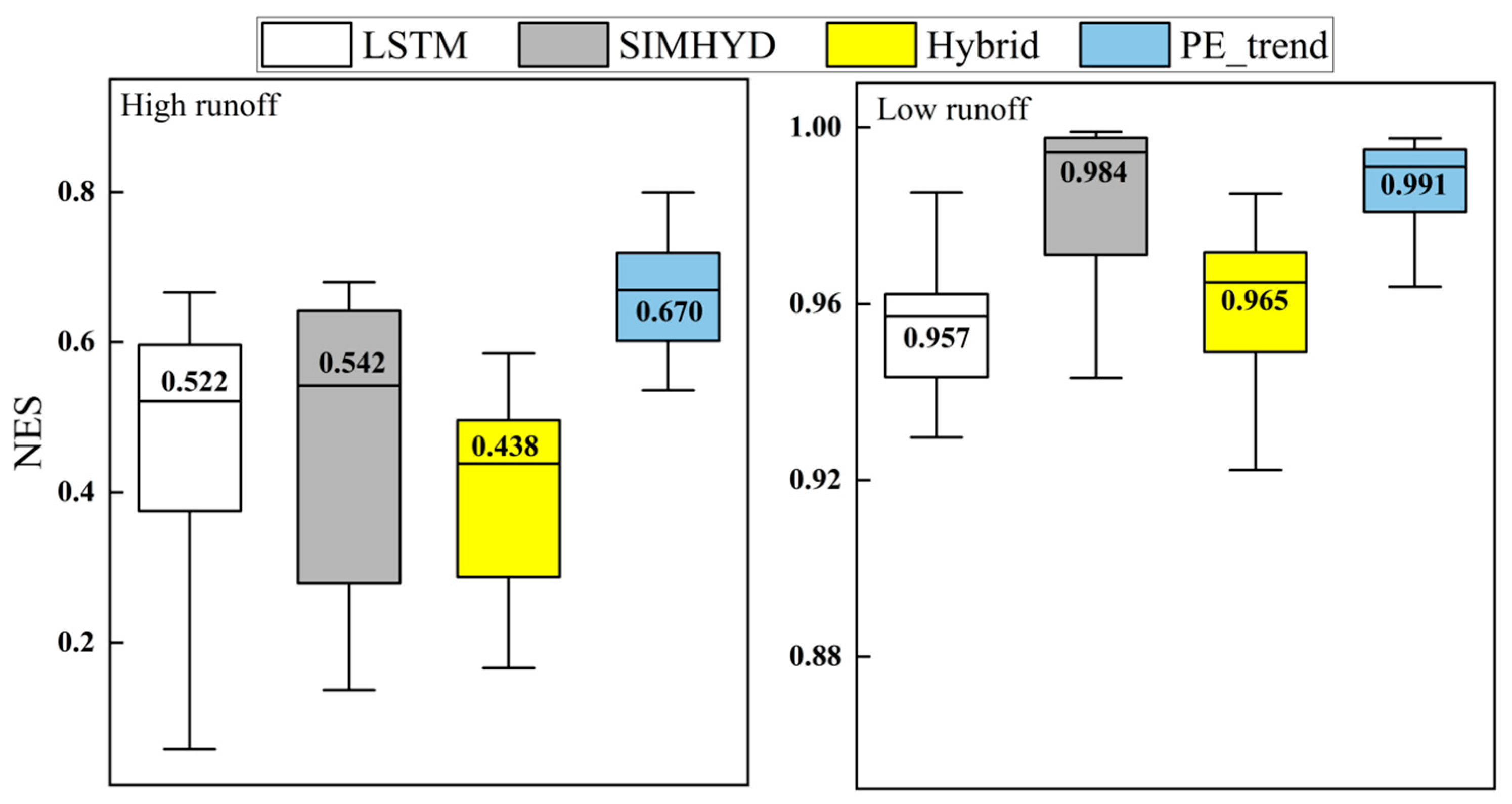
3.2. The Ability of the Model to Simulate Extreme Traffic

The key to whether the hybrid model can better forecast flood and drought disasters lies in whether the ability of the hybrid model to simulate extreme flows has been improved compared to that of the individual models [34]. In this study, the top 25% of observed runoff data during the validation period is selected as the relatively high-flow data, while the bottom 25% is selected as the relatively low-flow data for the basin. A boxplot of evaluation metrics for the model's simulation of extreme flows is then plotted (Figure 8).
The models exhibit significant differences in their ability to simulate high flows, with the PE_trend hybrid model demonstrating the best model performance. Compared to the SIMHYD model, the PE_trend model shows a 23.6% increase in the median NES for high-flow simulation. Compared to the LSTM model, the PE_trend model exhibits a 28.4% increase in the median NES of simulated high flows, and the length of the box-plot for this model is shorter, indicating more excellent stability in simulating high flows. In simulating low flows, both the individual models and the hybrid model perform very well. However, compared to the SIMHYD model, the PE_trend hybrid model shows significantly improved stability in simulating low flows. These results indicate that the PE_trend model outperforms the individual models in simulating extreme flows.

4. Discussion

4.1. The Predictive Performance of the Model Under Different Training Periods of Length

The training period length of the runoff prediction model is an important consideration affecting model performance [35]. An excessively long training period may lead to overfitting the model to the training data [36], resulting in poor performance on new data, while a too short training period may prevent the model from fully capturing the data's features, thereby affecting the model's accuracy and stability [37]. Determining the appropriate training period length is crucial for establishing an effective runoff pre-diction model. Therefore, this study analyzed the impact of three different training peri-od lengths on model performance and plotted the evaluation metrics in box plots for training periods of 6 years, 12 years, and 18 years (see Figure 9).
Selecting an appropriate training period length enhances the precision and efficiency of model predictions. As depicted in Figure 9, the predictive performance of the PE_trend model surpasses that of the standalone model in all three scenarios, further highlighting the superior predictive ability of this coupled model in runoff prediction. Comparing the model prediction outcomes for validation period lengths of 6 years and 12 years, it is evident that when the training period is set to 12 years, the performance of all hybrid models strengthens significantly. That indicates that the models needed more data for learning during the 6-year training period. In shorter training periods, models may struggle to capture the intricate patterns and trends within the data. Extending the train-ing period can provide the model with more data to learn from, thereby increasing the accuracy of predictions [38].
Comparing the model prediction results for training period lengths of 12 years and 18 years, the SIMHYD model and the combined prediction model PE_trend exhibit lower NES values when the training period is set to 18 years compared to the 12-year training period. That may be due to the models overfitting the training data, resulting in a de-creased generalization ability on new data [39]. A more extended training period may cause the model to overly rely on noise or specific patterns within the training data, po-tentially overlooking genuine trends and patterns, which could lead to poor predictive performance on new data [40].
In summary, setting an appropriate length for the training period helps the model learn the patterns and trends within the data, thereby enhancing its generalization ability on new data. Additionally, it can reduce the risk of the model overfitting the training data, improve training efficiency, and enable the model to make more accurate predictions.

4.2. The Runoff Simulation Ability of Individual and Combined Models

Compared to individual models, the combined model exhibits more robust runoff simu-lation capability, which confirms Mohammadi's [41] conclusion that combining hydro-logical models and machine learning models can enhance the accuracy of runoff simu-lation. The advantage of the combined model may stem from the complementarity of hydrological and machine learning models. Hydrological models utilize physical princi-ples and parameter estimation based on observed data to simulate runoff processes, of-fering high interpretability and reliability. Machine learning models enhance prediction accuracy by learning associations in data, particularly excelling in handling large amounts of nonlinear data. Combining the two can overcome their respective limitations and achieve a more accurate and robust runoff simulation.
Comparing our research with similar hydrological simulation studies in other regions, we can find some similar and different conclusions. For example, Zarei et al. [42] found that simulating high traffic presents challenges, and even with the use of composite models, the improvement obtained is very limited. This is consistent with our findings that although the composite model PE_trend exhibits good simulation ability for high traffic, underestimation of high traffic still occurs. Sezen and Sraj [43] also acknowl-edged the ability of combined models to simulate low traffic, but their research overes-timated low traffic. When conducting research on selecting training period lengths, Sharma and Kumari [44] found similar conclusions to ours, suggesting that an appro-priate training period length can yield better simulation results. Compared to previous research on runoff simulation combination models, such as the FT-LSTM model pro-posed by Sonali et al. [45] that combines Fourier transform and LSTM models (12.0%), and the Conv TALSTM model proposed by Liu et al. [46] that introduces convolution kernels and attention mechanisms into LSTM networks (5.1%), the PE_trend model has a greater improvement on individual models (12.8%).
Although the combined model performs well in runoff simulation, it still faces chal-lenges and limitations. Specifically, challenges primarily focus on model structure de-sign and prediction accuracy. Firstly, the reasonable combination of hydrological and machine learning models is crucial. According to Lee [47] and others, designing a com-bined model requires considering the integration of the physical principles of hydrolog-ical models and the data-driven capabilities of machine learning models to improve sim-ulation performance. Unreasonable model structure design may lead to reduced perfor-mance. For example, the Hybrid model only inputs primary hydrological data and the output of the SIMHYD model into the LSTM model, which may result in the model's inability to accurately capture the characteristics and patterns of hydrological processes, leading to inaccurate predictions. Secondly, the complexity of model inputs and the is-sue of overfitting. Research by Kavetski [48] and others indicates that machine learning models are prone to overfitting when there are too many input variables, meaning they excessively fit the training data and lose generalization ability. In such cases, the model's performance in simulating extreme flows may need improvement. Therefore, the com-plexity of model inputs may be one of the reasons for the decline in the performance of the Hybrid model during the validation period. In summary, a reasonable model struc-ture design for hybrid models and avoiding overfitting are directions for future im-provement.
In order to enhance the runoff simulation capability of the combined prediction model based on prediction effectiveness, this paper proposes the improved model PE_trend. The model can calculate the weighted coefficients of the individual model for the next step based on the runoff simulation results of the previous step. The results in Figure 7 and Figure 8 indicate that, compared to the individual model, the runoff simulation capability of the combined model PE_trend is more robust. In addition, the PE_trend model demonstrates superior performance in simulating extreme flow events, indicating its ca-pability to capture and forecast extreme flow conditions accurately. That further empha-sizes the robustness and reliability of the improved combination forecasting model in handling extreme flow scenarios, which is crucial for enhancing the overall predictive effectiveness of the model in hydrological applications.When evaluating the model per-formance, we utilized a subset of data from the US CAMELS dataset and did not assess the model's ability to simulate data from other regions. That may result in a slightly lower representation of the model evaluation outcomes. In future work, we plan to evaluate the model performance using data from various regions to enhance the gener-alizability of our findings.

4.3. Limitations and Future Challenges

Data reliability and continuity: The model has strict requirements for the accuracy of input data, and the model requires that the input data should be continuous and real. Continuous data can provide the model with better learning ability, and the model can only demonstrate better simulation ability during the validation period.
The ability to simulate high flow: Hydrological models provide better response to high flow, but still underestimate it. In the future, models for extreme flow need to have faster and more accurate response capabilities.

5. Conclusion

In order to improve the runoff simulation capability of traditional hydrological models, this study combines the machine learning model LSTM with the hydrological model SIMHYD. Two different hybrid models were constructed, and the runoff data of 30 watersheds in Washington State were simulated. The runoff simulation effects of the two model combination methods were evaluated, and further validation of the model's performance in simulating high and low flows was conducted. Based on the experi-mental results, the following main conclusions were drawn:
1. The hybrid model has better runoff simulation capability than traditional hydrological models, significantly improving the median NSE during the validation period.
2. The hybrid model PE_trend performs better in simulating extreme flow conditions than the individual model, contributing to better early warning of floods and droughts.
3. The overall improvement in the hybrid model's performance demonstrates the hybrid model's ability to improve runoff simulation accuracy. Although this study only selected river basins in Washington State, and the results may not be generalized to other basins, the excellent hybrid approach provided can be used as a reference for other regions. However, there are still some issues that need to be addressed in our future research:
(1) Further optimize the model combination method of the hybrid model to improve its learning ability.
(2) Explore the runoff simulation capability of hybrid models in different climatic re-gions.
(3) Enhance the model's ability to simulate high flows and improve its capability to forecast flood disasters.
In order to more intuitively demonstrate the enhancement of the runoff simulation capa-bility of the hybrid model over individual models, this study only selected the LSTM model and the SIMHYD model for combined analysis, which indeed needs a certain level of representativeness. This aspect will be further improved and modified in future work, where updated individual models and more efficient model combination methods will be used for evaluation.

Author Contributions

Conceptualization, Zhang Junqi and Lv Na.; methodology, Li Jing; software, Zhang Junqi; validation, Zhang Junqi, Yang Xinyu, Dong Yuhao, Zhang Bowen and Liu Yue; formal analysis, Dong Yuhao, Zhang Bowen; investigation, Zhang Junqi; resources, Zhang Junqi; data curation, Zhang Junqi.; writ-ing—orZhang Junqi nal draft preparation, Zhang Junqi; writing—review and editing, Zhang Junqi; visualization, Zhang Junqi; su-pervision, LiZhang Junqi Jing; project administration, Li Jing; funding acquisition,Li Jing. All authors have read and agreed to the published version of the manuscript.”

Funding

This research was funded by the National Natural Science Foundation of China (NSFC) (42277191,42377072, 2107087).

Data Availability Statement

US CAMLES dataset (https://gdex.ucar.edu/dataset/camels.html)

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Doycheva K, Horn G, Koch C, et al. Assessment and weighting of meteorolog-ical ensemble forecast members based on supervised machine learning with appli-cation to runoff simulations and flood warning[J]. Advanced Engineering Infor-matics, 2017, 33: 427–439.
  2. Kreibich H, Thieken A H, Petrow T, et al. Flood loss reduction of private households due to building precautionary measures–lessons learned from the Elbe flood in 02[J]. Natural hazards and earth system sciences, 2005, 5(1): 117-126. 20 August.
  3. Blöschl G, Sivapalan M. Scale issues in hydrological modelling: a review[J]. Hy-drological Processes, 1995, 9(3-4): 251-290.
  4. Wang X, Liu T, Yang W. Development of a robust runoff-prediction model by fusing the rational equation and a modified SCS-CN method[J]. Hydrological Sci-ences Jour-nal, 2012, 57(6): 1118–1140.
  5. Gebregiorgis A S, Hossain F. Understanding the dependence of satellite rainfall un-certainty on topography and climate for hydrologic model simulation[J]. IEEE Transac-tions on Geoscience and Remote Sensing, 2012, 51(1): 704–718.
  6. Burges S, J. Streamflow prediction: capabilities, opportunities, and challenges[J]. Hydrologic Sciences: Taking Stock and Looking Ahead, 1998, 5: 101–134.
  7. Talei A, Chua L H C. Influence of lag time on event-based rainfall–runoff mod-eling using the data driven approach[J]. Journal of Hydrology, 2012, 438: 223–233.
  8. Xiao W, Zhou J, Yang J, et al. Long-term runoff forecast in the middle and low-er reaches of the Yangtze River based on machine learning[J]. Water Resources and Power, 2022, 40(09): 31-34+26. [CrossRef]
  9. Nayak P C, Venkatesh B, Krishna B, et al. Rainfall-runoff modeling using con-ceptual, data-driven, and wavelet-based computing approaches [J]. Journal of Hy-drology, 2013, 493: 57–67.
  10. Chang C W, Dinh N T. Classification of machine learning frameworks for da-ta-driven thermal fluid models[J]. International Journal of Thermal Sciences, 2019, 135: 559–579.
  11. Gharari S, Razavi S. A review and synthesis of hysteresis in hydrology and hydro-logical modeling: Memory, path-dependency, or missing physics?[J]. Journal of Hy-drology, 2018, 566: 500–519.
  12. Noble W, S. What is a support vector machine?[J]. Nature Biotechnology, 2006, 24(12): 1565–1567.
  13. Rigatti S, J. Random forest[J]. Journal of Insurance Medicine, 2017, 47(1): 31-39.
  14. Yin C, Zhu Y, Fei J, et al. A deep learning approach for intrusion detection us-ing recurrent neural networks[J]. Ieee Access, 2017, 5: 21954–21961.
  15. Yang Y, McVicar T R, Donohue R J, et al. Lags in hydrologic recovery fol-lowing an extreme drought: Assessing the roles of climate and catchment charac-teristics[J]. Water Resources Research, 2017, 53(6): 4821–4837.
  16. Siami-Namini S, Namin A S. Forecasting economics and financial time series: ARIMA vs. LSTM[J]. arXiv:1803.06386, 2018.
  17. Amalou I, Mouhni N, Abdali A. Multivariate time series prediction by RNN archi-tectures for energy consumption forecasting[J]. Energy Reports, 2022, 8: 1084–1091.
  18. Man Y, Yang Q, Shao J, et al. Enhanced LSTM model for daily runoff predic-tion in the upper Huai river basin, China[J]. Engineering, 2022.
  19. Kanai S, Fujiwara Y, Iwamura S. Preventing gradient explosions in gated re-current units[J]. Advances in neural information processing systems, 2017, 30.
  20. Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computa-tion, 1997, 9(8): 1735-1780.
  21. Kim C, Kim C S. Comparison of the performance of a hydrologic model and a deep learning technique for rainfall-runoff analysis[J]. Tropical Cyclone Research and Review, 2021, 10(4): 215–222.
  22. Yuan X, Chen C, Lei X, et al. Monthly runoff forecasting based on LSTM–ALO model[J]. Stochastic environmental research and risk assessment, 2018, 32: 2199-2212.
  23. Adnan R M, Dai H L, Mostafa R R, et al. Modeling multistep ahead dissolved ox-ygen concentration using improved support vector machines by a hybrid me-taheuristic algorithm[J]. Sustainability, 2022, 14(6): 3470.
  24. [24]Adnan R M, Mostafa R R, Dai H L, et al. Pan evaporation estimation by rele-vance vector machine tuned with new metaheuristic algorithms using limited cli-matic data[J]. Engineering Applications of Computational Fluid Mechanics, 2023, 17(1): 2192258.
  25. Okkan U, Ersoy Z B, Kumanlioglu A A, et al. Embedding machine learning tech-niques into a conceptual model to improve monthly runoff simulation: A nested hybrid rainfall-runoff modeling[J]. Journal of Hydrology, 2021, 598: 126433.
  26. Liu J, Yuan X, Zeng J, et al. Ensemble streamflow forecasting over a cascade res-ervoir catchment with integrated hydrometeorological modeling and machine learn-ing[J]. Hydrology and Earth System Sciences, 2022, 26(2): 265-278.
  27. Yang S, Yang D, Chen J, et al. A physical process and machine learning com-bined hydrological model for daily streamflow simulations of large watersheds with limited observation data[J]. Journal of Hydrology, 2020, 590: 125206.
  28. Liu Q, Ma X, Yan S, et al. Lag in hydrologic recovery following extreme me-teorological drought events: implications for ecological water requirements[J]. Wa-ter, 2020, 12(3): 837.
  29. Yu Q, Jiang L, Wang Y, et al. Enhancing streamflow simulation using hybrid-ized machine learning models in a semiarid basin of the Chinese loess Plateau[J]. Journal of Hydrology, 2023, 617: 129115.
  30. Bai P, Liu X, Yang T, et al. Assessment of the influences of different potential evapotranspiration inputs on the performance of monthly hydrological models un-der different climatic conditions[J]. Journal of Hydrometeorology, 2016, 17(8): 2259-2274.
  31. Chiew F H S, Peel M C, Western A W. Application and testing of the simple rain-fall-runoff model SIMHYD[J]. Mathematical models of small watershed hy-drology and applications, 2002: 335–367.
  32. A: Bai, Xiaomang Liu, Jiaxin Xie, Simulating runoff under changing cli-matic conditions, 2021. [CrossRef]
  33. Lin F, Chen X, Yao H. Evaluating the use of Nash-Sutcliffe efficiency coeffi-cient in goodness-of-fit measures for daily runoff simulation with SWAT[J]. Journal of Hy-drologic Engineering, 2017, 22(11): 05017023.
  34. Michaud J, Sorooshian S. Comparison of simple versus complex distributed runoff models on a midsized semiarid watershed[J]. Water resources research, 1994, 30(3): 593–605.
  35. Elshorbagy A, Simonovic S P, Panu U S. Performance evaluation of artificial neural networks for runoff prediction[J]. Journal of Hydrologic Engineering, 2000, 5(4): 424–427.
  36. Piotrowski A P, Napiorkowski J J. A comparison of methods to avoid overfit-ting in neural networks training in the case of catchment runoff modeling [J]. Jour-nal of Hy-drology, 2013, 476: 97–111.
  37. Hong J, Wang Z, Yao Y. Fault prognosis of battery system based on accurate volt-age abnormity prognosis using long short-term memory neural networks[J]. Applied Energy, 2019, 251: 113381.
  38. Gu J, Zheng Z, Lan Z, et al. Dynamic meta-learning for failure prediction in large-scale systems: A case study[C]//2008 37th International Conference on Paral-lel Processing. IEEE, 2008: 157-164.
  39. Zheng Q, Yang M, Yang J, et al. Improvement of generalization ability of deep CNN via implicit regularization in two-stage training process[J]. IEEE Access, 2018, 6: 15844-15869.
  40. Zhang G P, Qi M. Neural network forecasting for seasonal and trend time se-ries[J]. European journal of operational research, 2005, 160(2): 501–514.
  41. Mohammadi B, Safari M J S, Vazifehkhah S. IHACRES, GR4J and MISD-based multi conceptual-machine learning approach for rainfall-runoff mod-eling[J]. Scientific Reports, 2022, 12(1): 12096.
  42. Zarei E, Saleh F N, Dalir A N. Comparing the hybrid-lumped-LSTM model with a semi-distributed model for improved hydrological modeling[J]. Journal of Water and Climate Change, 2024, 15(8): 4099-4113.
  43. Sezen C, Šraj M. Improving the simulations of the hydrological model in the karst catchment by integrating the conceptual model with machine learning mod-els[J]. Sci-ence of the Total Environment, 2024, 926: 171684.
  44. Sharma S, Kumari S. Comparison of machine learning models for flood fore-casting in the Mahanadi River Basin, India[J]. Journal of Water and Climate Change, 2024, 15(4): 1629-1652.
  45. Liu Y, Zhang T, Kang A, et al. Research on runoff simulations using deep-learning methods[J]. Sustainability, 2021, 13(3): 1336.
  46. Lee M H, Im E S, Bae D H. Impact of the spatial variability of daily precipita-tion on hydrological projections: A comparison of GCM-and RCM-driven cases in the Han River basin, Korea[J]. Hydrological Processes, 2019, 33(16): 2240–2257.
  47. Kavetski D, Fenicia F, Clark M P. Impact of temporal data resolution on pa-rameter inference and model identification in conceptual hydrological modeling: Insights from an experimental catchment[J]. Water Resources Research, 2011, 47(5).
  48. Sonali Swagatika, Jagadish Chandra Paul, Bibhuti Bhusan Sahoo, Sushindra Ku-mar Gupta, P. K. Singh; Improving the forecasting accuracy of monthly runoff time se-ries of the Brahmani River in India using a hybrid deep learning model. Journal of Wa-ter and Climate Change ; 15 (1): 139–156. 1 January. [CrossRef]
Preprints 138922 g001
Figure 1. Location of 30 Washington State River Basins.
Figure 1. Location of 30 Washington State River Basins.
Preprints 138922 g001
Preprints 138922 g002
Figure 2. The Structure of the SIMHYD_ Snow Model.
Figure 2. The Structure of the SIMHYD_ Snow Model.
Preprints 138922 g002
Preprints 138922 g003
Figure 3. Structure of Long Short Term Memory (LSTM) Model.
Figure 3. Structure of Long Short Term Memory (LSTM) Model.
Preprints 138922 g003
Preprints 138922 g004
Figure 4. Flow Chart of Hybrid Model Combination Method.
Figure 4. Flow Chart of Hybrid Model Combination Method.
Preprints 138922 g004
Preprints 138922 g005
Figure 5. Combination prediction model for prediction effectiveness (PE).
Figure 5. Combination prediction model for prediction effectiveness (PE).
Preprints 138922 g005
Preprints 138922 g006
Figure 6. Dynamic prediction effectiveness combination prediction model (PE_trend).
Figure 6. Dynamic prediction effectiveness combination prediction model (PE_trend).
Preprints 138922 g006
Preprints 138922 g007
Figure 7. The box plot and Taylor diagram of model evaluation indicators.
Figure 7. The box plot and Taylor diagram of model evaluation indicators.
Preprints 138922 g007
Preprints 138922 g008
Figure 8. Box diagram of evaluation indicators for predicting high and low traffic models.
Figure 8. Box diagram of evaluation indicators for predicting high and low traffic models.
Preprints 138922 g008
Preprints 138922 g009
Figure 9. Prediction results of individual model and dynamic prediction effectiveness hybrid model under different training periods.
Figure 9. Prediction results of individual model and dynamic prediction effectiveness hybrid model under different training periods.
Preprints 138922 g009
Table 1. LSTM Model Parameter Settings.
Table 1. LSTM Model Parameter Settings.
parameter Setting values parameter Setting values
Number of hidden units 32 Abandonment rate 0.4
Maximum Number Of Iterations 300 Gradient truncation threshold 1
optimizer Adam Learning rate reduction cycle 200
Batch size 32 Learning rate reduction factor 0.1
Initial learning rate 0.005
Table 2. Model Input and Output Variable Settings.
Table 2. Model Input and Output Variable Settings.
model input output target
SIMHYD PRE,Tmax,Tmin,PET Qsimhyd Qobs
LSTM PRE,Tmax,Tmin,PET Qlstm Qobs
Hybrid PRE,Tmax,Tmin,PET,Qsimhyd Qhybrid1 Qobs
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Alerts
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated