Rapid Vehicle Trajectory Prediction Based on Multi-Attention Mechanism for Fusing Multimodal Information

Preprint

Article

Rapid Vehicle Trajectory Prediction Based on Multi-Attention Mechanism for Fusing Multimodal Information

This version is not peer-reviewed.

Likun Ge^*,

Likun Ge^*,

This version is not peer-reviewed.

Altmetrics

Downloads

Views

Comments

Submitted:

08 November 2024

Posted:

09 November 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

Trajectory prediction plays a crucial role in autonomous driving tasks, as accurately and rapidly predicting the future trajectories of traffic participants can significantly enhance the safety and robustness of autonomous driving systems. This paper presents a novel trajectory prediction model that follows the encoder-decoder paradigm, achieving precise and rapid predictions of future vehicle trajectories by efficiently aggregating the spatiotemporal and interaction information of agents in traffic scenarios. We propose an agent-agent interaction information extraction module based on a sparse graph attention mechanism, which enables efficient aggregation of interaction information between agents. Additionally, we introduce a non-autoregressive query generation method that accelerates model inference speed by generating decoding queries in parallel. Comparative experiments with existing advanced algorithms show that our method improves the multimodal trajectory prediction metrics minADE, minFDE, and MR by an average of 9.1%, 11.8%, and 14.6%, respectively, while the inference time is only 33.7% of the average time taken by other algorithms. Finally, we demonstrate the effectiveness of the various modules proposed in this paper through ablation studies.

Keywords:

Subject:

Engineering - Mechanical Engineering

1. Introduction

The trajectory prediction task refers to predicting the future trajectories of the ego vehicle and surrounding traffic agents [1]. With the advancement of technologies such as autonomous vehicles and V2X (Vehicle to Everything), trajectory prediction has become one of the challenging topics in both academia and industry. Accurate prediction results can effectively reduce safety risks caused by scene uncertainties, playing a crucial role in enhancing the safety and robustness of autonomous driving systems [2].

The prediction component utilizes environmental information provided by the perception module to forecast the future trajectories of surrounding agents, based on data such as their positional information, historical trajectories, and interaction details. In traffic scenarios, the actions of agents are typically interdependent, influenced not only by their historical motion trends but also by other agents and the environment. The former refers to the temporal correlation of an agent's future trajectory, meaning that an agent's movement over a short period should remain consistent with its past motion, without abrupt changes. The latter is characterized by the impact of interactive behaviors on an agent's future trajectory, such as interactions with other agents (e.g., lane changes, overtaking) and interactions with the environment (e.g., avoiding obstacles), all of which can significantly affect the agent's future path [3]. This complexity presents substantial challenges for trajectory prediction.

Early trajectory prediction methods primarily relied on dynamics-based approaches, which involved constructing dynamic models of agents within traffic scenarios to compute future trajectories that adhere to physical constraints and traffic regulations. However, the process of developing dynamic models often involves numerous simplifications and assumptions about the agents, leading to significant discrepancies between the predicted outcomes and real-world situations. Moreover, dynamics-based methods struggle to account for the impact of interactive behaviors among agents, limiting their applicability to short-term prediction tasks in scenarios with relatively simple conditions.

Currently, deep learning-based trajectory prediction methods are regarded as promising approaches for achieving optimal prediction results. These methods leverage large datasets to train machine learning models, utilizing an encoder-decoder paradigm to aggregate multimodal information from the scene, thereby yielding relatively accurate predictions. Early machine learning models, such as Gaussian Processes (GP) [2], were limited by their simplicity and inability to capture a wide range of effective features from data, thus failing to meet the demands of autonomous driving. With the advancement of deep learning models, more sophisticated networks have been introduced to trajectory prediction tasks. These include Recurrent Neural Networks (RNN) [4] and their variants like Long Short-Term Memory networks (LSTM) [5], which excel at handling sequential information; Transformers [6], which are based on attention mechanisms; and Graph Neural Networks (GNN) [7], which are adept at aggregating interaction relationships. These network architectures have demonstrated significant effectiveness in processing temporal information and agent interaction data. Additionally, Generative Adversarial Networks (GANs) [8] have been introduced as a novel approach to trajectory prediction tasks. However, due to the complexity of training, their performance currently lags behind the aforementioned algorithms.

Despite the successes achieved in trajectory prediction tasks by the aforementioned studies, several issues remain unresolved. Firstly, Recurrent Neural Network (RNN) approaches, which are adept at handling temporal information, struggle to effectively aggregate spatial information and interaction data among agents within a scene. Secondly, although Transformer models based on attention mechanisms have certain advantages in aggregating scene information, their autoregressive decoding scheme results in slower inference speeds, making them less suitable for deployment in autonomous vehicles.

To address these challenges, we adopt the encoder-decoder paradigm and utilize various attention mechanisms to predict future trajectories. Specifically, we employ a sparse graph attention mechanism to extract interaction information from the surrounding agents' interactions and motion data. Additionally, we use self-attention and cross-attention mechanisms to aggregate spatial and temporal information. By leveraging these key pieces of information, the system can accurately predict the trajectories of other agents. The framework has been validated and tested on the Argoverse 1 [9] dataset. The results indicate that our model achieves performance comparable to state-of-the-art algorithms. Our main contributions are:

We propose a trajectory prediction framework based on the encoder-decoder paradigm, which effectively utilizes historical trajectory information, interaction data, and spatial information from traffic scenarios to achieve precise and efficient trajectory predictions.
We introduce a sparse graph attention learning method to capture interaction relationships among agents in traffic scenarios. This method efficiently extracts interaction features within local areas and adaptively eliminates redundant interactions.
We propose a stochastic non-autoregressive query generation method to obtain decoding queries in a single inference step. This leads to the construction of a fully non-autoregressive transformer network, enabling multi-modal trajectory prediction by leveraging rich interaction features.

2. Realated Work

Trajectory prediction is a sequence-to-sequence process that forecasts the future motion trajectories of agents based on their historical trajectory information, scene context, and interaction relationships among agents [10]. Trajectory prediction methods encompass physics-based approaches, classical machine learning methods, deep learning techniques, and reinforcement learning strategies [2]. Among these, deep learning methods are particularly notable for their ability to consider not only physical and road-related factors but also interaction-related factors, making them suitable for more complex scenarios. Deep learning algorithms such as Recurrent Neural Networks (RNNs) and Transformers have demonstrated outstanding performance in trajectory prediction tasks. Consequently, current trajectory prediction algorithms predominantly employ deep learning methods. In the following sections, we provide a review of trajectory prediction algorithms based on deep learning methods [11].

2.1. Recurrent Neural Networks

Unlike common Convolutional Neural Network (CNN) [12], RNNs can incorporate historical information, making them well-suited for handling temporal problems. In trajectory prediction tasks, commonly used recurrent networks include Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRU) [13]. LSTM, a special type of RNN, is a widely used method for aggregating sequential information and is extensively applied in trajectory prediction tasks. Studies [14] and [15] utilize LSTM as a sequence classifier to predict vehicle intentions, extracting historical trajectory features that are passed through hidden layers to the output layer for intention prediction. However, using LSTM alone for trajectory prediction captures only the long sequences of individual agents, failing to capture inter-agent relationships, resulting in low prediction accuracy. The Social LSTM [16] method addresses this by using LSTM to capture information from each sequence and employing a social pooling mechanism to capture relationships between aggregated sequences. Finally, a Multi-Layer Perceptron (MLP)-based decoder is used to decode future trajectories. This approach can automatically learn more complex interactions. However, the social pooling method proposed in Social LSTM has weak aggregation capabilities, leading to insufficient inter-agent interactions. To better aggregate interaction information, CS-LSTM [17] employs an improved social pooling layer using convolutional connections instead of fully connected layers, enabling more robust modeling and better generalization of various spatial configurations of interacting agents. DCS-LSTM [18] further improves CS-LSTM by introducing dilated convolutional social pooling and multimodal state inputs. These methods overlook much spatial information; MultiPath [19] utilizes spatial information and semantic maps to generate anchor trajectories. Additionally, Trajectron++ [20] employs CNNs to extract map features, gathering richer information and achieving more accurate future trajectories compared to previous work. Similarly, HOME [21] uses 2D convolutions to aggregate scene information and models interactions between the predicted agent and others through cross-attention, enabling complete trajectory prediction and simplifying and enhancing training efficiency.

2.2. Graph Neural Networks

GNN methods can aggregate scene information more efficiently than CNNs, making full use of the highly structured nature of semantic graphs. VectorNet [22] vectorizes structured semantic graphs, achieving precise trajectory predictions with fewer model parameters. TNT [23] uses a similar encoder to VectorNet to vectorize map information and agent features, addressing the challenge of modeling high uncertainty in agents' future trajectories. However, TNT has limitations, relying on predefined anchor points and being unable to make multiple predictions around a single anchor. DenseTNT [24] introduces an attention-based lane scoring mechanism to select the lane segment where the future trajectory endpoint lies, effectively addressing the multimodal trajectory prediction problem. GOHOME [21] improves upon HOME by more efficiently aggregating scene information, achieving faster computation speeds and reduced memory usage.

2.3. Transformer

Transformers can model complex temporal dependencies using self-attention and cross-attention mechanisms, addressing the issue of inconsistent multi-target trajectory prediction results. mmTransformer [25] employs a stacked Transformer network architecture to encode inter-agent relationships and uses a self-attention mechanism to generate trajectory proposals, enhancing model diversity and multimodality and significantly improving trajectory prediction performance. To better utilize spatial information, LAformer [26] considers both environmental and agent motion information, achieving precise trajectory predictions using VectorNet and attention-based encoders. Hivt [27] employs a hierarchical modeling approach, dividing scene interactions into local and global levels to reduce computational costs. At the local level, a VectorNet-like graph network models interactions within a certain range centered on the target agent, while at the global level, an attention mechanism constructs interactions between paired local-level features. QCNet [28] considers the translation and rotation invariance of trajectories in prediction tasks, reducing computational complexity and achieving unprecedented performance. Qcnext [29] improves upon the QCNet encoder, using a cross-attention module to update spatiotemporal features, and employing self-attention and column self-attention modules to model agent relationships and scene interactions, achieving better results than QCNet.

Inspired by previous studies, in our work we use multiple attentional mechanisms to achieve the aggregation of interaction, spatial, and temporal information of AGENTS in traffic scenarios in order to achieve accurate prediction of future trajectories. In addition, although the Transformer model is able to aggregate sequence information well, the inference speed is slow and delayed, inspired by related advances [30,31], we use a non-autoregressive query generation approach to generate decoded queries quickly thus significantly accelerating the inference speed.

3. Methods

3.1. Probem Foomulation

In this paper, the vectorized traffic scene includes agents, historical trajectory information of the participants, and map information. The scene contains N agents, where the trajectory information of the i -th participant can be represented as:

P_{i} = {P_{i}^{G}, P_{i}^{C}}

(1)

\{\begin{cases} P_{i}^{i} = {p_{i}^{t - n}, \dots, p_{i}^{t - 2}, p_{i}^{t - 1}, p_{i}^{t}, p_{i}^{t + 1}, \dots, p_{i}^{t + m}} \\ P_{i}^{G} = {ρ_{i}^{t - n}, \dots, ρ_{i}^{t - 2}, ρ_{i}^{t - 1}, ρ_{i}^{t}, ρ_{i}^{t + 1}, \dots, ρ_{i}^{t + m}} \end{cases}

(2)

Where

P_{i}^{G}

represents the trajectory information of agent i in the global coordinate system, and

P_{i}^{C}

represents the trajectory information in the local coordinate system, with the local coordinate system centered at the position of agent i at time t.

p_{i}^{t}

denotes the position information of agent i at time t,

p_{i}^{t - 1}

represents the historical position information of agent i at time t-1, and

p_{i}^{t + 1}

indicates the predicted position information of agent i at time t+1. Similar to

p_{i}^{t}

ρ_{i}^{t}

corresponds to the position information in the global coordinate system.

The position information of agent i at each time step can be expressed as:

\{\begin{cases} p_{i}^{t} = [x_{t}^{i}, y_{t}^{i}] \\ ρ_{i}^{t} = [x_{t}, y_{t}] \end{cases}

(3)

where

[x_{t}^{i}, y_{t}^{i}]

represents the coordinates in the local coordinate system, and

[x_{t}, y_{t}]

represents the coordinates in the global coordinate system.

3.2. Overview

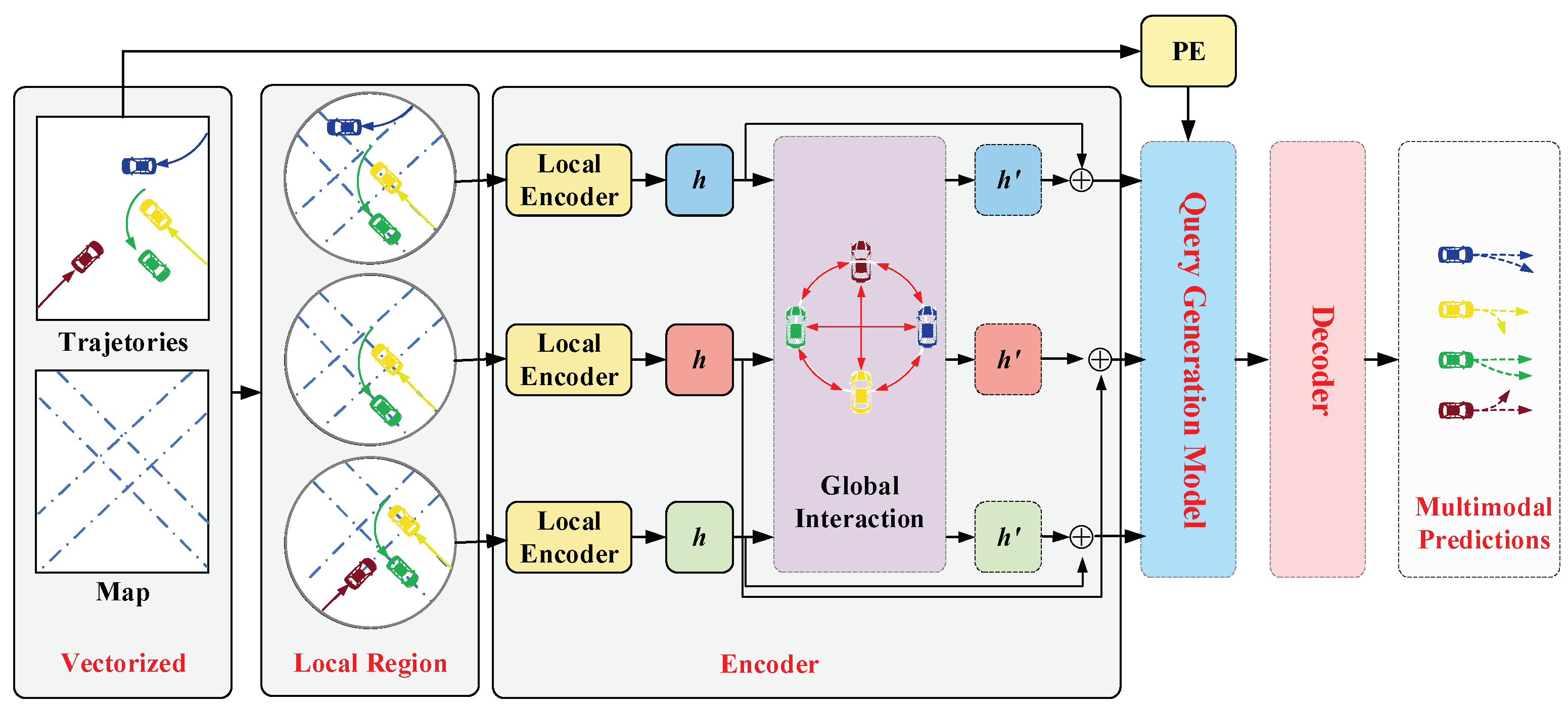
The overall structure of the trajectory prediction network is shown in Figure 1. The method proposed in this paper employs an encoder-decoder paradigm to achieve trajectory prediction. The encoder extracts features and transforms them into intermediate representations based on the temporal, spatial, and interaction information of agents in the traffic scene using both a local encoder and a global encoder. The decoder predicts future possible trajectories based on the information contained in these intermediate representations.

First, the agent information and scene information are vectorized. The local encoder utilizes a Sparse Graph Attention Network (SGAT) and a Temporal Transformer to aggregate the interaction information and spatiotemporal information of agents in the local scene. The global interaction module summarizes the local contextual features. Then, the non-autoregressive query generation module generates decoding queries in a parallel manner based on the features. Finally, a simple multilayer perceptron (MLP) is used to predict the future trajectory information for H time steps.

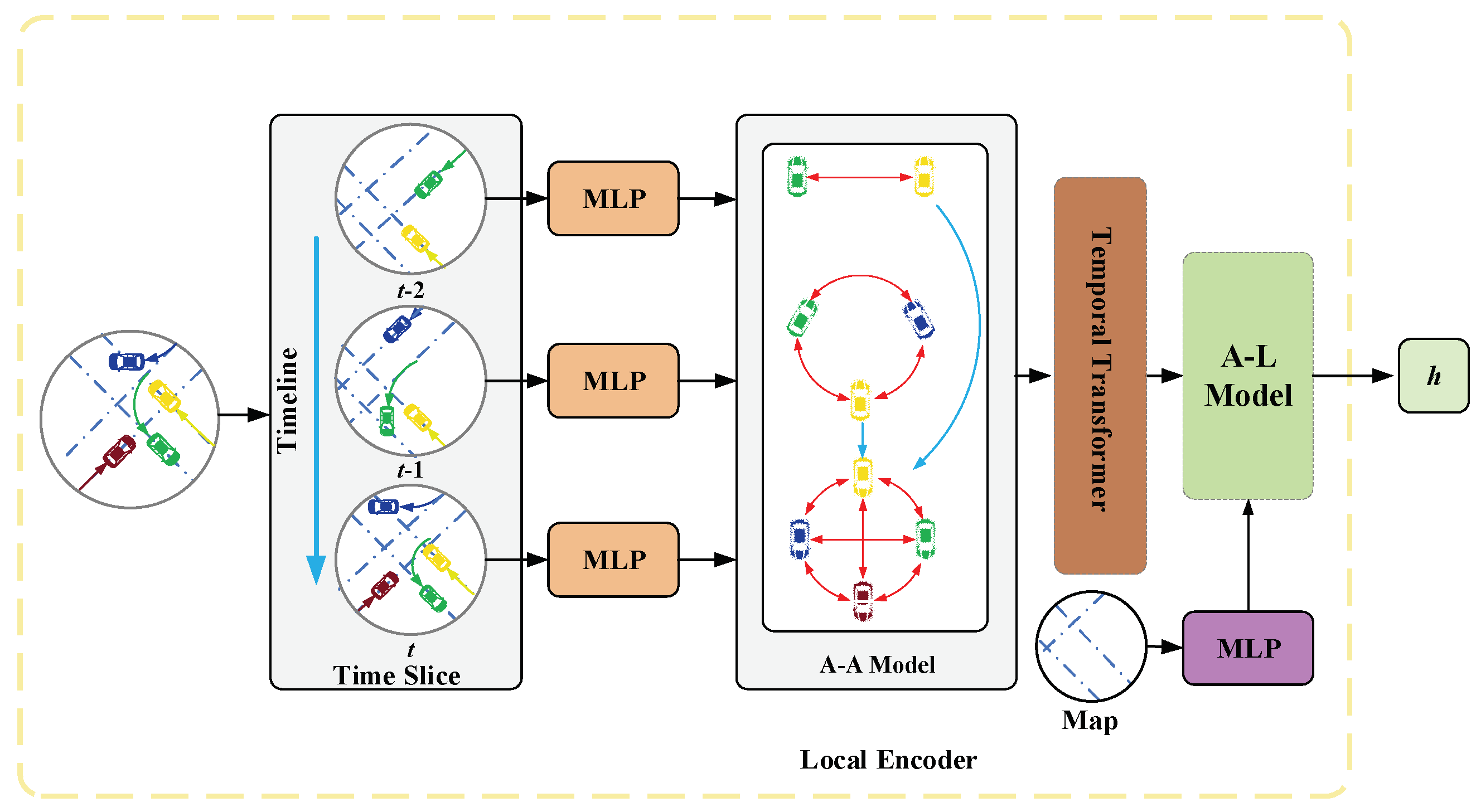
3.3. Local Encoder

The primary function of the local encoder is to aggregate the spatial, temporal, and interaction information of agents within a local range. The local encoder is divided into four components: trajectory data preprocessing, agent-agent interaction module, Temporal Transformer, agent-lane interaction module, and query generation module. Its main structure is illustrated in Figure 2.

3.3.1. Data Preprocessing Module

The data processing module projects the input historical trajectory information and road information into high-dimensional vectors to generate position embeddings and road embeddings through a multilayer perceptron (MLP), as shown in formulas (4)- (8).

e_{i}^{t} = ϕ (p_{i}^{t}, W_{1})

(4)

e_{i}^{t} = ϕ (ρ_{i}^{t}, W_{2})

(5)

Where

e_{i}^{t}

and

e_{i}^{t}

represent the position embeddings of agent i at time t, respectively.

ϕ (\cdot)

is the multilayer perceptron (MLP). While

W_{1}

and

W_{2}

are parameter matrices that can be learned through training.

e_{i, j}^{t} = ϕ (p_{i}^{t} - p_{j}^{t}, W_{3})

(6)

e_{i, j}^{t} = ϕ (ρ_{i}^{t} - ρ_{j}^{t}, W_{4})

(7)

Where

e_{i, j}^{t}

and

e_{i, j}^{t}

represent the relative position embeddings of agent i and agent j in the local and global coordinate systems, respectively.

ϕ (\cdot)

is the multilayer perceptron (MLP). While

W_{3}

and

W_{4}

are parameter matrices that can be learned through training.

e_{i, L}^{t} = ϕ (p_{L}^{e n d} - p_{L}^{s t a r t}, p_{i}^{t} - p_{L}^{s t a r t}, W_{5})

(8)

Where

e_{i, L}^{t}

represents the relative position embedding between agent i and lane L. While

W_{5}

is parameter matrices that can be learned through training.

3.3.1. Agent-Agent Interaction Module

To better aggregate interaction information between agents, we propose an agent-agent interaction module based on the graph attention mechanism. This module can learn the dependencies between agents in the same scene at a given time from the data. Each agent in the local scene at the same time is treated as a node to construct a directed graph. Considering that each node is typically influenced by only a few other nodes, the model should not focus on irrelevant nodes. Therefore, we introduce sparse attention coefficients in the form of an activation function to filter out unimportant interactions and retain significant ones.

First, the attention coefficient is calculated as:

α_{i, j}^{t} = \frac{α - entmax (LeakyReLU (a^{T} W_{5} [e_{i}^{t} \oplus e_{j}^{t}]) + ϕ (e_{i, j}^{t}, W_{6}))}{\sum_{k \in N} α - entmax (LeakyReLU (a^{T} W_{5} [e_{i}^{t} \oplus e_{j}^{t}]) + ϕ (e_{i, k}^{t}, W_{6}))}

(9)

Where

α_{i, j}^{t}

represents the influence of agent j on agent i at time t,

N

denotes the number of nodes in the graph,

LeakyReLU (\cdot)

is a leaky rectified linear unit with a negative input slope of 0.1,

a

is the weight vector of a single-layer feedforward neural network,

W_{5}

and

W_{6}

are learnable parameter matrices, and

ϕ (\cdot)

is an embedding function MLP with learnable parameter matrices

W_{6}

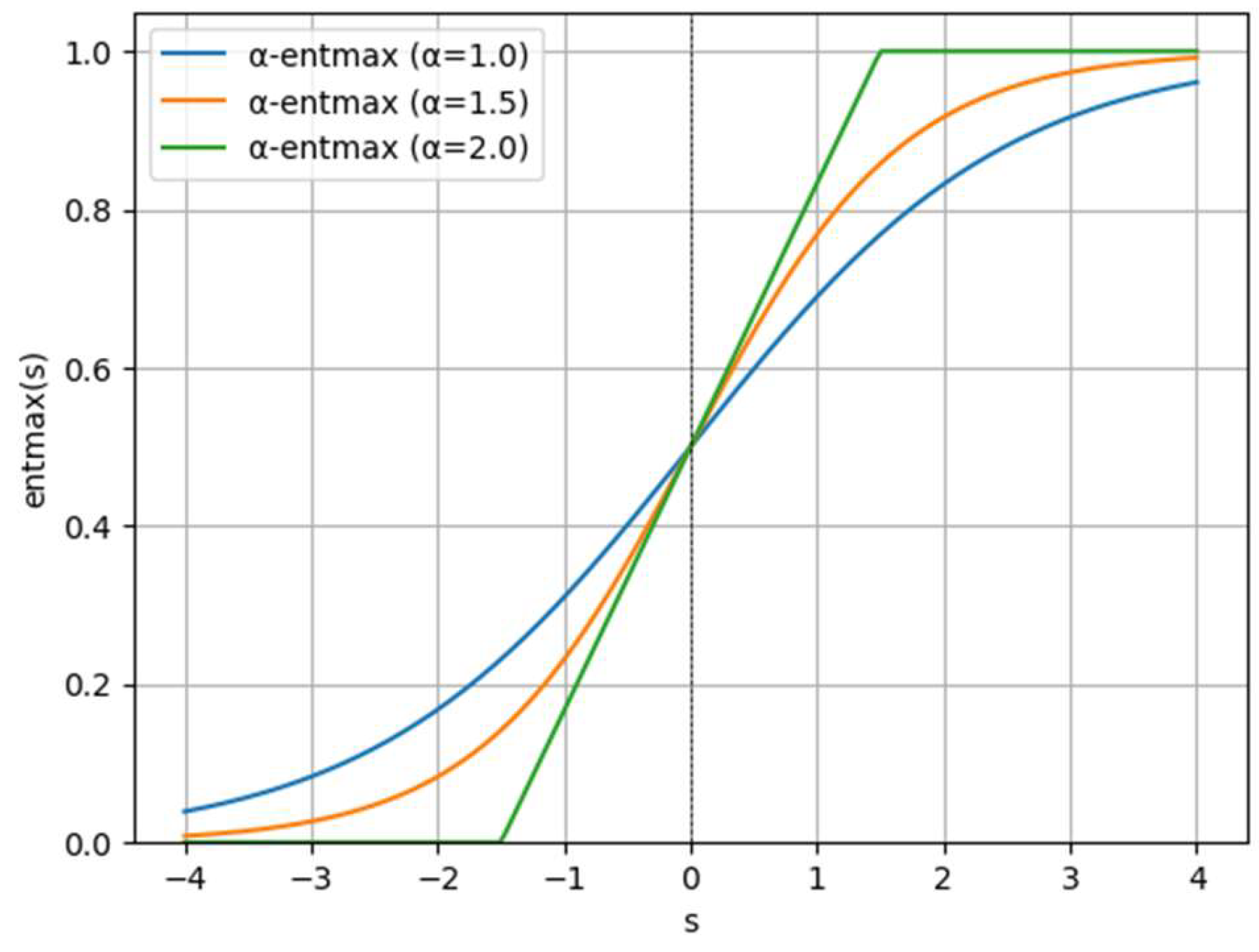
The definition of

α - entmax (\cdot)

in formula (9) is shown in formula (10):

α - entmax (s) = {[(α - 1) s - τ]}_{+}^{\frac{1}{α} - 1}

(10)

Where

{[x]}_{+} = \max (0, x)

and

τ

is the Lagrange multiplier.

The formula (10) is illustrated in Figure 3. Due to the presence of the

\max (\cdot)

operator in the formula, when

α = 1

，the formula becomes a softmax function; when

α = 2

, it becomes a sparsemax function. When

2 > α > 1

, the formula results in sparsity, which can be used to eliminate unimportant interactions between agents. In this paper, we set the parameter

α = 1.5

following the method in reference [32].

After obtaining the attention scores between agents, the feature representation of agent i at time t can be updated by propagating the features of its neighboring vehicles according to the corresponding attention scores, as shown in formula (11).

{\overset{⌢}{r}}_{i}^{t} = ELU (\sum_{k \in N} α_{i, k}^{t} W_{7} [e_{i}^{t} \oplus e_{k}^{t}]) LN (\cdot)

(11)

Where

{\overset{⌢}{r}}_{i}^{t}

is the feature vector of agent i at time t containing spatial and interaction information, and

ELU (\cdot)

is the activation function.

Similar to other Transformer network structures, our method follows the multi-head attention mechanism. The aforementioned feature aggregation process can be executed in multiple subspaces to enhance the expressiveness of the model. Let the number of heads be

K

; by aggregating multi-head information, we obtain a feature vector that includes interaction relationships, as shown in formula (12):

{\bar{r}}_{i}^{t} = ϕ (\sum_{k \in H} {\overset{⌢}{r}}_{i, k}^{t}, W_{7})

(12)

To facilitate training, we introduce residual connections and perform normalization operations before obtaining the final state, as shown in formula (13) and (14).

{\bar{r}}_{i}^{t}' = LN ({\bar{r}}_{i}^{t} + e_{i}^{t})

(13)

r_{i}^{t} = LN (MLP ({\bar{r}}_{i}^{t}', W_{8}) + {\bar{r}}_{i}^{t}')

(14)

Where

LN (\cdot)

denotes Layer Nom layer.

The final feature set serves as the input to the Temporal Transformer.

3.3.2. Temporal Transformer

The input feature set

R^{t} = \{r_{0}^{t}, r_{i}^{t}, \dots, r_{N}^{t}\}

contains only the positional and interaction features at time t and does not include temporal information, which is crucial for trajectory prediction. To address this, we design the Temporal Transformer module, which utilizes a self-attention mechanism to aggregate the temporal features of agents. Similar to the approach in reference [33], we add time-related positional embeddings to the feature vectors, as shown in formula (22):

S_{i} = R^{t} + T_{i}^{t} (k)

(15)

Here,

T_{i}^{t} (k)

represents the sinusoidal positional embedding, the definition of which is provided in formula (16).

T_{i}^{t} (k) = \{\begin{array}{l} \sin (t / 10000^{k / d}), & k is even \\ \cos (t / 10000^{(k - 1) / d}), & k is odd \end{array}

(16)

The resulting sequence set

S_{i}

, which includes temporal information, is used as the input to the temporal information aggregation module. Subsequently, the query Q, key K, and value V are computed, as illustrated in formula (17).

\{\begin{matrix} Q_{i}^{T} = S_{i} W^{Q} \\ K_{i}^{T} = S_{i} W^{K} \\ V_{i}^{T} = S_{i} W^{V} \end{matrix}

(17)

Where

W^{Q}

，

W^{K}

and

W^{V}

are learnable shared parameter matrices, respectively.

To capture different temporal dependencies, this paper employs a multi-head mechanism to project

S_{i}

into different subspaces for feature extraction, as shown in formula (18):

{\overset{⌢}{g}}_{i} = softmax (\frac{Q_{i}^{T} K_{i}^{T}}{\sqrt{d_{k}}} + M) V_{i}^{T}

(18)

Where

M

is a mask that allows the model to focus more on information from previous timestamps, with the definition of

M

provided in formula (19).

M = [\begin{matrix} 0 & - \infty & \dots & - \infty \\ 0 & 0 & \dots & - \infty \\ ⋮ & ⋮ & ⋱ & ⋮ \\ 0 & 0 & \dots & 0 \end{matrix}]

(19)

The multi-head information is then aggregated, as shown in formula (20), and normalization and residual connections are performed before outputting the final feature set, as illustrated in formulas (21) and formula (22).

{\bar{g}}_{i}^{t} = MLP (\sum_{k \in K} {\overset{⌢}{g}}_{i, k}^{t}, W_{9})

(20)

{\bar{g}}_{i}^{t}' = LN ({\bar{g}}_{i}^{t} + S_{i}^{t})

(21)

g_{i}^{t} = LN (MLP ({\bar{g}}_{i}^{t}', W_{10}) + {\bar{g}}_{i}^{t}')

(22)

3.3.3. Agent-Lane Interaction Module

Information in the local map can guide the intentions of agents; therefore, we designed the agent-lane interaction module to extract the implicit intentions of vehicles. This module employs a cross-attention mechanism to aggregate the interaction features between agents and lanes.

The computation process for the query

Q

, key

K

, and value

V

is illustrated in formula (23).

\{\begin{matrix} Q_{i}^{L} = g_{i}^{t} W^{Q} \\ K_{i}^{L} = e_{i, L}^{t} W^{K} \\ V_{i}^{L} = e_{i, L}^{t} W^{V} \end{matrix}

(23)

Where

W^{Q}

W^{K}

and

W^{V}

are parameter matrices that can be learned through training.

Similarly, we follow the multi-head mechanism to perform feature extraction in multiple subspaces. Let

K

denote the number of heads; the computation process for the multi-head temporal features is presented in Formulas (24) to (27).

{\overset{⌢}{h}}_{i} = softmax (\frac{Q_{i}^{L} K_{i}^{L}}{\sqrt{d_{k}}}) V_{i}^{L}

(24)

{\bar{h}}_{i}^{t} = MLP (\sum_{k \in K} {\overset{⌢}{h}}_{i, k}^{t}, W_{11})

(25)

{\bar{h}}_{i}^{t}' = LN ({\bar{h}}_{i}^{t} + g_{i}^{t})

(26)

h_{i}^{t} = LN (MLP ({\bar{h}}_{i}^{t}', W_{12}) + {\bar{h}}_{i}^{t}')

(27)

3.4. Global Encoder

The local encoder can only capture features from the local area; thus, relying solely on features from the local region for trajectory prediction may not yield optimal results. To address this, we designed a global interaction module based on the Transformer structure. This module aggregates the features provided by the local encoder using a multi-head cross-attention mechanism, with the computation process detailed in formulas (28) to (32).

\{\begin{cases} Q^{G} = h_{i} W^{Q} \\ K^{G} = [h_{i}, e_{i, j}^{t}] W^{K} \\ V^{G} = [h_{i}, e_{i, j}^{t}] W^{V} \end{cases}

(28)

{\overset{⌢}{h}}_{i}' = softmax (\frac{Q_{i}^{G} K_{i}^{G}}{\sqrt{d_{k}}}) V_{i}^{G}

(29)

{\bar{h}}_{i}^{t}' = MLP (\sum_{k \in K} {\overset{⌢}{h}}_{i, k}^{t}', W_{13})

(30)

{\bar{h}}_{i}^{t}'' = LN ({\bar{h}}_{i}^{t}' + h_{i}^{t})

(31)

h_{i}^{t}' = LN (MLP ({\bar{h}}_{i}^{t}'', W_{14}) + {\bar{h}}_{i}^{t}'')

(32)

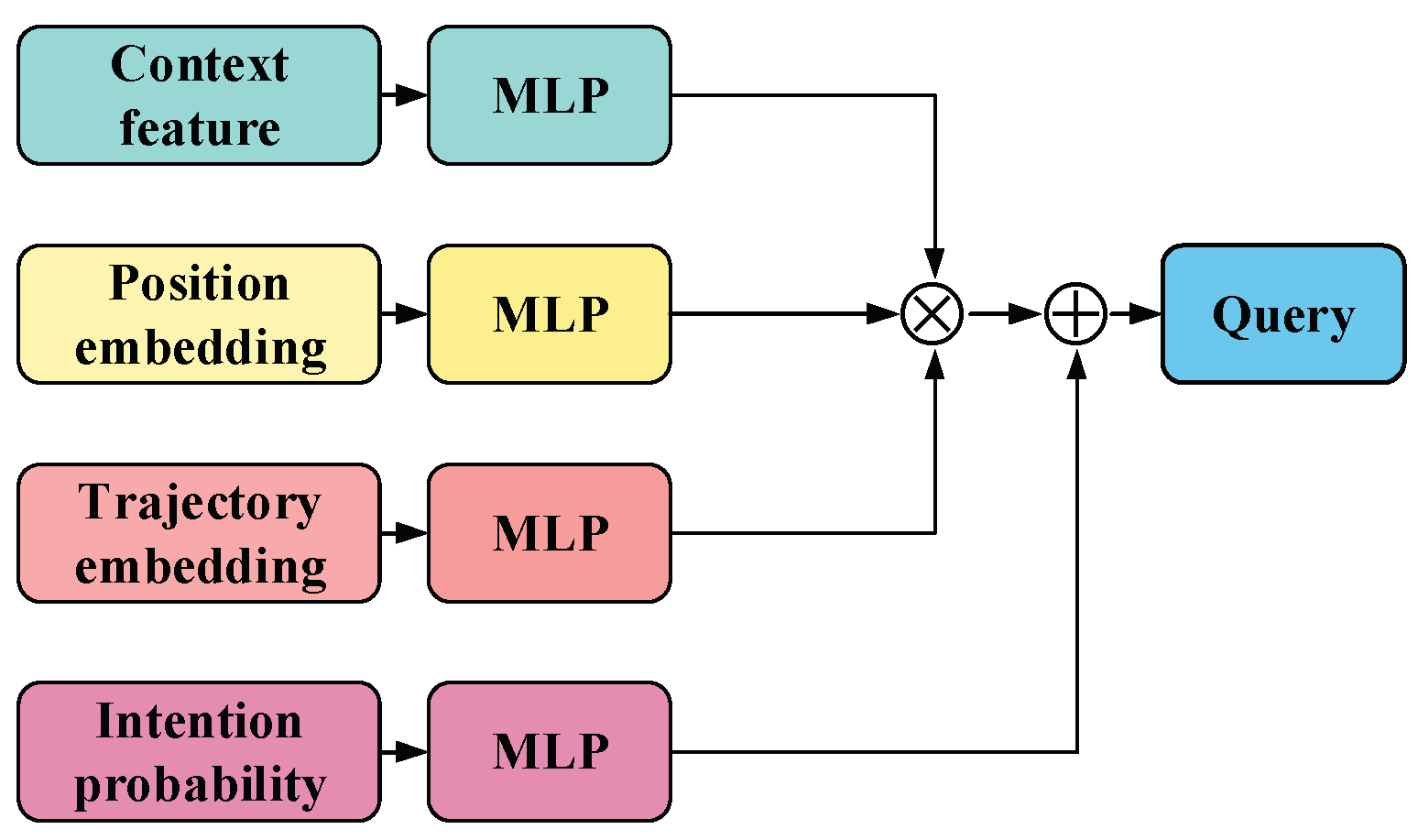
3.4. Query Generation Module

To improve prediction speed, inspired by reference [34], we adopt a non-autoregressive query generation method, the structure of which is illustrated in Figure 4. Unlike the conventional sequential query generation approach, our method allows for the parallel generation of multiple decoding queries for the decoder, enabling rapid generation of predicted trajectories. The proposed non-autoregressive query generation method is shown in formula (33).

Q = MLP (H^{t}') + MLP (H^{t}) + MLP (E^{t}) + MLP (P E)

(33)

Where

H^{t}' = \{h_{0}^{t}', h_{i}^{t}', \dots, h_{N}^{t}'\}

represents the feature set generated by the global encoder, and

H^{t} = \{h_{0}^{t}, h_{i}^{t}, \dots, h_{N}^{t}\}

represents the feature set generated by the local encoder,

E^{t} = \{e_{0}^{t}, e_{1}^{t}, \dots, e_{N}^{t}\}

is the set of trajectory embeddings generated in accordance with formula (5),

P E

represents the positional embeddings, which are the same as those in formula (16), and

T_{i}^{t} (k)

is the set of embeddings generated by the model.

3.4. Decoder

In this paper, we use a multilayer perceptron (MLP) as the decoder, which accepts the features of agents extracted by the local and global encoders to predict multimodal trajectories. Additionally, we employ a Laplace distribution to model the uncertainty of the trajectories. The output of the decoder is presented in formula (34).

T = MLP (Q, W_{14})

(34)

Where

T

is the trajectory tensor generated by the decoder, with a shape of

[K, N, H, 4]

, where

K

is the number of trajectories output for each agent,

N

is the total number of agents, and

H

is the number of predicted future time steps. The trajectory information is represented by the predicted position coordinates

[x, y]

and their associated uncertainties. To assist in training, we use another MLP along with a softmax function to predict the mixture coefficients of the mixture model for each agent, which has a shape of

[K, N]

3.5. Loss Function Define

During the training process, the loss function we defined consists of two parts: one is the regression loss function, and the other is the classification loss function, as shown in formula (35).

L = \min_{K} (L_{cls} + L_{reg})

(35)

Where

L_{cls}

represents the classification loss function, which is the cross-entropy loss function.

L_{reg}

denotes the regression loss function, which is the negative log-likelihood of the Laplace distribution, with its definition provided in formula (36). The weights of these two components are set to be equal.

L_{reg} = \frac{1}{N H} \sum_{i = 1}^{N} \sum_{t = T + 1}^{T + H} \log P ({(P_{i}^{t} - P_{i}^{T})}^{⊤} ∣ {\hat{μ}}_{i}^{t}, {\hat{b}}_{i}^{t})

(36)

Where

P (\cdot ∣ \cdot)

is the probability density function of the Laplace distribution, and

μ_{i}^{t}

and

b_{i}^{t}

represent the predicted positions and uncertainties of the optimal trajectory, respectively

4. Results

4.1. Implementation Detail

The multimodal trajectory prediction network designed in this paper will be trained on two RTX 3090 GPUs. During the training process, the Adam optimizer [35] will be used for parameter optimization, with a batch size of 32. The training will consist of a total of 50 epochs, with an initial learning rate set to 0.001, which will decay to 0.0001 after 40 epochs. The dropout rate is set to 0.1, and the number of heads in all multi-head attention mechanisms is set to 8. All network frameworks are implemented using the PyTorch deep learning framework.

4.2. Dataset and Metrics

This paper utilizes the Argoverse 1 Motion Forecasting Dataset [9] as the dataset for training and testing the trajectory prediction model. The Argoverse 1 Motion Forecasting Dataset is specifically designed for trajectory prediction tasks within Argoverse 1, containing a substantial amount of vehicle motion trajectory information along with high-definition map data corresponding to urban scenes. Data collection for the Argoverse 1 Motion Forecasting Dataset was conducted over 1006 hours in Miami and Pittsburgh using onboard sensor equipment, from which 320 hours of typical driving data were selected.

The driving data primarily includes a total of 324,557 driving sequences, each lasting 5 seconds, covering various scenarios such as left and right turns, lane changes, intersection navigation, and vehicle movements in dense traffic. These sequences are divided into training, validation, and test sets in a ratio of 5:1:2, resulting in 205,942 data samples for the training set, 39,742 for the validation set, and 78,143 for the test set. Each sequence contains the 2D centroid positions of tracked objects sampled at a frequency of 10 Hz, where the tracked objects can include vehicles, pedestrians, or bicycles. The training, validation, and test sets in the Argoverse 1 Motion Forecasting Dataset are derived from different parts of different cities, with one-eighth and one-fourth of the total data from each city allocated to the validation and test sets, respectively.

Before conducting the experiments, it is essential to clarify the evaluation metrics for the multimodal trajectory prediction task. This paper follows the conventional experimental setup for trajectory prediction and selects widely used evaluation metrics in the field, which include: Minimum Average Displacement Error (minADE), Minimum Final Displacement Error (minFDE), and Miss Rate (MR). The definitions of these three evaluation metrics are provided in formulas (36) to (38).

A D E = \frac{1}{K (t^{'} - T)} \sum_{t = T + 1}^{l} \sum_{k = 1}^{K} {‖p_{t}^{k} - p_{t}^{gt}‖}_{2}

(36)

F D E = \frac{1}{K} \sum_{k = 1}^{K} {‖p_{end}^{k} - p_{end}^{gt}‖}_{2}

(37)

MR = \frac{Number of predictions where ({‖p_{end}^{k} - p_{end}^{gt}‖}_{2} > δ_{MR})}{Total number of predictions}

(38)

Where

p_{t}^{k}

and

p_{t}^{gt}

represent the predicted and ground truth position information of the k-th trajectory at time t, respectively.

T

denotes the total time steps of the predicted trajectory, while

p_{end}^{k}

and

p_{end}^{gt}

represent the position information of the endpoints of the predicted trajectory and the ground truth trajectory, respectively.

4.3. Quantitative Analysis

4.3.1. Comparative Experiment

Conventional trajectory prediction tasks typically focus on vehicles classified as "Agents" in the dataset as the prediction targets. Therefore, this paper's simulation experiments first adhere to the standard experimental setup for trajectory prediction problems, conducting multimodal trajectory prediction analysis on the "Agent" vehicles in the dataset. Based on the aforementioned evaluation metrics for trajectory prediction, this paper will carry out comparative simulation experiments as well as ablation studies.

The reference methods in the comparative experiments include LaneRCNN [36], LaneGCN [37], TNT [23], Laformer [26], HiVT [27], and DenseTNT [24]. These network models have all demonstrated good performance on the Argoverse 1 Motion Forecasting Dataset and have been utilized by many other researchers for comparative testing, ensuring that the results of the comparative experiments are highly persuasive. Additionally, since the aforementioned methods and the model proposed in this paper use the same experimental dataset and scenarios, all methods will be compared using the official open-source models. The evaluation metric results of the proposed multimodal trajectory prediction model compared to other advanced methods are shown in Table 1 (as the models used by other advanced methods are open-source, the best publicly available results are used for comparison).

As shown in Table 1, the proposed multimodal trajectory prediction method outperforms other advanced methods in several key evaluation metrics, including minADE, minFDE, and MR (the best results for each metric are highlighted in bold). The performance improvement in these evaluation metrics is significant. Specifically, the multimodal trajectory prediction metric minADE shows an average improvement of 9.1% compared to other advanced methods, while minFDE and MR improve by 11.8% and 14.6%, respectively. And the inference time is only 33.7% of the average time taken by other algorithms. These experimental results effectively validate the efficacy of the proposed multimodal trajectory prediction method.

Although the proposed method did not achieve the best result in the minADE metric, it still performed very well (ranking second), with no significant gap from the best result. It is important to note that the Laformer model (which outperformed the proposed method in the minADE metric) optimizes the prediction results by adding vehicle dynamics information as a constraint to the initial multimodal prediction trajectories. While this approach reduces the average displacement error of the predicted trajectories, it significantly increases the scale and complexity of the prediction model. Therefore, the paper considers the minor differences in evaluation metrics to be acceptable. Additionally, the proposed method achieved the best results in inference time and outperformed the Laformer model in other evaluation metrics.

In summary, based on the experimental results, it can be concluded that the proposed multimodal trajectory prediction method effectively exploits prior information from driving scenarios, considers the impact of complex interactions between vehicles, and achieves more accurate multimodal trajectory predictions, outperforming existing advanced methods.

4.3.2. Ablation Experiment

To validate the effectiveness of the model proposed in this paper, we conducted ablation experiments on the Argoverse 1 dataset. We alternately removed certain modules constructed in the previous sections and tested the complete multimodal trajectory prediction model proposed in this paper. The experimental results are presented in Table 2.

From the experimental results in Table 2, we can observe the following:

Model_1 excludes the Temporal Transformer module. Experimental validation shows that the Temporal Transformer module has the most significant impact on overall performance, and increasing the number of layers in this module can enhance overall prediction performance. This is because the motion trajectories of agents in traffic scenarios typically do not undergo abrupt changes, allowing the extraction of motion patterns from historical trajectory information. Therefore, the historical information of agents has a greater impact on the accuracy of prediction results.

Model_2 excludes the Agent-Agent interaction module. Without this module, Model_2 cannot extract dependencies between agents in the scene, leading to a significant performance decline. Additionally, removing this module increases the inference time for scenes with the same radius.

Model_3 excludes the Agent-Lane interaction module. The experimental results validate the improvement in trajectory prediction accuracy provided by our proposed method. This is because the Agent-Lane interaction module can extract potential future trajectory guidance information from the relative positions of vehicles and lanes.

Model_4 excludes the global interaction module. The experimental results indicate that the global interaction encoder can improve trajectory prediction accuracy, although not as significantly as other modules. This is because the relatively small scenes in the validation set do not highlight the advantages of the global interaction module.

Model_5 excludes the query generation module. Model_5 achieves the highest accuracy because the autoregressive query generation method references previously generated trajectory results, offering a certain advantage in accuracy compared to the proposed non-autoregressive method. However, its inference time far exceeds that of other models, failing to meet the real-time requirements of trajectory prediction tasks. Therefore, considering both real-time performance and accuracy, the proposed method remains the superior choice.

In summary, the complete multimodal trajectory prediction model designed in this paper achieves ideal results across various evaluation metrics in the ablation study, further demonstrating that the proposed method is reasonable and effective. The method significantly enhances the accuracy and reliability of multimodal trajectory prediction.

4.4. Qualitative Analysis

In addition to the aforementioned quantitative experimental results, the following presents the visualization test results of the prediction model in various typical driving scenarios for qualitative analysis of the method.

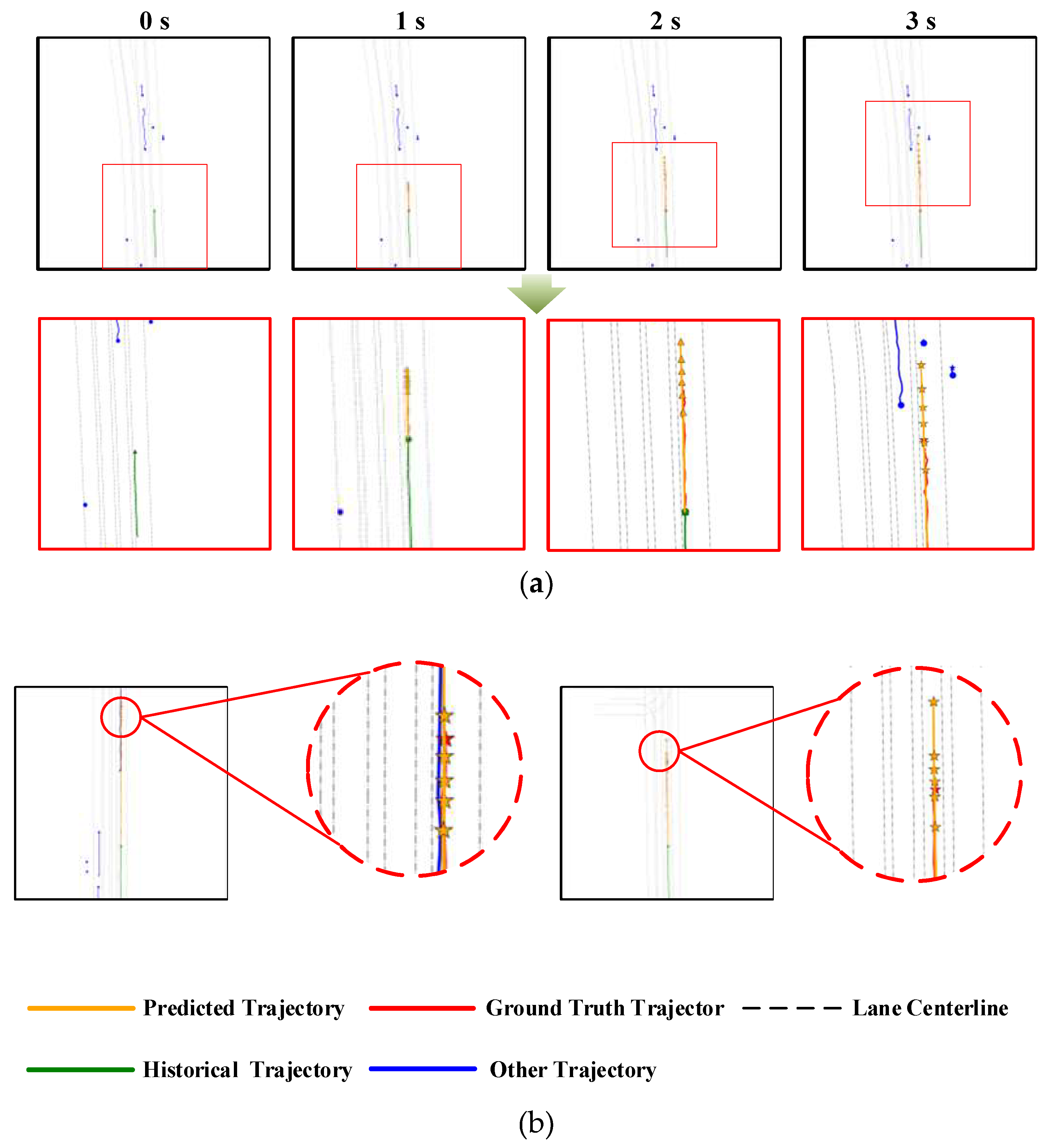
Figure 5 (a) shows the test results for some straight driving scenarios. For straight driving situations, the visual results displayed in the figure indicate that the multimodal trajectory prediction model effectively handles the dynamic interaction information of the driving scene. The output multimodal predicted trajectories exhibit high accuracy and rationality, closely aligning with the actual driving trajectories and adequately covering the trajectories that may arise from real driving behavior, thereby demonstrating the effectiveness of the method.

Furthermore, as shown in Figure 5 (b), the trajectory prediction results of the proposed algorithm under straight driving conditions are relatively accurate, with minimal overall trend differences. The distances between the predicted trajectories are relatively close, and the probability distribution is fairly uniform, aligning well with the characteristics of driving behavior in straight-line conditions.

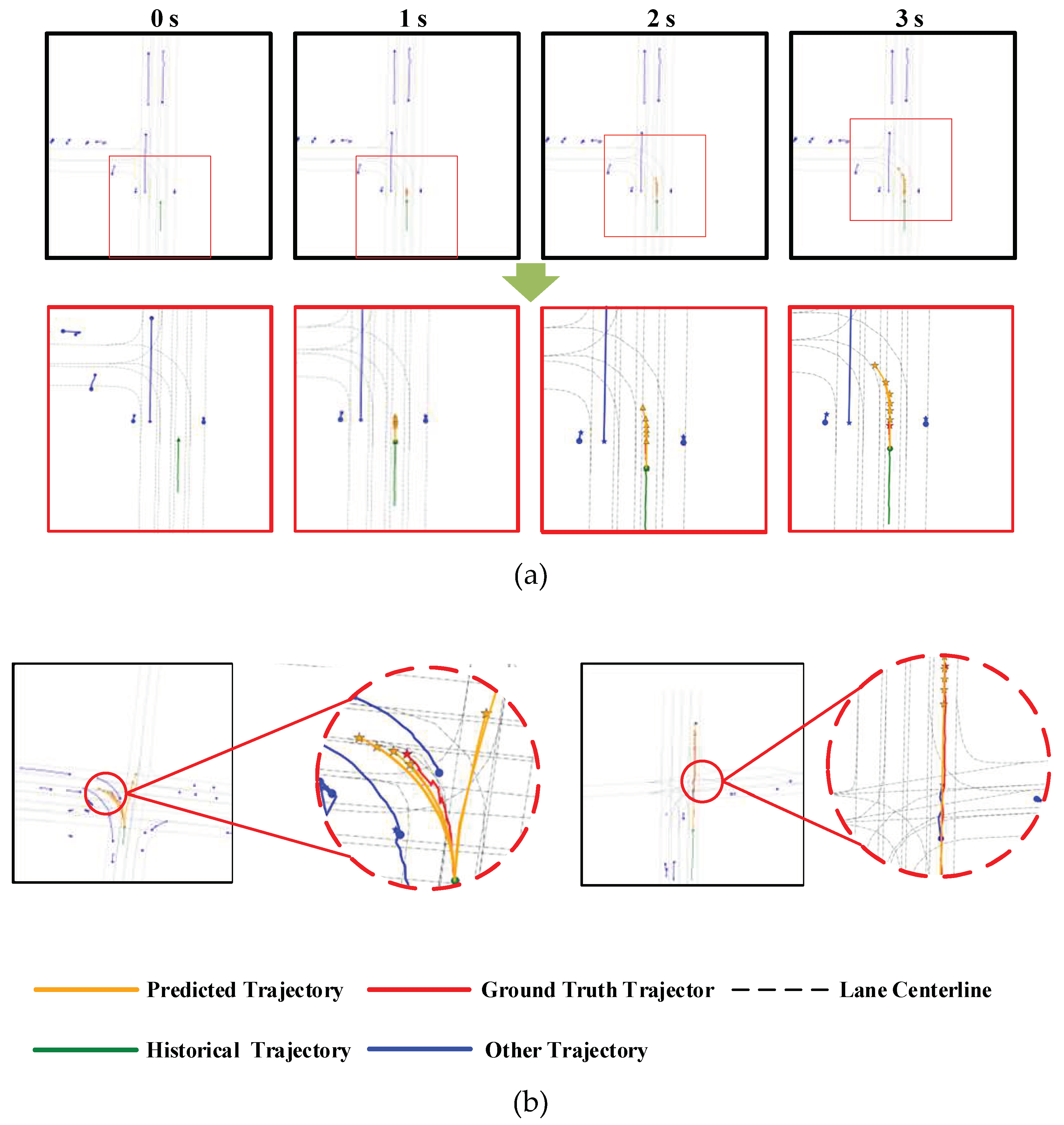
Figure 6 presents the simulation test results for some intersection scenarios. Compared to the straight driving segment shown in Figure 5, the road environment at intersections is more complex, with an increased number of traversable lanes for vehicles and more varied motion trajectories for agents. However, even with the significant increase in the complexity of the driving scene, the proposed method still effectively utilizes the interaction information of agents and scene information, successfully predicting the driving behavior of the target vehicle at the intersection. The endpoints of the multimodal trajectories are also very close to the actual trajectory endpoints.

Although there are some differences between the target lanes of certain predicted trajectories and the actual driving trajectories in Figure 6 (b), the driving behavior actions are consistent with the ground truth. Considering the diversity of trajectories reflected in the multimodal prediction results, this phenomenon is deemed reasonable and acceptable.

In summary, combining the quantitative analysis from the comparative experiments with the qualitative results from the visualizations in typical scenarios, it can be concluded that the multimodal trajectory prediction model proposed in this paper effectively leverages the interaction information of agents and scene information to produce accurate multimodal trajectory predictions, with accuracy surpassing that of existing advanced methods.

5. Conclusions

In this paper, we propose a novel trajectory prediction model that follows the encoder-decoder paradigm, capable of accurately and rapidly predicting future vehicle trajectories by aggregating the spatiotemporal and interaction information of agents in traffic scenarios. Within this model, we introduce a method based on a sparse graph attention mechanism to aggregate interaction information between agents in traffic scenarios. This method effectively filters out interactions with minimal impact on the target agent, allowing the model to focus more on significant interactions. Subsequently, we employ a temporal transformer based on a self-attention mechanism and an Agent-Lane module based on a cross-attention mechanism, along with a Global interaction module, to aggregate temporal and scene information. Finally, to accelerate the model's inference speed, we propose a non-autoregressive query generation method that rapidly generates decoding queries in parallel. Experimental results comparing our method with other algorithms demonstrate that our approach achieves optimal prediction results in the shortest time. We conducted ablation studies, and the results fully validate the effectiveness of the methods proposed in this paper. Our trajectory prediction model can be applied to trajectory prediction tasks in vehicle-road cooperative systems or V2X scenarios. In future work, we will continue to optimize the model to handle more challenging scenarios, such as those involving pedestrians and cyclists.

Author Contributions

Investigation, G.W.; Data curation, G.W.; Writing—original draft, L.G.; Writing—review and edit-ing, L.G.; Supervision, S.W.. All authors have read and agreed to the published version of the manuscript.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Wang, F.-Y. MetaVehicles in the Metaverse: Moving to a New Phase for Intelligent Vehicles and Smart Mobility. IEEE Trans. Intell. Veh. 2022, 7, 1–5. [Google Scholar] [CrossRef]
Huang, Y.; Du, J.; Yang, Z.; Zhou, Z.; Zhang, L.; Chen, H. A Survey on Trajectory-Prediction Methods for Autonomous Driving. IEEE Trans. Intell. Veh. 2022, 7, 652–674. [Google Scholar] [CrossRef]
Cao, D.; Wang, X.; Li, L.; Lv, C.; Na, X.; Xing, Y.; Li, X.; Li, Y.; Chen, Y.; Wang, F.-Y. Future Directions of Intelligent Vehicles: Potentials, Possibilities, and Perspectives. IEEE Trans. Intell. Veh. 2022, 7, 7–10. [Google Scholar] [CrossRef]
Zaremba, W.; Sutskever, I.; Vinyals, O. Recurrent Neural Network Regularization 2015.
Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Computation 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention Is All You Need 2023.
Scarselli, F.; Gori, M.; Ah Chung Tsoi; Hagenbuchner, M. ; Monfardini, G. The Graph Neural Network Model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef] [PubMed]
Krichen, M. Generative Adversarial Networks. In Proceedings of the 2023 14th International Conference on Computing Communication and Networking Technologies (ICCCNT); IEEE: Delhi, India, July 6 2023; pp. 1–7.
Chang, M.-F.; Ramanan, D.; Hays, J.; Lambert, J.; Sangkloy, P.; Singh, J.; Bak, S.; Hartnett, A.; Wang, D.; Carr, P.; et al. Argoverse: 3D Tracking and Forecasting With Rich Maps. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Long Beach, CA, USA, June, 2019; pp. 8740–8749. [Google Scholar]
Chen, X.; Zhang, H.; Zhao, F.; Cai, Y.; Wang, H.; Ye, Q. Vehicle Trajectory Prediction Based on Intention-Aware Non-Autoregressive Transformer With Multi-Attention Learning for Internet of Vehicles. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
Xing, H.; Liu, W.; Ning, Z.; Zhao, Q.; Cheng, S.; Hu, J. Deep Learning Based Trajectory Prediction in Autonomous Driving Tasks: A Survey. In Proceedings of the 2024 16th International Conference on Computer and Automation Engineering (ICCAE); IEEE: Melbourne, Australia, March 14, 2024; pp. 556–561. [Google Scholar]
Kim, Y. Convolutional Neural Networks for Sentence Classification 2014.
Dey, R.; Salem, F.M. Gate-Variants of Gated Recurrent Unit (GRU) Neural Networks. In Proceedings of the 2017 IEEE 60th International Midwest Symposium on Circuits and Systems (MWSCAS); IEEE: Boston, MA, August, 2017; pp. 1597–1600. [Google Scholar]
Phillips, D.J.; Wheeler, T.A.; Kochenderfer, M.J. Generalizable Intention Prediction of Human Drivers at Intersections. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV); IEEE: Los Angeles, CA, USA, June, 2017; pp. 1665–1670. [Google Scholar]
Zyner, A.; Worrall, S.; Ward, J.; Nebot, E. Long Short Term Memory for Driver Intent Prediction. In Proceedings of the 2017 IEEE Intelligent Vehicles Symposium (IV); IEEE: Los Angeles, CA, USA, June, 2017; pp. 1484–1489. [Google Scholar]
Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Las Vegas, NV, USA, June, 2016; pp. 961–971. [Google Scholar]
Deo, N.; Trivedi, M.M. Convolutional Social Pooling for Vehicle Trajectory Prediction. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW); IEEE: Salt Lake City, UT, USA, June, 2018; pp. 1549–15498. [Google Scholar]
Zhang, H.; Wang, Y.; Liu, J.; Li, C.; Ma, T.; Yin, C. A Multi-Modal States Based Vehicle Descriptor and Dilated Convolutional Social Pooling for Vehicle Trajectory Prediction 2020.
Chai, Y.; Sapp, B.; Bansal, M.; Anguelov, D. MultiPath: Multiple Probabilistic Anchor Trajectory Hypotheses for Behavior Prediction 2019.
Salzmann, T.; Ivanovic, B.; Chakravarty, P.; Pavone, M. Trajectron++: Dynamically-Feasible Trajectory Forecasting With Heterogeneous Data 2021.
Gilles, T.; Sabatini, S.; Tsishkou, D.; Stanciulescu, B.; Moutarde, F. GOHOME: Graph-Oriented Heatmap Output for Future Motion Estimation. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA); IEEE: Philadelphia, PA, USA, May 23, 2022; pp. 9107–9114. [Google Scholar]
Gao, J.; Sun, C.; Zhao, H.; Shen, Y.; Anguelov, D.; Li, C.; Schmid, C. VectorNet: Encoding HD Maps and Agent Dynamics From Vectorized Representation. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Seattle, WA, USA, June, 2020; pp. 11522–11530. [Google Scholar]
Zhao, H.; Gao, J.; Lan, T.; Sun, C.; Sapp, B.; Varadarajan, B.; Shen, Y.; Shen, Y.; Chai, Y.; Schmid, C.; et al. TNT: Target-driveN Trajectory Prediction 2020.
Gu, J.; Sun, C.; Zhao, H. DenseTNT: End-to-End Trajectory Prediction from Dense Goal Sets. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE: Montreal, QC, Canada, October, 2021; pp. 15283–15292. [Google Scholar]
Liu, Y.; Zhang, J.; Fang, L.; Jiang, Q.; Zhou, B. Multimodal Motion Prediction with Stacked Transformers. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Nashville, TN, USA, June, 2021; pp. 7573–7582. [Google Scholar]
Liu, M.; Cheng, H.; Chen, L.; Broszio, H.; Li, J.; Zhao, R.; Sester, M.; Yang, M.Y. LAformer: Trajectory Prediction for Autonomous Driving with Lane-Aware Scene Constraints 2023.
Zhou, Z.; Ye, L.; Wang, J.; Wu, K.; Lu, K. HiVT: Hierarchical Vector Transformer for Multi-Agent Motion Prediction. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: New Orleans, LA, USA, June, 2022; pp. 8813–8823. [Google Scholar]
Zhou, Z.; Wang, J.; Li, Y.; Huang, Y. Query-Centric Trajectory Prediction. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); IEEE: Vancouver, BC, Canada, June, 2023; pp. 17863–17873. [Google Scholar]
Zhou, Z.; Wen, Z.; Wang, J.; Li, Y.-H.; Huang, Y.-K. QCNeXt: A Next-Generation Framework For Joint Multi-Agent Trajectory Prediction 2023.
Chen, K.; Chen, G.; Xu, D.; Zhang, L.; Huang, Y.; Knoll, A. NAST: Non-Autoregressive Spatial-Temporal Transformer for Time Series Forecasting 2021.
Huang, Y.; Bi, H.; Li, Z.; Mao, T.; Wang, Z. STGAT: Modeling Spatial-Temporal Interactions for Human Trajectory Prediction. In Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision (ICCV); IEEE: Seoul, Korea (South), October, 2019; pp. 6271–6280. [Google Scholar]
Wu, S.; Xiao, X.; Ding, Q.; Zhao, P.; Wei, Y.; Huang, J. Adversarial Sparse Transformer for Time Series Forecasting. In Proceedings of the Proceedings of the 34th International Conference on Neural Information Processing Systems; Curran Associates Inc.: Red Hook, NY, USA, 2020.
Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image Is Worth 16x16 Words: Transformers for Image Recognition at Scale 2021.
Chen, N.; Watanabe, S.; Villalba, J.; Zelasko, P.; Dehak, N. Non-Autoregressive Transformer for Speech Recognition. IEEE Signal Process. Lett. 2021, 28, 121–125. [Google Scholar] [CrossRef]
Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization 2017.
Zeng, W.; Liang, M.; Liao, R.; Urtasun, R. LaneRCNN: Distributed Representations for Graph-Centric Motion Forecasting. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS); IEEE: Prague, Czech Republic, September 27, 2021; pp. 532–539. [Google Scholar]
Liang, M.; Yang, B.; Hu, R.; Chen, Y.; Liao, R.; Feng, S.; Urtasun, R. Learning Lane Graph Representations for Motion Forecasting 2020.

Figure 1. Algorithm Structure Diagram. This figure illustrates the structure of our model, where historical trajectories and map information are aggregated through the local encoder and global encoder to capture interaction information and spatiotemporal information. The query generator then generates decoding queries in parallel, and finally, the decoder produces the predicted trajectories.

Figure 2. Structure Diagram of the Local Encoder. The local encoder aggregates the interaction information between agents using a Sparse Graph Attention Network, aggregates temporal information through a Temporal Self-Attention Network, and aggregates the interaction information between agents and the road using a cross-attention mechanism.

Figure 3. The impact of different values of

α

on the formula.

Figure 3. The impact of different values of

α

on the formula.

Figure 4. structure of the query generation module

Figure 5. Straight driving scenario. (a) shows the trajectory prediction process for the next 3 seconds and its zoomed-in view. (b) presents the prediction results and zoomed-in views for other straight driving scenarios.

Figure 6. Typical intersection scenario. (a) illustrates the trajectory prediction process for the next 3 seconds and its zoomed-in view. (b) displays the prediction results and zoomed-in views for other intersection driving scenarios.

Table 1. Comparison results with other advanced algorithms.

Method	minADE (K=1)	minFDE (K=1)	MR (K=1)	minADE (K=6)	minFDE (K=6)	MR (K=6)	Time (K=6)
LaneRCNN	1.685	3.692	0.569	0.904	1.453	0.123	-
LaneGCN	1.702	3.762	0.588	0.870	1.362	0.162	-
TNT	2.174	4.959	0.710	0.910	1.446	0.166	531
HiVT	1.598	3.533	0.547	0.774	1.169	0.127	153
Laformer	1.553	3.453	0.547	0.772	1.163	0.125	115
DenseTNT	1.679	3.632	0.584	0.882	1.282	0.126	482
Ours	1.557	3.451	0.545	0.774	1.158	0.118	108

Table 2. Ablation study results.

	TT	A-A	A-L	Global	QG	minADE (K=6)	minFDE (K=6)	MR (K=6)	Time (K=6)
Model_1		√	√	√	√	1.251	2.132	0.287	84
Model_2	√		√	√	√	0.868	1.348	0.155	93
Model_3	√	√		√	√	0.811	1.175	0.132	100
Model_4	√	√	√		√	0.819	1.171	0.129	96
Model_5	√	√	√	√		0.751	1.141	0.120	443
Complete Model	√	√	√	√	√	0.774	1.158	0.118	108

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Alerts

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Rapid Vehicle Trajectory Prediction Based on Multi-Attention Mechanism for Fusing Multimodal Information

Abstract

Keywords:

Subject:

1. Introduction

2. Realated Work

2.1. Recurrent Neural Networks

2.2. Graph Neural Networks

2.3. Transformer

3. Methods

3.1. Probem Foomulation

3.2. Overview

3.3. Local Encoder

3.3.1. Data Preprocessing Module

3.3.1. Agent-Agent Interaction Module

3.3.2. Temporal Transformer

3.3.3. Agent-Lane Interaction Module

3.4. Global Encoder

3.4. Query Generation Module

3.4. Decoder

3.5. Loss Function Define

4. Results

4.1. Implementation Detail

4.2. Dataset and Metrics

4.3. Quantitative Analysis

4.3.1. Comparative Experiment

4.3.2. Ablation Experiment

4.4. Qualitative Analysis

5. Conclusions

Author Contributions

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe