Prerpints.org logo
Preprint
Article

Qualitative Analysis, and Novel Exact Solitons to the Compound Korteweg-De Vries Burgers Equation

Altmetrics

Downloads

37

Views

11

Comments

0

Submitted:

20 November 2024

Posted:

21 November 2024

You are already at the latest version

Alerts
Abstract
The paper consists on the exact wave results of the (1+1)-dimensional nonlinear compound Korteweg-De Vries, and Burgers (KdVB) equation with a truncated M- fractional derivative. This model represents the generalization of Korteweg-De Vries- modified Korteweg-De Vries and Burgers equations. We obtained the periodic, combo- singular,dark-bright, and other wave results with the use of the extended sinh-Gordon equation expansion (EShGEE), and the modified (G′/G2)-expansion techniques. The use of effective fractional derivative makes our results much better than the existing results. The gained solutions are useful as well as applicable in the various fields including the mathematical physics, plasma physics, ocean engineering, optics, etc. The obtained solutions are demonstrated by 2-D, 3-D, and Contour plots. The achieved results are fruitful in future research concerned equation. Stability analysis is used to check that the results are precise as well as exact. The modulation instability (MI) is performed to find stable steady-state solutions of the concerned model. At the end, it is suggested that the methods used are easy and reliable.
Keywords: 
Subject: Engineering  -   Other

1. Introduction

Non-linear mathematical models are used to depict phenomena that occur naturally. Non-linear partial differential equations are utilized to express a number of different models. Different kinds of fractional derivatives have only been utilized in recent years, including unstable nonlinear Schrödinger equation [1], Gross-Pitaevski model [2], Schrödinger-Hirota equation [3], Cahn-Hilliard equation [4], stochastic concatenation equation [5], Boiti-Leon-Manna-Pempinelli model [6], Estevez-Mansfield-Clarkson model [7] and others.
Two dependable and efficient methods were employed in our study: the modified ( G ′ / G 2 ) -expansion method and the extended sinh-Gordon equation expansion scheme (EShGEES). The relevant methods are applied to different models. Instantly; the extended sinh-Gordon equation expansion method is applied for the Biswas-Arshed model [8], Kundu-Eckhaus equation [9], generalized nonlinear Schrödinger equation [10], Boussinesq-Burgers model [11], Van der Waals model [12], Westervelt model [13]. The modified ( G ′ / G 2 ) -expansion technique is utilized for third-order dispersion nonlinear Schrödinger equation [14], Fokas-Lenells equation [15], classical Boussinesq model [16], coupled Drinfel’d-Sokolov-Wilson model [17], Wazwaz Kaur Boussinesq equation [18], and many others.
Our research’s primary goal is to utilize the modified ( G ′ / G 2 ) -expansion scheme and the EShGEE scheme to determine the new exact wave solutions of the compound KdVB equation in the context of truncated M-fractional derivative. To verify the accuracy and precision of the solutions obtained, as well as the stability of the relevant model, stability and modulation instability analyses are conducted.
The paper is divided into various sections. Section 2 presents the model description and mathematical analysis; Section 3 presents the extended sinh-Gordon equation expansion method and wave solutions; Section 4 presents the modified ( G ′ / G 2 ) -expansion scheme and wave solutions; Section 5 mentions a graphic explanation; Section 6 shows a physical description; Section 7 performs stability analysis; Section 7 modulates instability analysis; and Section 9 concludes.

Truncated M-fractional Derivative

Definition: Suppose h ( t ) : [ 0 , ∞ ) → ℜ , therefore truncated M-fractional derivative of h of order ϵ [19]
D M , t ϵ , ϱ h ( t ) = lim ϵ → 0 h ( t E ϱ ( ϵ t 1 − ϵ ) ) − h ( t ) ϵ , ϵ ∈ ( 0 , 1 ] , ϱ > 0 ,
here E ϱ ( . ) indicates a truncated Mittag-Leffler profile [20]
E ϱ ( z ) = ∑ m = 0 i z m Γ ( ϱ m + 1 ) , ϱ > 0 and z ∈ C .
Characteristics: Suppose a,b ∈ ℜ , and g , h are ϵ —differentiable at a point t > 0 , from [19]:
( a ) D M , t ϵ , ϱ ( a g ( t ) + b h ( t ) ) = a D M , t ϵ , ϱ g ( t ) + b D M , t ϵ , ϱ h ( t )
( b ) D M , t ϵ , ϱ ( g ( t ) . h ( t ) ) = g ( t ) D M , t ϵ , ϱ h ( t ) + h ( t ) D M , t ϵ , ϱ g ( t )
( c ) D M , t ϵ , ϱ ( g ( t ) h ( t ) ) = h ( t ) D M , t ϵ , ϱ g ( t ) − g ( t ) D M , t ϵ , ϱ h ( t ) ( h ( t ) ) 2
( d ) D M , t ϵ , ϱ ( A ) = 0 , where A is a constant .
( e ) D M , t ϵ , ϱ g ( t ) = t 1 − ϵ Γ ( ϱ + 1 ) d g ( t ) d t .

2. The Model Representation and Mathematical Treatment

Consider a (1+1)-dimensional compound KdVB model is given as [21];
h t + a h h x + b h 2 h x + θ h x x − τ h x x x = 0 .
The wave function in this case is denoted by h = h ( x , t ) , where the parameters are a, b, θ , and τ . Eq. The form of the Korteweg-De Vries-modified Korteweg-De Vries and Burgers equations is generalized in Eq.(1). Different wave solutions of Eq.(1) can be obtained by using different schemes, such as the novel ( G ′ / G ) -expansion scheme in [21], the ( G ′ / G ) -expansion technique in [22], the generalized ( G ′ / G ) -expansion scheme in [23], the extended ( G ′ / G ) -expansion scheme in [24], singular-kink, singular-periodic, and single soliton solutions in [25].
A (1+1)-dimensional KdVB model in truncated M-fractional derivative is given as;
D M , t ϵ , ϱ h + a h D M , x ϵ , ϱ h + b h 2 D M , x ϵ , ϱ h + θ D M , x 2 ϵ , ϱ h − τ D M , x 3 ϵ , ϱ h = 0 .
Let us apply the following wave transformation:
h ( x , t ) = H ( ℧ ) , ℧ = Γ ( 1 + ϱ ) ϵ ( x ϵ − λ t ϵ ) .
Here, H represents the amplitude where as ℧ denotes the argument of the wave profile, which represents the wave’s position and time dependence. The parameter λ represents the velocity of soliton.
By applying the Eq.(3) into Eq.(2), we gain the nonlinear ODE given as;
3 a H 2 + 2 b H 3 − 6 τ H ′ ′ + 6 θ H ′ − 6 H λ = 0 .
By utilizing Homogenous Balance method in Eq.(4) and balancing the terms H 3 and H ″ ; we gain the value of m is 1.

3. Explanation and Implementation of Extended sinh-Gordon Equation Expansion Scheme

3.1. Explanation

There are main stages for the concerned technique.
Stage 1:
Assume a nonlinear partial frctional differential equation:
Z ( g , D M , t ϵ , ϱ g 2 , g 2 D M , x ϵ , ϱ g , D M , x ϵ , ϱ g , … ) = 0 .
Here, g = g ( x , t ) indicates a wave-function.
Considering a given relation:
g ( x , t ) = G ( ℧ ) , ℧ = Γ ( 1 + ϱ ) ϵ ( x ϵ + κ t ϵ ) .
Inserting Eq. (6) in Eq. (5), yields:
H ( G , G 2 G ′ , G ″ , … ) = 0 .
Stage 2:
Consider the solution of Eq. (7) is shown below:
G ( p ) = α 0 + ∑ j = 1 m ( β j sinh ( p ) + α j cosh ( p ) ) j .
Here α 0 , α j , β j ( j = 1 , 2 , 3 , … , m ) are unknowns. Consider a novel function p of ℧, satisfies:
d f d ℧ = sinh ( f ) .
Positive integer "m" is calculated with the help of Homogenous balance method. Eq. (9) is obtained by using the following:
q x t = κ sinh ( v ) .
By [26], one gets the result of Eq. (10) shown as:
sinh p ( ℧ ) = ± csch ( ℧ ) O R cosh p ( ℧ ) = ± coth ( ℧ ) .
And
sinh p ( ℧ ) = ± ι s e c h ( ℧ ) O R cosh p ( ℧ ) = ± tanh ( ℧ ) .
ι 2 = − 1 .
Stage 3:
The system that results from putting Eqs. (8) and Eq. (9) in the Eq. (7) is p ′ k ( ℧ ) sinh l p ( ℧ ) cosh m p ( ℧ ) ( k = 0 , 1 ; l = 0 , 1 ; m = 0 , 1 , 2 , . . . ) . A system involving α j and β j ( j = 1 , 2 , 3 . . . m ) and others can be obtained by taking every co-efficient of p ′ k ( ℧ ) sinh l p ( ℧ ) cosh m p ( ℧ ) equal to 0.
Stage 4:
Get the answers for the unknown by solving the obtained system. The solutions for Eq. (7) are obtained by using Eqs. (11) and (12), which are displayed as follows:
G ( ℧ ) = α 0 + ∑ j = 1 m ( ± β j csch ( ℧ ) ± α j coth ( ℧ ) ) j .
and
G ( ℧ ) = α 0 + ∑ j = 1 m ( ± ι β j s e c h ( ℧ ) ± α j tanh ( ℧ ) ) j .
By using this scheme, we can gain the sech, csch, tanh and coth consisting solutions.

3.2. Implementation of EShGEE Technique

Eq.(8) takes the given form for m = 1 :
V ( ℧ ) = α 0 + α 1 cosh ( f ( ℧ ) ) + β 1 sinh ( f ( ℧ ) ) .
Using Eq.(15) into Eq.(4) along Eq.(9), we gain a system containing α 0 , α 1 , β 1 , λ and other parameters. With the help of Mathematica tool, one gains the sets:
Set 1:
α 0 = − 3 a 4 b , α 1 = 2 θ a , β 1 = − 2 θ a , λ = 4 b θ 2 3 a 2 − 3 a 2 16 b , τ = 8 b θ 2 3 a 2 .
h 1 ( x , t ) = − 3 a 4 b + 2 θ a ( ± coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ∓ csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) .
h 2 ( x , t ) = − 3 a 4 b + 2 θ a ( ± tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ∓ ι sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) .
Set 2:
α 0 = − 3 a 4 b , α 1 = 2 θ a , β 1 = 2 θ a , λ = 4 b θ 2 3 a 2 − 3 a 2 16 b , τ = 8 b θ 2 3 a 2 .
h 1 ( x , t ) = − 3 a 4 b ± 2 θ a ( coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) + csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) .
h 2 ( x , t ) = − 3 a 4 b ± 2 θ a ( tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) + ι sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 4 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) .
Set 3:
{ α 0 = − a 2 − 8 b θ + a 4 b , α 1 = − a 2 − 8 b θ + a 4 b , β 1 = − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b , λ = − a a 2 − 8 b θ + a 2 + 8 b θ 12 b , τ = a a 2 − 8 b θ + a 2 − 4 b θ 12 b } .
h 1 ( x , t ) = − a 2 − 8 b θ + a 4 b ∓ ( ( a 2 − 8 b θ + a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) + a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ) .
h 2 ( x , t ) = − a 2 − 8 b θ + a 4 b ∓ ( ι a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) + ( a 2 − 8 b θ + a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ) .
Set 4:
{ α 0 = − a 2 − 8 b θ + a 4 b , α 1 = − a 2 − 8 b θ + a 4 b , β 1 = a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b , λ = − a a 2 − 8 b θ + a 2 + 8 b θ 12 b , τ = a a 2 − 8 b θ + a 2 − 4 b θ 12 b } .
h 1 ( x , t ) = − a 2 − 8 b θ + a 4 b ∓ ( a 2 − 8 b θ + a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ± a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = − a 2 − 8 b θ + a 4 b ∓ ( a 2 − 8 b θ + a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ± ι a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
Set 5:
{ α 0 = a 2 − 8 b θ − a 4 b , α 1 = a 2 − 8 b θ − a 4 b , β 1 = − − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b , λ = − − a a 2 − 8 b θ + a 2 + 8 b θ 12 b , τ = − a a 2 − 8 b θ + a 2 − 4 b θ 12 b } .
h 1 ( x , t ) = a 2 − 8 b θ − a 4 b ± ( a 2 − 8 b θ − a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ∓ − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = a 2 − 8 b θ − a 4 b ± ( a 2 − 8 b θ − a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ∓ ι − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
Set 6:
{ α 0 = a 2 − 8 b θ − a 4 b , α 1 = a 2 − 8 b θ − a 4 b , β 1 = − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b , λ = − − a a 2 − 8 b θ + a 2 + 8 b θ 12 b , τ = − a a 2 − 8 b θ + a 2 − 4 b θ 12 b } .
h 1 ( x , t ) = a 2 − 8 b θ − a 4 b ± ( a 2 − 8 b θ − a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ± − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = a 2 − 8 b θ − a 4 b ± ( a 2 − 8 b θ − a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) ± ι − a a 2 − 8 b θ + a 2 − 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 8 b θ + a 2 + 8 b θ 12 b ) t ϵ ) ) .
Set 7:
{ α 0 = a 2 + 8 b θ − a 4 b , α 1 = a − a 2 + 8 b θ 4 b , β 1 = − − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b , λ = a a 2 + 8 b θ − a 2 + 8 b θ 12 b , τ = − a a 2 + 8 b θ + a 2 + 4 b θ 12 b } .
h 1 ( x , t ) = a 2 + 8 b θ − a 4 b ± ( a − a 2 + 8 b θ ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) ∓ − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = a 2 + 8 b θ − a 4 b ± ( a − a 2 + 8 b θ ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) ∓ ι − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) .
Set 8:
{ α 0 = a 2 + 8 b θ − a 4 b , α 1 = a − a 2 + 8 b θ 4 b , β 1 = − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b , λ = a a 2 + 8 b θ − a 2 + 8 b θ 12 b , τ = − a a 2 + 8 b θ + a 2 + 4 b θ 12 b } .
h 1 ( x , t ) = a 2 + 8 b θ − a 4 b ± ( a − a 2 + 8 b θ ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) ± − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = a 2 + 8 b θ − a 4 b ± ( a − a 2 + 8 b θ ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) ± ι − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 8 b θ − a 2 + 8 b θ 12 b ) t ϵ ) ) .
Set 9:
{ α 0 = − a 2 + 8 b θ + a 4 b , α 1 = a 2 + 8 b θ + a 4 b , β 1 = − a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b , λ = − a a 2 + 8 b θ + a 2 − 8 b θ 12 b , τ = a a 2 + 8 b θ + a 2 + 4 b θ 12 b } .
h 1 ( x , t ) = − a 2 + 8 b θ + a 4 b ± ( a 2 + 8 b θ + a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) ∓ a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = − a 2 + 8 b θ + a 4 b ± ( a 2 + 8 b θ + a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) ∓ ι a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) .
Set 10:
{ α 0 = − a 2 + 8 b θ + a 4 b , α 1 = a 2 + 8 b θ + a 4 b , β 1 = a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b , λ = − a a 2 + 8 b θ + a 2 − 8 b θ 12 b , τ = a a 2 + 8 b θ + a 2 + 4 b θ 12 b } .
h 1 ( x , t ) = − a 2 + 8 b θ + a 4 b ± ( a 2 + 8 b θ + a ) 4 b coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) ± a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b csc h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) .
h 2 ( x , t ) = − a 2 + 8 b θ + a 4 b ± ( a 2 + 8 b θ + a ) 4 b tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) ± ι a a 2 + 8 b θ + a 2 + 4 b θ 2 2 b sec h ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 8 b θ + a 2 − 8 b θ 12 b ) t ϵ ) ) .
Set 11:
α 0 = − 3 a 4 b , α 1 = 4 θ a , β 1 = 0 , λ = 16 b θ 2 3 a 2 − 3 a 2 16 b , τ = 8 b θ 2 3 a 2 .
h 1 ( x , t ) = − 3 a 4 b ± 4 θ a coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) .
h 2 ( x , t ) = − 3 a 4 b ± 4 θ a tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) t ϵ ) ) .
Set 12:
{ α 0 = − a 2 − 16 b θ + a 4 b , α 1 = − a 2 − 16 b θ + a 4 b , β 1 = 0 , λ = − a a 2 − 16 b θ + a 2 + 16 b θ 12 b , τ = a a 2 − 16 b θ + a 2 − 8 b θ 48 b } .
h 1 ( x , t ) = − a 2 − 16 b θ + a 4 b ( 1 ± coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 b θ + a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
h 2 ( x , t ) = − a 2 − 16 b θ + a 4 b ( 1 ± tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 b θ + a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
Set 13:
{ α 0 = a 2 − 16 b θ − a 4 b , α 1 = a 2 − 16 b θ − a 4 b , β 1 = 0 , λ = − − a a 2 − 16 b θ + a 2 + 16 b θ 12 b , τ = − a a 2 − 16 b θ + a 2 − 8 b θ 48 b } .
h 1 ( x , t ) = − a − a 2 − 16 b θ 4 b ( 1 ± coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 b θ + a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
h 2 ( x , t ) = − a − a 2 − 16 b θ 4 b ( 1 ± tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 b θ + a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
Set 14:
{ α 0 = a 2 + 16 b θ − a 4 b , α 1 = a − a 2 + 16 b θ 4 b , β 1 = 0 , λ = a a 2 + 16 b θ − a 2 + 16 b θ 12 b , τ = − a a 2 + 16 b θ + a 2 + 8 b θ 48 b } .
h 1 ( x , t ) = a − a 2 + 16 b θ 4 b ( − 1 ± coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 b θ − a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
h 2 ( x , t ) = a − a 2 + 16 b θ 4 b ( − 1 ± tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 b θ − a 2 + 16 b θ 12 b ) t ϵ ) ) ) .
Set 15:
{ α 0 = − a 2 + 16 b θ + a 4 b , α 1 = a 2 + 16 b θ + a 4 b , β 1 = 0 , λ = − a a 2 + 16 b θ + a 2 − 16 b θ 12 b , τ = a a 2 + 16 b θ + a 2 + 8 b θ 48 b } .
h 1 ( x , t ) = a 2 + 16 b θ + a 4 b ( − 1 ± coth ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 b θ + a 2 − 16 b θ 12 b ) t ϵ ) ) ) .
h 2 ( x , t ) = a 2 + 16 b θ + a 4 b ( − 1 ± tanh ( Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 b θ + a 2 − 16 b θ 12 b ) t ϵ ) ) ) .

4. Description of the Modified ( G ′ / G 2 ) − Expansion Technique

Here, we will brief fundamental steps of the concerned technique given as [14].
Step 1:
Let us assume the Eqs. (5), (6) and (7).
Step 2:
Assume the result for Eq.(7) given as;
Q ( η ) = ∑ i = 0 m α i ( G ′ G 2 ) i ,
Where α i ( i = 0 , 1 , 2 , 3 , … , m ) are undetermined where α j ≠ 0 . A new profile G= G ( η ) satisfies a mentioned equation,
( G ′ G 2 ) ′ = p + q ( G ′ G 2 ) 2 ,
here p and q indicate the constants. We obtain the given solutions to Eq. (62) depends on the values of p:
Case 1:when p q < 0 , we have
( G ′ G 2 ) = − | p q | q + | p q | 2 ( C 1 sinh ( p q η ) + C 2 cosh ( p q η ) C 1 cosh ( p q η ) + C 2 sinh ( p q η ) ) ,
Case 2: if p q > 0 , then
( G ′ G 2 ) = p q ( C 1 cos ( p q η ) + C 2 sin ( p q η ) C 1 sin ( p q η ) − C 2 sin ( p q η ) ) ,
Case 3: if p = 0 and q ≠ 0 , then
( G ′ G 2 ) = − C 1 q ( C 1 η + C 2 ) .
Here C 1 and C 2 are constants.
Step 3:
Putting Eq. (61) into the Eq. (7) along Eq. (62), and summing up coefficients of every order of ( G ′ G 2 ) i to 0, then solving the obtained system involving α i , p , q , ν and others.
Step 4:
Eq. (61) of which α i , ν and other parameters that are obtained in the step 3 in the Eq. (7), one can gain the results of Eq. (5).

4.1. Exact Soliton Solutions Through Modified ( G ′ / G 2 ) − Expansion Technique

For m = 1 , Eq.(61) changes into:
Q ( η ) = α 0 + α 1 G ′ ( η ) G 2 ( η ) .
Here α 0 and α 1 are undetermined. Using Eq. (66) and Eq. (62) in the Eq. (4) and with the use of Mathematica tool, yields the given sets:
Set 1:
α 0 = − 3 a 4 b , α 1 = 4 θ p a , λ = − 16 b θ 2 p q 3 a 2 − 3 a 2 16 b , τ = 8 b θ 2 3 a 2 .
h ( x , t ) = − 3 a 4 b + 4 θ p a ( − | p q | q + | p q | 2 ( ( C 1 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) + C 2 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) / ( C 1 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) + C 2 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) ) ) .
h ( x , t ) = − 3 a 4 b + 4 θ p a ( p q ( ( C 1 cos ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) + C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) / ( C 1 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) − C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( 16 b θ 2 p q 3 a 2 − 3 a 2 16 b ) t ϵ ) ) ) ) ) .
Set 2:
{ α 0 = − a + a 2 − 16 i b θ p q 4 b , α 1 = i p a + a 2 − 16 i b θ p q 4 b q , λ = − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b , τ = − a a 2 − 16 i b θ p q + a 2 − 8 i b θ p q 48 b p q } .
h ( x , t ) = − a + a 2 − 16 i b θ p q 4 b + i p ( a + a 2 − 16 i b θ p q ) 4 b q ( − | p q | q + | p q | 2 ( ( C 1 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
h ( x , t ) = − a + a 2 − 16 i b θ p q 4 b + i p ( a + a 2 − 16 i b θ p q ) 4 b q ( p q × ( ( C 1 cos ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) − C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
Set 3:
{ α 0 = − a + a 2 − 16 i b θ p q 4 b , α 1 = − i p − a + a 2 − 16 i b θ p q 4 b q , λ = − − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b , τ = a a 2 − 16 i b θ p q − a 2 + 8 i b θ p q 48 b p q } .
h ( x , t ) = − a + a 2 − 16 i b θ p q 4 b − i p ( − a + a 2 − 16 i b θ p q ) 4 b q ( − | p q | q + | p q | 2 ( ( C 1 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
h ( x , t ) = − a + a 2 − 16 i b θ p q 4 b − i p ( − a + a 2 − 16 i b θ p q ) 4 b q ( p q × ( ( C 1 cos ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) − C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( − a a 2 − 16 i b θ p q + a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
Set 4:
{ α 0 = − a + a 2 + 16 i b θ p q 4 b , α 1 = − i p a + a 2 + 16 i b θ p q 4 b q , λ = − a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b , τ = − a a 2 + 16 i b θ p q + a 2 + 8 i b θ p q 48 b p q } .
h ( x , t ) = − a + a 2 + 16 i b θ p q 4 b − i p ( a + a 2 + 16 i b θ p q ) 4 b q ( − | p q | q + | p q | 2 ( ( C 1 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) + C 2 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
h ( x , t ) = − a + a 2 + 16 i b θ p q 4 b − i p ( a + a 2 + 16 i b θ p q ) 4 b q ( p q × ( ( C 1 cos ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) − C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ + ( a a 2 + 16 i b θ p q + a 2 − 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
Set 5:
{ α 0 = − a + a 2 + 16 i b θ p q 4 b , α 1 = i p − a + a 2 + 16 i b θ p q 4 b q , λ = a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b , τ = − − a a 2 + 16 i b θ p q + a 2 + 8 i b θ p q 48 b p q } .
h ( x , t ) = − a + a 2 + 16 i b θ p q 4 b + i p ( − a + a 2 + 16 i b θ p q ) 4 b q ( − | p q | q + | p q | 2 ( ( C 1 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 cosh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sinh ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .
h ( x , t ) = − a + a 2 + 16 i b θ p q 4 b + i p ( − a + a 2 + 16 i b θ p q ) 4 b q ( p q × ( ( C 1 cos ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) + C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) / ( C 1 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) − C 2 sin ( p q Γ ( 1 + ϱ ) ϵ ( x ϵ − ( a a 2 + 16 i b θ p q − a 2 + 16 i b θ p q 12 b ) t ϵ ) ) ) ) ) .

5. Graphically Explanation

Here, we used 2-D, 3-D, and contour plots to display the obtained solutions. The 2-D graphs are displayed for various ϵ .

6. Physically Explanation

Now we will give the dynamical behaviour of the solutions obtained for the compound KdVB equation with fractional derivative.
Figure 1: denotes a combo singular solitons for; a = − 0.5 , b = 1 , θ = − 0.2 , and ϱ = 1 . Fig(a) shows the 2D plot for − 12 < x < 12 when ϵ = 1 , blue line at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 12 < x < 12 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .
Figure 2: denotes a dark-bright soliton for; a = 0.3 , b = 2 , θ = 0.2 , and ϱ = 1 . Fig(a) shows the 2D plot for − 12 < x < 12 when ϵ = 1 , blue curve at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 12 < x < 12 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .
Figure 3: represents a singular soliton for; a = 0.65 , b = − 0.45 , θ = 0.3 , and ϱ = 1 . Fig(a) shows the 2D plot for − 8 < x < 8 when ϵ = 1 , blue curve at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 8 < x < 8 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .
Figure 4: denotes a dark soliton for; a = 0.55 , b = 0.45 , θ = − 0.2 , and ϱ = 1 . Fig(a) shows the 2D plot for − 9 < x < 9 when ϵ = 1 , blue curve at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 9 < x < 9 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .
Figure 5: shows a combo kink soliton for; a = 1 , b = 0.9 , θ = − 0.2 , p = 0.5 , q = − 0.6 , c 1 = 0.5 , c 2 = − 0.4 and ϱ = 1 . Fig(a) shows the 2D plot for − 3 < x < 3 when ϵ = 1 , blue curve at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 3 < x < 3 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .
Figure 6: shows a periodic soliton for; a = 0.15 , b = 0.45 , θ = 0.1 , p = 0.5 , q = − 0.3 , c 1 = 0.5 , c 2 = 1 , and ϱ = 1 . Fig(a) shows the 2D plot for − 7 < x < 7 when ϵ = 1 , blue curve at value of t is 0, orange line when the t is 5, while green line when the t is 10. Fig(b) shows a 2D graph for − 7 < x < 7 at 0 < t < 10 , while red line when ϵ = 0.5 , black line when ϵ = 0.7 , while blue line if ϵ = 1 . Fig(c) indicates the 3D graph if ϵ = 0.6 when 0 < t < 10 . Fig(d) represents the Contour graph when ϵ = 0.6 for 0 < t < 10 .

7. Stability Analysis

We will conduct the crucial analysis for the relevant equation in this section. Many equations probably use the stability analysis [27,28]. The Hamiltonian transformation is taken into consideration for the stability analysis of Eq.(1).
S = 1 2 ∫ − ∞ ∞ h 2 d x
Here, S indicates a factor of momentum, and h ( x , t ) represents the possibility power. An important criterion for the stable-solution is shown as follows;
∂ S ∂ λ > 0 ,
here λ shows the soliton velocity, putting Eq.(48) in Eq.(82) yields;
S = 1 2 ∫ − 6 6 ( − 3 a 4 b + 4 θ a tanh ( x − ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) t ) ) ) 2 d x ,
by using the criterion given in Eq.(83), we get
( 24 a 2 b θ cosh ( 6 − t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) ) sec h ( t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) + 6 ) ( t sinh ( t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) + 6 ) sec h ( 6 − t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) ) + t cosh ( t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) + 6 ) tanh ( 6 − t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) ) sec h ( 6 − t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) ) ) − 64 b 2 θ 2 ( t sec h 2 ( t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) + 6 ) − t sec h 2 ( 6 − t ( 16 b θ 2 3 a 2 − 3 a 2 16 b ) ) ) ) / ( 8 a 2 b 2 ) > 0 .
Hence, Eq.(1) shows that, if the criterion is met, the model is stable.

8. MI Analysis

Consider the given relation for steady state solution of compound KdVB equation [29]:
h ( x , t ) = ( H ( x , t ) + δ ) e ι δ t .
Here δ represents the normalizing power of optical. Using Eq.(86) in Eq.(1). By linearizing, we get
θ H x x − τ H x x x + H t + δ ι H + δ 3 / 2 ι = 0 .
Let us assume the results of Eq.(87) given as;
H ( x , t ) = A 1 e ι ( p x − q t ) + A 2 e − ι ( p x − q t ) .
here q shows the frequency while p denotes the perturbation normalized wave number. Using the Eq.(88) in Eq.(87). By collecting the co-efficients of e ι ( p x − q t ) and e − ι ( p x − q t ) , we get the dispersion relation .
− δ 2 + p 6 τ 2 + θ 2 p 4 − 2 p 3 q τ + q 2 = 0 .
Finding for q, the dispersion relation derived from Eq.(89) provides
q = p 3 τ ± δ 2 − θ 2 p 4 .
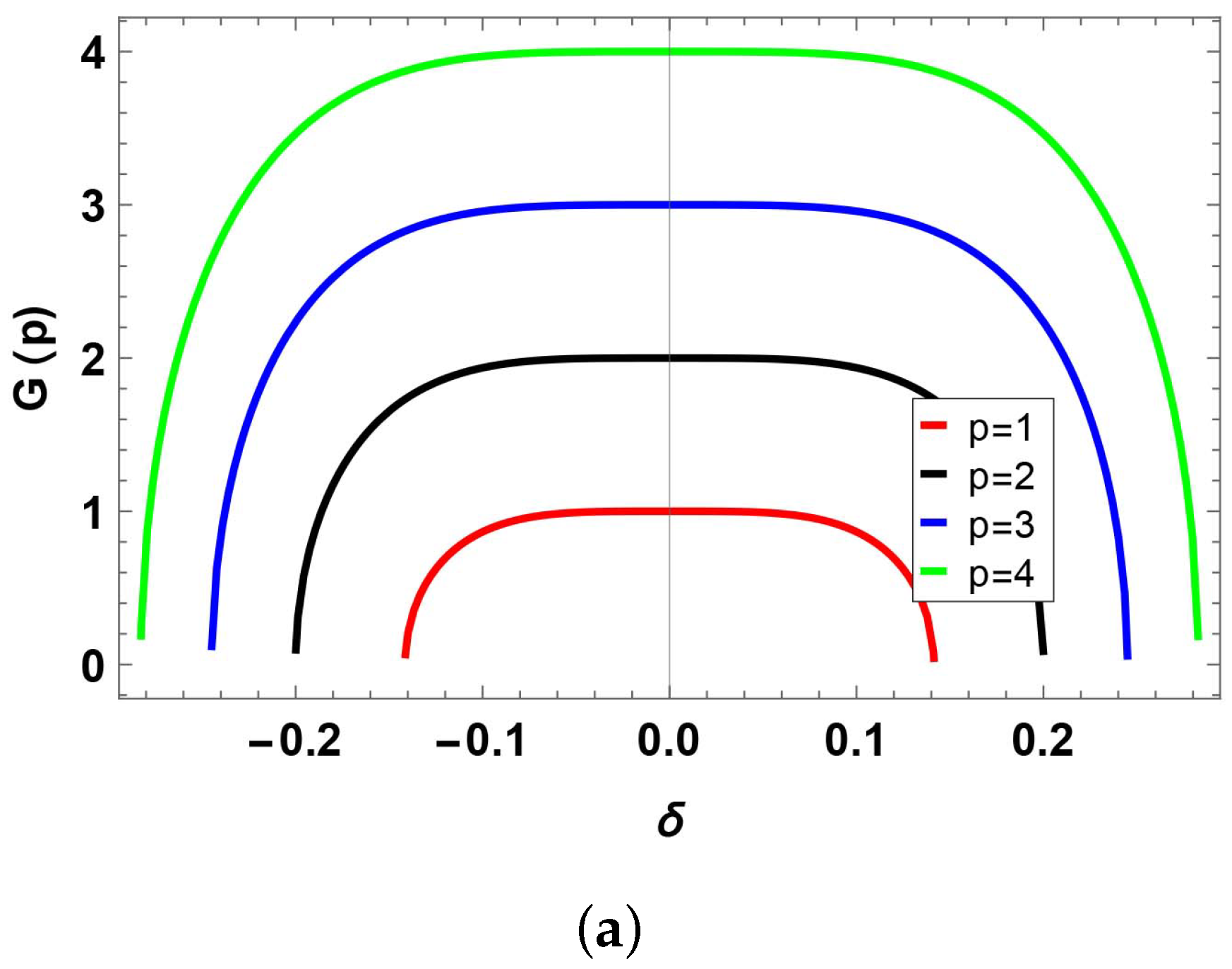
The stable steady state solutions are displayed by an attained dispersion relation. In the event that q is not real, the steadily increasing perturbation will make the solution unstable. If q is real, then small perturbations cause the steady state to transform into the stable state. The prerequisite for an unstable solution is;
δ 2 − θ 2 p 4 < 0 .
MI gain spectrum G ( p ) is obtained;
G ( p ) = 2 I m ( q ) = ± δ 2 − θ 2 p 4 .

9. Conclusion

We have successfully obtained new wave solutions for the non-linear compound KdVB equation along TMFD in this paper. We use the modified ( G ′ / G 2 ) -expansion methods and the EShGEE to obtain the kink, periodic, dark-bright, singular, and many other soliton solutions. Mathematica software is used to get and check the results. Using the Mathematica tool, the obtained results are displayed as contour, 2-dimensional, and 3-dimensional graphs. The outcomes aid in the development of a relevant equation. The solutions are also helpful in a variety of engineering and applied science fields. Ultimately, this study shows that the employed techniques are not only straightforward and easy to understand, but also effective in solving the unique non-linear partial fractional differential equations (NLPFDEs).
Moreover, a stability analysis and the MI of the governing model have been conducted to check the stability and precision of the achieved results. The methods utilised are not only straightforward but also exceptionally effective in solving non-linear partial differential equations (PDEs). Furthermore, these techniques prove to be valuable for addressing higher-order NLPDEs and larger systems of equations. The findings presented here offer substantial insights and potential applications across various scientific and engineering areas. The obtained solutions are beneficial in a variety of fields, including fluid dynamics, plasma physics, optical fibers, and telecommunications. At the end, it is concluded that the used techniques are reliable and provide the useful results. Now a days, exact solution, Since soliton-like solutions have emerged as a unique area of study in nonlinear science, they have gained significant attention. Because of the unique characteristics of soliton, soliton theory has become more significant. Following interaction and stability, the soliton retains its shape and velocity.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia [1234].

References

  1. Khan, Muhammad Ishfaq and Farooq, Aamir and Nisar, Kottakkaran Sooppy and Shah, Nehad Ali; Unveiling new exact solutions of the unstable nonlinear Schrödinger equation using the improved modified Sardar sub-equation method, Results in Physics, 59, 107593, (2024). [CrossRef]
  2. Qawaqneh, Haitham and Altalbe, Ali and Bekir, Ahmet and Tariq, Kalim U; Investigation of soliton solutions to the truncated M-fractional (3+ 1)-dimensional Gross-Pitaevskii equation with periodic potential, AIMS Mathematics, 9, 9, 23410–23433, (2024). [CrossRef]
  3. Tian, Guangyuan and Meng, Xianji; Exact Solutions to Fractional Schrödinger–Hirota Equation Using Auxiliary Equation Method, Axioms, 13, 10, 663, (2024). [CrossRef]
  4. Hussain, Akhtar and Ibrahim, Tarek F and Birkea, FM Osman and Alotaibi, Abeer M and Al-Sinan, Bushra R and Mukalazi, Herbert; Exact solutions for the Cahn–Hilliard equation in terms of Weierstrass-elliptic and Jacobi-elliptic functions, Scientific Reports, 14, 1, 13100, (2024). [CrossRef]
  5. Shehab, Mohammed F and El-Sheikh, Mohammed and Ahmed, Hamdy M and El-Gaber, AA and Mirzazadeh, M and Eslami, M; Extraction new solitons and other exact solutions for nonlinear stochastic concatenation model by modified extended direct algebraic method, Optical and Quantum Electronics, 56, 7, 1–34, (2024). [CrossRef]
  6. Qin, Chun-Yan and Zhang, Run-Fa and Li, Yao-Hong; Various exact solutions of the (4+ 1)-dimensional Boiti–Leon–Manna–Pempinelli-like equation by using bilinear neural network method, Chaos, Solitons & Fractals, 187, 115438, (2024). [CrossRef]
  7. Qawaqneh, Haitham and Alrashedi, Yasser; Mathematical and Physical Analysis of Fractional Estevez–Mansfield–Clarkson Equation, Fractal and Fractional, 8, 8, 467, (2024). [CrossRef]
  8. Zafar, Asim and Bekir, Ahmet and Raheel, M and Razzaq, Waseem; Optical soliton solutions to Biswas–Arshed model with truncated M-fractional derivative, Optik, 222, 165355, (2020). [CrossRef]
  9. Kumar, Dipankar and Manafian, Jalil and Hawlader, Faisal and Ranjbaran, Arash; New closed form soliton and other solutions of the Kundu–Eckhaus equation via the extended sinh-Gordon equation expansion method, Optik, 160, 159–167, (2018). [CrossRef]
  10. Bezgabadi, A Safaei and Bolorizadeh, MA; Analytic combined bright-dark, bright and dark solitons solutions of generalized nonlinear Schrödinger equation using extended sinh-Gordon equation expansion method, Results in Physics, 30, 104852, (2021). [CrossRef]
  11. Qawaqneh, Haitham and Jari, Hasan A and Altalbe, Ali and Bekir, Ahmet; Stability analysis, modulation instability, and the analytical wave solitons to the fractional Boussinesq-Burgers system, Physica Scripta, (2024). [CrossRef]
  12. Ali, Nawzad Hasan and Mohammed, Sizar Abid and Manafian, Jalil; New explicit soliton and other solutions of the Van der Waals model through the EShGEEM and the IEEM, J. Modern Tech. Eng, 8, 1, 5–18, (2023).
  13. Qawaqneh, Haitham and Zafar, Asim and Raheel, Muhammad and Zaagan, Abdullah A and Zahran, Emad HM and Cevikel, Adem and Bekir, Ahmet; New soliton solutions of M-fractional Westervelt model in ultrasound imaging via two analytical techniques, Optical and Quantum Electronics, 56, 5, 737, (2024). [CrossRef]
  14. Yanni Zhang, Liping Zhang, Jing Pang, Application of (G′/G2) Expansion Method for Solving Schrödinger’s Equation with Three-Order Dispersion, Advances in Applied Mathematics, 6, 2, 212-217, (2017). [CrossRef]
  15. Nadia Mahak, Ghazala Akram; Exact solitary wave solutions of the (1+1)-dimensional Fokas-Lenells equation, Optik. 2020. [CrossRef]
  16. Aljahdaly, Noufe H; Some applications of the modified (G′/G2)-expansion method in mathematical physics, Results in Physics, 13, 102272, (2019). [CrossRef]
  17. Behera, S and Aljahdaly, NH and Virdi, JPS; On the modified (G′/G2)-expansion method for finding some analytical solutions of the traveling waves, Journal of Ocean Engineering and Science, 7, 4, 313–320, (2022). [CrossRef]
  18. Saboor, Abdul and Shakeel, Muhammad and Liu, Xinge and Zafar, Asim and Ashraf, Muhammad; A comparative study of two fractional nonlinear optical model via modified (G′/G2)-expansion method, Optical and Quantum Electronics, 56, 2, 259, (2024). [CrossRef]
  19. Tukur Abdulkadir Sulaiman, Gulnur Yel and Hasan Bulut; M-fractional solitons and periodic wave solutions to the Hirota-Maccari system, Modern Physics Letters B, 1950052, (2019). [CrossRef]
  20. J. Vanterler D A C. Sousa, and E. Capelas D E Oliveira; A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties, International Journal of Analysis and Applications, 16, 1, 83-96, (2018). [CrossRef]
  21. Alam, Md Nur and Belgacem, Fethi Bin Muhammad; Exact Traveling Wave Solutions for the (1+ 1)-Dimensional Compound KdVB Equation via the Novel (G′/G)-Expansion Method, International Journal of Modern Nonlinear Theory and Application, 5, 1, 28–39, (2016). [CrossRef]
  22. Zayed, EME; The (G′/G)-Expansion Method Combined with the Riccati Equation for Finding Exact Solutions of Nonlinear PDEs, Journal of applied mathematics & informatics, 29, 1_2, 351–367, (2011). [CrossRef]
  23. Alam, Md Nur and Akbar, M Ali and Hoque, M Fazlul; Exact travelling wave solutions of the (3+ 1)-dimensional mKdV-ZK equation and the (1+ 1)-dimensional compound KdVB equation using the new approach of generalized (G′/G)-expansion method, Pramana, 83, 317–329, (2014). [CrossRef]
  24. El Morsy, SA and El-Azab, MS and El-Kalla, IL; Nonlinear Reaction-Diffusion Equation and Kdvb Equation, Electronic Journal of Mathematical Analysis and Applications, 3, 1, 97–110, (2015).
  25. Miah, M Mamun and Seadawy, Aly R and Ali, HM Shahadat and Akbar, M Ali; Abundant closed form wave solutions to some nonlinear evolution equations in mathematical physics, Journal of Ocean Engineering and Science, 5, 3, 269–278, (2020). [CrossRef]
  26. X. L. Yang, J. S. Tang; Travelling wave solutions for Konopelchenko-Dubrovsky equation using an extended sinh-Gordon equation expansion method, Communications in Theoretical Physics,(2008), 50, 10471051. [CrossRef]
  27. Tariq, Kalim U and Wazwaz, Abdul-Majid and Javed, Rizwan; Construction of different wave structures, stability analysis and modulation instability of the coupled nonlinear Drinfel’d–Sokolov–Wilson model, Chaos, Solitons & Fractals, 166, 112903, (2023). [CrossRef]
  28. Zulfiqar, Hina and Aashiq, Aqsa and Tariq, Kalim U and Ahmad, Hijaz and Almohsen, Bandar and Aslam, Muhammad and Rehman, Hamood Ur; On the solitonic wave structures and stability analysis of the stochastic nonlinear Schrödinger equation with the impact of multiplicative noise, Optik, 289, 171250, (2023). [CrossRef]
  29. ur Rehman, Shafqat and Ahmad, Jamshad; Modulation instability analysis and optical solitons in birefringent fibers to RKL equation without four wave mixing, Alexandria Engineering Journal, 60, 1, 1339–1354, (2021). [CrossRef]
Preprints 140275 g001
Figure 1. Graph of h ( x , t ) is given in Eq.(17).
Figure 1. Graph of h ( x , t ) is given in Eq.(17).
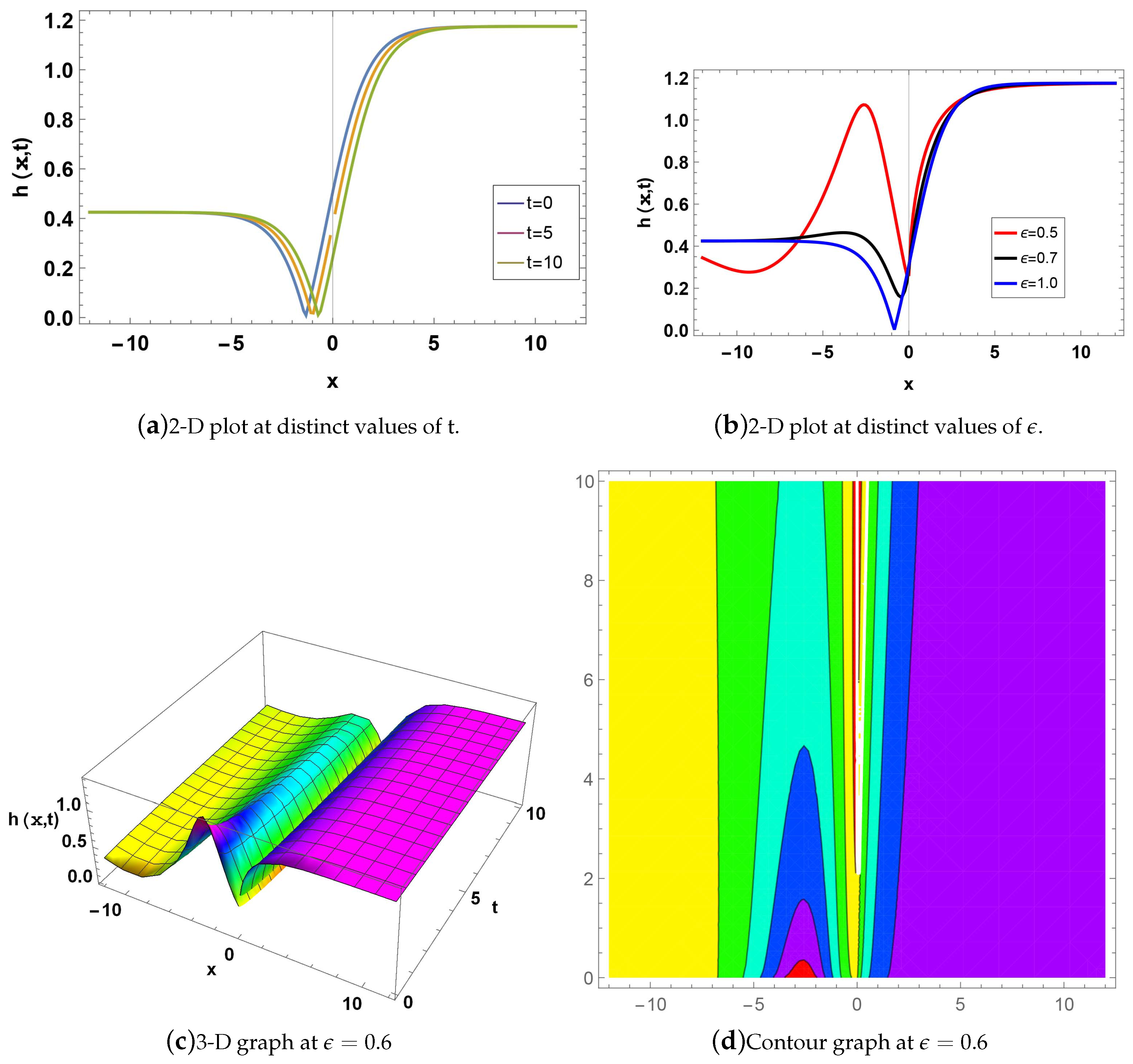
Preprints 140275 g001
Preprints 140275 g002
Figure 2. Graph of h ( x , t ) is given in Eq.(18).
Figure 2. Graph of h ( x , t ) is given in Eq.(18).
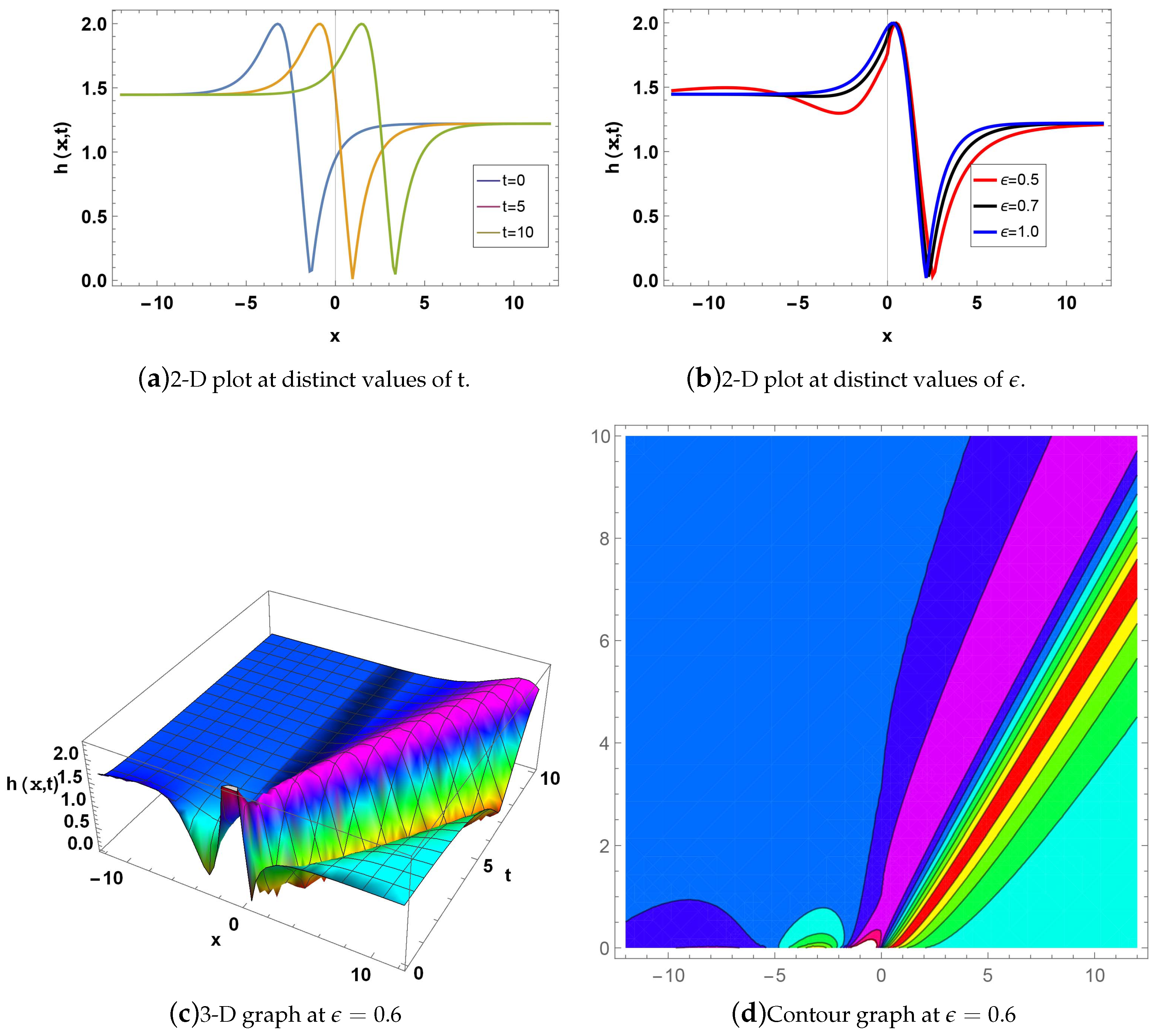
Preprints 140275 g002
Preprints 140275 g003
Figure 3. Graph of h ( x , t ) is given in Eq.(47).
Figure 3. Graph of h ( x , t ) is given in Eq.(47).
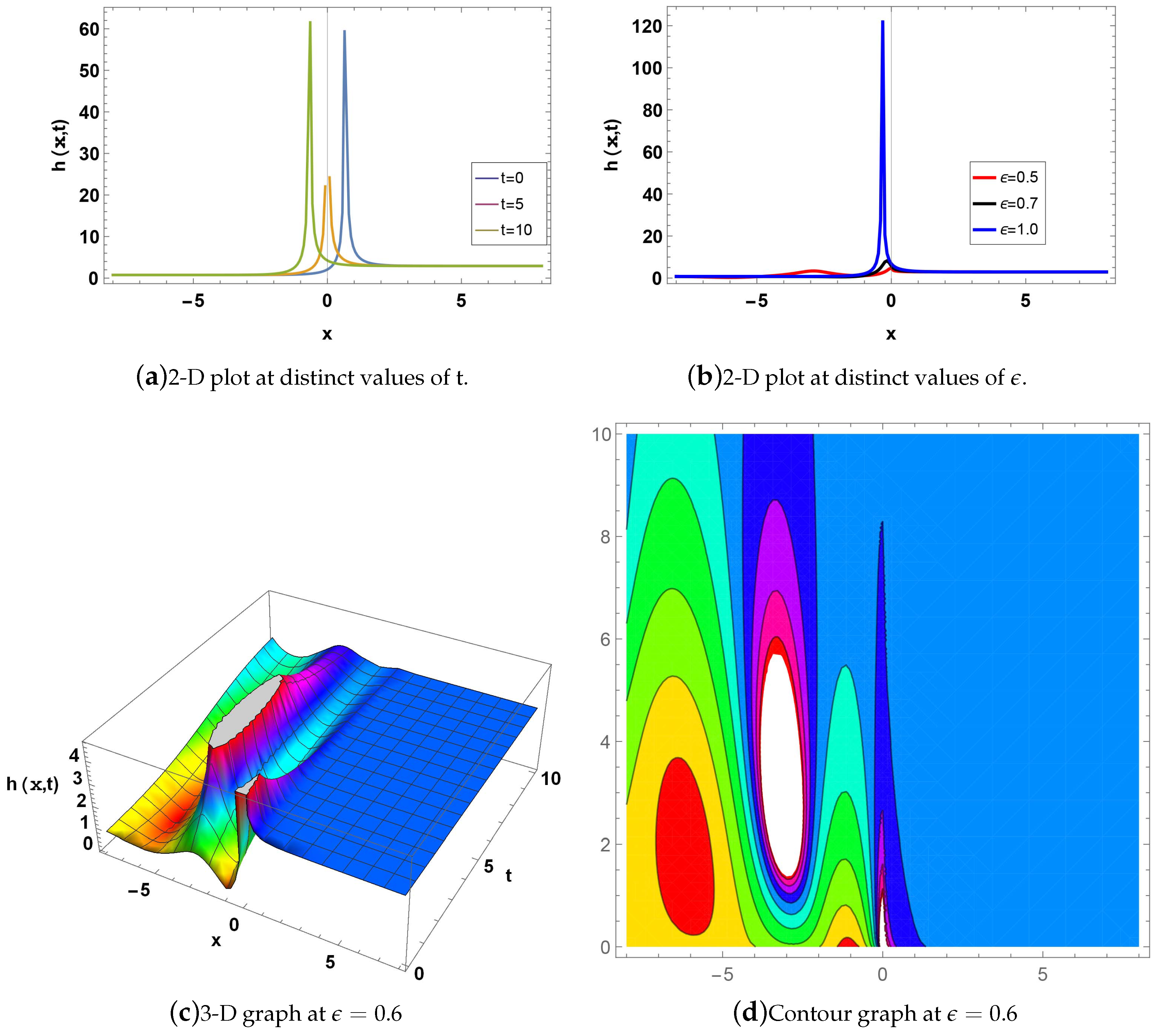
Preprints 140275 g003
Preprints 140275 g004
Figure 4. Graph of h ( x , t ) is given in Eq.(48).
Figure 4. Graph of h ( x , t ) is given in Eq.(48).
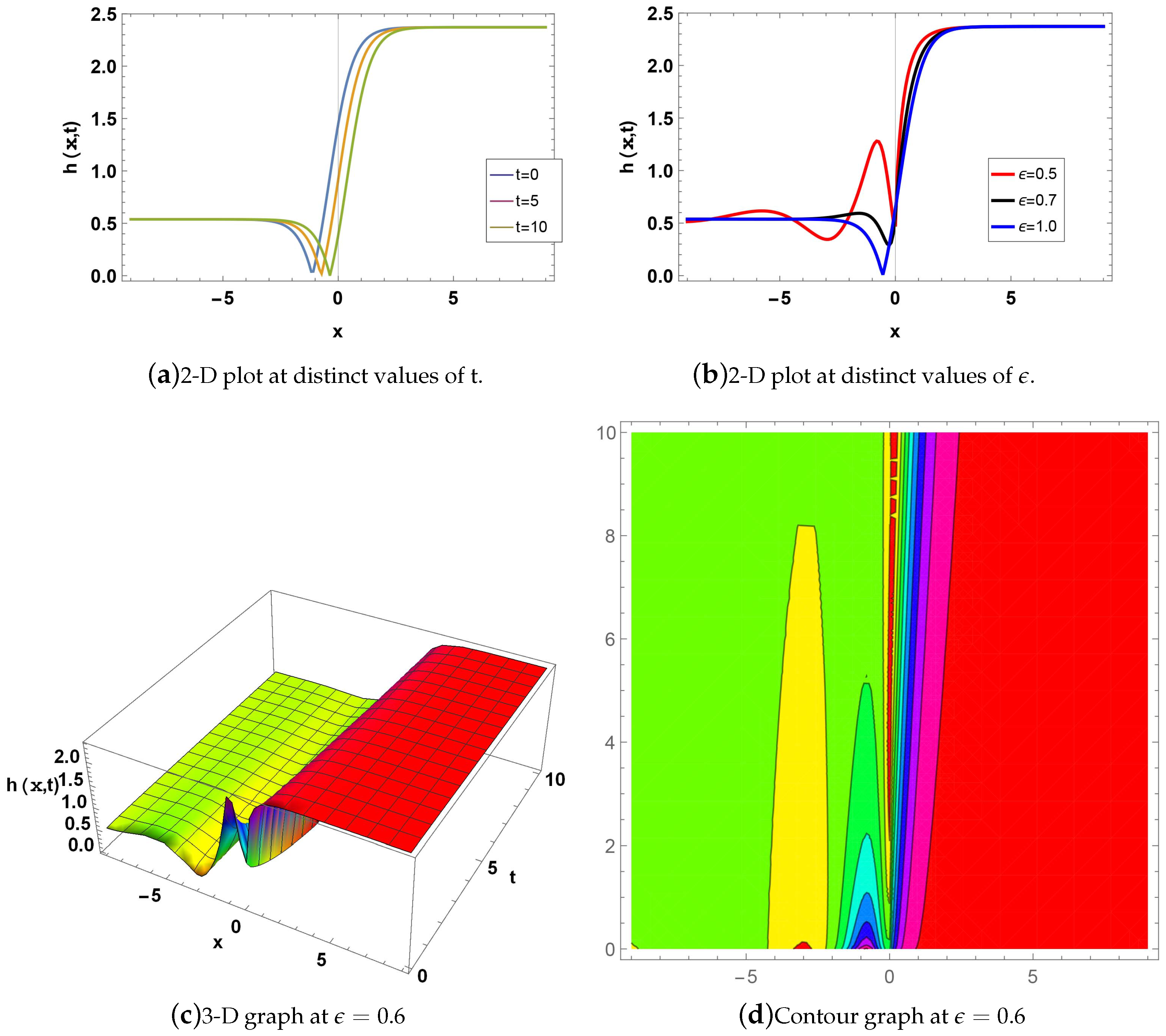
Preprints 140275 g004
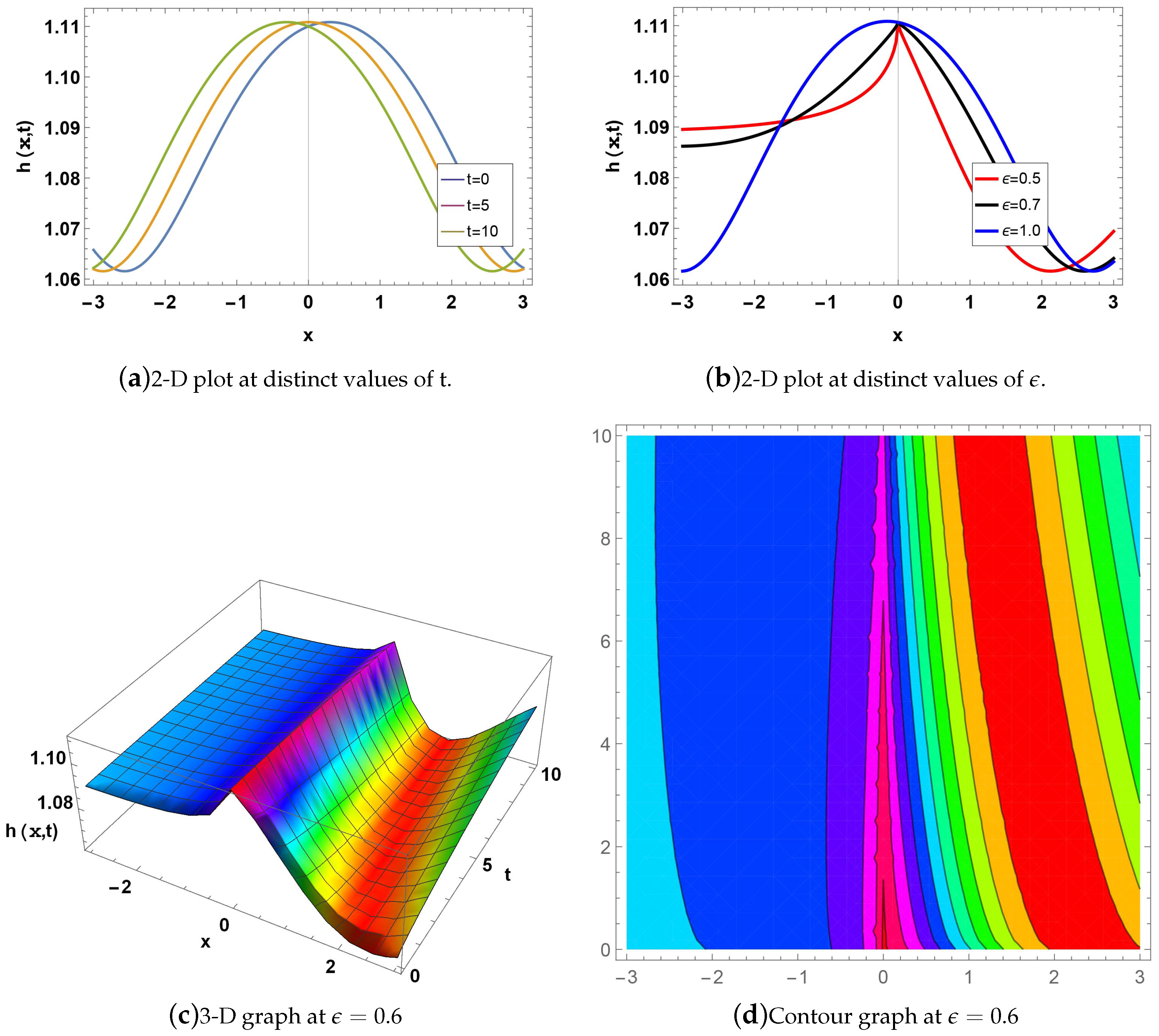
Preprints 140275 g005
Figure 5. Graph of h ( x , t ) is given in Eq.(68).
Figure 5. Graph of h ( x , t ) is given in Eq.(68).
Preprints 140275 g005
Preprints 140275 g006
Figure 6. Graph for h ( x , t ) is given in Eq.(69).
Figure 6. Graph for h ( x , t ) is given in Eq.(69).
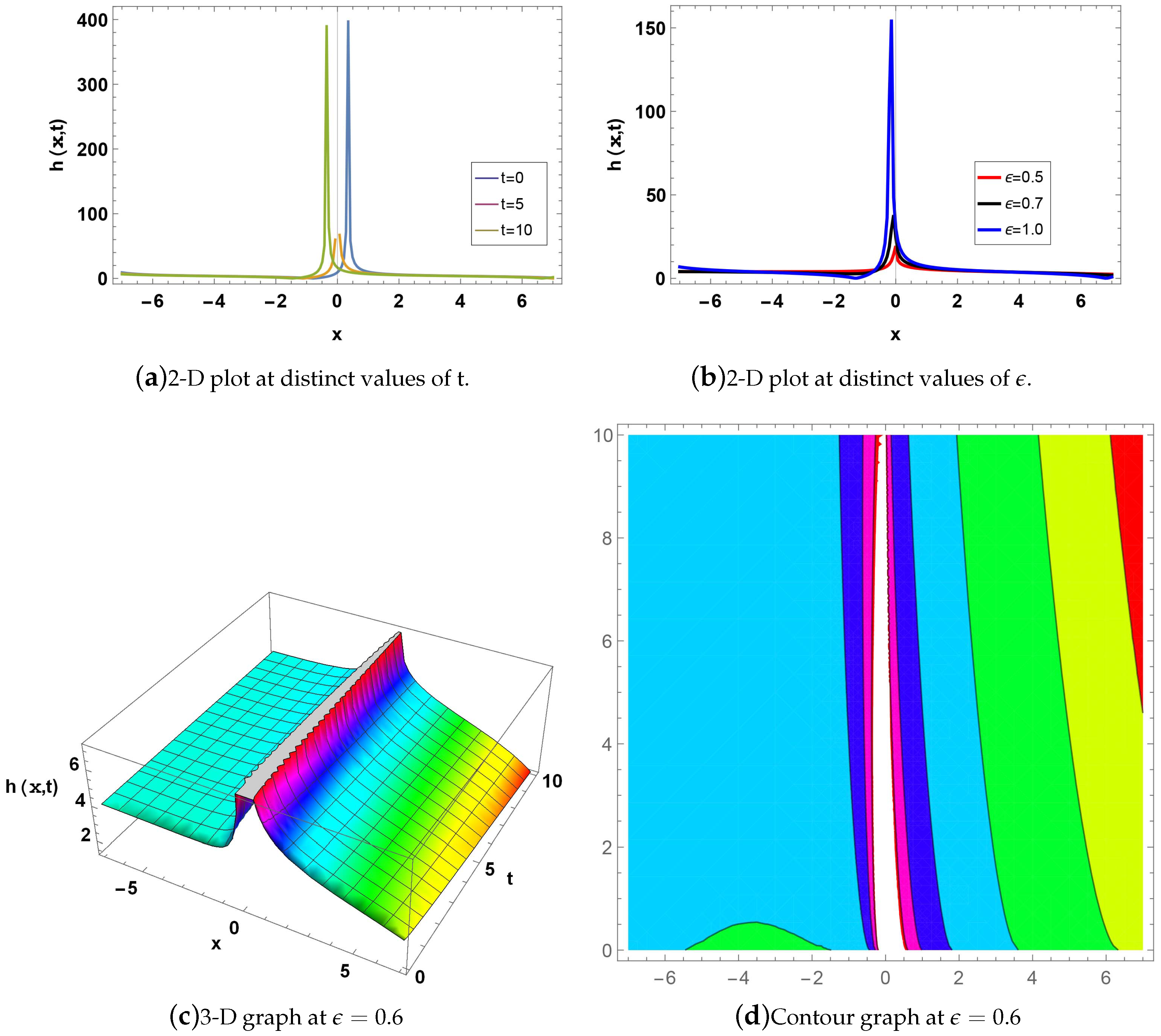
Preprints 140275 g006
Preprints 140275 g007
Figure 7. MI gain spectrum for distinct values of p.
Figure 7. MI gain spectrum for distinct values of p.
Preprints 140275 g007
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated