Submitted:
27 November 2024
Posted:
28 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
-
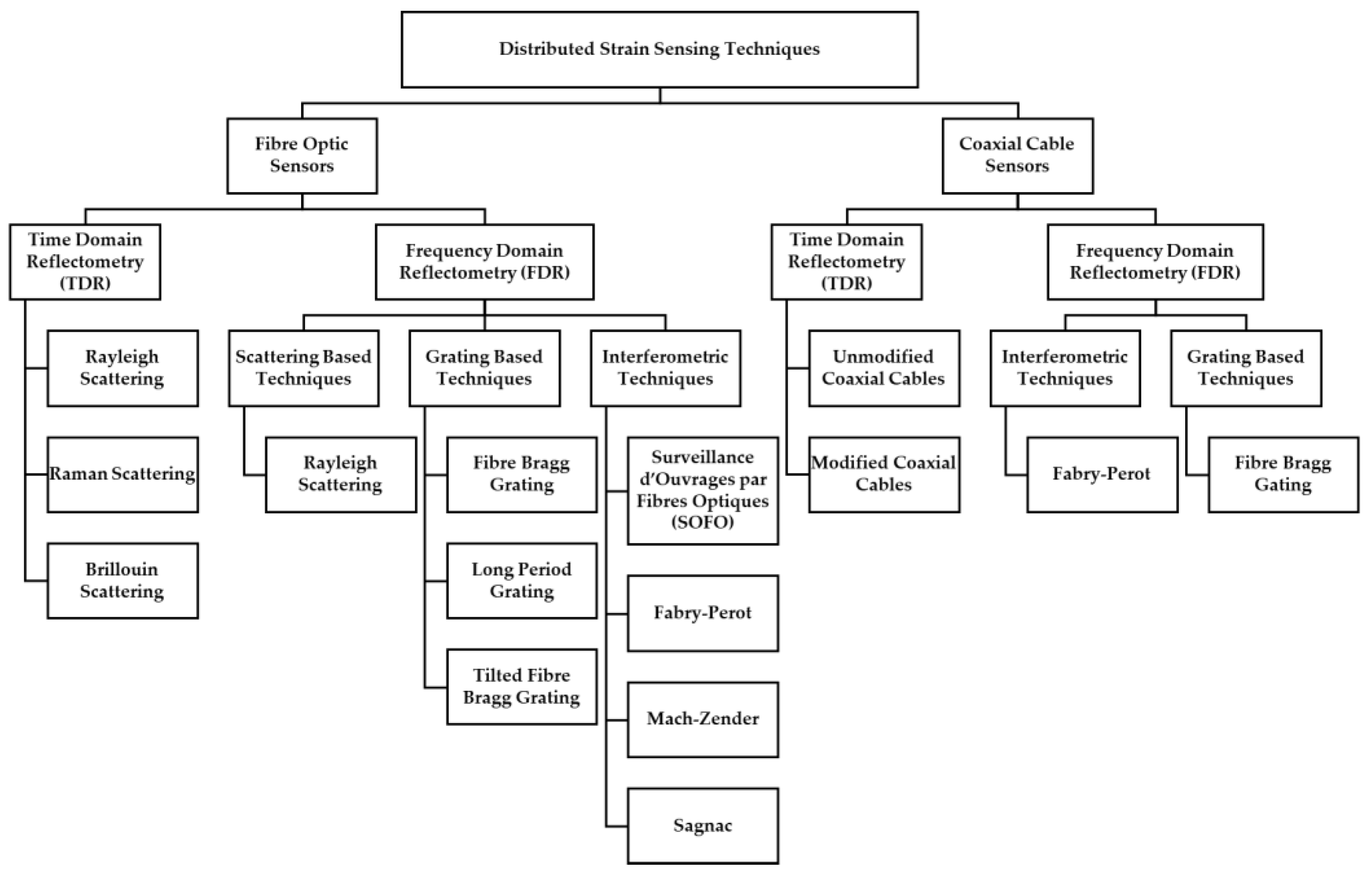
Section 2. Background on fibre optic distributed sensing
- ○
- Section 2.1. Time domain reflectometry in fibre optic sensing
- ○
- Section 2.2 Frequency domain reflectometry in fibre optic sensing
-
Section 3. Coaxial cable distributed strain sensing
- ○
- Section 3.1 Time domain reflectometry in coaxial cable distributed strain sensing
- ○
- Section 3.2 Frequency domain reflectometry in coaxial cable distributed sensing
- Section 4. Future research challenges in frequency domain coaxial cable strain sensing
2. Background on Fibre Optic Distributed Sensing
2.1. Time Domain Reflectometry in Fibre Optic Sensing
- Rayleigh scattering describes the elastic scattering of light by inhomogeneities much smaller than the wavelength of the incident light [20,21]. Under normal conditions in a fiber optic, as light interacts with the fiber, scattered light remains at an angle that supports forwards propagation. On interaction with a discontinuity, some of the light will be scattered at an angle which does not support forwards propagation, or scattered backwards, towards the light source, which is the principle behind Optical Time Domain Reflectometry (OTDR). Rayleigh scattering is used to analyze attenuation associated with breaks, splices, connectors and general health of a fiber [2,22]. Other applications explored include measuring landslide activity [23] and detecting cracks in concrete structures [24]. This technique offers the highest spatial resolution of the three scattering methods [18], but is highly sensitive to vibrations [25], so also finds application in acoustic sensing.. The sensing range of Rayleigh scattering is limited to around 70m.
- Raman scattering is nonlinear and arises from the interaction between light and the vibrational and rotational transitions of the atoms within the fiber material structure. Depending on the exact transitions, the scattered light will shift in frequency to two discrete bands; anti-Stokes transmission describes the shift to higher frequency and Stokes transmission describes the shift to lower frequency. The ratio of the magnitude of these peaks provides data on the temperature of the fiber [2]. This technique provides temperature information independent of strain, but does have a poor signal-to-noise-ratio [26].
- Brillouin scattering is nonlinear and is associated with electrostriction which couples electromagnetic waves with material structure-scale waves, phonons. Incident electromagnetic energy interacts with the optical fiber material to create backscattered electromagnetic energy of lower frequency, and a phonon of low frequency vibrational energy. The thermal energy within the fiber will influence the Brillouin scattering [20,21]. This technique is used for temperature sensing and also strain sensing (if a separate temperature measurement independent of strain can be taken, enabling strain to be inferred). One notable advantage, in the context of this paper, is the development of Brillouin optical time domain reflectometry (BOTDR) through which monitoring could be achieved from one end of the fiber. Single-ended sensing is an attractive practical advantage when considering the deployment of distributed sensors in engineering structures [8]. This has led to Brillouin scattering being the most common technique used in civil applications of structural health monitoring [27]. This method enables a long measurement range (kilometers (kms)) but with limitations on spatial resolution to around 1m [18].
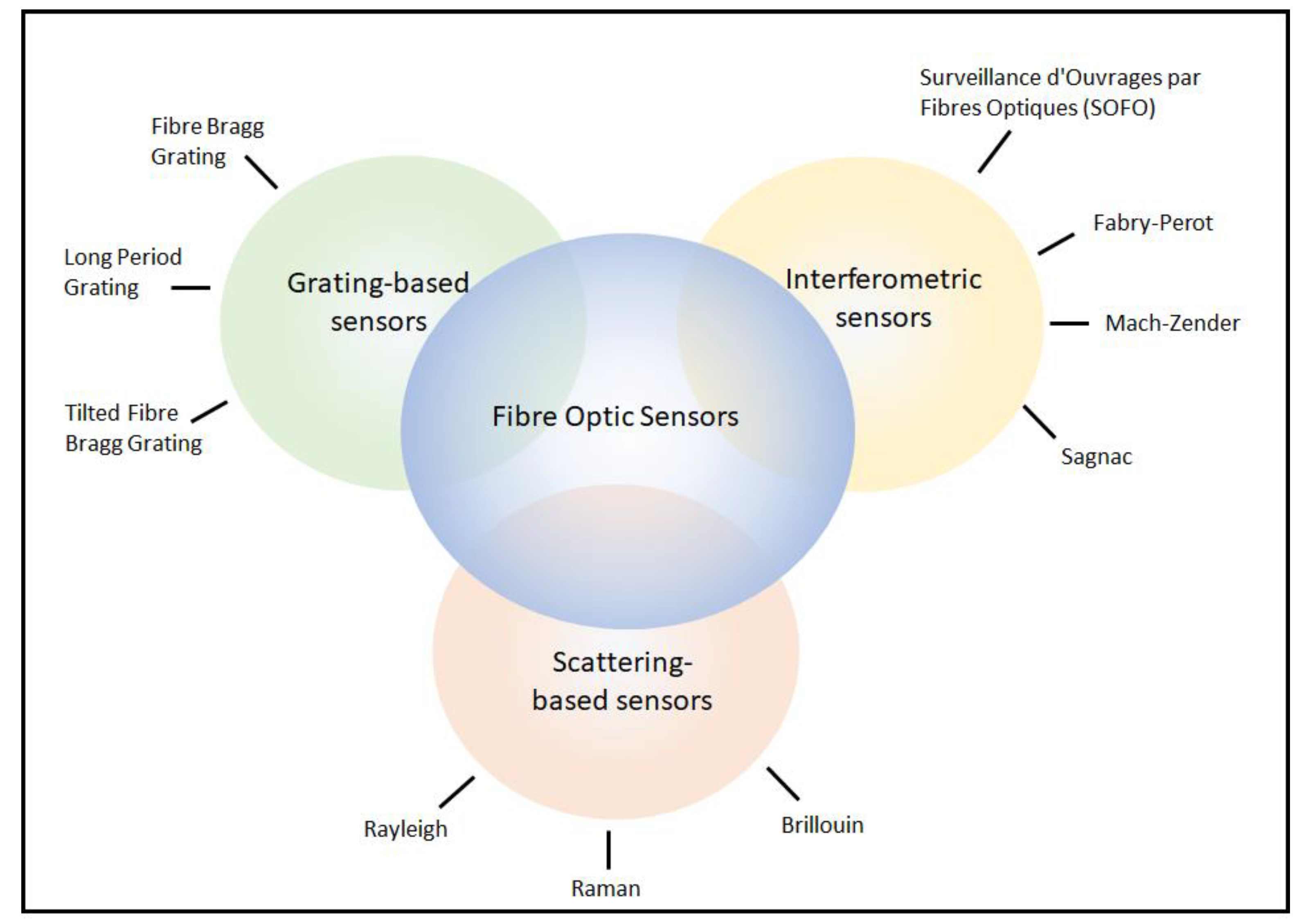
2.2. Frequency Domain Reflectometry in Fibre Optic Sensing
2.2.1. Scattering-Based Sensors
2.2.2. Grating Based Sensors
2.2.3. Interferometric Sensors
-
There are several references quoting strain limits of optical fibers:
- The fragility of the fiber optics makes installation difficult and great care must be taken not to damage the sensor itself. Bending stresses should be avoided during installation as this can impact on the weakly scattered signals necessary for monitoring [8].
- The expense of fiber-optic systems can limit their use to applications only where reliability is critical [2,40]. A more cost-effective solution could see SHM techniques applied where reliability or safety is less critical but nonetheless would benefit from the economic advantages in targeted O&M activities, or optimization of system operating parameters.
3. Coaxial Cable Distributed Strain Sensing
3.1. Coaxial Cable Time Domain Reflectometry
3.1.1. TDR Using Unmodified Coaxial Cables
3.1.2. TDR Using Modified Coaxial Cables
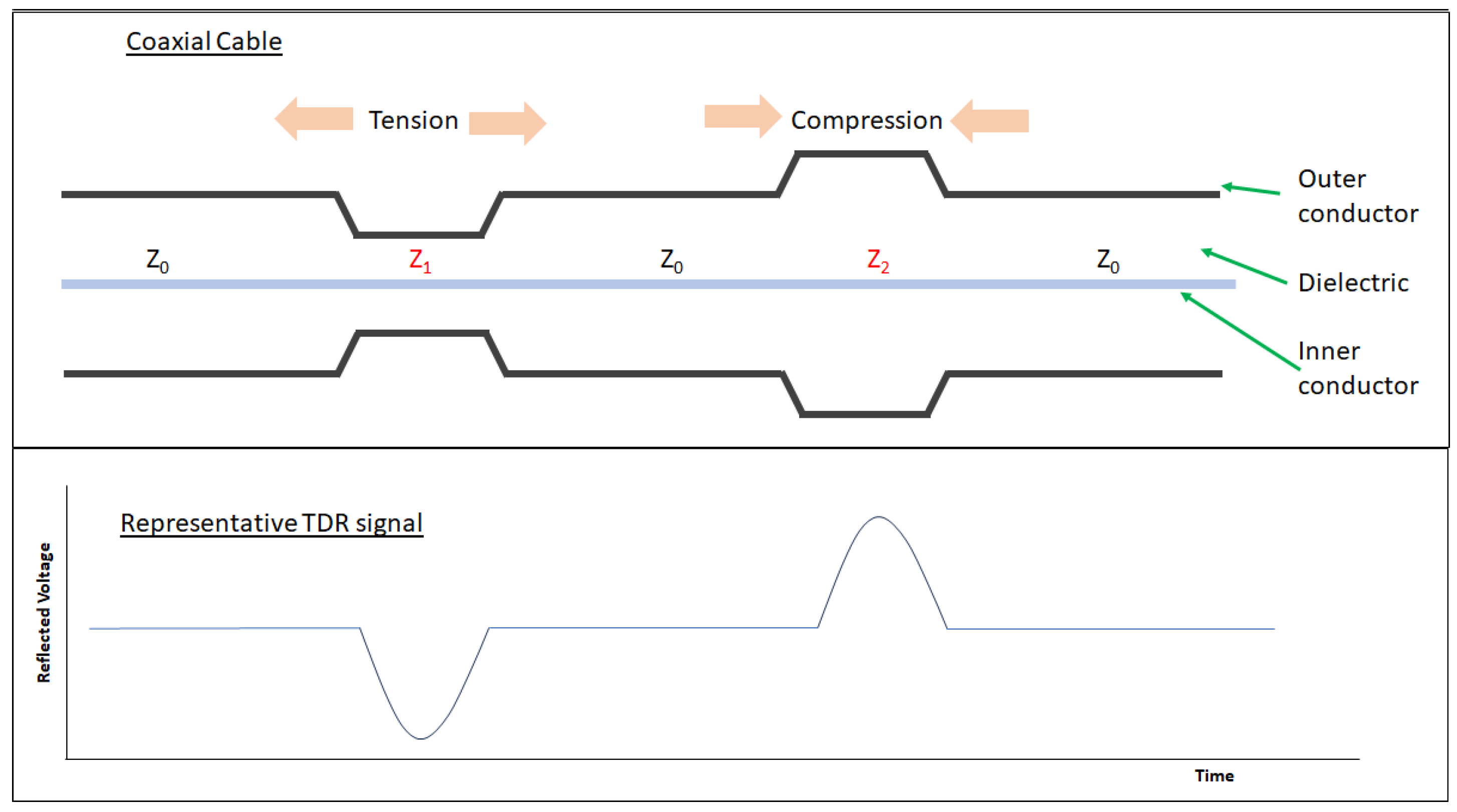
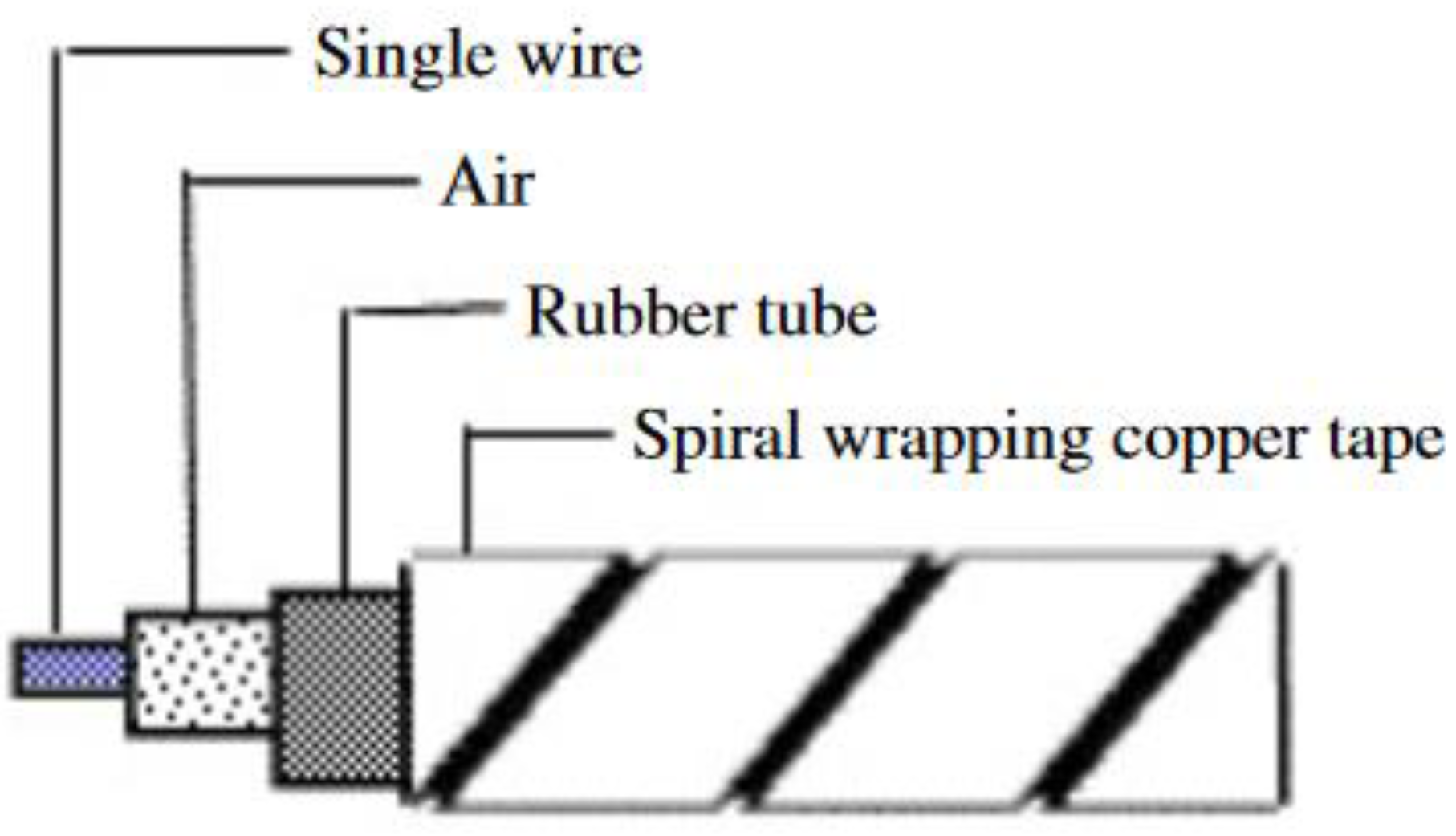
- Lack of sensitivity using coaxial cable for strain sensing remains a challenge using TDR [40,50,59]. As described earlier in the paper, reviewing progress of unmodified coaxial cable, Lin et al [41] explored the use of a more compliant rubber as the dielectric in a coaxial cable structure by way of increasing the sensitivity to strain. The sensitivity of a prototype rubber-based dielectric cable was shown, through experiment, to be approximately five to ten times that of standard RG-174 coaxial cable. This approach still relies on a geometric change with strain whereas a change in topology of the outer coaxial cable conductor with strain could inherently offer increased sensitivity.
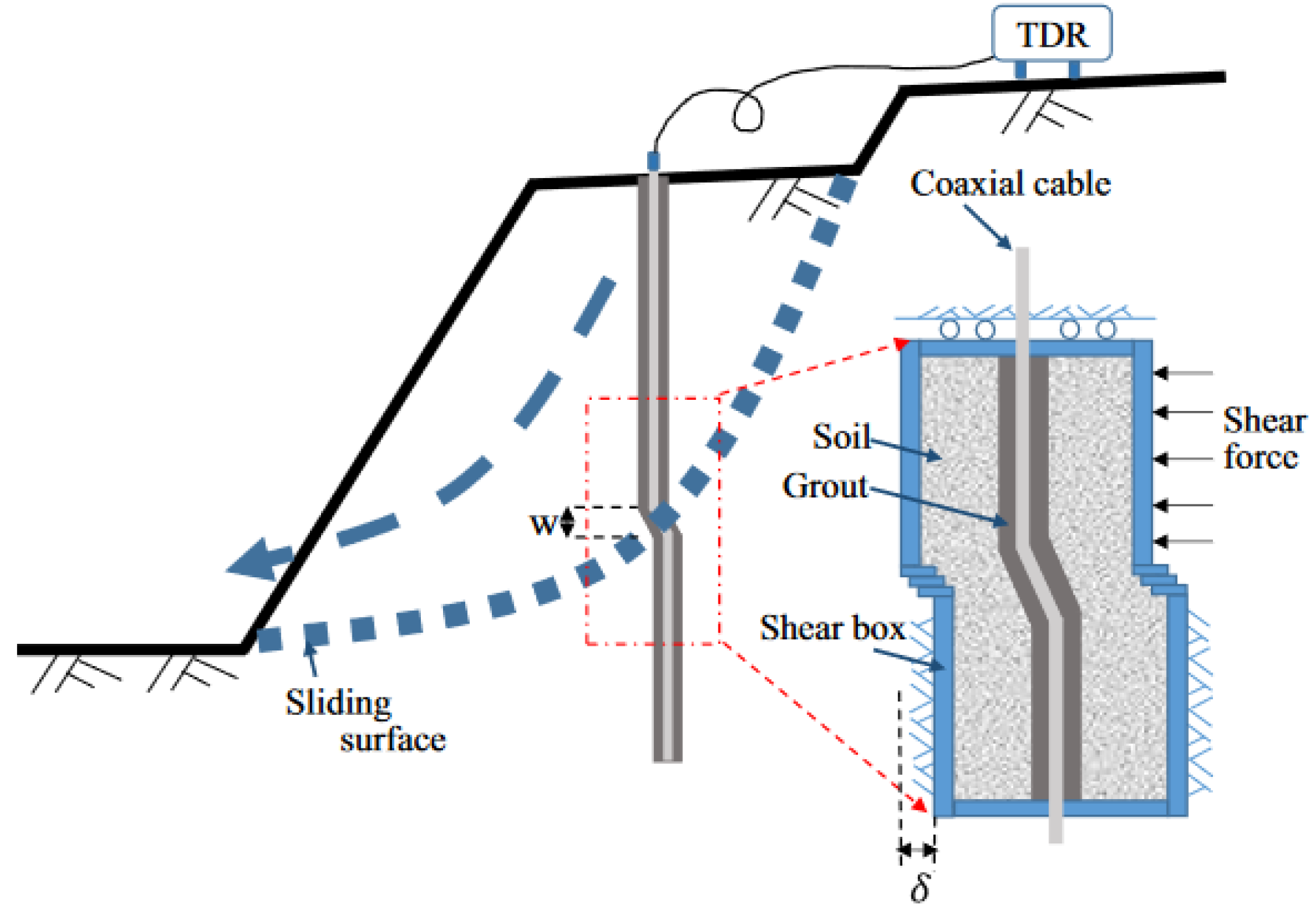
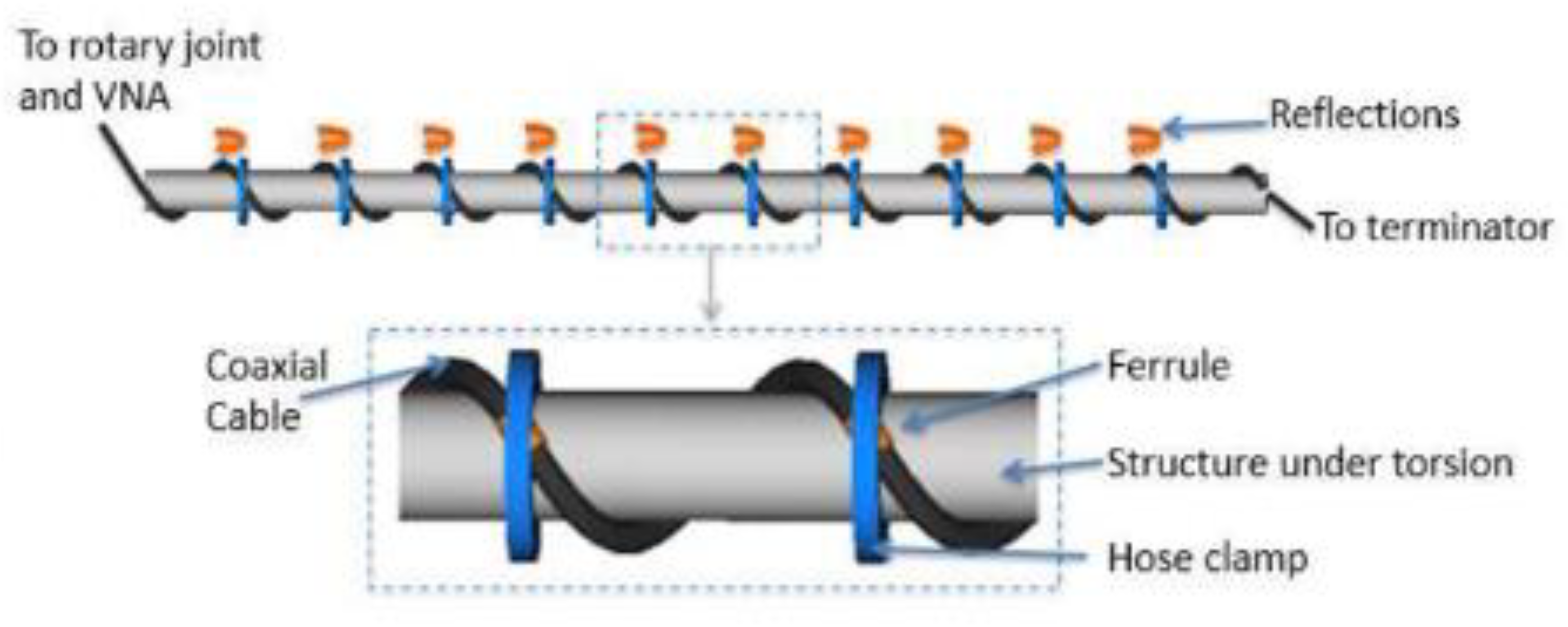
- Several published reports describe the use of helical wound outer conductors as a technique to induce a change in outer conductor topology with strain [7,38,40,64,65]. A lot of this work focused on crack detection in reinforced concrete beams. In 2004 Chen et al tested a prototype coaxial cable sensor constructed with helically wound adhesive copper tape forming the outer conductor (Figure 8) [7].
3.2. Coaxial Cable Frequency Domain Reflectometry
3.2.1. Interferometric Coaxial Cable Frequency Domain Reflectometry
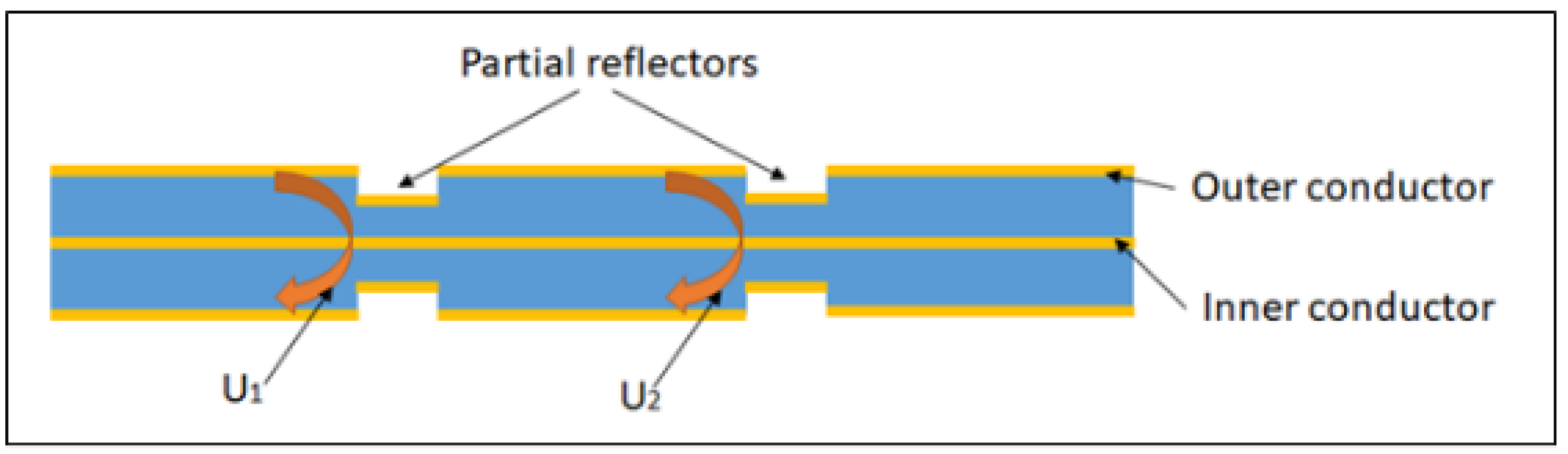
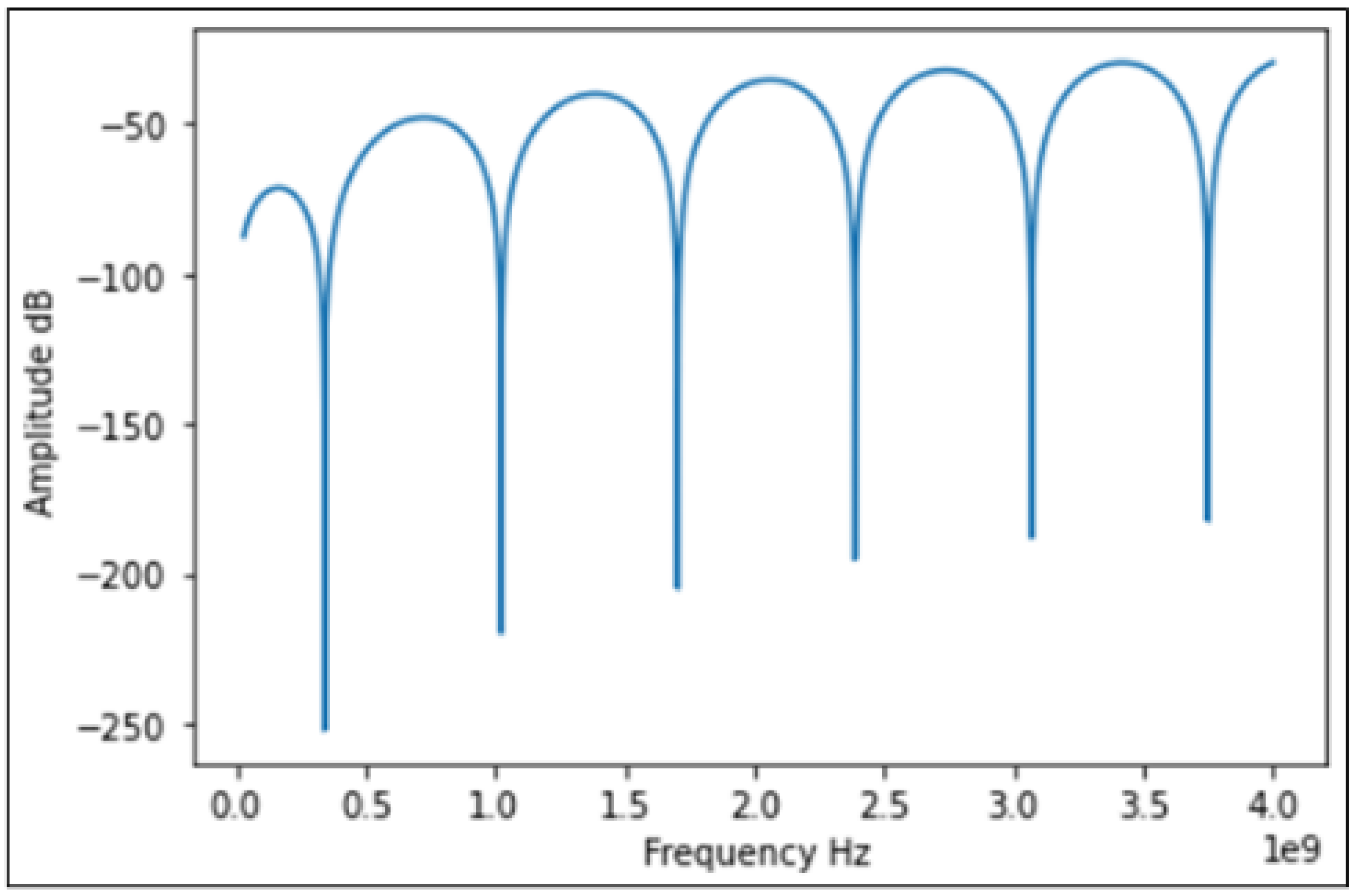
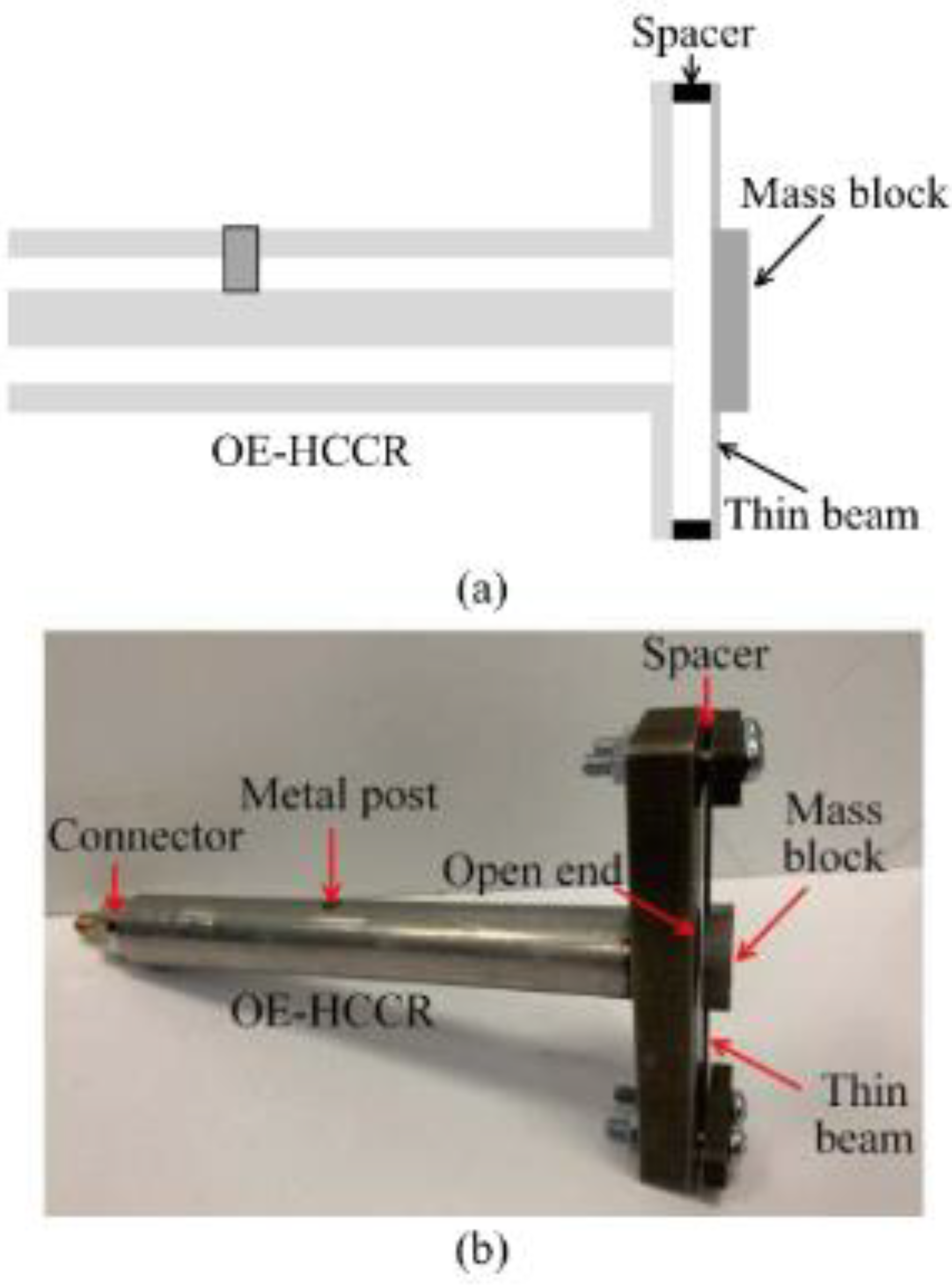
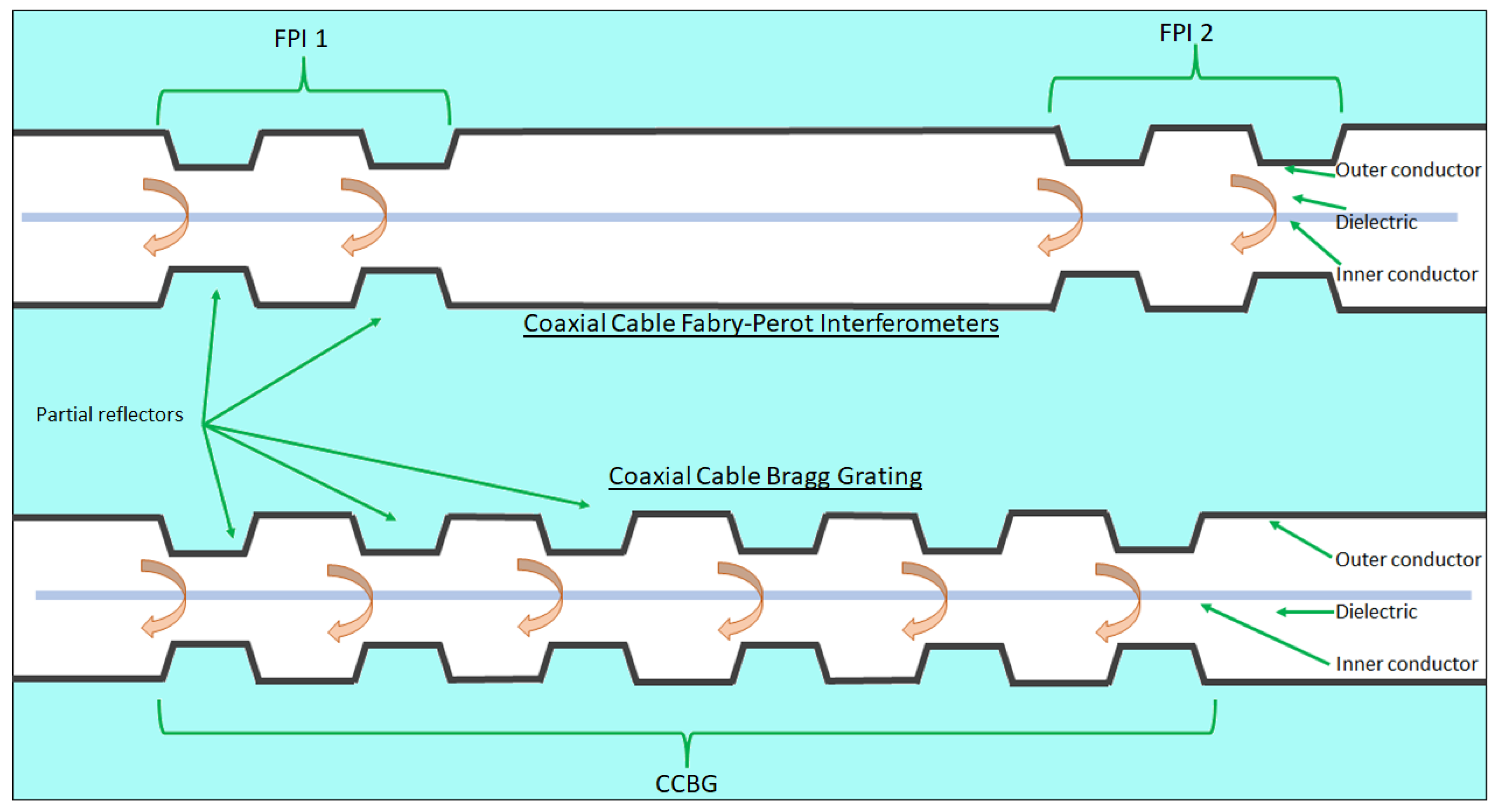
- On creating a pair of highly reflective reflectors in a coaxial structure a Fabry-Perot resonator (CCFPR) is constructed. Whilst only a single measurement can be made from this device, multiplexing is not possible as insufficient energy passes the reflectors, the multiple round trips of the energy within the cavity increase the Q-factor of the device, increasing the measurement resolution. The second reflector forming the resonant cavity can be placed beyond the open end of the coaxial structure, thereby forming ‘open-ended coaxial probes’ which are widely available for measuring material properties in the microwave range of the electromagnetic spectrum [82,83,84,85,86,87,88,89]. By adapting this arrangement, it was shown that the second reflector in the CCFPR could be formed by a metal plate positioned beyond the end of the coaxial structure. The lateral position of the plate could be measured to resolutions of the order of 1nm, comparable with the resolutions of analogous fiber optic techniques [90,91]. A diagram of this open-ended hollow coaxial cable resonator (OE-HCCR) is shown in Figure 22.
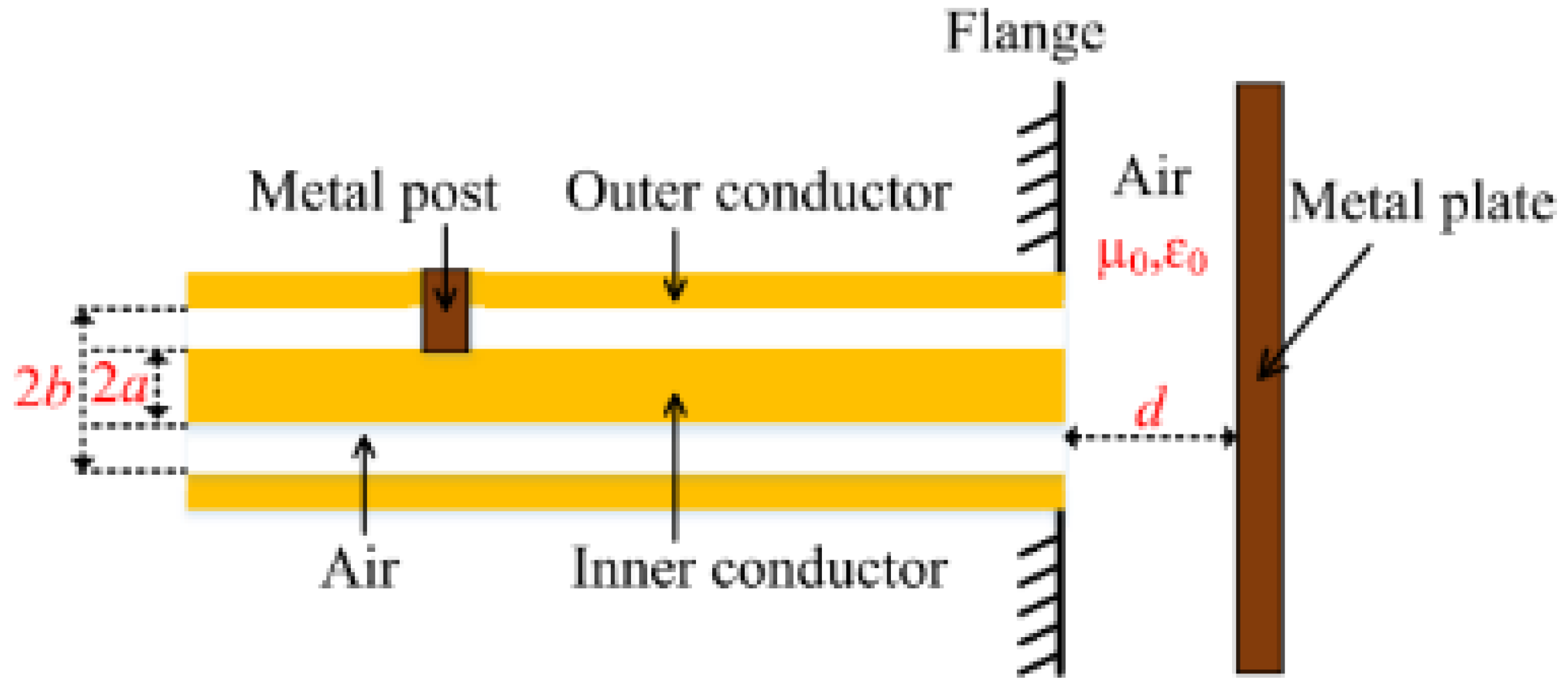
- A displacement sensor based on a hollow coaxial cable Fabry-Perot resonator (HCC-FPR) was developed and tested in 2018 [95]. A solid stainless steel inner conductor (6mm diameter) and a tubular stainless steel outer conductor (14mm diameter) form the basis of an air-dielectric coaxial structure. A single pair of highly reflective partial reflectors exist, one on a moveable handgrip, forming a resonant cavity. When the handgrip is moved, the reflector moves, changing the length of the resonant cavity and causing a shift in frequency. The device, shown in Figure 24, could measure displacement to a resolution of 10µm.
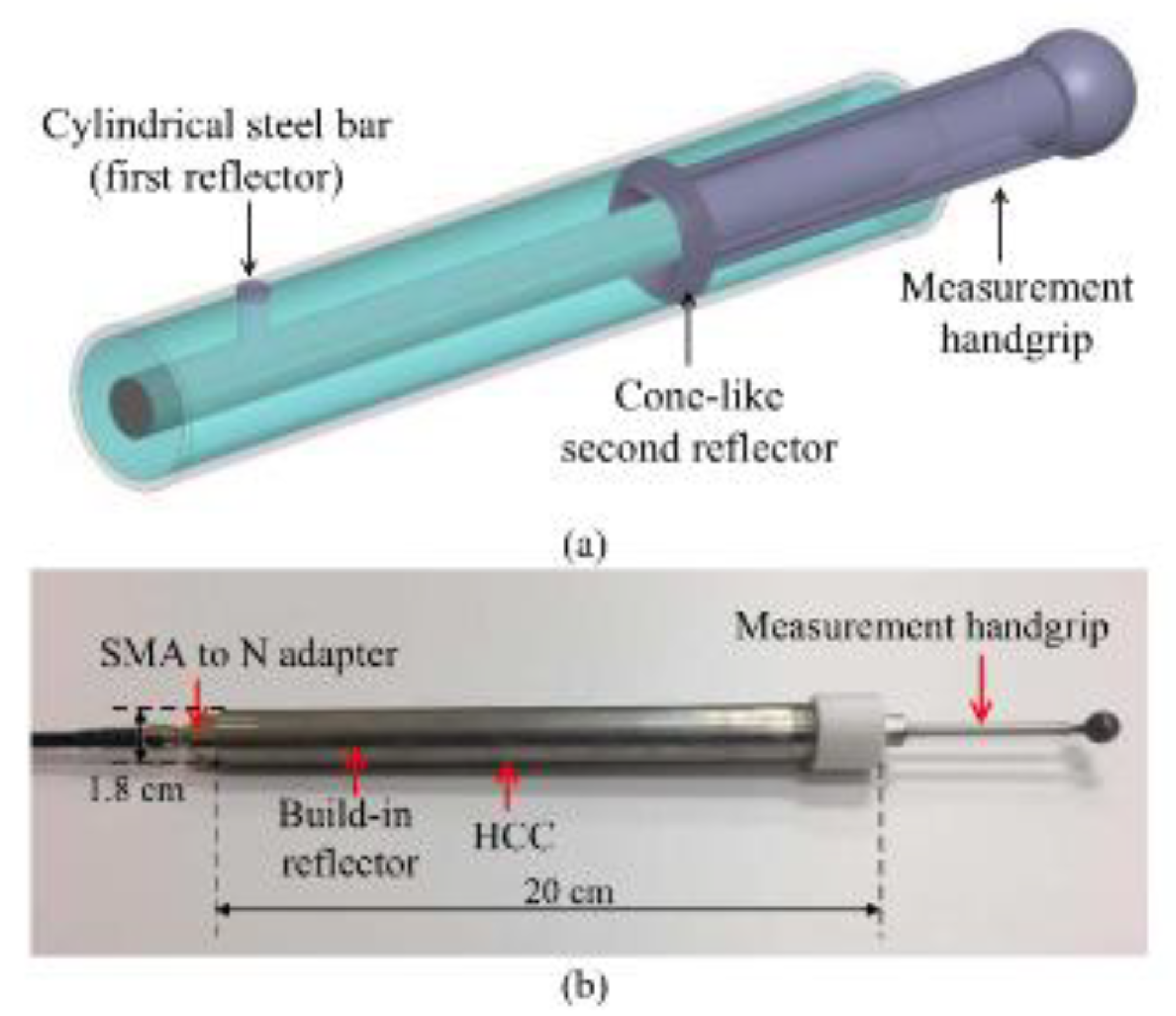
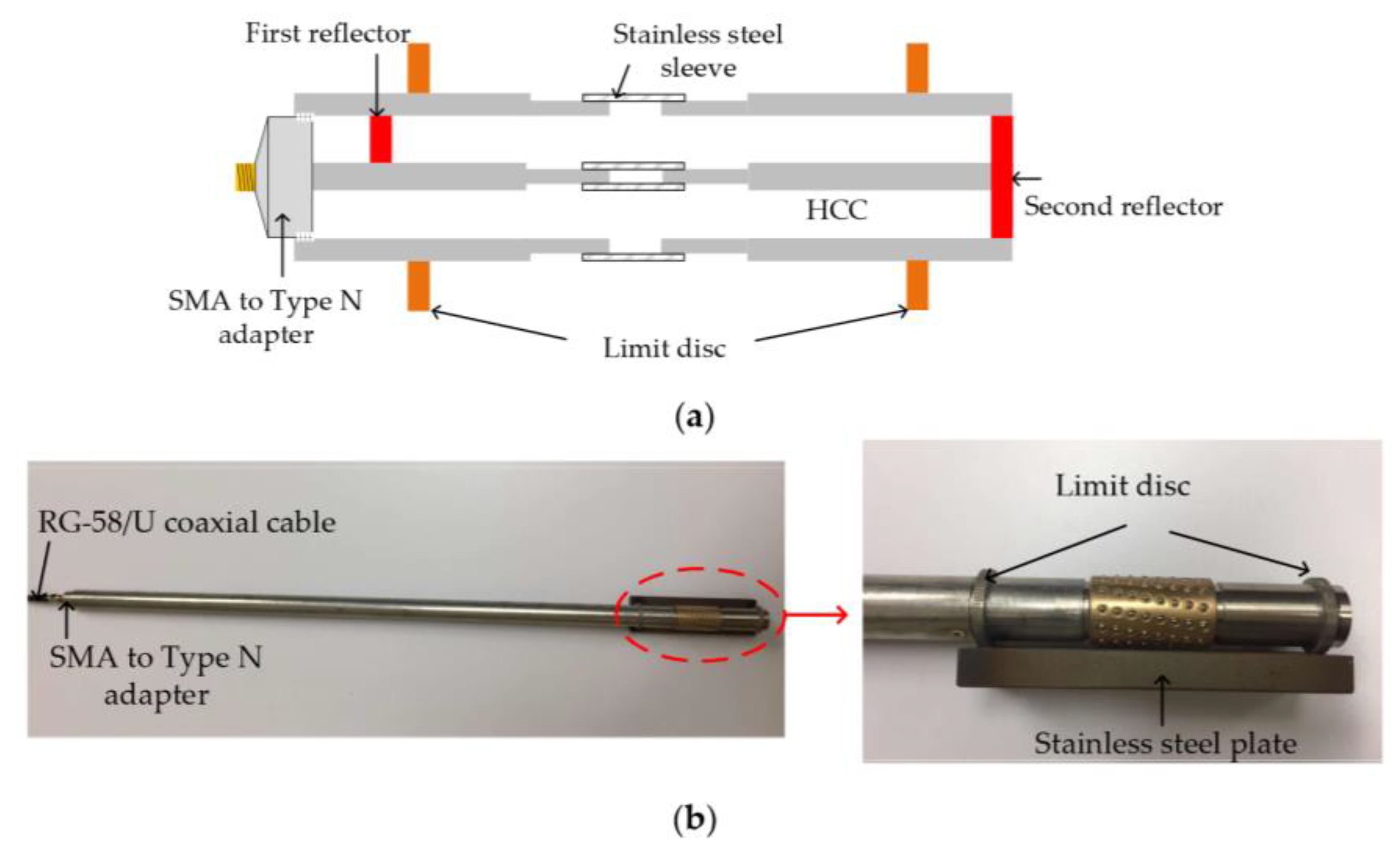
- Further developments on the HCC-FPR proved the principle of this device as a strain sensor for high temperature environments, up to 1000oC. The movable hand grip was replaced with a weld points (limit discs) to attach the device to a test steel plate. Now as the steel plate expands with temperature the cavity length of the FPR changes, shifting the resonant frequency, from which strain can be deduced. The nested arrangement of the coaxial structure is intended to remove effects of thermal expansion of the sensor itself [96]. The principle of the operation of this device is illustrated in Figure 25 along with photographs of the tested sensor.
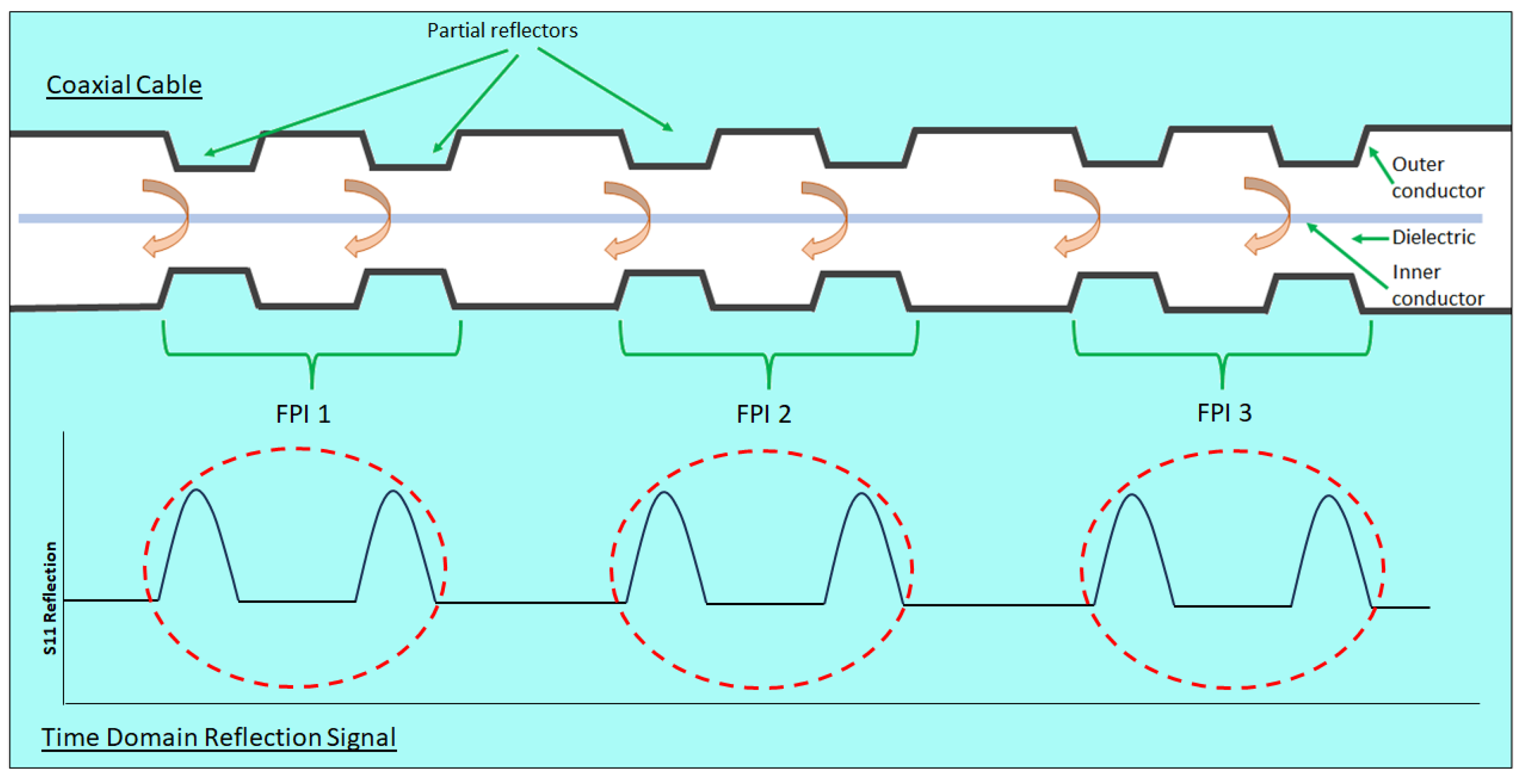
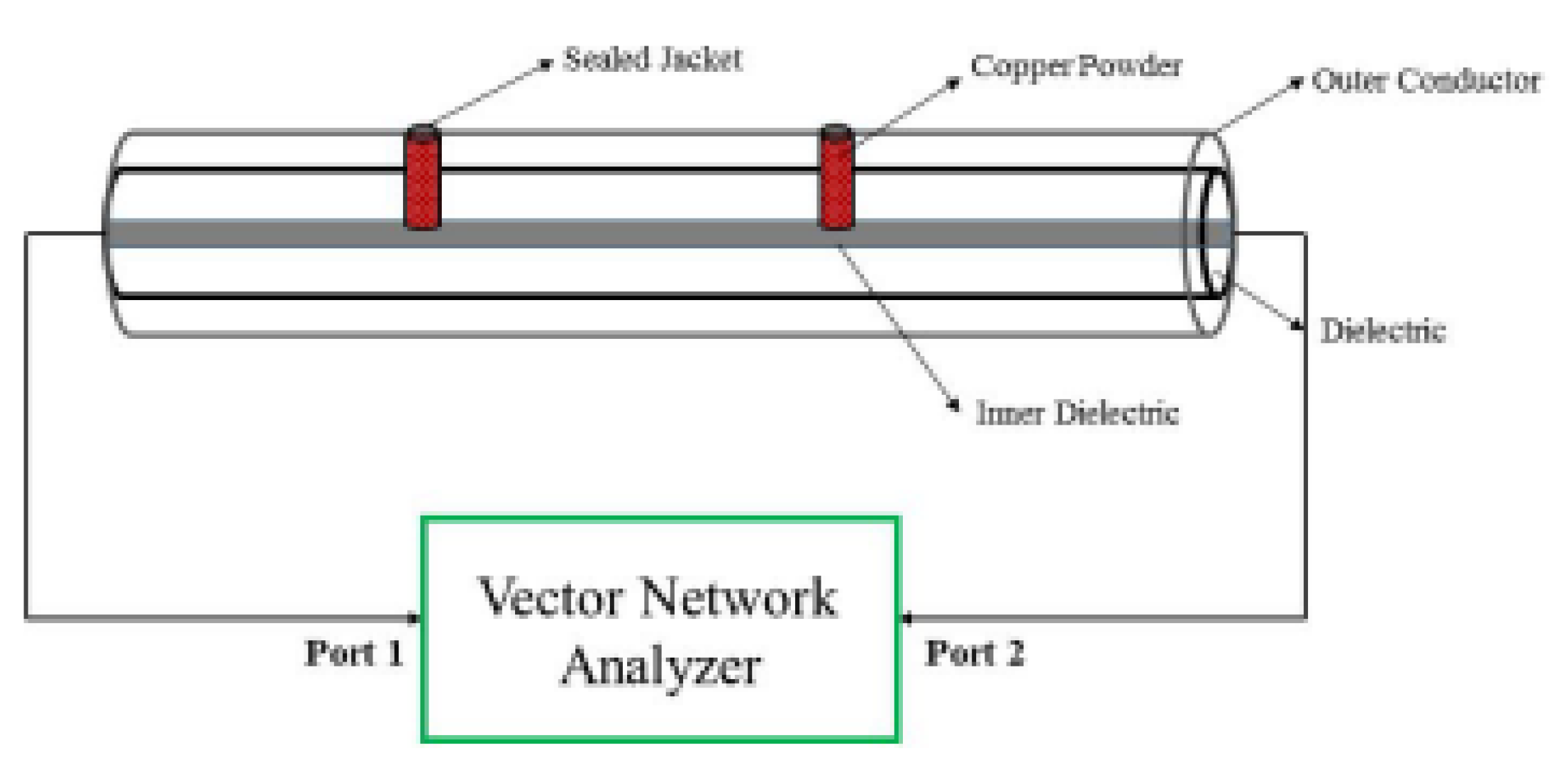
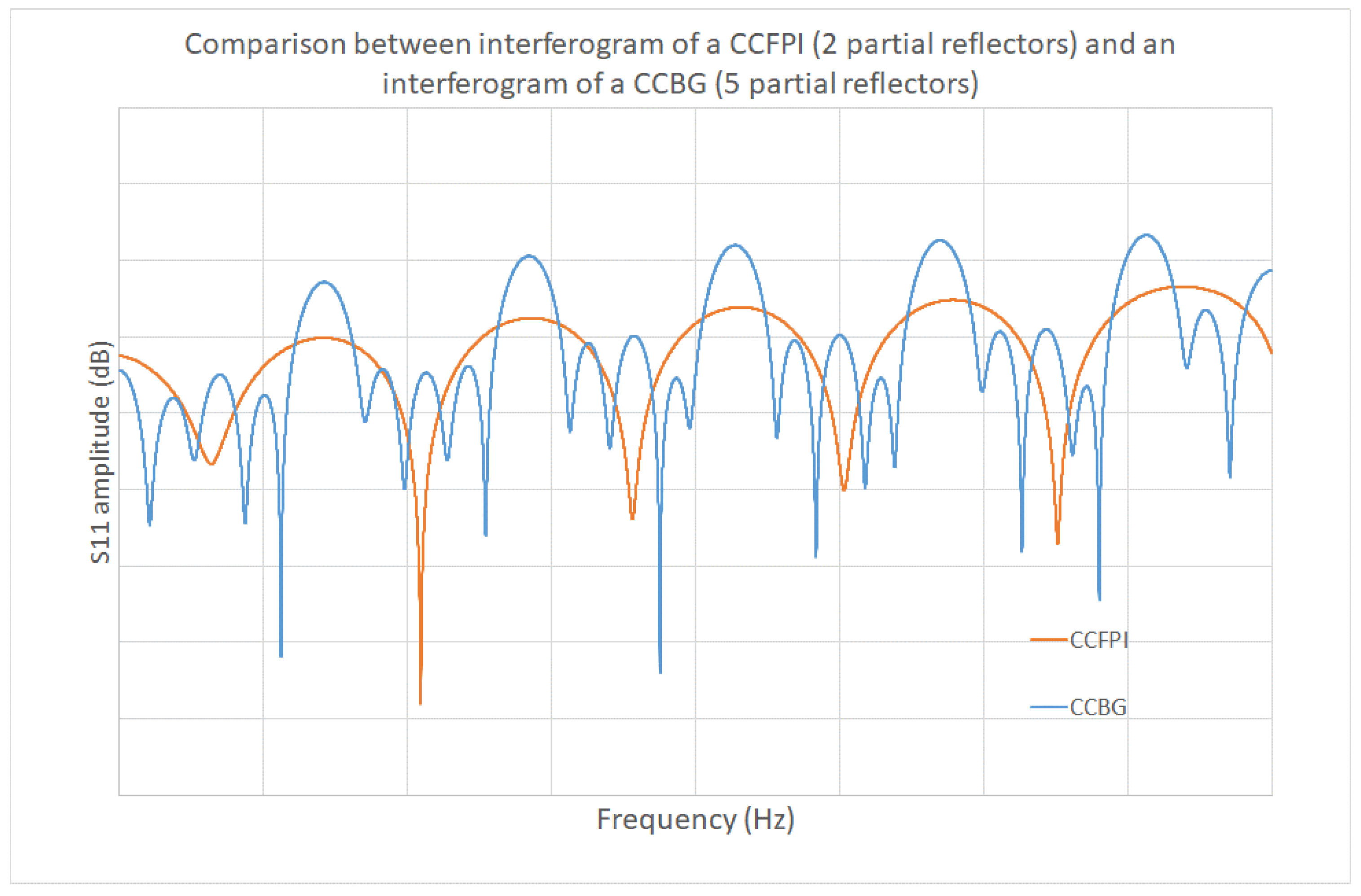
- Adapting a coaxial cable into a CCFPR for temperature measurements was described in 2017 [97]. In contrast to utilizing partial reflectors in distributed sensing using FPI arrangements along the entire length of the cable, CCFPRs use a single pair of highly reflective points, in this case constructed by filling drilled cavities in a coaxial cable with copper powder to form a short circuit (Figure 26). The high reflectivity results in increased measurement resolution [98] but limits the number of sensing points. This investigation noted the adaptability of the technique to strain sensing.
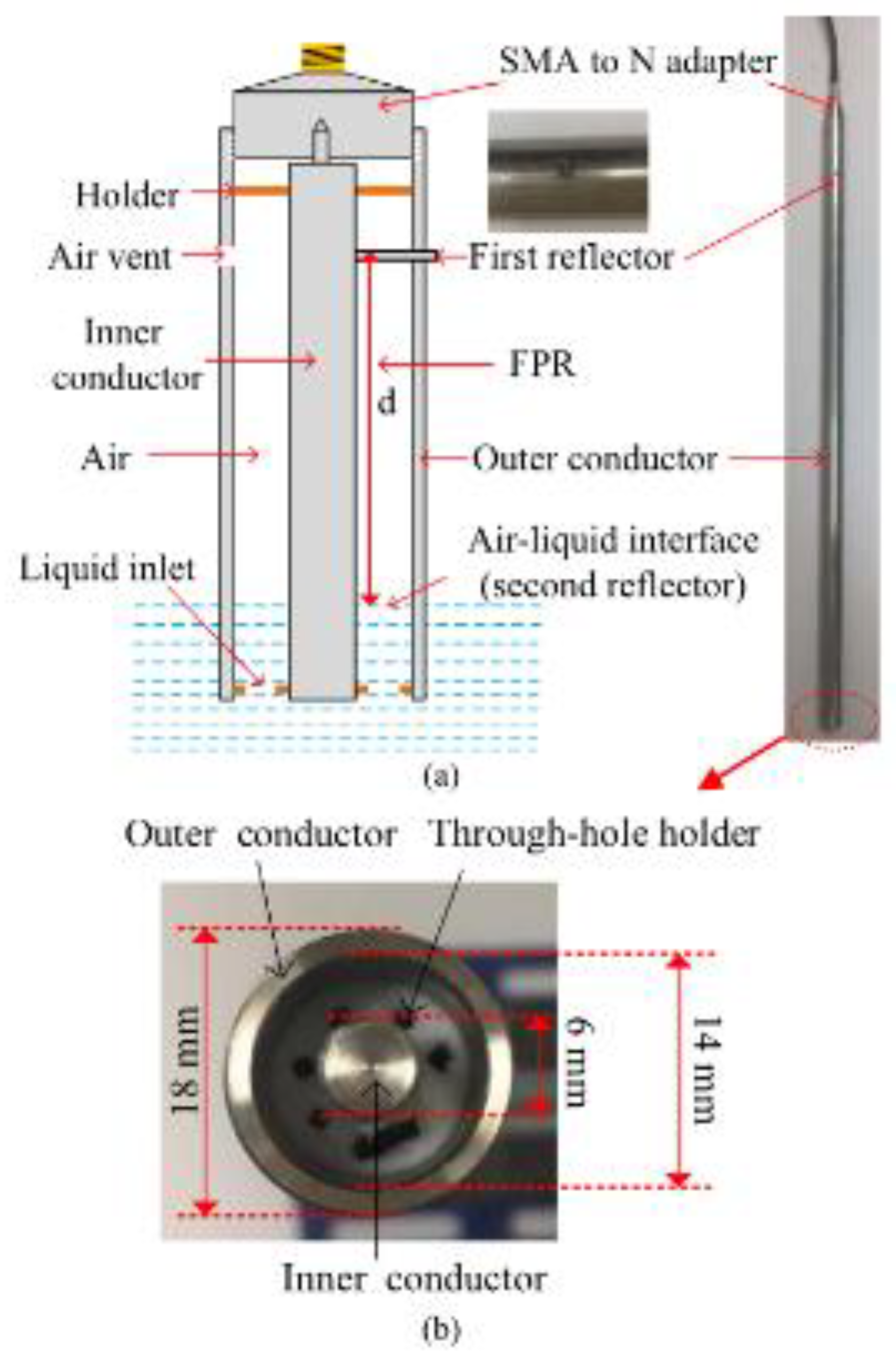
- The application of a HCC-FPR as a liquid-level sensor was researched in [99]. In this configuration, illustrate in Figure 27, the liquid forms the second reflector creating the resonant cavity, and hence the level of the liquid determines the frequencies of resonance. The sensor could measure liquid levels over a ~20cm range to resolutions in the order of micrometers.
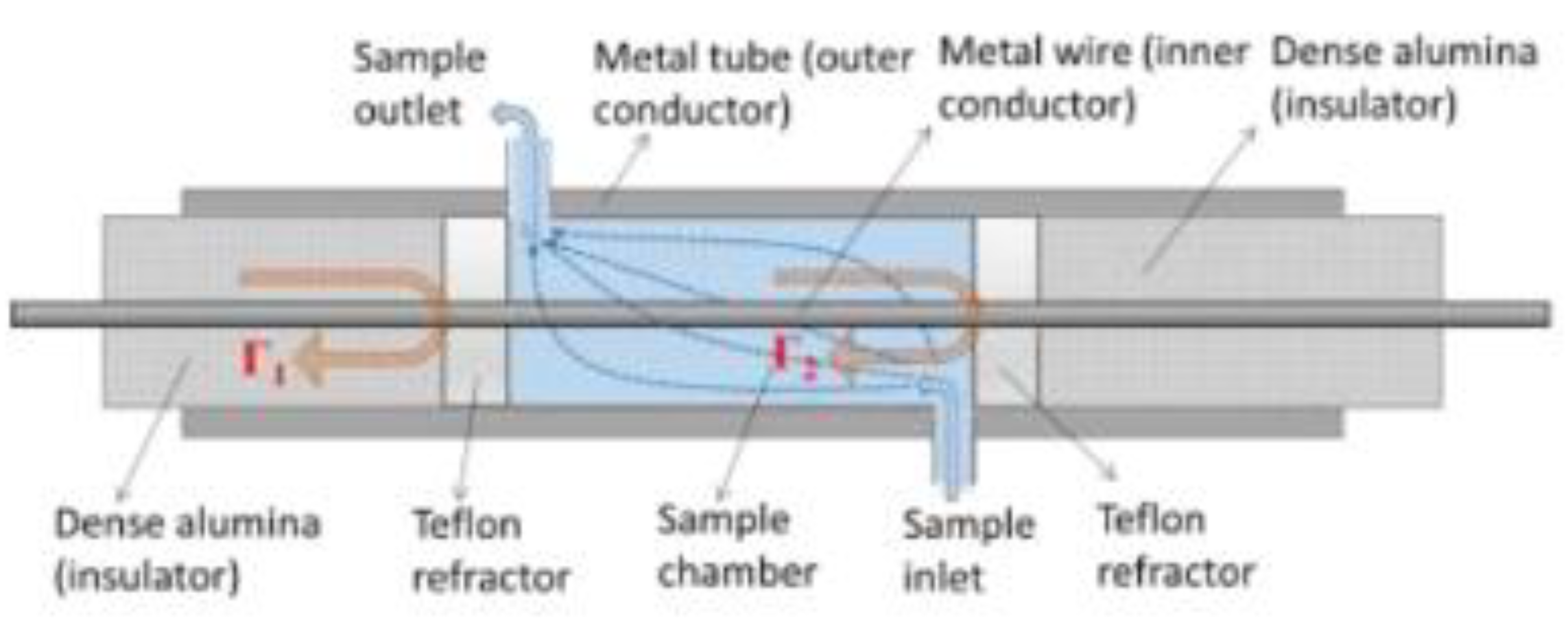
- Characterizing liquids through measurement of their dielectric properties is important for a range of functions such as food processing, biological analysis and the design of microwave communication systems. A sensor based on a CCFPI construction was developed for this application in 2017 [100]. A bespoke coaxial structure was manufactured using stainless steel tube and wire as the outer and inner conductors and ceramic (Al2O3) as the dielectric. Two Teflon discs formed the partial reflectors either side of a cavity formed by the omission of the ceramic dielectric for a ~10cm proportion of the structure. The construction of the device is shown in Figure 28. Different fluids were pumped through this cavity, in turn, and the resultant interferogram was shown to be dependent on the dielectric properties of the different fluids.
- A metal-ceramic coaxial cable design was proposed for high temperature monitoring using the Fabry-Perot interferometric technique [101]. The high temperature properties of the ceramic replace the temperature limited conventional polymer dielectrics. Successful operation was reported between 200oC and 500oC although thermal stability over longer time frames at these temperatures was yet to be explored. Two different partial reflector designs were tested; full-circle air gaps and half-circle air gaps, as shown in Figure 29.
- The use of CCFPI for temperature monitoring is also described in [102], where copper crimp rings are compressed onto a conventional coaxial cable to form an FPI (~10cm) long (Figure 30). The objective of this research was to design a sensor capable of monitoring temperatures downhole in order to indicate leakages in CO2 storage.
3.2.2. Grating-Based Coaxial Cable Frequency Domain Reflectometry
4. Future Research Challenges in Coaxial Cable Strain Sensing
- The robust coaxial cable structure means they can withstand installation procedures which are too severe for delicate fiber optics [8].
- A CCFPI response to strain is dependent on several factors, not just the physical distance between the two partial reflectors comprising the FPI. The response of the dielectric permittivity to strain has significant influence on the performance of a coaxial cable as a strain sensor using FPI features. Characterizing the dielectric permittivity with strain is an area for further work. This would enable the likely response of different coaxial cables as strain sensors, using FPI features, to be understood and predicted.
-
CCFPI distributed sensing measurements can be a result of the convolution of strain and temperature effects on the device. Both environmental factors influence the interferogram. Suggestions on how this challenge may be addressed are summarized below:
- Inference is made that the convolution of strain and temperature effects can be minimized by selecting dielectric materials that show preferential sensitivity to strain or temperature, depending on which condition is to be monitored [77]. There is a further reference to this technique in [7] where instead of using a commercially available coaxial cable with a Teflon or polyethylene dielectric, a coaxial cable with a low stiffness rubber dielectric was designed in an attempt to increase the sensitivity of the cable to strain.
- Another approach taken has been to use a reference CCFPI alongside the CCFPI monitoring the strain, to act as temperature compensation [77]. This is similar to the well-established practice of utilizing conventional electrical resistance strain sensors in a bridge arrangement to provide temperature compensation [113].
- Depending on the application and CCFPI design, temperature variations could be accounted for by presentation as an error on the strain reading, within reason.
- Signal analysis methods to monitor different characteristics of the interferogram might hold the key to inferring temperature effects on strain measurements. Latest developments in machine learning could more rapidly classify interferogram changes due to temperature and changes due to strain, deconvolving the environmental effects.
- Recent work on FBG sensors has applied machine learning techniques to discriminate between strain and temperature variations [120]. It would be interesting to pursue the role machine learning could play in advanced signal processing techniques for CCFPI.
- In the reviewed work there have been two main methods for creating the partial reflectors in the FPI arrangement; crimps/localized deformation and hole drilling [9,10,37,39] For the measurement of strain it was cited that localized deformations with metal ferrules ensure cable strength is retained, whereas hole drilling would create undesirable weaknesses [108] . One purpose of the development of the undulating cross-section CCBG was to propose a design that could be realistically fabricated [111]. The practicality and engineering challenges of manufacturing partial reflectors on a large-scale, integrated with coaxial cable manufacturing processes should not be overlooked in order to realize the full commercial potential of this technology. This is another aspect worthy of further work.
-
Optimal signal analysis techniques would further enhance the CCFPI technology for commercial success. Some techniques reviewed under this paper, but not necessarily applied yet to CCFPI devices include:
-
Deeper investigation into key features of the interferogram to track would be interesting; amplitude, Q-factor as well and position of frequency maxima and minima. The inclusion of machine learning methods into the signal analysis would be a novel approach to extracting greater information from the interferogram data. The objectives of more sophisticated signal analysis techniques would include:
- Increased sensitivity
- Improvement of SNR.
- Rapid analysis of multiple FPIs for real-time monitoring
- Potential to de-convolve strain and temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Glisic, B. Concise Historic Overview of Strain Sensors Used in the Monitoring of Civil Structures: The First One Hundred Years. Sensors 2022, 22, 2397. [Google Scholar] [CrossRef] [PubMed]
- Lopez-Higuera, J.M.; Rodriguez Cobo, L.; Quintela Incera, A.; Cobo, A. Fiber Optic Sensors in Structural Health Monitoring. J. Light. Technol. 2011, 29, 587–608. [Google Scholar] [CrossRef]
- Meng, W.; Bachilo, S.M.; Weisman, R.B.; Nagarajaiah, S. A Review: Non-Contact and Full-Field Strain Mapping Methods for Experimental Mechanics and Structural Health Monitoring. Sensors 2024, 24, 6573. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Liang, F.; Zhu, Q.; Zhang, H. An Overview on Structural Health Monitoring and Fault Diagnosis of Offshore Wind Turbine Support Structures. J. Mar. Sci. Eng. 2024, 12, 377. [Google Scholar] [CrossRef]
- Caithness Windfarm Information Forum Available online: https://stopthesethings.com/wp-content/uploads/2015/03/accidents.pdf.
- Wang, J.; Zhang, X.; Zeng, J. Optimal Group Maintenance Decision for a Wind Farm Based on Condition-based Maintenance. Wind Energy 2021, 24, 1517–1535. [Google Scholar] [CrossRef]
- Chen, G.; Mu, H.; Pommerenke, D.; Drewniak, J.L. Damage Detection of Reinforced Concrete Beams with Novel Distributed Crack/Strain Sensors. Struct. Health Monit. 2004, 3, 225–243. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Huang, J.; Wei, T.; Wu, S.; Lan, X.; Fan, J.; Xiao, H. Coaxial Cable Bragg Grating Sensors for Structural Health Monitoring. 2012, 5. [Google Scholar]
- Wei, T.; Wu, S.; Huang, J.; Xiao, H.; Fan, J. Coaxial Cable Bragg Grating. Appl. Phys. Lett. 2011, 99, 113517. [Google Scholar] [CrossRef]
- Cheng, B.; Hua, L.; Zhu, W.; Zhang, Q.; Lei, J.; Xiao, H. Distributed Temperature Sensing with Unmodified Coaxial Cable Based on Random Reflections in TDR Signal. Meas. Sci. Technol. 2019, 30, 015105. [Google Scholar] [CrossRef]
- Huang, J.; Lan, X.; Zhu, W.; Cheng, B.; Fan, J.; Zhou, Z.; Xiao, H. Interferogram Reconstruction of Cascaded Coaxial Cable Fabry-Perot Interferometers for Distributed Sensing Application. IEEE Sens. J. 2016, 16, 4495–4500. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, J. Coaxial Cable Sensing: Review and Perspective. IEEE Trans. Microw. Theory Tech. 2023, 1–20. [Google Scholar] [CrossRef]
- Lindsey, N.J.; Martin, E.R. Fiber-Optic Seismology. Annu. Rev. Earth Planet. Sci. 2021, 49, 309–336. [Google Scholar] [CrossRef]
- Roriz, P.; Carvalho, L.; Frazão, O.; Santos, J.L.; Simões, J.A. From Conventional Sensors to Fibre Optic Sensors for Strain and Force Measurements in Biomechanics Applications: A Review. J. Biomech. 2014, 47, 1251–1261. [Google Scholar] [CrossRef] [PubMed]
- Floris, I.; Adam, J.M.; Calderón, P.A.; Sales, S. Fiber Optic Shape Sensors: A Comprehensive Review. Opt. Lasers Eng. 2021, 139, 106508. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L. Recent Progress in Distributed Fiber Optic Sensors. Sensors 2012, 12, 8601–8639. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A Review of Recent Distributed Optical Fiber Sensors Applications for Civil Engineering Structural Health Monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Muanenda, Y.; Oton, C.J.; Di Pasquale, F. Application of Raman and Brillouin Scattering Phenomena in Distributed Optical Fiber Sensing. Front. Phys. 2019, 7, 155. [Google Scholar] [CrossRef]
- FOSCO. Available online: https://www.fiberoptics4sale.com/blogs/archive-posts/95048006-optical-fiber-loss-and-attenuation (accessed on 25 November 2024).
- Viavi Fiber Optics. Available online: https://www.viavisolutions.com/en-us/resources/learning-center/what-fiber-optic-sensing (accessed on 25 November 2024).
- Chamoin, L.; Farahbakhsh, S.; Poncelet, M. An Educational Review on Distributed Optic Fiber Sensing Based on Rayleigh Backscattering for Damage Tracking and Structural Health Monitoring. Meas. Sci. Technol. 2022, 33, 124008. [Google Scholar] [CrossRef]
- Kogure, T.; Okuda, Y. Monitoring the Vertical Distribution of Rainfall-Induced Strain Changes in a Landslide Measured by Distributed Fiber Optic Sensing With Rayleigh Backscattering. Geophys. Res. Lett. 2018, 45, 4033–4040. [Google Scholar] [CrossRef]
- Liu, T.; Huang, H.; Yang, Y. Crack Detection of Reinforced Concrete Member Using Rayleigh-Based Distributed Optic Fiber Strain Sensing System. Adv. Civ. Eng. 2020, 2020, 1–11. [Google Scholar] [CrossRef]
- Wheeler, L.N.; Take, W.A.; Hoult, N.A.; Le, H. Use of Fiber Optic Sensing to Measure Distributed Rail Strains and Determine Rail Seat Forces under a Moving Train. Can. Geotech. J. 2019, 56, 1–13. [Google Scholar] [CrossRef]
- Li, J.; Zhang, M. Physics and Applications of Raman Distributed Optical Fiber Sensing. Light Sci. Appl. 2022, 11, 128. [Google Scholar] [CrossRef] [PubMed]
- Bastianini, F.; Di Sante, R.; Falcetelli, F.; Marini, D.; Bolognini, G. Optical Fiber Sensing Cables for Brillouin-Based Distributed Measurements. Sensors 2019, 19, 5172. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Fan, X.; He, H.; Yan, L.; He, Z. Single-End Hybrid Rayleigh Brillouin and Raman Distributed Fibre-Optic Sensing System. Light Adv. Manuf. 2023, 4, 1. [Google Scholar] [CrossRef]
- Hill, K.O.; Meltz, G. Fiber Bragg Grating Technology Fundamentals and Overview. J. Light. Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef]
- Juraszek, J. Fiber Bragg Sensors on Strain Analysis of Power Transmission Lines. Materials 2020, 13, 1559. [Google Scholar] [CrossRef]
- You, R.; Ren, L.; Song, G. A Novel Fiber Bragg Grating (FBG) Soil Strain Sensor. Measurement 2019, 139, 85–91. [Google Scholar] [CrossRef]
- Purwasih, N.; Shinozaki, H.; Okazaki, S.; Kihira, H.; Kuriyama, Y.; Kasai, N. Atmospheric Corrosion Sensor Based on Strain Measurement with Active–Dummy Fiber Bragg Grating Sensors. Metals 2020, 10, 1076. [Google Scholar] [CrossRef]
- Jiang, T.; Ren, L.; Wang, J.; Jia, Z.; Li, D.; Li, H. Experimental Investigation of Fiber Bragg Grating Hoop Strain Sensor–Based Method for Sudden Leakage Monitoring of Gas Pipeline. Struct. Health Monit. 2021, 20, 3024–3035. [Google Scholar] [CrossRef]
- Zhu, T.; Wu, D.; Liu, M.; Duan, D.-W. In-Line Fiber Optic Interferometric Sensors in Single-Mode Fibers. Sensors 2012, 12, 10430–10449. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.H.; Kim, Y.H.; Park, K.S.; Eom, J.B.; Kim, M.J.; Rho, B.S.; Choi, H.Y. Interferometric Fiber Optic Sensors. Sensors 2012, 12, 2467–2486. [Google Scholar] [CrossRef] [PubMed]
- Islam, Md.; Ali, M.; Lai, M.-H.; Lim, K.-S.; Ahmad, H. Chronology of Fabry-Perot Interferometer Fiber-Optic Sensors and Their Applications: A Review. Sensors 2014, 14, 7451–7488. [Google Scholar] [CrossRef] [PubMed]
- Jiao, T.; Zhou, Z.; Liu, J.; Xiao, H.; Ou, J. Large Strain-Tolerated Smart Steel Strand with Built in Coaxial Cable Fabry–Perot Interferometer. Measurement 2020, 151, 107019. [Google Scholar] [CrossRef]
- Zhou, Z.; Jiao, T.; Zhao, P.; Liu, J.; Xiao, H. Development of a Distributed Crack Sensor Using Coaxial Cable. Sensors 2016, 16, 1198. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Wang, T.; Hua, L.; Fan, J.; Xiao, H.; Luo, M. A Coaxial Cable Fabry-Perot Interferometer for Sensing Applications. Sensors 2013, 13, 15252–15260. [Google Scholar] [CrossRef]
- Shishuang, Sun; Pommerenke, D.J.; Drewniak, J.L.; Genda, Chen; Liang, Xue; Brower, M.A.; Koledintseva, M.Y. A Novel TDR-Based Coaxial Cable Sensor for Crack/Strain Sensing in Reinforced Concrete Structures. IEEE Trans. Instrum. Meas. 2009, 58, 2714–2725. [Google Scholar] [CrossRef]
- Lin, M.W.; Thaduri, J.; Abatan, A.O. Development of an Electrical Time Domain Reflectometry (ETDR) Distributed Strain Sensor. Meas. Sci. Technol. 2005, 16, 1495–1505. [Google Scholar] [CrossRef]
- Fröbel, A. Cable Shielding to Minimize Electromagnetic Interference. Available online: http://www.eeeic.org/proc/papers/55.pdf (accessed on 8 October 2023).
- Shi, Q.; Kanoun, O. Wire Fault Location in Coaxial Cables by Impedance Spectroscopy. IEEE Sens. J. 2013, 13, 4465–4473. [Google Scholar] [CrossRef]
- Studying Time Domain Reflectometry to Predict Slope Failure in Open-Cast Mines. Физикo-Технические Прoблемы Разрабoтки Пoлезных Искoпаемых 2020. [CrossRef]
- Shreshthi, M.B.; V, H.R.D.; Ahamed, S.S. Comparison on Reflectometry Methods for Wire Fault Location.; October 18 2011; pp. 2011-01–2703.
- Lee, B.M.; Loh, K.J.; Lanza Di Scalea, F. Distributed Strain Sensing Using Electrical Time Domain Reflectometry With Nanocomposites. IEEE Sens. J. 2018, 18, 9515–9525. [Google Scholar] [CrossRef]
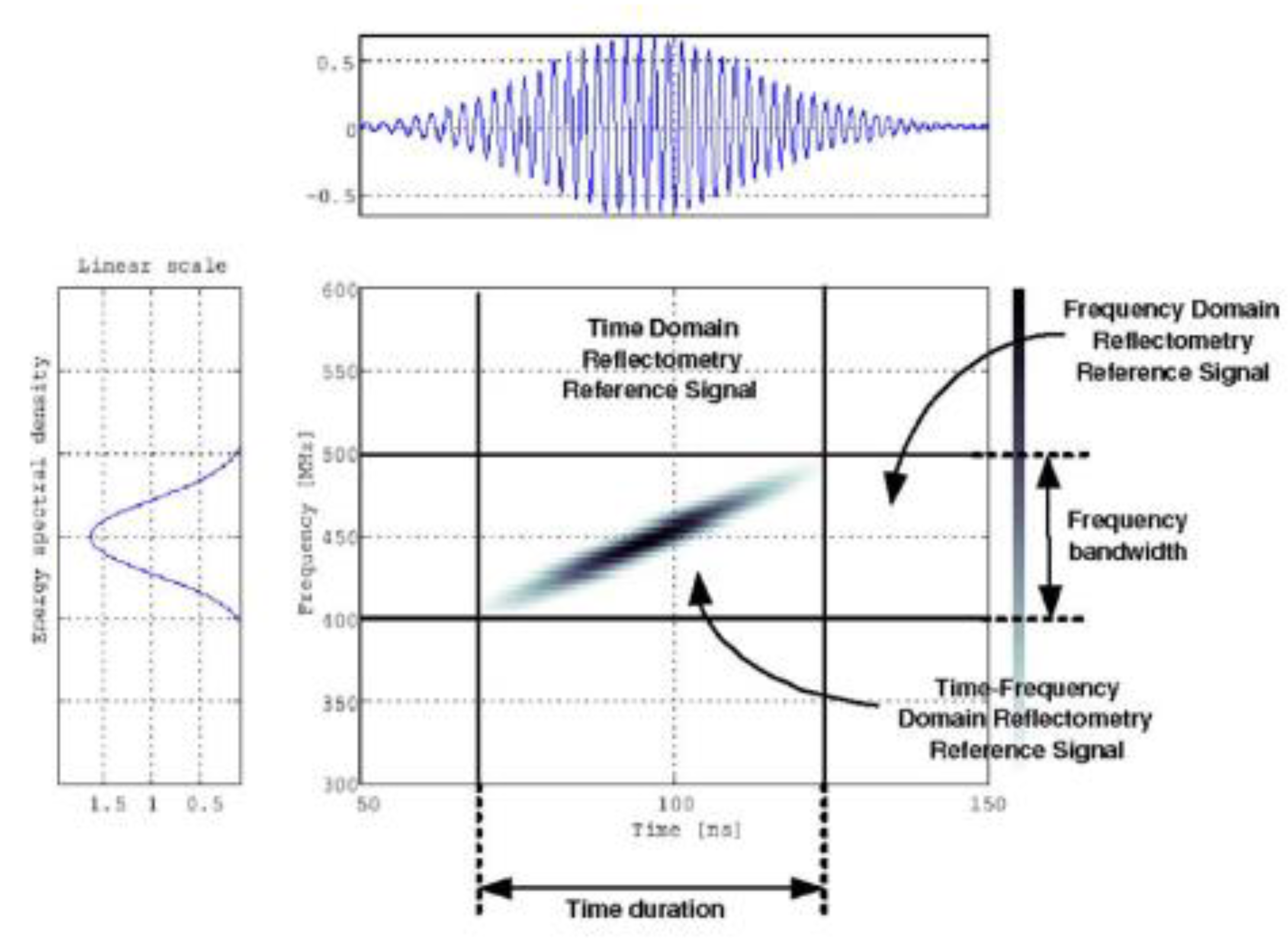
- Shin, Y.-J.; Powers, E.J.; Choe, T.-S.; Hong, C.-Y.; Song, E.-S.; Yook, J.-G.; Park, J.B. Application of Time-Frequency Domain Reflectometry for Detection and Localization of a Fault on a Coaxial Cable. IEEE Trans. Instrum. Meas. 2005, 54, 2493–2500. [Google Scholar] [CrossRef]
- Furse, C.M.; Kafal, M.; Razzaghi, R.; Shin, Y.-J. Fault Diagnosis for Electrical Systems and Power Networks: A Review. IEEE Sens. J. 2021, 21, 888–906. [Google Scholar] [CrossRef]
- Sisemore, C.J.; Stefani, R.E. Rock Fracture Measurements: A New Use for Time-Domain Reflectometry. J. Appl. Phys. 1971, 42, 2701–2710. [Google Scholar] [CrossRef]
- Tang, L.; Tao, X.; Choy, C. Possibility of Using a Coaxial Cable as a Distributed Strain Sensor by Time Domain Reflectometry. Smart Mater. Struct. 2001, 10, 221–228. [Google Scholar] [CrossRef]
- Dowding, C.H.; Su, M.B.; O’Connor, K. Measurement of Rock Mass Deformation with Grouted Coaxial Antenna Cables. Rock Mech. Rock Eng. 1989, 22, 1–23. [Google Scholar] [CrossRef]
- Su, M.-B.; Chen, Y.-J. MULTIPLE REFLECTION OF METALLIC TIME DOMAIN REFLECTOMETRY. Exp. Tech. 1998, 22, 26–29. [Google Scholar] [CrossRef]
- Paulter, N.G. An Assessment on the Accuracy of Time-Domain Reflectometry for Measuring the Characteristic Impedance of Transmission Lines. IEEE Trans. Instrum. Meas. 2001, 50, 1381–1388. [Google Scholar] [CrossRef]
- Renyuan Tong; Ming Li; Qing Li Design of Elastic Helical Time Domain Reflectometry Cable for Distributed Tensile Deformation Monitoring. In Proceedings of the 2011 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce (AIMSEC); IEEE: Deng Feng, China, August 2011; pp. 3887–3890.
- Applications of Time Domain Reflectometry in the Mining Industry. Available online: https://pe2bz.philpem.me.uk/Comm01/-%20TestEquip/-%20TDR/Info-900-TDR-InMiningIndustry/koc.html (accessed on 14 November 2022).
- Chung, C.-C.; Lin, C.-P.; Ngui, Y.J.; Lin, W.-C.; Yang, C.-S. Improved Technical Guide from Physical Model Tests for TDR Landslide Monitoring. Eng. Geol. 2022, 296, 106417. [Google Scholar] [CrossRef]
- Lin, C.-P.; Wang, K.; Chung, C.-C.; Weng, Y.-W. New Types of Time Domain Reflectometry Sensing Waveguides for Bridge Scour Monitoring. Smart Mater. Struct. 2017, 26, 075014. [Google Scholar] [CrossRef]
- Wang, K.; Lin, C.-P.; Jheng, W.-H. A New TDR-Based Sensing Cable for Improving Performance of Bridge Scour Monitoring. Sensors 2020, 20, 6665. [Google Scholar] [CrossRef]
- Bishop, J.A.; Pommerenke, D.J.; Chen, G. A Rapid-Acquisition Electrical Time-Domain Reflectometer for Dynamic Structure Analysis. IEEE Trans. Instrum. Meas. 2011, 60, 655–661. [Google Scholar] [CrossRef]
- Van Biesen, L.P.; Renneboog, J.; Barel, A.R.F. High Accuracy Location of Faults on Electrical Lines Using Digital Signal Processing. IEEE Trans. Instrum. Meas. 1990, 39, 175–179. [Google Scholar] [CrossRef]
- Osman, O.; Sallem, S.; Sommervogel, L.; Olivas Carrion, M.; Peltier, A.; Bonnet, P.; Paladian, F. METHOD TO IMPROVE FAULT LOCATION ACCURACY AGAINST CABLES DISPERSION EFFECT. Prog. Electromagn. Res. Lett. 2019, 83, 29–35. [Google Scholar] [CrossRef]
- Agrez, D. Approximation of the Skin Effect to Improve Cable-Fault Location by Tdr. In Proceedings of the Proceedings of the 20th IEEE Instrumentation Technology Conference (Cat. No.03CH37412); IEEE: Vail, Colorado, USA, 2003; Vol. 1, pp. 50–53.
- Zhu, C.; Zhuang, Y.; Chen, Y.; Huang, J. Truly Distributed Coaxial Cable Sensing Based on Random Inhomogeneities. IEEE Trans. Instrum. Meas. 2019, 68, 4600–4607. [Google Scholar] [CrossRef]
- Chen, G.D.; Sun, S.S.; Pommerenke, D.; Drewniak, J.L.; Greene, G.G.; McDaniel, R.D.; Belarbi, A.; Mu, H.M. Crack Detection of a Full-Scale Reinforced Concrete Girder with a Distributed Cable Sensor. Smart Mater. Struct. 2005, 14, S88–S97. [Google Scholar] [CrossRef]
- Chen, G.; McDaniel, R.; Brower, M.; Pommerenke, D. Crack Detectability and Durability of Coaxial Cable Sensors in Reinforced Concrete Bridge Applications. Transp. Res. Rec. J. Transp. Res. Board 2010, 2172, 151–156. [Google Scholar] [CrossRef]
- Li, S.; Chen, C.-L.; Loh, K.J. Laboratory Evaluation of Railroad Crosslevel Tilt Sensing Using Electrical Time Domain Reflectometry. Sensors 2020, 20, 4470. [Google Scholar] [CrossRef]
- Wu, X.; Tong, R.; Wang, Y.; Mei, C.; Li, Q. Using a Parallel Helical Sensing Cable for the Distributed Measurement of Ground Deformation. Sensors 2019, 19, 1297. [Google Scholar] [CrossRef]
- Lee, H.M.; Lee, G.S.; Kwon, G.-Y.; Bang, S.S.; Shin, Y.-J. Industrial Applications of Cable Diagnostics and Monitoring Cables via Time–Frequency Domain Reflectometry. IEEE Sens. J. 2021, 21, 1082–1091. [Google Scholar] [CrossRef]
- Song, E.; Shin, Y.-J.; Stone, P.E.; Wang, J.; Choe, T.-S.; Yook, J.-G.; Park, J.B. Detection and Location of Multiple Wiring Faults via Time–Frequency-Domain Reflectometry. IEEE Trans. Electromagn. Compat. 2009, 51, 131–138. [Google Scholar] [CrossRef]
- Ching-Wen Hsue; Te-Wen Pan Reconstruction of Nonuniform Transmission Lines from Time-Domain Reflectometry. IEEE Trans. Microw. Theory Tech. 1997, 45, 32–38. [CrossRef]
- Smith, P.; Furse, C.; Gunther, J. Analysis of Spread Spectrum Time Domain Reflectometry for Wire Fault Location. IEEE Sens. J. 2005, 5, 1469–1478. [Google Scholar] [CrossRef]
- Nick A Simple Guide to Spread Spectrum Time Domain Reflectometry. Available online: https://www.viperinnovations.com/a-simple-guide-to-sstdr/ (accessed on 14 November 2022).
- Qian, S.; Chen, D. Joint Time-Frequency Analysis Qian.Pdf; Part 2; 1st ed.; Prentice Hall, New Jersey, USA, 1996; Vol. 1 pp. 45–199; ISBN 0-13-254384-2.
- Mohr_CT100BOperatorsManualA4.Pdf. Available online: http://www.mohr-engineering.com/tdr-cable-tester-documents-CT100.php (accessed on 14 November 2022).
- User-Guide-Keysight-Agilent-N9912A-FieldFox-Handheld-RF-Combination-Analyzer-4-and-6-GHz.Pdf. Available online: https://www.testworld.com/wp-content/uploads/user-guide-Keysight-Agilent-N9912A-FieldFox-Handheld-RF-Combination-Analyzer-4-and-6-GHz.pdf (accessed on 14 November 2022).
- Hecht, Eugene Optics; 2nd ed.; Addison-Wesley, 1987; ISBN 0-201-11609-X.
- Cheng, B. Coaxial Cable Sensors Based on Fabry-Perot Interferometers and Their Applications in Distributed Sensing, Clemson University, USA, 2017.
- Cheng, B.; Zhu, W.; Hua, L.; Liu, J.; Li, Y.; Nygaard, R.; Xiao, H. Distributed Torsion Sensor Based on Cascaded Coaxial Cable Fabry–Perot Interferometers. Meas. Sci. Technol. 2016, 27, 075103. [Google Scholar] [CrossRef]
- Cheng, B.; Zhu, W.; Liu, J.; Yuan, L.; Xiao, H. 3D Beam Shape Estimation Based on Distributed Coaxial Cable Interferometric Sensor. Smart Mater. Struct. 2017, 26, 035017. [Google Scholar] [CrossRef]
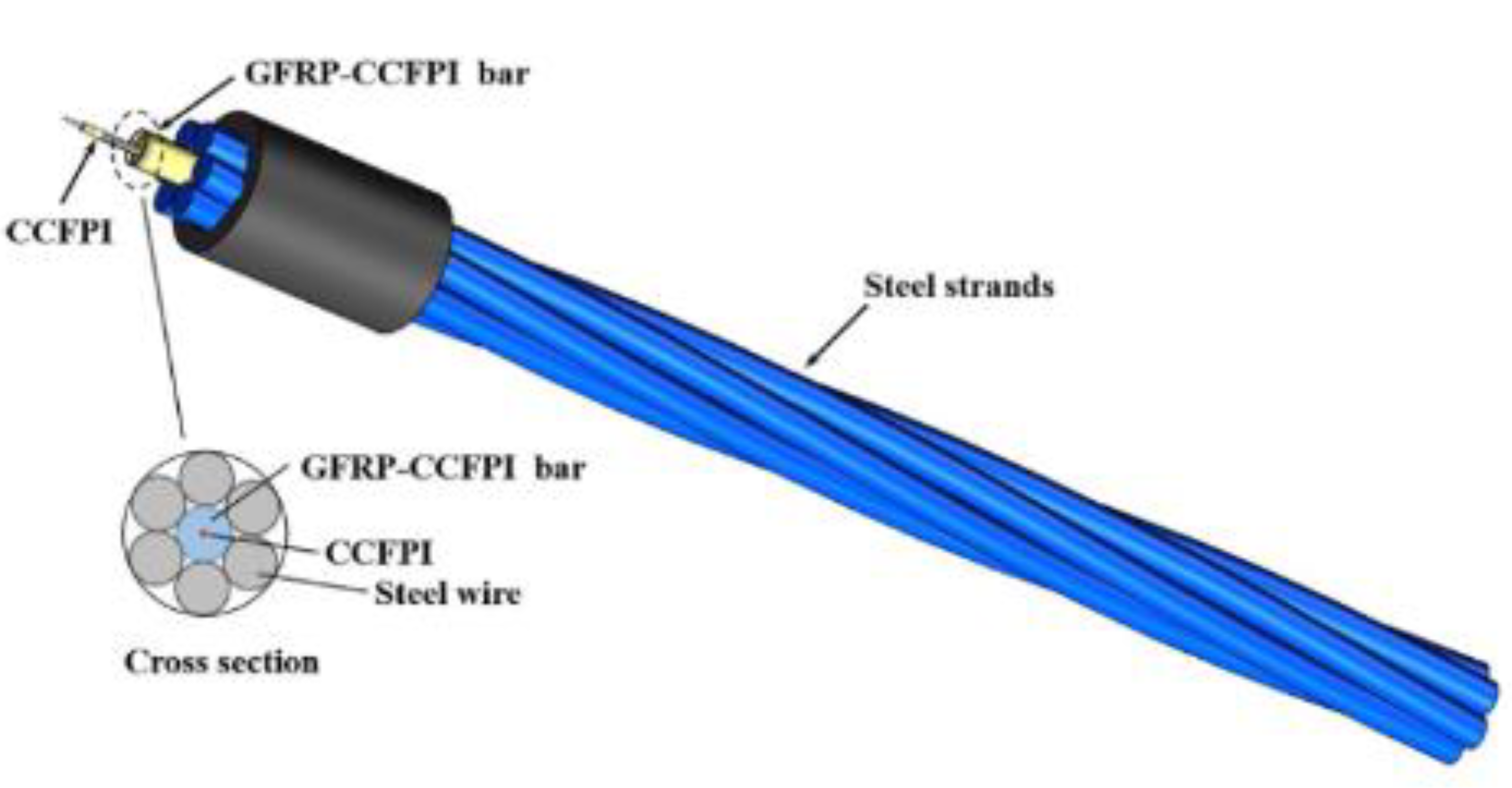
- Jiao, T.; Pu, C.; Xu, Q.; Tang, M.; Zhu, X.; Liu, C.; Li, J. Development and Characterization of a Coaxial Strain-Sensing Cable Integrated Steel Strand for Wide-Range Stress Monitoring. Rev. Adv. Mater. Sci. 2024, 63, 20230165. [Google Scholar] [CrossRef]
- Zhu, C.; Alsalman, O.; Huang, J. Cascaded Weak Reflector Coaxial Cable Structure for Point and Distributed Large-Strain Sensing. IEEE Sens. J. 2024, 24, 7788–7795. [Google Scholar] [CrossRef]
- Berube, D.; Ghannouchi, F.M.; Savard, P. A Comparative Study of Four Open-Ended Coaxial Probe Models for Permittivity Measurements of Lossy Dielectric/Biological Materials at Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 1996, 44, 1928–1934. [Google Scholar] [CrossRef]
- Kundu, A.; Gupta, B. Broadband Dielectric Properties Measurement of Some Vegetables and Fruits Using Open Ended Coaxial Probe Technique. In Proceedings of the Proceedings of The 2014 International Conference on Control, Instrumentation, Energy and Communication (CIEC); IEEE: Calcutta, India, January, 2014; pp. 480–484. [Google Scholar]
- Stuchly, M.A.; Stuchly, S.S. Coaxial Line Reflection Methods for Measuring Dielectric Properties of Biological Substances at Radio and Microwave Frequencies-A Review. IEEE Trans. Instrum. Meas. 1980, 29, 176–183. [Google Scholar] [CrossRef]
- Jiang, G.Q.; Wong, W.H.; Raskovich, E.Y.; Clark, W.G.; Hines, W.A.; Sanny, J. Measurement of the Microwave Dielectric Constant for Low-Loss Samples with Finite Thickness Using Open-Ended Coaxial-Line Probes. Rev. Sci. Instrum. 1993, 64, 1622–1626. [Google Scholar] [CrossRef]
- Wang, J.; Lim, E.G.; Leach, M.P.; Wang, Z.; Man, K.L. Open-Ended Coaxial Cable Selection for Measurement of Liquid Dielectric Properties via the Reflection Method. Math. Probl. Eng. 2020, 2020, 1–8. [Google Scholar] [CrossRef]
- Meaney, P.M.; Gregory, A.P.; Seppala, J.; Lahtinen, T. Open-Ended Coaxial Dielectric Probe Effective Penetration Depth Determination. IEEE Trans. Microw. Theory Tech. 2016, 1–9. [Google Scholar] [CrossRef] [PubMed]
- La Gioia, A.; Porter, E.; Merunka, I.; Shahzad, A.; Salahuddin, S.; Jones, M.; O’Halloran, M. Open-Ended Coaxial Probe Technique for Dielectric Measurement of Biological Tissues: Challenges and Common Practices. Diagnostics 2018, 8, 40. [Google Scholar] [CrossRef]
- Popovic, D.; McCartney, L.; Beasley, C.; Lazebnik, M.; Okoniewski, M.; Hagness, S.C.; Booske, J.H. Precision Open-Ended Coaxial Probes for in Vivo and Ex Vivo Dielectric Spectroscopy of Biological Tissues at Microwave Frequencies. IEEE Trans. Microw. Theory Tech. 2005, 53, 1713–1722. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Microwave Device Inspired by Fiber-Optic Extrinsic Fabry-Perot Interferometer: A Novel Ultra-Sensitive Sensing Platform. J. Light. Technol. 2020, 38, 6961–6966. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Gerald, R.E.; Chen, Y.; Huang, J. Probing the Theoretical Ultimate Limit of Coaxial Cable Sensing: Measuring Nanometer-Scale Displacements. IEEE Trans. Microw. Theory Tech. 2020, 68, 816–823. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Gerald, R.E.; Huang, J. Ultrasensitive Open-Ended Coaxial Cable-Based Microwave Resonator Learns to Sense Impacts. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Zhu, C.; Gerald, R.E.; Huang, J. Highly Sensitive Open-Ended Coaxial Cable-Based Microwave Resonator for Humidity Sensing. Sens. Actuators Phys. 2020, 314, 112244. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Y.; Zhang, Q.; Shi, B.; Huang, J. Enhanced Sensitivity and Robustness in an Embeddable Strain Sensor Using Microwave Resonators. IEEE Trans. Instrum. Meas. 2024, 73, 1–8. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Huang, J. A Centimeter-Range Displacement Sensor Based on a Hollow Coaxial Cable Fabry–Perot Resonator. IEEE Sens. J. 2018, 18, 4436–4442. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Zhuang, Y.; Huang, J. Displacement and Strain Measurement up to 1000 °C Using a Hollow Coaxial Cable Fabry-Perot Resonator. Sensors 2018, 18, 1304. [Google Scholar] [CrossRef]
- Ahmed, M.F.; Xue, T.; Wu, B.; Huang, J. High Quality Factor Coaxial Cable Fabry-Perot Resonator for Sensing Applications. IEEE Sens. J. 2017, 17, 3052–3057. [Google Scholar] [CrossRef]
- Gaborit, G.; Martin, G.; Coutaz, J.-L.; Duvillaret, L.; Kassi, S.; Romanini, D. High-Finesse Fabry-Perot Electro-Optic Sensors with Enhanced Sensitivity and High Spatial Resolution. Appl. Opt. 2007, 46, 2001. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Zhuang, Y.; Chen, Y.; Huang, J. A Liquid-Level Sensor Based on a Hollow Coaxial Cable Fabry–Perot Resonator With Micrometer Resolution. IEEE Trans. Instrum. Meas. 2018, 67, 2892–2897. [Google Scholar] [CrossRef]
- Zeng, S.; Trontz, A.; Zhu, W.; Xiao, H.; Dong, J. A Metal-Ceramic Coaxial Cable Fabry-Pérot Microwave Interferometer for Monitoring Fluid Dielectric Constant. Sens. Actuators Phys. 2017, 257, 1–7. [Google Scholar] [CrossRef]
- Trontz, A.; Cheng, B.; Zeng, S.; Xiao, H.; Dong, J. Development of Metal-Ceramic Coaxial Cable Fabry-Pérot Interferometric Sensors for High Temperature Monitoring. Sensors 2015, 15, 24914–24925. [Google Scholar] [CrossRef]
- Li, Y.; Nygaard, R.; Zhu, W.; Xiao, H. Robust and Cost Effective Distributed Coaxial Cable Sensors Verified As Real-Time Permanent Downhole Monitoring for Groundwater Safety in Geological CO2 Storage. In Proceedings of the All Days; CMTC: Sugar Land, Texas, November 17 2015; p. CMTC-438055-MS.
- Wei, C.Y.; James, S.W.; Ye, C.C.; Dykes, N.D.; Tatam, R.P.; Irving, P.E. Strain Capability of Optical Fibre Bragg Grating Sensing in Composite Smart Structures. 1999, 10.
- Mihailov, S.J. Fiber Bragg Grating Sensors for Harsh Environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef]
- Zaltieri, M.; Massaroni, C.; Lo Presti, D.; Bravi, M.; Sabbadini, R.; Miccinilli, S.; Sterzi, S.; Formica, D.; Schena, E. A Wearable Device Based on a Fiber Bragg Grating Sensor for Low Back Movements Monitoring. Sensors 2020, 20, 3825. [Google Scholar] [CrossRef]
- Consales, M.; Principe, S.; Iele, A.; Leone, M.; Zaraket, H.; Jomaa, I.; Cutolo, A.; Cusano, A. A Fiber Bragg Grating Liquid Level Sensor Based on the Archimedes’ Law of Buoyancy. J. Light. Technol. 2018, 36, 4936–4941. [Google Scholar] [CrossRef]
- Di Sante, R.; Donati, L. Strain Monitoring with Embedded Fiber Bragg Gratings in Advanced Composite Structures for Nautical Applications. Measurement 2013, 46, 2118–2126. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, Y.; Li, P.; Ou, J.; Xiao, H.; Zhao, P. Novel Coaxial Cable Sensors for Large Strain Measurement in SHM. In Proceedings of the Civial Structural Health Monitoring Workshop (CSHM-4); Berlin, Germany, November 2012.
- Fu, J.; Wang, X.; Wei, T.; Wei, M.; Shen, Y. A Cost-Effective Geodetic Strainmeter Based on Dual Coaxial Cable Bragg Gratings. Sensors 2017, 17, 842. [Google Scholar] [CrossRef]
- Shi, P.; Gao, R.; Liu, S.; Zhao, J. A New Design Method for a Strain Sensor Using the Cross-Section Modification of a Coaxial Cable. Sens. Actuators Phys. 2013, 203, 355–361. [Google Scholar] [CrossRef]
- Shi, P.; Li, Z.; Tang, Y.; Zhao, H.; Gao, R.; Liu, S. Strain Sensor Based on Coaxial Cable Bragg Grating with Gradient Cross Section. Sens. Actuators Phys. 2023, 349, 114082. [Google Scholar] [CrossRef]
- Cheng; et al. - 2016 - Distributed Torsion Sensor Based on Cascaded Coaxi.Pdf.
- Zymelka, D.; Yamashita, T.; Takamatsu, S.; Itoh, T.; Kobayashi, T. Printed Strain Sensor with Temperature Compensation and Its Evaluation with an Example of Applications in Structural Health Monitoring. Jpn. J. Appl. Phys. 2017, 56, 05EC02. [Google Scholar] [CrossRef]
- Zhang, H.; Jiang, C.; Hu, J.; Song, J.; Zhu, X.; Wang, P.; Li, H. Temperature-Insensitive Optical Fiber Strain Sensor Fabricated by Two Parallel Connection Fabry–Perot Interferometers with Air-Bubbles. Rev. Sci. Instrum. 2023, 94, 045001. [Google Scholar] [CrossRef] [PubMed]
- Yang, N.; Su, J.; Fan, Z.; Qiu, Q. High Precision Temperature Insensitive Strain Sensor Based on Fiber-Optic Delay. Sensors 2017, 17, 1005. [Google Scholar] [CrossRef]
- Gao, X.; Xu, J.; Zhang, W.; Lei, F.; Zheng, J.; Pei, L.; Wang, J.; Chai, J.; Ning, T. Temperature-Insensitive Strain Sensor Based on Few-Mode Fiber. Opt. Fiber Technol. 2022, 73, 103034. [Google Scholar] [CrossRef]
- Shen, C.; Zhong, C.; Chu, J.; Zou, X.; Jin, Y.; Wang, J.; Dong, X.; Li, Y.; Wang, L. Temperature-Insensitive Strain Sensor Using a Fiber Loop Mirror Based on Low-Birefringence Polarization-Maintaining Fibers. Opt. Commun. 2013, 287, 31–34. [Google Scholar] [CrossRef]
- Mokhtar, M.R.; Owens, K.; Kwasny, J.; Taylor, S.E.; Basheer, P.A.M.; Cleland, D.; Bai, Y.; Sonebi, M.; Davis, G.; Gupta, A.; et al. Fiber-Optic Strain Sensor System With Temperature Compensation for Arch Bridge Condition Monitoring. IEEE Sens. J. 2012, 12, 1470–1476. [Google Scholar] [CrossRef]
- Jeon, S.-J.; Park, S.Y.; Kim, S.T. Temperature Compensation of Fiber Bragg Grating Sensors in Smart Strand. Sensors 2022, 22, 3282. [Google Scholar] [CrossRef]
- Saha, S.; Hadigheh, S.A.; Rukhlenko, I.; Valix, M.; Uy, B.; Fleming, S. Machine Learning-Augmented Multi-Arrayed Fiber Bragg Grating Sensors for Enhanced Structural Health Monitoring by Discriminating Strain and Temperature Variations. J. Civ. Struct. Health Monit. 2024. [Google Scholar] [CrossRef]












| Sensing Technology | Transducer Type | Sensing Range | Spatial Resolution | Main Measurands | Single ended monitoring |
|---|---|---|---|---|---|
| Raman OTDR |
Distributed | 1 km 37 km |
1 cm 17 m |
Temperature | NO |
| Brillouin OTDR |
Distributed | 20-50 km | ~1 m | Temperature and Strain | YES |
| Brillouin OTDA |
Distributed | 150-200 km | 2cm (2km) 2m (150km) |
Temperature and Strain | NO |
| Rayleigh OFDR |
Distributed | 50-70 m | ~1mm | Temperature and Strain | YES (needs a reference fiber) |
| Fibre Bragg Grating | Quasi-distributed | ~100 channels | 2 mm (Bragg length) | Temperature, Strain and Displacement | YES |
| Type of modification | Purpose of modification | Citation |
|---|---|---|
| Dielectric material selection | Increased sensitivity to strain | [41] |
| Topology of outer conductor | Increased sensitivity to strain | [7,38,40,64,65] |
| Intentional creation of impedance changes | Tracking point to measure distance changes/act as ‘location tags’ | [55] |
| Inclusion of small in-line sensors | Increase sensitivity to strain, or increase functionality of cable | [46,66] |
| Coaxial Cable Sensor Type | Application | Cable Type | Partial Reflector | Sensor active length | Frequency | Key Results | Reference |
|---|---|---|---|---|---|---|---|
| CCFPI | Axial strain sensor | RG58 | Holes | 70mm | ~3.5GHz | -3.3kHz/µε | [39] |
| CCFPI | Axial strain sensor | Not stated | Not stated | Not stated | ~1.9GHz | 22.5kHz/ µε | [77] |
| CCFPI | Torsion sensor (cascaded FPIs) | RG58 | Crimping metal ferrules | 227mm (wrapped) | ~4.2GHz | 1.834MHz (rad/m)-1 | [112] |
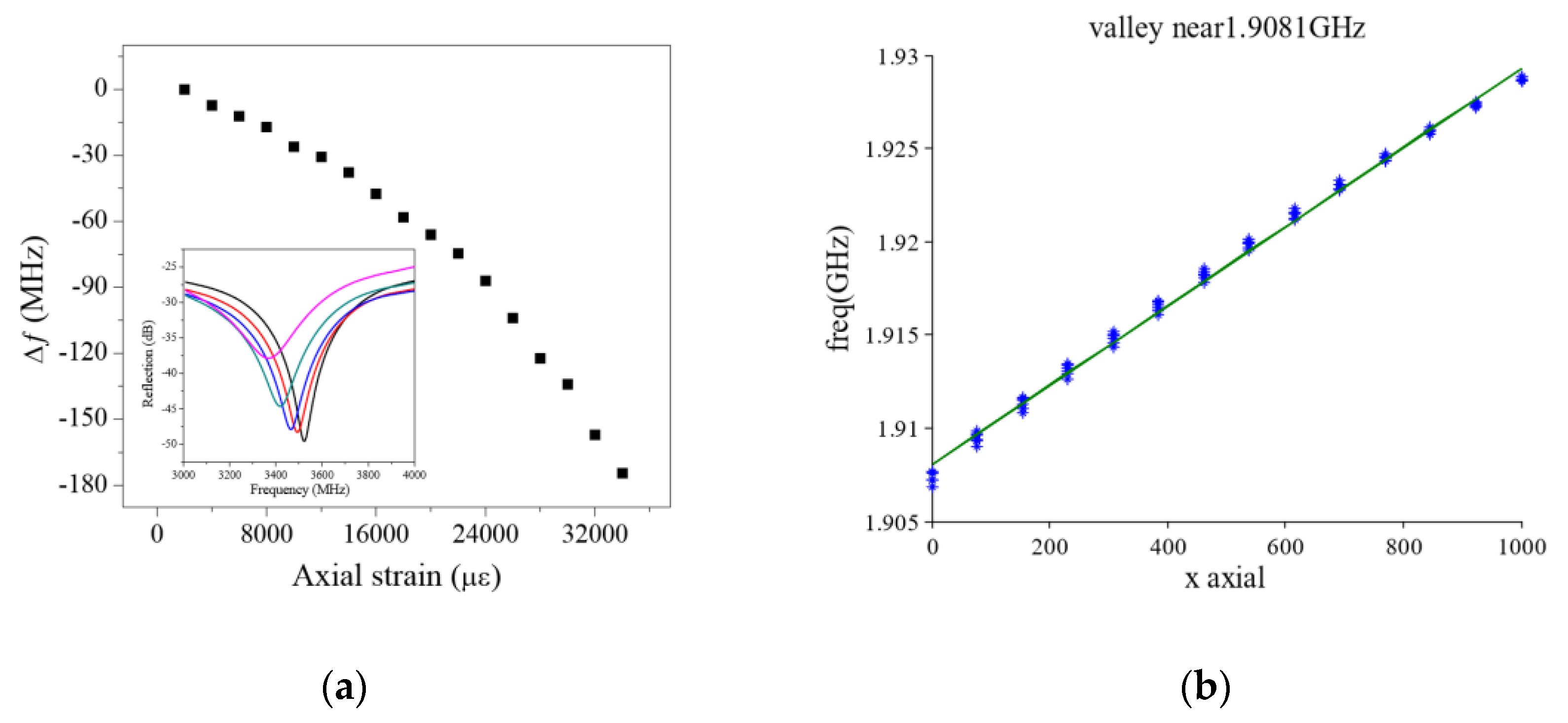
| CCFPI | Embedded in GFRP for core in steel stranded cable | SF047 | Crimping metal ferrules | 200mm | ~3GHz | -3.7kHz/µε | [37] |
| CCFPR | Measure lateral displacements | Bespoke structure | Metal post and metal plate | 75mm | ~1GHz | Lateral position resolutions measured to order of 1nm. | [91] |
| CCFPR | Strain-e.g. shrinkage strain | Bespoke structure | Metal post and gap/flange | 80mm | ~0.6GHz | Sensitivity of 2.5GHz/mm – nanoscale precision | [94] |
| CCFPR | Displacement sensor | Bespoke structure | Metal post and metal cone | 20cm | ~1.2GHz | Displacement to resolution of 10µm. | [95] |
| CCFPR | Strain sensor for high temperature environments | Bespoke structure | Metal inserts | 11.8cm | ~1GHz | Monitored thermal strain between 100 and 900oC. | [96] |
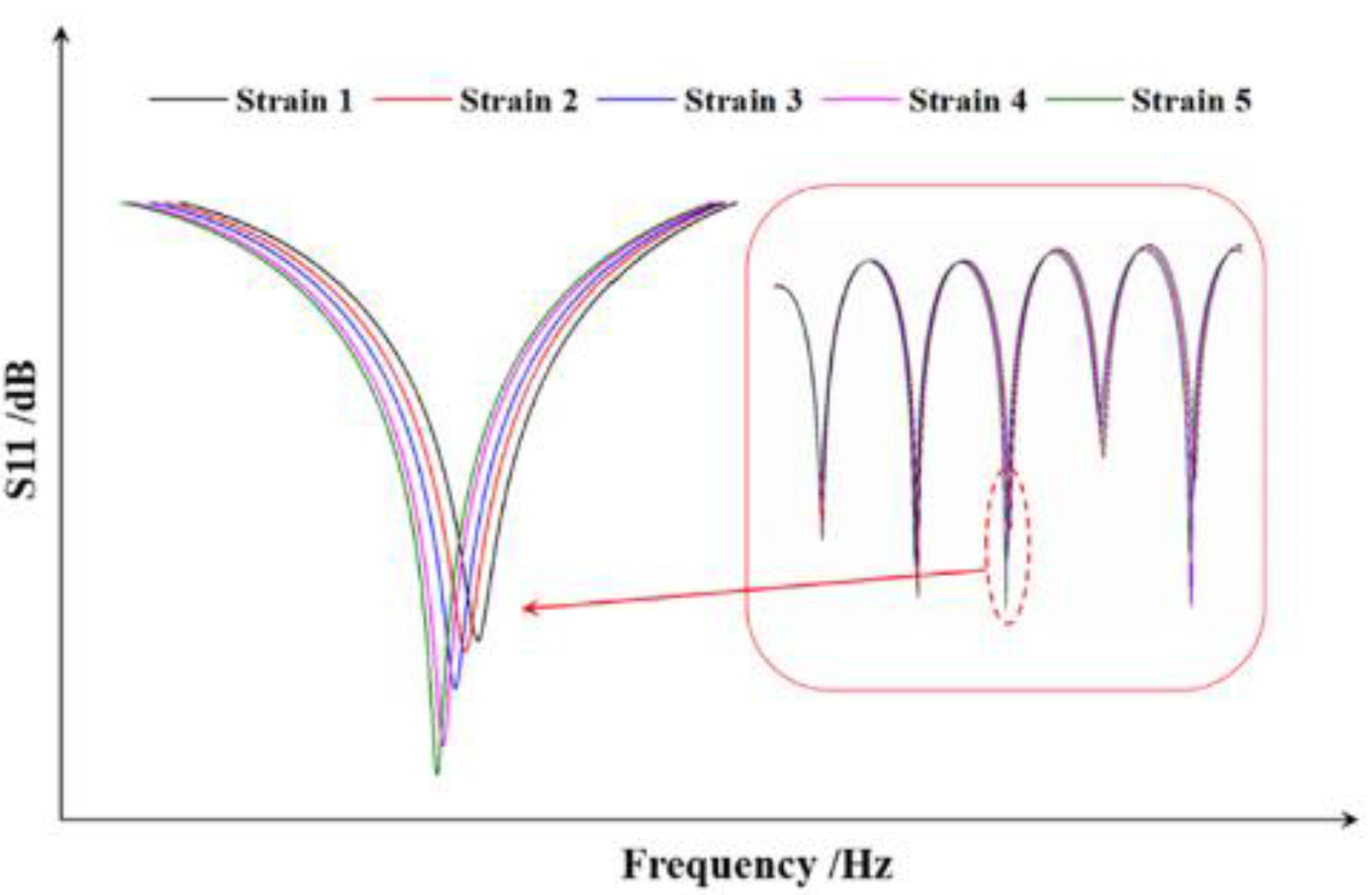
| CCBG | Axial strain sensor | RG58 | Holes | 1.408m (22 periods) | ~4.25GHz | -3kHz/µε | [10] |
| CCBG | Axial strain sensor | RG58 | Holes | 1m (40 periods) | ~4GHz | -2.1kHz/µε | [9] |
| CCBG | Strain sensor | Bespoke | Undulating dielectric | 200mm (10 periods) | ~4.5GHz | ~3.075kHz/µε | [111] |
| Irregular CCBG | Strain sensor | MIL-C_17 | Holes | 2m | 0-6GHz | -5.068 kHz/ µε | [81] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





