Operators in the Hilbert Space: the Ramsey Approach

1. Introduction

In this communication we consider Ramsey graphs emerging from operators defined in Hilbert space [1,2,3]. Ramsey theory, introduced by Frank Plumpton Ramsey, a British philosopher and mathematician, is devoted to the mathematical problems which seek for a sub-structure embedded into a given structure [4]. The well-known problem typical for the Ramsey theory is the so-called “party problem”, which defines the minimum number of persons labeled R(m,n) that must be invited so that at least m are acquainted each with other (they are called “friends” in the notions of the Ramsey theory), or at least n are not acquainted each with other (they are respectively labeled as “strangers”) [5,6,7,8,9]. The well-known result is $R\left(3,3\right)=6.$Important results in the Ramsey Theory were obtained by Paul Erdős, Ronald Graham and their collaborators [5,8,9]. When Ramsey Theory is formulated in the terms of the graph theory, it claims that any graph will necessarily contain an interconnected sub-graph [7,8,9,10,11,12,13]. The Ramsey theorem, reshaped in the notions of the theory of graphs, states that one will find monochromatic cliques in any edge color labelling of a sufficiently large complete graph [7]. In our communication, we address the Ramsey graphs emerging from operators acting in the Hilbert space. Applications of the introduced approach to quantum mechanics is discussed.

2. Ramsey Graphs Generated by Sets of Operators

Consider the Hilbert space $L^2.$ Let $\left(a,b\right)$ denote a finite (or infinite) interval on the real axis [1]. We denote $L^2\left(a,b\right)$ (or simply $L^2)$ the set of all complex value Lebesgue measurable functions f defined on $\left(a,b\right)$ such as ${\left|f\right|}^2$ is a Lebesgue integral on $\left(a,b\right).$ A pair of functions which differ only on a set of measure zero are not considered as distinct elements of $L^2$ [1]. Let D denote a subspace of $L^2.$ Consider the set of operators $\left\{T_i, i=1,\dots N\right\}$, each of one relates to each element $f\in D$; a particular element $T_{i}f=g\in L^2$ ; operators $\left\{T_i\right\}$ are defined in space $L^2$ with domain D. Let us assume that some of operators $\left\{T_i\right\}$ commute, and some of them do not commute. The operators commute (they are “friends” in terms of the Ramsey Theory) if Eq. 1 takes place:

$$\left[T_i,T_k\right]=T_i{T}_k-T_k{T}_i=0, i,k=1,\dots N$$

(1)

The operators do not commute (they are, in turn, “strangers”) if Eq. 2 is true:

$$\left[T_i,T_k\right]=T_i{T}_k-T_k{T}_i\ne 0, i,k=1,\dots N$$

(2)

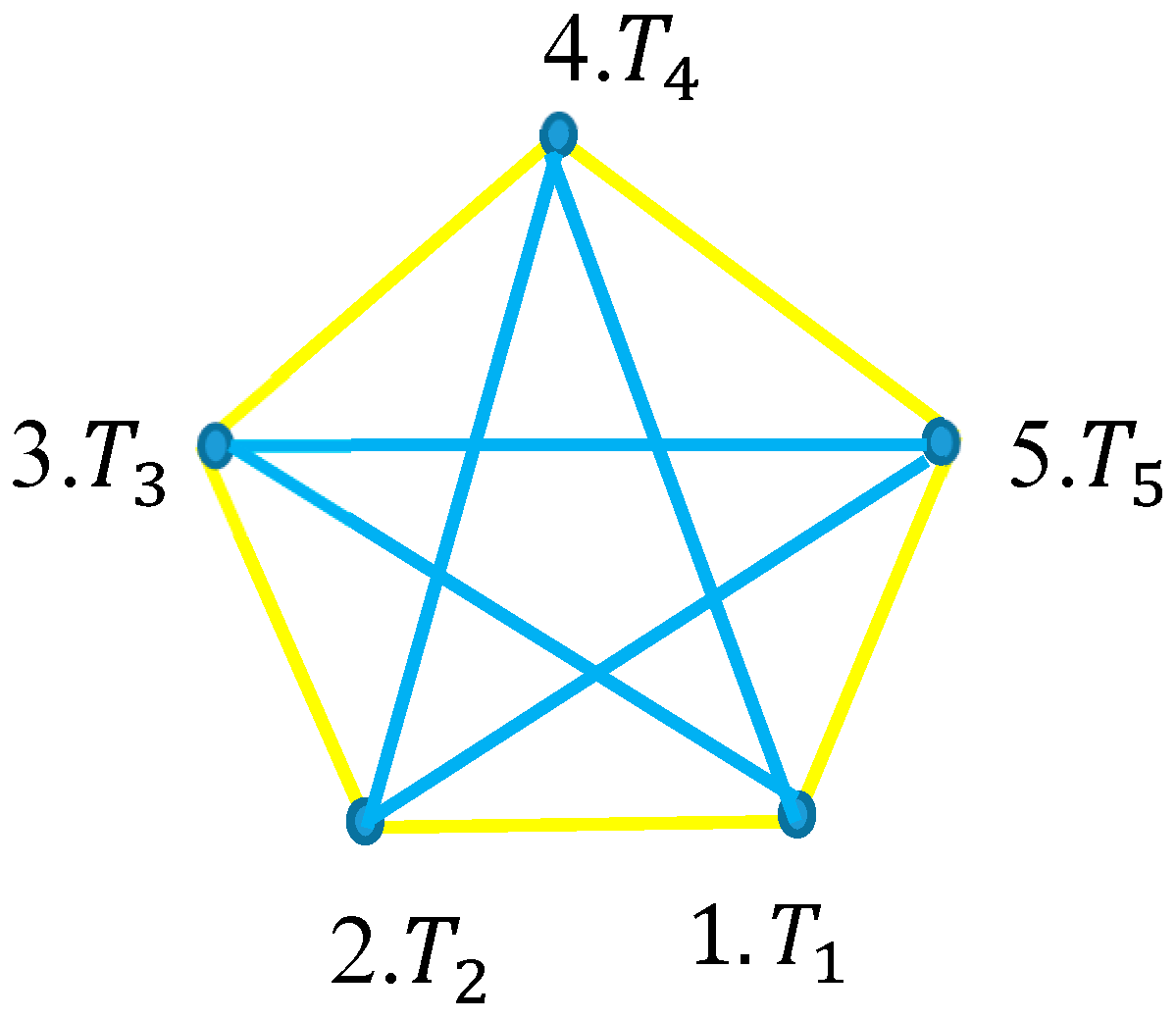
Thus, the Ramsey analysis becomes possible, when operators $\left\{T_i\right\}$ serve as a vertices of the graph. If the operators commute, they are joint with a yellow edge. If they do not commute, they are joint with a blue edge. Thus, the complete, bi-colored, non-directed, Ramsey graph is formed. Let us illustrate the introduced coloring procedure, with the graph, shown in Figure 1. It should be stressed, that commuting of operators is suggested to be non-transitive [13]; this is important for our future treatment.

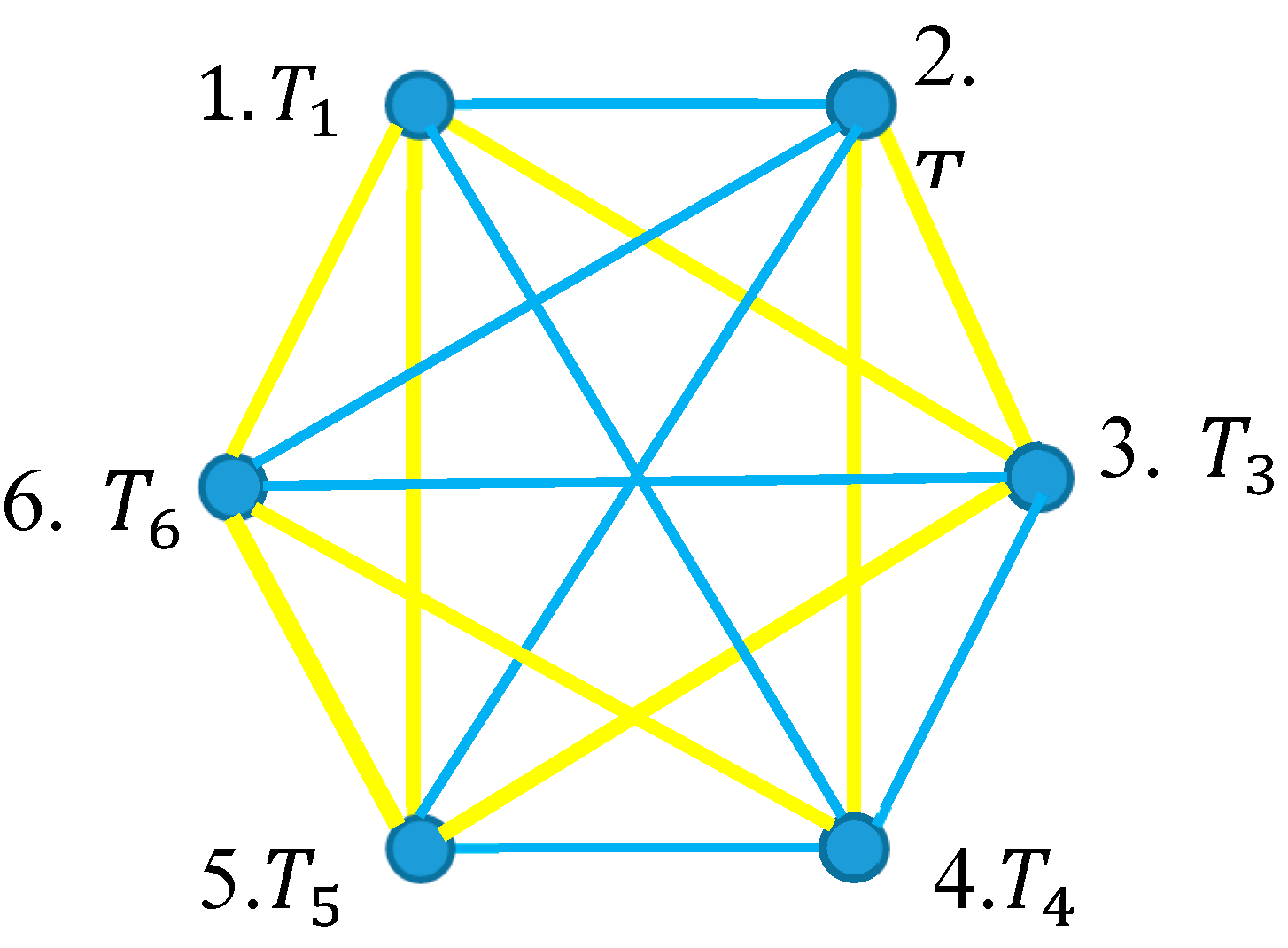
Consider the graph depicted in Figure 1: no monochromatic triangle is recognized in the graph built of five vertices/operators. This is quite understandable; indeed, the Ramsey number $R\left(3,3\right)=6.$ Now consider the bi-colored, complete, Ramsey graph emerging from six commuting/non commuting vertices/operators $\left\{T_i, i=1,\dots 6\right\}$, shown in Figure 2.

Any two operators that commute, have a common set of eigenfunctions, provided only that each has a complete set of eigenfunctions [1]. In other words, the operators do not necessarily have to be Hermitian, unitary, anti-Hermitian, etc. [1]. Thus, a triad of operators $\left\{T_1,T_3,T_5\right\}$ have a common set of eigenfunctions. It should be stressed, that that triad of non-commuting operators, forming a “blue” triangle may appear in the graph. The Ramsey Theorem does not fix the color of the monochromatic triangle, which will be found in the bi-colored, complete graph built of six vertices.

Thus, following theorem is proved:

Theorem 

Consider the graph emerging from six vertices/operators $\left\{T_i, i=1,\dots 6\right\}$ defined in the Hilbert space $L^2$. The operators are joint with a yellow link, when they commute; the operators are joint with a blue link, when they do not commute. At least one monochromatic (yellow or blue) triangle will be necessarily found in the graph.

3. Ramsey extension for the infinite sets of operators

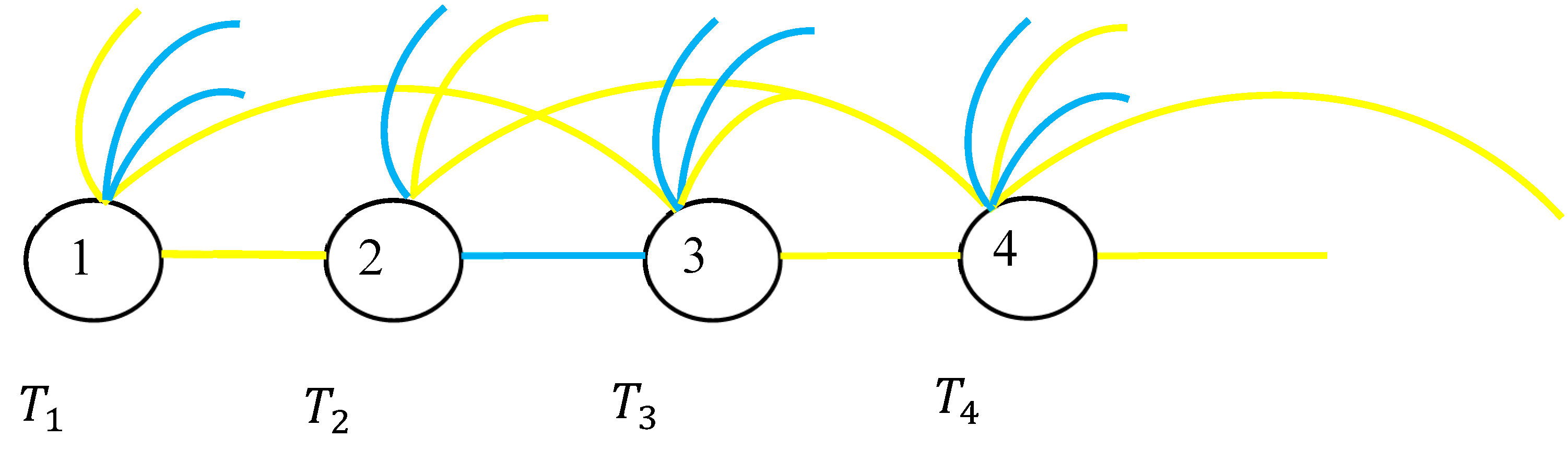
Consider infinite, however, countable set of operators $\left\{T_i, i=1,2,\dots \right\}$ defined in the Hilbert space $L^2$. This set generates infinite bi-colored graph, illustrated with Figure 3, when operators $\left\{T_i, i=1,2,\dots \right\}$ serve as vertices and coloring of the edges is defined by Eq. (1) and Eq. (2). According to the infinite Ramsey theorem there must be necessarily present an infinite monochromatic clique in the aforementioned graph (a clique of the undirected graph is a subset of vertices of the graph; every two distinct vertices in the clique are adjoining) [14].

Thus, an infinite monochromatic clique of operators will be necessarily be found in the graph. This proves the following theorem:

Theorem 

Consider infinite, however countable set of operators $\left\{T_i, i=1,2,\dots \right\}$ defined in the Hilbert space $L^2$. Operators $\left\{T_i, i=1,2,\dots \right\}$ act as the vertices of the infinite graph. The operators are joint with the yellow edge, when they commute; the operators are joint with a blue edge, when they do not commute. Infinite monochromatic clique will necessarily be found in the graph.

If this clique is “yellow” the operators forming the clique have a common set of eigenfunctions. The operators do not necessarily have to be Hermitian, unitary or anti-Hermitian. Again, the exact color of the infinite monochromatic clique remains unknown.

4. Discussion and applications

The mathematical technique enabling converting of sets of operators into the bi-colored, complete, non-directed, Ramsey graph is suggested. The operators play a role of the vertices of the graph. The dual relations between operators are prescribed by the relations of commutation between the operators. The introduced approach is applicable for the analysis of the motion of the rigid body and problems of quantum mechanics. Indeed, translations and rotations of a rigid body may be represented by the commuting and non-commuting operators of translations/rotations [15,16,17]. Observables of quantum mechanics (coordinates, energy, momenta, angular momenta, etc.) are also the commuting and non-commuting operators [19,20,21]. Thus, the introduced approach is also applicable for the quantum mechanics.