Prerpints.org logo
Preprint
Article

A Novel Bio-Inspired 3DOF Spherical Robotic Manipulator

Altmetrics

Downloads

56

Views

29

Comments

0

Submitted:

06 December 2024

Posted:

06 December 2024

You are already at the latest version

Alerts
Abstract
Studying the interactions between biological organisms and their environment provides engineers with valuable insights for developing complex mechanical systems, and fostering the creation of novel technological innovations. In this study, we introduce a novel bio-inspired three degrees of freedom (DOF) spherical robotic manipulator (SRM), designed to emulate the biomechanical properties observed in nature. The design utilizes the transformation of spherical Complex Spatial Kinematic Pairs (CSKPs) to synthesize bio-inspired robotic manipulators. Additionally, the use of screw theory and the Levenberg-Marquardt algorithm for kinematic parameter computation supports further advancements in human-robot interaction and simplifies control processes. By directly transmitting motion from the motors, the platform replicates the ball and socket mobility observed in biological joints, while minimizing mechanical losses and optimizing energy efficiency, thereby ensuring superior performance in spatial mobility. The proposed 3DOF SRM provides advantages including an expanded workspace, enhanced dexterity, and a lightweight, compact design. Experimental validation, conducted through SolidWorks, MATLAB, Python, and Arduino, demonstrates the versatility and broad application potential of the novel bio-inspired 3DOF SRM, positioning it as a robust solution for a wide range of robotic applications.
Keywords: 
Subject: Engineering  -   Mechanical Engineering

1. Introduction

Humans and animals possess complex body structures optimized for movement, enabling efficient interaction with their environments. Through this intelligent design, they have developed various joint types, including those with 3DOF, to adapt to their specific functional requirements (Figure 3b). In the literature review, detailed analyses of 3 DOF joints, such as the shoulder, hip, ankle, fin, and wing structures in various organisms, as well as 3 DOF mechanisms and robots, have been conducted. These studies highlight the complexity and adaptability of these systems across biological and engineered models.
Adams et al. (2016) analyzed the 3DOF glenohumeral joint in humans, emphasizing stabilizing structures, while Bakhsh & Nicandri (2018) expanded on its versatile motion. De Lange et al. (1985) and Han et al. (2024) explored wrist 3DOF, with Han focusing on rehabilitation modeling. Molini et al. (2011) and Kumar et al. (2023) studied the hip joint’s diagnostic potential and biomechanics. Brockett and Chapman (2016) analyzed ankle 3DOF, while Pol et al. (2021) addressed age-related mobility decline.
In animals, Arias-Martorell (2019) highlighted chimpanzees’ flexible 3DOF shoulder joints, while Larson (1993) and Larson (1995) explored functional variations in gorillas and orangutans. Evans & de Lahunta (2012) and Reis Silva et al. (2013) examined 3DOF joints in dogs, and Manafzadeh (2023) studied large carnivores like lions and cheetahs. Bledt et al. (2019) modeled these mechanics in the MIT Cheetah, while Becker et al. (2019) and Böhmer et al. (2020) studied joint mobility in horses, deer, and cheetahs. Brocklehurst et al. (2022) explored 3DOF shoulder joints in reptiles and marsupials. Gatesy et al. (2022) developed a 3DOF framework for guineafowl and alligators, expanded by Kambic et al. (2017) for bipedal locomotion. Stowers et al. (2017) and Baier et al. (2013) linked 3DOF flight mechanics in pigeons and Chukar Partridges. Fish fin dynamics, explored by Lauder and Tangorra (2015) [24], inspired bio-robotic designs such as Sudki et al.’s (2013) marine propulsor. Cortés Torres et al. (2024) and Pandey et al. (2013) applied 3DOF modeling to robotic fins and amphibious systems, respectively.
The initial wrist mechanism, described by Torii et al. (1990) [28], focuses on industrial robots that require powerful actuators. In contrast, Gosselin and Hamel (1993) developed the Agile Eye, refined by Gosselin et al. (1996) [30], who noted motion limitations. Leguay-Durand et al. (1997) enhanced dexterity with a redundant manipulator, while Vischer et al. (2000) and Birglen et al. (2002) focused on Argos and SHaDe, emphasizing industrial efficiency and user interaction, respectively. Lum et al. (2006) optimized a surgical mechanism, paralleled by Schuler et al. (2006) for space applications. Yu (2007) and Hess-Coelho (2007) developed 3DOF mechanisms focusing on compactness and rigidity, with Inada et al. (2009) introducing a lightweight wrist joint and Yu et al. (2009) improving smoothness. Wu et al. (2014) optimized a spherical manipulator facing similar challenges as Degirmenci et al. (2015) in microsurgery. Sadeqi et al. (2017) focused on a hip exoskeleton, while Lee et al. (2018) developed a human-machine interface to reduce interference. Li et al. (2018) introduced a spherical motion generator, while Bai et al. (2019) reviewed rehabilitation advances.
Hofer and D'Andrea (2020) emphasized simplicity in robotic arms, contrasting with Abe et al. (2021) [47], whose ABENICS mechanism is more functional and complex. Rommers et al. (2021) and Choi et al. (2022) developed flexure joint and microsurgical designs, respectively. Howard (2023) highlighted cost-effective solutions, while Ghaedrahmati and Gosselin (2023) focused on wrist-gripper systems. Zhang et al. (2023) developed a compact robotic wrist, with Schröder et al. (2023) advancing spherical robot control. Djennane et al. (2024) introduced a precise 3DOF manipulator, and Zhang et al. (2024) [55, 56] focused on rehabilitation and ultrasound technologies.
Krebs et al. (2007) and Pehlivan et al. (2014) developed 3DOF devices for stroke rehabilitation, with a focus on wrist and forearm improvements. Fite et al. (2008) and Fan et al. (2016) created prosthetics, with Fite’s gas-actuated arm offering more DOF and Fan’s wrist prosthetic covering most daily tasks. Amirabdollahian et al. (2014) and Singh et al. (2019) both targeted home-based stroke rehabilitation, while Jarrassé et al. (2010) and Rose et al. (2015) focused on transparency in human-robot interaction. Pezent et al. (2017) improved RiceWrist-S ergonomics, and Bajaj et al. (2019) emphasized dexterity in wrist mechanisms. Li et al. (2020) introduced an ankle rehab robot, and Vertongen et al. (2020) reviewed lightweight prosthetic systems. Eschweiler et al. (2022) examined wrist biomechanics for clinical use.
Soltanov et al. [70, 71, 72] contributed to structural synthesis of robot manipulators, improving dynamic performance, motion control, and design for industrial and medical applications. Yousaf et al. (2021) and Amal et al. (2024) explored bioinspired designs in MAVs and marine robotics, respectively. Morgansen et al. (2007) and Kim et al. (2012) developed bioinspired underwater robots, focusing on efficient mobility, similar to Li et al. (2024) with a biomimetic pectoral fin. Wyrobek et al. (2008) and Mahmoud et al. (2011) emphasized modular and safe robotic systems for human interaction, while Chernyak et al. (2012) and Bright et al. (2024) focused on quadrupedal and cheetah-inspired robots for rough terrain and speed. Hammond et al. (2013) and Hu et al. (2024) designed precision wrists for medical tasks, while Hwang et al. (2016) and Hernández-Flores et al. (2024) improved adaptive control in surgical and quadrupedal robots. Kuka AG (2017) and Selvamuthu et al. (2024) advanced precision robotics for industrial and robotic arm applications.
In this study, we present the design and development of a novel bio-inspired 3DOF SRM with advanced spatial mobility, capable of replicating the functional characteristics of a 3DOF joint observed in biological organisms. The proposed 3DOF SRM offers significant improvements over existing systems, including an expanded workspace, enhanced dexterity, and a lightweight, compact form factor. These features position the manipulator as a versatile solution for various applications in fields such as medicine, industrial automation, aerospace, robotics, consumer electronics, and defense.
In the preliminary phase of our research, we focused on human-robot interaction, particularly examining the human hand's medical functionality and the hand-eye coordination process. In the subsequent phase, we applied the transformation of spherical CSKPs to systematically perform the structural synthesis of the 3DOF SRM, accompanied by the determination of its mobility number. Furthermore, we employed the screw theory and Levenberg-Marquardt optimization to solve both forward and inverse kinematics of the 3DOF SRM, ensuring precise motion control and high maneuverability. The design is realized by 3D printing the 3DOF SRM’s components, followed by assembly and comprehensive experimental evaluation. In the final phase of the study, the exploration of human-robot interaction is integrated into the 3DOF SRM as a wrist joint, leading to a more refined and efficient control system that transitions from passive perception to active control through manipulation, thereby enhancing its operational performance. The results are analyzed to validate the performance of the manipulator, demonstrating its potential for widespread application in various technical domains.

2. The Anatomy of the Human Arm and its Implications for Robot Interaction.

The human arm is an intricate and sophisticated system comprised of bones, muscles, tendons, and nerves that work together seamlessly to facilitate a vast range of motion and enable interaction with the environment. In order to design robotic manipulators that can perform tasks similar to those carried out by humans, it is crucial to have a comprehensive understanding of the anatomy of the human arm.
The human arm has a wide range of mobility, including flexion (bending), abduction (moving away from the body's midline), medial rotation (inward rotation), lateral rotation (outward rotation), extension (straightening), pronation (turning the palm down), supination (turning the palm up), and combinations of flexion/abduction and abduction/extension (Figure 1). Among this system, the wrist joint permits movement in the spherical coordinate system, which includes flexion-extension, radial-ulnar deviation, and pronation-supination. Therefore, as a result of our extensive research, we have developed a novel bio-inspired 3DOF SRM that is capable of mimicking the mobility of the human wrist joint by using the method of transformation of spherical CSKPs, as shown in Figure 3a.
Manipulating an object allows us to modify our environment, serving as a crucial connection to the external world. It involves not only physical factors but also anticipating future outcomes. For example, when reaching for a book, visual attention shifts to coordinate motor actions, guided by sensorimotor and visual feedback. The hand approaches the object, adjusts its orientation, and closes around it. Tactile signals confirm contact and any deviation prompts immediate corrective adjustments to achieve the intended outcome. We often adjust our initial approach for end-state comfort [89], a skill that develops over time. Experience also helps us handle fragile, hazardous objects, or handovers [90], guided by prior knowledge and the action's intended purpose.
Dexterous manipulation follows a consistent hand-arm kinematic pattern, where hand aperture peaks according to object size before closing upon contact, as observed by Jeannerod and confirmed in further studies exploring other object and kinematic factors. However, individuals with neurological conditions like Dyspraxia, or Developmental Coordination Disorder (DCD), experience difficulty in planning and executing movements [92]. This impairment in hand-eye coordination often results in challenges during object interactions, such as unintentional dropping or breakage. The eyes must accurately assess distance and object placement during movement, which can be especially difficult for individuals with DCD (Figure 1).
Consequently, the second phase of our research focuses on simplifying the control system of the novel bio-inspired 3DOF SRM, enhancing precision and reliability in object manipulation (Figure 8).

3. Design and Methodology of the Novel Bio-Inspired 3DOF SRM

This section systematically outlines the development of a novel class of robotic manipulators, emphasizing the transition from conceptual to analytical design principles. The research involves structural synthesis by examining the interactions between geometric entities and their transformation into robotic manipulators. Our current focus is on designing a bio-inspired 3DOF SRM, where the end effector's motion is mapped within a spherical coordinate system. A key aspect of this design process is the analysis of the end effector’s movement trajectory, which necessitates a thorough investigation of the mobility within spherical CSKPs.
In this context, the mobility of two concentric spheres depicted in Figure 2a serves as a fundamental spherical CSKPs. A sphere with center O 2 and radius r is positioned concentrically within a fixed sphere of center O 1 and radius R , forming a system with 3DOF. This connection is exemplified in biological organisms by the ball and socket joint. These DOFs correspond to rotational motions about the x , y , and z axes, represented by the angles α , β , and γ , respectively, thereby constituting a higher-order kinematic pair. By establishing a spherical coordinate system on sphere 2, the motion equation for any point P on this sphere relative to sphere 1 can be determined, facilitating the precise control and movement of the end effector within the spherical coordinate system.
The platform of the novel 3DOF SRM, structurally synthesized from the transformation of the spherical CSKPs, exhibits the same spatial mobility, denoted as { λ i   } 1 3 , as sphere 2. In the design of this novel bio-inspired 3DOF SRM, we employ revolute kinematic pairs along each coordinate axis ( A x i s 1 ,   A x i s 2 ,   A x i s 3 ) to achieve the desired spherical motion. These revolute joints drive the arms, which function as the generator of the spheres, maneuvering the mobile platform relative to the fixed reference frame of sphere 1, which serves as the support in Figure 2b. Furthermore, it is feasible to select the grounding points ( G 1 ,   G 2 ,   G 3 ,   G 4 ) for the novel 3DOF SRM at any arbitrary location on the stationary sphere 1, providing flexibility in the system’s configuration.
To determine the mobility and kinematic parameters of the mobile platform in the novel bio-inspired constrained 3DOF SRM, it is essential to analyze the mobility and kinematics of the spherical CSKPs for the specified configuration. The rotational motion of the spherical CSKPs about the x and y axes can be represented using the rotation matrices R x ( α ) and R y ( β ) , as shown in Equation (1).
R x ( α ) = [ 1 0 0 0 cos ( α ) − sin ( α ) 0 sin ( α ) cos ( α ) ] ,   R y ( β ) = [ cos ( β ) 0 sin ( β ) 0 1 0 − sin ( β ) 0 cos ( β ) ]
where the angles α and β represent the rotations about the x and y axes, respectively. To achieve simultaneous rotation about both axes, the product of the R x ( α ) and R y ( β ) matrices must be defined, as shown in Equation (2).
T = R x ( α ) R y ( β ) = [ cos ( β ) 0 sin ( β ) sin ( α ) sin ( β ) cos ( α ) − cos ( β ) sin ( α ) − cos ( α ) sin ( β ) sin ( α ) cos ( α ) cos ( β ) ]
This transformation matrix T represents the combined rotational motion around the x and y coordinate axes at angles α and β . If we attempt to rotate the sphere simultaneously along both axes, the result is a rotation around a diagonal axis passing through the sphere's center. This outcome is explained by Euler's rotation theorem, which states that any arbitrary rotation can be represented as a single rotation around a unique axis [93]. Therefore, under the given conditions, it is impossible to achieve independent rotations along both the x and y axes simultaneously with a fixed center point.
The kinematic parameters of the novel bio-inspired constrained 3DOF SRM's mobile platform are obtained in the next step by applying the transformation matrix ( T ) on the spherical CSKPs to the selected central coordinate origin and point ( P ) with radius r. In order to represent a point P on sphere 2, we can utilize spherical coordinates ( r ,   φ ,   θ ), where the polar angle (measured from the positive z -axis) is represented by φ and the azimuth angle (measured from the positive
-axis) is represented by θ (Figure 2a). In order to obtain the kinematic parameters, we need to convert the given spherical coordinates into Cartesian coordinates ( x , y , z ) using the following formula (3):
{ x = r s i n ( θ ) c o s ( φ ) y = r s i n ( θ ) s i n ( φ ) z = r c o s ( θ )
In the subsequent stage, we can calculate the position vector ( P x y z ) of point P after rotation by multiplying the transformation matrix ( T ) with the transformed coordinates (3), which can be expressed as follows (4):
P x y z = T [ x y z ] = [ r s ( β ) c ( θ )   +   r c ( β ) c ( φ ) s ( θ ) r c ( α ) s ( φ ) s ( θ )   −   r c ( β ) s ( α ) c ( θ )   +   r c ( φ ) s ( α ) s ( β ) s ( θ ) r c ( α ) c ( β ) c ( θ )   +   r s ( α ) s ( φ ) s ( θ )   −   r c ( α ) c ( φ ) s ( β ) s ( θ ) ]
The P x y z matrix (4) obtained will serve to characterize the displacement of the mobile platform for any given instant of time in the novel bio-inspired constrained 3DOF SRM. The matrix P x y z will consist of post-rotation state vectors of the point P for each row element, where the state vectors correspond to the coordinates x t , y t , and z t . We can consider the parameters θ and φ of the spherical coordinate system, placed in the spherical CSKPs, as constant, while the parameter r can be defined as the synthesis parameter and remains variable. The Jacobian matrix ( J ) is used to determine the linear velocity of point P on sphere 2 and the mobile platform simultaneously, as shown in equation (5).
J = T R z ( φ ) R y ( θ ) [ 0 − c ( β ) s ( φ ) c ( φ ) 0 s ( β ) s ( θ ) − c ( β ) c ( φ ) c ( θ ) − s ( φ ) c ( θ ) 1 0 0 ] [ 1 0 0 0 r 0 0 0 r ]
The matrix J (5) contains linear velocity vectors of point P after rotation along the x , y , and z axes represented by V x t , V y t , and V z t respectively. The term R is excluded from equation (5) because the Jacobian matrix concerns the linear velocity of the mobile platform, with the stationary sphere acting as a fixed reference point. The determinant of the Jacobian matrix is utilized to extract valuable information regarding the kinematic behavior of the designed novel bio-inspired constrained 3DOF SRM (6), including singular configuration, volume expansion, and contraction. The relationship between the kinematic and geometric parameters of the novel bio-inspired constrained 3DOF SRM is established through the determinant, which defines the motion of the moving sphere 2 relative to the fixed sphere 1 as a scaling factor, represented by the ratio r / R (where R   =   1 in this particular case), capturing the interaction between these parameters.
det ( J ) = r a t i o 2 ( c ( β ) c ( θ ) − s ( β ) c ( φ ) s ( θ ) )
The formula (7) is used to determine the angular velocity of point P on both sphere 2 and the mobile platform simultaneously.
ω = J − 1 [ V x t V y t V z t ]  
Each row element ω x t , ω y t , and ω z t of the obtained ω matrix (7) will be the post-rotation angular velocity vectors of point P respectively. As a result, the kinematic parameters such as displacement, linear velocity, and angular velocity of the mobile platform of the novel bio-inspired constrained 3DOF SRM can be determined using formulas (4), (5), and (7) for any selected point on it.
The equation (8) demonstrates the representation of a rigid body's velocity (sphere2 or moving platform) as a point in ℝ 6 by utilizing a spatial velocity or twists ( V t w i s t ), which is a combination of three angular and three linear velocities.
V t w i s t = [ ω x t ω y t ω z t V x t V y t V z t ]   ∈   ℝ 6
Based on the geometric and mathematical analysis conducted, it has been determined that the mobility of the mobile platform in the novel bio-inspired constrained 3DOF SRM, designed by transforming the spherical CSKPs mirrors the spatial mobility of the spherical CSKPs. Consequently, the spatial mobility, denoted as { λ i   } 1 3 , can be established through a defined process: first, rotating one arm around a chosen coordinate axis ( A x i s 1 ) and returning it to its original position, followed by the rotation of the second arm ( A x i s 2 ) in a similar manner. Additionally, the mobile platform of the novel bio-inspired constrained 3DOF SRM can perform unrestricted rotational motion ( γ ) around the z -axis ( A x i s 3 ) at any spatial position. This constrained configuration is well-suited for applications where spherical arms and the body are subjected to high loads, such as in robotic arms or legs undergoing heavy weight-bearing, rocket maneuvers, or bio-inspired underwater robotic systems. It helps prevent motor overload, ensuring reliable and efficient operation under demanding conditions.
To achieve smooth 3DOF motion of the mobile platform within a spherical space and eliminate the joint constraint in the novel bio-inspired constrained 3DOF SRM (as illustrated in Figure 2b), two movable spherical platforms are introduced by releasing one of the spherical arms (previously fixed sphere1). Figure 3a demonstrates the newly designed bio-inspired 3DOF SRM, which mimics the ball and socket joint movement observed in biological systems, as shown in Figure 3b.
Through our research process, we have formulated and presented the following three axioms, which establish a foundational basis for developing this type of novel bio-inspired robotic manipulator.
Axiom 1: Kinematic pairs that converge at a point, line, or surface, based on theoretical geometric parameters such as coordinate systems, angles of rotation, planes of symmetry, or imaginary axes within spatial configurations, are classified as Complex Spatial Kinematic Pairs (CSKPs).
Axiom 2: By selecting supports on the kinematic pairs that form Complex Spatial Kinematic Pairs, a mobile platform can be created with the same degree of freedom as those kinematic pairs.
Axiom 3: The kinematic parameters of the end effector in the robotic manipulator, developed through the transformation of Complex Spatial Kinematic Pairs, will reflect the kinematic parameters inherent to those kinematic pairs.
The novel bio-inspired 3DOF SRM, illustrated in Figure 3a, features a sequential configuration, where the number of revolute pairs ( ∑ i = 1 j f i = 3 ) directly corresponds to its degree of freedom ( M   =   3 ). At this stage, the motion is directly transmitted from the motors to the spherical arms and the mobile platform of the novel bio-inspired 3DOF SRM, minimizing slippage, wear, and the number of mechanical components. This direct transmission also lowers energy consumption during operation, leading to a more dexterous, compact, reliable, and cost-efficient design. Furthermore, one of the notable advantages of the proposed design is the ability to modify the manipulator's support, as shown in Figure 3a, to adapt it to various joints found in biological organisms, as illustrated in Figure 3b. The designed spherical platform mirrors the structure of a spherical ball bearing, facilitating the potential attachment of an additional redundant spherical arm if necessary. Redundant configurations in robotic manipulators are often crucial for enhancing flexibility, dexterity, and fault tolerance. In the case of the novel bio-inspired 3DOF SRM (Fig. 3), this redundancy can be implemented through the symmetrical arrangement of the support and spherical arm, thereby improving the system's adaptability to various tasks and operational conditions. This design not only increases the system’s reliability but also contributes to its robustness in complex environments.

3.1. Degree of Freedom Calculations for the Novel Bio-Inspired 3DOF SRM

Determining the DOF in robotic manipulators is a fundamental process, as it provides a comprehensive understanding of the number of independent movements that the system can perform. This insight is critical for both the precise design and the accurate control of the robot’s motion, ensuring that the manipulator operates with maximum efficiency and optimal performance. Understanding the DOF is essential for preventing self-collisions and avoiding interference with external objects, thus contributing to the overall safety and reliability of the system. The DOF of the novel bio-inspired 3DOF SRM, depicted in Figures 2b and 3, can be calculated using the Euler and Kutzbach formulas [94, 95], as shown in Equation (9), since the constraints imposed by the kinematic pairs are not entirely independent.
M = λ L + ∑ i = 1 j f i + q ,   L = l − j − 1
where
j – is the number of joints in the manipulator;
l – is the number of links in the manipulator;
λ – closed loop motion parameter that describes the positions and orientations of the couple in the loop; f i – DOF of kinematic pairs on the manipulator;
q – is the number of independent coordinates required to describe the motion.
For the given expressions, we can calculate the complete count of constraints { d } 0 5 within the subspace of the end effector as follows (10):
d = 6 − λ
By inputting the values of l =4, j =4, λ =3, ∑ i = 1 j f i = 5 , and q =1 into the novel 3DOF SRM shown in Figure 2b, we can determine its DOF to be M =3. Since Figure 3a represents an open configuration, both configurations maintain a degree of freedom of M   =   3 .
In addition to defining movement capabilities, calculating the DOF optimizes mechanical design by preventing over- or under-constraining, improving energy efficiency, and reducing wear. It also aids in integrating control algorithms to enhance precision and responsiveness, ensuring the manipulator operates efficiently in dynamic environments.

4. Kinematic Analysis of the Novel Bio-Inspired 3DOF SRM

The introduction of the geometric entities transformation approach, which integrates both forward and inverse kinematics concepts, is significantly enhanced by the application of the screw theory. This methodology provides a cohesive and comprehensive framework for elucidating the intricate relationship between joint motions and end-effector movements. Such a holistic perspective fosters a more intuitive understanding of the robot's behavior, thereby facilitating improved decision-making regarding trajectory planning, obstacle avoidance, and overall system optimization.
The kinematic structure of the proposed manipulator is designed with two revolute pairs that drive concentric arcs, in addition to a third revolute pair located on a platform (Figure 4). In this specific isocenter configuration, the joints of the manipulator are arranged such that all perpendicular axes intersect at a common point. The centers of the arcs, designated as O 1 and O 2 , are positioned at specific locations as illustrated in Figure 4.
According to Chasles-Mozzi's theorem [96], it is a well-established principle that any rigid body displacement can be effectively represented as a motion along a fixed screw axis S within three dimensional space. Brockett demonstrates that the forward kinematic equations of an open chain robot, comprising either revolute or prismatic joints, can consistently be expressed as a product of matrix exponentials. This underscores the significance of the product of exponentials (PoE) formula as a valuable modeling tool in robot kinematics.
In the subsequent phase, the PoE representation is employed to determine both the position and orientation of the end effector, which is to be positioned on the mobile platform of the novel bio-inspired 3DOF SRM, using a forward kinematic approach. In our design, for the fixed frame { s } and the end-effector frame { b } as illustrated in Figure 4, the forward kinematics in PoE formulation is represented as follows (11):
T ( θ ) = e [ S 1 ] θ 1   e [ S 2 ] θ 2   e [ S 3 ] θ 3   M
The zero position configuration of the end effector, denoted as M , is defined by the following equation (12):
M = [ 0 0 − 1 − r 0 1 0 0 1 0 0 R 0 0 0 1 ]
The values of the screw parameters S i = ω i ,   v i are listed in the following Table 1:
The variables ω i , q i , and V i represent the angular velocity, coordinate, and linear velocities, respectively, for each frame i of the zero position of the designed manipulator, as listed in Table 1.
The kinematic matrix T ( θ ) , which represents the orientation and position of the selected point { b } on the z rotation axis of the novel bio-inspired 3DOF SRM, with respect to the fixed frame { s } at any given moment, is defined as follows (13):
T ( θ ) = [ − c 1 s 2 c 3 − s 1 s 3 c 1 s 2 s 3 − s 1 c 3 − c 1 c 2 R c 1 s 2 −  rc 1 c 2 −  R ( s 1 s 3 +  c 1 c 3 s 2 ) − s 1 s 2 c 3 + c 1 s 3 s 1 s 2 s 3 + c 1 c 3 − s 1 c 2 R ( c 1 s 3 −  c 3 s 1 s 2 ) −  rc 2 s 1 +  Rs 1 s 2   c 2 c 3 − c 2 s 3 − s 2 Rc 2 c 3 −  R ( c 2 −   1 ) −  rs 2 0 0 0 1 ]
where, the variables c 1 ,   c 2 ,   c 3 , and s 1 ,   s 2 ,   s 3 in the matrix (13), represent the trigonometric functions cosine and sine of angles θ 1 ,   θ 2 , and θ 3 respectively.
The Jacobian J s ( θ ) , which establishes the relationship between the angular velocity of the end effector and the linear velocity of the joints of the designed novel bio-inspired 3DOF SRM, is determined by the following formula (14):
J s ( θ ) = [ ω S 1 ω S 2 ω S 3 V S 1 V S 2 V S 3 ] = [ 0 sin ( θ 1 ) − cos ( θ 1 ) cos ( θ 2 ) 0 − cos ( θ 1 ) − cos ( θ 2 ) sin ( θ 1 ) 1 0 − sin ( θ 2 ) 0 R cos ( θ 1 ) 0 0 R sin ( θ 1 ) − r sin ( θ 2 ) 0 0 r cos ( θ 2 ) sin ( θ 1 ) ]
The post-rotation angular and linear velocities for each joint of the novel 3DOF SRM can be expressed as follows: ω S 1 = [ 0 ,   0 ,   1 ] ′ , ω S 2 = [ sin ( θ 1 ) ,   − cos ( θ 1 ) ,   0 ] ′ , ω S 3 = [ − cos ( θ 1 ) cos ( θ 2 ) ,   − cos ( θ 2 ) sin ( θ 1 ) ,   − sin ( θ 2 ) ] ′ and V S 1 = [ 0 ,   0 ,   0 ] ′ , V S 2 = [ R cos ( θ 1 ) ,   R sin ( θ 1 ) ,   0 ] ′ , V S 3 = [ 0 ,   − r sin ( θ 2 ) , r cos ( θ 2 ) sin ( θ 1 ) ] ′ .
The spatial velocity or twist of the end effector of the novel bio-inspired 3DOF SRM can be calculated by utilizing the formula (15) and taking into account the given velocities ( θ ˙ = [ θ 1 ,     ˙ θ 2 ,     ˙ θ 3 ˙ ] ′ ) as follows:
V t w i s t = J s ( θ )   θ ˙

4.1. Inverse Kinematic Analysis of the Novel Bio-Inspired 3DOF SRM

Inverse kinematics is a fundamental aspect of robotic manipulators as it allows for the determination of joint angles and positions required to achieve a desired end-effector configuration ( T ( θ ) ). This capability is essential for controlling the movement and positioning of robotic arms in various applications such as industrial robotics, medical robotics, mobile robotics, animation, virtual reality, and computer graphics. When it comes to achieving inverse kinematics, there are several approaches available, including analytical solutions, closed-form solutions, numerical optimization methods, geometric methods, and machine learning-based techniques.
Numerical optimization methods play a crucial role in the inverse kinematics of robotic manipulators, as they provide an advantageous approach for solving complex mathematical equations and constraints, allowing for accurate and efficient determination of joint angles and positions, leading to improved robot control, motion planning, and task execution. These methods allow for a more flexible and adaptable approach to problem-solving, enabling researchers to tackle intricate scenarios that would otherwise be challenging or impossible to solve analytically. Even if an analytic solution is theoretically possible, it is often advantageous to employ numerical optimization methods to improve the accuracy of the results.
In this study, the implementation of the inverse kinematics problem for a novel bio-inspired 3DOF SRM is carried out by utilizing the Levenberg-Marquardt numerical optimization algorithm [98, 99]. The Levenberg-Marquardt algorithm is a numerical optimization method that combines the strengths of the Gauss-Newton algorithm and the method of gradient descent. It is designed to solve nonlinear least squares problems, where the goal is to find the parameters that minimize the sum of squared differences between observed and predicted values. In comparison to the Gauss-Newton algorithm, the Levenberg-Marquardt algorithm demonstrates greater robustness, enabling it to converge towards a solution even when the initial guess is far from the desired minimum.
In order to gain a comprehensive understanding of the mathematical expressions underlying the Levenberg-Marquardt algorithm, it is essential to delve into the intricacies of a general nonlinear least squares problem. We have a set of m data points ( x i ,   y i ) and a model function f ( x ,   p ) , where x is the independent variable and p represents the vector of parameters to be optimized. The goal is to find the optimal parameter vector p * = [ θ 1 ′ , θ 2 ′ ,   θ 3 ′ ] T that minimizes the sum of squared residuals (16):
S ( p ) = ∑ i = 1 m [ y i − f ( x ,   p ) ] 2  
The Levenberg-Marquardt algorithm operates by iteratively updating a parameter vector, denoted as p , until convergence is achieved. Each iteration involves computing a search direction, represented as Δ p , which indicates how much each parameter should be updated. The update rule can be expressed as follows (17):
p n e w =   p o l d +   Δ p
The search direction Δ p is obtained by solving a linear system of equations, which involves the Jacobian matrix   J and the residual vector r r e s . The Jacobian matrix J is defined as (18):
J i j = ∂ f ( x i ,   p ) ∂ p j
where ∂ f ( x i ,   p ) ∂ p j denotes the partial derivative of f with respect to the j -th parameter. The residual vector r r e s is defined as follows (19):
r r e s i =   y i −   f ( x i ,   p )
To solve the linear system of equations, the Levenberg-Marquardt algorithm introduces a damping factor λ that controls the trade-off between the Gauss-Newton method (which assumes a locally linear model) and gradient descent (which assumes a locally quadratic model). The update rule for Δ p can be written as (20):
(   J T   J   +   λ   I   ) Δ p   =   J T   r r e s  
where, J T denotes the transpose of the Jacobian matrix, I is the identity matrix, and λ I is added to ensure the system is well-conditioned.
The damping factor λ is adjusted at each iteration based on the improvement in the objective function. If the new parameter vector p n e w leads to a decrease in the objective function, λ is decreased to favor the Gauss-Newton method. Conversely, if the objective function increases, λ is increased to favor gradient descent. This adaptive adjustment of λ allows the algorithm to efficiently navigate through parameter space and converge to a local minimum.
The successful solution of the inverse kinematics for the developed novel bio-inspired 3DOF SRM is achieved by implementing the Levenberg-Marquardt numerical optimization algorithm in the MATLAB program and utilizing the T ( θ ) transformation matrix (13), leading to the determination of the angles [ θ 1 ′ , θ 2 ′ ,   θ 3 ′ ]. The angles θ 1 ′ , θ 2 ′ , and   θ 3 ′ required to determine the new position of the end effector of the robotic manipulator in space can be effortlessly derived by utilizing the expressions of the observed and expected transformation matrices provided below (21):
e [ S 1 ] θ 1 ′   e [ S 2 ] θ 2 ′   e [ S 3 ] θ 3 ′ = e [ S 1 ] θ 1   e [ S 2 ] θ 2   e [ S 3 ] θ 3   M
where, the observed transformation matrix on the right-hand side of expression (21) can be determined by utilizing expression (13), while the expected transformation matrix on the left-hand side.
The Levenberg-Marquardt algorithm is implemented using the " l s q n o n l i n " function in the MATLAB environment. The objective function, called " c a l c u l a t e R e s i d u a l s " , is responsible for computing the residuals between the observed and expected transformation matrices (21) based on the current parameter values. Through an iterative process, the algorithm adjusts these parameters to minimize the residuals. Upon completion of the optimization process, the resulting values of θ 1 ` ,   θ 2 ` and θ 3 ` are extracted from the optimization result.
The Levenberg-Marquardt algorithm continues iterating until a stopping criterion is met, such as reaching a maximum number of iterations or achieving a desired level of convergence. The final parameter vector p * = [ θ 1 ′ , θ 2 ′ ,   θ 3 ′ ] T obtained represents the optimal solution to the nonlinear least squares problem.

5. Experimental Validation and Performance Results of the Novel Bio-Inspired 3DOF SRM

This experimental study aims to rigorously assess the performance of the novel bio-inspired 3DOF SRM, designed as an application of the wrist joint observed in humans (Figure 1). A straightforward control methodology has been developed to compute the target angles (roll ( α ), pitch ( β ), and yaw ( γ )) required for the rotation of the manipulator's mobile platform. The inverse kinematic calculations leverage the specified target orientation to derive the necessary rotational angles for the three motors, thereby facilitating precise control of the manipulator’s movements. Following the theoretical analysis, the dynamic modeling of the system is conducted within the MATLAB environment to facilitate usability. Once the updated 3D CAD model is developed with the appropriate assembly constraints, it is imported into the SimMechanics module of MATLAB for trajectory planning purposes (Figure 5).
In the analyzed system, input signals and their associated constraints are presented as MATLAB functions, allowing for a comprehensive understanding of the sequence of connections between the control system elements and the parameters that require measurement.
Following the theoretical design and simulation phases, the components of the manipulator are fabricated using a 3D printer and subsequently assembled with the aid of three servo motors, as illustrated in Figure 6a. A Teensy 4.0 microcontroller is employed to facilitate connectivity among the various components. The system is powered by a lithium polymer (LiPo) battery, which provides a nominal voltage of 12 volts. This voltage is then regulated to five volts for the microcontroller, encoders, and logic signal levels, while the unregulated voltage is transmitted directly to the controlling motors.
The motion trajectory of the end effector, represented by the reflector indicated by the red sphere in Figure 6a, is analyzed using Python, employing the OpenCV library for object tracking and NumPy for numerical computations. Additionally, MATLAB is integrated into the analysis, and the resulting workspace of the manipulator is illustrated in Figure 6b, demonstrating its operational range along with the corresponding angles.

5.1. Lagrangian Dynamics and Analytical Discussions of the Novel Bio-Inspired 3DOF SRM

The dynamics of the novel bio-inspired 3DOF SRM are theoretically analyzed using the Lagrangian method, based on the homogeneous transformation matrix T ( θ ) as presented in equation (13), to validate the results obtained from the MATLAB Simulink simulations. The Lagrangian ℒ ( q _ ,   q ˙ _ ) , defined as the difference between the system’s total kinetic energy K ( q _ ,   q ˙ _ ) and potential energy P ( q _ ,   q ˙ _ ) , is formulated as (22):
ℒ ( q _ ,   q ˙ _ ) = K ( q _ ,   q ˙ _ ) −   P ( q _ )
In this context, q _ = [ θ 1 , θ 2 , θ 3 ] denotes the generalized joint angles, and q ˙ _ = [ θ 1 ˙ ,   θ 2 ˙ ,   θ 3 ˙ ] denotes their corresponding generalized angular velocities. The equations of motion are derived from the Lagrangian using the Euler-Lagrange equation (23):
F i = d d t ( ∂ ℒ ∂ q i ˙ _ ) − ∂ ℒ ∂ q i _
where, F i denotes the generalized external forces acting on the system, such as torques or external loads, while the angles θ 1 , θ 2 , θ 3 correspond to the roll ( α ), pitch ( β ), and yaw ( γ ) motor angles of the manipulator, respectively. For this study, the analysis is confined to internal forces, with no external forces applied to the system. Consequently, the Euler-Lagrange equation simplifies to F i = 0 . During the analysis, MATLAB's symbolic toolbox is employed to implement constraints on the motor angles to avoid collisions between mechanical components. These constraints around the initial position, set at 90 degrees, are specified as 30 0 ≤ β ≤ 150 0 , 60 0 ≤ α ≤ 120 0 , 0 0 ≤ γ ≤ 180 0 .
To analyze the kinematic and dynamic properties of the examined manipulator, performance measurements are conducted over a 12 second interval, incorporating both simulation and experimental results, as shown in Figure 7. The solid lines represent the outcomes of the simulation for Motor 1, Motor 2, and Motor 3, while the dashed lines illustrate the roll ( α ), pitch ( β ), and yaw ( γ ) angles for Servo X, Servo Y, and Servo Z, as obtained from the experimental data (Figure 7a).
The investigation revealed that the maximum range of motion is ±30 degrees along the roll ( α ) axis, ± 60 degrees along the pitch ( β ) axis, and ± 90 degrees along the yaw ( γ ) axis. Notably, the difference between the simulation and experimental results is found to be less than ± 1 degree, indicating a high level of accuracy in the designed model.
Figure 7b presents the comparative torque profiles obtained from MATLAB Simulink and Lagrangian dynamics for the three motors in the manipulator design. Motor 1 exhibits significant torque fluctuations, peaking at approximately 9.5 × 10 − 4   N m during initial operation, indicating a high torque demand during movement initiation. In contrast, Motor 2 maintains lower and more stable torque values, peaking at 4.6 × 10 − 4   N m , with a brief peak followed by a rapid decline, suggesting a relatively consistent torque requirement. We observe that Motor 3 shows no torque output throughout the duration due to the absence of weight along the z -axis, indicating that this motor does not encounter significant loading under the tested conditions. The maximum torque values for each motor, obtained experimentally via current measurements using the ACHS-7124 Current Sensor Carrier and MG996R Metal Gear servo motors, are marked by star symbols. The comparison between the MATLAB simulation, Lagrangian dynamics, and current sensor data reveals a minor deviation, with a percentage error of approximately 0.21%, demonstrating the accuracy and consistency between the different methods used for torque analysis. This analysis offers valuable insights into the operational limits and capabilities of the manipulator, paving the way for further advancements in robotic design and control strategies.

5.2. Human-Robot Interaction Through the Novel Bio-Inspired 3DOF SRM

In the subsequent phase of the research, the novel bio-inspired 3DOF SRM is utilized as a model for the 3DOF wrist mechanism observed in humans, as illustrated in Figure 8a. This study introduces an innovative control system for a bio-inspired 3DOF wrist robotic manipulator that utilizes real-time hand tracking to facilitate intuitive and adaptive manipulation. As previously discussed, the development of robotic systems that can interact seamlessly with human users represents a critical advancement in the field of robotics (Figure 1).
Figure 8a depicts the book as the target object for retrieval, facilitated by establishing a connection between the mini wireless surveillance camera system and the 3DOF wrist manipulator. The control system is engineered to leverage hand tracking data to compute the requisite angles for the servo motors that govern the manipulator's movements, utilizing real-time data sourced from the Arduino interface. Specifically, the positions of the 3DOF wrist and finger joints are extracted through MediaPipe, allowing for the computation of a centroid that represents the palm's position, as defined by a proximity sensor. This centroid is pivotal in adjusting the end effector's position, enabling precise control for object detection within the operational capabilities of the robotic manipulator. The integration of Python with the OpenCV and MediaPipe libraries facilitates accurate gesture recognition and effective tracking of hand landmarks, thereby significantly enhancing the manipulator's responsiveness to user inputs (Figure 8b).
During human-robot interaction, the acquisition of objects is facilitated by a E18-D80NK proximity sensor that displays the message "Object Detected" on the screen when the robotic hand detects an object, aiding in tracking and guiding the manipulator's approach.
The presented control system represents a significant advancement in the development of intelligent robotic manipulators capable of real-time interaction. Future research will concentrate on optimizing gesture recognition algorithms and expanding the range of manipulative tasks, thereby enhancing the practical applications of bio-inspired robotic systems.
The novel bio-inspired 3DOF SRM developed in this study has significant potential for various applications, including military, industrial, and medical fields. Its advanced control system and intuitive human-robot interaction capabilities enhance precision and efficiency in tasks such as bomb disposal, automated assembly, and minimally invasive surgeries. Furthermore, our proposed human-robot interaction system eliminates the need for specially designed gloves to control the manipulator, as the user-friendly interface accommodates any hand size by tracing its components. In comparison to other teleoperation systems [101 − 105], the novel bio-inspired 3DOF SRM offers cross-platform compatibility, a mobile base, lower costs, an expanded workspace, and a more efficient end-effector. This adaptability facilitates integration with advanced technologies, such as virtual reality headsets (e.g., Oculus Rift, HTC Vive) and augmented reality glasses (e.g., Microsoft HoloLens, Google Glass), enabling intuitive control and enhancing user experience. Besides this, our system supports various input devices, including motion capture sensors (e.g., Leap Motion, Microsoft Kinect) and wearable technologies (e.g., smart rings, smart bracelets), which provide supplementary feedback and enhance interaction. As technology continues to evolve, this manipulator could play a pivotal role in addressing complex challenges across multiple sectors.

Conclusion and Future Work

In this research, we investigated biological organisms exhibiting 3DOF joint configuration and explored innovative robotic designs, culminating in the development of a novel bio-inspired 3DOF SRM. The design is performed by the transformation of CSKPs to effectively replicate the movements of ball and socket joints observed in biological organisms. Throughout this process, we established three foundational axioms for the design and analysis of novel bio-inspired manipulators. Employing the screw theory and the Levenberg-Marquardt algorithm, we successfully addressed the forward and inverse kinematics challenges associated with the manipulator.
Our research utilized SolidWorks, MATLAB, Python, and Arduino software for comprehensive design and comparative analysis of the manipulator. We presented extensive results detailing the spherical workspace of the novel bio-inspired 3DOF SRM, achieving roll ( α )   =   ± 30 degrees, pitch ( β ) =   ± 60 degrees, and yaw ( γ ) =   ± 90 degrees. Additionally, we measured a peak torque value of 9.5 × 10 − 4   N m , which underscores the manipulator’s lightweight, dexterity, and compact dimensions of 95   m m in height, width, and length.
In the subsequent phase of this research, we implemented advanced methodologies and developed a user-friendly interface to enhance human-robot interaction. The novel bio-inspired 3DOF SRM is utilized as a model for the 3DOF wrist mechanism observed in humans, facilitating a more reliable eye-hand coordination process through the incorporation of a proximity sensor and a camera. This system could be applicable across military, industrial, medical, and other domains that require 3DOF joint configurations.
Future research will focus on refining the 3DOF SRM platform for enhanced compactness and incorporating haptic feedback to improve control precision. The existing 3DOF spherical platform may be directly augmented with specially designed spherical roller bearings to yield enhanced performance. Furthermore, the designed novel bio-inspired 3DOF SRM can be adapted for application in other bio-inspired robotic systems, improving their operational and dynamic capabilities. In the next phase, we plan to integrate haptic systems into the designed novel bio-inspired 3DOF SRM to provide more precise control [106, 107], ensuring tactile and force feedback [108, 109], which will contribute to achieving robust and stable control mechanisms [110]. We believe that the proposed methods for human-robot interaction, combined with advancements in AI technology and modern automation, will contribute significantly to the development of effective solutions in robotics.

Data availability statement

The data are not publicly available at the time of publication because they are not in a format that is easily accessible or reusable by other researchers. However, the data supporting the findings of this study are archived and can be provided by the corresponding author upon reasonable request.

Acknowledgments

We extend our gratitude to the Florida State University and its technical staff at the Digital Fabrication Lab (Fablab) for their invaluable support during the fabrication of the robotic system.

Conflicts of Interest

The authors declare no conflict of interest.

Ethics Statement

This research does not involve human participants or animals.

Funding Statement

This research was not supported by any external funding.
ORCID iDs
Suleyman Soltanov https://orcid.org/0009-0006-6992-3649
Rodney Roberts https://orcid.org/0000-0001-9255-3216

References

  1. Adams CR, DeMartino AM, Rego G, Denard PJ, Burkhart SS. The rotator cuff and the superior capsule: why we need both. Arthroscopy: The Journal of Arthroscopic & Related Surgery. 2016 Dec 1;32(12):2628-37. [CrossRef]
  2. Bakhsh W, Nicandri G. Anatomy and Physical Examination of the Shoulder. Sports Med Arthrosc Rev. 2018 Sep;26(3):e10-e22. [CrossRef]
  3. De Lange A, Kauer JM, Huiskes R. Kinematic behavior of the human wrist joint: A roentgen-stereophotogrammetric analysis. Journal of Orthopaedic Research. 1985;3(1):56-64. [CrossRef]
  4. Han L, Cheng L, Li H, Zou Y, Qin S, Zhou M. Hierarchical Optimization for Personalized Hand and Wrist Musculoskeletal Modeling and Motion Estimation. IEEE Transactions on Biomedical Engineering. 2024 Sep 9. [CrossRef]
  5. Molini L, Precerutti M, Gervasio A, Draghi F, Bianchi S. Hip: anatomy and US technique. Journal of ultrasound. 2011 Jun 1;14(2):99-108. [CrossRef]
  6. Kumar S, Mohanan S, Vattoth AL, Bajaj G, Pandey T. Anatomy and Biomechanics of Lower Extremity Tendons: Imaging Implications. InSeminars in Ultrasound, CT and MRI 2023 Aug 1 (Vol. 44, No. 4, pp. 364-385). WB Saunders. [CrossRef]
  7. Brockett CL, Chapman GJ. Biomechanics of the ankle. Orthopaedics and trauma. 2016 Jun 1;30(3):232-8.
  8. Pol F, Baharlouei H, Taheri A, Menz HB, Forghany S. Foot and ankle biomechanics during walking in older adults: A systematic review and meta-analysis of observational studies. Gait & posture. 2021 Sep 1;89:14-24. [CrossRef]
  9. Arias-Martorell J. The morphology and evolutionary history of the glenohumeral joint of hominoids: a review. Ecology and Evolution. 2019 Jan;9(1):703-22. [CrossRef]
  10. Larson, S. G. (1993). Functional morphology of the shoulder in primates. In D. L. Gebo (Ed.), Postcranial adaptation in nonhuman primates (pp. 45–69). DeKalb, IL: Northern Illinois University Press.
  11. Larson, S. G. (1995). New characters for the functional interpretation of primate scapulae and proximal humeri. American Journal of Physical Anthropology, 98, 13–35. [CrossRef]
  12. (ISSN)1096-8644.
  13. Evans HE, de Lahunta A. Miller’s Anatomy of the Dog. 4th ed. St. Louis, MO: Elsevier Saunders; 2012. p. 871.
  14. Reis Silva H, Uosyte R, Clements DN, Bergkvist GT, Schwarz T. Computed tomography and positive contrast computed tomographic arthrography of the canine shoulder: normal anatomy and effects of limb position on visibility of soft tissue structures. Veterinary Radiology & Ultrasound. 2013 Sep;54(5):470-7. [CrossRef]
  15. Manafzadeh AR. Joint mobility as a bridge between form and function. Journal of Experimental Biology. 2023 Jan 1;226(Suppl_1): jeb245042. [CrossRef]
  16. Bledt G, Powell MJ, Katz B, Di Carlo J, Wensing PM, Kim S. Mit cheetah 3: Design and control of a robust, dynamic quadruped robot. In 2018 IEEE. InRSJ International Conference on Intelligent Robots and Systems (IROS) 2019 (pp. 2245-2252).
  17. Becker J, Emmanuel M, Jean-Marc L. Joint loading estimation method for horse forelimb high jerk locomotion: jumping. Journal of Bionic Engineering. 2019 Jul; 16:674-85. [CrossRef]
  18. Böhmer C, Theil JC, Fabre AC, Herrel A. Atlas of terrestrial mammal limbs. CRC Press; 2020 Apr 3.
  19. Brocklehurst RJ, Fahn-Lai P, Regnault S, Pierce SE. Musculoskeletal modeling of sprawling and parasagittal forelimbs provides insight into synapsid postural transition. Iscience. 2022 Jan 21;25(1). [CrossRef]
  20. Gatesy SM, Manafzadeh AR, Bishop PJ, Turner ML, Kambic RE, Cuff AR, Hutchinson JR. A proposed standard for quantifying 3-D hindlimb joint poses in living and extinct archosaurs. Journal of Anatomy. 2022 Jul; 241(1):101-18. [CrossRef]
  21. Kambic RE, Roberts TJ, Gatesy SM. 3-D range of motion envelopes reveal interacting degrees of freedom in avian hind limb joints. Journal of Anatomy. 2017 Dec;231(6):906-20. [CrossRef]
  22. Stowers AK, Matloff LY, Lentink D. How pigeons couple three-dimensional elbow and wrist motion to morph their wings. Journal of The Royal Society Interface. 2017 Aug 31;14(133):20170224. [CrossRef]
  23. Baier DB, Gatesy SM, Dial KP. Three-dimensional, high-resolution skeletal kinematics of the avian wing and shoulder during ascending flapping flight and uphill flap-running. PloS one. 2013 May 15;8(5): e63982. [CrossRef]
  24. Heers AM, Baier DB, Jackson BE, Dial KP. Flapping before flight: high resolution, three-dimensional skeletal kinematics of wings and legs during avian development. PLoS One. 2016 Apr 21;11(4):e0153446.
  25. Lauder GV, Tangorra JL. Fish locomotion: biology and robotics of body and fin-based movements. Robot fish: bio-inspired fishlike underwater robots. 2015:25-49.
  26. Sudki B, Lauria M, Noca F. Marine propulsor based on a three-degree-of-freedom actuated spherical joint. InProceedings of the 3rd International Symposium on Marine Propulsors 2013 May (pp. 481-485).
  27. Cortés Torres ED, García Gonzales LE, Villamizar Marin LE, García Cena CE. Mechanical Design of a New Hybrid 3R-DoF Bioinspired Robotic Fin Based on Kinematics Modeling and Analysis. InActuators 2024 Sep 11 (Vol. 13, No. 9, p. 353). MDPI.
  28. Pandey J, Reddy NS, Ray R, Shome SN. Biological swimming mechanism analysis and design of robotic frog. In2013 IEEE international conference on mechatronics and automation 2013 Aug 4 (pp. 1726-1731). IEEE.
  29. Torii N, Mizuno H, Iwasaki K, inventors; Fanuc Corp, assignee. Wrist assembly for an industrial robot. United States patent US 4,972,735. 1990 Nov 27.
  30. Gosselin CM, Hamel JF. The Agile Eye: a high-performance three-degree-of-freedom camera-orienting device. In IEEE International Conference on Robotics and Automation 1993 Jan 1 (Vol. 1, No. 1, pp. 781-781). IEEE.
  31. Gosselin CM, Pierre ES, Gagne M. On the development of the agile eye. IEEE Robotics & Automation Magazine. 1996 Dec; 3(4):29-37. [CrossRef]
  32. Leguay-Durand S, Reboulet C. Optimal design of a redundant spherical parallel manipulator. Robotica. 1997 Jul;15(4):399-405. [CrossRef]
  33. Vischer P, Clavel R. Argos: A novel 3-DoF parallel wrist mechanism. The International Journal of Robotics Research. 2000 Jan;19(1):5-11.
  34. Birglen L, Gosselin C, Pouliot N, Monsarrat B, Laliberté T. SHaDe, a new 3-DOF haptic device. IEEE Transactions on Robotics and Automation. 2002 Apr;18(2):166-75.
  35. Lum MJ, Rosen J, Sinanan MN, Hannaford B. Optimization of a spherical mechanism for a minimally invasive surgical robot: theoretical and experimental approaches. IEEE Transactions on Biomedical Engineering. 2006 Jun 19;53(7):1440-5. [CrossRef]
  36. Schuler S, Kaufmann V, Houghton P, Székely GS. Design and development of a joint for the dextrous robot arm. InNinth ESA Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands, Nov 2006 Nov (pp. 28-30).
  37. Yu Y, Narita Y, Harada Y, Tsujio S. Development of 3-DOF active rotational ball joint. In 2007 IEEE International Conference on Robotics and Biomimetics (ROBIO) 2007 Dec 15 (pp. 1966-1971). IEEE.
  38. Hess-Coelho, Tarcisio A. "A redundant parallel spherical mechanism for robotic wrist applications." (2007): 891-895. [CrossRef]
  39. T. Inada, T. Tsujimori, S. Kitamura, and R. Taniuchi, “Robot,” U.S. Patent 7 622 001, 2009.
  40. Yu Y, Narita Y, Harada Y, Nakao T. Research of 3-DOF active rotational ball joint. In2009 IEEE/RSJ International Conference on Intelligent Robots and Systems 2009 Oct 10 (pp. 5153-5158). IEEE.
  41. Wu G, Caro S, Bai S, Kepler J. Dynamic modeling and design optimization of a 3-DOF spherical parallel manipulator. Robotics and Autonomous Systems. 2014 Oct 1;62(10):1377-86. [CrossRef]
  42. Degirmenci A, Hammond FL, Gafford JB, Walsh CJ, Wood RJ, Howe RD. Design and control of a parallel linkage wrist for robotic microsurgery. In2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) 2015 Sep 28 (pp. 222-228). IEEE.
  43. Sadeqi S, Bourgeois SP, Park EJ, Arzanpour S. Design and performance analysis of a 3-rrr spherical parallel manipulator for hip exoskeleton applications. Journal of Rehabilitation and Assistive Technologies Engineering. 2017 May; 4:2055668317697596. [CrossRef]
  44. Lee J, Song BW, Yang W. Design of exoskeleton-type wrist human–machine interface based on over-actuated coaxial spherical parallel mechanism. Advances in Mechanical Engineering. 2018 Feb;10(2):1687814017753896. [CrossRef]
  45. Li X, Liu J, Chen W, Bai S. Integrated design, modeling and analysis of a novel spherical motion generator driven by electromagnetic principle. Robotics and Autonomous Systems. 2018 Aug 1;106:69-81. [CrossRef]
  46. Bai S, Li X, Angeles J. A review of spherical motion generation using either spherical parallel manipulators or spherical motors. Mechanism and Machine Theory. 2019 Oct 1; 140:377-88. [CrossRef]
  47. Hofer M, D’Andrea R. Design, fabrication, modeling and control of a fabric-based spherical robotic arm. Mechatronics. 2020 Jun 1;68:102369. [CrossRef]
  48. Abe K, Tadakuma K, Tadakuma R. ABENICS: Active ball joint mechanism with three-DoF based on spherical gear meshings. IEEE Transactions on Robotics. 2021 Apr 26;37(5):1806-25.
  49. Rommers J, van der Wijk V, Herder JL. A new type of spherical flexure joint based on tetrahedron elements. Precision Engineering. 2021 Sep 1;71:130-40. [CrossRef]
  50. Choi D, Kim C, Song JB. Development of microsurgical robot arm using spherical serial RCM mechanism and commercial laparoscopic surgical robot instrument. In 2022 19th International Conference on Ubiquitous Robots (UR) 2022 Jul 4 (pp. 159-164). IEEE.
  51. Howard IS. Design and kinematic analysis of a 3D-printed 3DOF robotic manipulandum. In Annual Conference Towards Autonomous Robotic Systems 2023 Sep 8 (pp. 227-239). Cham: Springer Nature Switzerland.
  52. Ghaedrahmati R, Gosselin C. Kinematic Analysis of a New 3-DOF Parallel Wrist-Gripper Assembly with a Large Singularity-Free Workspace. In Actuators 2023 Nov 10 (Vol. 12, No. 11, p. 421). MDPI. [CrossRef]
  53. Zhang P, Deng Z, Hou X, Wang S. Development of a miniaturized bedside robotic wrist with multifunctional movement capabilities: An analysis based on a simulation environment. In 2023 IEEE 3rd International Conference on Digital Twins and Parallel Intelligence (DTPI) 2023 Nov 7 (pp. 1-5). IEEE.
  54. Schröder K, Garcia G, Chacón R, Montenegro G, Marroquín A, Farias G, Dormido-Canto S, Fabregas E. Development and control of a real spherical robot. Sensors. 2023 Apr 11;23(8):3895. [CrossRef]
  55. Djennane M, Chehaidia SE, Yakoub C, Mesbah K, Aljohani M, Mosaad MI. Design, Analysis and Implementation of a 3-DOF Spherical Parallel Manipulator. IEEE Access. 2024 Apr 9. [CrossRef]
  56. Zhang L, Yu Z, Su P, Li J, Ge R. Design of a Parallel Wrist Rehabilitation Robot and Analysis of Physiological Effect on Training. IEEE/ASME Transactions on Mechatronics. 2024 Jan 8. [CrossRef]
  57. Zhang P, Deng Z, Hou X, Wang S. Development of a Parallel-Mechanism-Based Robotic Wrist With Remote Center of Motion Capability to Assist Ultrasound Scanning. IEEE Journal of Radio Frequency Identification. 2024 Mar 20. [CrossRef]
  58. Krebs HI, Volpe BT, Williams D, Celestino J, Charles SK, Lynch D, Hogan N. Robot-aided neurorehabilitation: a robot for wrist rehabilitation. IEEE transactions on neural systems and rehabilitation engineering. 2007 Sep 17;15(3):327-35.
  59. Pehlivan AU, Sergi F, Erwin A, Yozbatiran N, Francisco GE, O'Malley MK. Design and validation of the RiceWrist-S exoskeleton for robotic rehabilitation after incomplete spinal cord injury. Robotica. 2014 Dec;32(8):1415-31. [CrossRef]
  60. Fite KB, Withrow TJ, Shen X, Wait KW, Mitchell JE, Goldfarb M. A gas-actuated anthropomorphic prosthesis for transhumeral amputees. IEEE Transactions on Robotics. 2008 Feb 25;24(1):159-69. [CrossRef]
  61. Fan S, Fan S, Jiang L, Liu H. A design of a miniaturized prosthetic wrist based on repetition rate of human wrist daily tasks. In2016 IEEE International Conference on Robotics and Biomimetics (ROBIO) 2016 Dec 3 (pp. 1643-1648). IEEE.
  62. Amirabdollahian F, Ates S, Basteris A, Cesario A, Buurke J, Hermens H, Hofs D, Johansson E, Mountain G, Nasr N, Nijenhuis S. Design, development and deployment of a hand/wrist exoskeleton for home-based rehabilitation after stroke-SCRIPT project. Robotica. 2014 Dec;32(8):1331-46. [CrossRef]
  63. Singh N, Saini M, Anand S, Kumar N, Srivastava MP, Mehndiratta A. Robotic exoskeleton for wrist and fingers joint in post-stroke neuro-rehabilitation for low-resource settings. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2019 Sep 23;27(12):2369-77. [CrossRef]
  64. Jarrassé N, Tagliabue M, Robertson JV, Maiza A, Crocher V, Roby-Brami A, Morel G. A methodology to quantify alterations in human upper limb movement during co-manipulation with an exoskeleton. IEEE Transactions on neural systems and Rehabilitation Engineering. 2010 Jul 19;18(4):389-97. [CrossRef]
  65. Rose CG, Sergi F, Yun Y, Madden K, Deshpande AD, O'Malley MK. Characterization of a hand-wrist exoskeleton, READAPT, via kinematic analysis of redundant pointing tasks. In 2015 IEEE International Conference on Rehabilitation Robotics (ICORR) 2015 Aug 11 (pp. 205-210). IEEE.
  66. Pezent E, Rose CG, Deshpande AD, O'Malley MK. Design and characterization of the Open Wrist: A robotic wrist exoskeleton for coordinated hand-wrist rehabilitation. In 2017 international conference on rehabilitation robotics (ICORR) 2017 Jul 17 (pp. 720-725). IEEE.
  67. Bajaj NM, Spiers AJ, Dollar AM. State of the art in artificial wrists: A review of prosthetic and robotic wrist design. IEEE Transactions on Robotics. 2019 Jan 23;35(1):261-77. [CrossRef]
  68. Li J, Zuo S, Zhang L, Dong M, Zhang Z, Tao C, Ji R. Mechanical design and performance analysis of a novel parallel robot for ankle rehabilitation. Journal of Mechanisms and Robotics. 2020 Oct 1;12(5):051007. [CrossRef]
  69. Vertongen J, Kamper DG, Smit G, Vallery H. Mechanical aspects of robot hands, active hand orthoses, and prostheses: A comparative review. IEEE/ASME Transactions on Mechatronics. 2020 Aug 4;26(2):955-65.
  70. Eschweiler J, Li J, Quack V, Rath B, Baroncini A, Hildebrand F, Migliorini F. Anatomy, biomechanics, and loads of the wrist joint. Life. 2022 Jan 27;12(2):188. [CrossRef]
  71. [70]. Soltanov S. Structural synthesis of the robot manipulators with general constraint one using the transformation of the higher kinematic pare. Tran. Natl. Acad. Sci. Azerb. Ser. Phys.-Tech. Math. Sci. Mechanics, 39 (8), 37–43 (2020).
  72. [71]. Alizade R, Soltanov S, Hamidov A. Structural synthesis of lower-class robot manipulators with general constraint one. Robotics. 2021 Jan 11;10(1):14. [CrossRef]
  73. [72]. Soltanov S. Structural synthesis of the new type 4DOF robot manipulators for industry and medicine. Australian Journal of Mechanical Engineering. 2023 Apr 2:1-3. [CrossRef]
  74. Yousaf R, Shahzad A, Qadri MM, Javed A. Recent advancements in flapping mechanism and wing design of micro aerial vehicles. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2021 Oct;235(19):4425-46. [CrossRef]
  75. Amal P, Nair AR, Arunav H, Raj R, Akhil VM, Tawk C, Shankar KV. Bioinspiration and biomimetics in marine robotics: a review on current applications and future trends. Bioinspiration & Biomimetics. 2024 Mar 11. [CrossRef]
  76. Morgansen KA, Triplett BI, Klein DJ. Geometric methods for modeling and control of free-swimming fin-actuated underwater vehicles. IEEE Transactions on Robotics. 2007 Dec 18;23(6):1184-99. [CrossRef]
  77. Kim HJ, Song SH, Ahn SH. A turtle-like swimming robot using a smart soft composite (SSC) structure. Smart Materials and Structures. 2012 Dec 10;22(1):014007. [CrossRef]
  78. Li B, Li Z, Li H, Du Y. Optimization of Three-Degree-of-Freedom Biomimetic Pectoral Fin Propulsion Law. Journal of Shanghai Jiaotong University (Science). 2024 Jul 24:1-4.
  79. Wyrobek KA, Berger EH, Van der Loos HM, Salisbury JK. Towards a personal robotics development platform: Rationale and design of an intrinsically safe personal robot. In2008 IEEE International Conference on Robotics and Automation 2008 May 19 (pp. 2165-2170). IEEE.
  80. Mahmoud RA, Ueno A, Tatsumi S. An assistive tele-operated anthropomorphic robot hand: Osaka city university hand ii. In Proceedings of the 6th International Conference on Human-robot Interaction 2011 Mar 6 (pp. 85-92).
  81. Chernyak V, Flynn T, O'Rourke J, Morgan J, Zalutsky A, Chernova S, Nestinger SS, Padir T. The design and realization of a high mobility biomimetic quadrupedal robot. InProceedings of 2012 IEEE/ASME 8th IEEE/ASME International Conference on Mechatronic and Embedded Systems and Applications 2012 Jul 8 (pp. 93-98). IEEE.
  82. Bright D, Shield S, Patel A. AeroDima: Cheetah-Inspired Aerodynamic Tail Design for Rapid Maneuverability. In2024 IEEE International Conference on Robotics and Automation (ICRA) 2024 May 13 (pp. 1451-1456). IEEE.
  83. Hammond FL, Howe RD, Wood RJ. Dexterous high-precision robotic wrist for micromanipulation. In 2013 16th International Conference on Advanced Robotics (ICAR) 2013 Nov 25 (pp. 1-8). IEEE.
  84. Hu T, Lu X, Yi J, Wang Y, Xu D. Biomimetic soft robotic wrist with 3-DOF motion and stiffness tunability based on ring-reinforced pneumatic actuators and a particle jamming joint. Science China Technological Sciences. 2024 Mar;67(3):774-90. [CrossRef]
  85. Hwang YH, Kang SR, Cha SW, Choi SB. An electrorheological spherical joint actuator for a haptic master with application to robot-assisted cutting surgery. Sensors and Actuators A: Physical. 2016 Oct 1;249:163-71.
  86. Hernández-Flores EA, Hernández-Rodríguez YM, Munguía-Fuentes R, Bayareh-Mancilla R, Cigarroa-Mayorga OE. Acinonyx jubatus-Inspired Quadruped Robotics: Integrating Neural Oscillators for Enhanced Locomotion Control. Biomimetics. 2024 May 27;9(6):318. [CrossRef]
  87. Kuka AG, Augsburg, Germany, 2017. [Online]. Available: www.kuka.com.
  88. Selvamuthu MG, Abe K, Tadakuma K, Tadakuma R. Metal ABENICS: Metallic Spherical Gear Mechanism with Orientation Correction using Embedded IMU Sensor. In 2024 IEEE International Conference on Advanced Intelligent Mechatronics (AIM) 2024 Jul 15 (pp. 256-263). IEEE.
  89. E. J. McCormick, Ed., Human Factors Engineering, 3rd ed. New York: McGraw-Hill, (1970).
  90. Rosenbaum DA, Jorgensen MJ. Planning macroscopic aspects of manual control. Human Movement Science. 1992 Feb 1;11(1-2):61-9. [CrossRef]
  91. Chan WP, Parker CA, Van der Loos HM, Croft EA. Grip forces and load forces in handovers: implications for designing human-robot handover controllers. InProceedings of the seventh annual ACM/IEEE international conference on Human-Robot Interaction 2012 Mar 5 (pp. 9-16).
  92. Jeannerod M. The timing of natural prehension movements. Journal of motor behavior. 1984 Sep 1;16(3):235-54.
  93. Zwicker JG, Missiuna C, Harris SR, Boyd LA. Developmental coordination disorder: a review and update. European Journal of Paediatric Neurology. 2012 Nov 1;16(6):573-81. [CrossRef]
  94. H Goldstein, C Pool, and J Safko. Classical Mechanics 3rd edn. Miami, FL. 2001.
  95. R. Courant, H. Robbins, I. Stewart, 1996, What is mathematics, Euler’s formula, NY, USA, 1752, pp. 235–240.
  96. K. Kutzbach, Mechanische leitungsverzweigung, ihre gezetze und anwendungen, Maschinenbau. Betrieb 8 (1929) 710–716.
  97. Ceccarelli M. Screw axis defined by Giulio Mozzi in 1763 and early studies on helicoidal motion. Mechanism and machine theory. 2000 Jun 1;35(6):761-70. [CrossRef]
  98. R. Brockett, "Robotic manipulators and the product of exponential formula," Mathematical Theory of Networks and Systems, P.A. Fuhrman, Ed., Springer-Verlag, New York, 1984, pp. 120–129.
  99. K. Levenberg, “A method for the solution of certain problems in least squares, Quart. Appl. Math., 1944, Vol. 2, pp. 164–168.
  100. D. Marquardt, “An algorithm for least-squares estimation of nonlinear parameters,” SIAM J. Appl. Math., 1963, Vol. 11, pp. 431–441. [CrossRef]
  101. Lynch, Kevin M., and Frank C. Park. Modern Robotics: Mechanics, Planning, and Control. Cambridge University Press, 2017, ISBN 9781107156302.
  102. Ohkawa T, He K, Sener F, Hodan T, Tran L, Keskin C. Assemblyhands: Towards egocentric activity understanding via 3d hand pose estimation. InProceedings of the IEEE/CVF conference on computer vision and pattern recognition 2023 (pp. 12999-13008).
  103. Zhao TZ, Kumar V, Levine S, Finn C. Learning fine-grained bimanual manipulation with low-cost hardware. arXiv preprint arXiv:2304.13705. 2023 Apr 23.
  104. Wu P, Shentu Y, Yi Z, Lin X, Abbeel P. Gello: A general, low-cost, and intuitive teleoperation framework for robot manipulators. arXiv preprint arXiv:2309.13037. 2023 Sep 22.
  105. Wang C, Shi H, Wang W, Zhang R, Fei-Fei L, Liu CK. Dexcap: Scalable and portable mocap data collection system for dexterous manipulation. arXiv preprint arXiv:2403.07788. 2024 Mar 12.
  106. Qin Y, Yang W, Huang B, Van Wyk K, Su H, Wang X, Chao YW, Fox D. Anyteleop: A general vision-based dexterous robot arm-hand teleoperation system. arXiv preprint arXiv:2307.04577. 2023 Jul 10.
  107. Gillespie RB, Colgate JE, Peshkin MA. A general framework for cobot control. IEEE Transactions on Robotics and Automation. 2001 Aug;17(4):391-401.
  108. Moore CA, Peshkin MA, Colgate JE. Cobot implementation of virtual paths and 3D virtual surfaces. IEEE Transactions on Robotics and Automation. 2003 Apr 8;19(2):347-51.
  109. Colgate JE, Brown JM. Factors affecting the z-width of a haptic display. InProceedings of the 1994 IEEE International Conference on Robotics and Automation 1994 May 8 (pp. 3205-3210). IEEE.
  110. Faulring EL, Lynch KM, Colgate JE, Peshkin MA. Haptic display of constrained dynamic systems via admittance displays. IEEE Transactions on Robotics. 2007 Feb 5;23(1):101-11. [CrossRef]
  111. Roberts RG, Moore CA, Colgate JE. A New Expression for the Passivity Bound for a Class of Sampled-Data Systems. IEEE Transactions on Robotics. 2024 Jul 25. [CrossRef]
Preprints 142048 g001
Figure 1. The depiction of human arm kinematic mobility and hand-eye coordination in human-object interaction. .
Figure 1. The depiction of human arm kinematic mobility and hand-eye coordination in human-object interaction. .
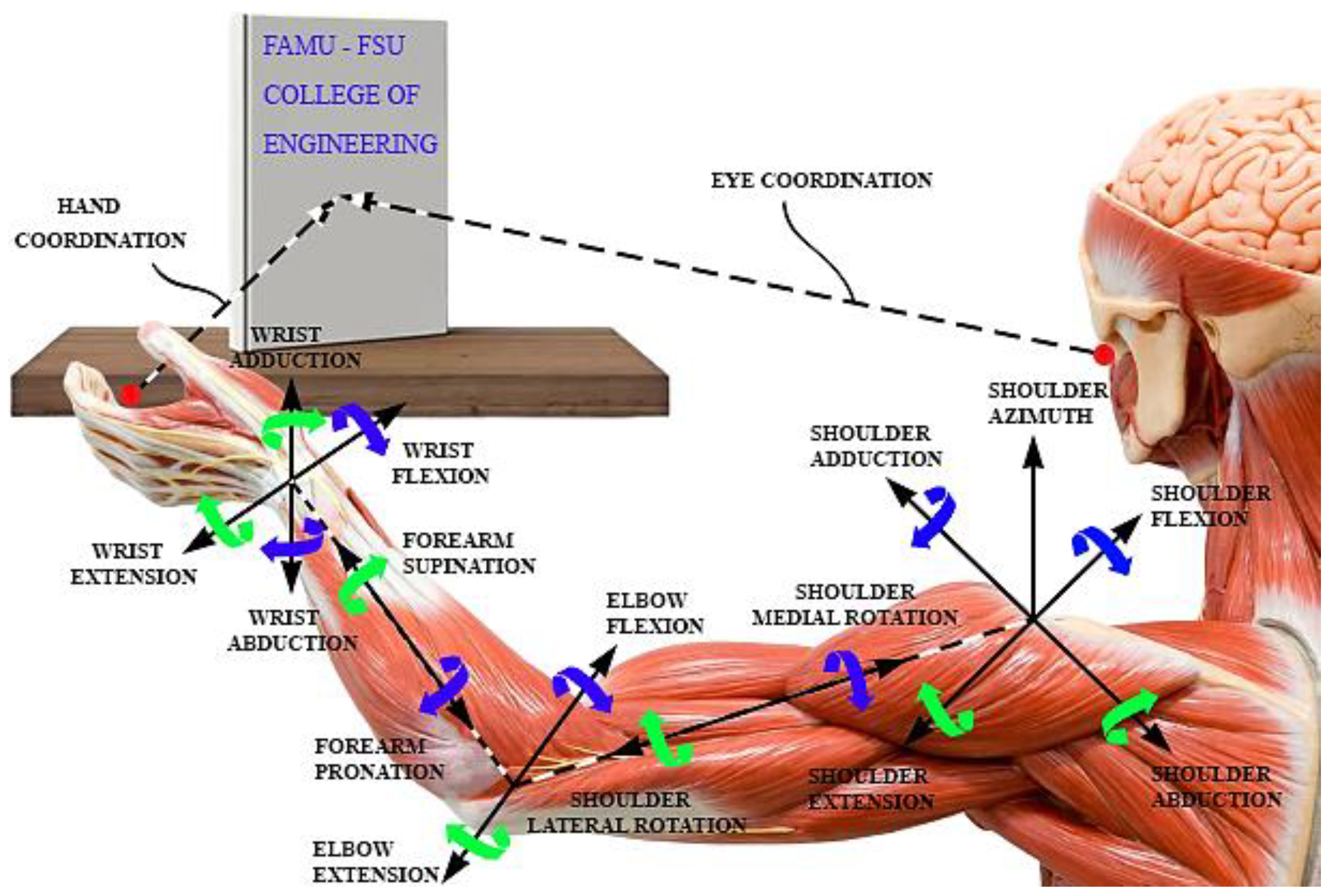
Preprints 142048 g001
Preprints 142048 g002
Figure 2. a) The mutual concentric configuration of the fixed sphere 1, with center O 1 and radius R , and sphere 2, with center O 2 and radius r . b) A novel bio-inspired constrained 3DOF SRM derived from the transformation of the spherical CSKPs.
Figure 2. a) The mutual concentric configuration of the fixed sphere 1, with center O 1 and radius R , and sphere 2, with center O 2 and radius r . b) A novel bio-inspired constrained 3DOF SRM derived from the transformation of the spherical CSKPs.
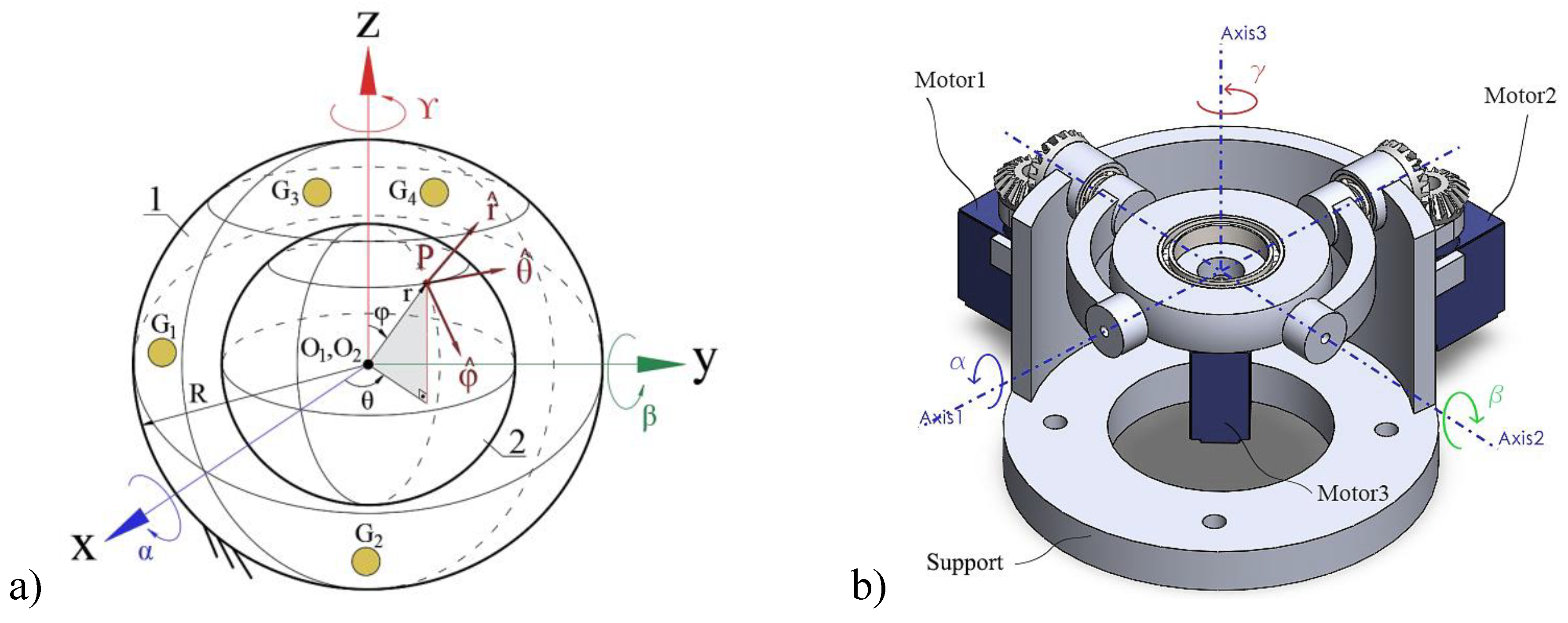
Preprints 142048 g002
Preprints 142048 g003
Figure 3. a) A novel bio-inspired 3DOF SRM designed from the transformation of a spherical CSKPs. b) Anatomical illustration of the human right hip joint, highlighting the ball and socket connection between the femoral head and acetabulum.
Figure 3. a) A novel bio-inspired 3DOF SRM designed from the transformation of a spherical CSKPs. b) Anatomical illustration of the human right hip joint, highlighting the ball and socket connection between the femoral head and acetabulum.
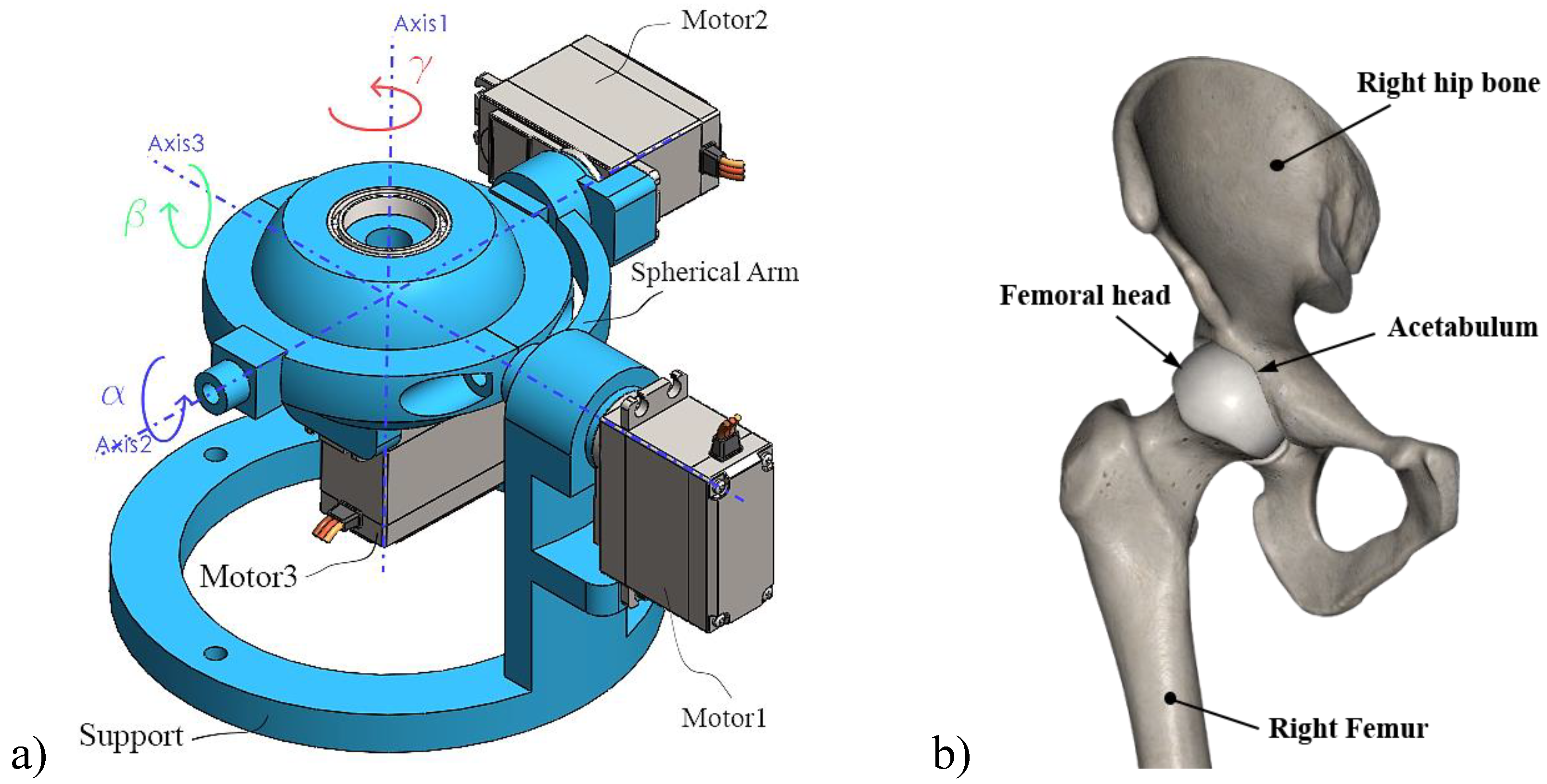
Preprints 142048 g003
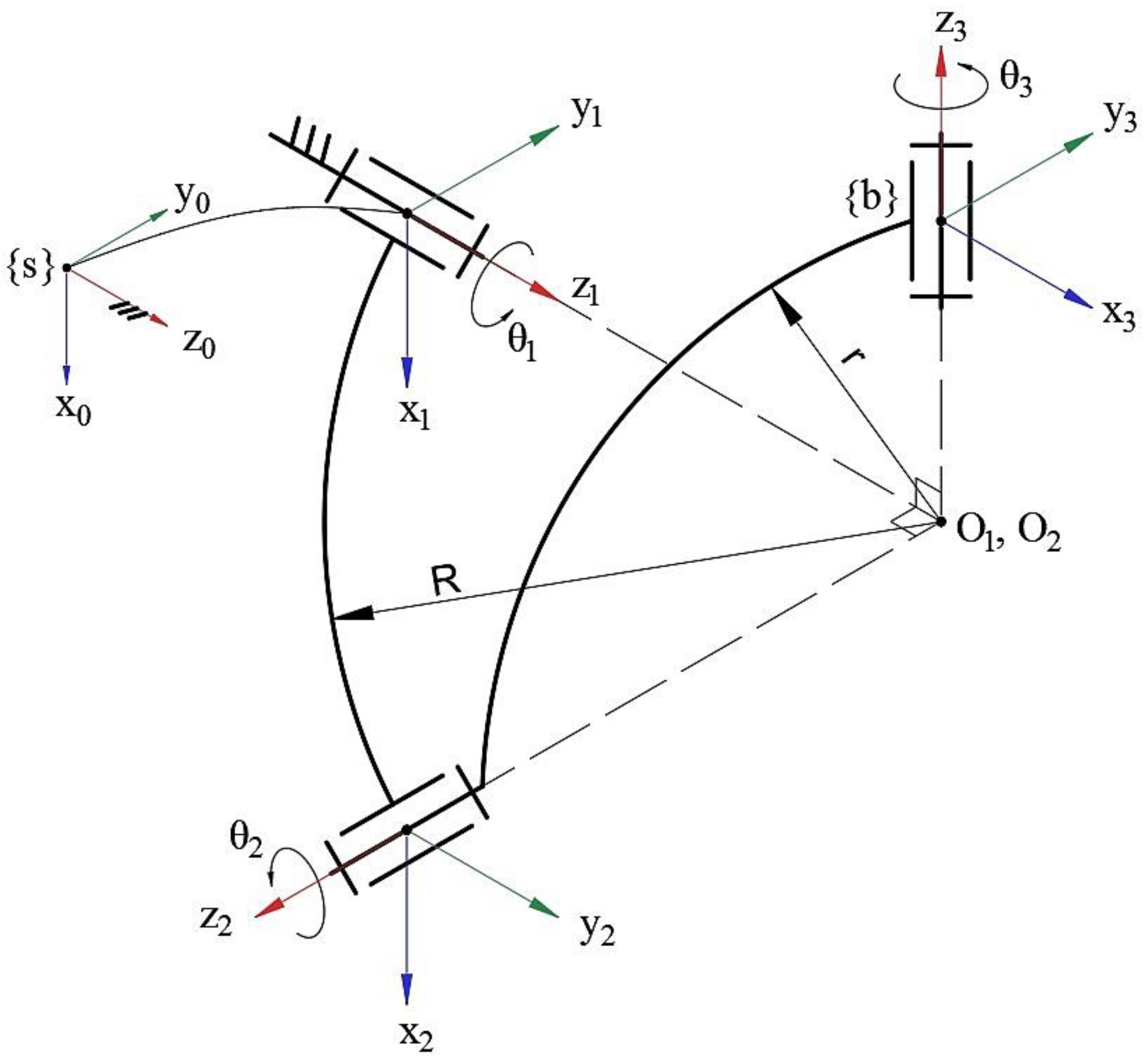
Preprints 142048 g004
Figure 4. Kinematic structure of the proposed novel bio-inspired 3DOF SRM.
Figure 4. Kinematic structure of the proposed novel bio-inspired 3DOF SRM.
Preprints 142048 g004
Preprints 142048 g005
Figure 5. Implementation of the novel bio-inspired 3DOF SRM in the MATLAB SimMechanics environment.
Figure 5. Implementation of the novel bio-inspired 3DOF SRM in the MATLAB SimMechanics environment.
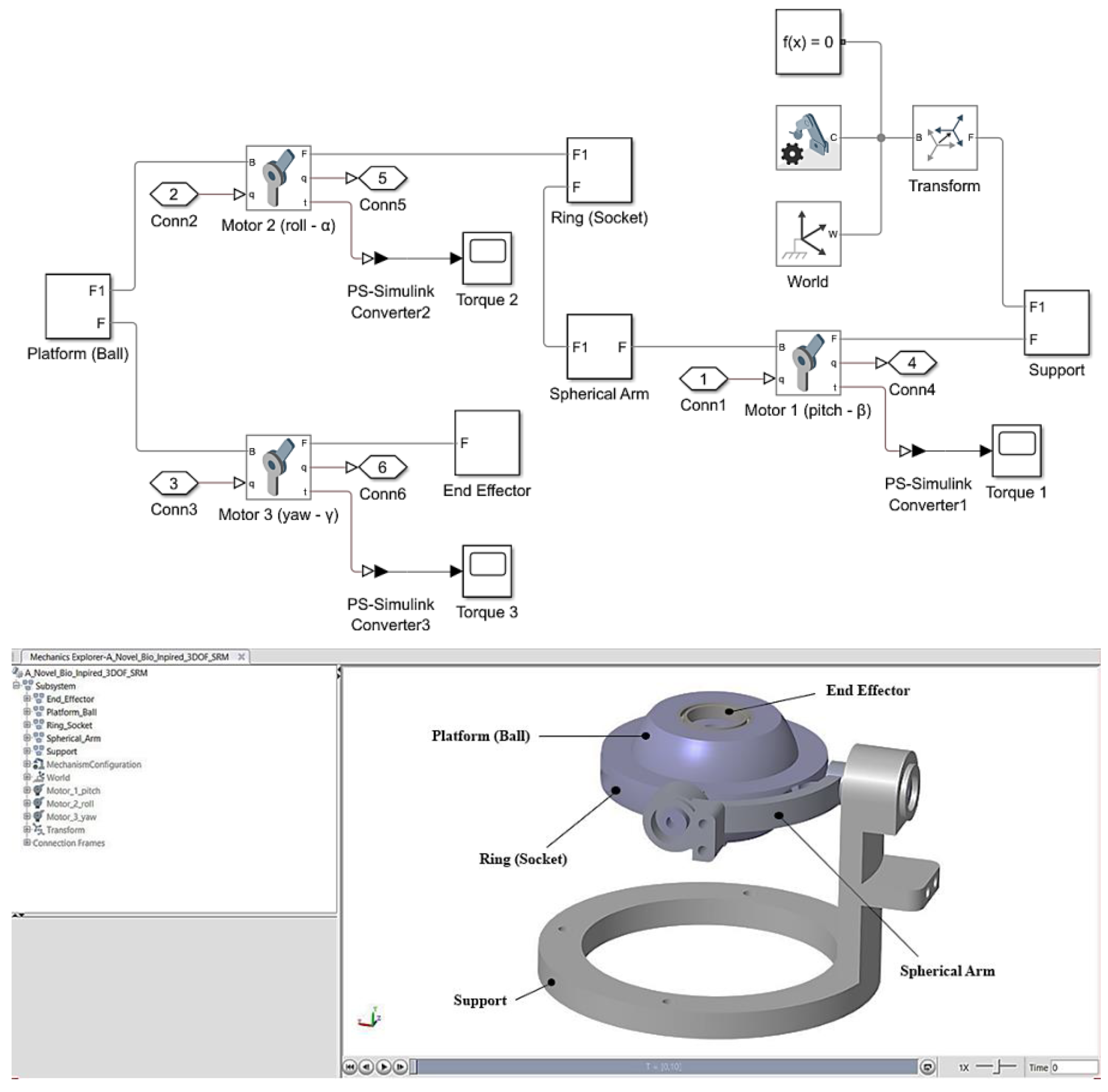
Preprints 142048 g005
Preprints 142048 g006
Figure 6. a) Configuration and dimensions of the novel bio-inspired 3DOF SRM. b) Workspace representation of the end effector's motion trajectory in the novel bio-inspired 3DOF SRM.
Figure 6. a) Configuration and dimensions of the novel bio-inspired 3DOF SRM. b) Workspace representation of the end effector's motion trajectory in the novel bio-inspired 3DOF SRM.
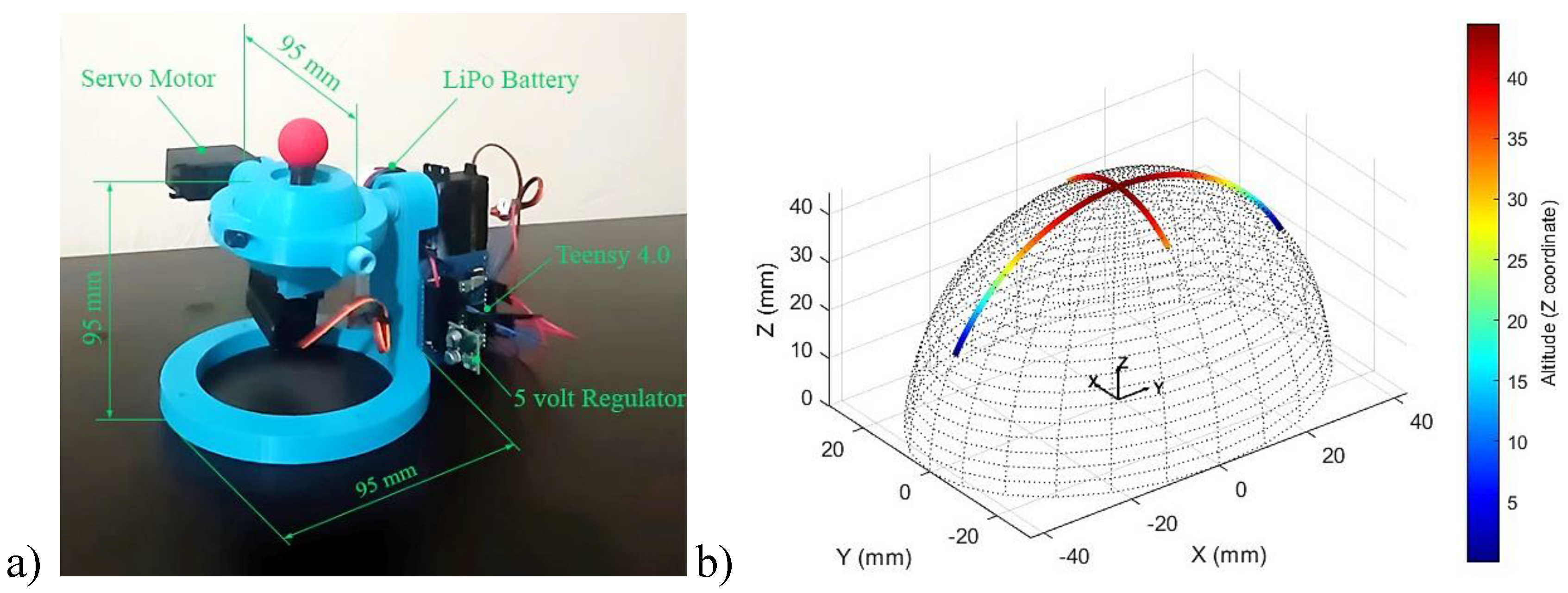
Preprints 142048 g006
Preprints 142048 g007
Figure 7. a) Comparative analysis of simulation and experimental plots depicting the angular displacement profiles of the motors for the novel bio-inspired 3DOF SRM. b) Torque profiles of the motors for the novel bio-inspired 3DOF SRM.
Figure 7. a) Comparative analysis of simulation and experimental plots depicting the angular displacement profiles of the motors for the novel bio-inspired 3DOF SRM. b) Torque profiles of the motors for the novel bio-inspired 3DOF SRM.
Preprints 142048 g007
Preprints 142048 g008
Figure 8. a) Coordination framework of the novel bio-inspired 3DOF SRM for human-robot interaction. b) Real-time hand tracking, object detection and servo angle measurements for the bio-inspired 3DOF SRM.
Figure 8. a) Coordination framework of the novel bio-inspired 3DOF SRM for human-robot interaction. b) Real-time hand tracking, object detection and servo angle measurements for the bio-inspired 3DOF SRM.
Preprints 142048 g008
Table 1. Screw parameters table for novel bio-inspired 3DOF SRM.
Table 1. Screw parameters table for novel bio-inspired 3DOF SRM.
frame   i ω i q i V i = − ω i  x  q i
1 (0, 0, 1) (0, 0, 0) (0, 0, 0)
2 (0, -1, 0) (0, 0, R ) (R, 0, 0)
3 (-1, 0, 0) (-r, 0, 0) (0, 0, 0)
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated