Could There be Method Behind Kepler's Cosmic Music?

Preprint

Article

Could There be Method Behind Kepler's Cosmic Music?

Altmetrics

Downloads

Views

Comments

Paul Redding^*

This version is not peer-reviewed

Submitted:

06 December 2024

Posted:

06 December 2024

You are already at the latest version

Alerts

Abstract

While Kepler is regarded as a major figure in standard historical accounts of the scientific revolution of early modern Europe, he is typically seen as having one foot in the new scientific culture and one in the old. In some of his work Kepler appears, along with Galileo, to be on a trajectory towards Newton’s celestial mechanics. Besides his advocacy of Copernicus’s heliocentrism, he appeals to physical causes in his explanations of the movements of celestial bodies. But other work expresses a neo-Platonic “metaphysics” or “mysticism”, as most obvious in his self-alignment with the ancient tradition of the “music of the spheres”. Here I problematize this distinction. Kepler’s purported neo-Platonic “metaphysics”, I argue, had been tied to Platonic and neo-Platonic features of the methodology of a tradition of mathematical astronomy that would remain largely untouched by his shift to heliocentrism and that would be essential to his actual scientific practice. Importantly, certain inherited geometric practices—one’s later formalized as “projective geometry”—would carry those “harmonic” structures expressed in the thesis of the music of the spheres.

Keywords:

Subject: Arts and Humanities - History

1. Introduction

Johannes Kepler (1571–1630) has long occupied an ambiguous position in the history of modern science. He was one of the first to defend Copernicus’s revolutionary heliocentric thesis set out in De Revolutionibus Orbium Coelestium of 1543 (Copernicus 1992).i Copernicus had challenged the evidence of everyday experience which had suggested (and surely still does) that the Sun moves daily around a stationary Earth—the conception of the universe inherited from the ancient Greeks. In contrast, the new conception demanded that we picture ourselves as located on a planet that not only rotates daily on its own axis but also, like other planets, circles the Sun. With this “Copernican principle” (Dunér 2023) that questions immediate experience on the basis of a theoretical conception of the conditions under which that experience unfolds, the question of the relation of “empirical evidence” to “theory” would become complex.

Construed in this way, Kepler standardly appears, along with his approximate contemporary Galileo Galilei (1564–1642), as one of the earliest instigators of the “scientific revolution” that would break with scholastic Aristotelianism and its theological interpretation and profoundly reshape Western thought (c.f., Koyre 1973, Kuhn 1995). Kepler’s theoretically guided analysis of years of astronomical data accumulated by the greatest sixteenth-century observational astronomer, Tycho Brahe, would lead to the formation of his three geometrically described laws of planetary motion, laws that Isaac Newton (1642–1726) would subsume within his own algebraically expressed universal laws of gravitation.

Such “modernism” in this regard is typically described as on display in Kepler’s Astronomica Nova of 1609, where he had introduced a “celestial physics” at the heart of astronomy in the spirit of Galileo’s attempts to unify the explanations of celestial and terrestrial phenomena.ii With such a focus, Kepler is understood to have helped redefine astronomy as cosmology qua branch of natural philosophy rather than as simply “mathematics” devoted to “saving the phenomena”, that is, as being construed merely instrumentally as means to predict celestial phenomena such as eclipses of the sun.iii

All agree, however, that aspects of Kepler’s astronomical commitments resist being fitted neatly into this progression from Copernicus to Newton. Despite the approach introduced in Astronomica Nova, his carefully constructed empirically based laws were linked to what, from a modern perspective, appears as a distinctly unscientific conception of the universe. While Einstein had nominated “Kepler’s marvellous achievement” as “a particularly fine example of the truth that knowledge cannot spring from experience alone but only from the comparison of the inventions of the intellect with observed fact” (Einstein 1954, 266), not all of Kepler’s intellectual inventions would prove fruitful. As Gerald Holton noted half a century ago, from our perspective we see Kepler’s “probing for the firm ground on which our science could later build” as often leading into “regions which we now know to be unsuitable marshland” (Holton 1988, 54). The path alluded to had been guided by a “commitment to neo-Platonic metaphysics” which sat beside his otherwise “sound instinct for physics” (55). More recently David Love has asserted that Kepler’s “free-ranging imagination” would “sometimes led him to the truth and sometimes into the realms of fantasy” (Love 2015, 57), it being the very “contrast between a deep insight into the nature of reality and a hopelessly wrong mysticism, that makes Kepler such an endearing and fascinating character in the story of the scientific revolution” (Love 2015, 12). While it is generally assumed that these antithetical aspects of his attitude to the universe can at least be distinguished analytically, I will argue, that Kepler the scientific astronomer could not have existed without a commitment to the fundamental structures underlying Kepler’s purported neo-Platonic metaphysical or mystical beliefs.

With the label “neo-Platonic” commentators typically have in mind those features of Kepler’s proffered model of the universe that relate to the cosmos as portrayed in Plato’s dialogue Timaeus that had been taken up in the later neo-Platonic tradition of the “music of the spheres”—the concept of the universe as designed by God so as to emit the most beautiful harmonies and melodies with its moving parts. Kepler did indeed embrace a Christianized version of this tradition, but this commitment must be unraveled from the “musical” features that were integral to the advances made by ancient Greek astronomy and integral to Kepler’s own success as an astronomer. And while his astronomy was overlaid by a type of metaphysics that went well beyond the limits of empirical science, this metaphysics, I suggest, was more of the familiar Christianized Aristotelian form, and indifferent to the neo-Platonic “musical” features it adopted in Kepler.

More specifically, those musical features of Kepler’s purported “neo-Platonic metaphysics” were, I will suggest, simply features of the ancient geometrically based Greek astronomical models upon which Copernicus, Tycho and Kepler had all drawn.iv Such models, stretching from that of Eudoxus of Cnidus, a contemporary and colleague of Plato, to Ptolemy of Alexandria five centuries later, had been constructed with the resources of mathematics very different to those opened up to Europe in the sixteenth century when the non-Greek discipline of algebra was imported from Arabic sources to be seized upon by the likes of Descartes and Newton. Moreover, for the Greek mathematical astronomers this mathematics was generally understood in relation to the computational role it played in predicting cosmological phenomena that were both bound up with astrology and also of practical significance within agricultural societies. The German theologian Andreas Osiander had tried to save Copernicus’s heliocentric thesis from theological controversy by proposing an instrumentalist interpretation in a prefatory “To the Reader” to De Revolutionibus but this effort was strenuously resisted by Copernicus’s followers.v Kepler too would criticise the instrumentalist interpretation of the heliocentric model, and in buying into the type of “instrumentalist-realist” debate that has continued to the present, was adopting a metaphysical stance more in line with a Christianized version of Aristotle’s cosmology than with any neo-Platonist astronomy.

Kepler’s attraction to neo-Platonic astronomical models would have two linked phases. In the first, as set out in his book Mysterium Cosmographicum published in 1596, he had proposed a model for Copernicus’s heliocentric conception in which the orbits about the sun of the then known six planets (counting earth as a planet as per the Copernican hypothesis) correlated with a series of six concentric spheres constructed about, within and between a homocentrically nested structure of the five regular polyhedra or “Platonic solids”—the cube, tetrahedron, dodecahedron, icosahedron, and octahedron. This structure revealed that, despite the Copernican break with ancient geocentric astronomy, Kepler was, as had Copernicus himself (Swerdlow and Neugebauer 1984), still relying upon the ancient approach to astronomy found in the likes of Plato, Eudoxus, Hipparchus and Ptolemy.

Later, Kepler’s neo-Platonic approach would more explicitly embrace the more dramatic musical idea that the crucial parameters structuring the cosmos were derived from the ratios and proportions of musical harmony, as is obvious from the title of his major work of 1619, Harmonice Mundi, “The Harmony of the World” (Kepler 1997). This approach had originated in an extension of the mathematics of musical relations to cosmology by Pythagorean natural philosophers such as Philolaus of Croton and Archytas of Tarentum, and would most known from Plato’s Timaeus, but even in Plato’s time it had been already dismissed by Aristotle as a mere metaphor and untrue (Aristotle 1984, On The Heavens 290b12-14).vi

Kepler did not believe that the orbiting planets actually gave off audible sounds, but he nevertheless took the “harmonies” of the planetary movements as much more than a metaphor. The movements of the planets gave expression to the most conceivably beautiful music entertained by the mind of God. Thus Kepler became involved in contemporary debates over music theory itself, criticising the form of music theorized by the ancient Greeks as based on inadequate conceptions of the musical intervals.vii But this does not entirely exhaust his reasons for pursuing a “harmonic” astronomy. The Greek musical intervals were indeed, deeply embedded into the most scientific aspects of this practice of astronomy, and so here I question the usual way of partitioning Kepler’s approach into a modern physics-based empirical astronomy on the one hand and a discardable neo-Platonic “metaphysical” model on the other. Rather, I suggest, an alternative orthogonal partitioning into his fundamentally “neo-Platonic” form of astronomy and his Christian-Aristotelian cosmology, with the literalness of his conception of the music of the spheres linked to the latter.

In this I will be guided by Stephen Gaukroger’s description of science as “a complex amalgam of (among other things) theory, engineering, technology, and invention” (Gaukroger 202, 285) and argue that such an amalgam in Kepler’s scientific work was run through with observational techniques and forms of instumentation that cannot be freed from those “neo-Platonic” features to which they had been bound in antiquity. In particular, it will be suggested that such features of Platonic and post-Platonic models were implicit in the geometry that would be inherited by Kepler via his appropriation of the methods and instruments of ancient astronomy, methods and instruments fundamental to the astronomical progress made by the ancients and by Kepler himself. This was a conception of geometry different to the classically Euclidean geometry that, with the aid of modern algebra, would be modified by Descartes in his Geometrie of 1637 into “analytic” geometry” (Descartes 1954) and that would become the framework for modern Newtonian celestial mechanics.

The geometry underlying Kepler’s astronomy, it will be argued, shows fundamental features of projective geometry, a form of geometry with roots in ancient Greece, Medieval Arabic astronomy, as well as Renaissance neo-Platonic theories of perspective in painting.viii Projective geometry would only start to be differentiated from Euclidean geometry in the decades after Kepler’s death in the work of Gerard Desargues and Blaise Pascal, and its final separation from Euclidean geometry would wait until the “Erlangen Program” of Felix Kline in the final decades of the nineteenth century. The projective geometry of Desargues and Pascal would be eclipsed by Descartes’s analytic geometry and forgotten for a century and a half, but would re-emerge in the nineteenth century as one of a number of non-Euclidean geometries that would later prove crucial in the subsequent “revolutionary” transformation from Newtonian to post-Newtonian physics and astronomy. As the nature of projective geometry and its difference to Euclidean geometry is not widely known about, a short historical sketch is warranted before its features are traced in relation to the neo-Platonic features of Kepler’s astronomy, and from there to the astronomical tradition upon which he drew.

2. Projective Geometry: A Historical Sketch

Euclidean geometry is a geometry of distances and angles. What makes one line-segment identical to another is that one could imagine both lines as, say pieces of wire, such that one could move next to the other to check they were the same length. Similarly with angles, one could superimpose one on the other to see that they were aligned.ix In 1637, Descartes would make the implicit idea of such a metric explicit by introducing “Cartesian” coordinates on the plane on which such geometrical shapes were inscribed, helping to create “analytic geometry”. Not only could lengths of lines be calculated by means of the numerical “x” and “y” values of their extremities, with the idea of the continuum as isomorphic with the “real number line”, geometrical shapes could now be identified with algebraic equations linking variables x and y.x The effect of the new analytic geometry on the European sciences would be massive.

Euclidean geometry, however, had been found to be unhelpful in relation to certain purposes for which geometry might be thought to be useful—for example, that of dealing with spatial relations between two-dimensional perspectival representations of three-dimensional arrays of objects, the problem facing those trying to deal with the issue of perspective that had been introduced into Renaissance painting. Viewed perspectivally as when projected onto a two-dimensional picture plane, the sides the tiles of a square-tiled floor appear to shrink when receding into the distance while nevertheless understood as being of the same length, and lines understood to be parallel appear to meet at a “vanishing point” on or just above the horizon, as described by Leon Battista Alberti in 1480.xi What was needed was a type of geometrical optics that went beyond that topic as dealt with by Euclid. Kepler would be a transitional figure in introducing the type of approach to geometry that modern theories of perspective would demand. This was “projective geometry”, officially introduced in 1639, albeit fleetingly, by the French mathematician Girard Desargues in his Rough Draft of an Essay on the results of taking plane sections of a cone (in Field and Gray 1987, ch. 6). The idea of shapes resulting from “taking plane sections of a cone”, Desargues had taken from the Conics of Hellenistic mathematician Apollonius of Perga.xii

Being published only two years after Descartes’s massively influential Geometrie, that introduced his analytic geometry, Desargues’s work, along with that of his small group of followers including Blaise Pascal, would not catch on and would remain largely unknown until the turn of the nineteenth century. But a few decades earlier, in 1604 and in relation to the optical needs of his own astronomical work, Kepler had published a work that, besides revolutionizing the field of optics, had anticipated key features of Desargues’s projective geometry. This was his Paralipomena to Witelo whereby The Optical Part of Astronomy is Treated (Kepler 2000), the “Witelo” of the title referring to a thirteenth-century Polish monk who had popularised the optics of the tenth- to eleventh-century Arab mathematician and astronomer, Hasan Ibn al-Haytham, referred to in Europe by the Latinized “Alhazen”.

Ibn al-Haytham (956-1040) had been a major figure within a branch of Arabic mathematics in which had been developed the geometry of the conic sections—circle, ellipse, parabola and hyperbola—as earlier theorized by Apollonius of Perga in the second century BCE. But while Desargues had attempted to capture those “projective” relations explored by Alberti, Durer and others, within an axiomatizable two-dimensional geometry,xiii the Arab’s development of geometry science had been at least partly motivated by the need to understand the use of the astrolabe, an astronomical instrument whose use dated back to Greek astronomers. Thus in the nineth century, Abmad al-Farghani (c 800-870) had devoted a chapter of a book, The Perfect (al Farghani 2005), to its geometrical underpinnings, a presentation described as “the first truly geometrical study of geometrical projections” (Rashed 2017, 2; c.f., Abgrail 2015, 159-160). The Arabs had conceived of Apollonius’s work Conics as having given rise to a whole new branch of mathematics, “ilm al-tastih”, the “science of projection” (Rashed 2017, 2).

Al-Farghani, Ibn-al-Haytham and other Arab geometers, as later would Kepler and Desargues, had taken Apollonius’s approach to conic sections well beyond that found in Apollonius himself. While Apollonius had conceived the four conics as produced by sectioning a cone different angles, he still treated them as essentially different figures. The Arabs, and later, Kepler and Desargues, had sought “projective” principles linking these shapes when considered entirely as plane shapes abstracted from their perspectival qualities. All introduced into geometry the idea of a type of movement or transformation between shapes which had earlier, with certain exceptions, been conceived in static way.xiv Like the Arabs, Kepler would appeal to a principle of analogy, linking the various conic shapes in ways that would later be referred to as their “projective equivalence”.xv An ellipse, for example, could easily be thought of as a stretched circle, appealing to the type of intuitions that would be later used in discipline of topology. Using a type of dynamic vocabulary, Kepler would thus note, “a straight line goes over into a parabola through infinite hyperbolas, and further through infinite ellipses into a circle […] the most obtuse hyperbola is a straight line, and the most acute, a parabola; the most acute ellipse is a parabola, and the most obtuse, a circle” (quoted in Rosenfeld 1988, 134-135).

A second feature of Kepler’s optics that would relate to Desargues’s geometry was the notion of “points at infinity”. Renaissance theories of perspectival painting had already come up with the conception of infinitely distant “vanishing points” at which perspectivally represented lines that are “objectively” parallel appear to meet, and for Kepler, the existence of points at infinity would be a consequence of stretching an ellipse to an infinite extent. Kepler had determined that an ellipse had two “foci”, and if one “stretched” an ellipse far enough one would be left with a parabola with one focus, the other now residing an infinite distance apart. In his work The Knowns, Ibn al-Haytham had also discussed points at infinity in a projective context (Rashed 2017, 313-321). The existence of points at infinity for Desargues, however, would, as we will see, be integrated more systematically into his new geometry than had been achieved by Kepler, differentiating its conception of the plane from the traditional Euclidean plane. Both Kepler and Desargues would thus counter Euclid’s infamous “fifth postulate” (Euclid 1956, vol. 1, postulate 5), that asserted that even at infinite distances parallel lines would remain apart.xvi Again in the nineteenth century, Euclid’s fifth postulate would be denied a variety of different “non-Euclidean” geometries.

In the early nineteenth century, Desargues’ fundamental ideas would be revived in France by Gaspard Monge and Lazare Carnot together with their students (Gray 2007), and the discipline of projective geometry would blossom during the century, taking advantage of the contemporary development of algebraic resources, giving projective geometry its own “analytic” form, to rival that of Euclidean geometry deriving from Descartes.

As military engineers active during the revolutionary years of France, Monge and Carnot sought techniques analogous to those of Renaissance painters, allowing them to relate measurable distances between points on two-dimensional maps to points in the landscapes represented on those maps, and projective geometry served such purposes. For this they would employ the central “invariant” of projective geometry that replaced the invariance of distance and angle in Euclidean geometry. This had been discovered by Desargues, but was seemingly unknown to Kepler. Again, this idea had been present in the work of the Arabs. The invariant allowing perspectival mapping in space was a double-ratio, that is, a ratio of ratios, among distances separating four points on a straight line. 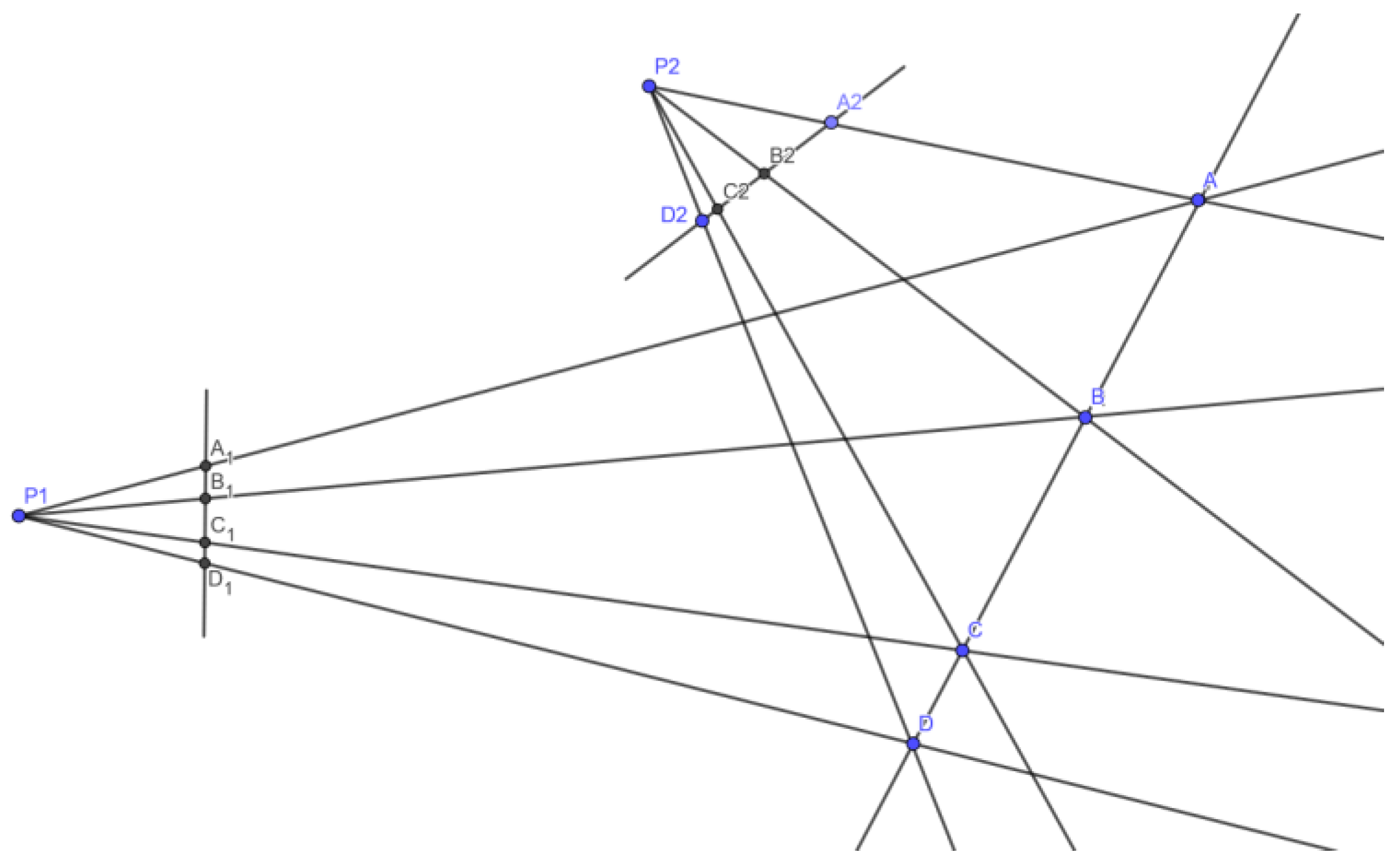This double ratio, later called the “cross-ratio,” was grasped as holding for different projections of such arrays or “ranges” of points, as illustrated in Figure 1.xvii

Here, two “pencils” of rays, each of four rays, radiating from points P1 and P2, are both sectioned by a line to form on that line a range of four points, A, B, C, D. Each pencil is also sectioned by a shorter line creating two further ranges, A₁, B₁, C₁, D₁, and A₂, B₂, C₂, D₂. Some principle is needed to relate the way the four points are proportioned differently over the three sectioning lines. What Desargues had discovered was that a certain double ratio holding among the points was constant. Specifically, the ratio between the ratios AB and BC and AD and DB (AB:BC :: AD:DB) was equal to that between A₁B₁ and B₁C₁ and A₁D₁ and D₁B₁ (A₁B₁: B₁C₁ :: A₁D₁: D₁B₁) as well as equal to that between A₂B₂ and B₂C₂ and A₂D2 and D₂B₂ (A₂B₂::B₂C₂::A₂D₂:D₂B₂). Furthermore, the same cross-ratio was found to hold between the angles formed among the four rays of the different pencils radiating from P1 and P2. More generally, this cross-ratio of ranges and pencils would hold for any further line intersecting these pencils, regardless of its orientation, and similarly of any further pencil of rays intersecting any of these ranges.

Regarded in this way, this diagram is meant to be taken as a two dimensional one—the theorems here hold regardless of any three-dimensional interpretation given to the lines or points involved. Projective geometry simply studies various configurations of points and lines. Nevertheless, we might imagine the diagram as a schematic representation of the viewpoints of, say, two painters, viewed from above, their viewpoints represented by P1 and P2, with the nearer, short sectioning lines representing the picture planes of the canvases on which each is portraying a common scene. Thinking of points A, B, C, and D, as points on common objects within the scene, we can now appreciate how the constancy of the cross ratio might allow us to think of relations among perspectivally different representations of some common scene.

It would take some time for the realization that projective geometry was not simply Euclidean geometry with some added theorems of this kind. For example, it might be thought that such ratios could have determinate values only because such values are able to be assigned to them by the underlying metric made explicit by Descartes’s coordinates. In the second-half of the nineteenth century, however, this would be shown to be mistaken, when the mathematician Felix Klein, having classified the various existing geometries with the resources of algebraic group theory, would raise the question of “the sense in which it seems psychologically justified to construe projective geometry before metrical geometry and to regard it as the very basis of the latter”.xviii Klein was relying on the fact that a special instance of the cross-ratio relation called the “harmonic cross-ratio”, was able to be constructed within an entirely non-metrical form of geometry. Rather than presupposing Euclidean geometry, the latter in fact presupposed it.

In this harmonic cross-ratio, the cross-ratio itself has a value of 1—that is, a ratio like that of AB:BC in the figure above would be equal to that of AD:DC.xix Here the adjective “harmonic” hints at the ultimate Greek “musical” sources of projective geometry. The harmonic cross-ratio was, in fact, the “most beautiful bond” that Plato had regarded as responsible for the coherence of the different parts of the cosmos as a whole. We are now in a better position to examine this “harmonic” conception of space and its role in Kepler’s astronomy and the neo-Platonic astronomy upon which Kepler had drawn.

3. Kepler’s Early Polyhedral Model

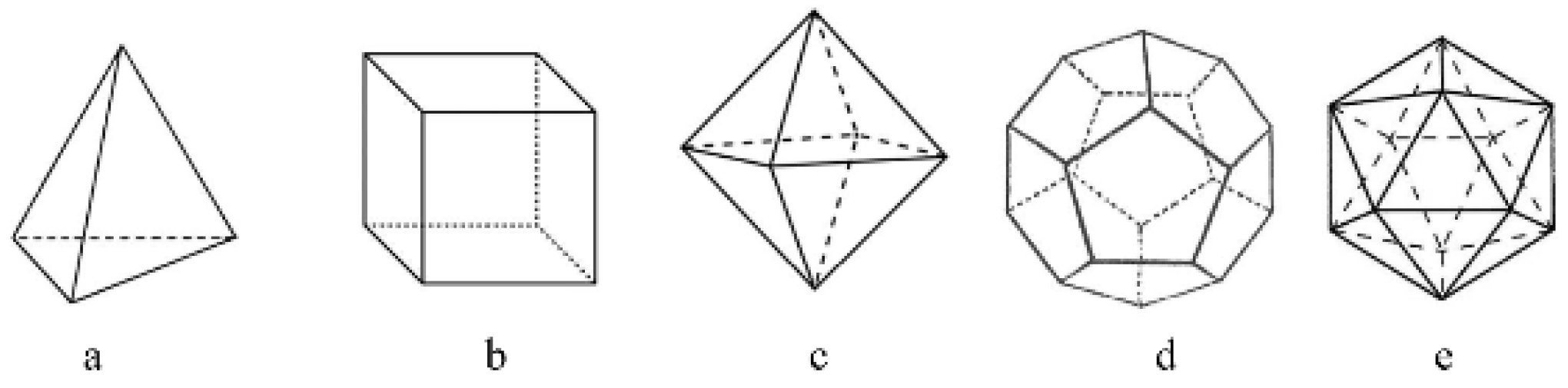
The regular polyhedral of the astronomical model of Kepler’s Mysterium Cosmographium are three-dimensional geometric structures with identical regular polygonal faces that meet each other along edges that themselves converge on points of intersection or “vertices”. Theaetetus, a younger colleague of Plato in his Academy, is the presumed author of Proposition 18, of Euclid’s Elements, Book XIII (Euclid 1956) proving that there are only five such solids, the ones illustrated in Figure 2 below: the tetrahedron, with 4 triangular faces, 6 edges, and 4 vertices; the cube, with 6 square faces, 12 edges and 8 vertices; the octahedron, with 8 triangular faces, 12 edges and 6 vertices, the dodecahedron, with 12 pentagonal faces, 30 edges and 20 vertices; and the icosahedron, with 20 triangular faces, 30 edges, and 12 vertices.

The five regular polyhedra had played a fundamental role in the cosmology of Plato’s dialogue Timaeus, but not the same role as that to which they would be assigned by Kepler.xx In Kepler’s model, these five “Platonic solids” are arranged in a nested homocentric configurationxxi—from the inside out: octahedron; icosahedron; dodecahedron; tetrahedron and cube—such that between any two of these shapes, a sphere could be inserted with the vertices of the enclosed polyhedron touching its surface from within and the faces of the surrounding polyhedron touching the sphere as tangents from without. The five solids thus determined the spacing of six spheres with which he correlated the orbits of the six known planets. Kepler gives as a direct quotation the form of words (presumably from God himself, to whom Kepler credited the experience) within which the insight had come to him: “The Earth is a circle which is the measure of all. Construct a dodecahedron round it. The circle surrounding that will be Jupiter. Round Jupiter construct a cube. The circle surrounding that will be Saturn. Now construct an icosahedron inside the Earth. The circle inscribed within that will be Venus. Inside Venus inscribe an octahedron. The circle inscribed within that will be Mercury” (Kepler 1981, 69). In relation to Copernicus’s measurements of the relative distances of the planets upon which Kepler relied, this model had, in fact, been surprisingly accurate (Field 1988, 64-69). The most obvious failing of the model would come in 1871, a century and a half after Kepler’s death when a new planet, Uranus, would be discovered—a mathematical impossibility according to Kepler’s model. But within his own lifetime, with the availability of more accurate data, Kepler would see the need to revise the model himself, although its basic structure would remain intact. It is now accepted that the original “fit” between model and observation was simply a happy coincidence, and that the discovery of Uranus had put an end to any possible significance for Kepler’s Platonic speculations. I suggest, however, that Kepler’s attachment to the relations among the Platonic solids would remain highly significant for other reasons.

The underlying mathematical principle determining this structure, according to Kepler, was to be found in the relations among the polyhedral themselves, which he classified into three “primary” (cube, tetrahedron, and dodecahedron), and two secondary forms (icosahedron and octahedron) (Kepler 1981, 105). Kepler’s reasoning here certainly seems ad hoc. For example, the radii of the orbits of the three planets further from the sun than the Earth correlate with the primary polyhedra while those of the two closer to the sun correlate with those of the secondary polyhedra, Kepler declaring that “nothing could be more appropriate than that our Earth, the pinnacle and pattern of the whole universe, and therefore the most important of the moving stars, should by its orbit differentiate between the two classes of polyhedra” (Kepler 1981, 105). However, from the point of view of our task of showing how Platonic features of Kepler’s model point to features of its underlying geometry, his starting point of the division of the polyhedral into two classes is highly relevant.

A fundamental feature of projective geometry is its principle of “duality”—a type of functional equivalence between points and lines, such that for all theorems concerning relations among points, a similar theorem can be found concerning relations among lines.xxii Kepler’s partition of the five polyhedra into two groups follows from the role the principle of duality plays among the polyhedral themselves. Minus the tetrahedron, the remaining four polyhedra can be divided into two pairs, such that in each pair one figure is understood as the dual in the sense of the inverse of the other. Thus, while the square has 6 faces and 8 vertices, the octahedron has 8 faces and 6 vertices, and while the dodecahedron has 12 faces and 20 vertices, the icosahedron has 20 faces and 12 vertices.

This implies that an octahedron could be constructed inside a cube, such that each of its vertices is located at the middle of each of the six faces of the cube. Similarly, a cube can be constructed inside the octahedron, such that each of its eight vertices are located at the centres of each of the eight faces of the octahedron. An analogous arrangement holds with respect to the dodecahedron and the icosahedron. Each of Kepler’s two secondary solids are thus the “duals” of one or other of the two primary solids. As for the tetrahedron, it can be understood as being dual to itself, or “self-similar”.xxiii

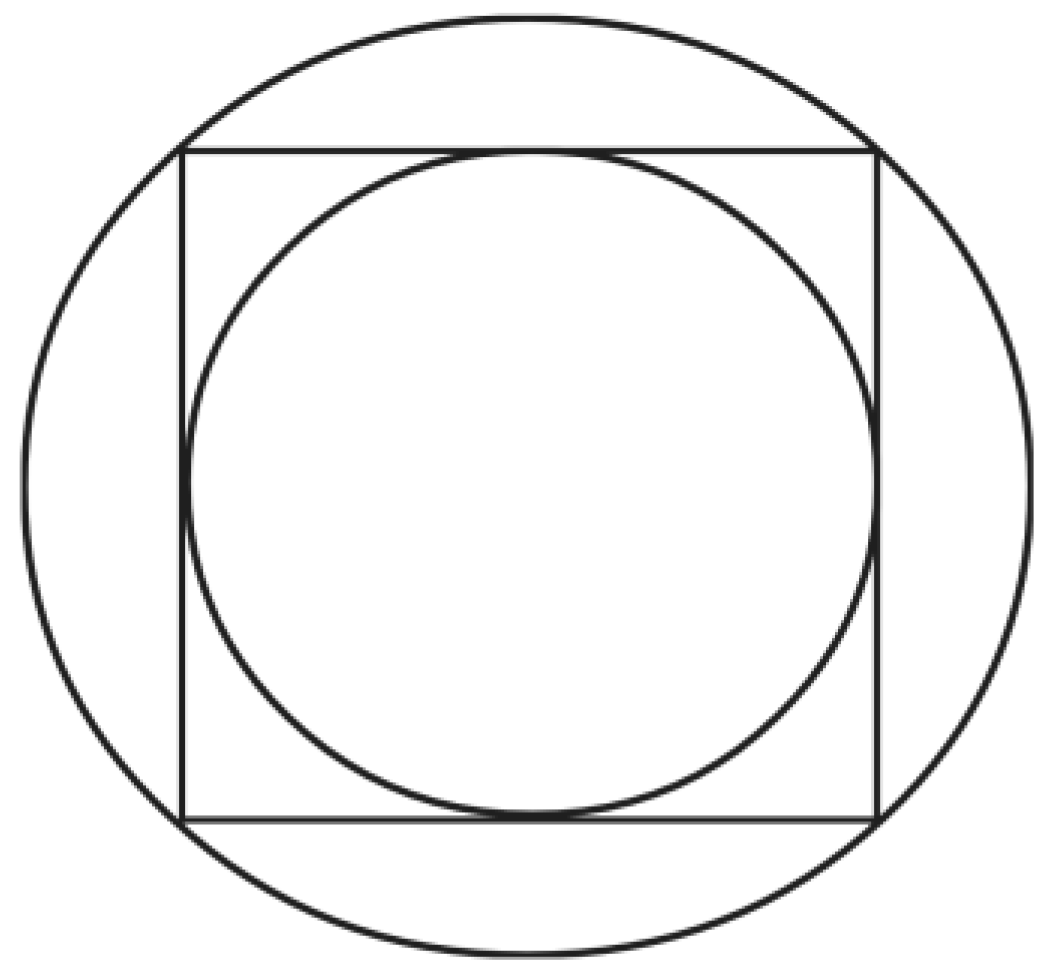
Such duality will prove highly relevant to the principles according to which polyhedra can be homocentrically nested, and to see this we might try to simplify the idea of nesting them by starting, as had Kepler initially,xxiv with the nesting of two-dimensional polygons separated by inner and outer circles. Consider, for example, a simple square with its inner and outer circles, as in Figure 3.

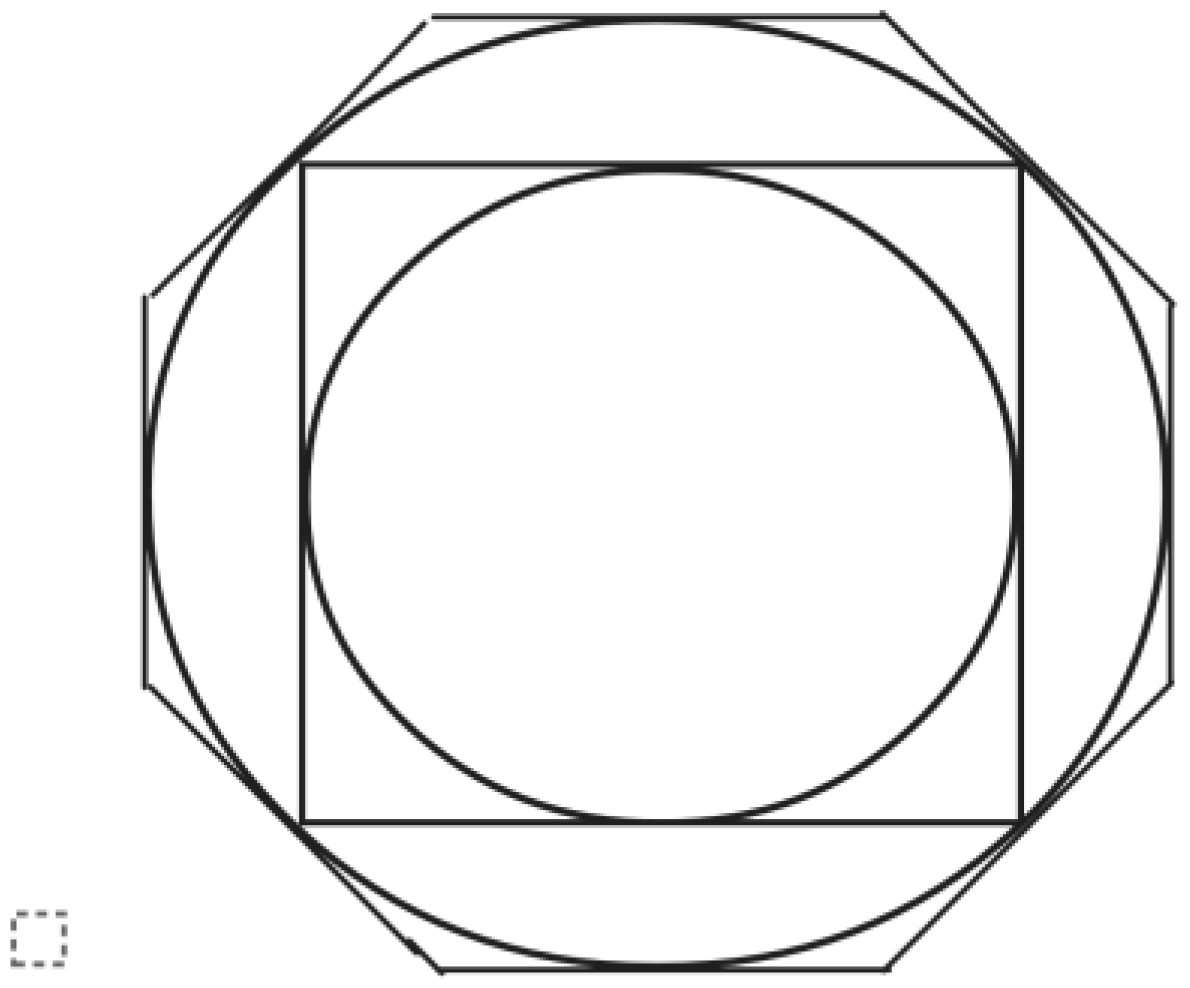
Here a square contains a circle that touches each of its sides and is circumscribed by a second circle that passes through each of its vertices. It is now easy enough to envisage how another regular polygon, concentric with both the square and the two circles, might be constructed such that its sides touch the square’s outer circle as tangents, as does the added octagon, for example, in Figure 4.

Of course, a further circumscribing circle could be now constructed passing through its eight vertices, and so on, building up a nested series of polygons from the inside out, and from this simple model we might now try to imagine a three-dimensional analogue by interpreting the square in Figure 2 as a section through a cube and its inner and outer circles as the great circles of inner and circumscribing spheres.

We soon discover, however, that adding this new third dimension has considerably complicated the relations involved. For example, while the octagon in Figure 3 might be considered as a section through the middle of some possible polyhedron, exactly which polyhedron it might be is not clear, as the sides of the octagon can be interpreted in different ways: a particular side might represent an edge joining two faces of the three-dimensional analogue, or it may represent a section through a particular face. As Pythagorean mathematicians had learnt in ancient Greece, moving between two- and three-dimensional forms of geometry introduces complex problems—in fact, the conic sections had first been investigated in Greece in relation to problems of three-dimensional geometry.xxv In this case, what is needed is some kind of underlying principles accounting for the way two dimensional faces can be combined into three-dimensional figures. One such principle—simple but with a vast array of applications—had been discovered more than a century after Plato by Apollonius of Perga (c 240–190 BCE) in the context of his study of conic sections, and this principle would be rediscovered in the nineteenth-century revival of projective geometry in France. It is a basic instance of the duality found in projective geometry, in this context that between a point and a line, a “pole” and its “polar”. 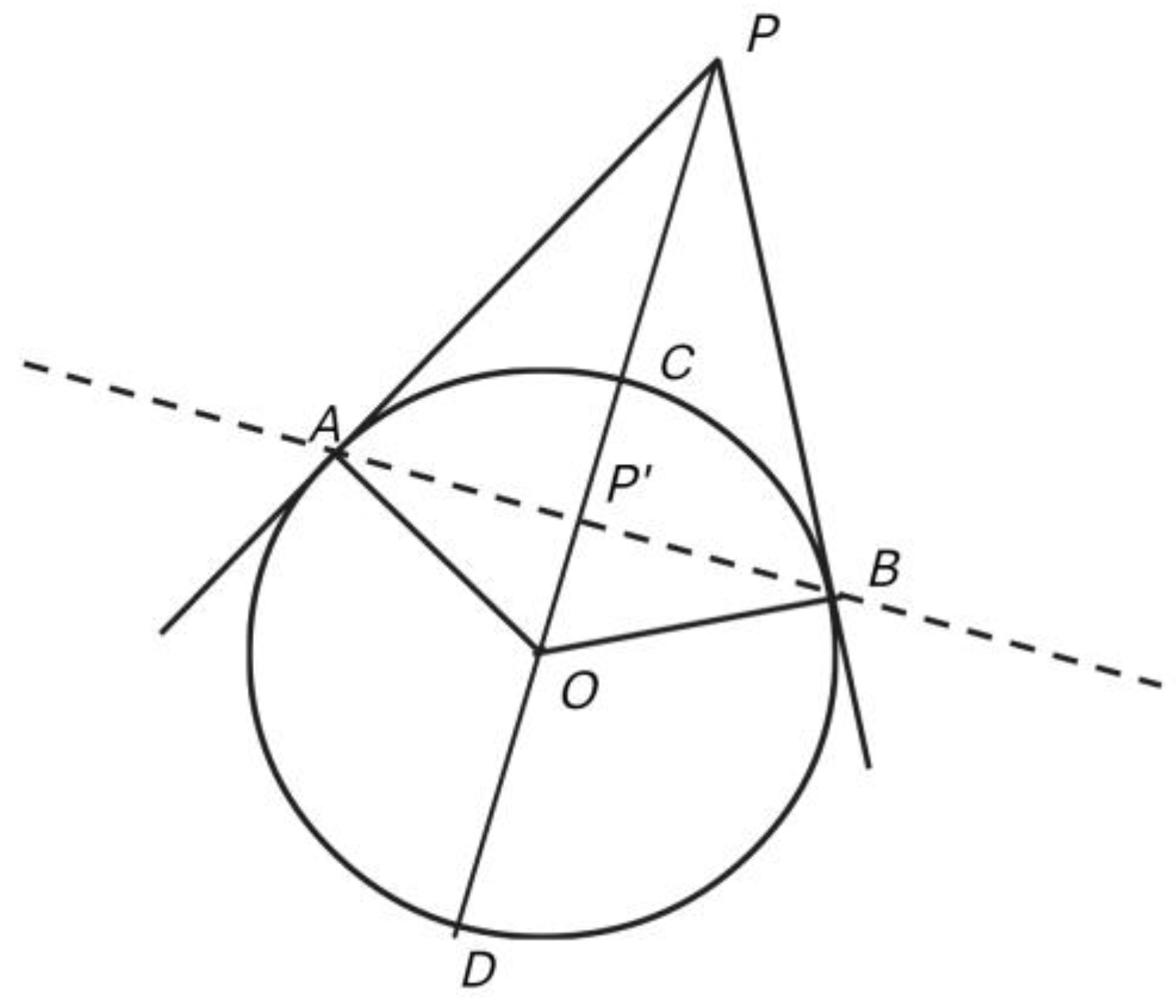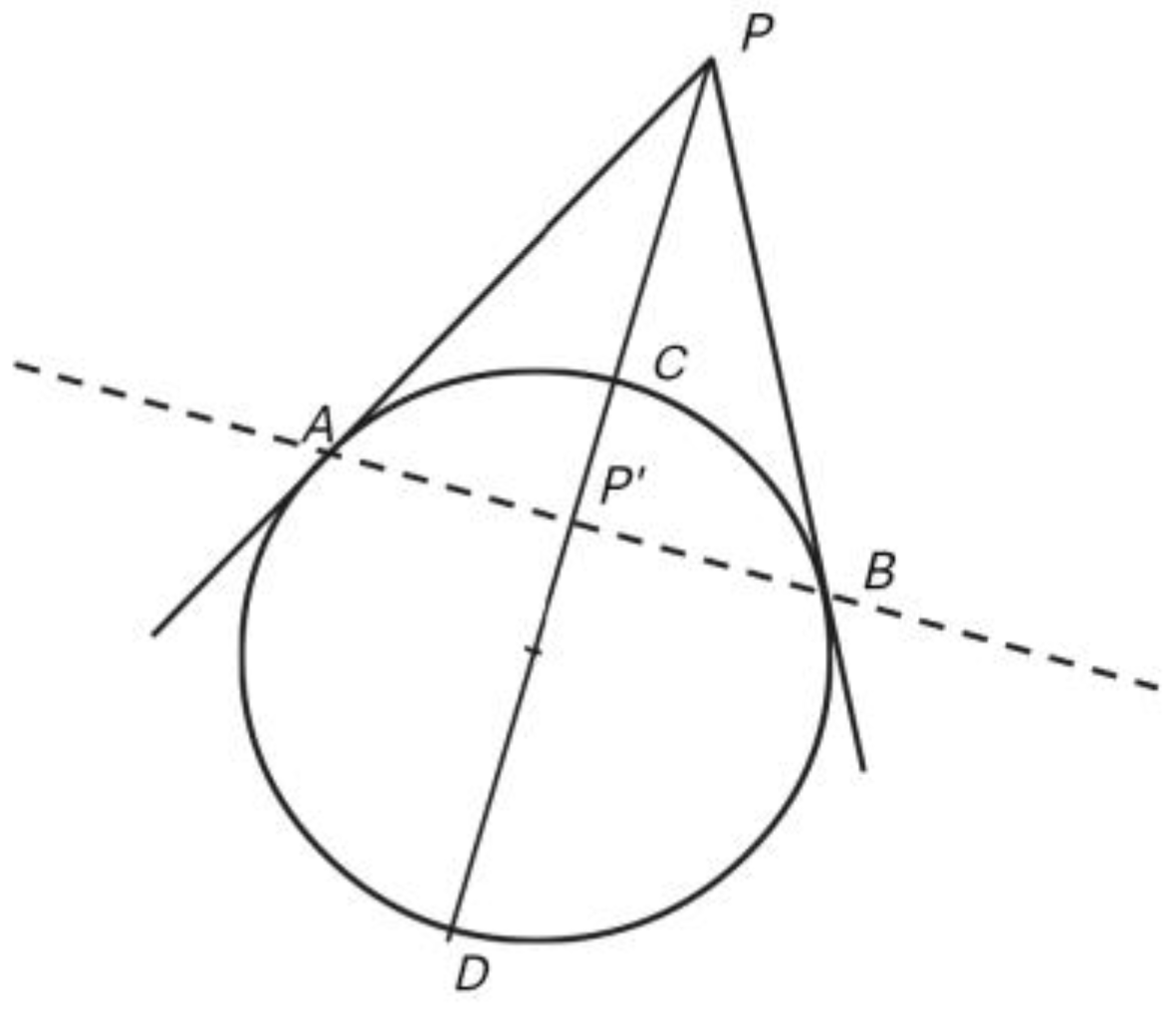The relation of pole and polar exists in relation to a circle (or any conic, but for simplicity let’s keep to the circle), can be illustrated in Figure 5 below.xxvi

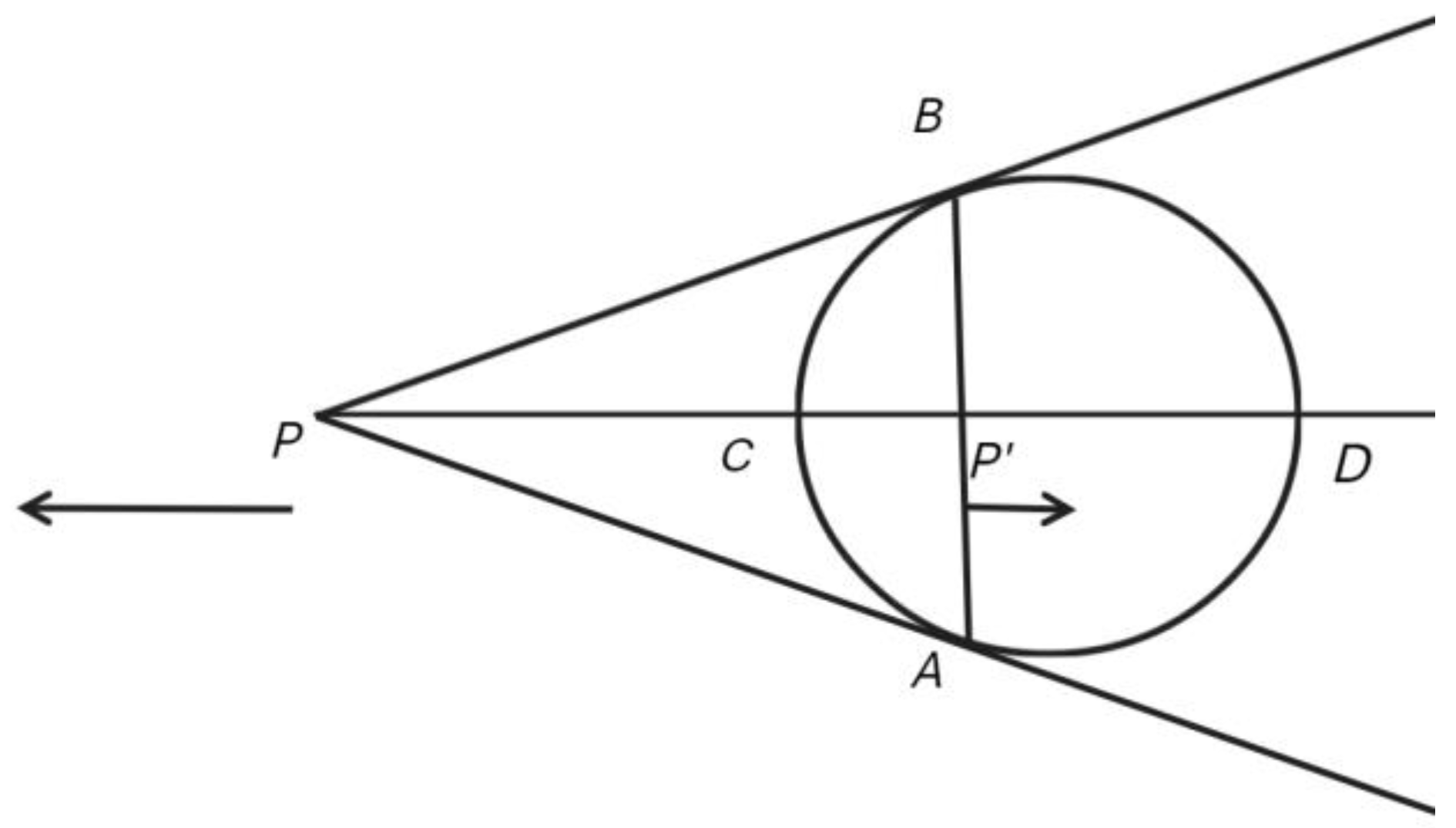
A circle inscribed on a plane separates the area inside the circle from that outside it in a peculiar way, such that for any point outside the circle (the pole) there will exist a unique line (the polar) that transects the circle, and for any point inside the circle, there will coincide a unique line wholly outside the circle. (Again, we will only consider the situation with a pole P lying outside the circle.)

For the pole P, the corresponding polar, the line AB, is found as illustrated in Figure 4. When two lines are drawn from P so as to tangentially touch the circle at points A and B, line joining points A and B will be the polar of P with respect to that circle. The point P', at which the polar intersects the line joining the pole (P) to the centre of the circle (O), is called the inversion of P,xxvii and it turns out that a particular relation will hold among distances marked out by the pole and its inverse with respect to the circle, in that the product OP⋅OP' = OA². Without much algebra, the Greeks would have expressed this in terms of areas, such that the area of a rectangle with sides OP and OP' would be said to be equal to the area of a square with side the length of the radius of the circle.

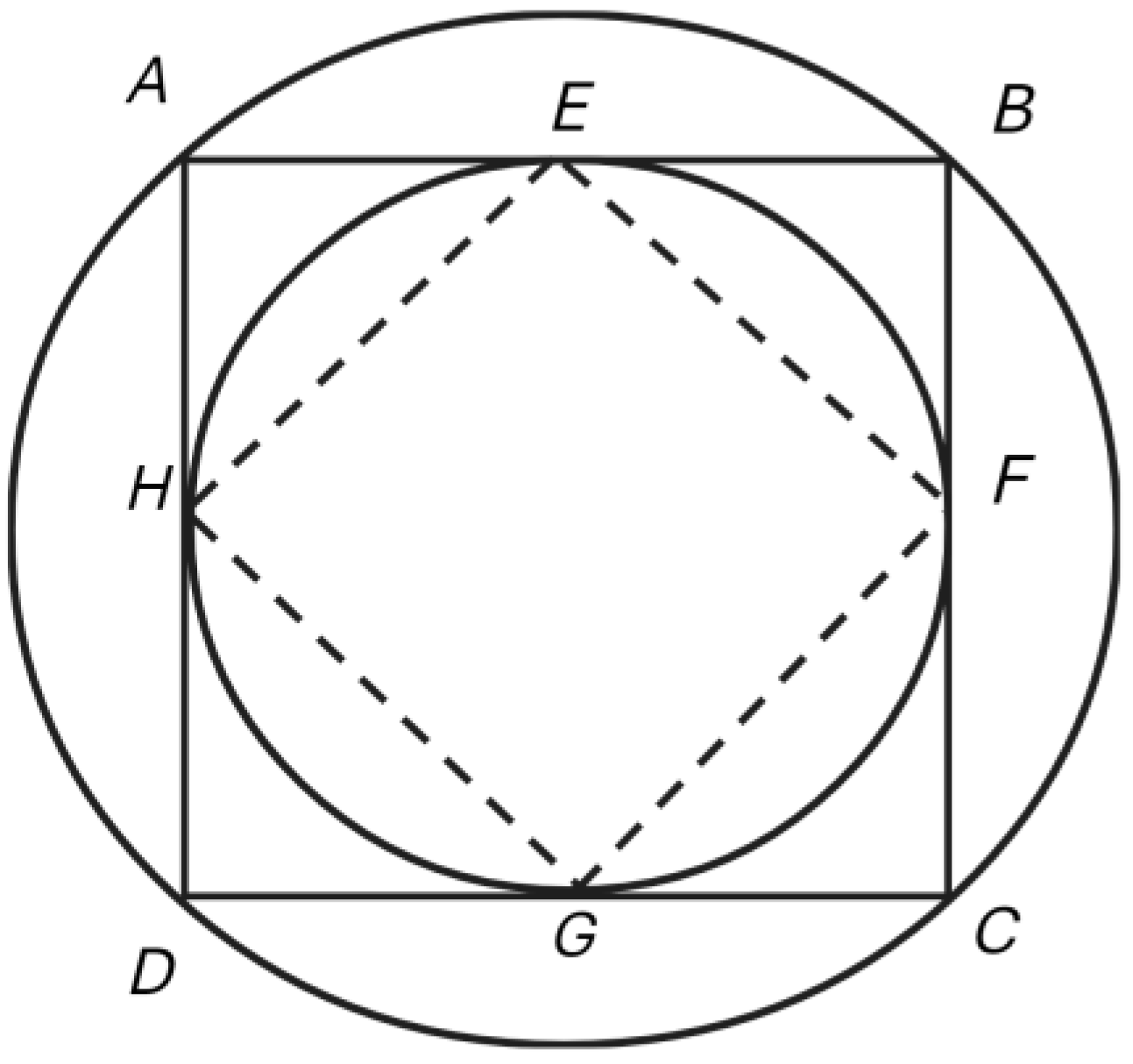
It is easy to see how the pole–polar relation might be relevant to Kepler’s nested polyhedra by returning to the simpler example of a square with inner and outer circles. Were we to construct a further square inside the circle contained in the first square and rotated 90° in relation to it, it can be appreciated that the sides of the innermost square are the polars of the poles represented by vertices of the surrounding square, just as, in Figure 6, A is the pole of polar HE, B that of EF, C that of FG, and D that of GH.

Adding a third dimension now eliminates the constraint that the inner and outer polygons be the same (in the figure above, squares). The analogous constraint is now that the inner polyhedron has the same number of vertices as the outer has faces. The dual relation now understood in three dimensions can thus be described as follows: “Take any point within the polyhedron as the center of a sphere of arbitrary radius. Let the vertices of the polyhedron be poles with respect to this sphere. The dual is defined to be the envelope formed by the planes polar to the vertices. [...] If we restrict ourselves to symmetric polyhedra that have circumscribing spheres, such as the platonic solids, the poles can be taken to be the vertices intercepted by the circumsphere while the polars are tangent planes to this sphere (the inscribed sphere of the dual)” (Kappraff 2001, 292).

We will see variants on this figure of Apollonius, relating pole to polar and its inverse, reappear in many guises in relation to the implicit conception of space that had been imported from antiquity into Kepler’s cosmological models, but significantly it also has deep direct connections with the harmonic theory that the Pythagoreans and Plato had extended to astronomy, the “harmonic” principle to which Kepler would appeal in his second model in the Harmonices Mundi of 1619.

4. Kepler’s Later Harmonic Model

In Mysterium Cosmographium Kepler had flirted with ancient harmonic theory in a somewhat confusing way in relation to trying to justify the partitioning of the zodiac into its traditional twelve constellations or “houses” (Kepler 1981, Chapter XII. 131-135). In Harmonices Mundi, however, the harmonic model is expanded to effectively become the dominant structure, Book III being devoted to the development of harmonic theory itself, independently of any astronomical application, and Book V, to its application to the orbits of the planets. However, here we must distinguish between the way that Kepler thought of harmony as relevant to astronomy and the way that Plato had envisaged this.

That Kepler had regarded the thesis of the “music of the spheres” as much more than a metaphor is apparent in Book III of Harmonices Mundi which is devoted to a full-blown theory of musical intonation adequate to contemporary European music. Thus, Kepler criticises the limitations of the conception of intonation as theorized by Pythagoreans of Plato’s time and adopts the extension of this earlier approach found later in Ptolemy to be developed in the sixteenth century in a more modern musical context by Gioseffo Zarlino.xxviii

The traditional Pythagorean conception of the musical consonances, Kepler holds, showed the limits of their willingness to trust their senses for discerning consonantal intervals (Kepler 1997, 137), as they had restricted concordant intervals to three: the diapason (or octave, as in middle C to the C immediately above it, C4 to C5) and, within the octave, the diatessaron (the fourth, as in C to F, and the diapente (the fifth, as in C to G) (Kepler 1997, 133-134). The Greeks had set great store on the fact that for the tones emitted from a vibrating string, the ratios for dividing the string into these three intervals could be constructed from the tetrad or tetraktys of numbers 1, 2, 3, and 4. Thus the octave coincided with dividing the string in half and so with the ratio 2:1, while the fifth coincided with dividing the string in the ratio 3:2, and the fourth in the ratio 4:3. While the octave, the fourth and the fifth are still thought of as fundamental concords, for the needs of musical theory, especially one relevant to the complex polyphonic music of the Renaissance, many more consonant intervals needed to be recognized.

The three early Pythagorean intervals had been based on the simple arithmetic of the way a “mean” could divide two terms: the geometric mean in the case of the octave, the arithmetic mean in the case of the fifth, and the harmonic mean in the case of the fourth. The geometric mean, g_m, of two terms, a and b, understood according to the ratio a:g_m = g_m:b (understood algebraically, g_m=√ab), had been given special status in Greek culture, but with a number system limited to the positive natural numbers with no zero, the idea of a square root fell outside of Greek arithmetic, and so could not be given a determinate value for non-square numbers such as 2. This meant that the geometric mean, while defining the interval of the octave itself, could not divide the octave, the task of which fell to the arithmetic and harmonic means. Algebraically, the arithmetic mean m_a of terms, a and b, is

\frac{a + b}{2},

while the harmonic mean had been described as holding between three terms such that “the part of the third by which the middle term exceeds the third is the same as the part of the first by which the first exceeds the second” (Barker 1989, 42).xxix This, in fact, turns out to be the mathematical inverse of the arithmetic mean.xxx After Plato, Eratosthenes (276–194 BCE), an astronomer famed for his having measured the size of the Earth,xxxi had apparently written two books (now both lost), on the mathematics underlying Plato’s cosmology: Platonicus and On Means (Heath 1921 vol. II, 105-106).

A peculiar arrangement of the three means called the “musical tetraktys” and comprising the numbers 6, 8, 9 and 12 arranged into a double-ratio, 6:9 :: 8:12 (Barbera 1984, 200), had been interpreted by a number of important neo-Platonic thinkers as the “best bond” that Plato, in the Timaeus, had described as holding the diverse parts of the cosmos into a whole (Plato 1997, 31b-c).xxxii In particular, Plato had spoken of the need for two mean terms to mediate the extremes of a three-dimensional body while only one mean was required to mediate the relation of two extremes on a plane surface (Plato 1997, 32a-b)). In short, the three means of Pythagorean harmonic theory were seen as having properties significant at the level of the application of numbers to the measurement of space itself, independently of their specific application to music.xxxiii

It can be easily appreciated that double ratio formed among the numbers 6, 8, 9, 12 instantiates the harmonic cross-ratio of modern projective geometry, as the ratio of 8-6 to 9-8 (2:1) is equivalent to the ratio 12-6 to 12-9 (6:3 = 2:1). That is, the modern harmonic cross-ratio can be thought of as a generalization of the Greeks “musical tetraktys”. Without the resources of a well-developed algebra and an appropriate number system, the Greeks had, in their so-called “geometrical algebra”, exploited relations between the ratios of numbers and ratios of the continuous magnitudes of geometry on the other, ratios that had been discovered to be incommensurable. The system of means could be employed in ways that paired magnitudes unrepresentable in the number system, “irrational numbers” such as the square root of 2 (√2), with approximations expressed in ratios of natural numbers. In fact, the musical tetraktys can be used as the basis of an algorithm for the calculation of a numerical value for √2 itself. Crucially, an early instance of the geometric construction of the harmonic cross-ratio would appear within Apollonius’s Conics (Apollonius of Perga 2000). Thus, in Book I, Proposition 34, a construction is described in which a line is drawn from a point P passing through a circle (or an ellipse or a parabola) as its diameter, and cutting the circumference at points C and D, as below in Figure 7. If a perpendicular drawn to that line cuts it at point P' so as to form a harmonic cross-ratio, PD:DC::DP': P'C, then straight lines drawn from P to points A and B where the perpendicular cuts the circumference will touch the circle as tangents.xxxiv

Along with the formulae of the harmonic cross-ratio these constructions can certainly seem confusing, and a simpler way to think of such a “harmonic division” of a line is to think of there being two ways in which a line segment, DC, can be divided in a certain ratio. It can be divided internally, as here by P' forming the ratio DP': P'C and it can be divided externally in the same ratio, as here by P, to form the ratio DP:PC. In such a case the four points on the line stand in the harmonic cross-ratio, the fundamental invariant of projective geometry as indicated by Desargues and validated by Felix Klein.

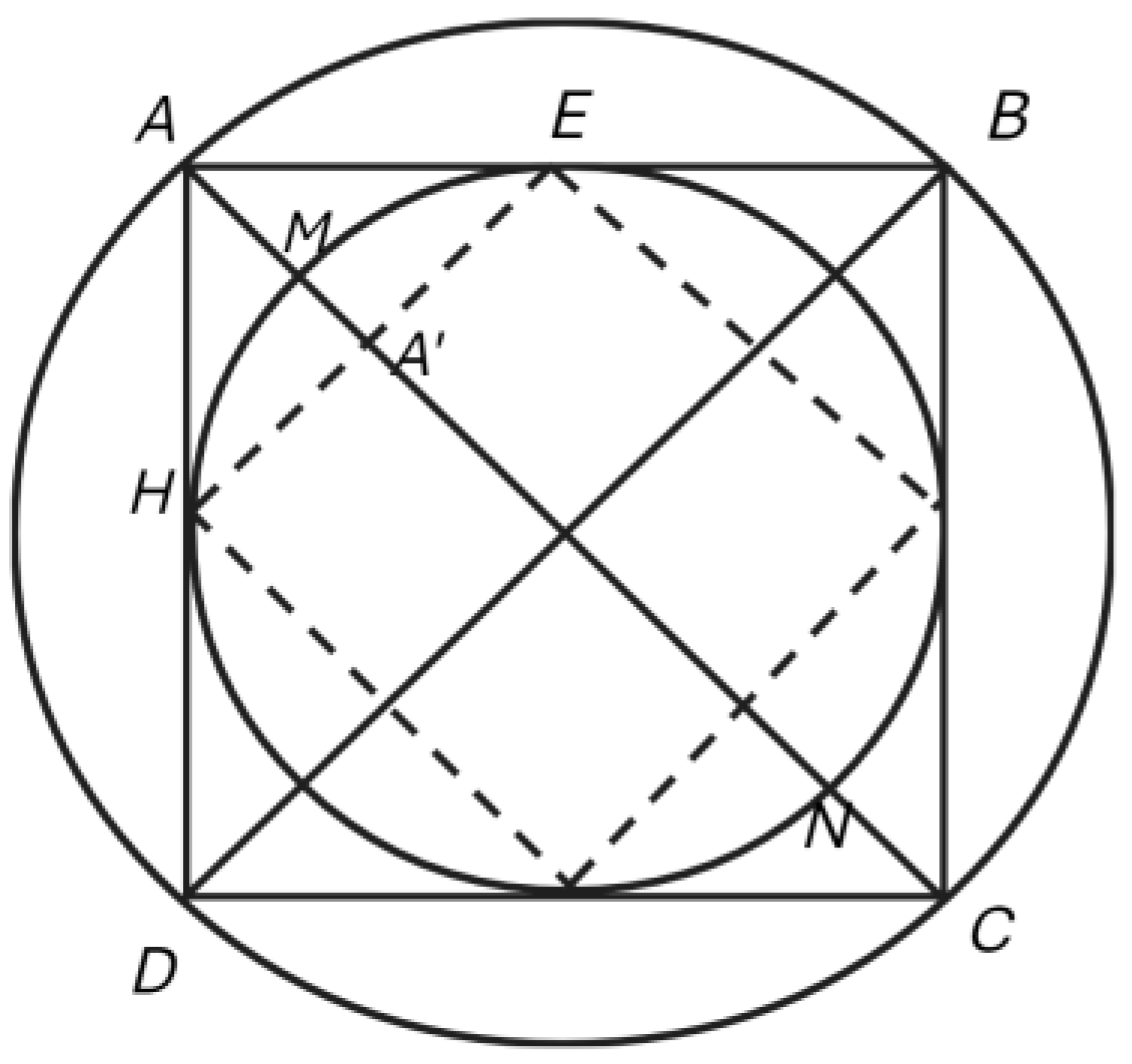
Were we to now construct diagonals through the corners of the outer squares in Figure 6 such that that they transect the circumference of its inner circle (as AC transects it at points M and N), and transect the sides of the inner square (as AC transects HE A') as in Figure 8 below, it can be appreciated how deeply the harmonic cross ratio is implicit within the space of the circles related as circumscribing the respective squares in this way, and, by extension, the three dimensional equivalents of such two-dimensional structures, the nested dual polyhedra.

Kepler was committed to the idea of finding the proportions found in the intonation of his contemporary music in the cosmos, believing it to express those most beautiful proportions entertained in the divine mind and in 1694 believed he had found them with the ratios of the orbits of the planets. Were space itself assumed to be Euclidean, finding such music features would surely be in need of some external explanation. But what if such harmonic relations were features of the structure of the space itself as presupposed by the astronomer in their investigations? Then such an extraneous explanation would not be needed. Kepler’s commitment to the music of the spheres might then be thought of as a variant of the “transcendental illusion” that Kant had believed responsible for the more usual belief that space was “in itself” Euclidean when, in terms of his transcendental idealism, the form of space was a construction imposed on sensory experience by the mind itself (Kant 1998, Transcendental Aesthetic, section I). This is, it was an illusion created by the projection of features of the explanatory resources employed onto the explanandum.

As the inheritor of a particular scientific tradition, Kepler could not help but incorporate various aspects of the amalgam constituting it. In the following section it will be shown how projective geometry itself had been a part of that amalgam constituting Greek mathematical astronomy. The space of the observed and measured universe would thus be “harmonic”.

5. The Role of Projective Geometrical Relations with the Amalgam of Astronomical Practices from Eudoxus to Kepler

When Plato established his Academy in Athens in 387 BCE, Greek astronomy was already at a relatively advanced stage, but it would benefit by the rapid growth of geometry among Plato’s associates such as Theaetetus (c 417-369 BCE)) and Eudoxus of Cnidus (c 390–340 BCE). The earth had, by this time, come to been conceived as a stationary spherical body, “floating” unsupported at the centre of a closed spherical cosmos,xxxv and so the cosmos was fundamentally structured by the idea of a relation between two homocentric spheres, an outer, celestial sphere, onto the inner surface of which the fixed stars were attached, able to be viewed by observers on the surface of the earth, the second, much smaller sphere located at the centre of the celestial sphere. Such homocentric spheres allow the idea of any point on either sphere to be projected onto an equivalent point on the other.xxxvi

The outer sphere was understood to revolve around the earth daily, based on observations carried out at night of the westward movements of the constellations in their counter-clockwise circling about the pole star. A similar east-west rotation, although a little slower, characterized the sun, which rose each morning, a little behind the position relative to the stars that it had risen the day before. In relation to the celestial sphere, then, the sun appears to complete an annual circuit against the heavens, tracing a circular path, the “ecliptic”. The ecliptic, however, was tilted in relation to the celestial equator, that is, the axis on which the sun revolved around the earth was on a tilt (approximately 23 degrees) to the axis on which the celestial spheres rotated. This coincided with the observation that the sun did not rise in the east at the same point on the horizon each day, but throughout the year moved between north and south solstices in a way that coincided with the seasons. From the Babylonians, the Greeks had learnt to partition the stars close to the ecliptic on either side into the twelve constellations of the zodiac, and for such agricultural economies, knowledge of the location of the sun with respect to the zodiac at any time was crucial for the practical know-how of when to plant and harvest.xxxvii Besides the movements of the sun, those of the moon and the five planets or “wanderers” could be similarly traced against the starry landmarks of the zodiac.

A sophisticated geometric model of the universe capturing these phenomena was put forward by Plato’s colleague, Eudoxus of Cnidus, as described by Aristotle (Aristotle, Metaphysics 1073b18 – 30; c.f., the summary in Crowe 2001, 22). Eudoxus’s complex model involved 27 homocentric spheres,xxxviii and the underlying idea of such homocentric spheres would persist with modifications through Ptolemy ultimately to Kepler’s specific version. After Eudoxus, however, more and more observational evidence would be accumulated, showing its need for further elaboration. Hipparchus of Nicaea (c 190- 120 BCE), the first to apply trigonometry to astronomy, had access to a vast collection of celestial observations from the Babylonians and attempted to deal with the anomalies of the existing approach that this data revealed. For example, the annual orbit of Sun had now been shown to be irregular,xxxix and to explain this Hipparchus located the earth excentrically, some distance from the geometric centre of the spherical celestial space around which all else rotated (Crowe 2001, 30-31). On the other hand, irregularities had been discovered in the paths of the moon and the planets, with planets such as Mars and Venus capable of “retrograde motion”, observed at points of their celestial circling as stopping and reversing direction, before resuming their paths.xl In relation to this, Hipparchus employed the “epicycle-deferent” system (Crowe 31-37; Timberlake and Wallace 2019, Ch 4.3). In this system, a planet, instead of revolving directly around the earth, revolved in an “epicycle” around a point which itself revolved on a circular path, the “deferent”, around the earth. Ptolemy would continue the combination of eccentric and epicycle-deferent systems in a model that would be the accepted until Copernicus.

The measurements taken in mathematical astronomy fundamentally related to changes in the measurement of angles subtended by objects over time in relation to the observer, and calculation of relative distances between planets would rely on the phenomenon of parallax, the difference in the apparent position of an object against a background when viewed from different locations. Thus an object such as the moon, when observed at a specific time, would appear in a different place in relation to the stars than it would appear when viewed from some distant point on the earth at the same time, or at the same place at a later time. Here the fixed stars provided the points of reference, like marks on a ruler as it would not be until the nineteenth century, that instruments were powerful enough to reveal parallax among the stars themselves.xli Measuring the angles between celestial objects of course required some sort of instrument, and the predominant instrument upon which all astronomical observation depended, was the astrolabe, which, as the Arabs would later show, was constructed on “projective” principles.

In his Almagest, the most influential astronomical work from antiquity, Ptolemy had described a spherically shaped instrument—the spherical astrolabe or armillary sphere (Ptolemy 1998, 217-219). It consisted of a central sphere, representing the earth, surrounded by a series of metal rings,xlii each representing one of the astronomically significant circles inscribed on the celestial vault, such as the celestial equator, the ecliptic, and the paths of the moon and planets.xliii The outer moveable band provided positions of prominent fixed stars situated around the ecliptic, sometimes divided into the houses of the zodiac, while the positions of the sun, moon and planets were represented on further fixed bands that could move independently so as to be aligned positions of the fixed stars. In short, this instrument was essentially a simplified metal instantiation of Eudoxus’s theoretical model of the cosmos with its multiple homocentric spheres from which the bands were, as if, cut out. A more common and practical flat form, usually referred to simply as the astrolabe, had also been described by Ptolemy in his Planisphere or Flattening the Surface of the Sphere (Ptolemy 2007), a work lost in the Greek but which had been preserved in Arabic translation. Besides reproducing the modelling functions of the armillary sphere, the astrolabe contained a type of quadrant for taking angular measurements, and suspended vertically it could be used in order to find the user’s bearings.xliv The astrolabe would later be perfected by Arabic scientists and craftsmen and in relation to which they would develop their “science of projection”. From Muslim Spain it would be reintroduced into the rest of Europe in the 12^th century.

The astrolabe consisted of a series of flat plates that could turn around a central fulcrum, each performing tasks performed by the parts of the armillary sphere. The base plate, the “mother”, sat inside a raised annulus divided into 360 degrees against which angles could be measured and on the mother was engraved a coordinate grid.xlv On top of this, and able to be rotated on the mother, was a mesh-like disc, the “rete” (web), containing a ring representing the ecliptic, as well as various pointers representing the positions of prominent stars. Around these discs, and attached from the back, rotated the “alidade” or sighting arm, something like a doubled long-hand of a clock, at the end of which small holes pierced raised processes allowing visual alignment of the instrument with distant objects as with the quadrant. With this coordination of parts, the astrolabe has been described as combining the functions of “a compass, a clock, a calendar, a measuring tape, a sextant, a planetarium, an astrological ruler” (Aterini 2019, 242).

In order for the relative positions of lines or points as represented on a sphere to be now represented on a two-dimensional surface, a form of “projection” had to be used, but this was of a different type to the linear projection that would be explored in the Renaissance and that would lead into Desargues’s style of projective geometry. It was rather “stereographic projection”. While the Greeks used the geometry of stereographic projection (In the Almagest, Ptolemy describes it and had attributes it to Hipparchus, while Virtruvius had earlier attributed it to Eudoxus)xlvi, there is no evidence that they had found proofs that would justify this use. That advance would await the Arab mathematicians of the nineth and tenth centuries (Abgrall 2015).

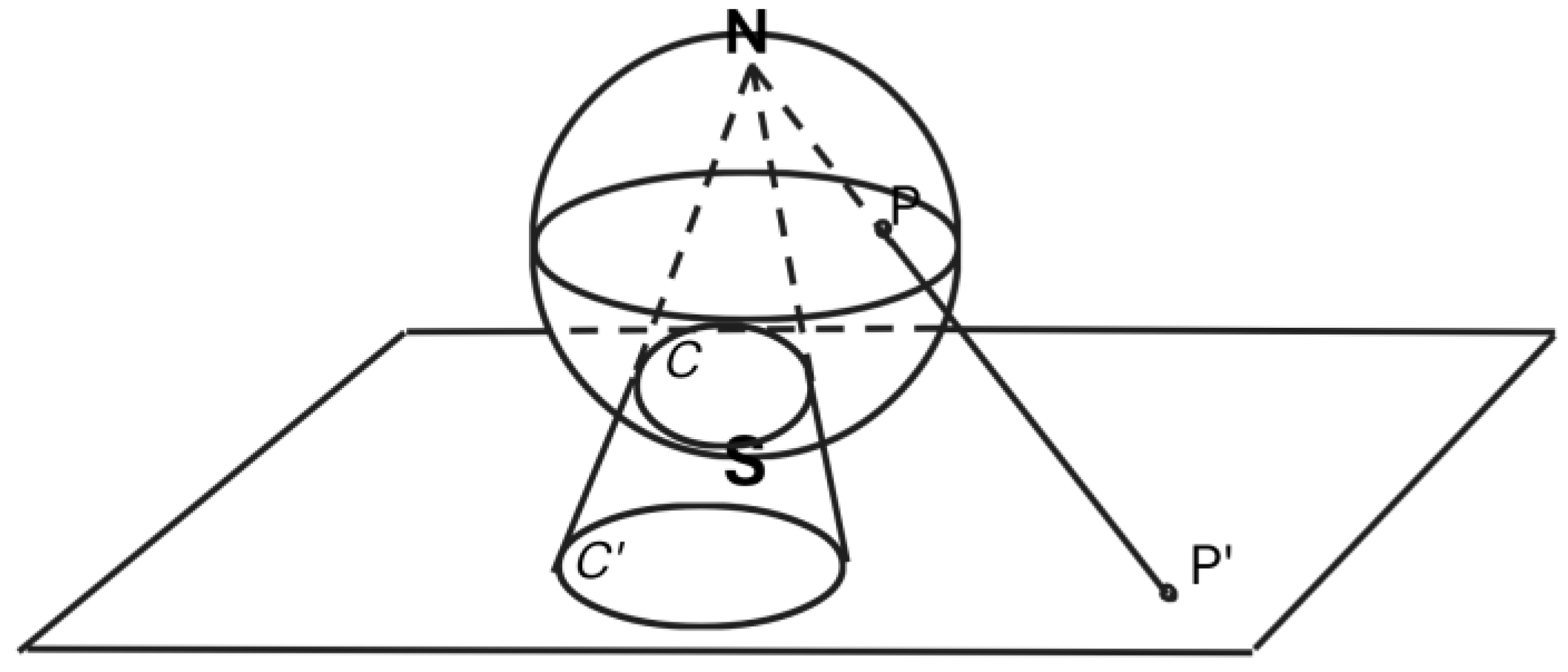
In stereographic projection, rays are taken as emanating from a pole of a sphere, passing through the surface of the sphere at points in such a way as so as to map those points onto points on a plane, conceived as passing tangentially through the opposite pole, as in Figure 9 below.

Analogous to linear projection, equalities of distance are not preserved in stereographic projection, but certain other relationships between points are preserved, analogous to the preservation of the cross-ratio in linear projection. Most importantly for the operation of the astrolabe, is the preservation of circles on the sphere when projected onto the planar surface, as in Figure 9 where the circle C is projected onto the circle C'. If a circle on the sphere, like the merideans, pass through a pole, they are onto straight lines.xlvii

The proof of the invariance of the circle within stereographic projection would be first given by a mathematician working in Bagdad, Abmad al-Farghani, in a book devoted to the constructure of the astrolabe (Al-Farhhani 2006; Abgrail 2015, sect. II;). Not surprisingly, given the basically conical nature of the projection of circles onto circles, it seems clear that al-Farghani had built upon the approach to conic sections in Apollonius’s Conics. That is, the principles of stereographic projection were effectively grounded in the same geometry as that of the cross-ratio of linear projection.

After the use of the astrolabe had spread into the rest of Europe from Arabic Spain around the twelfth century, a simpler but more robust version suitable for use at sea, the “mariner’s astrolabe”, would be used by Portuguese navigators in the fifteenth century (Mott 2007). By the sixteenth century different variants of the astrolabe, including cheap paper constructions, were being widely used for surveying and navigation as well as astronomy and astrology. In the last third of that century another form of non-linear projection would be introduced by Geradus Mercator, a Flemish globe, map and instrument maker. In 1569 Mercator published the first map using the now familiar “Mercator projection”, which, somewhat analogous to the astronomer’s stereographic projection, projected points on a spherical surface—in this case the terrestrial sphere—onto a flat surface, but now conceived as wrapped around the sphere to form a cylinder from which it could be “unwrapped”.xlviii In the Mercator projection great circles on the globe were mapped onto straight lines on the plane, in this case, the longitudinal meridians meeting at the poles on the sphere appearing as parallel lines. As with stereographic projection, Mercator projection is “conformal” or angle-preserving, and with a Mercator map, sextant, ruler and protractor, navigator could plot their journeys as straight lines (“rhumb lines”) on the map and with a mariner’s astrolabe, at any time locate their own position on the map.xlix

In the last quarter of the century, Tycho Brahe would be able to take advantage of this great development of instrumentation. Having been given control of an island, Hven, located between Denmark and Sweden, he had there established a castle/laboratory filled with such types of instruments, often designed by himself and capable of measuring angles with unprecedented accuracy (Timberlake and Wallace 2019, 154).l After the death of his patron, the King of Denmark, Tycho would relocate to Prague, where he would soon be joined by Kepler. The patron there of both Tycho and Kepler, the Holy Roman Emperor Rudolf II, being said to have possessed eight astrolabes. Figure 10 below shows an instrument combining of armillary sphere at the top with an astrolabe below, constructed by the Swiss watchmaker, Jost Bürgi, who had worked with both Tycho in Hven and Kepler in Prague. This instrument is described as having been used by Kepler.li

In his Optics Kepler had shown himself to be working within the spirit of a tradition that, starting with the Greeks had become developed into a systematic science in the Arab world in the centuries of its great scientific development. Even had Kepler been unconscious of the way that the tradition he worked within was shaped by projective geometry, this could still be described as implicit in his practice. Nevertheless, it seems clear from his conception of the geometry underlying his innovations in optics that he would have had the “feel” of such a projective features of space. In conclusion we might turn to differences separating his attitude to Copernicanism to that of Geordano Bruno to see this as guiding his actual calculations.

6. Conclusion: Two Senses of the “Copernican Principle”

A sign that Kepler was self-consciously relying on those projective features of astronomical space implicit within the ancient tradition of mathematical astronomy might be found in his rejection of the cosmology of another infamous Copernican at the time, Giordano Bruno. Bruno had been executed by burning in Rome in 1600 for the Copernican heresy as well as others, but Kepler’s copernicanism was not that of Bruno’s. From a contemporary point of view Bruno’s seems the distinctively more modern, as he had hypothesized that the fixed stars were suns like our own, with their own exoplanets perhaps supporting life. As Field points out, however, in neither Mysterium Cosmographium nor Harmonice Mundi did Kepler embrace such Brunoean features of the universe, even though he was certainly aware of Bruno’s claims (Field 1988, 17).

While this conservatism has been attributed to religious factors, Field assesses Kepler’s rejection of Bruno’s infinite universe in terms of his adherence to what could be established at the time by empirical methods. “If the Universe is immense or infinite, in the sense that we must believe it to contain objects we cannot observe, such as stars that are sometimes too far away for us to see them … then we cannot know how to construct theories to explain what we observe.” “[I]n modern terms” she adds, “the word ‘Universe’ must be taken to mean ‘observable Universe’” (Field 1988, 18). In a similar spirit, Christopher Graney positively contrasts Kepler’s heliocentric universe with Bruno’s centreless one: “[I]n the early seventeenth century, science reveals the Copernican universe to consist of exactly that which Kepler describes in the sixteenth chapter of De Stella Nova: a vast shell of huge but dull stars, surrounding a tiny but brilliant sun and its lively planets, and at least one of these planets teems with life; and among that life are these motes of dust called human beings, which beget themselves, clothe themselves, and so forth. A universe of sun-like stars, on the other hand, is the creation of those who do not do their science carefully enough…. It is not the universe observed by careful astronomers” (Graney 2019, 166). If science is an amalgam of various techniques, forms of instrumentation that cannot be entirely separated from its theories, the components of that amalgam will clearly be subject to historical change. We now have observation evidence that supports Bruno’s belief that the stars are other suns, but that evidence would not be available until centuries later. Now, regions of the universe unimaginable to Kepler or Bruno have been opened up by instruments such as the James Webb Telescope, but we are still not in a situation entirely different to Kepler. We can conceive of regions of the universe that are still beyond observation as light from them has yet to reach the earth, and it is still not known whether the universe itself is infinite or finite. Nevertheless, like Kepler, astronomers still assume the infinity of the universe for their mathematical calculations.

Field notes how in a diagram in Ch. XIV of Mysterium Cosmographicum, a narrow space separates the “circle of the Zodiac” from the orbit of Saturn, but this space is described as being “like infinity” (Field 1988, 41-43). That is, for the purpose of calculating the relative distances of the planets from the sun, the distance of the stars from the sun can be considered as infinite—an infinity meant in the sense of “immeasurable” or “immense”, and in comparison to which the orbits of the planets would be considered “insensibly small” (Field 1988, 43). Might not such an infinite be understood on the model of those “points at infinity” within projective space”? These are points that Kepler had conjectured must exist from his understanding of the dynamic relations among the conic sections and are points that Desargues would relate to the vanishing points of perspectival representations.

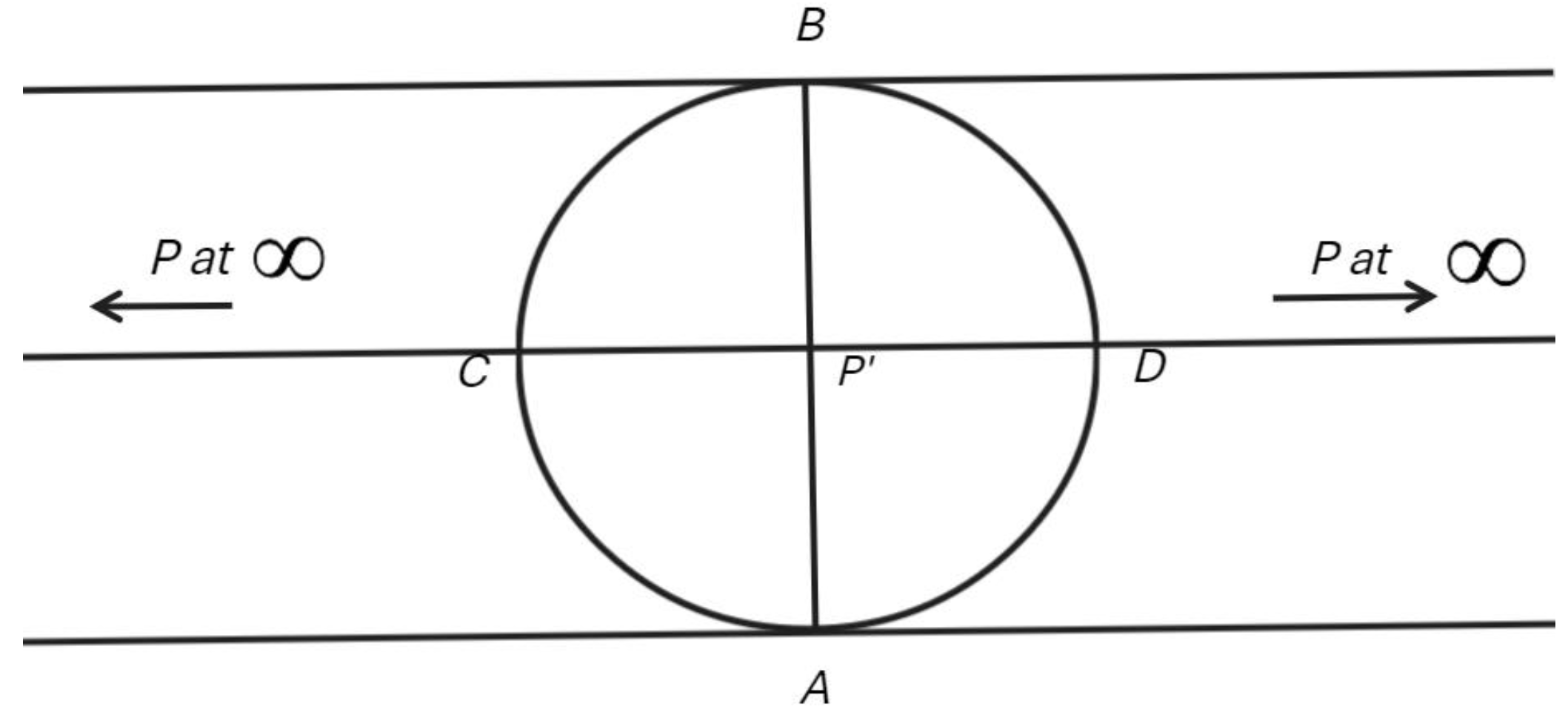
Points at infinity can be understood from the orientation of projective geometry’s central “invariant”, the harmonic cross-ratio, which, as we have seen, following Apollonius, can be conceived in terms of the harmonic properties of a pole and its inverse, with respect to a circle as found in Figure 11a.lii

The Arab mathematicians as well as Kepler and Desargues had thought of diagrams of the sort found in Apollonius’s investigations of conic sections as dynamic rather than static, and this idea of movement is relevant here. If pole P is thought of as moving to the left away from the circle, its inverse, P', will move to the right towards the circle’s centre. A consequence of the harmonic cross-ratio will be that as P' approaches the centre of the circle, P will approach infinity. Thus, when P' reaches the centre, the tangents radiating from P will be parallel—in projective terms, they will meet at infinity, exemplifying the difference between the Euclidean and projective planes.

A further peculiarity of projective geometry is that, unlike Euclidean geometry in which a line extends infinitely in both directions, in projective geometry a line extended infinitely to the left approaches a point which is the same point at infinity approached in leftward movement.liii Thus, as P' in figure 11b continues to move to the right after passing through the centre, P, which had been moving left, will be now found to approach the circle from the right. The analytic projective geometry of the nineteenth century would be devoted to finding algebraic proofs underlying such peculiar geometric intuitions.

Accepting Kepler’s immeasurable, or “immense”, as equivalent to a projective sense of “infinite”, we might now think of the Copernican principle as able to be employed in different ways by Kepler and Bruno. The principle is typically invoked to distinguish the spirit of Copernican astronomy from that of “unreflective” everyday experience, but it clearly does not distinguish Copernican astronomy from Ptolemaic astronomy. The pre-Copernican astronomers were surely, in one sense, as equally Copernican as Copernicus himself.

That complex Greek amalgam of practices that Ptolemy would inherit from Plato, Eudoxus and Hipparchus and would transmit to later generations had been redolent with devices to explain the difference between the observed paths of celestial bodies and their paths as plotted theoretically with the resources of geometry. For example, the theoretical moves of displacing the earth from the centre of the cosmos or postuating deferents and their epicycles were made to try to show the stars as not simply wandering as they appeared to Apollonius, the proto-projective geometer par excellence, had in fact demonstrated that these two theoretical devices employed to explain the regressions of planets were, in fact, observationally equivalent (Neugebauer 1975, 190-196). As Crowe notes “the epicycle-deferent system can be used to replicate any motion resulting from an eccentric circle. To achieve this, simply set the epicycle radius equal to the eccentricity of the eccentric circle” (Crowe 2001, 34).liv

Surely it had been an implied projective geometry, given the fundamental role played in it by notions of duality and inversion and its links to the ability to theorize the relation of the perspectivally opposed points of view, that had been perfectly fitted to the type reversal of perspective invoked in the “Cartesian principle”? Moreover, we might then think, that when applied without such geometric resources, as in Bruno, what remained of the Copernican principle was simply a contrast between a conception of how the universe appears from some specific point of view within it and one of how it really is, or, in a more seventeenth-century idiom, how it appears from God’s “point of view”, on the other. As no human observer can be understood to be located at such a “view from nowhere”, this interpretation of the Copernican principle could not be a part of empirical astronomy itself. Rather, it could only play the role of a type of superadded “metaphysical” gloss.

Kepler had indeed strayed into the territory of such non-empirically based metaphysical conceptions with his embrace of the thesis of the music of the spheres. This cosmic “music” had to be perfect because it was the artistry of the divine, and hence perfect, musician. This clearly had “neo-Platonic” provenance, and the neo-Platonists certainly had also extended Plato’s ideas about space from being astronomical notions to “metaphysical” or “mystical” ones. I have suggested, however, that such ideas about the relevance of the application of musical intervals to the world was in no way limited to this metaphysical gloss. It had been integral to the scientific practice of astronomy inherited by Kepler. The reemergence of non-Euclidean geometries in the nineteenth century might also suggest that such ideas remain relevant to the present.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

No new data were created or analyzed in this study. Data are contained within the article.

Conflicts of Interest

The author declares no conflicts of interest.

References

Abgrall, Philippe. 2015. Les Debuts de la Projection Steretographique: Conception et Principles. Arabic Sciences and Philosophy, 25: 135–166.
Al-Farghani. 2005. On the Astrolabe. Arabic text edited with a translation by R. Lorch. Stuttgart: Franz Steiner Verlag.
Andersen, Kirsti. 2007. The Geometry of an Art: The History of the Mathematical theory of Perspective from Alberti to Monge. New York: Springer.
Apollonius of Perga. 2000. Conics, Books I–III, new revised edition. Edited by D Densmore; translated by R. C. Taliaferro. Santa Fe: Green Line Press.
Aristotle. 1984. The Complete Works of Aristotle: The Revised Oxford Translation. Edited by Jonathan Barnes, Princeton: Princeton University Press.
Aterini, B. 2019. The Astrolabe: A Mechanism for Reading the Stars. In Explorations in the History and Heritage of Machines and Mechanisms. Edited by B. Zhang and M. Ceccarelli. Cham: Springer, pp. 227-242.
Baltus, Christopher. 2020. Collineations and Conic Sections: An Introduction to Projective Geometry and its History. Cham: Springer.
Caspar, Max. 1993. Kepler. Translated and edited by C. Doris Hellman. New York: Dover.
Copernicus, Nicholas. 1992. On the Revolutions. Translated by E. Rosen. Baltimore: Johns Hopkins University Press.
Crowe, Michael J. 2001. Theories of the World from Antiquity to the Copernican Revolution. Second Revised Edition. Mineola, NY: Dover Publications.
Daners, Daniel. 2012. “The Mercator and Stereographic Projections, and Many in Between”. American Mathematical Monthly 119: 199-210.
Dear, Peter. 1988. Mersenne and the Learning of the Schools. Ithaca: Cornell University Press.
Descartes, René. 1954. The Geometry of Rene Descartes with a facsimilie of the first edition. Translated by David E. Smith and Marcia L. Latham. New York: Dover Publications. Original publication, 1637.
Duner, David. 2023. “The Copernican Principle”. In Gargaud, M., et al. Encyclopedia of Astrobiology, 666–668. Berlin: Springer. [CrossRef]
Einstein, Albert. 1954. Johannes Kepler. In Ideas and Opinions. Translated by S. Bargemann. New York: Crown, 262–266.
Ellerman, D. A. Fundamental Duality in the Exact Sciences: The Application to Quantum Mechanics. Foundations 2024: 175–204. [CrossRef]
Euclid. 1956. The Thirteen Books of Euclid’s Elements. 3 Vols. Translated by Sir. Thomas L. Heath. New York: Dover.
Field, J. V. 1986. Two Mathematical Inventions in Kepler’s ‘Ad Vitellionem ParalipomenaI’. Studies in the History and Philosophy of Science 17(4): 449−468. [CrossRef]
Field, Judith. V. 1988. Kepler’s Geometrical Cosmology. Chicago: University of Chicago Press.
Field, J. V. and J. J. Gray. 1987. The Geometrical Work of Girard Desargues. New York: Springer.
Gaukroger, Stephen. 2020. The Failures of Philosophy. Princeton: Princeton University Press.
Granada, . 2004.
Gray, J. 2007. Worlds Out of Nothing: A Course in the History of Geometry in the 19th Century. London: Springer.
Heath, Thomas. 1921. A History of Greek Mathematics, 2 volumes. Oxford: Clarendon Press.
Kant, Immanuel. 1998. Critique of Pure Reason. Edited and translated by Paul Guyer and Allen W. Wood. Cambridge: Cambridge University Press.
Kappraff, Jay. 2001. Connections: The Geometric Bridge Between Art and Science. Singapore: World Scientific Publishing. [CrossRef]
Kepler, Johannes 1981. Mysterium Cosmographicum: The secret of the universe. Translation by A. M. Duncan, Introduction and Commentary by E. J. Aiton, with a Preface by I. Bernard Cohen. New York: Abaris Books.
Kepler, Johannes. 1997. The Harmony of the World. Translated by E. J. Aiton, A. M. Duncan, and J. V. Field. Philadelphia, P.A.: American Philosophical Society.
Kepler, Johannes. 2000. Optics: Palipomena to Witelo and optical part of astronomy. Translated by William H. Donahue. Santa Fe: Green Lion Press.
Klein, Felix. 1890. Zur Nicht-Euklidische Geometrie. Mathematische Annalen 37: 544–572.
Kleiner, I. 2012. Excursions in the History of Mathematics. Cham: Springer.
Koyré, Alexandre. 1973. The Astronomical Revolution: Copernicus-Kepler-Borelli. New York: Dover.
Kuhn, Thomas S. 1995. The Copernican Revolution. Massachusetts: Harvard University Press.
Love, David K. 2015. Kepler and the Universe: How One Man Revolutionized Astronomy. Amherst, N.Y.: Promethius Books.
Mott, Lawrence V. 2007. Navigational Techniques. In The Oxford Companion to World Exploration. Edited by David Buisseret. Oxford: Oxford University Press.
Netz, Reviel. 2022. A New History of Greek Mathematics. Cambridge: Cambridge University Press.
Neugebauer, Otto. 1975. A History of Ancient Mathematical Astronomy. Berlin: Springer. [CrossRef]
Nicomachus of Gerasa. 1926. Introduction to Arithmetic. Translated by Martin Luther D’Ooge; with studies in Greek arithmetic by Frank Egleston Robins and Louis Charles Karpinski. New York: Macmillan Co.
Plato. 1997. Timaeus. In Complete Works. Edited by John M. Cooper. Indianapolis: Hackett, pp. 1224 - 1291.
Ptolemy, 1998. Almagest. Translated by G. J. Toomer, with a foreword by Owen Gingerich. Princeton: Princeton University Press.
Rashed, Roshdi. 2017. Ibn al-Haytham’s Geometrical Methods and the Philosophy of Mathematics: A History of Arabic Sciences and Mathematics, Vol 5. Translated by J. V. Field. Abingdon, Ox.: Routledge.
Reid, Mark J. and Karl M. Menten. 2020. The First Stellar Parallaxes Revisited. Astronomische Nachrichten, 341: 860-869. [CrossRef]
Rosenfeld, B. A. 1988. A History of Non-Euclidean Geometry: Evolution of the Concept of a Geometrical Space. Translated by Abe Shenitzer. New York: Springer.
Swerdlow, N. M. and Otto Neugebauer, Otto. 1984. Mathematical Astronomy in Copernicus’s De Revolutionibus. In Two Parts. New York: Springer.
Timberlake, Todd, and Paul Wallace. 2019. Finding our Place in the Solar System, Cambridge: Cambridge University Press.
Vitrac, Bernard 2006. Les mathématiques dans le Timée de Platon: le point de vue d’un historien des sciences. Etudes platoniciennes 2: 11-78.
Voelkel, James R. 2001. The Composition of Kepler’s Astronomica nova. Princeton NJ: Princeton University Press.

i	Kepler had encountered Copernicus via his teacher at Tübingen, Michael Maestlin.
ii	See, for example, the accounts in Love (2015, ch 4), and Timberlake and Wallace (2019, ch. 7.2). Voelkel, 2002, gives an account of the rhetorical strategies behind Kepler’s presentation of his work in Astronomica nova.
iii	Thus, Kepler was critical of Copernicus who, he thought, still fudged the difference between computational astronomy and cosmology or natural philosophy (Granada 2004, 101).
iv	On what we can reconstruct of the actual mathematics implicit in Plato’s Timaeus, see, for example, Vitrac 2006.
v	See, for example, Swerdlow and Neugebauer, ch 1. Copernicus himself had died during the publication of De Revolutionibus and his reaction to Osiander’s preface, if he had been aware of it, is unknown.
vi	Nevertheless, it would be revived at various times in European history. A christian interpretation given by Augustine of Hippo would in turn be revived by Marin Mersenne in his Traité de l’harmonie universelle of 1627 , while more pagan Pythagorean/Platonist interpretations would be advanced by Ficino in the fifteenth century and by the Paracelsian occultist Robert Fludd in the sixteenth. See Dear 1988, ch 5. Mersenne’s scientific meetings would be the context in which Desargues would first present his ideas of projective geometry.
vii	Thus Kepler insisted that the cosmos had to reflect a music of the complexity of modern polyphonic music, which, he believed, was more suited to express the magnificence of God’s creation.
viii	Kepler is standardly regarded as a Euclidean in geometry. E.g., “In the domain of geometry, Euclid is his master and guide. To him he pays the highest praise. His Elements are for him an unequalled master work” (Caspar 1993, 273).
ix	Euclid seemed to have conceived of equalities among lines and angles in such a way despite the Platonic assumption that such lines were essentially without width or depth.
x	As, for example, when a straight line can be described by the equation x + y = 2 or a circle by x² + y² = 1. Such algebraic resources had not been available to the Greeks.
xi	This was in his thesis on painting, Della pittura, published in Florence in 1480 (Rosenfeld 1988, 134).
xii	A Latin edition of parts of this work had been published in Europe in 1566.
xiii	On the history of such attempts see Andersen 2007.
xiv	Roshdi Rashed has described Ibn al-Haytham’s attempts to theorise the introduction of motion into geometry as had been taken up by Arab mathematicians in this way. While this idea had been found in Greece, especially in the work of Archimedes, “it is a different matter, again, to introduce motion as one of the fundamental notions in geometry” and “to take such a step requires a reformulation of geometrical ideas […] Ibn al-Haytham is, as far as I know, the first to have attempted to carry out this reformulation” (Rashed 2017, 8).
xv	Leibniz, especially, would take up this idea into his own plans for a non-metrical form of geometry, “analysis situs”. For an account of the history of the “principle of continuity” after Kepler see Kleiner 2019, ch. 9.
xvi	In the nineteenth century, the idea of internally coherent geometries without this postulate would appear with specifically non-Euclidean geometries.
xvii	Analogous to this, an equivalent double ratio can be considered as holding among the angles of a “pencil” of four rays. For the sake of simplicity I will focus on ratios of line-lengths.
xviii	“We can distinguish between mechanical and optical properties of space. The former find their mathematical expression in the free mobility of solid bodies, the latter in the grouping of the straight lines that run through space (the rays of light, or the lines of sight emitted by the rays). The question here is not how our idea of space comes about (or has come about over the course of generations): no one will doubt that mechanical and optical experiences work together or have worked together. The question is whether the properties of one or the other type should be given priority in the methodical construction of spatial science. For Mr. von Helmholtz, as we have examined in detail, the mechanical properties are preferred: but one can also begin with the optical properties. The developments can be viewed side by side and each of them has its own particular advantages” (Klein 1890, 570).
xix	Strictly, the value is −1, as Carnot had introduced the idea of assigning line-segments a value of + or − on the basis of their direction or “orientation”. Thus, if the segment AB is deemed positive, that of BA is negative. For simplicity sake I will ignore this dimension.
xx	For Plato, four of the solids defined the nature of the four basic elements of the cosmos: fire (tetrahedron); air (octahedron); water (icosahedron); and earth (cube) (Plato 1997, 54e–56e). He assigned the dodecahedron to the shape of the cosmos as a whole (55c).
xxi	That is, all with the same centre.
xxii	The significance of duality for modern mathematics and science is now regarded as extending well beyond the area of projective geometry. See, for example, Ellerman 2024.
xxiii	For its part, the tetrahedron is its own dual (is “self-similar”) in that with four faces and four vertices, a similar but inverted tetrahedron can be constructed within it, the mid-points of the faces serving as vertices for the second internal tetrahedron. This process can be iterated indefinitely.
xxiv	Kepler lists the various approaches taken leading up to the polyhedral theory. The penultimate was the attempt to fit the orbits to circles between nested polygons (Kepler 1981, 67).
xxv	Menaechmus (c 380-320 BCE) had employed the conic sections in an attempt to solve the famous “Delian problem”, the problem of finding the size of a cube such that its volume would be double that of another cube. Menaechmus is sometimes taken as the discoverer of the conic sections (Netz 2022, 101-104).
xxvi	The properties of the pole and polar are spread over various theorems Apollonius’s Conics (Apollonius of Perga 2000, Book III propositions 30–34).
xxvii	The theorems of such an “inversion geometry” would be widely studied in the nineteenth century.
xxviii	Zarlino had been involved in a protracted dispute with Galileo’s father, Vincenzo Galilei, who advocated the new way of dividing the octave equally in steps of the proportion, 1:¹²√2. The idea of non-square numbers as having “square roots” had only been introduced into Europe in the sixteenth century. As for the Greeks, numbers were limited to the positive natural numbers, this proportion used a number entirely unimaginable to the Greeks.
xxix	Archytas seems to have been counting down the scale, reversing the sequence. Thus, the part of 6 by which the harmonic mean, 8, exceeds it (2, or one third of 6) equals the part of the 12 by which it exceeds 8 (4, or one third of 12).
xxx	The harmonic mean can thus be calculated as ( $\frac{\frac{1}{a} + \frac{1}{b}}{2}$ )^-1, which simplifies to $\frac{(2 a b)}{a + b}$ .
xxxi	Eratosthenes had estimated the circumference of the earth to be equivalent to 250,000 stades, though to be approximately 23,100 miles, while its present estimate is 24,900 miles (Crowe 2001, 29).
xxxii	Thus, Nicomachus of Gerasa, for example, in his Introduction to Arithmetic, discussing Plato’s “most perfect proportion, that which is three-dimensional and embraces them all”, notes that it “would properly and truly be called harmony […] since it is not a plane, nor bound together by one mean term, but with two, so as thus to be extended in three dimensions” and goes on to describe this as a structure unifying the three musical means, that he equates with the musical tetraktys” (Nicomachus of Gerasa 1926, 284–286). Similar identifications of Plato’s best bond with the musical means are found in Proclus and Iamblichus of Chalcis.
xxxiii	Kepler’s complaint about the limitations of the musical tetraktys was not in the spirit of Plato, who criticized the musical theorists’ exclusive identification of this structure with the perceived consonances of music itself. For Plato, musical phenomena and astronomical phenomena were to be explained by some common underlying mathematical principles, principles whose more general application was not to be understood as the application of musical principles qua music.
xxxiv	This is usually found expressed in the reverse way. From a point P a line is drawn through the centre of a circle, cutting its circumference at points C and D. If tangents are drawn from P to the circle, touching it at A and B, and the line AB transects the line PD at P', then the points P, C, P', D form a harmonic range.
xxxv	Anaximander (c 610–546BCE) is credited with having first conceived of the earth as unsupported at the centre of the cosmos, earlier conceptions having the earth float in water. Anaximander, however, conceived of the earth as a cylindrical disc, with diameter three times its height. (Crowe 2001, 114).
xxxvi	There had been various alternatives on offer. Famously, Aristarchus of Samos (310 – 230 BCE) had proposed a heliocentric model. Earlier, Philolaus of Croton had conjectured that a fire other than the sun was at the centre. This could not be seen from Greece, as it was on the side of the earth always facing “outwards” as it rotated around this fire.
xxxvii	From the modern heliocentric perspective, of course, the “movement” of this outer sphere is illusory. It is we observers on the surface of the earth who rotate daily.
xxxviii	The outermost sphere was, of course, that of the fixed stars arranged into the 12 constellations of the zodiac, and within this was a second, inclined to it at an angle of 23.5 degrees and rotating in the same direction but at a different rate. The Moon was located on a third sphere, with a 5-degree inclination to the second, and rotating in the opposite direction to the first two. Similarly, three spheres were needed to accurately account for the movement of the Sun on its ecliptic path, while a further four spheres were required for each for the five planets (Crowe 2001, 23).
xxxix	From the perspective of the heliocentric model, this would be shown to be an expression of the fact that, as Kepler would show, the earth’s orbit is an ellipse rather than a circle.
xl	This was already known to Eudoxus, and the multiple spheres associated with each star had been used to account for this phenomenon in a way anticipating Hipparchus’s solution.
xli	With the available instruments, in Kepler’s time parallax phenomena could not be overserved between the stars. The first time that parallax could be used to measure the distance of a star itself was in 1838 and needed relied on the measurement of an angle of 0.125 arcseconds (Reid and Menten 2020, 660). It will be remembered that Tycho Brahe had achieved an accuracy of only 1 arcminute (ie, 60 arcseconds).
xlii	The word “armillary” referred to bracelets or arm-bands.
xliii	Ptolemy, in Book V of the Almagest (Ptolemy 1998, 217-218), attributes the invention of the armillary sphere to Eratosthenes of Cyrene, a contemporary of Archimedes.
xliv	Ptolemy had also described quadrants in The Almagest.
xlv	This “altitude–azimuth” grid was a coordinate system that functioned somewhat like that of latitude and longitude, with altitude measuring the angle of an object above the horizon and azimuth an angle around the horizon, eastward from the north. Unlike the latitude – longitude coordinates, the altitude–azimuth coordinates were specific to the location at which the measurements were made. See Timberlake and Wallace 2019, ch. 2.1.
xlvi	In his Ten Books on Architecture Vitruvius had discusses an instrument known as the arachne (spider) attributed to Eudoxus working on the principle of “analemma” stereographic projection.
xlvii	Also, angles between intersecting lines on the surface of the sphere project onto similar angles on the plane, while equal rotations are preserved with respect to the sphere and its planar image (Rosenfeld 121-122).
xlviii	Here, the projection is conceived as one in which points on the surface of a terrestrial globe are projected onto a flat surface understood as wrapped around the globe as an encompassing cylinder, which will later be “unfurled”.
xlix	In 1772, the Alsacian mathematican Johann Heinrich Lambert would show that both the Mercator projection and stereographic projections were derived from a projection that went back to the Greeks favoured shape in the exploration of three-dimensional space, the cone (Lambert 1972; Daners 2012, 199-201). Lambert’s “conformal conic projection” would henceforth be introduced into the realm of mapping.
l	He had, for example, the then biggest existing quadrant built into a room dedicated to its use.
li	The instrument is currently located in the Nordiska Museet in Stockholm. An accompanying note reads: “Johannes Kepler studied the stars with the help of this armillary sphere”. Photo,
lii	It will be remembered that the inversion of P is the point of intersection between the polar of P and a line drawn from passing through the centre of the circle.
liii	This consequence had been accepted by both Desargues and Kepler.
liv	Kepler too, in the same spirit, had shown that the systems of Ptolemy, Copernicus and Tycho Brahe could be considered to be identical in relation to their observational consequences.

Figure 1. The invariance of the cross-ratio across different lines sectioning two separate pencils of rays.

Figure 2. a, Tetrahedron; b, Cube; c, Octahedron; d, Dodecahedron; e, Icosahedron.

Figure 3. a square with circumscribed and circumscribing circles.

Figure 4. an added eight-sided polygon for which the square’s circumscribing circle forms the inner circle.

Figure 5. A pole P and its polar AB in relation to a circle.

Figure 6. Poles and Polars in embedded similar polygons.

Figure 7. A simplification of Apollonius’s construction of the harmonic cross-ratio in Conics Book I, proposition 34.

Figure 8. The polar of point A, HE, transects the diagonal of the inner circle to form a harmonic cross-ratio, A,A'; MN.

Figure 9. Stereographic projection through the north pole onto a plane through the south pole. Points map onto points, as in P to P', and circles map onto circles, as in C to C'.

Figure 10. Armillary sphere and astrolabe constructed by the Swiss watchmaker Jost Bürgi and Antonius Eisenhoit, in Kassel, 1585 (photograph, Chris Bainbridge).

Figure 11. a. A pole P and its inversion P' with P moving to the left, and P' to the right.

Figure 11. b: Pole P at “point at infinity”, with its inversion P' at the centre of the circle. Note, the point at infinity is located equally to the right as to the left.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Could There be Method Behind Kepler's Cosmic Music?

Abstract

1. Introduction

2. Projective Geometry: A Historical Sketch

3. Kepler’s Early Polyhedral Model

4. Kepler’s Later Harmonic Model

5. The Role of Projective Geometrical Relations with the Amalgam of Astronomical Practices from Eudoxus to Kepler

6. Conclusion: Two Senses of the “Copernican Principle”

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe