Regional Housing Supply and Demand Imbalance Qualitative Analysis in U.S. Based on Big Data

Preprint

Article

Regional Housing Supply and Demand Imbalance Qualitative Analysis in U.S. Based on Big Data

Altmetrics

Downloads

Views

Comments

Yiqiu Tang,

Yanjun Chen,Shenghan Zhao^*

Yiqiu Tang,

Yanjun Chen,Shenghan Zhao^*

This version is not peer-reviewed

Submitted:

06 December 2024

Posted:

09 December 2024

You are already at the latest version

Alerts

Abstract

The United States housing market has historically exhibited regional imbalances in housing supply and demand, which have contributed to reduced housing affordability and market volatility. The application of big data technology enables the utilisation of data to enhance comprehension of these imbalances, thereby informing the formulation of policy. We put forth a model for analyzing the housing supply and demand based on big data, which employs a comprehensive approach to examine both the demand and supply sides. With regard to the demand side, the model incorporates a multitude of data sources to ascertain and delineate the pivotal elements influencing housing demand. These include population growth rate, household income level, employment opportunity distribution, migration and flow trends, and cost of living. By constructing cubes, the model is capable of capturing the characteristics of dynamic demand changes in different regions. With regard to the supply side, the model assesses land use, building materials and labor costs, the timeliness of building permitting and approval processes, and the impact of regional policies and regulations. By means of a quantitative analysis of the aforementioned factors, the model is able to identify housing supply bottlenecks in different regions. The model's efficacy in identifying significant imbalances between supply and demand in the United States housing market was validated through experimental analysis of historical data.

Keywords:

Subject: Business, Economics and Management - Business and Management

1. Introduction

The issue of housing is not solely concerned with the fundamental living requirements of the population; it also has a significant bearing on the country's economic growth and social stability. This issue has a significant impact on the well-being, quality of life, economic performance, and social cohesion of individuals. In recognition of the pressing need to address the housing crisis, governments have identified it as a core objective of their governance [1]. By implementing a range of measures, the government aims to enhance the quality of life for the population and improve their living environment.

As one of the largest capitalist countries in the world, the United States occupies a pivotal position and exerts an exemplary effect in the field of housing security. Since the Great Depression of the 1930s, the United States government has consistently advanced the development and enhancement of the housing security system through legislative action, financial investment, and policy innovation. The United States' housing security system encompasses federal, state, and local governmental entities and is characterized by a multi-layered and diversified policy design, financial support, and service delivery structure [2]. For instance, augmenting the availability of public housing enables the government to directly intervene in the housing market and rectify the disequilibrium between supply and demand. Moreover, the government offers housing subsidies to low- and middle-income families, thereby facilitating greater access to adequate housing for these demographic groups [3].

The United States' housing security system is notable for its innovative policy design and relatively mature construction and management of public housing. The federal government collaborates closely with local governments and civil society organizations to advance inclusive and sustainable housing initiatives. For instance, the government is partnering with nonprofit organizations to guarantee that housing policies continue to bolster the rights and interests of low- and middle-income groups, while also preventing policy "gaps." These strategies not only safeguard the housing rights and interests of low- and middle-income groups [4], but also effectively mitigate social contradictions and promote social equity and stability.

The advent of big data has provided policymakers and researchers with an unparalleled opportunity to gain insights into the nuances of housing market imbalances [5]. The use of big data allows for a more detailed examination of housing market trends, encompassing information such as demographics, migration patterns, economic conditions, and housing inventory in real time. This enables a more comprehensive evaluation of the qualitative and quantitative factors influencing housing supply and demand across regions [6].

The objective of this study is to conduct a qualitative analysis of the imbalance between housing supply and demand in the United States, and to use big data to identify the key indicators that affect these dynamic changes. By examining demand-side factors, including population growth, income levels, and migration patterns, as well as supply-side constraints, such as land availability, construction costs, and regulatory policies, this study will identify the regions most affected by these imbalances. Furthermore, we will employ clustering techniques to categorize regions with analogous housing characteristics.

2. Related Work

Initially, Hsieh et al. [7] sought to quantify the extent of spatial mismatch of labor and its overall economic cost between cities in the United States. The study revealed that high-productivity cities, such as New York and the San Francisco Bay Area, have experienced a reduction in overall United States economic growth due to the presence of significant restrictions on the supply of new housing. Further, Stacy et al. [8] investigate the influence of relaxed land-use regulations on the supply and cost of housing. The study revealed that the relaxation of restrictions was linked to an expansion in the housing supply and a decline in prices, although the impact was observed to vary across regions. Furthermore, the study indicates that the influence of such reforms on the high-end rental market is more discernible.

Alig and colleagues [9] examined the influence of population growth and individual income levels on urbanization since World War II, and the subsequent alterations to forest ecosystems. The study observes that between 1982 and 1997, the population of the United States increased by 17 percent, while the area of urbanization grew by 47 percent. During this period, more than 60 percent of new housing was constructed in or near areas of wild vegetation, resulting in a significant reduction in forest area. Furthermore, the authors project that as the United States population is anticipated to increase by over 120 million (approximately 40%) by 2050, the area associated with deforestation will surpass 20 million hectares, representing 13% of the existing private forest area.

Reifschneider et al. [10] conducted an analysis of the impact of the 2007-2009 financial crisis and subsequent recession on the productive capacity of the United States economy, with a particular focus on changes in the aggregate supply side. The model employs a methodology based on non-observed variables to estimate the change in the United States' potential gross domestic product (GDP) subsequent to the financial crisis. The findings indicate that potential GDP is approximately 7% lower than the projected trajectory prior to 2007.

3. Methodologies

3.1. Supply and Demand Models

It is assumed that the demand for housing in region

i

at time

t

D_{i, t}

and that the supply is

S_{i, t}

. These are multivariate functions that are driven by a variety of dynamic factors. Let us initially define the demand function,

D_{i, t}

, and the supply function,

S_{i, t}

, which are represented by Equations 1 and 2.

\begin{matrix} D_{i, t} = f (X_{i, t}) = α_{1} ∆ P_{i, t} + α_{2} I_{i, t} + α_{3} E_{i, t} \\ + α_{4} M_{i, t} + α_{5} C_{i, t} + ϵ_{i, t}, \end{matrix}

(1)

\begin{matrix} S_{i, t} = g (Y_{i, t}) = β_{1} A_{i, t} + β_{2} B_{i, t} + β_{3} R_{i, t} + β_{4} T_{i, t} + η_{i, t} . \end{matrix}

(2)

In this model, the variables represented by

X_{i, t}

are demand-side variables, including population growth rate

∆ P_{i, t}

, income level

I_{i, t}

, employment rate

E_{i, t}

, migration rate

M_{i, t}

, and cost of living

C_{i, t}

. In contrast, the variables represented by

Y_{i, t}

are supply-side variables, including land availability

A_{i, t}

, construction cost

B_{i, t}

, policy environment

R_{i, t}

, and permit approval time

T_{i, t}

. Both sets of variables are modelled comprehensively through supply and demand models, which reflect the state of the market more comprehensively.

The limitations of simple linear models in capturing the intricate interdependencies between supply and demand are well-documented. To address this challenge, we propose the incorporation of interaction terms, which are defined as nonlinear interactions between demand-side and supply-side variables. These interactions are employed to elucidate the dynamics of demand and supply, such as the impact of population growth on housing supply within a specified policy context. The interaction item

H_{i, t}

is defined as Equations 3.

\begin{matrix} H_{i, t} = \sum_{k = 1}^{5} \sum_{l = 1}^{4} γ_{k l} (X_{i, t}^{k} \cdot Y_{i, t}^{l}), \end{matrix}

(3)

where

γ_{k l}

represents the interaction coefficient, which reflects the intensity of the interaction between the

k

variable on the demand side and the

l

variable on the supply side. To illustrate, the interaction of construction cost

B_{i, t}

with income level

I_{i, t}

may demonstrate that regions with higher incomes are more capable of bearing higher construction costs and, consequently, demonstrate greater sensitivity to income growth on supply side. The incorporation of these interactions into the demand and supply functions allows for the expression of the integrated model as Equation 4 and 5.

\begin{matrix} D_{i, t} = α_{1} ∆ P_{i, t} + α_{2} I_{i, t} + α_{3} E_{i, t} + α_{4} M_{i, t} + α_{5} C_{i, t} + \\ \sum_{k = 1}^{5} \sum_{l = 1}^{4} γ_{k l} (X_{i, t}^{k} \cdot Y_{i, t}^{l}) + ϵ_{i, t}, \end{matrix}

(4)

\begin{matrix} S_{i, t} = g (Y_{i, t}) = β_{1} A_{i, t} + β_{2} B_{i, t} + β_{3} R_{i, t} + β_{4} T_{i, t} + \\ \sum_{k = 1}^{5} \sum_{l = 1}^{4} γ_{k l} (X_{i, t}^{k} \cdot Y_{i, t}^{l}) + η_{i, t} . \end{matrix}

(5)

By means of the demand and supply functions, we define the regional supply-demand deficit measurement

I_{i, t}

as Equation 6.

\begin{matrix} I_{i, t} = D_{i, t} - S_{i, t} . \end{matrix}

(6)

In order to gain further insight into and predict the dynamic changes of supply and demand imbalance, we minimise the squared error of supply and demand imbalance in order to obtain the optimal solution of the model parameters

α

β

and

γ

. The objective function is given by Equation 7.

\begin{matrix} \min_{α, β, γ} \sum_{i = 1}^{N} \sum_{t = 1}^{T} {(D_{i, t} - S_{i, t})}^{2} . \end{matrix}

(7)

By solving this function, the optimal combination of parameters can be estimated in order to minimise the imbalance between supply and demand. In practice, certain variables in the supply and demand model may be constrained by external factors. For instance, land availability

A_{i, t}

and construction costs

B_{i, t}

are frequently contingent upon local government policies and market conditions. These constraints are then introduced into the model, whereupon the Lagrange multiplier method is employed to solve the nonlinear optimisation problem with constraints. The aforementioned constraint can be expressed as Equation 8.

\begin{matrix} A_{i, t} \leq {\bar{A}}_{i}, B_{i, t} \leq {\bar{B}}_{i}, T_{i, t} \leq {\bar{T}}_{i} . \end{matrix}

(8)

The introduction of the Lagrange multiplier

λ_{A}

λ_{B}

λ_{T}

allows us to define Lagrange objective function as Equation 9.

\begin{matrix} L (α, β, γ, λ) = \sum_{i, t} {(D_{i, t} - S_{i, t})}^{2} + \\ λ_{A} (A_{i, t} - {\bar{A}}_{i}) + λ_{B} (B_{i, t} - {\bar{B}}_{i}) + λ_{T} (T_{i, t} - {\bar{T}}_{i}) . \end{matrix}

(9)

By solving the aforementioned Lagrangian function, the optimal supply-demand equilibrium solution, taking into account the constraints, can be obtained.

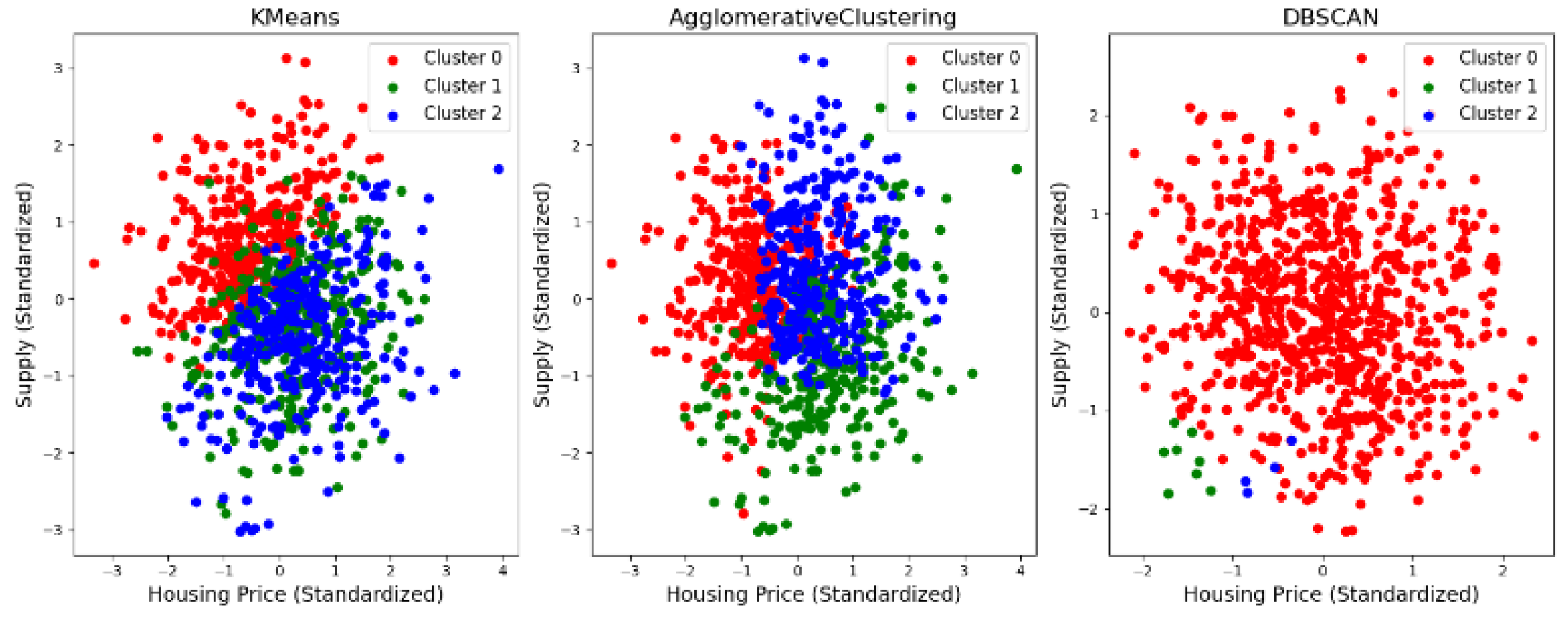
3.2. Cluster Analysis

The initial step in the classification process is the utilisation of cluster analysis, which facilitates the grouping of regions with analogous characteristics pertaining to the housing market. Let us suppose that the supply-demand characteristics of region

i

at time

t

are represented by the pair of values

Z_{i, j} = [X_{i, j}, Y_{i, j}]

, where

X_{i, j}

denoting the demand-side feature and

Y_{i, j}

denoting the supply-side feature. In order to facilitate the interpretation of complex multidimensional data, the k-means clustering algorithm is employed to divide the

N

regions into

k

clusters. This is done with the objective of minimising intra-class variance, as illustrated in Equation 10.

\begin{matrix} \min_{μ_{1}, \dots, μ_{k}} \sum_{i = 1}^{N} \sum_{j = 1}^{k} w_{i j} {∥ Z_{i, j} - μ_{j} ∥}^{2}, \end{matrix}

(10)

where

μ_{j}

denotes the centroid of class

j

, while

w_{i j}

represents the indicator function. If region

i

is deemed to belong to class

j

, then

w_{i j}

is assigned a value of

1

; otherwise, it is assigned a value of

0

. By employing an iterative approach and adjusting the centroid position, it is possible to group regions with analogous supply and demand dynamics into a single class.

This classification not only facilitates the identification of the supply and demand characteristics of specific regions, but also allows for the implementation of disparate models or strategies for varying categories of regions in subsequent predictive analysis. In order to predict future imbalances between supply and demand, we have employed the use of machine learning algorithms based on regional clustering. The measurement of the supply-demand deficit is defined by the following Equation 11.

\begin{matrix} I_{i, t} = D_{i, t} - S_{i, t}, \end{matrix}

(11)

where

D_{i, t}

represents the housing demand of the

i

region at the time

t

, while

S_{i, t}

denotes the housing supply of the region. The objective is to forecast a de-measured

I_{i, t + 1}

at a future point in time based on historical data. In order to capture the complex non-linear relationships between supply and demand variables, machine learning methods such as gradient boosted trees (GBMs) are employed.

The input features of the machine learning model comprise demand-side feature

X_{i, t}

and supply-side feature

Y_{i, t}

, in addition to the results of cluster classification. By utilising the training set, the model is able to discern the historical trends associated with imbalances in supply and demand. The predictive model is expressed by the following Equation 12.

\begin{matrix} {\hat{I}}_{i, t + 1} = h (X_{i, t}, Y_{i, t}, C_{i}), \end{matrix}

(12)

where

h (\cdot)

represents the prediction function of the machine learning model, whereas

C_{i}

denotes the cluster classification result for the

i

region. The clustering results,

C_{i}

, provide specific supply and demand dynamics for different categories of regions. Consequently, similar prediction models are employed for regions of the same class.

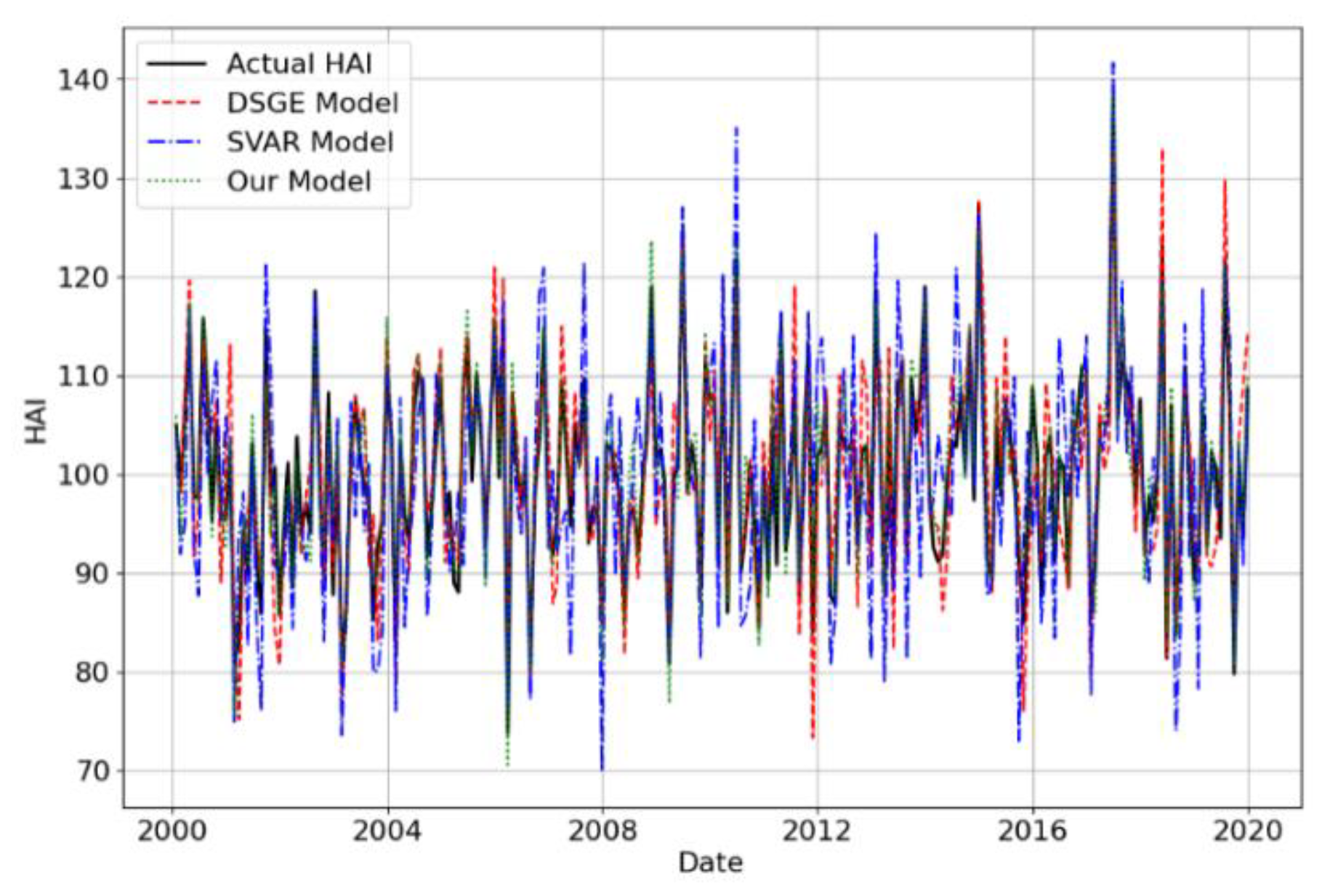
4. Experiments

4.1. Experimental Setup

The dataset encompasses the period from 2010 to 2020 and comprises approximately 5 million real estate transactions and over 1,000 regional economic indicators from all 50 states and major cities in the United States. The dataset includes a number of specific variables, including population growth, which exhibits an average annual growth of between 2% and 5% across different regions. Additionally, it encompasses median household income, which is approximately $50,000 in most areas but exceeds $80,000 in some. The dataset also incorporates unemployment rates, which fluctuate between 2% and 10%. Furthermore, it comprises housing stock data, covering approximately 12 million residential units, of which 2% to 4% are vacant. Furthermore, the influence of building permits and land use regulations on the housing supply is examined.

In the experiments, we undertake a comparative analysis of the proposed model with the Dynamic Stochastic General Equilibrium (DSGE) model and the Structural Vector Autoregressive (SVAR) model. The DSGE model employs a dynamic approach to analyze changes in housing prices and supply. It incorporates the supply and demand dynamics of the housing market, coupled with fluctuations in the economic cycle. The SVAR model employs time series data to examine the interrelationship between housing supply, demand, and prices.

4.2. Experimental Analysis

The Housing Affordability Index (HAI) is a metric that assesses the capacity of middle-income households to procure housing at a reasonable cost. It considers a range of variables, including household income, housing prices, and loan interest rates, to determine the extent to which middle-income households can afford to purchase housing. A higher HAI value indicates a greater degree of affordability with respect to housing.

K-Means was chosen for its simplicity and efficiency in dividing data into predefined clusters, making it ideal for analyzing large-scale real estate data like regional house prices. Hierarchical clustering captures nested patterns, while DBSCAN excels at identifying irregular clusters and handling noise, such as new constructions or rare transactions. Together, these methods offer a flexible and robust analysis of the real estate market.

Figure 1 depicts the actual Housing Affordability Index (HAI) in comparison to the projections of the three models (DSGE, SVAR, and the proposed model) for the period from January 2000 to December 2019. As illustrated in the figure, the prediction curve of the Ours model is the most proximate to the actual HAI value, exhibiting greater precision than the DSGE and SVAR models. This suggests that the Ours model demonstrates superior accuracy in forecasting housing affordability.

Figure 2 shows the clustering effect of three different clustering algorithms (KMeans, hierarchical clustering, and DBSCAN) on simulated housing supply and demand imbalance data in United States. Each subgraph corresponds to an algorithm, with different colored dots representing different clusters. The horizontal axis represents the normalized housing price, and the vertical axis represents the normalized housing supply. KMeans and hierarchical clustering generate a clear cluster structure, while DBSCAN can identify noisy data, demonstrating its advantages in dealing with outliers.

The results of the clustering analysis indicate that there is a shortage of affordable housing in some regions, while there is an excess of such housing in others. These results can inform the prioritisation of investment in infrastructure and affordable housing construction, particularly in areas where supply is inadequate. Furthermore, it may be advisable to consider implementing specific land-use adjustments or tax incentives for developers in these areas. In areas where there is a surplus of properties, policies can be implemented to encourage the conversion of vacant properties to other uses or to adjust rental control policies. In the long term, these findings could provide guidance for sustainable urban planning, enabling a balance to be struck between population growth and housing supply.

5. Conclusions

In conclusion, the comparative analysis of different clustering algorithms, including KMeans, Agglomerative Clustering, and DBSCAN, on simulated U.S. housing supply and demand imbalance data reveals distinct advantages and limitations of each approach. KMeans and Agglomerative Clustering provided clear and consistent cluster structures, making them suitable for well-separated data. Meanwhile, DBSCAN demonstrated its strength in handling noise and identifying outliers, making it advantageous for more complex datasets. These findings highlight the importance of selecting the appropriate clustering algorithm based on the specific characteristics of housing market data, allowing for more accurate and meaningful insights into regional housing supply and demand imbalances. Future research can further improve the dynamics and timeliness of the model by integrating real-time data from online real estate platforms.

References

Xu, Zihan, et al. "Spatial correlation between the changes of ecosystem service supply and demand: An ecological zoning approach." Landscape and Urban Planning 217 (2022): 104258. [CrossRef]
Adabre, Michael Atafo. "Developing a model for bridging the gap between sustainable housing and affordable housing (low-cost housing) in the Ghanaian housing market." (2021).
Giusino, Davide, et al. "“We all held our own”: job demands and resources at individual, leader, group, and organizational levels during COVID-19 outbreak in health care. A multi-source qualitative study." Workplace health & safety 70.1 (2022): 6-16. [CrossRef]
Humphreys, Helen, et al. "Long COVID and the role of physical activity: a qualitative study." BMJ open 11.3 (2021): e047632. [CrossRef]
Li, Han, et al. "Energy flexibility of residential buildings: A systematic review of characterization and quantification methods and applications." Advances in Applied Energy 3 (2021): 100054. [CrossRef]
Shirmohammadi, Melika, Wee Chan Au, and Mina Beigi. "Remote work and work-life balance: Lessons learned from the covid-19 pandemic and suggestions for HRD practitioners." Human Resource Development International 25.2 (2022): 163-181. [CrossRef]
Hsieh, Chang-Tai, and Enrico Moretti. "Housing constraints and spatial misallocation." American economic journal: macroeconomics 11.2 (2019): 1-39. [CrossRef]
Stacy, Christina, et al. "Land-use reforms and housing costs: Does allowing for increased density lead to greater affordability?." Urban Studies 60.14 (2023): 2919-2940. [CrossRef]
Alig, Ralph. "Urbanization in the US: Land use trends, impacts on forest area, projections, and policy considerations." Journal of Resources, Energy and Development 7.2 (2010): 35-60. [CrossRef]
Reifschneider, Dave, William Wascher, and David Wilcox. "Aggregate supply in the United States: recent developments and implications for the conduct of monetary policy." IMF Economic Review 63.1 (2015): 71-109. [CrossRef]

Figure 1. Housing Affordability Index Comparison.

Figure 2. Clustering Comparison Comparison.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Regional Housing Supply and Demand Imbalance Qualitative Analysis in U.S. Based on Big Data

Abstract

1. Introduction

2. Related Work

3. Methodologies

3.1. Supply and Demand Models

3.2. Cluster Analysis

4. Experiments

4.1. Experimental Setup

4.2. Experimental Analysis

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe