Prerpints.org logo
Preprint
Article

Landslide Susceptibility Mapping Considering the Landslide Spatial Aggregation Using Dual Frequency Ratio Method: A Case Study on the Middle Reaches of Tarim River Basin

Altmetrics

Downloads

24

Views

13

Comments

0

Submitted:

09 December 2024

Posted:

09 December 2024

You are already at the latest version

Alerts
Abstract
The phenomenon of landslide spatial aggregation is widespread in nature, which can affect the result of landslide susceptibility prediction (LSP). In order to eliminate the uncertainty caused by landslide spatial aggregation in LSP study, scholars have proposed some methods to quantify the degree of landslide spatial aggregation, such as class landslide aggregation index (LAI), which is widely used. However, due to the limitations of the existing LAI method, it is still uncertain when applied to the LSP study of the area with complex engineering geological conditions. Considering the landslide spatial aggregation, a new method, dual frequency ratio (DFR), was proposed in this paper to establish the relationship between the landslide occurrence and twelve predisposing factors (namely, slope, aspect, elevation, relief amplitude, engineering geological rock group, fault density, river density, annual average rainfall, NDVI, distance to road, quarry density and hy-dropower station density). And in the DFR method, an improved LAI was used to quantify the degree of landslide spatial aggregation in the form of frequency ratio. Taking the middle reaches of Tarim River Basin as the study area, the application of DFR method in LSP study was verified. Meanwhile, four models were adopted to calculate the landslide susceptibility indexes (LSIs) in this study, including frequency ratio (FR), analytic hierarchy process (AHP), logistic regression (LR) and random forest (RF). Finally, the prediction performance of each LSP model was evalu-ated by the receiver operating characteristic curves (ROCs) and distribution patterns of LSIs. The results showed that DFR method could reduce the adverse effect of landslide spatial aggregation on LSP study and enhance the prediction performance of LSP model better. In addition, models of LR and RF had superior prediction performance, among which DFR-RF model had the highest prediction accuracy value and quite reliable result of LSIs.
Keywords: 
Subject: Environmental and Earth Sciences  -   Remote Sensing

1. Introduction

Landslide is one of the most widespread geohazards worldwide, characterized with sudden occurrence, destructive force and fast movement, and often causes great damage to settlements and constructions located in landslide-prone zone [1-5]. Therefore, the research of landslide susceptibility prediction (LSP) is vital for providing guidance to the land-use, urban-rural planning, and disaster prevention and mitigation [6-8]. According to the landslide susceptibility map (LSM) obtained by LSP study, site location strategy of engineering construction including road, hydropower station and residential district, can be reasonably determined to reduce or even avoid the loss of lives and property caused by landslides [9-11].
Landslide formation is actually a complicated process that involves a number of predisposing factors, such as geomorphology, tectonic action, stratum lithology, climate, hydrological condition, human activity and so on. And it is the key step for LSP study to determine a link between the landslide occurrence and predisposing factors [12-14]. Aiming at the analysis on this relationship, scholars have proposed many different models including geomorphological mapping, heuristic terrain and susceptibility zoning, physically-based numerical modelling, and statistically-based classification methods, to quantify the impact of factor and calculate the landslide susceptibility index (LSI) [6,10,13-15]. Current researches show that statistically-based models are widely used in regional studies with good prediction performance, such as heuristic methods [10,16,17], frequency ratio (FR) analysis [14,15,18], general statistical approaches [7,10], machine learning models [18-22]. In addition, the machine learning models, including logistic regression (LR) model, random forest (RF) model, etc., are being used more and more frequently due to reliable results and high precision [17,19-23]. However, each LSP model often displays different prediction performance as a result of the discrepancies in model type, characteristics of study areas, landslide spatial datasets and predisposing factors. And it is recommended that the LSP result should not be determined by a single model because each model usually has its own uncertainty [13,14,17].
Besides, the accuracy of model prediction is significantly influenced by the landslide inventory, which is a necessary precondition for LSP research [8,22]. Although the production of landslide inventory is more convenient and accessible by high-resolution remote sensing imagery datasets and developed investigation techniques, there is still uncertainty in landslide inventory caused by the lack of high-level professional interpretation, challenge of investigation in inaccessible area and the non-homogeneity of landslide spatial distribution [14,16,24]. The non-homogeneity of landslide spatial distribution is an inherent attribute of landslide spatial datasets and is one of the challenges in creating a landslide inventory. Due to the complexity of the landslide formation mechanism, the predisposing factors have a significant impact on the landslide distribution pattern. For instance, it is often found that landslides in a specific region happened in the form of clusters of landslides in areas with nearby faults or roads, and have a banding distribution. In other words, the landslide distribution usually shows a high degree of heterogeneity in space and is affected by changes in controlling factors, especially when the study area is large [16,24,25]. Some scholars have introduced relevant landslide aggregation index (LAI) to realize the quantification of landslide spatial aggregation [16,24,26,27]. In particular, the often-used FR without considering landslide spatial aggregation was modified to enhance the LSP model's prediction performance [16,26]. And a new index for quantifying the degree of landslide spatial aggregation is proposed in this study as well, which shows a good effect on regional LSP study.
In order to quantify the aggregation degree of landslide spatial distribution, a comparison is made between different LAIs used in improving FR. And four typical models including FR, analytic hierarchy process (AHP), LR and RF, are used in calculating LSIs to test the application effect of LAIs. Then, the prediction performance of four LSP models is also compared in this study. The middle reaches of Tarim River Basin, situated where the Tarim Basin and South Tianshan Mountains converge, is taken as the study area because of serious landslide hazard. Based on different LSP models and modified FR values, LSMs of the study area are obtained, and the receiver operating characteristic curves (ROCs) and LSI distribution patterns are used to validate the performance of each LSP model.

2. Methods

2.1. LSP Modeling Procedure

In this study, it is the primary objective to analyze the impact from landslide spatial aggregation on the LSP model's prediction performance in the middle reaches of the Tarim River basin. As shown in Figure 1, all the processes required to complete the landslide susceptibility prediction in this study, can be encapsulated by the following six steps:
(1)
Landslide inventory building through remote sensing interpretation, field investigation and historical record;
(2)
Spatial datasets collecting and integration of landslide predisposing factors;
(3)
Establishing the correlation between the incidence of landslide and corresponding impact factors by indicators including FR, adjusted FR (FRa) and DFR, and the influence of landslide spatial aggregation is considered by the latter two indicators;
(4)
Creating LSP models using the FR, AHP, LR and RF models, and adopting the FRs values of each predisposing factor as input variables in this step;
(5)
LSIs calculation by LSP models and LSMs generating using ArcGIS 10.4 software;
(6)
Model evaluation based on LSI distribution patterns and accuracy analysis.

2.2. Analysis of Landslide Spatial Aggregation

Based on the analyzed statistic correlations, the frequency ratio is often used as an indicator to reflect the impact of each subclass of predisposing factors to landslide occurrence, which can be easily applied to visually display the geographic connection of landslide distribution with related predisposing factors [7,14-16,24]. As shown in Equation (1), FR is also often regarded as the ratio of landslide density of a specific subclass under a predisposing factor to that of the whole study area. In general, a low correlation between landslide incidence and related factor is indicated by a FR value less than 1, and a high connection is indicated by a FR value larger than 1 [17,18].
FRij = (lij / aij) / (L / A)
where FRij denotes the frequency ratio of subclass i under the predisposing factor j; lij refers to the count of landslides under subclass i of the predisposing factor j, aij stands for the area of class i under the predisposing factor j, L denotes the whole amount of landslides in the total research area, and A refers to the total area.
However, the heterogeneity of landslide spatial distribution is a result of the fact that landslide formation is influenced by a variety of internal and external dynamics and varies significantly across different regions [5,12,25,28]. Therefore, using the FR alone without taking into account the landslide spatial aggregation makes it irrational to create a correlation between the occurrence of landslide and associated predisposing factors [16,24,26,27]. In other words, the principle of FR method ignores the influence of landslide spatial aggregation, which leads to uncertainty in the results.

2.2.1. Existing Landslide Aggregation Index

In order to quantify the degree of landslide spatial aggregation and eliminate the uncertainty caused by it, some scholars have introduced new adjusted indexes used in improving FR calculation, such as class landslide aggregation index (CLAI), normalized spatial-correlated scale index (NSCI) and normalized spatial distance index (NSDI) [16,24,26,27]. Among these indexes, the CLAI index has been widely used in LSP study because it is easy to be adopt in combination with FR and its representation form is more closely related to FR [16,26]. The first two cases in Figure 2 served as the foundation for the initial introduction of CLAI. The level of landslide aggregation in four distinct scenarios can be observed in Figure 2, representing the typical situations of landslide spatial distribution. The chosen area is split into the same grid with an equal area of Sa in each of the cases depicted in Figure 2. Since the subclass i1 in case 1 and subclass i2 in case 2 both have the same number of grids (five) and landslide points (ten), the lij / aij in each of the above two cases is same as 10 / (5 × Sa). They are equally susceptible to landslides, as indicated by their same FR values. However, since only one grid of subclass i1 has landslide points in case 1, and every grid of subclass i2 has landslide points in case 2, it is evident that the degree of landslide spatial aggregation varies in each case. According to this situation, the CLAI was proposed to quantify the degree of landslide spatial aggregation and its calculation is shown in Equation (2) [16]:
CLAI = UL / UT
Where UL is the number of basic evaluation units in which landslide points are present in a specific subclass i under certain predisposing factor, and UT denotes the total amount of basic evaluation units in the subclass i. In general, the smaller the CLAI, the higher degree of landslide spatial aggregation. Then, the FR can be modified by applying CLAI, as shown in Equation (3) [16,26]:
FRa = FR × CLAI
Where FRa represents the adjusted frequency ratio.

2.2.2. A New Index of Analyzing Landslide Spatial Aggregation

However, there are also other cases including case 3 and case 4 where the subclass i is divided into ten identical grids, just as the area of each subclass is usually different in fact, reflecting other different situations in which the uncertainty may be caused by the landslide spatial aggregation. Regarding to case 2 and case 3 shown in Figure 2, the CLAI value in both cases is equal to 1. However, in case 3, there is actually less landslide spatial aggregation, because each grid only has one landslide point. In addition, the CLAI in case 4 is unreasonably reduced to 0.1 compared to the CLAI value of 1 in case 2. In a word, CLAI index cannot really quantify the degree of landslide spatial aggregation due to the limitations in theory. Aiming to achieve the quantitative degree assessment of landslide spatial aggregation, a new indicator called LAIFR is proposed in this study, which can be conveniently obtained on the basis of CLAI, as shown in Equation (4):
LAIFR = CLAI / (LS / UT)
where LAIFR represents the landslide spatial aggregation index calculated in the form of frequency ratio; CLAI can be obtained from Equation (2), LS stands for the total amount of landslide points of a certain subclass i under specific predisposing factor, while UT represents the total amount of basic evaluation units in subclass i. Similarly, the smaller the LAIFR, the higher degree of landslide spatial aggregation. Significantly, the LAIFR is equal to 0 when there is no landslide point in a subclass. In fact, it is can be found that the LAIFR is able to be deduced as UL / LS. However, for the sake of visual expression and comparison with CLAI and FR, the LAIFR is decided to be displayed as Equation (4) in this study. Furthermore, FR can be improved by the LAIFR considering landslide spatial aggregation, as shown in Equation (5):
DFR = FR × LAIFR
Where DFR is the optimized frequency ratio expressed in the form of dual frequency ratio participating in the calculation. And in this study, FR, FRa and DFR are also collectively referred to as the FRs.

2.3. LSP Modeling Approaches

To test the related LAI methods, four LSP models including FR, AHP, LR and RF are applied for LSIs. FR and AHP are often-used classical statistical models, while LR and RF belong to typical machine learning models. And the FR values without considering landslide spatial aggregation, and values of FRa and DFR considering landslide spatial aggregation, are input as basic data in the above four LSP models.

2.3.1. FR Model

The frequency ratio model is a popular statistical methodology that may be applied to GIS methods to obtain the LSM quantitatively. Equation (1) shows how the frequency ratio model is used to ascertain the spatial relationships between the location of landslides and contributing factors. And then the frequency ratio of each factor is summed as following Equation (6) to calculate the LSIs [7,14,15,17].
LSIFR = FR1 + FR2 + FR3 + … + FRj,
where FRj stands for the FR value of the type or range of each factor.

2.3.2. AHP Model

As a typical multi-criteria heuristic method, AHP model is a semi-qualitative decision-making approach, which is usually used to resolve complicated multi-objective decision-making problems, such as engineering location selection, resource allocation and so on [9,11,29]. Each factor’s weight value in the AHP model ranges from 1 to 9 and is calculated by comparing different factors in pairs. The consistency of the comparison matrix made up of the aforementioned weight values is tested using the consistency ratio (CR), which is determined by Equation (7). The comparison matrix is approved if the CR value is less than 0.1. [8,10,16]:
CR = CI / RI
where RI stands for the random index for the comparison matrix and CI is the consistency index of the matrix as determined by Equation (8). In Equation (8), λmax refers to the comparison matrix's maximum eigenvalue, and n denotes the total amount of factors (twelve in this case).
CI = (λmax-n) / (n-1)
Then, the normalized weight value of each predisposing factor is gained according to the comparison matrix. And finally, the LSIs can be calculated using Equation (9):
LSIAHP = FR1 × w1 + FR2 × w2 + FR3 × w3 + … + FRj × wn
where FRj is the type or range rating of each factor, and wn indicates the weight value of the corresponding predisposing factor.

2.3.3. LR Model

The LR approach is a commonly used analysis model that enables a quantitative assessment of the correlationship between a set of independent variables (impact factors in this study) and dependent variable (landslide occurrence in this study) quantitatively [18,21,22]. It explains how a series of independent variables contribute to a binary dependent variable (whether a landslide occurs). In this study, the dependent variable is the likelihood that landslide will occur and the corresponding predisposing factors are taken as independent variables in SPSS software. In the LR model, the dependent variable is the binary variable of whether landslide occur (1) or not (0). Additionally, the following Equation (10) can be used to determine the likelihood of landslide occurrence:
P =1 / (1+e-z)
where Z denotes the linear combination given by Equation (11) and P is the likelihood of landslide incident, which ranges from 0 to 1.
Z = b0 + b1 × x1 + b2 × x2 + … + bn × xn
where the regression intercept is denoted by b0, bn (n = 1, 2, 3 ... n) refers to regression coefficient, and the independent variable is represented by xn (n= 1, 2, 3 ... n) which is the corresponding FRs value of each predisposing factor in this study.

2.3.4. RF Model

The RF model, which was first presented by Breiman in 2001, is an ensemble technique made up of a series of tree classifiers that combines the random subspace and bagging ensemble learning [30]. And RF model is one of the most often used methods for addressing multi-classification and prediction issues, including LSP study [19,20,26]. In terms of missing and unbalanced data, the RF algorithm's outcomes are comparatively consistent and its susceptibility to multicollinearity is low. The RF model's primary steps are as follows [23,30]: (1) using bootstrap to resample the original dataset in order to produce a subset that is equivalent to the original data set; (2) the optimal segmentation index is chosen for segmentation after a random selection of m indexes is made from n indexes in each classification tree node; (3) combining the classification or prediction outcomes of every decision tree to arrive at the final findings. Furthermore, the RF model's prediction performance is significantly impacted by the quantity of decision trees and candidate attributes included in the subsets [31].

2.4. Uncertainty Evaluation Indexes

2.4.1. ROCs

The Receiver Operating Characteristic Curves (ROCs), one of the popular methods for model evaluation in LSP research, are used to assess the prediction performance of each LSP model [7,14,22]. Shown in Equation (12) and Equation (13), When plotting ROCs, the horizontal coordinate is the false positive rate (FPR), while the vertical coordinate is the true positive rate (TPR). The model's accuracy in forecasting the likelihood of landslide events is indicated by the area under the curve (AUC), which ranges from 0.5 to 1. Generally, the AUC values can be classified into following grades, such as 0.5~0.6 (very low accuracy), 0.6~0.7 (low accuracy), 0.7~0.8 (moderate accuracy), 0.8~0.9 (good accuracy) and 0.9~1 (excellent accuracy) [32-34].
TPR = TP / (TP+FN)
FPR = FP / (FP+TN)
Where TP indicates the quantity of correctly categorized landslide samples, FN represents the quantity of incorrectly categorized non-landslide samples, FP denotes the quantity of incorrectly categorized landslide samples, and TN refers to the quantity of correctly categorized non-landslide samples. As shown in Equation (14), the model's prediction performance improves with a greater AUC value [26].
AUC = (ΣTP + ΣTN) / (P + N)

2.4.2. Distribution Patterns of LSIs

The mean and standard deviation values in this study are adopted to describe the distribution patterns of LSIs, which are displayed as a type of histogram. As assistant indexes for assessing the LSP model performance, the mean value can give an index to the predicted LSIs’ central tendency, and the degree of dispersion is reflected by standard deviation [26]. In general, LSIs deviate from the mean value less when the standard deviation is lower, and vice versa. Furthermore, a low mean value and a high standard deviation generally mean small calculated results of LSIs on the whole, which can illustrate the strong ability of the LSP model to differentiate between LSIs of various grid cells. In addition, if the model also has a high AUC value of landslide prediction, it indicates that this model is not only reliable, but also has high prediction accuracy [17].

3. Materials

3.1. Description of Study Area

The Tarim River basin is composed of nine river systems, including Aksu River, Hetian River, Yerqiang River, Qarqan River, Keriya River, Dina River, Kashgar River, Kaidu-Kongque River and Ugan-Kuqa River [35]. As shown in Figure 3, the study area is located in the middle reaches of Tarim River Basin, situated in Xinjiang Province of China (38°47′04″~42°38′44″N, 76°36′23″~86°30′53″E), adjacent to Kyrgyzstan Republic and Kazakhstan Republic in the northwest bounded by the middle beam of the South Tianshan Mountains. It covers a total area of 185829 km2, with about 818 kilometers long from east to west and 428 kilometers wide from north to south. The entire population of this studying area is around 4.86 million.
Geographically speaking, the studying area’s elevation spans from 655 to 7435 m, and it is located on the northern edge of the Tarim Basin and the southern edge of the South Tianshan Mountains. Additionally, the overall terrain decreases from north to south, characterized with three-step pattern, with continuous mountains in the north, vast Taklimakan Desert in the south, and gravel fan-shaped foothills, alluvial plain area, gobi and oasis alternating in the middle. The Tomur Peak in the South Tianshan Mountains is the highest point in the study area at 7435.3 m. Geologically, the studying area is situated on the southwest margin of the Central Asian orogenic belt, and the junction of Kazakhstan-Yili block and Tarim block [36-38], so it is characterized by active structures and developed faults. The strike of most active faults is close to E-W, and the distribution density of faults in the south is less than that in the north. Furthermore, faults can produce canyons with large surface fluctuations, and their vicinity is often a landslide prone area.
In addition, the Tarim River basin belongs to the typical temperate continental climate zone and arid-semiarid region, with rare rainfall, high evaporation and dry climate. The average annual temperature, average annual precipitation, and potential evaporation for the majority of the study area are 9.2 to 11.5°C, 64 mm, and 1890 mm, respectively. [39]. Moreover, the studying area's precipitation distribution is incredibly unequal in space. The north mountainous regions near Tomur Peak and Khan-Tengri Peak receive almost 600 mm of precipitation annually, while the annual precipitation in the southern Tarim Basin is less than 50 mm.

3.2. Landslide Inventory Information

The necessary initial operation in the LSP study is creating a landslide inventory [14,40]. The landslide dataset of the study area was obtained, validated, and further enhanced based on remote sensing interpretation, field work and literature research. Landslides are widely developed in the study area, especially in northern mountains, and 663 landslide points which occurred between 1985 and 2023 were identified in total (Figure 3). The quality of data collection and compilation is controllable as a whole, mainly in the following measures: (1) the interpretation of landslide points was based on comparisons of high-precision remote sensing images, considering morphological structure of landslide, altered landscape and the influence of other background conditions including surrounding engineering facilities and vegetation growth; (2) field researches were performed in the landslide areas to eliminated wrong data caused by construction excavation or misjudgment of remote sensing interpretation; (3) the publications were fully mined to supplement and verify the remote sensing interpretation results; (4) the landslide points were identified according to multi-period historical images, which can not only overcome the identification limitation of snow and cloud, but also comprehensively compare the spatial relationship between the geohazard and threatened target. Based on the above data verification and selection, the dataset has reliable quality and good usability [4,41].

3.3. Landslide Predisposing Factors

Numerous factors influence the formation of landslide, which is the consequence of both internal and external dynamics [14,42,43]. Predisposing factors that cause landslide are chosen for this study based on field investigation and previous studies on landslide susceptibility, which could reflect local geomorphologic conditions (slope, aspect, elevation and relief amplitude), geological settings (engineering geological rock group (EGRG) and to fault density), hydrological factors (river density and average annual rainfall) and surface cover factors (NDVI, distance to road, quarry density and hydropower station density). There may be specific correlations among these factors, and high correlation of factors would affect the prediction accuracy of LSP model. So, Pearson correlation test is applied to validate these factors’ independence in this study. Each of the twelve predisposing factors satisfies the independence criterion since the absolute values of their pairwise correlation values are all less than 0.5 [8]. Next, as shown in Table 1, the discrete factors are categorized under the actual determined state or homologous action mechanism, while the continuous factors are categorized into eight subtypes based on the natural breakpoint method [13,17]. In Table 1, considering landslide spatial aggregation, the FRs values are attained to reflect whether the subclass of predisposing factor is conducive to the formation of landslide or not. Additionally, the data layers of above factors are processed into raster format with the size of each grid being 30×30 m for LSIs calculation.

3.3.1. Geomorphologic Factors

In terms of geomorphologic conditions, the slope (Figure 4a), aspect (Figure 4b), elevation (Figure 4c) and relief amplitude (Figure 4d) are the primary controlling factors of landslide formation in study area, and the relevant data of these three factors can be generated by digital elevation model (DEM). Thereinto, slope degree could change the stress field of slope body, so as to affect slope evolution including stress distribution, strain accumulation and the formation of potential slip surface. Therefore, landslide development has close correlation with the slope, and within a certain range, lower slope gradient is usually associated with higher slope stability [3,14]. Aspect has an impact on hydrothermal conditions including sunshine and precipitation, which plays a controlling role in rock weathering, vegetation growth and melting of ice and snow. Thus, there is a certain relationship between aspect and landslide distribution in space [8,26]. As with many LSP studies, the aspect factor has nine subclasses in Table 1, with the subclass of -1 representing the plane area [7,17,19]. Various climate elements change with the increase of elevation, among which precipitation and temperature change quite acutely. The resulting changes of some conditions, such as microclimatic characteristics, type of plant communities and human activities, would affect the evolution of landslide [43]. Relief amplitude denotes to the difference between the highest and lowest elevation points in a given area. In general, a higher relief amplitude can cause the increase of landslide potential energy, which in turn improves the landslide velocity and ultimately raises the intensity of landslide activity [44,45].

3.3.2. Geological Factors

With respect to geological setting, lithology factor controls the strength of slope material, which profoundly determines the slope stability [7,46]. In this study, according to the National Standard of China (GB/T 50218-2014), engineering geological rock group (EGRG) (Figure 4e) used in reflecting the influence of lithology, is divided into six subclasses as shown in Table 2: hard, less hard, less soft, soft, softer and water. The original data of EGRG factor is generated based on the 1:250,000 scale geological map. And because of more structure planes and lower strength, landslides of the study area are prone to developed in areas of the less hard, less soft and soft rock groups (Table 1). Fault density (Figure 4f) is positively correlated with landslide occurrence [8,11]. Faults result in the formation of rock mass structural planes and considerable topographic relief [44,46]. Thus, landslides are common in the northern mountainous regions with a high fault density in the research area.

3.3.3. Hydrological Factors

River density (Figure 4g) can affect the slope stability by causing pore water pressure and scouring the slope foot, which is generally unfavorable to the structural strength of slope body and conductive to the landslide occurrence [14]. In addition, groundwater often develops near river, which can lead to infiltration failure and soften the structural surface, resulting in slope instability [15]. Rain infiltration and direct ground erosion caused by rainfall is less favorable to slope stability, thereby landslide is often triggered by rainfall in the study area [47]. The average annual rainfall data (Figure 4h) of the research area is produced using ArcGIS 10.4 software, based on rainfall data gathered from the local meteorological service and an open database published by the WorldClim website (https://www.worldclim.org/). Table 1 shows that the regions with high average annual rainfall are exactly associated with high frequence of landslide occurrence.

3.3.4. Surface Cover Factors

Based on the spectral characteristics of vegetation cover, NDVI (Figure 4i) can reflect the status and biomass of surface vegetation, which is adopted to measure the surface vegetation cover in this study. Generally speaking, the higher the NDVI value, the better the vegetation growth [17]. The research area's NDVI values, varying from -1 to 1, are separated into eight subclasses using the natural breakpoint approach, as indicated in Table 1. On the whole, Table 1 also shows that a relatively high NDVI value is more closely connected with a low landslide occurrence.
What’s more, the human activities are also important predisposing factors to the landslide occurrence [1]. According to field investigation, the engineering constructions including road, hydropower station and quarry are considered as the main human activities triggering landslides in the study area. These engineering activities could not only break the original stress equilibrium of slope by hill cutting or variation of reservoir level, but also cause the occurrence of unstable slope due to unreasonable surface loading [15]. In Table 1, the natural breakpoint approach is used to categorize the quarry density (Figure 4j) and the hydropower station density (Figure 4l) into eight different groups. However, the factor of distance to road (Figure 4k) is classified into eight classes under the specific intervals of distance [11]: 0-100 m, 100-200 m, 200-400 m, 400-800 m, 800-1600 m, 1600-3200 m, 3200-6400 m, >6400 m. Moreover, Table 1 shows a negative correlation between the landslide occurrence and the distance to road as a whole.

4. Results

4.1. Preparation of Spatial Datasets for building LSP model

Twelve landslide predisposing factors' FRs values are utilized in this study as input independent variables for LSP models, as follows: (1) FR value without considering landslide spatial aggregation; (2) FRa value considering landslide spatial aggregation based on CLAI; (3) DFR value considering landslide spatial aggregation based on LAIFR. Both landslide and non-landslide types make up the spatial datasets used as the dependent variable in the LSP models. The former is given a value of 1 after being derived from known landslide grid units, whereas the same number of samples belonging to the latter type is given the value 0 after being chosen at random from the non-landslide units. For the sake of model validation in the LSP process, all of the landslide and non-landslide samples are split into two groups at arbitrary: 30% are used to validate the LSP model's performance, and 70% are utilized as training data to construct the model [7,26].

4.2. LSP by FR Model

The FRs values including FR, FRa and DFR are calculated through Equation (1) to Equation (5), and Table 1 displays each factor's results. Then, according to Equation (6), values of each FRs type is summed up respectively to get the LSIs by ArcGIS 10.4 software. With the frequently-used natural breakpoint method, the LSMs obtained by the FR models are categorized as five susceptibility levels (Figure 5a-c): very low, low, moderate, high and very high [20,40]. Additionally, the other three LSP models also follow the natural breakpoint approach for LSM classification.
As shown in Figure 5, the majority of the high and very high LSI areas are scattered in northern mountains, and all the gained LSMs have high similarity in this respect. However, the LSM based on the FRa model clearly displays the fewest areas in high and very high LSIs (Figure 5b), accounting for 3.06% and 1.68% of the entire area, respectively, mostly around constructions of quarries and hydropower stations. Besides, due to the gentle topography, most districts of the study area, such as Aksu, Awati, Keping, Alar, Tiemenguan, Tumushuke, Shaya and Bachu, are almost entirely in very low degree of landslide susceptibility.

4.3. LSP by AHP Model

As the values of the CI, RI and CR are 0.0305, 1.54 and 0.0198, respectively, which shows that the pairwise comparison matrix (Table 3) provided in the calculation process of AHP model has a reasonable consistency. Then, according to Equation (9), the calculated weight value of each predisposing factor is input into the AHP model to calculate LSIs, as shown in Equation (15). Next, the LSMs of AHP model are generated using ArcGIS 10.4 software. Finally, the LSMs of study area are also listed as five grades based on the natural breakpoint approach (Figure 5d-f): very low, low, moderate, high and very high.
LSIAHP = 0.170 × F1 + 0.031 × F2 + 0.020 × F3 + 0.127 × F4 + 0.092 × F5 + 0.127 × F6 + 0.046 × F7 - 0.092 × F8 + 0.012 × F9 + 0.92 × F10 + 0.127 × F11 + 0.065 × F12
On the whole, it is evident that the high and very high susceptibility areas are almost concentrated in alpine valleys of the South Tianshan Mountains, especially in the upper and middle reaches of the Tarim River’s tributaries (Figure 5d-f). Most of the aforementioned areas are primarily found in the northern portions of Kuqa, Wensu, Luntai, Baicheng, Akqi, Wushi and Korla. In addition, the results of FR-AHP model and DFR-AHP model are significantly similar in the spatial distribution characteristics of LSIs. But according to Figure 5e, the LSM by FRa-AHP model has fewest areas with very high (0.63%) and high (3.85%) landslide susceptibility levels, which is consistent with the result based on FRa model.

4.4. LSP by LR Model

In the initial step of the LR model’s prediction process, the datasets about twelve various predisposing factors and related samples should be firstly converted into XLS-formatted data for SPSS software to access. And then, the FRs of each predisposing factor are imported into LR model through adopting binary logistic regression analysis, where the occurrence of landslide corresponds to the dependent variable and the input factors are the independent variables [7]. According to the initial result of LR model analysis, since the significance values of aspect and annual mean rainfall are both greater than 0.05, both of them should be removed from the LR model in the later model building process [17]. Next, the remaining 10 predisposing factors are re-input into the LR model. Then, each factor's regression coefficient is determined, as shown in Equation (16-18). These regression coefficients are all positive, indicating that each factor contributes to the landslide occurrence of the middle reaches of Tarim River basin.
The equation of FR-LR model:
ZFR = - 7.022 + 0.170 × F1 + 0.177 × F3 + 0.278 × F4 + 0.200 × F5 + 0.512 × F6 + 1.348 × F7 + 0.283 × F9 + 1.168 × F10 + 0.696 × F11 + 0.356 × F12
The equation of FRa-LR model:
ZFRa = - 4.078 + 446.474 × F1 + 982.629 × F3 + 1101.208 × F4 + 6273.457 × F5 + 5954.789 × F6 + 22037.404 × F7 + 2714.528 × F9 + 3586.338 × F10 + 593.037 × F11 + 894.978 × F12
The equation of DFR-LR model:
ZDFR = - 6.086 + 0.153 × F1 + 0.210 × F3 + 0.372 × F4 + 0.226 × F5 + 0.591 × F6 + 1.009 × F7 + 0.124 × F9 + 1.145 × F10 + 0.995 × F11 + 0.479 × F12
Furthermore, because each model's chi-square significance is greater than 0.05, the Hosmer-Lemeshow test indicates that the goodness-of-fit of these equations based on the FR-LR model (0.232), FRa-LR model (0.210), and DFR-LR model (0.830) can be adopted [22]. In addition, the values of Cox-Snell R2 and Nagelkerke R2 are also much higher than 0.05 and close to 1, indicating that the performance of models is good. Finally, through Equation (16-18), the LSMs are acquired by calculating the LSI of each grid unit based on ArcGIS 10.4 software. Additionally, the natural breakpoint approach is applied to reclassify the LSMs predicted by the LR models into five grades, namely, very low, low, moderate, high and very high (Figure 5g-i).
As a whole, compared with models of FR and AHP, the discrepancy of LSIs distribution patterns in each LSM obtained by the LR model is not very apparent under different types of FRs. Figure 5g-i shows that high and very high landslide susceptibility zones are mainly distributed in Akqi, Kuqa, Wushi, Luntai, Baicheng, Wensu and Korla, accounting for 4.92%~5.33% and 4.36%~4.63% of the total area, respectively.

4.5. LSP by RF Model

In general, for an RF model, more decision trees could result in more modeling time, whereas less decision trees would result in errors [23,26,31]. Hence, in the first step of establishing the RF model for LSP, the optimal numbers of factor features and decision trees used in the models are attained by using MATLAB R2022a software through the analysis of factor feature number and out-of-bag error [48-50]. Then, the RF model under the optimal parameters is adopted to carry out LSI prediction. Finally, the calculated results of LSI are loaded into ArcGIS 10.4 software for producing the LSMs (Figure 5i-l).
Similarly, the LSMs obtained by the RF model are ranked into five different categories based on natural breakpoint approach, including very low, low, moderate, high, and very high. Furthermore, the LSM obtained by FR-RF model has the most areas of high and very high landslide susceptibility among these LSMs by RF model, making up 9.59% and 10.21% of the total area, respectively. While the LSM by FRa-RF model has the fewest areas of high and very high landslide susceptibility, covering the proportion of 5.6% and 4.3% of the total area, respectively. Likewise, the majority of the high and very high landslide susceptibility zones in the middle reaches of Tarim River basin are primarily found in the northern part of the South Tianshan Mountains where gullies and valleys developed.

5. Discussion

In this section, the predictive performance of adopted LSP models is validated by the AUC values and LSIs distribution characteristics. Then, according to the LSP results of this study and existing studies, the features of LSP model and FRs are discussed. In addition, the limitations of LSP model are analyzed, and a briefly prospect of the potential research work is also given.

5.1. Evaluation of LSP Models

5.1.1. AUC Values of the LSP Models

Based on validation datasets, the LSP models are evaluated by the ROCs, and the AUC values are obtained to reflect models' prediction accuracy. As shown in Figure 6, based on the DFR datasets, the LSP models considering the landslide spatial aggregation have higher AUC values, indicating that the accuracy of LSP model can be improved by the application of DFR method. Compared with the prediction results under unadjusted FR datasets, the prediction accuracy of LSP model using DFR method is significantly improved by 0.9%-3.0%. On the contrary, as far as the AUC value is concerned, the models using FRa datasets are even lower than the models using FR datasets that do not consider landslide spatial aggregation.
From the view of the whole results of AUC (Figure 6), the AUC value of the RF model is greater, indicating a good prediction ability, followed by LR model, AHP model and FR model. And in terms of the RF models, the variation trend of AUC value is as follows: DFR-RF (0.910) > FR-RF (0.880) > FRa-RF (0.861). Furthermore, because of the very good performance and distinctly higher accuracy, the DFR-RF model's prediction result is the most reliable and accurate when compared to the other LSP models. And the FR model using FRa dataset have the lowest AUC value of 0.828. Additionally, regardless of which FRs type dataset is used, the AHP model and the FR model both have lower AUC values. On the other hand, in the LSP of this study area, the LR and RF models both perform better in terms of prediction precision.
Besides, it is evident that the RF models based on different FRs datasets differ greatly in terms of accuracy, while the accuracy difference of the FR or AHP models is smaller. This phenomenon suggests that the performance of RF models with better prediction ability is more affected by the type of FRs datasets.

5.1.2. Distribution Patterns of LSIs

The mean value and standard deviation are employed as the two primary indicators in this study to analyze the LSIs features of each LSP model using the histogram and compare the prediction performance of various models. The former can reflect the central tendency of all calculated LSIs, while the latter is proposed to indicate the degree of dispersion of LSIs. Generally speaking, low mean value suggests that the majority of the LSIs generated by the LSP model fall within the low value category. In terms of the standard deviation, the higher the standard deviation, the more LSIs deviates from the mean value, the better the distinguish capacity for the differences of LSIs, and the lower the uncertainty of the prediction results, and vice versa. In summary, a low mean value and a high standard deviation illustrate that the corresponding LSP model can better reflect each grid unit's landslide susceptibility by using fewer high LSIs, namely, the prediction performance of this model is reliable and accurate [17,26].
As shown in Figure 7, the LSIs distribution histogram of each LSP model is generated according to the prediction results. And in this process, the LSIs of FR models and AHP models are normalized in ArcGIS 10.4 software in advance. As far as the FRs dataset type is concerned, compared with the FR datasets, the LSIs results predicted with the DFR datasets considering landslide spatial aggregation have a lower mean value and higher standard deviation. In other words, the DFR method can actually enhance the LSP model's prediction performance. However, the standard deviation of the LSP model based on FRa datasets is the lowest in each corresponding LSP model group. Especially in the models of RF and LR, the models based on FRa datasets also have the highest mean value. In addition, due to the limitations of the CLAI method, the LSIs obtained by FR model and AHP model built on the FRa datasets are generally very low, resulting in extremely low mean values. That is to say, in this study, the FRa datasets based on the CLAI method do not perform well in improving the LSP models’ prediction abilities.
In the case of different LSP models, the RF model and LR model have obviously better prediction performance than other LSP models according to the lower mean value and higher standard deviation. Furthermore, the DFR-RF model has the lowest mean value and the highest standard deviation, indicating that its prediction performance is very good in this study. On the whole, according to the histograms shown in Figure 7, the LSP models are ranked as follows by the prediction performance: the RF model is the best, followed by the LR model, AHP model and FR model.
In a word, each LSP model built on DFR datasets not only has higher AUC value, but also shows better prediction capacity with lower mean value and higher standard deviation. In other words, the results show that DFR method can effectively enhance the prediction performance of LSP model. Oppositely, according to the AUC values and distribution patterns of LSIs, the FRa dataset based on the CLAI method performs poorly in improving the LSP models’ prediction performance in this study. What’s more, machine learning models, including RF model and LR model, have much better performance in LSP study, with RF model performing the best.

5.2. Synthetical Analysis of LSP Results

Although based on different LSP models and FRs datasets, all the LSMs with various ranges of LSIs show generally consistent features as a whole: the northern mountains, which range in elevation from 2104 to 3817 m, are the primary areas of high and very high landslide susceptibility zones. Besides, these mountains are characterized by active tectonic activities and intense human activities, such as road construction and mining. This phenomenon suggests that these landslide predisposing factors can play a significant role in landslide occurrence, and the reasonable selection of landslide predisposing factors should not be underestimated [7,13,14].
Meanwhile, the LSP Results also are affected by LSP model’s prediction performance. Generally speaking, the traditional statistical models, including FR model and AHP model, are inherently linear and cannot reflect the nonlinear relationship between landslide occurrence and correlative predisposing factors, so their prediction ability is relatively low. In contrast, this complex relationship can be well handled by machine learning models, such as LR model and RF model. Furthermore, the RF model can improve prediction accuracy by integrating multiple decision trees, which is helpful to avoid overfitting and enhance generalization ability [23,26,31]. By and large, the RF model outperforms the other LSP models with regard to prediction performance in this study.
Landslide spatial aggregation is worth considering in LSP study, as it brings uncertainty to model building [24]. According the LSP Results and model evaluation, there is no doubt that the DFR method proposed in this study can practically enhance the LSP model’s prediction capacity. However, the CLAI method which has been used successfully in some past researches [16,26], does not have a good performance. As explained within section 2.2.2, the CLAI method's poor performance is caused by theoretical limitations that would result in significant levels of uncertainty in LSP studies, especially when the research region is broad and landslide predisposing factors are complex. In any case, the DFR method shows a more stable and favorable effect on enhancing the prediction performance of LSP model.

5.3. For Further Study

As the basic premise of LSP study, the establishment of reliable and complete landslide inventory is generally determined by skilled professional interpreters and high-resolution remote sensing datasets used for landslide identification [4]. The combination of multi-period remote sensing data datasets analysis and landslide samples validation by field investigation is conducive to reduce the uncertainties caused by interpreters’ misjudgment and overlapped areas of multiple landslides [26,41]. In addition, automatic landslide identification using deep learning method can lighten the workload of obtaining landslide datasets, especially when the study area is large.
Besides, evaluation units like the hydrologic slope unit, which are frequently employed in current research, are capable of better describing the relationship between the incidence of landslide and geomorphic factors [11,14,20]. The DFR method considering landslide spatial aggregation should be applied and even optimized in different evaluation unit types, such as hydrologic slope unit, to play a better role in improving landslide prediction ability. Additionally, the techniques employed for automatic slope unit extraction can effectively achieve quick modeling and improve the aforementioned studies, ensuring that the LSP model's prediction performance is continuously enhanced going forward. However, the existing automatic extraction methods of slope units often produce unreasonable results when processing the datasets with complex geomorphological conditions, so the elaborate extraction method still needs further research [51].
What’s more, the LSM produced by a single type of LSP model frequently contains inevitable uncertainty because the association between landslide formation and numerous predisposing factors is typically complicated [7,46,52]. Since each LSP model has its own data classification principle, adopting multiple models in LSP study would contribute to lessen the uncertainty raised by the feature importance analysis of a series of predisposing conditions. Furthermore, some studies have shown that integrating deep learning methods with more progressive semi-supervised machine learning approaches can enhance LSP model’s capacity to predict landslide susceptibility [14,33,53].

6. Conclusions

In this study, the LSP process of the middle reaches of the Tarim River basin has been performed using four different LSP models applying different FRs datasets, taking into account the landslide spatial aggregation. Based on the landslide inventory with 663 identified landslide points, twelve landslide predisposing factors are adopted in LSP study, and a series of LSMs are obtained with various LSIs distribution patterns. The novel findings and main conclusions of this study can be drawn:
(1)
DFR method proposed in this study can not only perform well in quantifying the degree of landslide spatial aggregation, but also improve the prediction performance of LSP model effectively. According to the obtained LSMs and model evaluation, each LSP models using DFR method in this study has better prediction performance.
(2)
On the whole, the RF model outperforms the other LSP models in terms of prediction ability, followed by LR model, AHP model and FR model. Furthermore, the machine learning models, including RF model and LR model, have much better prediction performance than the traditional statistic models represented by AHP model and FR model.
(3)
The vast majority of the high and very high landslide susceptibility zones are primarily located in the northern mountainous regions of the studying area, according to a combination of different LSMs produced by LSP models. In addition, the LSP result of a single type of model is often uncertain, and the final LSM should be determined by the comprehensive analysis on the various LSP models’ results.

Author Contributions

Conceptualization, X.Y. and Y.S.; methodology, Y.S.; software, X.Y.; validation, S.L., Q.M. and H.M.; formal analysis, P.S.; investigation, Y.S., X.Y. and Q.M.; resources, X.Y.; data curation, Y.S.; writing—original draft preparation, X.Y.; writing—review and editing, Y.S. and Z.C.; project administration, Y.S.; funding acquisition, Z.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the Third Xinjiang Scientific Expedition Program (Grant No. 2022xjkk1305), the Science and Technology Partnership Program of the Shanghai Cooperation Organization and International Science and Technology Cooperation Program, the Xinjing Department of Science and Technology (Grant No. 2023E01005), the Second Tibetan Plateau Scientific Expedition and Research Program (STEP) (Grant No. 2019QZKK0904) and Key R&D Program of Xinjiang Uygur Autonomous Region (Grant No. 2022B03001-2).

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat Hazard Earth Sys 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
  2. Park, J.Y.; Lee, S.R.; Lee, D.H.; Kim, Y.T.; Lee, J.S. A regional-scale landslide early warning methodology applying statistical and physically based approaches in sequence. Eng Geol 2019, 260. [Google Scholar] [CrossRef]
  3. Li, G.K.; Moon, S. Topographic stress control on bedrock landslide size. Nature Geoscience 2021, 14, 307–313. [Google Scholar] [CrossRef]
  4. Xu, Q.; Zhao, B.; Dai, K.; Dong, X.; Li, W.; Zhu, X.; Yang, Y.; Xiao, X.; Wang, X.; Huang, J.; Lu, H.; Deng, B.; Ge, D. Remote sensing for landslide investigations: A progress report from China. Eng Geol 2023, 321. [Google Scholar] [CrossRef]
  5. Yang, Z.J.; Pang, B.; Dong, W.F.; Li, D.H.; Huang, Z.Y. Interaction of landslide spatial patterns and river canyon landforms: Insights into the Three Parallel Rivers Area, southeastern Tibetan Plateau. Sci Total Environ 2024, 914. [Google Scholar] [CrossRef] [PubMed]
  6. van Westen, C.J.; Castellanos, E.; Kuriakose, S.L. Spatial data for landslide susceptibility, hazard, and vulnerability assessment: An overview. Eng Geol 2008, 102, 112–131. [Google Scholar] [CrossRef]
  7. Bourenane, H.; Meziani, A.A.; Benamar, D.A. Application of GIS-based statistical modeling for landslide susceptibility mapping in the city of Azazga, Northern Algeria. Bull Eng Geol Env 2021, 80, 7333–7359. [Google Scholar] [CrossRef]
  8. Chang, M.; Cui, P.; Dou, X.; Su, F. Quantitative risk assessment of landslides over the China-Pakistan economic corridor. Int J Disast Risk Re 2021, 63, 102441. [Google Scholar] [CrossRef]
  9. Shang, Y.J.; Wang, S.J.; Li, G.C.; Yang, Z.F. Retrospective case example using a comprehensive suitability index (CSI) for siting the Shisan-Ling power station, China. Int J Rock Mech Min 2000, 37, 839–853. [Google Scholar] [CrossRef]
  10. Singh, K.; Kumar, V. Hazard assessment of landslide disaster using information value method and analytical hierarchy process in highly tectonic Chamba region in bosom of Himalaya. J Mt Sci-Engl 2018, 15, 808–824. [Google Scholar] [CrossRef]
  11. Li, Y.; Qi, S.; Zheng, B.; Yao, X.; Guo, S.; Zou, Y.; Lu, X.; Tang, F.; Guo, X.; Waqar, M.F.; Zada, K. Multi-Scale Engineering Geological Zonation for Linear Projects in Mountainous Regions: A Case Study of National Highway 318 Chengdu-Shigatse Section. Remote Sens-Basel 2023, 15. [Google Scholar] [CrossRef]
  12. Li, C.J.; Ma, T.H.; Sun, L.L.; Li, W.; Zheng, A.P. Application and verification of a fractal approach to landslide susceptibility mapping. Nat Hazards 2012, 61, 169–185. [Google Scholar] [CrossRef]
  13. Aditian, A.; Kubota, T.; Shinohara, Y. Comparison of GIS-based landslide susceptibility models using frequency ratio, logistic regression, and artificial neural network in a tertiary region of Ambon, Indonesia. Geomorphology 2018, 318, 101–111. [Google Scholar] [CrossRef]
  14. Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci Rev 2018, 180, 60–91. [Google Scholar] [CrossRef]
  15. Yalcin, A.; Reis, S.; Aydinoglu, A.C.; Yomralioglu, T. A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistics regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. Catena 2011, 85, 274–287. [Google Scholar] [CrossRef]
  16. Wang, X.; Zhang, L.; Wang, S.; Lari, S. Regional landslide susceptibility zoning with considering the aggregation of landslide points and the weights of factors. Landslides 2014, 11, 399–409. [Google Scholar] [CrossRef]
  17. Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
  18. Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
  19. Liu, L., L.; Zhang, Y., L.; Xiao, T.; Yang, C. A frequency ratio-based sampling strategy for landslide susceptibility assessment. Bull Eng Geol Env 2022, 81, 360. [Google Scholar] [CrossRef]
  20. Alvioli, M.; Loche, M.; Jacobs, L.; Grohmann, C.H.; Abraham, M.T.; Gupta, K.; Satyam, N.; Scaringi, G.; Bornaetxea, T.; Rossi, M.; Marchesini, I.; Lombardo, L.; Moreno, M.; Steger, S.; Camera, C.A.S.; Bajni, G.; Samodra, G.; Wahyudi, E.E.; Susyanto, N.; Sincic, M.; Gazibara, S.B.; Sirbu, F.; Torizin, J.; Schüssler, N.; Mirus, B.B.; Woodard, J.B.; Aguilera, H.; Rivera-Rivera, J. A benchmark dataset and workflow for landslide susceptibility zonation. Earth-Sci Rev 2024, 258. [Google Scholar] [CrossRef]
  21. Lin, L.; Lin, Q.; Wang, Y. Landslide susceptibility mapping on a global scale using the method of logistic regression. Nat Hazard Earth Sys 2017, 17, 1411–1424. [Google Scholar] [CrossRef]
  22. Broeckx, J.; Vanmaercke, M.; Duchateau, R.; Poesen, J. A data-based landslide susceptibility map of Africa. Earth-Sci Rev 2018, 185, 102–121. [Google Scholar] [CrossRef]
  23. Chen, W.; Li, Y.; Xue, W.F.; Shahabi, H.; Li, S.J.; Hong, H.Y.; Wang, X.J.; Bian, H.Y.; Zhang, S.; Pradhan, B.; Bin Ahmad, B. Modeling flood susceptibility using data-driven approaches of naive Bayes tree, alternating decision tree, and random forest methods. Sci Total Environ 2020, 701. [Google Scholar] [CrossRef] [PubMed]
  24. Liu, L.; Li, S.; Li, X.; Jiang, Y.; Wei, W.; Wang, Z.; Bai, Y. An integrated approach for landslide susceptibility mapping by considering spatial correlation and fractal distribution of clustered landslide data. Landslides 2019, 16, 715–728. [Google Scholar] [CrossRef]
  25. Liu, B.; Han, S.Y.; Gong, H.; Zhou, Z.L.; Zhang, D. Disaster resilience assessment based on the spatial and temporal aggregation effects of earthquake-induced hazards. Environmental Science and Pollution Research 2020, 27, 29055–29067. [Google Scholar] [CrossRef] [PubMed]
  26. Huang, F.; Tao, S.; Li, D.; Lian, Z.; Catani, F.; Huang, J.; Li, K.; Zhang, C. Landslide Susceptibility Prediction Considering Neighborhood Characteristics of Landslide Spatial Datasets and Hydrological Slope Units Using Remote Sensing and GIS Technologies. Remote Sens-Basel 2022, 14, 4436. [Google Scholar] [CrossRef]
  27. Chang, Z.L.; Huang, F.M.; Huang, J.S.; Jiang, S.H.; Liu, Y.T.; Meena, S.R.; Catani, F. An updating of landslide susceptibility prediction from the perspective of space and time. Geoscience Frontiers 2023, 14. [Google Scholar] [CrossRef]
  28. Dornik, A.; Drăguţ, L.; Oguchi, T.; Hayakawa, Y.; Micu, M. Influence of sampling design on landslide susceptibility modeling in lithologically heterogeneous areas. Scientific Reports 2022, 12, 2106. [Google Scholar] [CrossRef]
  29. Shang, Y.J.; Park, H.D.; Yang, Z.F. Engineering geological zonation using interaction matrix of geological factors: An example from one section of Sichuan-Tibet Highway. Geosciences Journal 2005, 9, 375–387. [Google Scholar] [CrossRef]
  30. Breiman, L. Random forests. Machine Learning 2001, 45, 5–32. [Google Scholar] [CrossRef]
  31. Hasan, M.; Kotov, A.; Idalski Carcone, A.; Dong, M.; Naar, S.; Brogan Hartlieb, K. A study of the effectiveness of machine learning methods for classification of clinical interview fragments into a large number of categories. Journal of Biomedical Informatics 2016, 62, 21–31. [Google Scholar] [CrossRef] [PubMed]
  32. Akobeng, A.K. Understanding diagnostic tests 3: receiver operating characteristic curves. Acta Paediatr 2007, 96, 644–647. [Google Scholar] [CrossRef] [PubMed]
  33. Wu, Y.L.; Ke, Y.T.; Chen, Z.; Liang, S.Y.; Zhao, H.L.; Hong, H.Y. Application of alternating decision tree with AdaBoost and bagging ensembles for landslide susceptibility mapping. Catena 2020, 187, 104396. [Google Scholar] [CrossRef]
  34. de Hond, A.A.H.; Steyerberg, E.W.; van Calster, B. Interpreting area under the receiver operating characteristic curve. Lancet Digit Health 2022, 4, E853–E855. [Google Scholar] [CrossRef]
  35. Chen, Y.; Xu, Z. Possible impacts of global climate change on water resources in Tarim River Basin, Xinjiang. Science in China 2004, 34, 1047–1053. [Google Scholar]
  36. Xiao, W.; Zhang, L.-C.; Qin, K.Z.; Li, J.-L. Paleozoic accretionary and collisional tectonics of the Eastern Tianshan (China): Implications for the continental growth of central Asia. American Journal of Science 2004, 304. [Google Scholar] [CrossRef]
  37. Xiao, W.; Windley, B.F.; Allen, M.B.; Han, C. Paleozoic multiple accretionary and collisional tectonics of the Chinese Tianshan orogenic collage. Gondwana Research 2013, 23, 1316–1341. [Google Scholar] [CrossRef]
  38. Zhou, J.B.; Wilde, S.A.; Zhao, G.C.; Han, J. Nature and assembly of microcontinental blocks within the Paleo-Asian Ocean. Earth-Sci Rev 2018, 186, 76–93. [Google Scholar] [CrossRef]
  39. Xu, J.H.; Chen, Y.N.; Lu, F.; Li, W.H.; Zhang, L.J.; Hong, Y.L. The Nonlinear trend of runoff and its response to climate change in the Aksu River, western China. Int J Climatol 2011, 31, 687–695. [Google Scholar] [CrossRef]
  40. Huang, F.; Teng, Z.; Yao, C.; Jiang, S.-H.; Catani, F.; Chen, W.; Huang, J. Uncertainties of landslide susceptibility prediction: Influences of random errors in landslide conditioning factors and errors reduction by low pass filter method. J Rock Mech Geotech 2024, 16, 213–230. [Google Scholar] [CrossRef]
  41. Yi, X.; Shang, Y.; Shao, P.; Meng, H. A dataset of spatial distributions and attributes of typical rockfalls and landslides in the China-Pakistan Economic Corridor from 1970 to 2020. China Scientific Data 2021, 6, 1–1. [Google Scholar]
  42. Nadim, F.; Kjekstad, O.; Peduzzi, P.; Herold, C.; Jaedicke, C. Global landslide and avalanche hotspots. Landslides 2006, 3, 159–173. [Google Scholar] [CrossRef]
  43. Wang, Y.; Lin, Q.; Shi, P. Spatial pattern and influencing factors of casualty events caused by landslides. Acta Geographica Sinica 2017, 72, 906–917. [Google Scholar]
  44. Shang, Y.J.; Park, H.D.; Yang, Z.F.; Zhang, L.Q. Debris formation due to weathering, avalanching and rock falling, landsliding in SE Tibet. Int J Rock Mech Min 2004, 41, 839–845. [Google Scholar] [CrossRef]
  45. Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S.; Baum, R.L.; Coe, J.A.; Schulz, W.H.; Bower, J.B. Landslide mobility and hazards: implications of the 2014 Oso disaster. Earth Planet Sc Lett 2015, 412, 197–208. [Google Scholar] [CrossRef]
  46. Wang, X.L.; Clague, J.J.; Crosta, G.B.; Sun, J.; Stead, D.; Qi, S.; Zhang, L. Relationship between the spatial distribution of landslides and rock mass strength, and implications for the driving mechanism of landslides in tectonically active mountain ranges. Eng Geol 2021, 292, 106281. [Google Scholar] [CrossRef]
  47. Luo, S.-l.; Huang, D.; Peng, J.-b.; Tomás, R. Influence of permeability on the stability of dual-structure landslide with different deposit-bedding interface morphology: The case of the three Gorges Reservoir area, China. Eng Geol 2022, 296, 106480. [Google Scholar] [CrossRef]
  48. Lagomarsino, D.; Tofani, V.; Segoni, S.; Catani, F.; Casagli, N. A Tool for Classification and Regression Using Random Forest Methodology: Applications to Landslide Susceptibility Mapping and Soil Thickness Modeling. Environmental Modeling & Assessment 2017, 22, 201–214. [Google Scholar] [CrossRef]
  49. Raghu, S.; Sriraam, N. Classification of focal and non-focal EEG signals using neighborhood component analysis and machine learning algorithms. Expert Systems with Applications 2018, 113, 18–32. [Google Scholar] [CrossRef]
  50. Islam, N.; Rashid, M.M.; Wibowo, S.; Xu, C.Y.; Morshed, A.; Wasimi, S.A.; Moore, S.; Rahman, S.M. Early Weed Detection Using Image Processing and Machine Learning Techniques in an Australian Chilli Farm. Agriculture-Basel 2021, 11. [Google Scholar] [CrossRef]
  51. Chang, Z.L.; Huang, J.S.; Huang, F.M.; Bhuyan, K.; Meena, S.R.; Catani, F. Uncertainty analysis of non-landslide sample selection in landslide susceptibility prediction using slope unit-based machine learning models. Gondwana Research 2023, 117, 307–320. [Google Scholar] [CrossRef]
  52. Cantarino, I.; Carrion, M.A.; Goerlich, F.; Martinez Ibañez, V. A ROC analysis-based classification method for landslide susceptibility maps. Landslides 2019, 16, 265–282. [Google Scholar] [CrossRef]
  53. Moayedi, H.; Mehrabi, M.; Mosallanezhad, M.; Rashid, A.S.A.; Pradhan, B. Modification of landslide susceptibility mapping using optimized PSO-ANN technique. Engineering with Computers 2019, 35, 967–984. [Google Scholar] [CrossRef]
Preprints 142274 g001
Figure 1. The methodological flowchart for LSP modelling.
Figure 1. The methodological flowchart for LSP modelling.
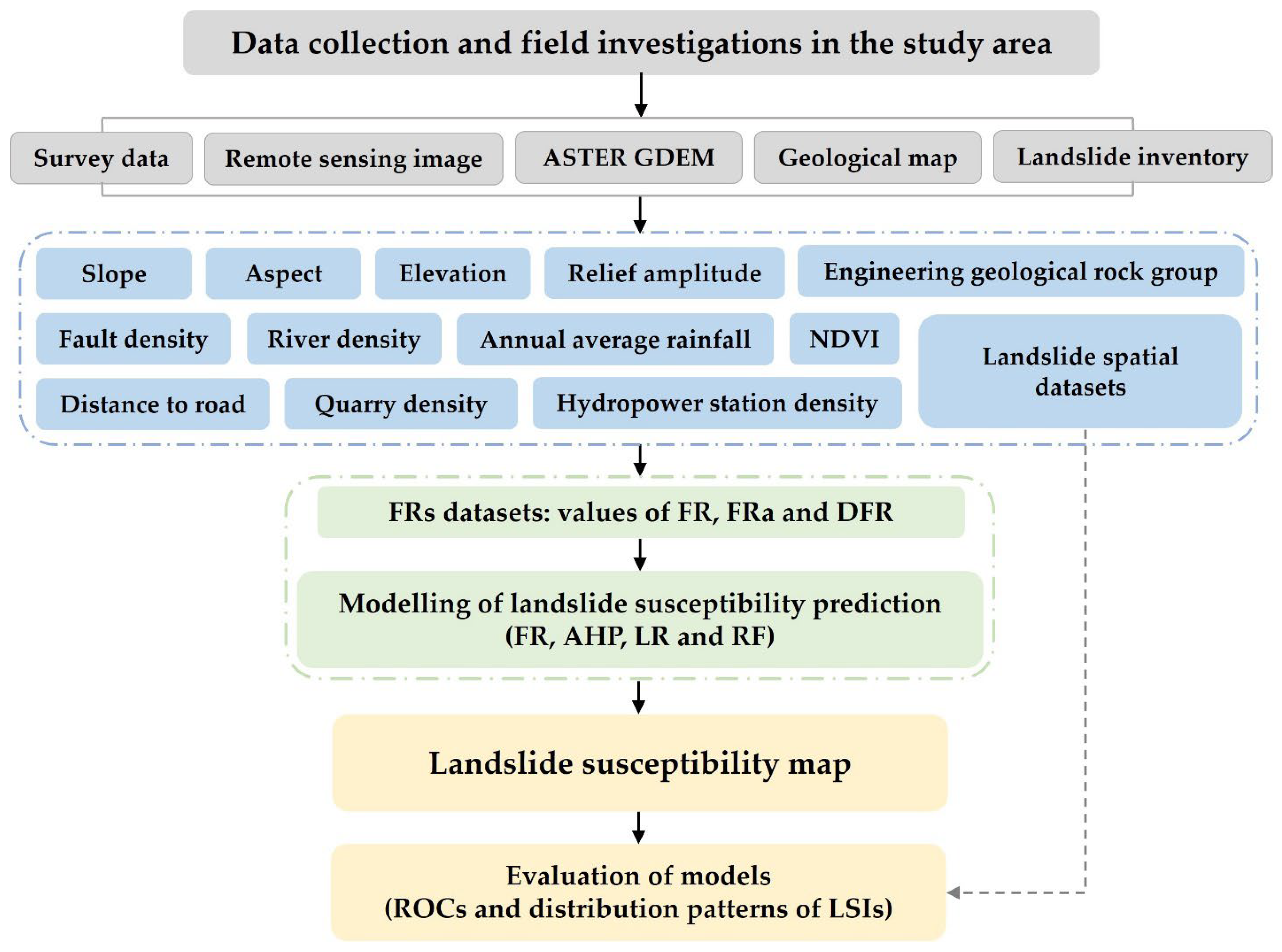
Preprints 142274 g001
Preprints 142274 g002
Figure 2. Four cases of landslide spatial aggregation. (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
Figure 2. Four cases of landslide spatial aggregation. (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.
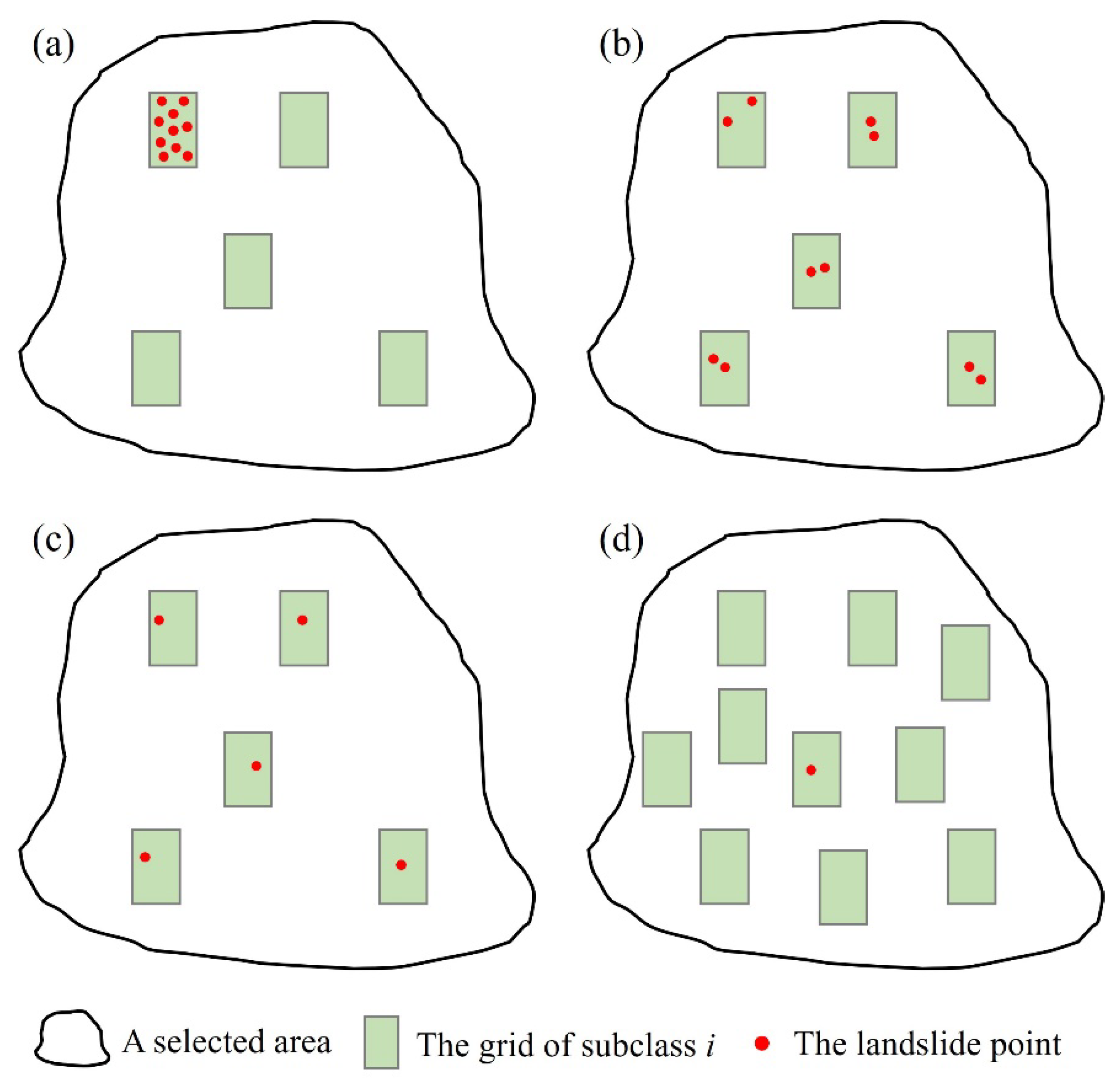
Preprints 142274 g002
Preprints 142274 g003
Figure 3. Location and landslides spatial distribution of the study area.
Figure 3. Location and landslides spatial distribution of the study area.
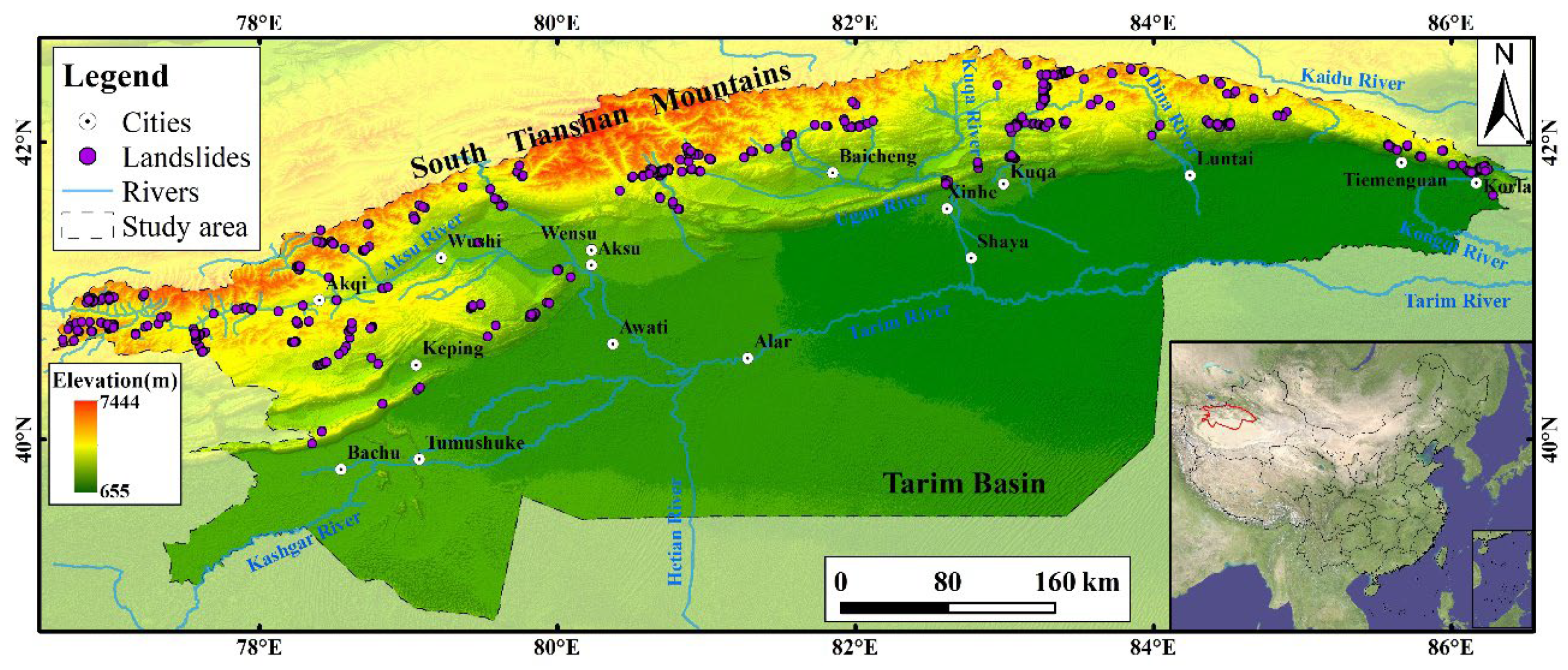
Preprints 142274 g003
Preprints 142274 g004
Figure 4. Landslide predisposing factors: (a) Slope; (b) Aspect; (c) Elevation; (d) Relief amplitude; (e) Engineering geological rock group; (f) Fault density; (g) River density; (h) Average annual rainfall; (i) NDVI; (j) Quarry density; (k) Distance to road; (l) Hydropower station density.
Figure 4. Landslide predisposing factors: (a) Slope; (b) Aspect; (c) Elevation; (d) Relief amplitude; (e) Engineering geological rock group; (f) Fault density; (g) River density; (h) Average annual rainfall; (i) NDVI; (j) Quarry density; (k) Distance to road; (l) Hydropower station density.
Preprints 142274 g004
Preprints 142274 g005
Figure 5. Landslide susceptibility maps obtained using LSP models under different FRs values. (a) FR model; (b) FRa model; (c) DFR model; (d) FR-AHP model; (e) FRa-AHP model; (f) DFR-AHP model; (g) FR-LR model; (h) FRa-LR model; (i) DFR-LR model; (j) FR-RF model; (k) FRa-RF model; (l) DFR-RF model.
Figure 5. Landslide susceptibility maps obtained using LSP models under different FRs values. (a) FR model; (b) FRa model; (c) DFR model; (d) FR-AHP model; (e) FRa-AHP model; (f) DFR-AHP model; (g) FR-LR model; (h) FRa-LR model; (i) DFR-LR model; (j) FR-RF model; (k) FRa-RF model; (l) DFR-RF model.
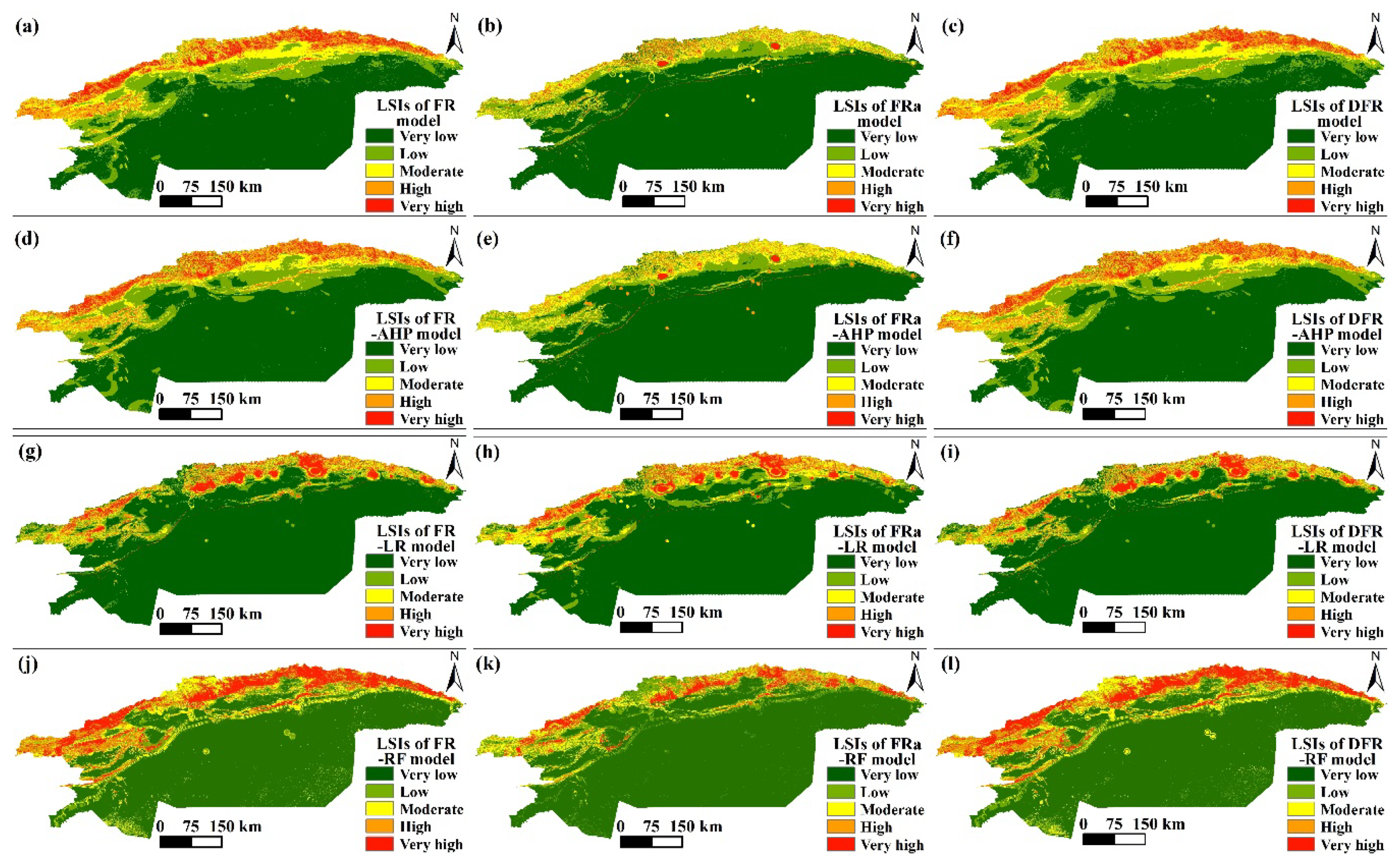
Preprints 142274 g005
Preprints 142274 g006
Figure 6. The ROCs representing the quality of the LSP models. (a) FR model; (b) AHP model; (c) LR model; (d) RF model.
Figure 6. The ROCs representing the quality of the LSP models. (a) FR model; (b) AHP model; (c) LR model; (d) RF model.
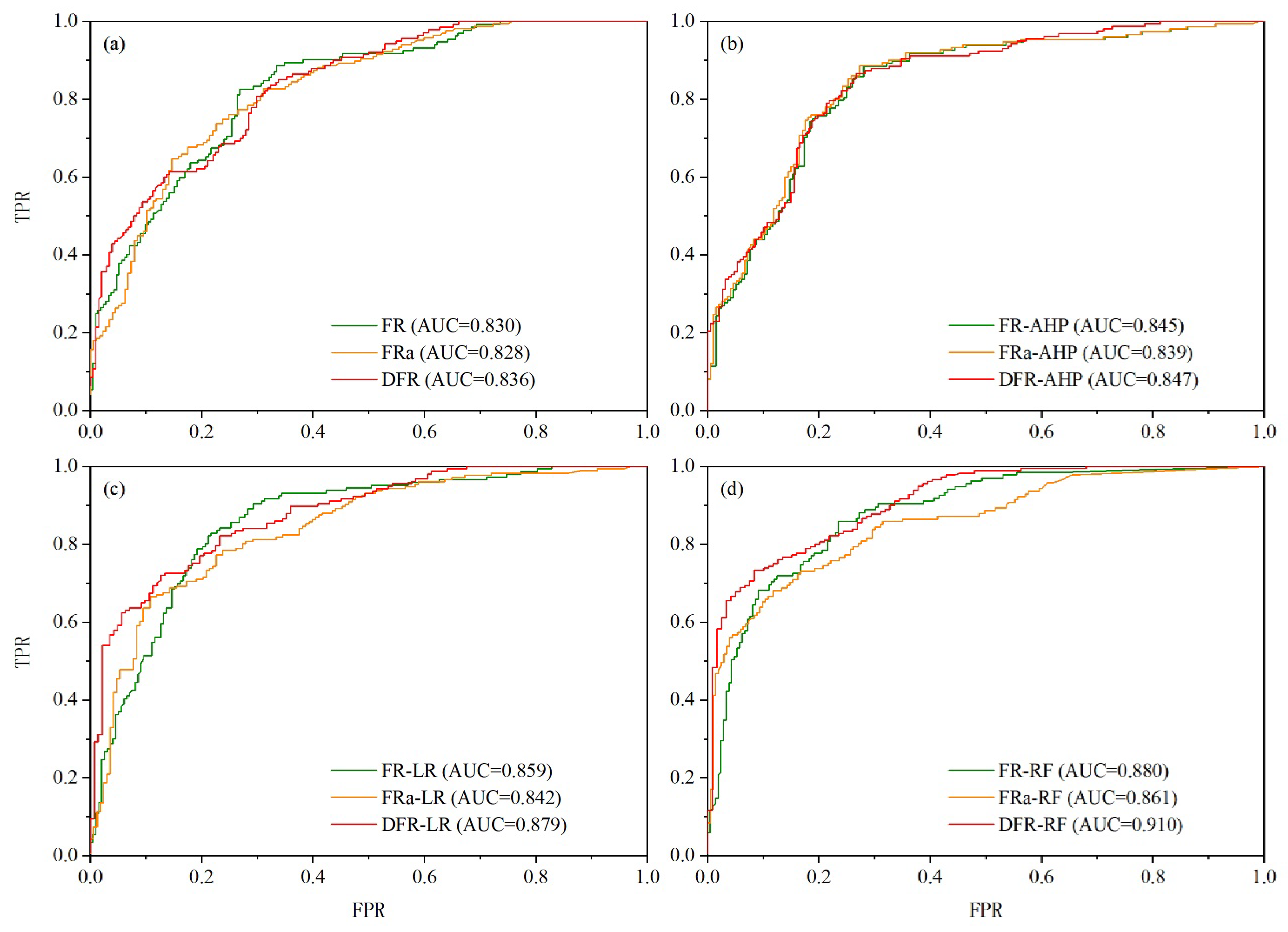
Preprints 142274 g006
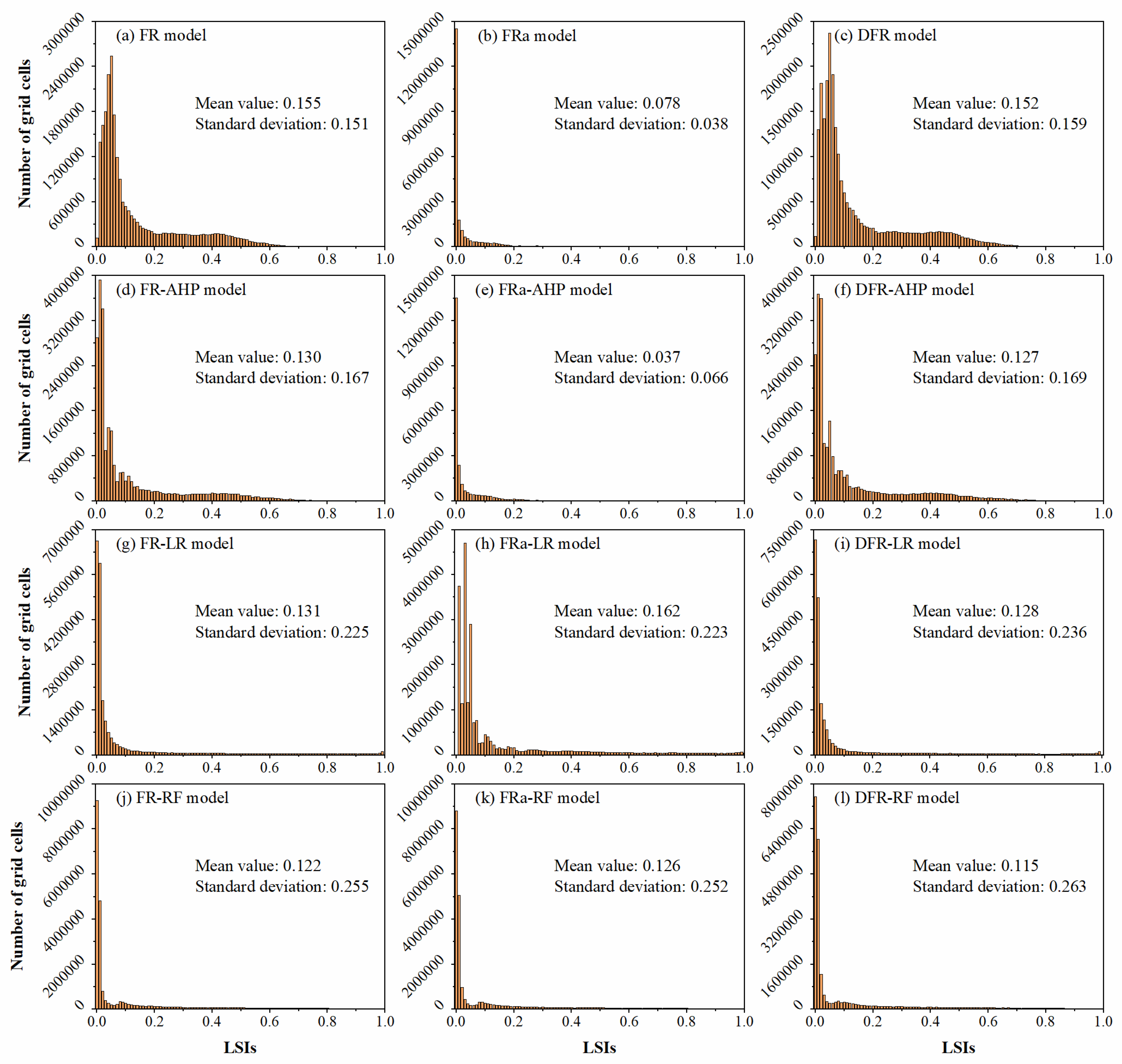
Preprints 142274 g007
Figure 7. LSIs distribution characteristics of the LSP models. (a) FR model; (b) FRa model; (c) DFR model; (d) FR-AHP model; (e) FRa-AHP model; (f) DFR-AHP model; (g) FR-LR model; (h) FRa-LR model; (i) DFR-LR model; (j) FR-RF model; (k) FRa-RF model; (l) DFR-RF model.
Figure 7. LSIs distribution characteristics of the LSP models. (a) FR model; (b) FRa model; (c) DFR model; (d) FR-AHP model; (e) FRa-AHP model; (f) DFR-AHP model; (g) FR-LR model; (h) FRa-LR model; (i) DFR-LR model; (j) FR-RF model; (k) FRa-RF model; (l) DFR-RF model.
Preprints 142274 g007
Table 1. FRs values considering landslide spatial aggregation.
Table 1. FRs values considering landslide spatial aggregation.
Predisposing Factors Values FR CLAI FRa LAIFR DFR
Slope (°)
(F1)		 0~4 0.008 0.000000 0.000000 1.000 0.008
4~10 0.149 0.000003 0.000001 1.000 0.149
10~17 1.314 0.000029 0.000038 0.939 1.234
17~25 3.469 0.000072 0.000251 0.894 3.102
25~33 5.331 0.000092 0.000493 0.742 3.956
33~41 6.308 0.000136 0.000857 0.922 5.816
41~52 10.064 0.000220 0.002214 0.936 9.417
52~90 8.354 0.000179 0.001498 0.919 7.677
Aspect (°)
(F2)		 -1 0.000 0.000000 0.000000 0.000 0.000
0~22.5, 337.5~0 0.829 0.000017 0.000014 0.885 0.734
22.5~67.5 0.856 0.000020 0.000017 1.000 0.856
67.5~112.5 0.708 0.000013 0.000009 0.769 0.544
112.5~157.5 1.418 0.000029 0.000041 0.866 1.228
157.5~202.5 1.597 0.000032 0.000051 0.847 1.352
202.5~247.5 1.218 0.000023 0.000028 0.802 0.977
247.5~292.5 0.717 0.000016 0.000012 0.964 0.691
292.5~337.5 0.905 0.000021 0.000019 1.000 0.905
Elevation (m)
(F1)		 655~1209 0.112 0.000002 0.000000 0.854 0.096
1209~1623 1.261 0.000028 0.000035 0.946 1.193
1623~2104 1.503 0.000033 0.000049 0.935 1.405
2104~2643 3.384 0.000075 0.000254 0.956 3.234
2643~3212 6.130 0.000115 0.000707 0.811 4.969
3212~3817 4.531 0.000093 0.000423 0.888 4.023
3817~4587 0.463 0.000011 0.000005 1.000 0.463
4587~7444 0.000 0.000000 0.000000 0.000 0.000
Relief amplitude (m)
(F4)		 0~17 0.010 0.000000 0.000000 0.800 0.008
17~47 0.691 0.000013 0.000009 0.829 0.572
47~83 3.336 0.000067 0.000223 0.857 2.859
83~118 4.053 0.000095 0.000384 1.000 4.053
118~155 5.650 0.000111 0.000625 0.838 4.732
155~204 9.098 0.000180 0.001636 0.846 7.698
204~285 10.305 0.000224 0.002307 0.930 9.581
285~989 5.239 0.000140 0.000733 1.143 5.988
Engineering geological rock group
(F5)		 Hard 1.940 0.000045 0.000087 1.000 1.940
Less hard 3.649 0.000071 0.000260 0.841 3.070
Less soft 2.769 0.000062 0.000173 0.972 2.692
Soft 2.864 0.000059 0.000169 0.887 2.541
Softer 0.187 0.000004 0.000001 1.000 0.187
water 0.000 0.000000 0.000000 0.000 0.000
Fault density
(F6)		 0~0.06 0.000 0.000000 0.000000 0.000 0.000
0.06~0.18 0.015 0.000000 0.000000 1.000 0.015
0.18~0.29 1.461 0.000033 0.000049 0.981 1.433
0.29~0.4 0.484 0.000011 0.000005 1.000 0.484
0.4~0.5 3.471 0.000065 0.000226 0.808 2.804
0.5~0.6 2.197 0.000050 0.000110 0.981 2.155
0.6~0.76 1.896 0.000036 0.000068 0.811 1.538
0.76~1.00 0.121 0.000003 0.000000 1.000 0.121
River density
(F7)		 0~0.08 0.000 0.000000 0.000000 0.000 0.000
0.08~0.18 1.252 0.000023 0.000029 0.790 0.989
0.18~0.28 1.506 0.000035 0.000052 0.989 1.490
0.28~0.38 1.067 0.000024 0.000026 0.979 1.045
0.38~0.49 1.320 0.000024 0.000032 0.795 1.050
0.49~0.59 1.018 0.000020 0.000021 0.855 0.870
0.59~0.69 1.598 0.000031 0.000050 0.844 1.349
0.69~1.00 0.709 0.000016 0.000012 1.000 0.709
Average annual rainfall (mm)
(F8)		 31~59 0.000 0.000000 0.000000 0.000 0.000
59~88 0.456 0.000010 0.000005 0.986 0.450
88~123 0.301 0.000007 0.000002 1.000 0.301
123~168 1.299 0.000026 0.000034 0.870 1.130
168~223 4.467 0.000091 0.000406 0.876 3.914
223~283 4.325 0.000096 0.000415 0.955 4.129
283~346 4.037 0.000073 0.000294 0.777 3.136
346~609 0.109 0.000001 0.000000 0.500 0.054
NDVI
(F9)		 -1.00~-0.40 2.246 0.000031 0.000070 0.600 1.348
-0.40~-0.23 2.885 0.000065 0.000188 0.974 2.810
-0.23~-0.15 0.767 0.000015 0.000011 0.830 0.636
-0.15~-0.06 1.232 0.000026 0.000032 0.900 1.109
-0.06~0.08 1.071 0.000022 0.000023 0.873 0.935
0.08~0.26 1.325 0.000028 0.000037 0.920 1.219
0.26~0.45 0.734 0.000019 0.000014 1.143 0.839
0.45~1.00 0.104 0.000002 0.000000 1.000 0.104
Quarry density
(F10)		 0~0.03 0.188 0.000010 0.000002 0.797 0.149
0.03~0.1 0.436 0.000030 0.000013 1.000 0.436
0.1~0.19 1.273 0.000085 0.000108 0.970 1.235
0.19~0.3 1.852 0.000127 0.000235 1.000 1.852
0.3~0.42 2.960 0.000199 0.000590 0.981 2.903
0.42~0.57 4.560 0.000308 0.001403 0.983 4.482
0.57~0.76 2.271 0.000156 0.000354 1.000 2.271
0.76~1.00 9.046 0.000576 0.005206 0.927 8.384
Distance to road (m)
(F11)		 0~100 9.496 0.047747 0.008396 0.703 6.675
100~200 2.258 0.003842 0.000676 1.000 2.258
200~400 1.273 0.001220 0.000215 1.000 1.273
400~800 0.550 0.000228 0.000040 1.000 0.550
800~1600 0.399 0.000104 0.000018 0.870 0.347
1600~3200 0.537 0.000165 0.000029 0.759 0.408
3200~6400 0.367 0.000074 0.000013 0.726 0.267
>6400 0.104 0.000008 0.000001 0.980 0.102
Hydropower station density
(F12)		 0~0.04 0.309 0.000017 0.000005 0.932 0.288
0.04~0.14 1.435 0.000047 0.000068 0.565 0.811
0.14~0.24 1.713 0.000095 0.000163 0.952 1.631
0.24~0.35 2.269 0.000088 0.000201 0.667 1.512
0.35~0.47 8.546 0.000389 0.003324 0.778 6.647
0.47~0.62 4.410 0.000258 0.001138 1.000 4.410
0.62~0.77 1.712 0.000100 0.000171 1.000 1.712
0.77~1.00 2.900 0.000170 0.000492 1.000 2.900
Table 2. The classification criteria of EGRG in study area.
Table 2. The classification criteria of EGRG in study area.
Class Major rock types
Hard Un-weathered to slightly weathered: granite, syenite, diorite, diabase, basalt, andesite, gneiss, siliceous slate, quartzite, siliceous consolidated conglomerate, quartz sandstone, siliceous limestone, etc.
Less hard (1) moderately (weakly) weathered hard rock; (2) un-weathered to slightly weathered: fused tuff, marble, slate, dolomite, limestone, calcareous sandstone, coarse crystal marble, etc.
Less soft (1) strongly weathered hard rock; (2) moderately (weakly) weathered less hard rock; (3) un-weathered to slightly weathered: tuff, phyllite, sandy mudstone, marl, argillaceous sandstone, siltstone, sandy shale, etc.
Soft (1) strongly weathered less hard rock; (2) moderately (weakly) weathered less soft rock; (3) un-weathered to slightly mudstone, argillaceous shale, chlorite schist, sericite schist, etc.
Softer (1) completely weathered rock; (2) strongly weathered less soft rock; (3) moderately (weakly) weathered to strongly weathered soft rock; (4) various semi-diagenetic rock; (5) quaternary loose accumulation.
Water Lakes, reservoirs, etc.
Table 3. Pair-wise comparison matrix and weight values of the data layers in AHP model.
Table 3. Pair-wise comparison matrix and weight values of the data layers in AHP model.
Factors F1 F2 F3 F4 F5 F6 F7 F8 F9 F10 F11 F12 Weight
F1 1 0.170
F2 1/6 1 0.031
F3 1/7 1/2 1 0.020
F4 1/2 5 6 1 0.127
F5 1/3 4 5 1/2 1 0.092
F6 1/2 5 6 1 2 1 0.127
F7 1/5 2 3 1/4 1/3 1/4 1 0.046
F8 1/3 4 5 1/2 1 1/2 3 1 0.092
F9 1/8 1/3 1/2 1/7 1/6 1/7 1/4 1/6 1 0.012
F10 1/3 4 5 1/2 1 1/2 3 1 6 1 0.092
F11 1/2 5 6 1 2 1 4 2 7 2 1 0.127
F12 1/4 3 4 1/3 1/2 1/3 2 1/2 5 1/2 1/3 1 0.065
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated