Dynamic Spatial-Temporal Graph Neural Network for Cooling Capacity Prediction in HVDC Systems

1. Introduction

Predicting the cooling capacity of converter valves is a critical aspect of maintaining the stability and efficiency of high-voltage direct current (HVDC) transmission systems. As the cornerstone of modern energy grids, HVDC systems play a vital role in long-distance power transmission due to their high efficiency and low energy loss. Within these systems, the cooling system ensures the thermal stability of key power components, such as thyristors and IGBTs, by regulating their operating temperatures. This process is essential to prevent overheating, which can lead to equipment failure, reduced lifespan, and unplanned maintenance costs. Furthermore, the increasing adoption of renewable energy sources and the integration of HVDC grids with intermittent energy inputs place additional stress on cooling systems, making predictive maintenance and performance optimization more important than ever. However, accurate prediction of cooling capacity remains a challenging task due to the inherent complexity of these systems, which involve non-linear interactions among multiple variables, such as voltage, current, coolant flow rate, and ambient temperature.

In recent years, data-driven approaches have gained increasing attention for predictive maintenance and performance optimization in industrial systems [1,2]. Traditional machine learning models, such as support vector machines (SVM) [3] and gradient boosting machines (GBM) [4], have been widely used due to their ability to model static relationships in data. However, these methods often struggle to capture temporal dependencies and inter-variable relationships, which are crucial for dynamic environments like cooling systems. For instance, the cooling capacity at any given time is not only influenced by current system states but also by historical trends, requiring models that can effectively learn from time-series data. Moreover, traditional models rely on handcrafted features and domain expertise, which may limit their ability to generalize to diverse operational conditions.

Deep learning techniques, particularly recurrent neural networks (RNNs) [5] and convolutional neural networks (CNNs) [6], have emerged as powerful tools for handling time-series data. RNNs are well-suited for capturing temporal dependencies, while CNNs excel in extracting local patterns. However, both approaches primarily treat the input variables independently, limiting their ability to model complex interactions between variables. These limitations underscore the need for a unified framework that can jointly model spatial and temporal dependencies to accurately predict cooling capacity in HVDC systems. Furthermore, scaling such methods to industrial-scale systems introduces challenges related to computational efficiency and interpretability, both of which are essential for real-world deployment.

Graph Neural Networks (GNNs) have recently shown great potential in capturing the spatial relationships in structured data [7]. By representing data as graphs, GNNs encode relationships between variables as edges and attributes as node features, enabling the modeling of complex interdependencies. For instance, in a cooling system, variables such as voltage, current, and temperature can be treated as nodes, while their correlations form the edges. Temporal Graph Neural Networks (TGNNs), such as the Temporal Graph Convolutional Network (TGCN) [8], extend this framework by incorporating temporal dynamics, allowing the model to jointly learn spatial and temporal features. Additionally, these methods offer a natural way to handle non-Euclidean data structures, making them particularly suitable for systems with inherently graph-like properties. Furthermore, attention mechanisms [9] have been introduced in GNNs to dynamically adjust the importance of relationships, improving model interpretability and adaptability in varying conditions.

Despite their success in other domains, such as traffic flow prediction [10] and social network analysis [11], the application of GNN-based methods to industrial cooling systems remains underexplored. Existing methods either fail to capture the dynamic nature of inter-variable relationships or require extensive domain knowledge to construct the graph structure. This gap highlights the need for a method that dynamically learns these dependencies while maintaining scalability and robustness in industrial scenarios.

To address these challenges, we propose a novel framework that integrates Graph Neural Networks (GNN) with Temporal Dynamics for cooling capacity prediction in HVDC systems. The contributions of this work are threefold:

• We propose a hybrid framework that combines GNN with temporal modeling to simultaneously capture spatial and temporal dependencies in multi-dimensional time-series data.
• We introduce a graph attention mechanism that dynamically prioritizes feature relationships, enhancing the interpretability and adaptability of the model.
• We validate the proposed method on real-world cooling system data, demonstrating its superior performance compared to traditional machine learning and deep learning models.

2. Related Work

2.1. Cooling Capacity Prediction

Cooling capacity prediction plays a crucial role in ensuring the stability and efficiency of high-voltage direct current (HVDC) systems. Traditional approaches to predicting cooling performance often rely on physical models, which simulate the thermal behavior of components based on governing equations. While these models provide a theoretical basis for understanding cooling mechanisms, their accuracy heavily depends on precise parameter calibration, which is often challenging in real-world applications due to the complexity of operational environments.

To overcome these limitations, data-driven methods have been increasingly adopted. Machine learning algorithms, such as support vector machines (SVM), random forests, and gradient boosting methods, have shown promise in modeling cooling performance based on historical data. However, these methods primarily capture static relationships within the data and fail to account for temporal dependencies critical to dynamic systems. Recent advancements in deep learning, particularly recurrent neural networks (RNNs) and convolutional neural networks (CNNs), have demonstrated superior performance in time-series prediction tasks. Nevertheless, these models often overlook inter-variable relationships, which are crucial in multi-dimensional systems like cooling networks.

2.2. Graph Neural Networks for Structured Data

Graph Neural Networks (GNNs) have emerged as a powerful tool for analyzing structured data by leveraging the inherent graph structure of relationships among entities. GNNs generalize traditional neural networks to graph domains by incorporating node and edge information, enabling effective modeling of spatial dependencies. Recent variants, such as Graph Convolutional Networks (GCNs), Graph Attention Networks (GATs), and Temporal Graph Networks, have expanded GNNs’ applicability to various domains, including traffic forecasting, recommendation systems, and industrial process monitoring.

In cooling systems, variables such as voltage, current, and ambient temperature naturally form a graph, where nodes represent individual variables and edges capture their dependencies. GNNs are particularly well-suited for modeling such systems, as they can capture both local and global dependencies among variables. However, most existing GNN-based approaches focus on static graphs and do not account for temporal dynamics, which are essential for time-series prediction tasks.

2.3. Temporal Graph Modeling

Temporal Graph Neural Networks (TGNNs) extend traditional GNNs by integrating temporal dynamics into the graph structure. For instance, Temporal Graph Convolutional Networks (TGCNs) combine graph convolution operations with recurrent layers (e.g., LSTM or GRU) to capture spatial and temporal dependencies simultaneously. Similarly, attention-based mechanisms, such as those employed in Graph Attention Networks (GATs), enhance TGNNs by dynamically weighting the importance of edges and nodes, making them highly interpretable.

Despite their success in other domains, the application of TGNNs to cooling capacity prediction remains underexplored. Most existing studies focus on specific domains, such as traffic flow forecasting and social network analysis, and their methodologies are not directly transferable to industrial cooling systems. Furthermore, these approaches often assume a fixed graph structure and fail to account for dynamic changes in relationships among variables.

2.4. Summary and Research Gap

Existing studies in cooling capacity prediction and temporal graph modeling highlight the following gaps:

• Limited Temporal-Spatial Integration: Traditional methods fail to simultaneously capture temporal dependencies and spatial relationships among variables.
• Lack of Dynamic Relationship Modeling: Most graph-based approaches assume a fixed graph structure, overlooking the dynamic nature of variable interactions in real-world cooling systems.
• Insufficient Interpretability: Many existing methods lack mechanisms to explain the importance of relationships or variables in the prediction process.

To address these limitations, this paper proposes a hybrid framework that combines GNN with temporal modeling and incorporates a graph attention mechanism. This approach enables the simultaneous modeling of temporal and spatial dependencies while dynamically adjusting relationship weights, improving both prediction accuracy and model interpretability.

3. Proposed Framework

To predict the cooling capacity of converter valves, we propose a framework that integrates Graph Neural Networks (GNN) with Temporal Dynamics. This hybrid approach captures both spatial dependencies among variables (e.g., voltage, current, temperature) and their temporal evolutions over time. By leveraging the graph structure to encode relationships and temporal modeling for sequential patterns, our method provides accurate and robust predictions. The proposed framework is designed to handle the complex, dynamic, and multi-dimensional nature of cooling systems, offering both high precision and scalability.

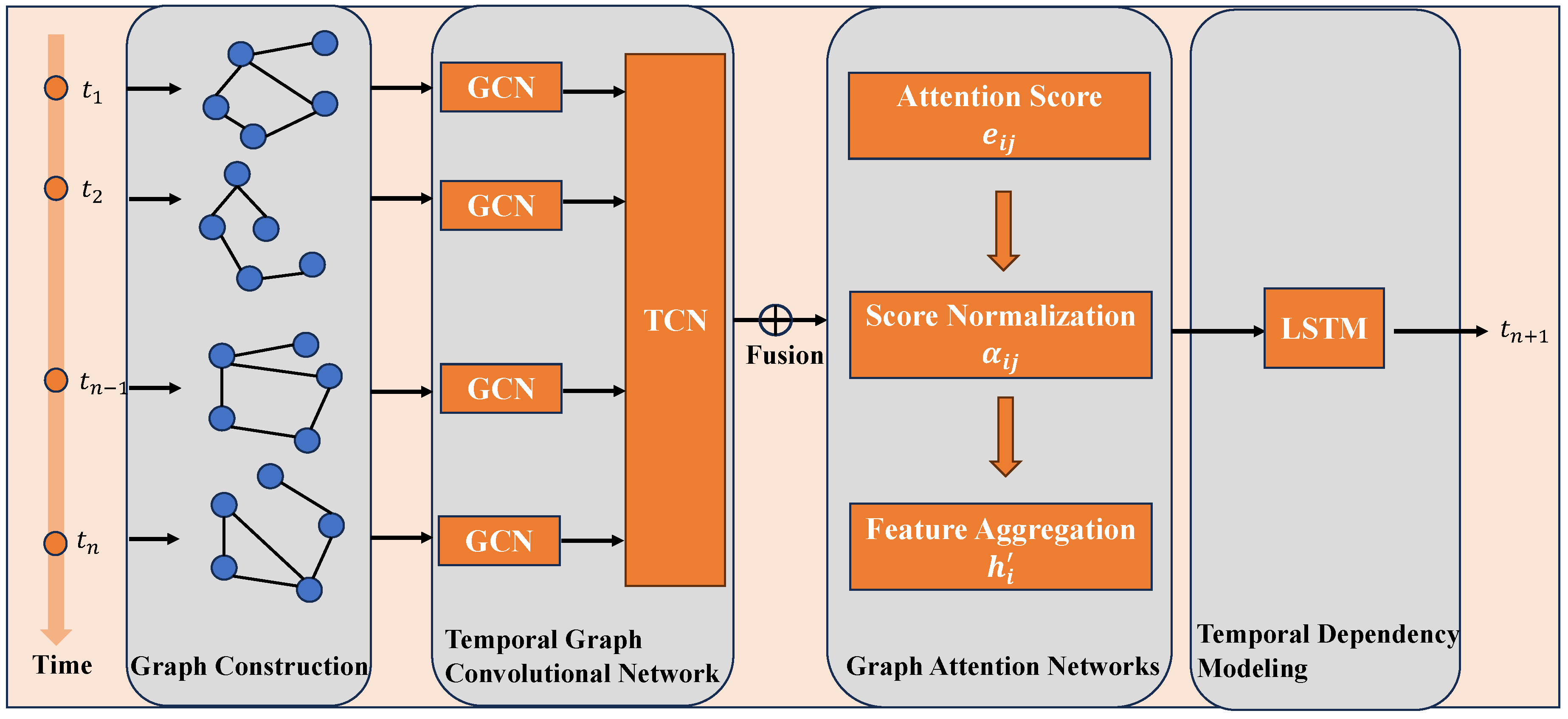
The framework is composed of four key components, each designed to address specific challenges:

• Graph Construction: Encodes relationships among features into a graph structure, allowing spatial dependencies to be explicitly modeled.
• Temporal Graph Convolutional Network (TGCN): Integrates graph convolution and temporal convolution to jointly capture spatial and temporal dependencies.
• Graph Attention Mechanism (GAT): Dynamically adjusts the importance of relationships between variables, enhancing model interpretability and predictive performance.
• Temporal Dependency Modeling: Utilizes recurrent layers (e.g., LSTM or GRU) to capture long-term dependencies across time steps.

Figure 1. The proposed framework for cooling capacity prediction. The framework consists of four main components: Graph Construction, Temporal Graph Convolutional Network (TGCN), Graph Attention Mechanism (GAT), and Temporal Dependency Modeling. Input data (e.g., voltage, current, temperature) is first transformed into a graph structure, where nodes represent variables and edges encode relationships. The TGCN combines graph convolution and temporal convolution to extract spatial-temporal features, which are refined by the GAT for dynamic edge weighting. Finally, the temporal dependencies are captured using LSTM to predict the cooling capacity.

Figure 1. The proposed framework for cooling capacity prediction. The framework consists of four main components: Graph Construction, Temporal Graph Convolutional Network (TGCN), Graph Attention Mechanism (GAT), and Temporal Dependency Modeling. Input data (e.g., voltage, current, temperature) is first transformed into a graph structure, where nodes represent variables and edges encode relationships. The TGCN combines graph convolution and temporal convolution to extract spatial-temporal features, which are refined by the GAT for dynamic edge weighting. Finally, the temporal dependencies are captured using LSTM to predict the cooling capacity.

3.1. Graph Construction

Cooling systems involve multiple interdependent variables such as voltage, current, coolant flow rate, and ambient temperature. To explicitly model the relationships between these variables, we construct a graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, where:

• Nodes ($\mathcal{V}$): Each node represents a variable in the dataset.
• Edges ($\mathcal{E}$): Each edge represents a relationship between two variables. For example, the correlation between voltage and current might be strong, while the correlation between ambient temperature and coolant flow rate might be weaker.

To quantify these relationships, the adjacency matrix $\mathbf{A}$ is computed using Pearson correlation:

$${\mathbf{A}}_{ij}={\displaystyle \frac{\mathrm{Cov}({\mathbf{x}}_i,{\mathbf{x}}_j)}{{\sigma }_i·{\sigma }_j}},$$

where $\mathrm{Cov}({\mathbf{x}}_i,{\mathbf{x}}_j)$ is the covariance between variables ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$, and ${\sigma }_i$ and ${\sigma }_j$ are their standard deviations. This ensures that ${\mathbf{A}}_{ij}$ captures the strength and direction of the linear relationship between variables.

To enhance numerical stability and improve the effectiveness of graph convolution, the adjacency matrix is normalized [12]:

$$\widehat{\mathbf{A}}={\mathbf{D}}^{-1/2}\mathbf{A}{\mathbf{D}}^{-1/2},$$

where $\mathbf{D}$ is the degree matrix of $\mathbf{A}$. This normalization ensures that the impact of highly connected nodes is balanced during graph convolution.

3.2. Temporal Graph Convolutional Network (TGCN)

The Temporal Graph Convolutional Network (TGCN) is the core component of our framework, combining spatial and temporal modeling into a unified structure:

• Graph Convolution: Captures spatial dependencies by propagating information across the graph. Each graph convolutional layer updates the representation of each node by aggregating features from its neighbors:

  $${\mathbf{H}}^{(l+1)}=\sigma \left(\widehat{\mathbf{A}}·{\mathbf{H}}^{\left(l\right)}·{\mathbf{W}}^{\left(l\right)}\right),$$

  where ${\mathbf{H}}^{\left(l\right)}$ is the node embedding matrix at layer l, ${\mathbf{W}}^{\left(l\right)}$ is a learnable weight matrix, and $\sigma$ is an activation function such as ReLU [13]. This operation ensures that each node’s representation reflects information from its neighbors, enabling the model to capture local spatial patterns.
• Temporal Convolution: Extracts short-term temporal features by applying 1D convolution along the time dimension:

  $${\mathbf{H}}_t^{(l+1)}=\mathrm{Conv}1\mathrm{D}\left({\mathbf{H}}_t^{\left(l\right)}\right),$$

  where ${\mathbf{H}}_t^{\left(l\right)}$ represents temporal features at time step t for layer l. The convolution kernel size is chosen to balance between capturing immediate temporal dependencies and maintaining computational efficiency.

By alternating graph and temporal convolutions, the TGCN effectively integrates spatial and temporal features, enabling robust predictions even in highly dynamic environments.

3.3. Graph Attention Mechanism (GAT)

The Graph Attention Mechanism (GAT) [14] is introduced to dynamically prioritize important relationships, allowing the model to focus on the most relevant connections:

• Attention Score Calculation: For each pair of connected nodes, the attention score is computed as:

  $$e_{ij}=\mathrm{LeakyReLU}\left({\mathbf{a}}^T·\left[{\mathbf{W}}_h{\mathbf{h}}_i\parallel {\mathbf{W}}_h{\mathbf{h}}_j\right]\right),$$

  where ${\mathbf{h}}_i$ and ${\mathbf{h}}_j$ are node embeddings, ${\mathbf{W}}_h$ is a learnable weight matrix, and $\mathbf{a}$ is the attention vector.
• Score Normalization: The attention scores are normalized using softmax:

  $${\alpha }_{ij}={\displaystyle \frac{exp\left(e_{ij}\right)}{{\sum }_{k\in \mathcal{N}\left(i\right)}exp\left(e_{ik}\right)}}.$$
  This ensures that the sum of attention weights for each node is 1, improving stability.
• Feature Aggregation: The updated embedding for each node is computed as a weighted sum of its neighbors’ features:

  $${\mathbf{h}}_i^{\prime }=\sigma \left(\sum _{j\in \mathcal{N}\left(i\right)}{\alpha }_{ij}·{\mathbf{W}}_h·{\mathbf{h}}_j\right).$$

The GAT improves the interpretability of the model by highlighting the most influential relationships.

3.4. Temporal Dependency Modeling

To capture long-term temporal dependencies, we use recurrent layers such as LSTM [15]. The LSTM processes the temporal embeddings generated by the TGCN, producing a final temporal representation:

$${\mathbf{h}}_t=\mathrm{LSTM}\left({\mathbf{H}}_t\right),$$

where ${\mathbf{H}}_t$ represents the temporal embeddings at time step t. The LSTM’s ability to maintain a memory of previous time steps ensures that the model can capture sequential patterns over long durations.

3.5. Optimization

The model is trained using the Mean Squared Error (MSE) loss function, defined as:

$$\mathcal{L}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{({\widehat{y}}_i-y_i)}^2,$$

where ${\widehat{y}}_i$ and $y_i$ are the predicted and true cooling capacities, respectively. The Adam optimizer [16] is employed to minimize the loss, with dropout and weight decay applied to prevent overfitting. The detailed steps of the training process are summarized in Algorithm 1.

Algorithm 1 Graph Neural Networks with Temporal Dynamics

Input: Time-series data $\mathbf{X}\in {\mathbb{R}}^{T\times N}$, adjacency matrix $\mathbf{A}$, window size T. 1: Normalize adjacency matrix $\widehat{\mathbf{A}}$. 2: Extract spatial features using $\mathbf{A}$ and $\mathbf{H}$. 3: Extract temporal features from ${\mathbf{H}}_t$. 4: Compute attention scores $e_{ij}$ and normalized weights ${\alpha }_{ij}$. 5: Aggregate features into ${\mathbf{h}}_i^{\prime }$. 6: Model temporal dependencies with LSTM to obtain ${\mathbf{h}}_t$. 7: Predict ${\widehat{y}}_{t+1}$ using fully connected layers. 8: Minimize the loss $\mathcal{L}$ to optimize model parameters. Output: Predicted cooling capacity ${\widehat{y}}_{t+1}$.

4. Experiments

This section evaluates the performance of the proposed method in predicting the cooling capacity of converter valves. The experiments were conducted on a real-world dataset collected from HVDC systems, focusing on the effectiveness, accuracy, and interpretability of the proposed model. Additionally, we compare the performance of the proposed framework with several baseline methods and analyze its scalability.

4.1. Dataset and Experimental Setup

4.1.1. Dataset Description

To evaluate the performance of the proposed framework, we used a dataset collected from an industrial High-Voltage Direct Current (HVDC) cooling system over six months. The data consists of multi-dimensional time-series variables sampled every 10 minutes. Key variables include:

• Voltage (V): Describes the input voltage of the system, ranging from 450V to 550V.
• Current (A): Represents the system load current, with values between 250A and 350A.
• Coolant Flow Rate (L/s): Measures the flow rate of the coolant, ranging from 2.0L/s to 3.0L/s.
• Ambient Temperature (°C): Reflects the external environmental influence on cooling efficiency, with values between 20°C and 35°C.
• Cooling Capacity (kW): The target variable, indicating the cooling power per unit time, ranging from 100kW to 150kW.

To enhance model performance, the following preprocessing steps were applied to the raw dataset:

• Timestamp Alignment: Missing data were imputed using interpolation to ensure a complete time-series.
• Noise Removal: High-frequency noise was filtered using wavelet transformation.
• Normalization: All input variables were normalized to the range $[0,1]$ to eliminate dimensional effects.
• Sliding Window Construction: A sliding window of size 24 (corresponding to 4 hours) was used to transform the time-series into input samples. Each sample contains 24 historical time steps as input and the next time step as the output cooling capacity.

To further validate the robustness of the proposed framework, synthetic data were generated to simulate system behavior under diverse conditions:

• High-Load Scenario: Increased current values to 400A to simulate extreme operating conditions.
• Low-Temperature Environment: Reduced ambient temperature to 10°C to examine the cooling system under cold environments.
• Non-Periodic Disturbances: Introduced random disturbances at specific time intervals to test model stability.

To ensure fair evaluation, the dataset was divided into training (70%), validation (15%), and testing (15%) subsets. A sliding window approach was adopted for sample generation, with the past 24 time steps used to predict the next cooling capacity value [15].

4.1.2. Experimental Setup

The following baseline models were selected for comparison:

• Support Vector Machine (SVM): A traditional machine learning model for static prediction tasks [17].
• Gradient Boosting Machine (GBM): A boosting-based ensemble learning model [18].
• Long Short-Term Memory (LSTM): A deep learning model designed for sequential data [15].
• Graph Convolutional Network (GCN): A graph-based model for spatial dependency modeling [19].
• Temporal Graph Convolutional Network (TGCN): A hybrid model combining GCN and RNN for spatial-temporal modeling [20].

All models were implemented in Python using PyTorch. The experiments were conducted on an NVIDIA Tesla V100 GPU with 32 GB of memory. The Adam optimizer was used with a learning rate of 0.001, and all models were trained for 100 epochs with a batch size of 64.

4.2. Evaluation Metrics

The performance of the models was evaluated using the following metrics:

• Mean Squared Error (MSE): Measures the average squared difference between predicted and actual values.
• Root Mean Squared Error (RMSE): A square root of MSE, representing the standard deviation of prediction errors.
• Coefficient of Determination ($R^2$): Indicates the proportion of variance explained by the model [21].

4.3. Results and Analysis

4.3.1. Overall Performance

Table 1 presents the performance comparison of the proposed method and baseline models on the test dataset.

The proposed method achieves the lowest MSE and RMSE and the highest $R^2$, outperforming all baseline models. This demonstrates its ability to capture both spatial and temporal dependencies effectively.

4.3.2. In-Depth Analysis of Prediction Performance

To comprehensively evaluate the proposed method, we conducted experiments on prediction accuracy, prediction time, and prediction efficiency. These metrics provide a holistic understanding of the model’s performance in terms of precision, computational cost, and practical applicability. The general prediction method in this study is represented by the best-performing baseline, Graph Convolutional Network (GCN).

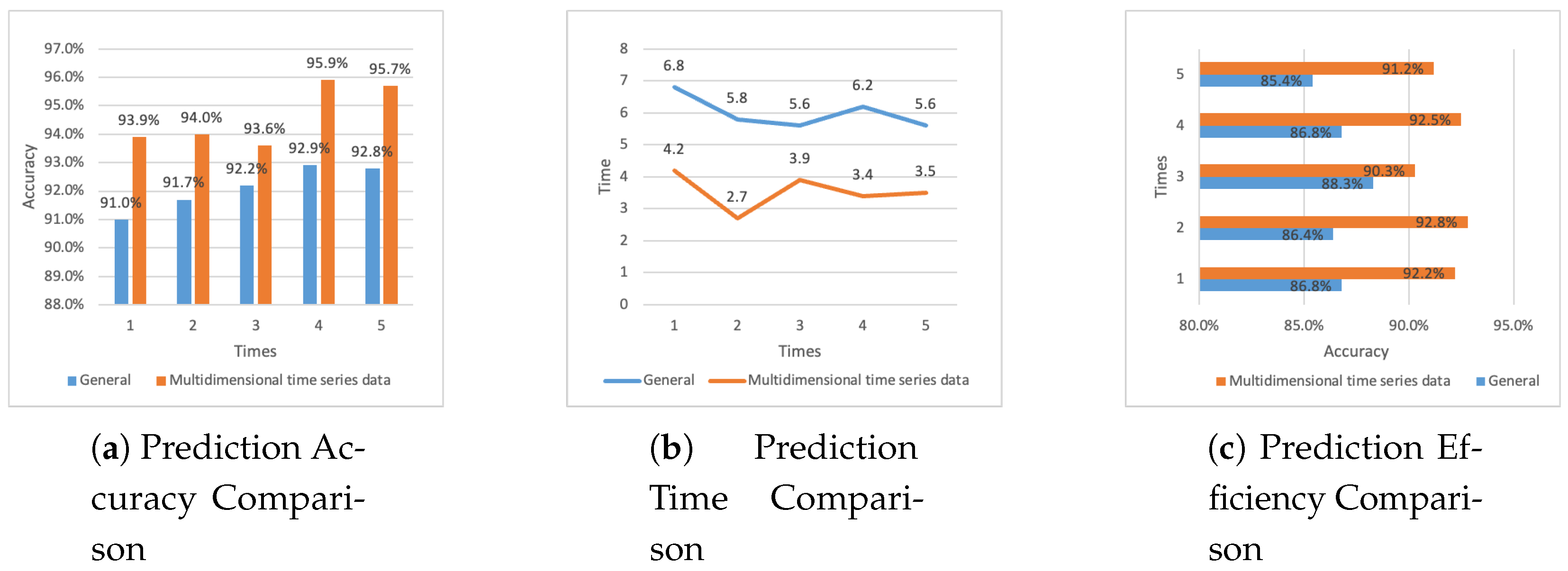
Prediction Accuracy. The prediction accuracy results are shown in Figure 2(a). The proposed method, based on multidimensional time-series data, achieves a significantly higher accuracy compared to the general GCN-based method. Specifically:

• The accuracy of the general method ranges from 91.0% to 92.9%, with an average accuracy of 92.12%.
• The accuracy of the proposed method ranges from 93.6% to 95.9%, with an average accuracy of 94.62%.

These results indicate that the proposed method outperforms the general method in accuracy, demonstrating its ability to better capture the spatial-temporal dependencies in cooling capacity prediction.

Prediction Time. The prediction time results are presented in Figure 2(b). The proposed method demonstrates superior computational efficiency compared to the general GCN-based method. Key observations include:

• The general method requires 5.6 to 6.8 seconds for prediction, with an average time of 6 seconds.
• The proposed method reduces the prediction time to a range of 2.7 to 4.2 seconds, with an average time of 3.54 seconds.

This reduction in prediction time highlights the computational efficiency of the proposed method, making it more suitable for real-time industrial applications.

Prediction Efficiency. The prediction efficiency, defined as the ratio of successful accurate predictions within a fixed time frame, is depicted in Figure 2(c). The proposed method significantly improves prediction efficiency compared to the general GCN-based method. The results show:

• The prediction efficiency of the general method ranges from 85.4% to 88.3%, with an average efficiency of 86.74%.
• The prediction efficiency of the proposed method ranges from 90.3% to 92.8%, with an average efficiency of 91.80%.

The higher prediction efficiency achieved by the proposed method further validates its practical value in industrial settings where timely and accurate predictions are crucial.

5. Discussion

The experimental results demonstrate the effectiveness of the proposed method in accurately predicting the cooling capacity of converter valves. Compared to traditional machine learning models (e.g., SVM, GBM) and deep learning models (e.g., LSTM, GCN), our approach achieves superior performance by leveraging both spatial and temporal dependencies in the data. Specifically, the integration of a graph attention mechanism allows the model to dynamically prioritize relationships between variables, thereby improving prediction accuracy and interpretability.

5.1. Advantages of the Proposed Method

The success of the proposed method can be attributed to its unique combination of spatial and temporal modeling. Unlike conventional methods that treat variables independently, the proposed model uses a graph structure to capture their interdependencies, which are critical in complex cooling systems. Additionally, the temporal modeling component enables the model to learn both short-term variations and long-term trends, further enhancing its predictive capabilities. The ablation study confirms the contributions of individual components, highlighting the importance of the graph attention mechanism and temporal modeling.

5.2. Limitations and Future Work

Despite its advantages, the proposed method has certain limitations:

• Dependence on Graph Structure: The performance of the model relies on the accuracy of the initial graph structure, which is currently constructed based on predefined rules (e.g., correlation coefficients). In scenarios where relationships among variables are complex or non-linear, the predefined graph may not fully capture their dependencies.
• Scalability: While the model demonstrates excellent performance on medium-sized datasets, its computational complexity increases with the number of variables and the length of time-series data. This may pose challenges when scaling to very large datasets or real-time applications.
• Data Availability: The proposed method requires a sufficient amount of high-quality labeled data for training. In industrial settings, such data may not always be available due to sensor limitations or data privacy concerns.

To address these limitations, future research will focus on dynamically learning the graph structure from data using techniques such as neural architecture search or attention-based graph learning. Additionally, we plan to explore more efficient architectures to improve scalability and extend the model’s applicability to other domains with similar challenges.

6. Conclusion

In this paper, we proposed a novel method that integrates Graph Neural Networks (GNN) with Temporal Dynamics for predicting the cooling capacity of converter valves. The method effectively captures both spatial dependencies among variables and temporal dependencies over time, addressing the challenges posed by multi-dimensional time-series data. By incorporating a graph attention mechanism, the proposed method dynamically adjusts the importance of relationships, enhancing both interpretability and performance.

The experimental results demonstrate that the proposed method outperforms traditional machine learning and deep learning baselines, achieving the lowest MSE and RMSE scores while maintaining high interpretability. The ablation study further validates the significance of the graph attention mechanism and temporal modeling components.

This work contributes to the growing body of research on graph-based temporal modeling and provides a practical solution for industrial applications, such as cooling system monitoring and fault prediction. In future work, we aim to explore dynamic graph learning techniques and optimize the model for real-time deployment.