Description of the Lubricant Behavior Based on the Theory of Viscoelastoplasticity

1. Introduction

1.1. Research Objectives

The research objective: to describe the lubricants viscoelastoplastic behavior based on the Anand model by means of multi-parameter optimization using a numerical procedure for identifying material constants based on experimental data.

Research tasks:

1. Conduct an experiments series to determine the thermophysical properties for greases over a range of operating temperatures (from -40 to +80 degrees Celsius) and exposure frequencies (0.01 to 100 Hz).

2. Describe the viscoelastoplastic behavior of grease using the extended Anand model. Formulate hypotheses about the temperature dependence of the parameters.

3. Extend the functional of numerical procedures to identify the mathematical model [1].

4. To find the parameters allowing to obtain the minimum error between experimental and numerical data (not more than 5 %).

1.2. Problem Context

The effective transport links, the connectivity of territories within the country and with neighboring countries, the creation of modern functional transport systems are priority areas for the development of countries around the world [2,3]. The research relevance in this industry is associated with its significant influence on the country economic development [3]. Research is being conducted in different directions [4,5]: ensuring safety, increasing the load capacity, increasing the elements lifespan, etc. Measures set for monitoring and predicting the behavior of critical components, their elements and the materials from which they are made is actively developing [6,7,8,9]. This research area is mainly related to the creation of numerical analogs of structures and mathematical descriptions of the behavior: metallic and non-metallic materials; objects under study [4].

The bridges bearings are critical elements of transport systems [10,11]. They perceive load complexes from the bridge span and external climatic and man-made influences. In addition, allow the bridge to effectively perform its assigned functions. A number of research areas related to increasing durability, reliability, strength and wear resistance of bearing elements exists: influence analysis of the geometric configuration on the stress-strain state of design [12], influence analysis of material element on the unit performance [13], etc. Spherical bearings are widely used [4,10]. The design consists of a spherical steel balancer and a lower steel plate, which interact through a polymer sliding layer with technological hollows filled with grease (Figure 1).

One variant for the hollow geometric configuration of bearing with annular grooves filled with lubricant is presented in Figure 1.

The bearings are designed for long periods of operation under constantly changing cyclical and dynamic loads [14,15]. The effective operation of the structure largely depends on materials of the sliding layer (polymer or composite) and grease [16,17,18]. The environment has a negative impact on the structure operation, in particular temperature conditions and their changes [19,20,21]. The construction of effective numerical analogues is required to predict the bearing operation and monitor its condition. The necessity arises for a mathematical description of the material behavior of the sliding layer (antifrictional materials and lubricants) taking into account the temperature and strain rate. Viscoelasticity theories and viscoelastoplasticity theory can be applied to describe the materials behavior.

1.3. Problem Description

This study is aimed at greases nonlinear behavior describing, which are widely used in the bridge industry, including in the production of bearing sliding layers [22,23]. Lubricants are used in other industries: mechanical engineering [24,25,26], aerospace [27,28], biomedicine [29], etc. It can significantly increase the durability of the structure by functions number performing: maintaining the required temperature in the construction, reducing frictional effects, damping the interaction between mating surfaces, etc. Researchers are considering the tasks of changing the geometric configuration of the structure to provide lubrication of the required contact areas, improving its functionality by adding various additives and elements. For example, rationalization of the bearing geometric configuration to effectively improve the structure performance was performed in [30]. The research focuses on preventing the risk of metal-to-metal contact by ensuring stable lubrication of the contact surfaces. The similar study was conducted by our group previously and aimed at increasing the amount of grease by changing the sliding layer geometry [22]. In [31] it was show that the effect of different graphene-based additives on lubricants. The increase in mechanical efficiency is highly dependent on the addition of graphene to the base. There is quite a research related large volume to changes in the lubricant composition. One of the options for lubricant modifying to improve performance characteristics is the introduction of polymer materials into the composition.

Lubricants are divided into: liquid [32], solid [33], paste-like (grease) [34], etc. Liquid lubricants are often used in engines, transmissions, metalworking, hydraulic systems and other mechanisms [25,35]. Solid lubricants [36,37] contain solid particles, for example, graphite, due to which it can be used in highly loaded mechanisms: bearings, gears, etc. Greases are widespread in the bridges bearing.

Three directions of research related to lubricants exist at present:

1. Study of tribological, thermophysical, electromechanical and other lubricants properties.

2. Experimental study of the lubricants behavior under thermal and force influence.

3. Mathematical description of lubricant behavior for possible use in computer aided design (CAD) systems.

This study engages all three of the outlined research areas.

The creation of numerical analogs of structures based on data on the behavior of materials is also relevant [40,41]. CAD active development makes it possible to create design numerical analogues that differ slightly from the real object [42,43]: ANSYS Mechanical APDL (ANSYS Inc., Canonsburg, PA, USA); ABAQUS (ABAQUS Inc., Velizy-Villacoublay, France), etc. [44] notes the importance of creating numerical analogs of designs for the development of society as a whole the transition to Industry 4.0.

A thorough approach to the description of materials mathematical models is necessary to minimize the error between the real design and the numerical analogue. This is the reason for a series of problems related to the selection of an adequate model of material behavior [45,46] and the search for the necessary system parameters to implement the tasks in modern CAD.

In [46] presents a description of the materials work like Maxwell solid using two mathematical models (Prony series and simplified Anand model). This work was carried out earlier by our research group.

The article found that:

- the mathematical model describes quite accurately the behavior of materials under temperature changes and at frequency from 1 Hz to 100 Hz;

- there is an increase in the error relative to experimental data at frequencies from 0.01 to 1 Hz.

This effect may be associated with the choice of a fairly simple mathematical model to describe the greases behavior. For this reason, a decision was made to consider the possibility of describing the lubricants behavior in a wide range of operating temperatures and deformation rates using more complex mathematical models, such as the Anand model.

The article presents a study related to the description of the lubricant behavior model within the framework of the viscoelastoplasticity theory. Modification of the Annad model taking into account the dependence of a material constants number on temperature is implemented. Descriptions of the material behavior model are based on experimental data obtained over a wide range of temperatures (from -40 to +80 degrees Celsius) and strain rates (from 0.01 to 100 Hz). A number of greases developed by the Central Institute of Aviation Fuels and Oils (CIATIM, Russian Federation) were selected as study objects: CIATIM-221 and CIATIM-221F. Petroleum oil with the addition of paraffin or ceresin is the grease basis. CIATIM-221F is different from CIATIM-221by the presence of PTFE in the grease. The analysis of the influence of the PTFE inclusion in the grease on the material properties is also reflected in the work.

2. Materials and Methods

2.1. Experimental study

Dynamic modal analysis (DMA) is widely used as one of the methods for experimental determination of thermophysical characteristics. The paper performed an experimental study on a Discovery Hybrid Rheology 2 (DHR 2) rotosimeter, which allows the determination of rheological characteristics of materials for a wide range of temperatures [46].

The torque $M$ and the displacement angle $\phi$ are the output data of the DHR 2. The values of true stresses (1) and true strains (2) are calculated using the following formulas:

$$\mathsf{\tau }=K_{\mathsf{\tau }}\cdot M,$$

(1)

$$\mathsf{\gamma }=K_{\mathsf{\gamma }}\cdot \mathsf{\phi },$$

(2)

where $K_{\mathsf{\tau }}$ and $K_{\mathsf{\gamma }}$ are stress and strain constants respectively depending on the mating surfaces geometry, $\mathsf{\tau }$ is tangential stress, $\mathsf{\gamma }$ is shear strain.

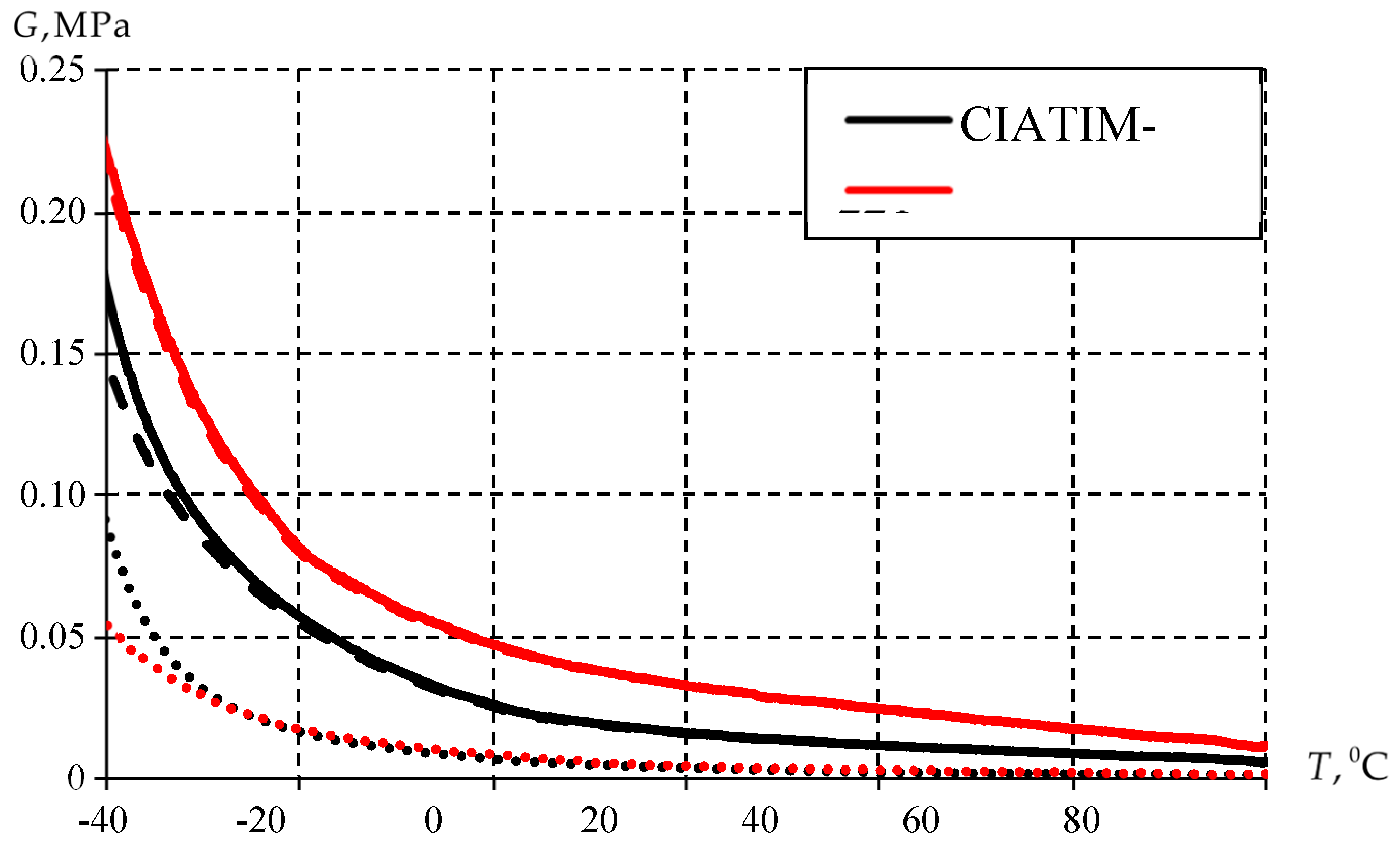
The previously tested procedure [46] will be applied for the determination of viscoelasticity parameters. The first step is to determine the possibility of its use. The following conditions have to be met for the material: it has a constant aggregate state over the entire range of temperatures considered (from -40 to +80 degrees Celsius); it is elastic or gel. For this purpose, the article analyzed the aggregate state of the material by the dependence of the complex shear modulus $G^{*}$, storage modulus $G\text{'}$ and loss modulus $G\text{'}\text{'}$ on temperature (Figure 2).

A material is elastic or gel if over the entire temperature range the loss modulus is lower than the storage modulus [47,48]. This distribution of experimental data is observed in Figure 2. Consequently, the application of the procedure for the calculation of viscoelastic parameters is reasonable.

2.2. Mathematical Model

Previously, the simplified Anand model was used to describe the viscoelastic behavior of grease [46]. However, the paper notes that such a description is only suitable for frequencies greater than 1 Hz. Significant error is observed at small frequencies (0 Hz to 1 Hz). Therefore, this paper considers the full Anand model to describe the behavior of grease.

The basic equation has the form:

$${\stackrel{.}{\mathsf{\gamma }}}_v=A{e}^{-U/RT}{\left[\sinh \left(\mathsf{\xi }\mathsf{\tau }/S\right)\right]}^{1/m},$$

(3)

It is includes an evolutionary equation:

$$\dot{S}=\left\{h_0{\left(\left|B\right|\right)}^{a}B/\left|B\right|\right\}{\stackrel{.}{\mathsf{\gamma }}}_v,$$

(4)

where $B=1-S/S^{*}$; $S^{*}=S_1{\left[{\stackrel{.}{\mathsf{\gamma }}}_v{e}^{U/RT}/A\right]}^n$, $A$is pre-exponential factor, $\mathsf{\xi }$ is dimensionless scalar constant, $m$ is strain rate sensitivity of stress, $\tau$ is tangential stress, $S$ is deformation resistance, $S_0$ is initial deformation resistance; $S^{*}$ is saturation value of the hardening function, $h_0$ is hardening/softening constant, $R$ is universal constant gas, $U$ is activation energy, $T$ is absolute temperature, $n$ is sample saturation as a function of shear rate, $a$ is strain rate sensitivity of hardening/softening. The majority of modern engineering packages (for FEM analysis) require a vector of constants to be specified to describe the material behavior by the Anand model:

$$\overline{x}=\left\{S_0;A;U/R;\xi ;m;h_0;S_1;n;a\right\},$$

(5)

According to authors [49, 50] and experimental data, a hypothesis of dependence of initial strain resistance, and strain-rate-sensitivity of the material on temperature is possible. Here let present these parameters in the form of (6) and (7), respectively, to confirm this hypothesis:

$$S_0\left(T\right)=C_1\left(1+C_2{\mathrm{e}}^{C_3/T}\right)\left(1+C_4{\mathrm{e}}^{C_5/T}\right),$$

(6)

$$m\left(T\right)=C_6\left(1+C_7{\mathrm{e}}^{C_8/T}\right)\left(1+C_9{\mathrm{e}}^{C_{10}/T}\right),$$

(7)

where $C_1-C_5$, $C_6-C_{10}$ are coefficients for describing the behavior of the initial strain resistance and strain-rate-sensitivity depending on the temperature respectively. The vector of unknowns is formed by substituting equations (6)-(7) into the vector of coefficients (5) $\overline{x}=\left\{A;U/R;h_0;S_1;n;a;C_i,i=\overline{1,10}\right\}$.

2.3. Anand Model Identification Procedure

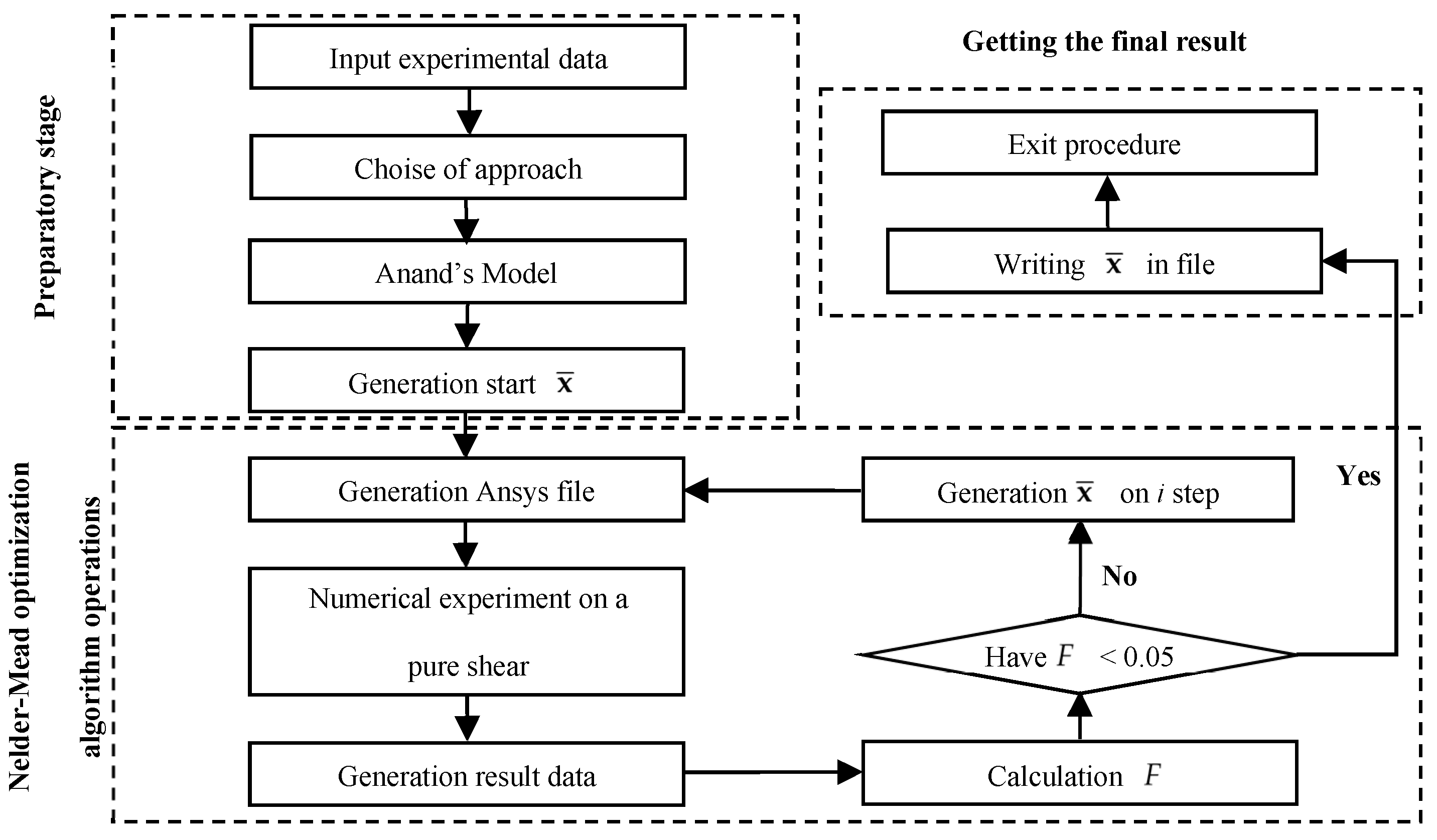
Figure 3 illustrates the numerical procedure for identifying the mathematical model of grease behavior. The algorithm is implemented by Python and ANSYS Mechanical APDL.

The numerical procedure consists of several steps:

1) Experimental data are loaded. The type of mathematical model is selected. The initial vector of unknowns is formed. Subsection 2.2 describes the mathematical equations of the algorithm detailed.

2) A numerical experiment is realized.

Two variants of numerical simulations of the shear stress were implemented. (Figure 4):

- the changes in the frequency from 0.01 to 100 Hz at constant temperatures;

- the temperature change from -40 to +80 ⁰С in a step of 2 degrees per minute, with a constant frequency (1 Hz).

The search for the unknown coefficients $\overline{x}$ occurs as step-by-step procedure. The residual function has the form (9). The procedure is stopped when the residual is less than 1 %:

$$F=\left({\overline{\tau }}^{\exp }-{\overline{\tau }}^{\mathrm{num}}\left(\overline{x}\right)\right)/{\overline{\tau }}^{\exp }\to \min ,$$

(9)

Nelder-Mead multi-parameter optimization is selected for the task implementation.

3) The work of the numerical procedure is completed. The file with the found parameters of the vector of unknowns is formed.

The presented approach can be applied to a wide range of materials. Previously, the applicability of the first algorithm version was evaluated to describe the polymer behavior [51].

3. Results

3.1. Results of the Experimental Study

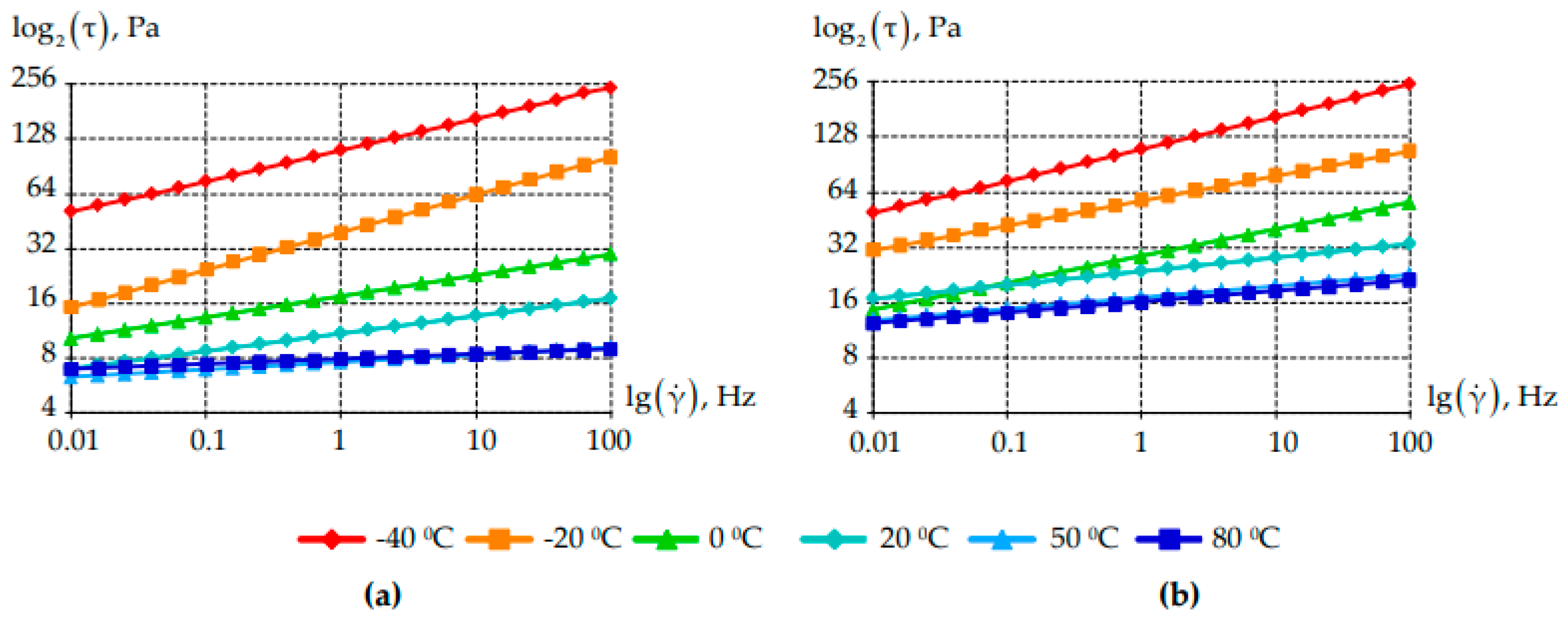
The first stage of the study is to analyze the dependence of the grease stress state on frequency stimulation. For this purpose, a frequency in the range from 0.01 to 100 Hz was applied to the samples. Figure 5 is shows the dependence of tangential stresses on frequency at different temperatures.

The pattern of the dependence of tangential stresses on frequency is linear. For all the lubricants considered, tangential stresses increase with increasing frequency. It can be noted that the introduction of PTFE into the lubricant composition affects tangential stresses at temperatures −20 °C and above.

The second stage consists in studying the dependence of material properties on temperature. The sample is cooled from +80 to -40 °C in steps of 2 degrees per minute while being subjected to cyclic deformation with a frequency of 1 Hz. The results are presented in Figure 6.

The physical and mechanical properties of the grease improved with the introduction of PTFE into its composition. It is observed that it is necessary to increase the torque value with decreasing temperature to keep the magnitude of sample deformation at the same level (0.1%).

3.2. Results of the Anand Mathematical Model Identification

Identification of equations (3-4), (6-7) parameters was performed within the developed numerical procedure. The initial vector of unknowns is the same for both greases. The initial and final values of the unknowns independent of temperature are presented in Table 1.

Sample saturation as a function of shear rate and strain-rate-sensitivity differ by no more than 6% for each material. Significant differences are observed in the pre-exponential factor $A$ (about 65 %). The material hardening/softening constant $h_0$ has maximum differences, namely: $h_0$ of Ciatim-221F is approximately 5.5 times greater than at Ciatim-221.

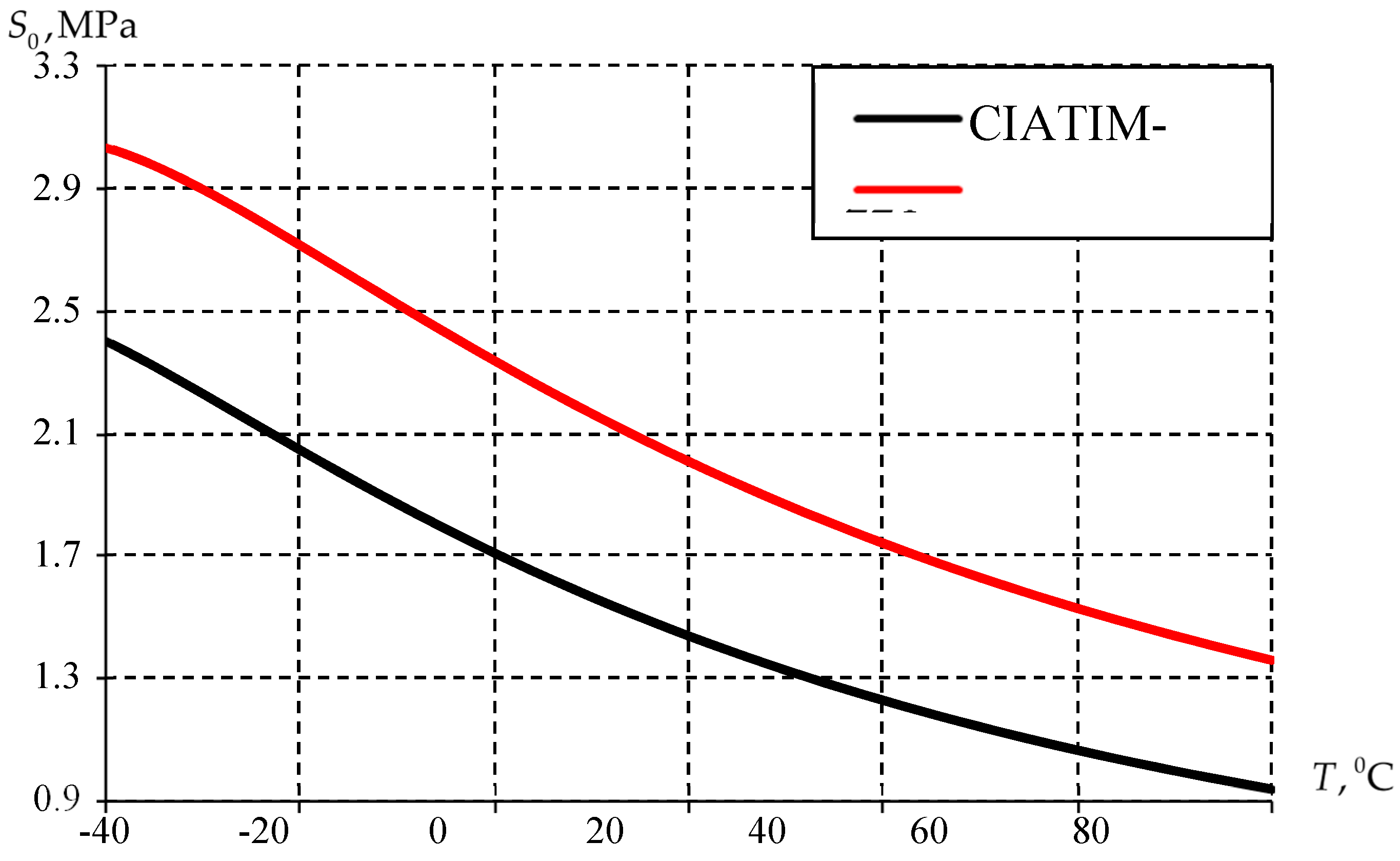
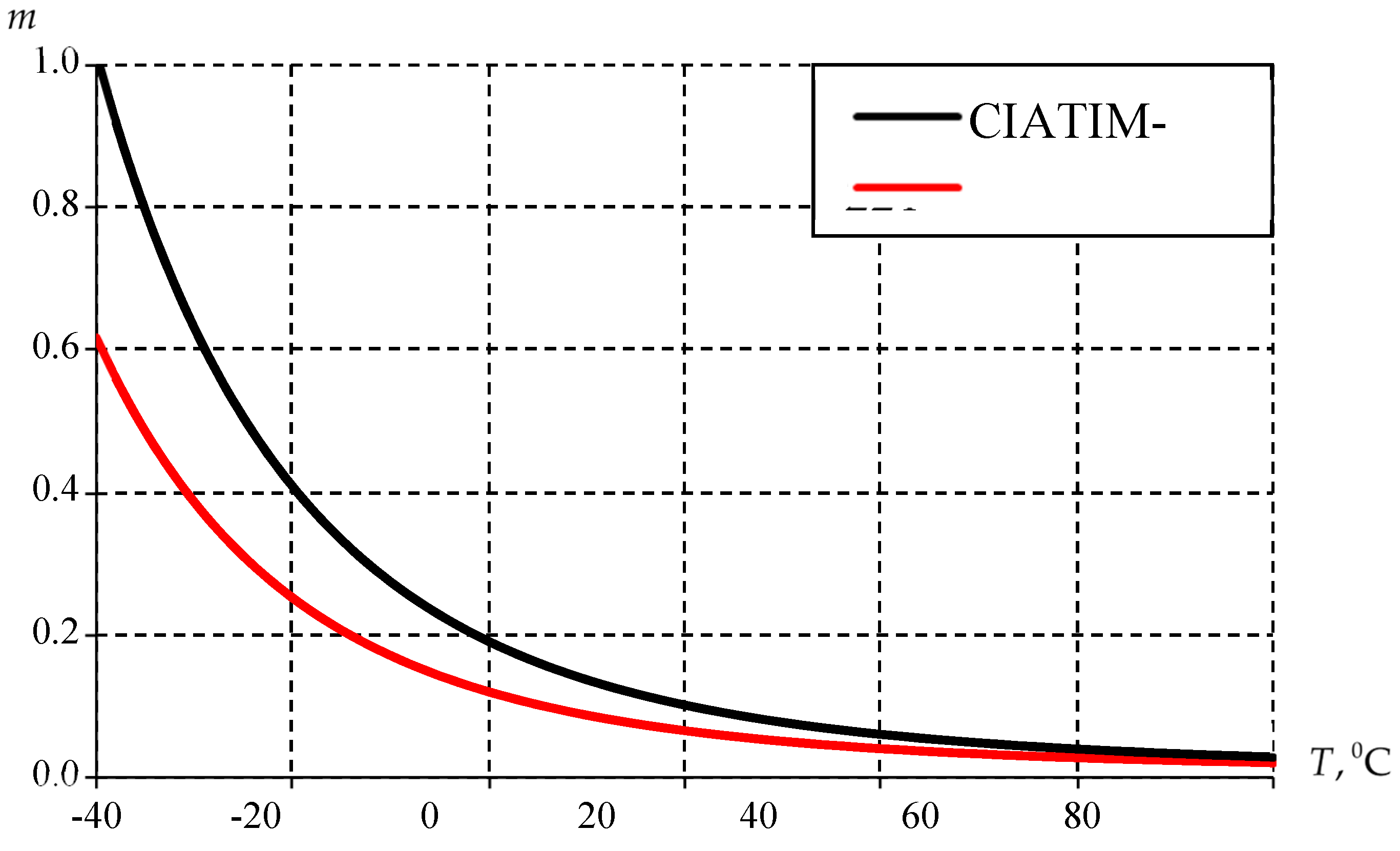
The temperature dependence of the grease parameters was obtained: the initial deformation resistance (Table 2, Figure 7); strain-rate-sensitivity (Table 3, Figure 8).

The distribution of the initial deformation resistance $S_0$ is illustrated in Figure 7.

The temperature dependences of the initial strain resistance are qualitatively similar. The initial deformation resistance decreases over the entire operating temperature range. The dependence of the initial deformation resistance on temperature is nonlinear. After further increase in temperature, there is a decrease in the values according to a close to linear law. The initial deformation resistance of the CIATIM-221F is almost 20 % times higher than CIATIM-221.

Figure 8 shows the distributions of strain rate sensitivity of stress $m$over the entire temperature range.

The temperature dependence of strain rate sensitivity of stress has a similar distribution pattern as the temperature dependence of the activation energy. However, in this case, the highest value prevails in the Ciatim-221 in the temperature range from -40 °C to 5 °C. It follows that the Ciatim-221 is more susceptible to shear rate in this temperature range.

The identification procedure was performed on a personal computer equipped with Intel Core i9-10900F, 128 GB RAM and 4 TB SSD. The procedure finds solutions of a given accuracy from 2 to 30 days. The convergence rate of the solution strongly depends on the initial vector of unknown parameters. It can be increased by implementing the problem on modern server platforms and clusters. In further research, it is planned to evaluate the stability of the numerical procedure.

In addition, it is planned to compare experimental data and numerical calculation implementing the full Anand model to describe the grease behavior.

3.3. Frequency and Temperature Dependence of Physical and Mechanical Characteristics

The identification procedure of unknown material parameters allowed to obtain coefficients for describing greases by Anand model. Numerical simulation of the pure shear experiment was performed in ANSYS. The paper implemented a custom script using APDL to automate a series of numerical calculations on the temperature and deformation parameters of the system. In addition, the algorithms include automatic processing of the numerical solutions.

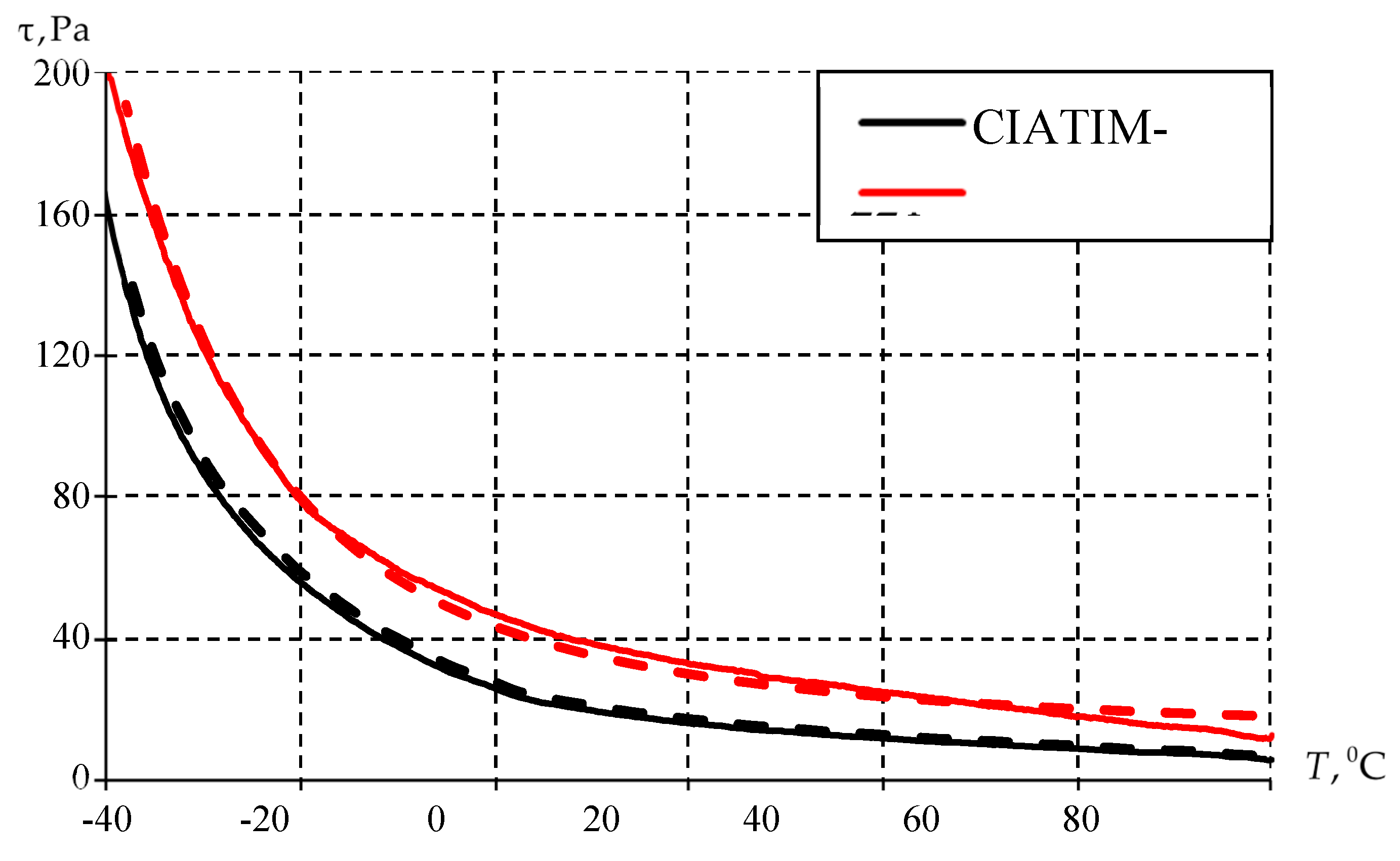
Figure 9 demonstrates the frequency-shear dependence of the tangential stress values at specific temperatures in the range from -40 °C to 80 °C.

The numerical calculation qualitatively and quantitatively corresponds to the experiments data over the entire temperature range. The total error at the points under study does not exceed 1 %.

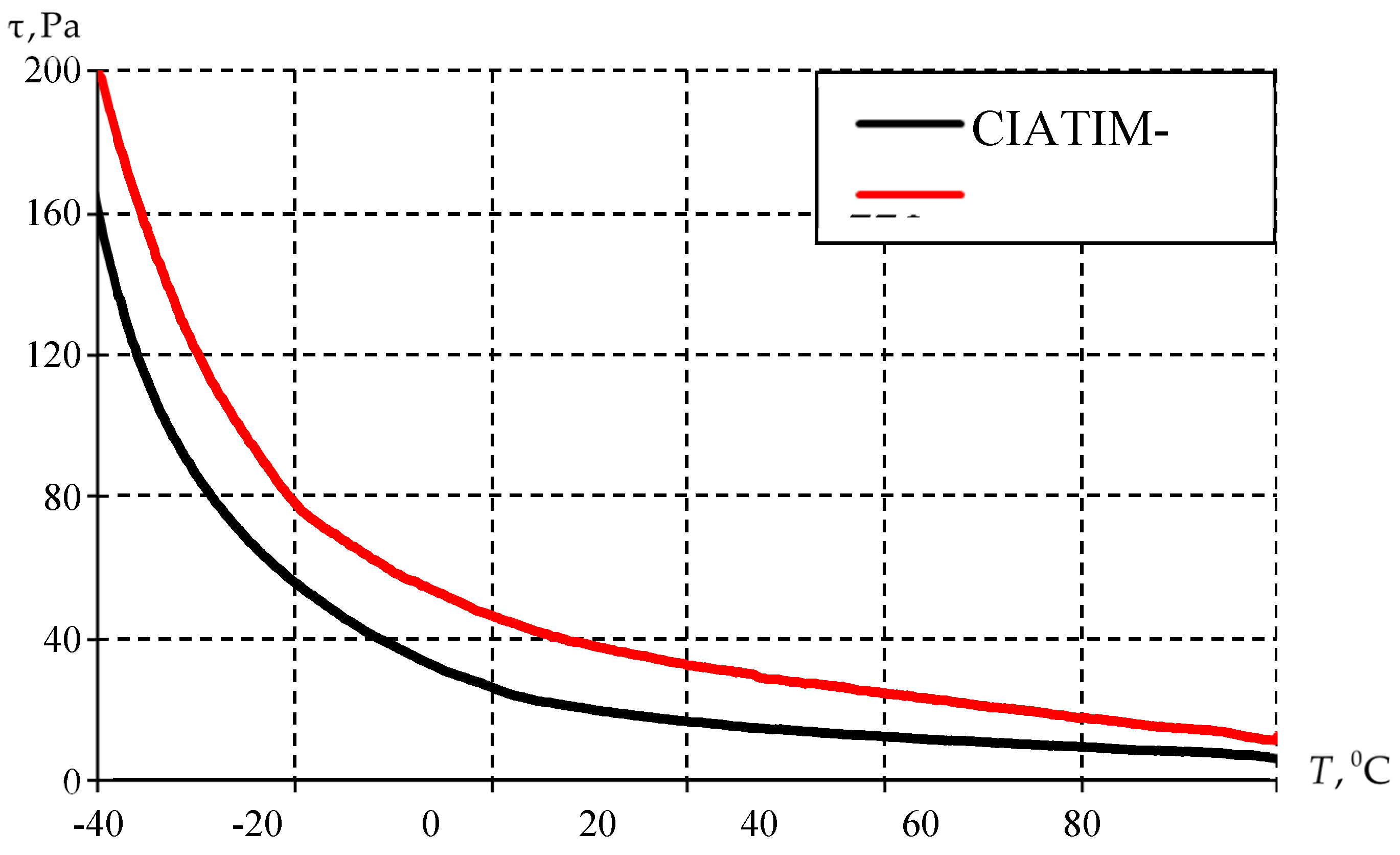
The temperature dependence of the tangential stresses is shown in Figure 10. The numerical model was exposed to temperatures from +80 to −40 °С in steps of 2 °С per minute. The frequency is constant and equal to 1 Hz. The conditions of numerical calculations completely repeat the experiment.

Numerical calculations qualitatively and quantitatively correspond to the experimental data. The difference between the results of the numerical model and the experimental data is less than 5%. The full Anand model allows us to describe the viscoelastic grease behavior. It can be used for a wide class of problems on predicting the behavior of materials and structures over a wide range of temperatures under dynamic loads.

4. Discussion

4.1. Limitation Statement

The paper investigated the applicability of the Anand model to describe the grease behavior. The following constraints are established as part of the study:

- considered a temperature range of -40°C to +80°C, with -60°C and +150°C being the minimum and maximum temperature values for the feasibility of the grease respectively;

- there is no possibility to carry out the experiment by means of non-contact impact on the sample using DWS technology [52];

- there is no open database of test materials and information on initial vectors for equation (5), which leads to increased time for identification of the mathematical model of material behavior;

- there are no separate experimental studies on determination of rheology and creep of greases in open sources.

In the future, the researchers will have to complete a number of tasks:

- conducting material studies at near critical temperatures (-60°C and +150°C);

- enriching the experimental database to reduce the time required to identify mathematical models of greases for future studies;

- conducting additional experiments on rheology and creep of materials;

- conducting experiments by means of non-contact impact on the sample using DWS technology;

- extending the applicability of the mathematical model to describe the behavior of polymers and composites.

4.2. About Mathematical Model

The application of the Anand mathematical model is widespread at present. This model is used to describe the behavior of many materials: metal alloys [53]; 3D printed structures [54,55], polymers [56], composites [57], rubbers [58], glasses [59] and other materials. Anssari-Benam notes that the large number of parameters of the Anand model complicates the identification and interpretation [60]. However, the model allows us to obtain higher-quality results on the materials and structures behavior that brings us closer to understanding the work real objects. Despite the complexity of the model, many scientists are engaged in modifying the mathematical model to suit their own problems [61,62], in order to minimize the error between experimental studies and numerical data.

Description of lubricants within the model of a series connection of an elastic spring and a viscous element (Maxwell body) is widely used [63,64,65]. Prony series and a simplified Anand model are used to describe a lubricant as a Maxwell body. However, the research team previously found that description of materials by Maxwell-type equations has serious limitations: the model works only at high deformation rates [47]. The modified Anand model for describing the behavior of lubricants obtained in the study will allow analyzing the work of the material, including in the bearings, for long periods in a wide range of operating temperatures. The results of the study will find wide application in the design of bridge bearings, especially in regions with difficult climatic conditions.

4.3. About the Procedure of Numerical Identification

A previously developed procedure for numerical identification of materials viscoelastic properties was tested on lubricants [47] and polymeric materials [51]. An assessment of the possibility of using the procedure to describe the photopolymer material Envisiontec SI500 behavior, used in additive manufacturing and 3D printing, was performed [66,67]. The effectiveness of the numerical identification procedure was confirmed by the agreement of the Envisiontec SI500 material model obtained using it with the results of Shumkov et al. [68].

An important result of this work is the expansion of the procedure functionality by describing the full and modified Anand model, which can be applied to a wide range of materials: polymers, composites, lubricants, etc.

These studies also allowed us to obtain a parameter changes range that significantly accelerates the mathematical description of a lubricants class, which include CIATIM-221 and CIATIM-221F.

A fairly large set of complex models that allow one to obtain a description of a lubricant as a viscoelastic or viscoelastoplastic body, including taking into account rheological properties, exists [69,70,71,72,73,74]. In the context of further research, we will consider the possibility of expanding the procedure for identifying properties to these models. This in turn will allow us to more fully evaluate the effectiveness of describing a lubricant using the modified Anand model. The main disadvantage of the modified Anand model is the large set of unknown parameters, which leads to significant costs of computational and time resources when implementing the task.

5. Conclusions

The article carried out a series of experiments to determine the thermophysical properties of greases in a wide range of temperatures (from -40 to +80 degrees Celsius) and shear rates (0.01 to 100 Hz). The hypothesis is proposed about temperature dependence of the Anand model parameters. New data on the temperature dependence of the activation energy distribution, initial resistance and shear rate sensitivity are obtained.

The numerical procedure has been created to determine the Anand model coefficients in the synergy of ANSYS Mechanical APDL and Python.

The following conclusions are drawn:

- The strength properties of greases increase with decreasing temperature.

- Consideration of the temperature effect on material behavior is necessary for qualitative and quantitative description of thermophysical greases properties.

The article obtained the coefficients of the extended Anand model for describing the grease behavior. Temperature dependences are determined for some of its parameters. The error is less than 1% between experimental and numerical data when using the extended Anand model.

In the development of the work it is planned to evaluate the possibility of using these algorithms to describe the performance of sliding layer polymers of bearing.

6. Patents

A state registration certificate of a computer program of the Russian Federation “Mathematical model identification of the Maxwell body viscoelastic behavior based on Prony series” No. 2023618695, registration date 04/27/2023. The authors are Anna A. Kamenskikh and Yuriy Nosov. The holder is Perm National Research Polytechnic University.