Wave-Like Behavior in the Source-Detector Resonance

1. The Source-Detector Resonance

We would like to ask the question: ‘is it possible to manifest wave interference characteristics with independent non-interacting elementary particles?’, where by ‘elementary’ we mean classical particles with no internal degrees of freedom (i.e., no ‘hidden variables’). Feynman famously quoted that wave-like characteristics are ‘impossible, absolutely impossible to explain in any classical way’ (Feynman Lectures on Physics [1]). We will challenge this statement with our model of the ‘Source-Detector Resonance’ (hereafter SDR) that we will now present below. Let us begin by considering a mass M attached to a macroscopic oscillator which follows the equation

$$M\ddot{x}=-k(x-L_0).$$

(1)

Here, $(x-L_0)$ is the particle displacement around the equilibrium position $x=L_0$. We do not define the particular physical form of the oscillator. The resonance frequency of the system is

$${\nu }_0={\displaystyle \frac{1}{2\pi }}\sqrt{{\displaystyle \frac{k}{M}}}.$$

(2)

Let us now assume that this oscillator is at the heart of a classical system that releases one elementary particle of mass $m\ll M$ every period

$$P\equiv {\displaystyle \frac{1}{{\nu }_0}}.$$

(3)

This consistent periodic release of particles does not have any effect on this large classical system. In particular, its eigenfrequency ${\nu }_0$ remains unchanged, and its supply of elementary particles is unphased and practically unlimited. We call such a system a ‘Source’ (see Figure 1).

The time series of particles emitted by the Source may be represented as in figure a if particles are emitted every period P, or as in Figure 2b–d if they are emitted randomly $80\%,50\%,20\%$ of the time of the full time-series respectively, at random integer multiples of the period P. In both cases, the Fourier Power Spectrum Density (hereafter PSD) of the time series has strong peaks around $\nu =0$ and $\nu ={\nu }_0$, plus some extra noise at all frequencies. If the signal becomes too weak (i.e., if too many particles are missing from the continuous time-series of Figure 2a), the peak at $\nu ={\nu }_0$ will disappear inside the noise, and there will remain no information of periodicity in the signal. The PSD is rescaled so that the value $\mathrm{PSD}(\nu =0)=1$ corresponds to the power of the full time series of Figure 2a.

Let us now consider a ‘Resonant Oscillator’ that may absorb these particles only if the particle time series it receives has the same eigenfrequency ${\nu }_0$. In other words, the periodic sequence of particles can stimulate this Resonant Oscillator only at its resonance frequency. The Resonant Oscillator then responds and announces the detection of (i.e., detects) a particle with a finite probability. In particular if the stream of particles reaches a Resonant Oscillator with a frequency different from its resonance frequency, these particles will not be fully absorbed (i.e., detected). Some fraction of them will be absorbed, and some fraction of them will continue their motion unimpeded behind the Resonant Oscillator (see Figure 3). We will further assume that

The probability of detecting a particle in a time-series by a Resonant Oscillator is proportional to the square of the ratio of the time-series PSD at its resonance frequency ${\nu }_0$ over the time-series PSD at zero frequency.

Mathematically, we express the probability of absorption of a particle in the time series as

$${Prob}_{\mathrm{abs}}={\left({\displaystyle \frac{\mathrm{PSD}(\nu ={\nu }_0)}{\mathrm{PSD}(\nu =0)}}\right)}^2.$$

(4)

When the Resonant Oscillator announces a particle absorption, this will result in a ‘Detection’. Particles that are not absorbed/detected by the Resonant Oscillator pass through it unimpeded.

2. Interference between Two Particle Streams

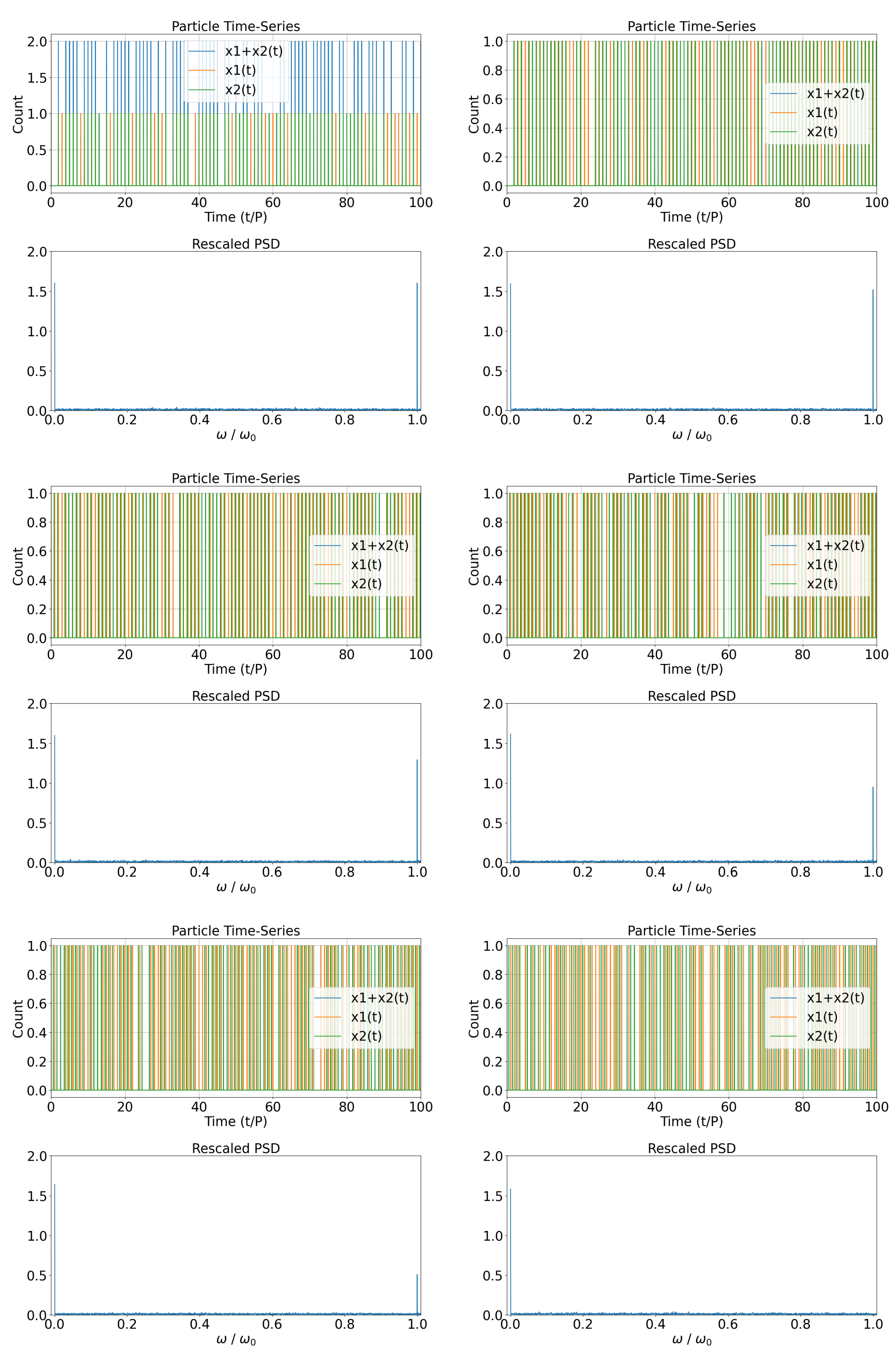
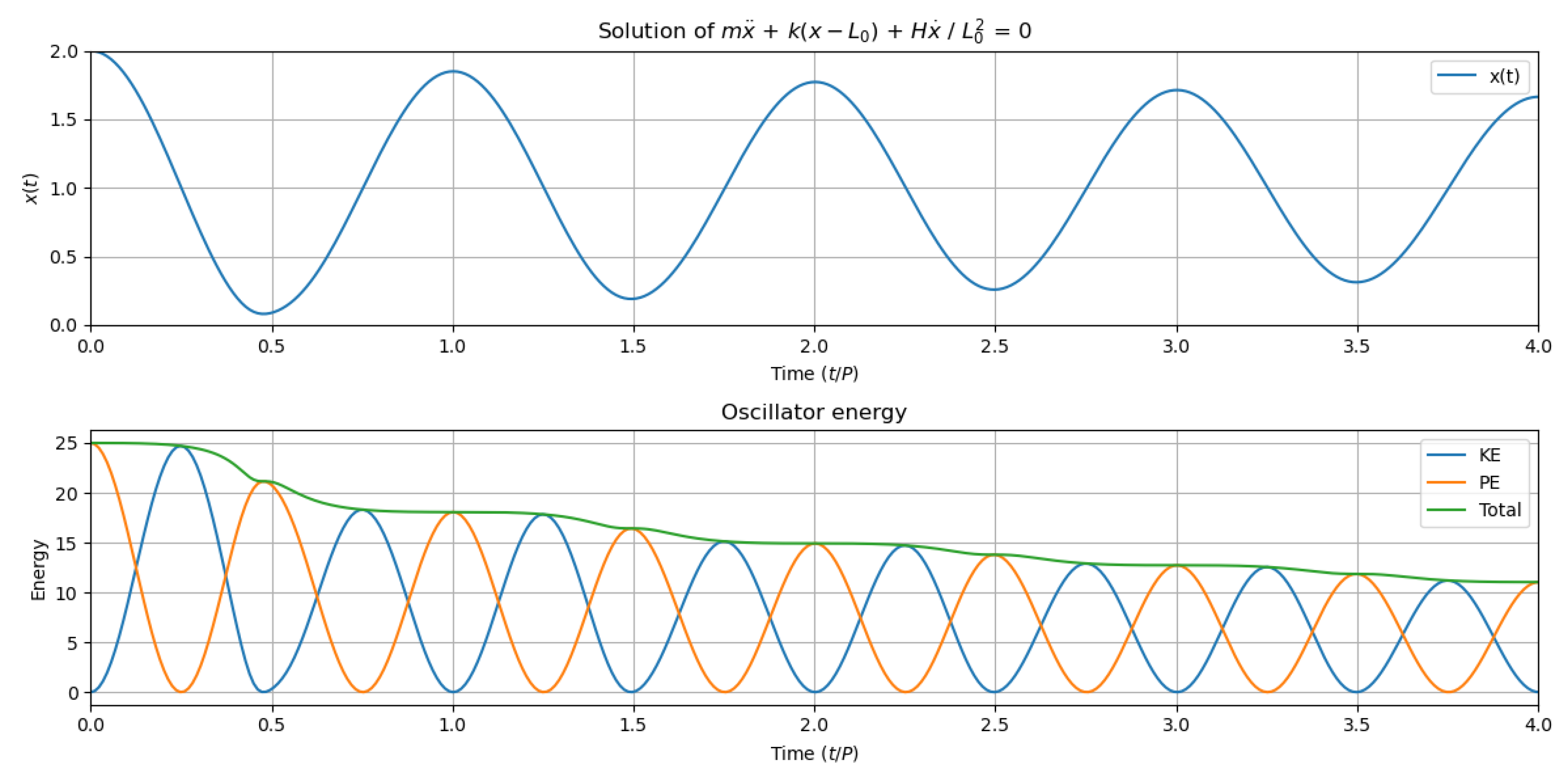
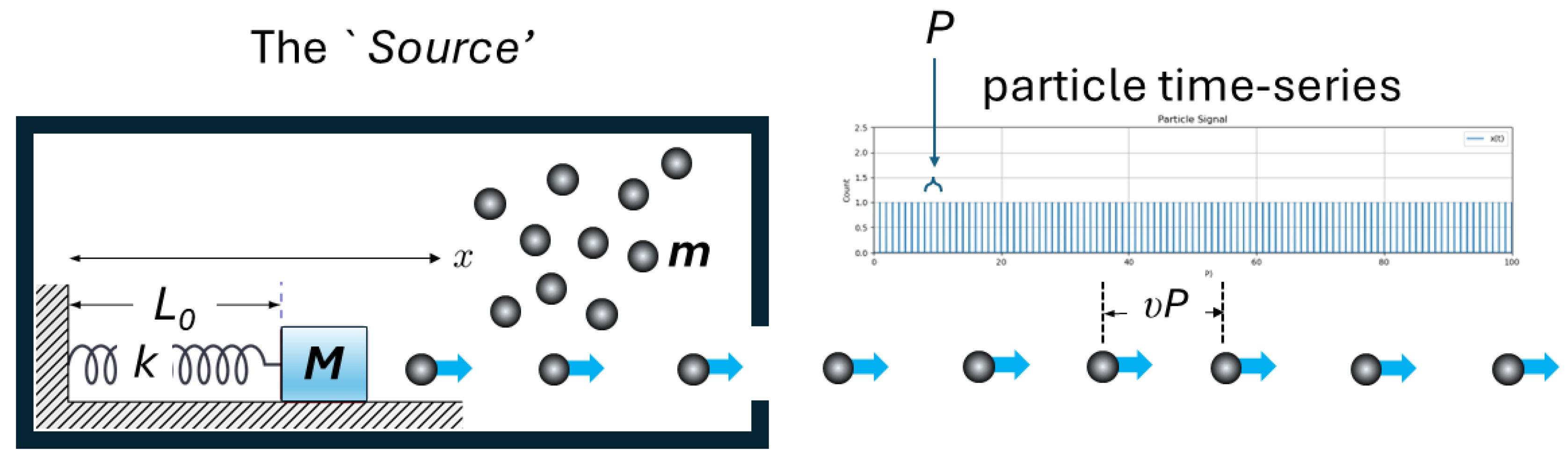
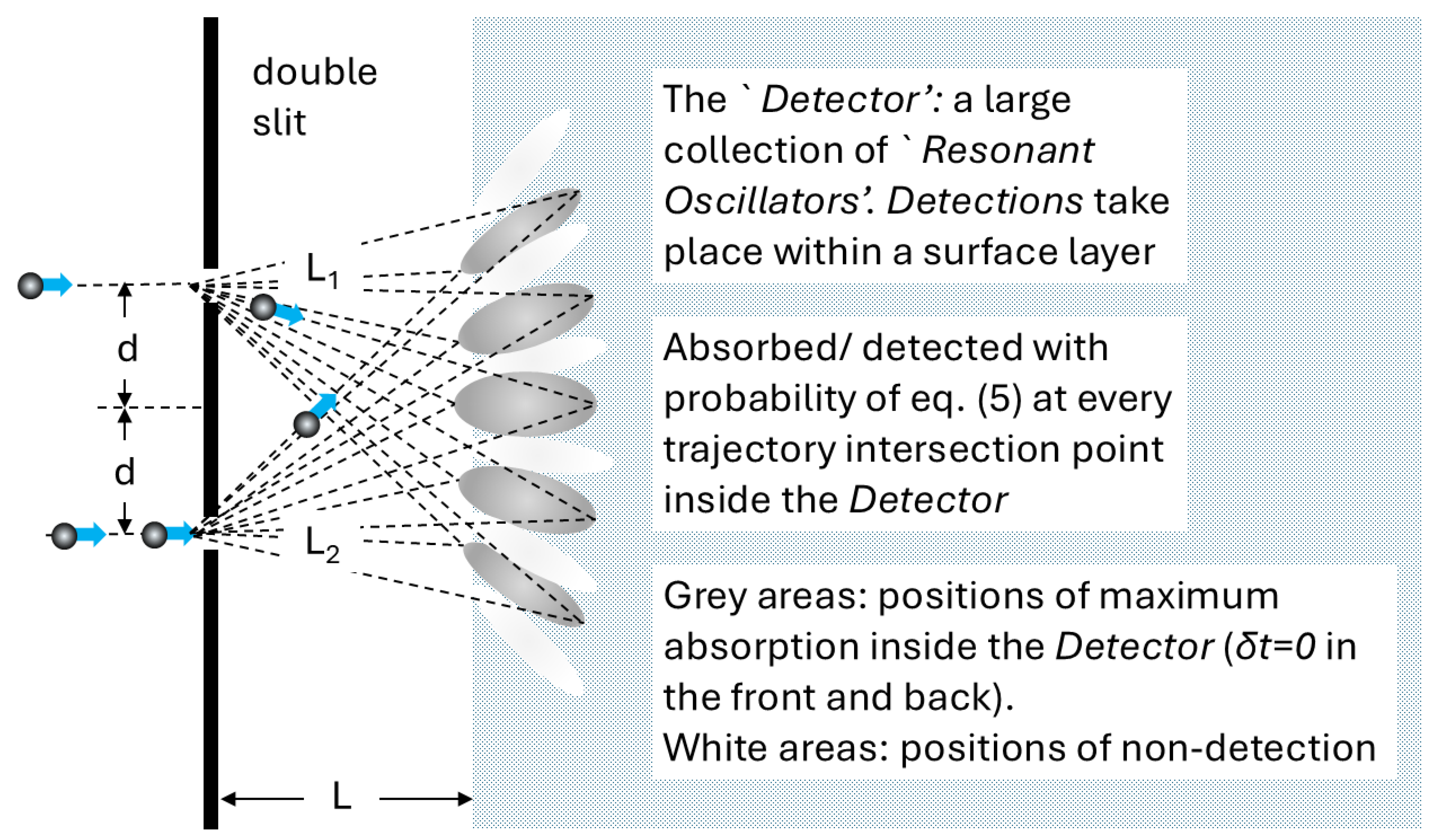
Let us assume that the Source emits random particle sequences (i.e., with particles emitted at random integer multiples of the resonance period P) that travel either through path 1, either through path 2. Both particle time sequences reach a Resonant Oscillator at a certain position in which the particles going through path 2 have a certain time delay $\delta t$ with respect to those going through path 1. Let us start with no time-delay, or a time delay equal to an integer multiple of the period P. In that case, the Resonant Oscillator receives the time sequence and corresponding spectrum of Figure 4a. For a time delay equal to $10\%,20\%,30\%,40\%$ of P plus an integer multiple of the period P, the Resonant Oscillator receives the time sequences and corresponding spectra of Figure 4b-e. Finally, for a time delay equal to $50\%$ of P plus an integer multiple of the period P, the Resonant Oscillator receives the time sequence and corresponding spectrum of Figure 4f. In that particular case, the power of the spectrum at the resonance frequency $\nu ={\nu }_0$ disappears! The reason is that, because of the superposition, the shortest periodic time interval between particles that reach the Resonant Oscillator is $P/2$, not P as in the original time series, thus the fundamental frequency of the combined series is $2{\nu }_0$, not ${\nu }_0$. 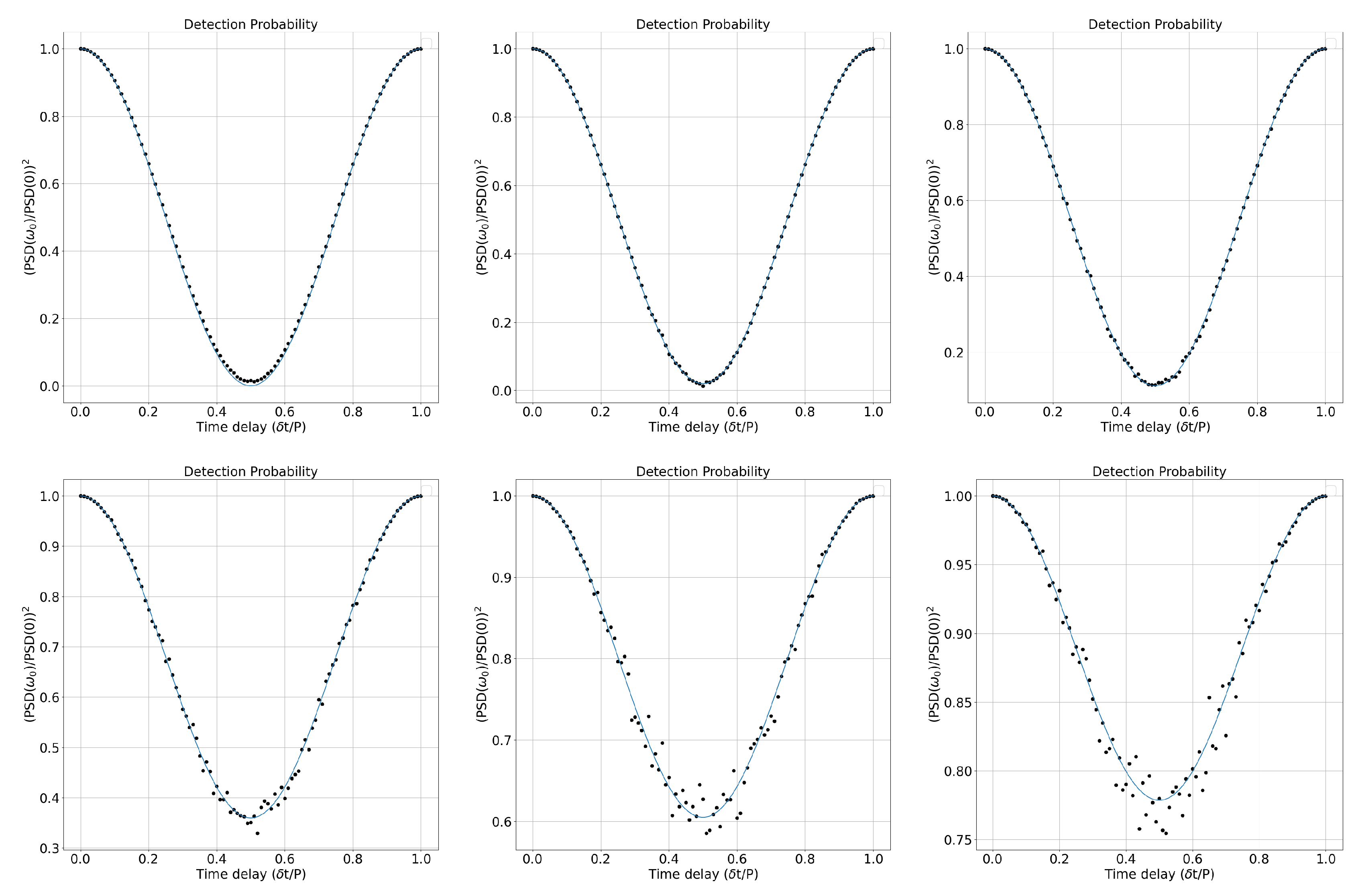In Figure 7a we performed multiple numerical experiments for multiple values of the time delay $\delta t$ and plotted the probability of absoprtion of a particle in the combined time series according Equation (4). This is the distribution of the square of the ratio of the combined stream’s PSD at resonance over the PSD of the combined stream at zero frequency (the total power of the combined stream) as a function of the time delay $\delta t$. We also plot the function ${cos}^2(\pi \delta t/P)$ obtained from Equation (5) below for $\alpha =\beta =0.8$. The fit to the numerical experiments is almost perfect, except around $\delta \approx P/2$ where the PSD at resonance reaches the noise level.

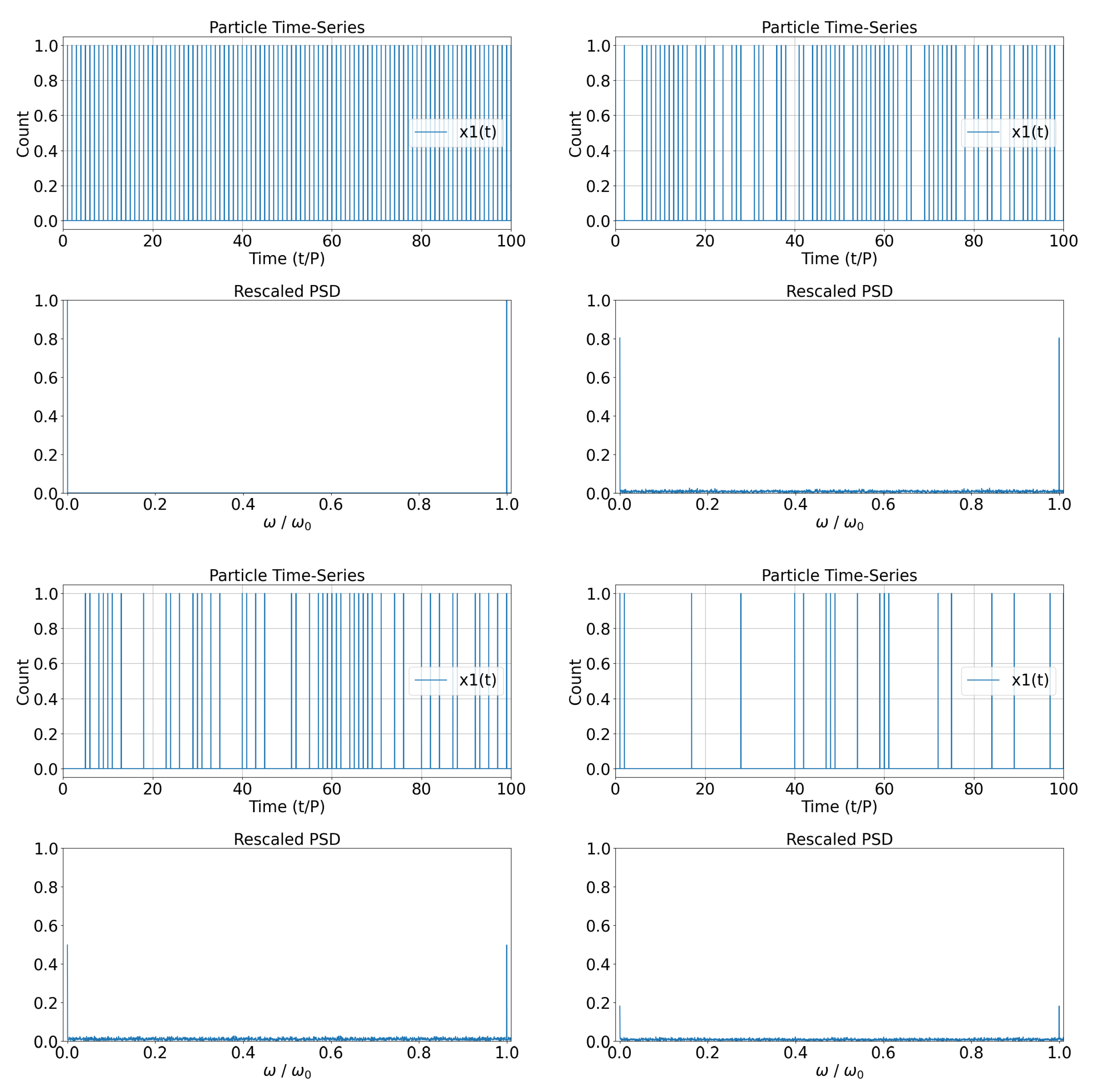
Figure 4. Top/Bottom rows of panels: The superposition of two equal power time-series of particles emitted intermittently by the Source with fixed period P and a time delay between them equal to $\delta t=0,0.1,0.2,0.3,0.4,0.5$ times the period P (plus an integer multiple of P). These time-series of particles are collected by the Resonant Oscillator/Detector. Shown also the corresponding spectra. We see very clearly that when $\delta t=0.5P$, the spectrum power at resonance vanishes.

Figure 4. Top/Bottom rows of panels: The superposition of two equal power time-series of particles emitted intermittently by the Source with fixed period P and a time delay between them equal to $\delta t=0,0.1,0.2,0.3,0.4,0.5$ times the period P (plus an integer multiple of P). These time-series of particles are collected by the Resonant Oscillator/Detector. Shown also the corresponding spectra. We see very clearly that when $\delta t=0.5P$, the spectrum power at resonance vanishes.

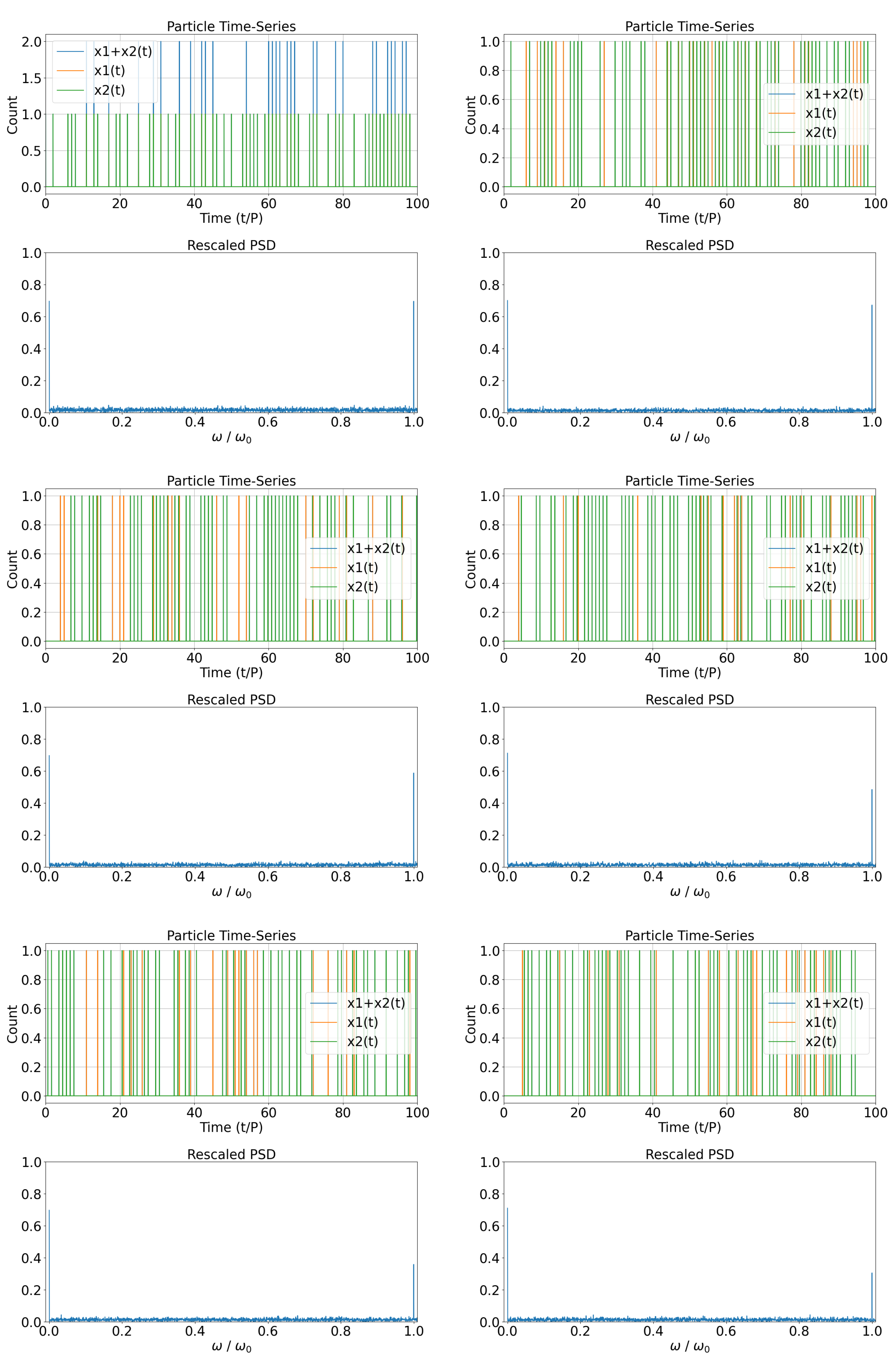
Figure 5. Top/Bottom rows of panels: The superposition of two unequal time-series of particles emitted intermittently by the Source with fixed period P and a time delay between them equal to $\delta t=0,0.1,0.2,0.3,0.4,0.5$ times the period P (plus an integer multiple of P). The first time-series contains only $20\%$ of the particles of the continuous time-series of figure a, and the second only $50\%$. These time-series of particles are collected by the Resonant Oscillator/Detector. Shown also the corresponding spectra. We see very clearly that when $\delta t=0.5P$, the spectrum power at resonance does not vanish. The ratio of the number of particles ar resonance over the total number of particles emitted by the Source is given by Equation (5).

Figure 5. Top/Bottom rows of panels: The superposition of two unequal time-series of particles emitted intermittently by the Source with fixed period P and a time delay between them equal to $\delta t=0,0.1,0.2,0.3,0.4,0.5$ times the period P (plus an integer multiple of P). The first time-series contains only $20\%$ of the particles of the continuous time-series of figure a, and the second only $50\%$. These time-series of particles are collected by the Resonant Oscillator/Detector. Shown also the corresponding spectra. We see very clearly that when $\delta t=0.5P$, the spectrum power at resonance does not vanish. The ratio of the number of particles ar resonance over the total number of particles emitted by the Source is given by Equation (5).

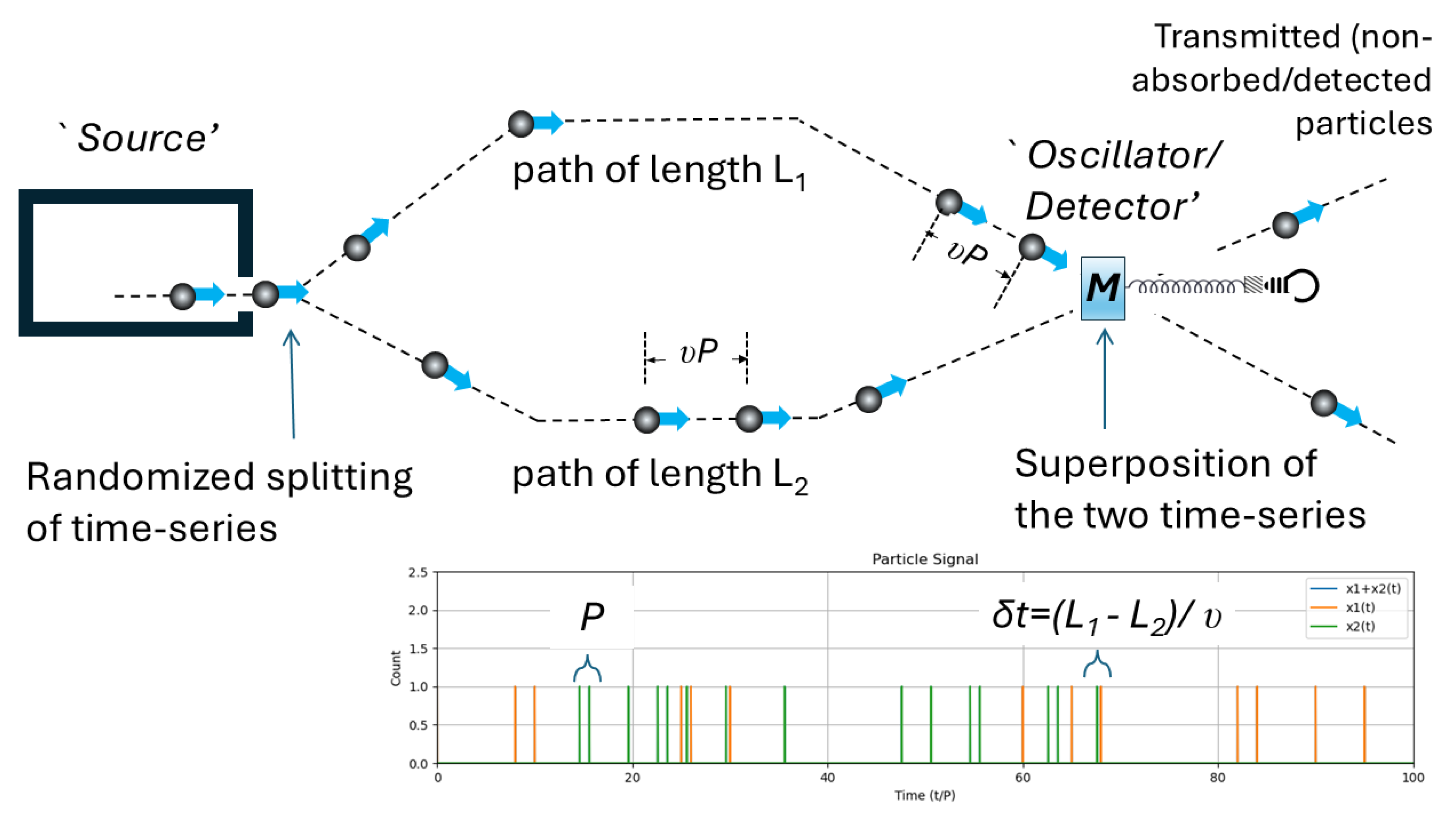
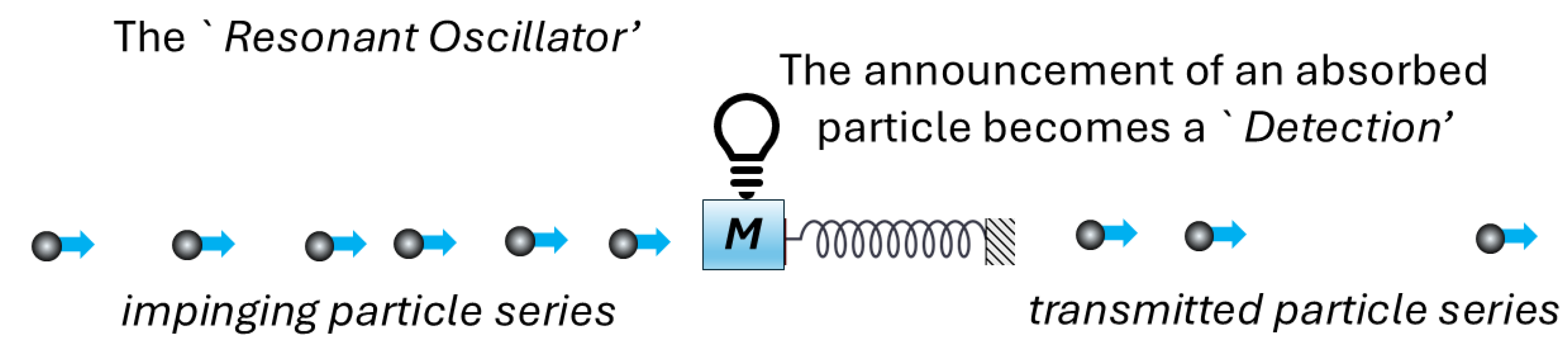
Figure 6. Sketch of interference between two different streams of particles that originate at the same Source and have a time delay of $\delta t=(L_1-L_2)/v$ between themselves. Such superposition manifests intereference characteristics at the Detector.

Figure 6. Sketch of interference between two different streams of particles that originate at the same Source and have a time delay of $\delta t=(L_1-L_2)/v$ between themselves. Such superposition manifests intereference characteristics at the Detector.

Figure 7. Distribution of the square of the ratio of the PSD at resonance over the PSD at zero frequency as a function of the time delay $\delta t$. We consider here the combination of two power time-series with $(\alpha ,\beta )=(0.8,0.8)/(0.8,0.6)/(0.8,0.4)/(0.8,0.2/(0.8,0.1)/(0.8,0.05\left)\right)$ from top left to bottom right respectively. Shown also the fits to the expression of Equation (5) for the correponding values of $\alpha$ and $\beta$. Except for the case of zero time delay $\delta t$, this distribution leaves a fraction $(1-{\mathrm{Prob}}_{\mathrm{abs}})$ of particles undetected. Clearly, when either one of $\alpha$ or $\beta$ is equal to zero (i.e., if we have only one and not two combined particle time-series), the detection probability ${\mathrm{Prob}}_{\mathrm{abs}}$ is equal to unity (not shown).

Figure 7. Distribution of the square of the ratio of the PSD at resonance over the PSD at zero frequency as a function of the time delay $\delta t$. We consider here the combination of two power time-series with $(\alpha ,\beta )=(0.8,0.8)/(0.8,0.6)/(0.8,0.4)/(0.8,0.2/(0.8,0.1)/(0.8,0.05\left)\right)$ from top left to bottom right respectively. Shown also the fits to the expression of Equation (5) for the correponding values of $\alpha$ and $\beta$. Except for the case of zero time delay $\delta t$, this distribution leaves a fraction $(1-{\mathrm{Prob}}_{\mathrm{abs}})$ of particles undetected. Clearly, when either one of $\alpha$ or $\beta$ is equal to zero (i.e., if we have only one and not two combined particle time-series), the detection probability ${\mathrm{Prob}}_{\mathrm{abs}}$ is equal to unity (not shown).

We see that when the two streams of particles have the same power and are in phase (i.e., $\delta t=0$ or some integer multiple of P), the Resonant Oscillator detects the same number of particles as the combined two particle time-series, i.e., the same number of particles as those emitted by the Source. No more, no less. In the other limit when the two streams of particles have the same power and are out of phase (i.e., $\delta t=P/2$ plus some integer multiple of P), the combined stream’s spectrum power at resonance vanishes. In general, in the case of a superposition of two intermittently periodic time-series with magnituted $\alpha$ and $\beta$ respectively, the probability of detection at the Resonant Oscillator/Detector as defined by Equation (4) is found numerically to be equal to

$${\mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}}_{\mathrm{abs}}={\left({\displaystyle \frac{\mathrm{P}\mathrm{S}\mathrm{D}\left({\nu }_0\right)}{\mathrm{P}\mathrm{S}\mathrm{D}\left(0\right)}}\right)}^2={\displaystyle \frac{{\alpha }^2+{\beta }^2}{{(\alpha +\beta )}^2}}\left(1+{\displaystyle \frac{2\alpha \beta }{{\alpha }^2+{\beta }^2}}cos\left(2\pi {\displaystyle \frac{\delta t}{P}}\right)\right)$$

(5)

(see Figure 7b-d). Once again, particles from both particle streams that are not absorbed/detected by the Resonant Oscillator pass through it unimpeded, and reach a deeper point inside the Detector.

3. A Double-Slit Experiment with Particles

Now imagine a large (infinite) collection of Resonant Oscillators. We will call such a system a macroscopic ‘Detector’. It is important that the Detector has enough thickness to absorb (thus also detect) all particles from the combined time-series that reach it. The interference setup that we propose is the one from a typical double-slit experiment. Particle series reach points of the Detector coming from both slits, and the time-difference $\delta t$ between the two time-series is proportional to the difference in the particle trajectory lengths over the particle speed. Particles are absorbed by the Resonant Oscillators/Detectors at each layer of the Detector according to the probability distribution of Equation (5). The particles that are not absorbed continue to travel along the same line that they followed after emerging from their respective slit and are combined with the stream of non-absorbed particles that emerged from the other slit. Some of them will be absorbed/detected in that second layer of the Detector, and so on and so forth. Eventually, all particles emerging from both slits will be absorbed, and the interference pattern shown schematicallyt in Figure 8 will emerge in the interior of the Detector. No particle will be left undetected. What is important though is that, in order for the Detector to absorb/detect all particles, it needs a certain finite thickness.

It is interesting that the same distribution as that of Equation (5) is obtained when we superpose two delayed periodic signals of amplitudes $\alpha$ and $\beta$ respectively, expressed mathematically as $\alpha exp(i2\pi t/P)+\beta exp\left(i2\pi \right(t+\delta t)/P)$. This sum may represent for example the addition of the electric field of two interfering electromagnetic waves. Classically, the power of the combined signal is proportional to the square of the amplitude of the electric field superposition, namely ${(\alpha +\beta cos(2\pi \delta t/P))}^2+{\beta }^2{sin}^2(2\pi \delta t/P)=({\alpha }^2+{\beta }^2)(1+2\alpha \beta cos(2\pi \delta t/P)/({\alpha }^2+{\beta }^2))$. If we further divide this expression by ${(\alpha +\beta )}^2$, we obtain the result of Equation (5). In our picture of periodic sequences of elementary particles, the power is proportional to the number of detected particles per unit of time at the Detector. Figure 7 is telling us that when two independent periodic signals from our Source reach a certain point in the resonant Detector with a time delay of $\delta t$ between them, the Resonant Oscillator at that position collects the sum of the two particle streams, i.e., a power that is double the power of each particle stream, but absorbs (detects, announces) a number of particles proportional to Equation (5) times the power of the Source particle stream. This result applies on average even if the periodic sequences of particles are not complete and certain particles are randomly missing. As long as particles of each stream are emitted and collected at integer multiples of the resonance period P, the same illusion of interference is obtained.

It should be obvious to the reader that the number of particles that reach the Detector per unit of time is equal to the sum of the number of particles per unit of time in the two particle streams, irrespective of the time delay $\delta t$ between the two streams. In the case of destructive interference at a certain position ($\delta t=P/2$), the Detector announces zero particles at that position. As a result of this ‘non-detection’, the two particle streams continue their travel unimpeded, and eventually all of them are detected deeper inside the Detector (see Figure 8). In the case of constructive interference ($\delta t=0$) the Detector absorbs the two streams of particles, but if we also count the particles also absorbed behind that point of constructive interference, the Detector announces on average double the number of particles detected at the first surface point of constructive interference. Thus, the Detector conserves the number of particles, provided we are willing to account for all detections, even those in the interior of the Detector.

If we collect all detections along the various angles of the experiment, we obtain the result of a double-slit experiment. The new result of our present numerical experiment is that the same illusion of interference is obtained only if we are willing to consider a Detector with a finite width. Had we considered only the surface layers of the Detector, we would have obtained the same intereference pattern with one-half the number of particles that reach the Detector.

4. Conclusions

We have shown that interference patterns may arise from the superposition of two particle streams generated by the same classical Resonant Oscillator that reach a second classical Resonant Oscillator tuned to the same resonance frequency. These two Resonant Oscillators are

• The Source that emits a series of particles at integer multiples of its resonance period,
• The Detector that receives these particle streams at each point and announces detections at that point with a probability proportional to the square of the PSD of the particle time-series at the Source-Detector Resonance (SDR) frequency. The particles that are not detected at that point continue their motion unimpeded deeper inside the Detector.

What we have shown essentially is that two such streams of independent non-interacting particles emitted with the same velocity at times that are integer multiples of P manifest on average the characteristics of a continuous wave, provided the detector operates only at the resonance frequency ${\nu }_0=1/P$. We have shown this result with a simple numerical experiment of interference when there is a time delay $\delta t$ between two such streams of particles. Our numerical result is valid even when the two streams carry unequal numbers of particles per unit time (on average). The resulting interference pattern is the same as that of continuous sinusoidal waves with equal or unequal amplitudes.

When we applied the above result to reproduce a double-slit experiment with particles, only one half of the particles were detected when they first reached the surface layer of the Detector. The other one half of the particles continued their respective motions in deeper layers of the Detector and were eventually absorbed/detected by it. The interference pattern integrated over the thickness of the Detector, creates the same effect as the interference pattern resulting from two interfering sinusoidal waves. This result is currently only qualitative, and we plan to provide a rigorous proof in the future.

Several researchers have tried in the past to generate similar interference patterns with particles that carry some type of internal ‘hidden variables’ in the form of an internal clock (e.g., [2,3]). The detector collects and processes that information before it announces a detection, similarly to our present model. The problem with such approaches is that they do not work for photons which cannot carry any internal clock. In our present model, the necessary information of the time delay is carried collectively by the two streams of particles, not by each individual particle as in the previous approaches quoted above.

Our current model applies only to free particles. Up to now we have said nothing about the particle velocity v which is important for the manifestation of the time delay $\delta t$ between the two different paths of lengths $L_1$ and $L_2$ ($\delta t=(L_1-L_2)/v$). In the Appendix, we offer a tentative physical model of how these particles may have obtained their velocity v and their kinetic energy.

In summary, if there exist macroscopic sources and detectors that operate as proposed, wave-like interference phenomena may be explained if the detectors absorb and announce particles with a particular probability distribution that at each point is described by Equation (5). If all macroscopic detectors in nature operate as proposed in this paper, wave-like phenomena may consist an illusion of the detectors, not a fundamental property of nature.