PV Farm Power Generation Forecast using PV-Battery Model with Machine Learning Capabilities

1. Introduction

Photovoltaic (PV) forecasting is crucial in modern power system planning and management, enabling grid operators to integrate renewable energy sources effectively. By predicting solar power generation, it supports grid stability, optimizes energy dispatch, and enhances market participation. Accurate PV forecasting is particularly important for managing the variability of solar energy, which is influenced by weather conditions, shading, and operational factors. The increasing integration of photovoltaic (PV) systems into energy grids has necessitated the development of accurate forecasting models to ensure grid stability, efficient energy management, and enhanced market participation. Advancements in forecasting methodologies, including statistical models, machine learning, and hybrid approaches, have significantly improved prediction accuracy and reliability, addressing challenges such as nonlinear dependencies, temporal correlations, and data variability. These innovations help mitigate the challenges of integrating intermittent PV generation into power grids, ensuring efficient resource allocation, reducing operational costs, and enhancing renewable energy penetration. As the adoption of PV systems continues to grow, forecasting remains essential for sustainable and reliable energy system operations.

1.1. States of the Arts

Several research studies have addressed various challenges in PV forecasting. For instance, a CNN-based model was developed to predict the Maximum Power Point (MPP) voltage in pavement PV arrays under complex shading conditions, achieving minimal prediction errors (MAE: 2.54, MSE: 11.13) and outperforming ResNet and MLP in speed and accuracy [1]. Another study proposed a hybrid architecture integrating Convolutional Graph Neural Networks (ConvGNNs) and LSTM networks to model spatial-temporal dependencies in PV systems, outperforming methods like ARIMA, SVM, and CNN+LSTM [2]. A probabilistic ensemble method (PEM) improved PV forecasting under cloudy conditions by excluding statistical outliers, reducing normalized RMSE by up to 15.12% [3]. To address inconsistencies in multi-horizon forecasts, a seamless probabilistic model, the Analog Ensemble (AnEn), was proposed, delivering accurate predictions for timeframes from 5 minutes to 36 hours [4]. Furthermore, an adaptive ML framework was introduced for behind-the-meter PV disaggregation, leveraging models like Random Forest (RF), Decision Tree (DT), and Multilayer Perceptron (MLP) to achieve R-squared values up to 0.98% [5].

Hybrid approaches have also shown promise. A Boot-LSTM-ICSO-PP model, integrating Improved Chicken Swarm Optimization (ICSO) and Prey-Predator mechanisms, achieved over 60% error reductions in probabilistic forecasting [6]. A combination of numerical weather predictions (NWP) with satellite data for nowcasting demonstrated reductions in MAE and RMSE in diverse geographic contexts [7]. Feature selection techniques like PCA and XGBoost reduced RMSE by 30% in mid-term PV forecasting [8]. A stacking ensemble model combining GRNN, ELM, ElmanNN, and LSTM provided robust performance across weather scenarios [9]. Additionally, a scalable ANN-based method for distributed regional-scale PV forecasting reduced RMSE by 29% using non-irradiance meteorological data [10]. Further advances include comparisons of deep learning architectures, with BiLSTM achieving a 96% correlation coefficient for GHI forecasting in arid regions [11].

Ensemble tree-based methods effectively predicted SPV power in the Qassim region, achieving RMSE values as low as 19.66 W [12]. A feature-selective ensemble framework combining ARIMA and LSTM models reduced RMSE by up to 64% for long-term regional PV generation [13]. ConvLSTM demonstrated superiority in hourly solar radiation forecasting in regions with variable weather, achieving an nRMSE of 1.51% [14]. In Turkey, a comparison between Random Forest and LSTM showed the latter’s superior predictive performance for nonlinear relationships in solar datasets [15]. Efforts to enhance model transparency have focused on explainable AI (XAI) tools, such as SHAP and LIME, which improved RMSE and user trust for Random Forest models [16]. A hybrid model integrating SDS, WPT, and IBBO demonstrated ultra-short-term forecasting accuracy, achieving RMSE as low as 0.0693 kW [17]. LSTM-based models optimized with advanced preprocessing techniques improved short-term PV forecasting metrics like MAE and RMSE [18]. To address harmonics forecasting in PV-wind hybrid systems, a hybrid ANN-ANFIS model achieved significant accuracy gains across various scenarios [19]. A hybrid MOSMA-SVM model further enhanced PV forecasting, achieving MAPE reductions of up to 27.13% [20].

Recent studies have also explored multi-source data integration. Combining remote sensing techniques with NWP data in CNN-LSTM ensembles achieved MAE reductions of 33.7% [21]. A review of ML methods found Random Forest to be the most robust for PV forecasting, reducing forecasting errors by 37.33% [22]. Advanced architectures like GSTANN, which integrate graph convolutional and attention mechanisms, demonstrated MAE reductions of up to 20% in very short-term forecasts [23]. Enhancements to LSTM models with two-stage attention mechanisms achieved RMSE as low as 0.0638 [24]. Hybrid MOSMA models for uncertainty analysis further improved deterministic accuracy in PV forecasts [25].

Temporal convolutional networks optimized for PV forecasts using CEEMDAN achieved RMSE values as low as 1.206 [26]. CNN-LSTM hybrid models validated for multiscale PV systems demonstrated superior scalability [27]. A domain-adaptive learning framework enabled real-time forecasting in dynamic climates, achieving significant MAE reductions without requiring test labels [28]. Forecasting applications extended to battery-integrated PV systems focused on operational reliability [29]. Lastly, integrating synthetic weather data with LSTM models improved short-term forecasts by 33%, outperforming traditional methods [30].

1.2. Practical Decision-Making and Operational Efficiency Needs

Despite the achievements of these previous studies, there are still some significant gaps to fill. For example, many of these existing studies focus solely on PV power generation forecasting without integrating battery management systems, which are essential for energy storage and grid reliability. For instance, [6] and [28] proposed advanced hybrid models for PV power prediction, but these do not include mechanisms for monitoring or optimizing battery performance. Study in [29] explored battery-integrated PV systems but lacked robust forecasting frameworks that combine PV generation predictions with battery energy management, leaving a gap in comprehensive energy management systems. Several methods, including LSTM [18] and CNN-LSTM hybrids [27], perform well under relatively stable conditions but often fail to maintain accuracy under highly variable or extreme weather conditions. For example, refs. [9] and [19] highlighted the limitations of hybrid models under complex meteorological scenarios, where prediction errors increase due to overfitting or limited adaptability. This underscores the need for models capable of handling such variability without compromising accuracy.

Furthermore, the computational intensity of advanced architectures like ConvGNNs [2] and MOSMA-SVM hybrids [20] presents significant challenges to their scalability and real-time applications. These models often require considerable computational resources, making them impractical for large-scale or real-time energy management systems. This limits their utility in scenarios where fast and efficient forecasting is critical. Many existing models focus on forecasting single variables, which restricts their ability to predict multiple interdependent factors simultaneously. While studies such as [24,25] have achieved high prediction accuracy, they lack the multivariate capabilities necessary for simultaneously forecasting temperature, irradiance, and PV power output. This gap reduces the efficiency and practicality of these models in real-world applications. Some studies, such as [3,26], have integrated uncertainty quantification into their models, but these approaches often rely on ensemble or statistical methods that significantly increase computational demands. Furthermore, their robustness under dynamic weather conditions remains questionable, as they often fail to adapt to unexpected variations effectively.

Moreover, deep learning models, including those in [11] and [23], are frequently labelled as "black-box" systems due to their lack of interpretability, which hampers operator trust and understanding. Although efforts such as [16] utilized XAI tools to improve interpretability, these tools are external and not inherently part of the forecasting models, creating additional complexity for operational use. Many studies, including [30] and [7], focus on improving forecasting accuracy but fail to address downstream applications such as load scheduling and resource coordination. This limitation reduces the applicability of these models in integrated energy systems, where such capabilities are essential for practical decision-making and operational efficiency.

2. Proposed ANFIS-Based PV Prediction Model

The proposed study integrates PV power forecasting with battery energy management, providing a unified approach to energy utilization and grid stability. Unlike models such as [6,28], which separate forecasting from battery management, this study ensures robust SOC stability and achieves long hours of battery autonomy under specified load conditions. This integration enables seamless energy planning and resource allocation. The ANFIS-based model demonstrates high accuracy in predicting PV power under diverse meteorological conditions, achieving better accuracy for temperature and irradiance. This adaptability addresses the limitations of hybrid models like [9] and [19], which struggle with fluctuating weather patterns. Additionally, the model surpasses the performance of single-variable frameworks such as LSTM [18] and CNN-LSTM [27]. By employing a MIMO algorithm, the proposed study enables simultaneous prediction of temperature, irradiance, and PV power output, enhancing prediction efficiency and utility. This capability improves upon methods like [24,25], which lack multivariate prediction capabilities and focus on single-variable outputs. The integration of MIMO with ANFIS provides a comprehensive forecasting approach. The computational efficiency of the ANFIS model makes it superior to architectures like ConvGNNs [2] and MOSMA-SVM [20], which are computationally intensive. The lightweight nature of ANFIS ensures scalability and real-time applicability, making it practical for large-scale energy management systems and real-world deployments.

Furthermore, the inherent explainability of ANFIS models, combining neural networks with fuzzy logic, offers transparent and interpretable predictions without requiring external XAI tools like those used in [16]. This feature significantly enhances operator trust and usability, bridging the gap between accuracy and operational applicability found in existing "black-box" models like [23]. The study also focuses on battery integration and load scheduling, providing direct applications in energy planning, resource coordination, and operational efficiency. Unlike [7,30], which concentrate purely on forecasting, the proposed model extends its functionality to downstream energy management tasks, offering a holistic solution for integrated energy systems. Finally, the robustness of the ANFIS model under complex data variations and its ability to maintain high accuracy across diverse datasets make it ideal for real-world scenarios. Its performance surpasses that of [3,26], ensuring reliability under dynamic and extreme weather conditions without significant computational overhead.

The major contributions of the paper can be summarized as follows.

• Integrating PV forecasting with battery SOC management, maintaining SOC stability (0.88% drop over 7 days) and providing 11 hours of battery autonomy, supporting energy planning and load scheduling.
• High prediction accuracy with ANFIS, reaching 95.10% for temperature and 98.06% for irradiance, outperforming traditional methods like ANN under complex meteorological conditions.
• Employing a MIMO algorithm to simultaneously predict temperature, irradiance, and PV power, improving forecasting efficiency over single-variable methods.
• Computational efficiency with ANFIS, surpassing resource-intensive methods like ConvGNNs, ensuring scalability and real-time applicability for energy systems.
• Combining fuzzy logic and neural networks for interpretable predictions, removing the need for additional outputs to explain model outputs, and enhancing practical utility in energy management.

3. Materials and Methods

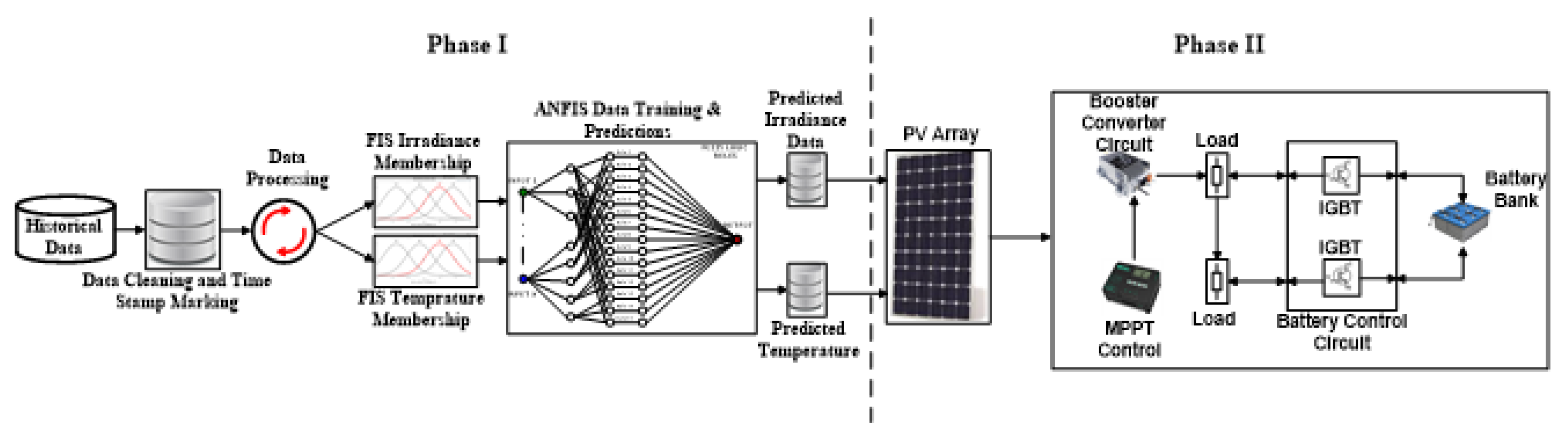
This research utilizes a hybrid approach integrating machine learning (ML) techniques to forecast the power generation of a solar photovoltaic (PV) farm. The proposed ANFIS-based prediction and energy management framework is presented in Figure 1.

As shown in Figure 1, the research framework is divided into two major phases, namely the (i) prediction phase and (ii) energy management phase. The first phase of the research framework represents the machine learning application, which predicts irradiance and temperature for the PV farm using the ANFIS algorithm, with these variables serving as inputs for the energy management phase.

3.1. Phase 1: ANFIS-Based PV Prediction System

3.1.1. Method Design and Data Preparation

The first stage involves the collection of historical meteorological data. The historical irradiance and temperature data are sourced from the West Texas MESONET database pertaining to the solar farm’s geographical location. This dataset includes timestamps, solar irradiance, and ambient temperature values, which form the core variables for the predictive model.

The raw data undergo preprocessing steps to enhance its suitability for modeling purposes. These steps include:

• Data Cleaning: Removal of erroneous entries and outliers to maintain data consistency;
• Interpolation: Estimation of missing values using statistical techniques to ensure completeness;
• Normalization: Scaling the data to a standard range, reducing variability, and improving model performance.

The processed data is structured in a matrix format and stored in an Excel file. Each entry comprises of Timestamps representing the temporal aspect of the dataset, Solar irradiance values, and Ambient temperature values.

3.1.2. Model Implementation

The ANFIS framework is employed to model and predict the temporal variation of solar irradiance and temperature. The design and implementation process follows a systematic workflow:

• Data Loading: The algorithm imports the Excel-stored matrix, where the timestamp column serves as the time index, and the irradiance and temperature columns represent the input variables.
• Feature Engineering: Lag features are created to capture temporal dependencies and recognize patterns in the dataset, which are critical for accurate predictions. These features enable the model to identify trends and seasonal effects in the historical data.
• Data Splitting: The dataset is divided into input matrices and target vectors, ensuring systematic utilization during the training phase. The input matrix comprises time-dependent features, while the target vector includes corresponding irradiance and temperature values.
• Model Training: The ANFIS algorithm trains on the input data, employing fuzzy logic to address uncertainties and adaptive learning to refine predictive capabilities. The training process is iterative, optimizing model parameters to minimize prediction errors.
• Prediction and Validation: Once trained, the ANFIS model forecasts the next day’s irradiance and temperature values. Validation involves comparing predictions against known historical data to ensure the model’s reliability.

3.1.3. Accuracy Enhancement Techniques

To improve the accuracy of the results, additional measures are incorporated:

• Cleansing and Conditioning: Rigorous preprocessing ensures the data is free from inconsistencies and suitable for modeling.
• Normalization/Denormalization: Scaling reduces the effect of variable magnitudes, enhancing the stability of the training process. The normalized data set is guided by Equation 1. The output results are then denormalized and compared with the historical data using Equation 2.

  $$x_{\mathrm{norm}}\left(i\right)={\displaystyle \frac{x_i-x_{min}}{x_{max}-x_{min}}}$$

  (1)

  $$x_i=x_{\mathrm{norm}}\left(i\right)*\left(x_{max}-x_{min}\right)+x_{min}$$

  (2)

  where $x_i$ is the historical data, $x_{min}$ is the minimum raw data, $x_{max}$ is the maximum raw data, and $x_{\mathrm{norm}}\left(i\right)$ is the normalized data set.
• Pattern Recognition: Temporal lag features and multivariate analysis allow the model to learn complex interdependencies within the dataset.

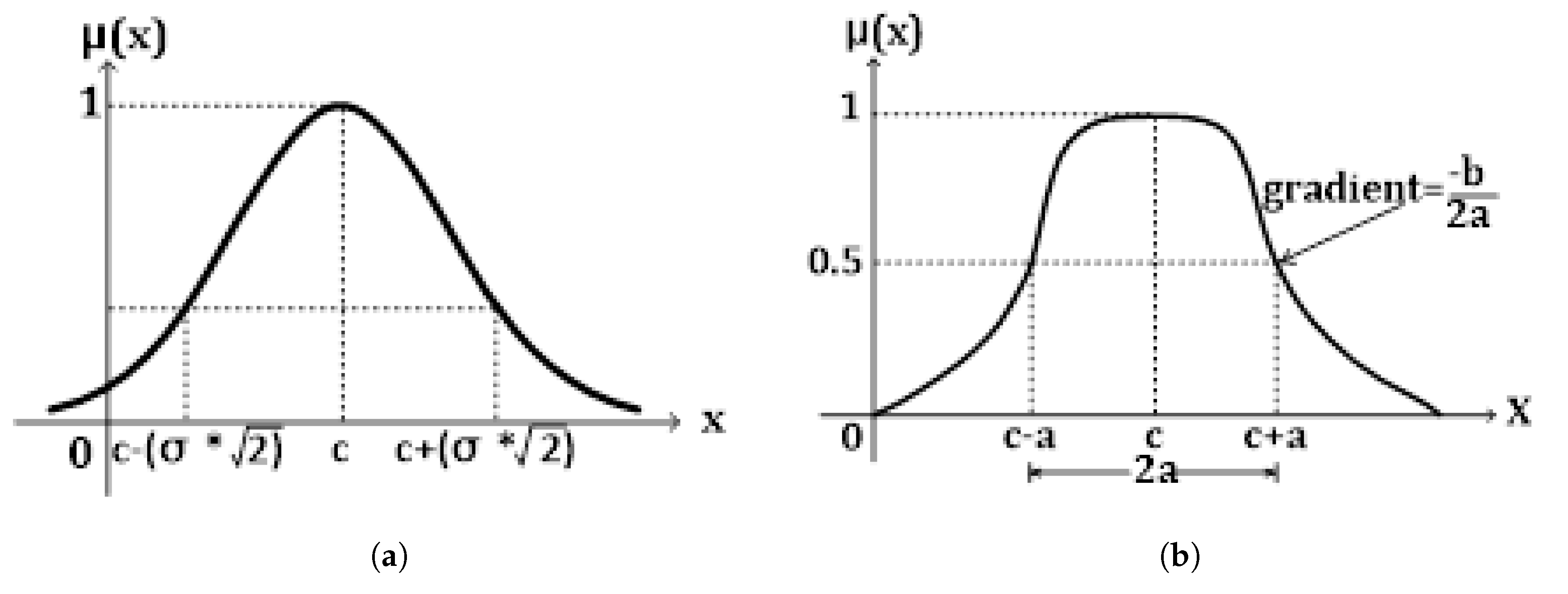
3.1.4. Gaussian and Bell Membership Functions

Two Adaptive Neuro-Fuzzy Inference System (ANFIS) membership functions, namely the Gaussian and Generalized Bell membership functions, are defined for the input variables to enhance the prediction process. The ANFIS implementation facilitates comprehensive data training, prediction, and validation, while also providing graphical visualization to compare the forecasted values with the time-stamped historical data used during training. The Gaussian and Bell membership functions (gaussmf), as defined by Equations (3) and (4) respectively, and illustrated in Figure 2, is employed to compute smooth and continuous membership values, enabling effective handling of input uncertainties.

$$\mu \left(x\right)=e^{-\left[{\displaystyle \frac{{(x-c)}^2}{2{\sigma }^2}}\right]}$$

(3)

$$\mu \left(x\right)={\displaystyle \frac{1}{1+{\left|\frac{x-c}{a}\right|}^{2b}}}$$

(4)

where $\mu \left(x\right)$ is the Gaussian function c is the mean, and $\mathsf{\sigma }$ is the standard deviation. The function is smooth and symmetric, controlled by the mean c and standard deviation $\sigma$, which better represent the data’s seasonality over a given period. a, b, and c are the adjustable shape parameters as shown in Figure 2b.

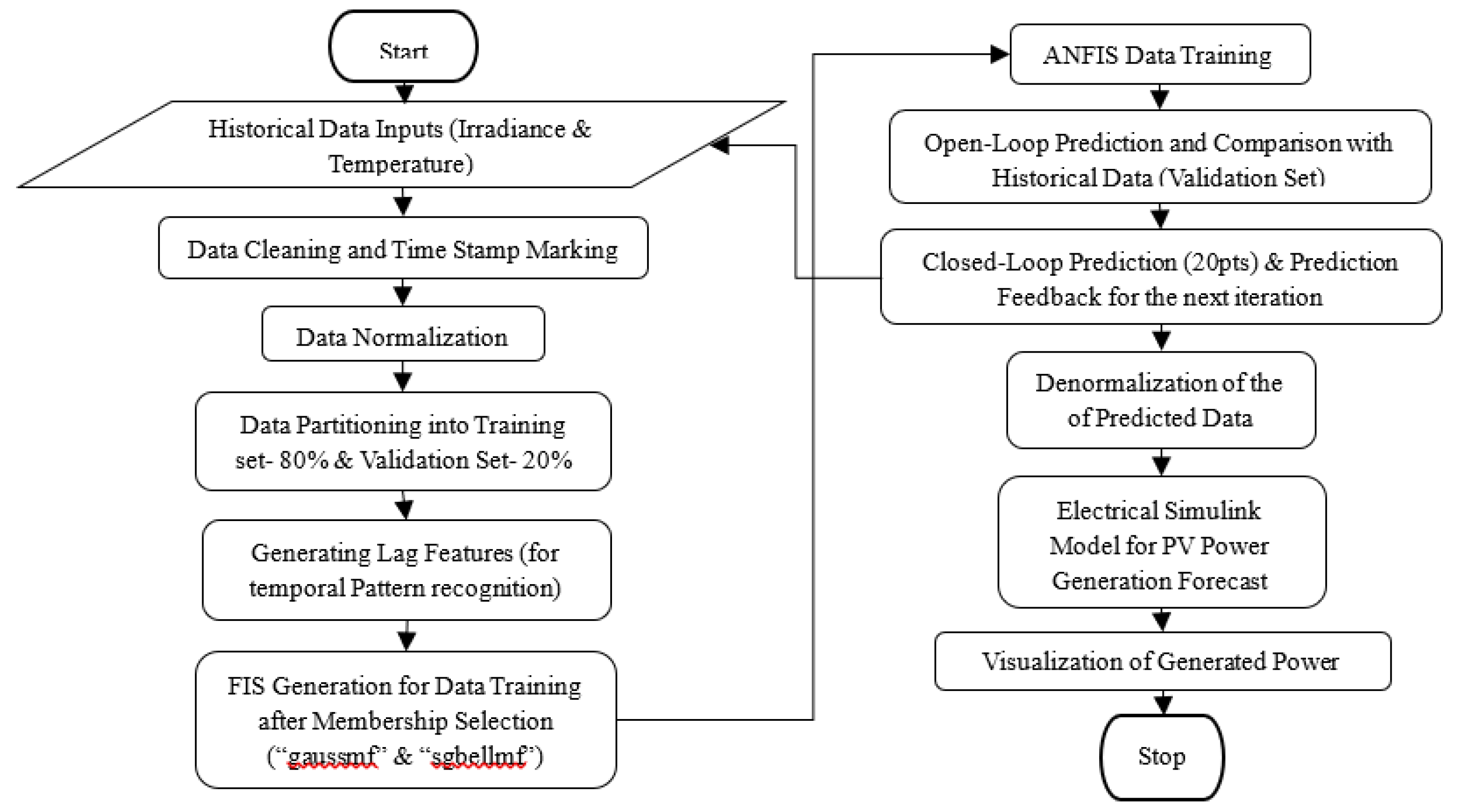
The design flowchart of the ANFIS training and prediction network is shown in Figure 3.

3.2. Phase 2: Energy Management System

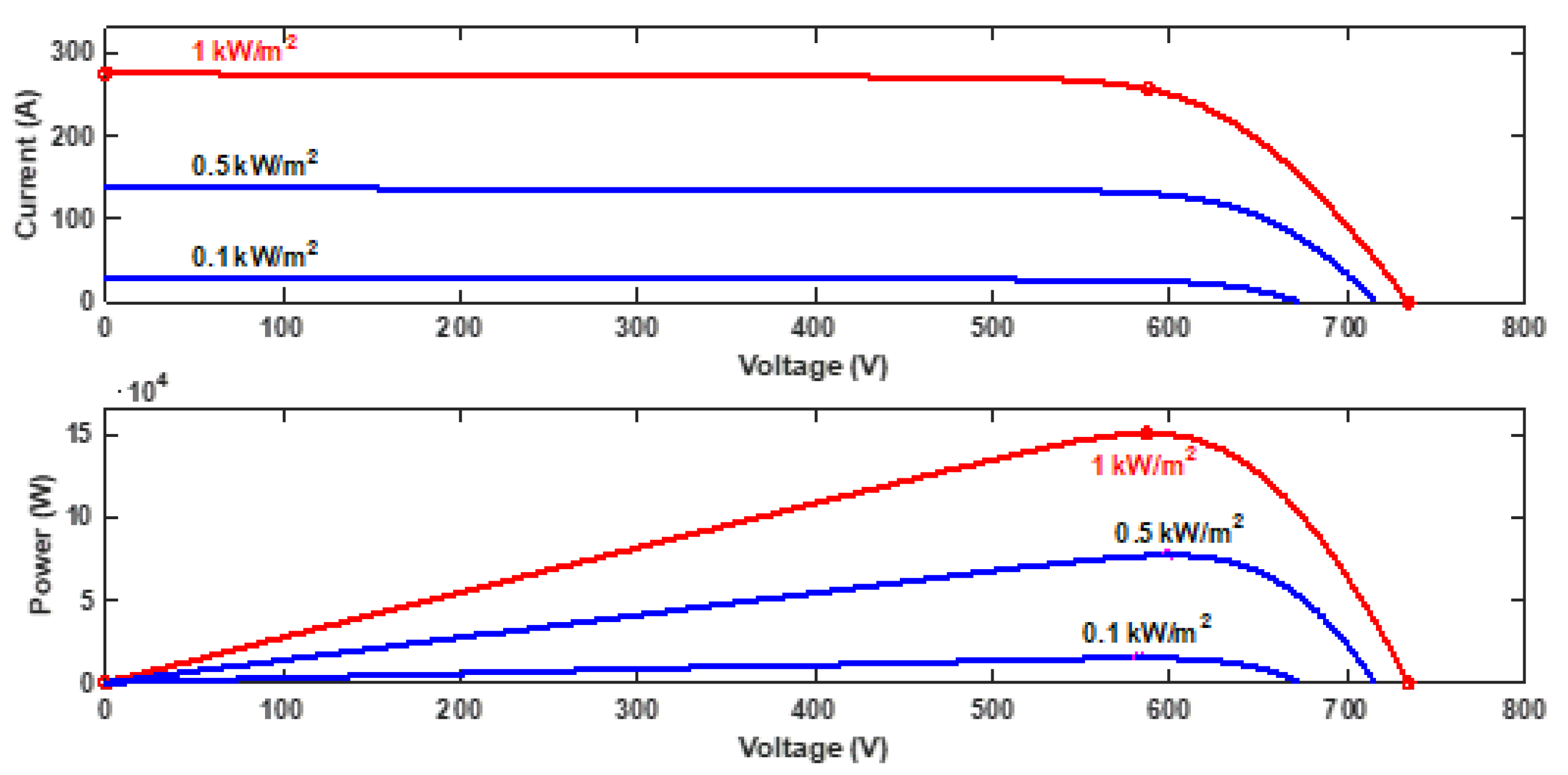
The energy management phase consists of three major subsystems: the (i) PV array, (ii) boost converter/load, and (iii) battery control. The electrical system of the PV farm is modeled in Simulink, incorporating a PV array, boost converter, and shunt load to replicate the real PV farm configuration. The PV array simulates the I-V and P-V characteristics of the entire PV-farm configuration as shown in Figure 4, while the boost converter regulates output voltage for efficient energy transfer between the PV array and the load.

The shunt load models the system’s interaction with the grid or storage, enabling analysis of performance under varying conditions. The electrical model includes the following components:

• Signal Builders: These extract forecasted irradiance and temperature data from an Excel data bank, feeding the values into the PV-array model. The model accurately represents the real PV farm with a capacity of 150 kW and utilizes SolarWorld Sunmodule SWA 320 XL mono modules.
• Boost Converter Circuit: This circuit consists of an IGBT, a diode, and a PV-side filtering capacitor. A boost signal applied to the IGBT gate controls power flow on the PV side, while the diode ensures unidirectional current flow and enhances capacitor efficiency. The converter operates using PWM signals generated by the MPPT algorithm to optimize energy transfer.
• Bi-Directional Converter for Battery: This component supports seamless battery charging and discharging. It ensures the battery charges when excess PV energy is available and discharges to meet load demands during deficits, using switching signals for both positive and negative sides.
• PWM Generator: Generates boost signals for both PV and battery-side controls, based on a duty cycle computed by the MATLAB PV control function, enabling precise energy management within the system.

The maximum power point transfer (MPPT) and maximum load (shunt resistance, $R_{sh}$) are determined by Equations (5) and (6), respectively.

$$R_{sh}={\displaystyle \frac{V_{MPPT}}{I_{MPPT}}}$$

(5)

$$\mathrm{Maximum}\mathrm{Load}=I_{MPPT}^2*R_{sh}$$

(6)

where $V_{MPPT}$ and $I_{MPPT}$ are the voltage and current at MTTP.

PV-side capacitance, $C_{PV}$ and inductance, $L_{PV}$ are estimated by Equations (7) and (8), respectively.

$$C_{PV}={\displaystyle \frac{I_o\left(V_0-V_i\right)}{f_{SW*\Delta V*V_0}}}$$

(7)

$$L_{PV}={\displaystyle \frac{V_i\left(V_0-V_i\right)}{f_{sw}*\Delta I*V_0}}$$

(8)

where $V_i$ is the Boost converter input voltage, $V_o$ is the boost converter output voltage, $f_{s}w$ is the Boost converter switching frequency, $I_o$ is the Output current of the converter, $\Delta V$ is the Ripple voltage, and $\Delta I$ is the Ripple current.

The battery side capacitance value is set to be equal to the PV side capacitance value to ensure maximum power transfer to the load side. The duty cycle is adjusted in relation to Equation (9).

$$R_{\mathrm{load}}={\displaystyle \frac{R_{\mathrm{source}}}{{(1-D)}^2}}$$

(9)

where $R_{\mathrm{source}}$ is the source resistance given by Equation (6).

3.3. Use Cases

3.3.1. Parameter Settings

The ANFIS Training for both irradiance and temperature is set at 600 Epochs with an appropriate number of membership functions. The training failed to converge accurately above two (2) membership functions defined for each of the variables while the number of iterations was carefully tuned from 300 to 600 Epochs for best forecast accuracy, above which the performance of the algorithm remains the same. The open-loop ANFIS prediction algorithm deploys temporal pattern recognition with the introduction of lag features, while the closed-loop algorithm feeds back the current prediction into the historical data for the next prediction capturing the dynamics of an erratic data set.

4. Results

The prediction results for both the open-loop and closed-loop are presented in the following subsections. Open-loop prediction utilizes pattern learning during training and predicts the next iteration while continuously updating its historical dataset for subsequent predictions. This approach ensures that the model remains responsive to new data during the forecasting process. In contrast, closed-loop prediction uses its own predicted data as the basis for generating subsequent forecasts, without incorporating historical data updates. This involves a single training phase, relying on the learned patterns to iteratively predict future points.

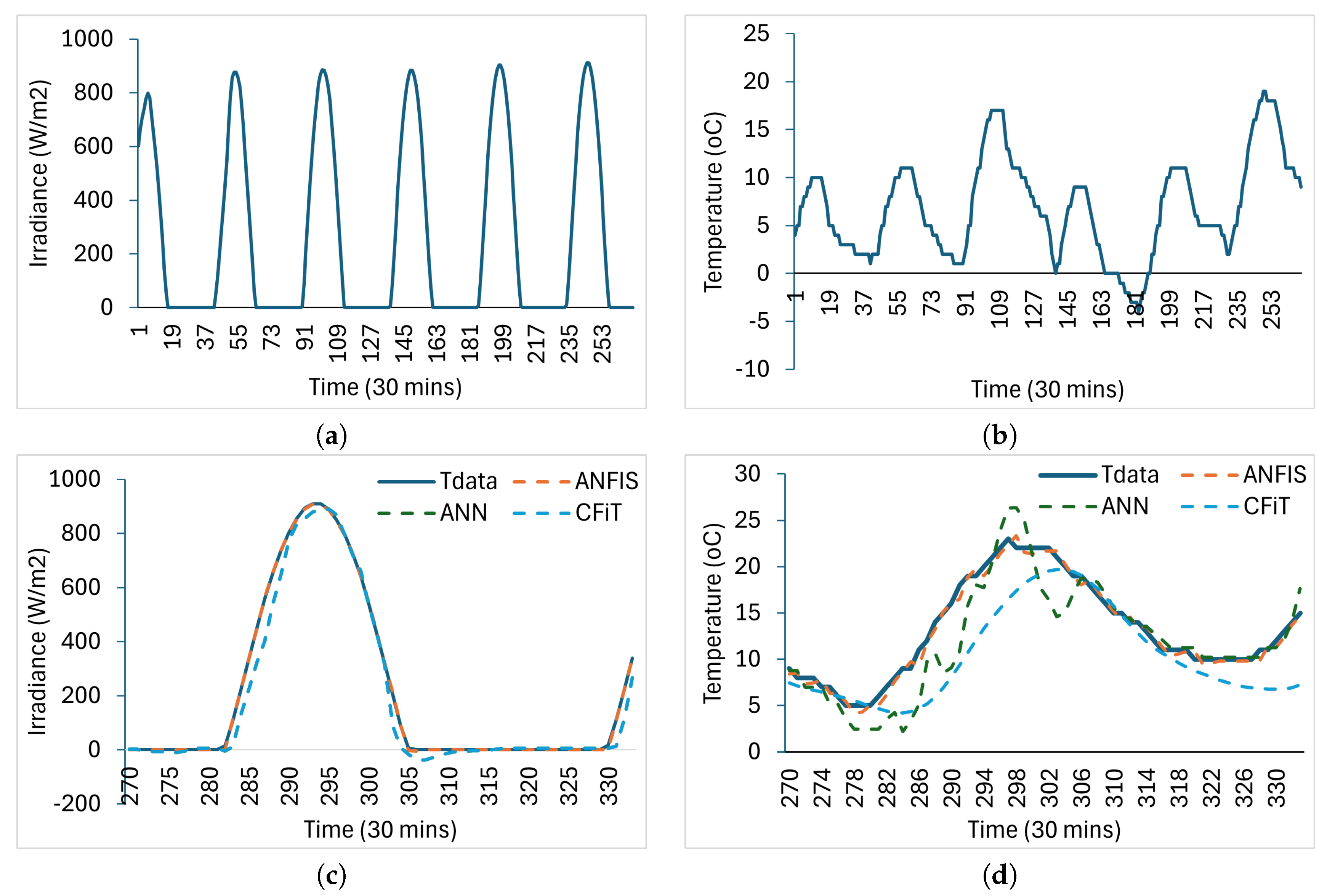
4.1. Open-Loop Predictions

For the open-loop prediction, the irradiance and temperature historical data are trained with the training data using ANFIS, ANN, LSTM, and curve-fitting algorithms at suitable numbers of epochs. The algorithm performances are then evaluated with the test dataset as presented in Figure 5. As could be observed, the ANFIS model outperformed the ANN and curve-fitting models. The prediction performances, including the accuracy and root mean square error, are presented in Table 1.

4.2. Closed-Loop Predictions

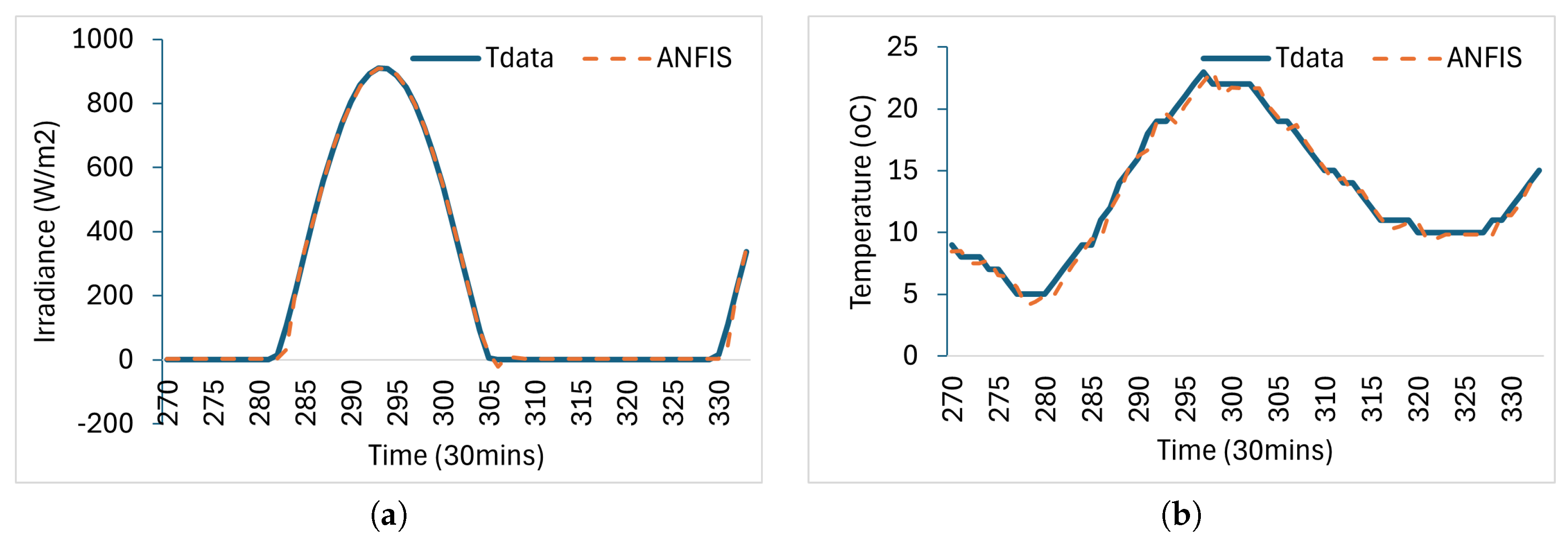
Closed-loop prediction leverages the training knowledge of the historical data and predicts the next iteration using the feedback closed-loop data. Thus closed-loop prediction is carried out without historical data update. The closed-loop prediction of the irradiance and temperature at 600 epochs is presented in Figure 6.

The ANFIS network effectively predicts 10 hours of irradiance and temperature data, above which the prediction accuracy cannot be guaranteed due to the amount of data deployed for training. The historical data bank is dynamically updated with new data as it becomes available during the simulation. These predicted values are then input into the electrical model to forecast the power generation of the site.

4.3. PV-Farm Power Generation Forecast

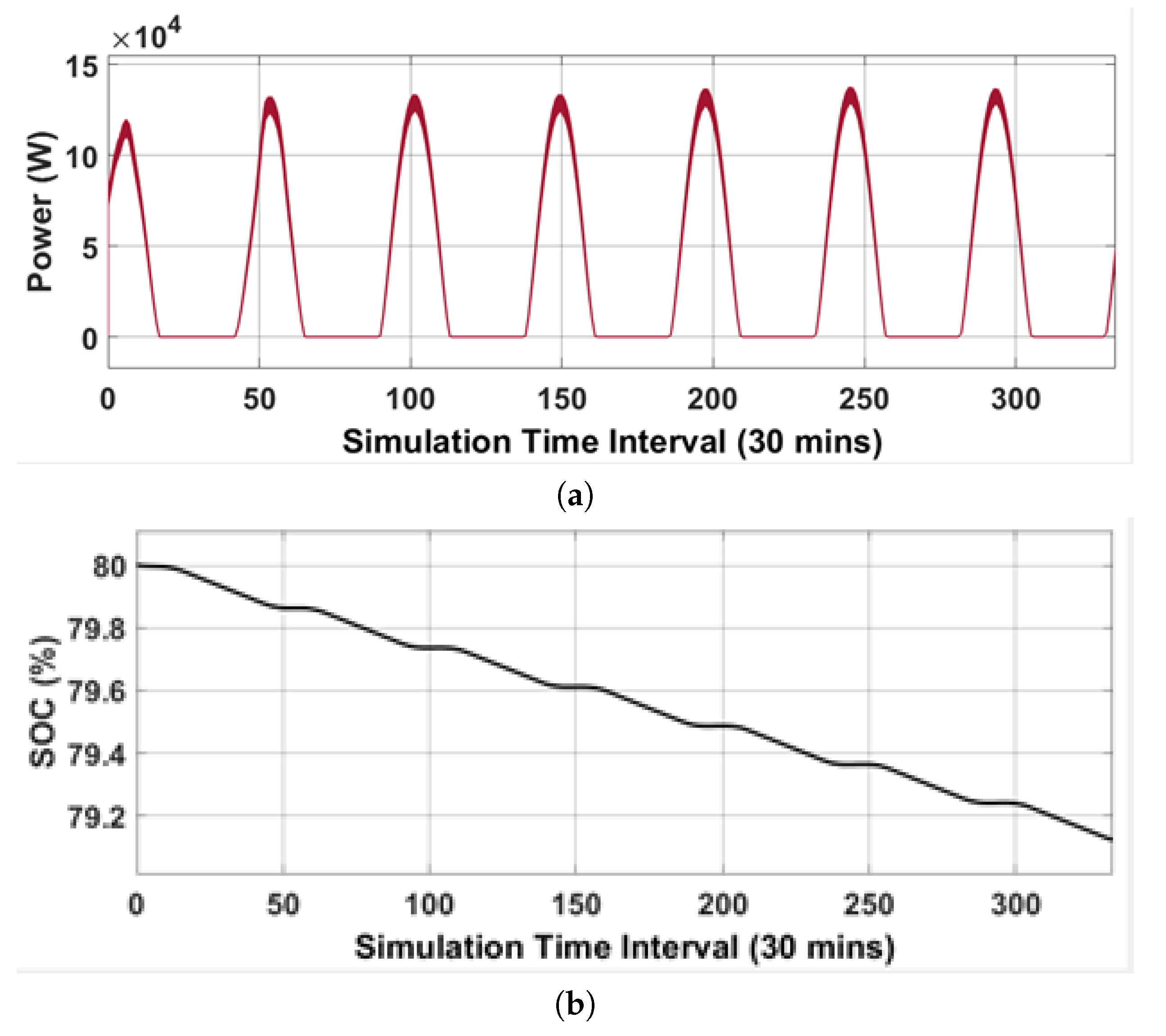
The electrical model’s accuracy is validated using actual historical data under ideal conditions of maximum generation (150 kW) at 1000 W/m² and 25°C.

As shown in Figure 7a, the generation remains within the expected limits and varies with irradiance and temperature as anticipated. The model demonstrates excellent performance, achieving a validation accuracy of 98%. Similarly, the battery state of charge (SOC) in percentage was equally measured. Battery bank design is based on the plant’s nominal voltage of 480 V and battery maximum capacity of 1600 AH. This is very important for expansion purposes and battery autonomy planning as can be observed from Figure 7b, the battery SOC, discharged from 80% to 79.1212% over 7 days with cyclic charging and discharging of the battery bank.

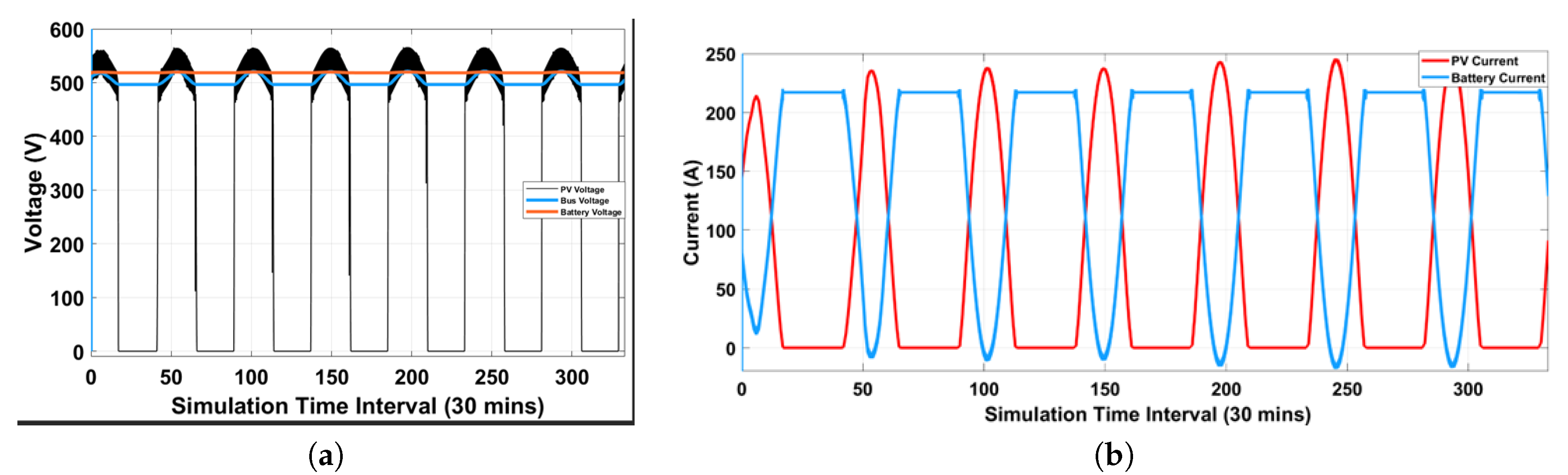
Figure 8a is a combined voltage view of the PV-array generated, DC Bus, and Battery Voltages. The Battery Voltage (DC Source) is linear as expected, and the bus voltage is maintained within the permissible range. (> 480 V). Figure 8b is the combined current view. The Battery current, as shown in Figure 8b, went negative at peak sunlight hours as the PV array produces more energy than the load demands, especially during peak sunlight hours. The excess current generated is used to charge the battery. Thus, the battery is in a charging cycle and current flows into the battery.

5. Discussion

This research introduces a new model for energy management in a microgrid with PV resources, integrating a PV-battery system with ANFIS capabilities. The model operates in two phases: the ANFIS prediction phase and the electrical modeling phase. The ANFIS prediction model uses site-specific irradiance and temperature as inputs to forecast variables, which are then fed into the electrical model for accurate power forecasting. The ANFIS algorithm demonstrates superior accuracy compared to ANN and curve-fitting techniques, effectively predicting solar farm power generation over a 10-hour period. The model’s predictions align closely with the actual site power capacity, making it a reliable tool for informed energy management decisions. Future work will focus on incorporating a load profile estimator to enhance load management and implement demand response strategies for improved energy planning.

6. Conclusions

In conclusion, a robust PV-battery model incorporating the ANFIS algorithm has been developed to forecast power generation in a solar farm effectively. The electrical model benefits from the ANFIS algorithm’s superior capability to accurately predict irradiance and temperature, providing reliable input for the electrical simulations. The clear distinction between the ML prediction algorithm and the electrical model highlights the modularity and adaptability of the approach, enabling precise power forecasting and facilitating informed energy management.