Newtonian Theory of Orbit Perturbation and Revalued Mass of Sgr A*

1. Newtonian Theory of Orbit Perturbation and Galactic Dynamics

1.1. Newtonian Theory of Orbit Perturbation Is Needed to Understand the Orbits About a Stellar Cluster in a Galaxy

It is generally known that the orbit in the solar system is stable. But, there is a very famous old problem: Calculated with $F=GMm/R^2$, the force of the Sun on the Moon is almost 2.2 times that of the Earth. It should have made the Moon run to the Sun and made the orbit of the Moon around the Earth broken of very quickly.[11] But, it is clear, the orbit of the Moon around the Earth is stable. This problem cannot be answered for a very long time until it has been understood with the Newtonian theory of orbit perturbation in recent.[12]

The Newtonian theory of orbit perturbation is written as

$$g=G{\displaystyle \frac{M_{center}}{R^2}}+\sum G{\displaystyle \frac{m_i}{r_i^3}}\mathit{R}$$

(1)

where $M_{center}$ is the center mass, $m_i$ is the mass of other objects; R is the distance between the center mass and the orbit body, r is the distance between perturbative body and the orbit body.

It is very important, in the Newtonian theory of orbit perturbation, there is a center mass to determine the radius of the orbit around it.[12,13] In the Earth-Moon system, the Earth is the center mass. Eq.(1) means that, the radius of an orbit is fundamentally determined with the mass of the center body, the Earth, and only the center mass has the gravitational acceleration $g_{center}=G{\displaystyle \frac{M_{center}}{r^2}}$ on the orbit. The mass of other bodies, including the Sun, only can have the perturbative acceleration $g_{perturb}=G{\displaystyle \frac{m_i}{r_i^3}}\mathit{R}$ on it. This is the reason why the orbit of the Moon around the Earth cannot be broken off by the Sun. Therefore, the famous old problem why the orbit around the Earth cannot be broken off by the Sun was well explained with Eq.(1).

It is important that, $\mathit{R}$ is a vector of R; which results in that $\sum G{\displaystyle \frac{m_i}{r_i^3}}\mathit{R}$ can be very little under the condition that $i$ is very large. So, Eq.(1) is still valid to a system with a lot of stars.[12] So, the Newtonian theory of orbit perturbation could be easily applied in understanding the orbits in a galaxy.

Compared with the famous old problem,[11] for the Sgr A*--Sun system, we know, the Sun is orbiting around the Sgr A* with the velocity of $~220km/s$ and the radius of $~\mathrm{26,000}lightyears$. From $v=\sqrt{GM/r}$, we know, a mass of $~1.8\times {10}^{11}{M}_{Sun}$ is needed to form such an orbit.[4] But, if there was a gravitational acceleration produced from a mass of $~1.8\times {10}^{11}{M}_{Sun}$ on the Oort cloud which is on the edge of the Sun system, it is easy to know that the acceleration from this mass is larger than 100 times that from the Sun; which should have made the Oort cloud run away from the Sun system. But, we know, the Oort cloud is stably orbiting around the Sun. Therefore, that the Oort cloud around the Sun cannot be broken off by the force from the mass of $~1.8\times {10}^{11}{M}_{Sun}$ clearly shows that the Newtonian theory of orbit perturbation is needed to understand the orbits in the Sgr A*--Sun system.

It may be argued that in current theory for the orbits in a galaxy, according to the Poisson equation, the mass of $~1.8\times {10}^{11}{M}_{Sun}$ is the sum of all the mass enclosed in the sphere with the radius of 26,000 light years. But, here, what we need focus on is that the orbit of the Oort cloud around the Sun cannot be broken off by the mass of $~1.8\times {10}^{11}{M}_{Sun}$; which clearly means that the center mass for the orbit is the Sun while the mass of $~1.8\times {10}^{11}{M}_{Sun}$ is only a perturbative one; just as the orbit of the Moon around the Earth in which the center mass is the Earth while perturbative mass is the Sun. It certainly shows that the Newtonian theory of orbit perturbation for the orbit in a galaxy is just as that for the orbit in the solar system. It also shows that, just as the orbit of the Moon around the Earth cannot be related with the sum of the masses of the Sun and Earth,[12] the orbits in a galaxy also cannot be related with the sum of masses of all the stars in a sphere. Further, it also showed that the Poisson equation is invalid. (The invalidity of the Poisson equation shall be discussed in detailed lately.)

In recent, it was found that, at the center of the ω Centauri there is an intermediate black hole with a mass of $~\mathrm{8,200}{M}_{Sun}$.[14] For the same way, it is easy to know that, as a mass of $~1.8\times {10}^{11}{M}_{Sun}$ is acting on the orbit of the ω Centauri around the Sgr A*, the calculated force of it on the orbits on the edge of the ω Centauri around the intermediate black hole at the center of the ω Centauri is larger than that of the black hole with the mass of $~\mathrm{8,200}{M}_{Sun}$. It should make the orbits on the edge of the ω Centauri broken off. And, factually, the orbits in the ω Centauri are stable. This is another case to show that the Newtonian theory of orbit perturbation is needed to understand the orbit in a galaxy.

1.2. The Mass of the Sgr A* and Hill Sphere

Hill sphere can be approximately written as

$$r=d\sqrt[3]{{\displaystyle \frac{m}{3M}}}$$

(2)

where m is the mass of the star, M is the large mass that m is orbiting around, r is the Hill radius of the star in which the orbits of the planets around the star are stable, d is the distance between m and M.

Hill sphere was well used: 1) to understand the stability of the orbits around a star,[15,16,17] 2) to look for the exoplanets or habitable planets,[18,19] and 3) to design the interstellar orbit.[20] But, it has not been used to understand the orbits in the galaxy.

In the Milky Way, our solar system and a lot of other stellar clusters are orbiting around the Sgr A*. Therefore, the mass of the Sgr A* can be calculated from Eq.(2) with the solar system. And, recently, it was observed that there is a black hole with the mass of ${\mathrm{8,200}M}_{Sun}$ at the center of ω Centauri. From Eq.(2), the mass of the Sgr A* also can be calculated with the ω Centauri as shown in the Table 1.

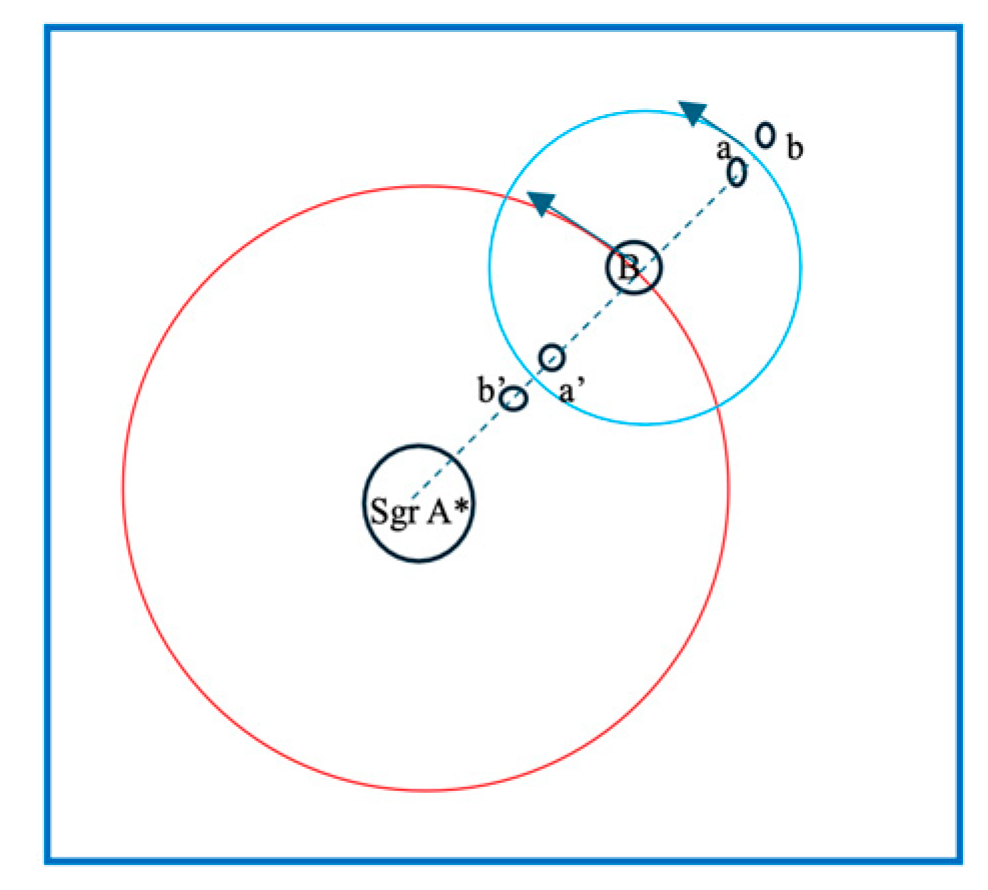
• Note 1: The Oort cloud is with 1.5 light years from the Sun. We select $r=3$ light years as the Hill radius of the Sun.
• Note 2: the radius of the ω Centauri is almost 75 light years. Here, the Hill radius is selected as $r=150$ light years. The largest distance from the Sgr A* is $d_{\mathsf{\omega }}=\mathrm{21,000}ly$.

Table 1 shows that, with $r=d\sqrt[3]{{\displaystyle \frac{m}{3M}}}$, from the Sgr A*--Sun system, the predicted mass of the Sgr A* is on the level of ${~10}^{11}{M}_{Sun}$. It is highly accordant with that predicted from the Newtonian theory of orbit perturbation. Both the predictions are in the level of ${~10}^{11}{M}_{Sun}$. While, that for the Sgr A*--ω Centauri system is only ${~10}^9{M}_{Sun}$. We think, maybe, further measurement for the ω Centauri is needed for that it was first measured recently.

From Eq.(1) we know, a center body, such as a black hole or other massive body, is needed to form a stellar cluster with stable orbits around it. Therefore, it could be concluded that, at the center of every stellar cluster, there should be a center body (black hole or other massive body). The mass of the center body could be known from two ways. First, from the Newtonian theory of orbit perturbation we know, it could be known from any one of the orbits around the center body. As the radius and velocity of the orbit is known, the mass of the center body can be obtained from $v=\sqrt{Gm/r}$. Second, it could be obtained from the Hill sphere. The mass of the Sgr A* is known, and the radius of a stellar cluster, r, and the distance between the cluster and the Sgr A*, d, were observed. The mass of the center body of the stellar cluster can be known from Eq.(2).

2. Discussion

2.1. The Center Mass in a Galaxy

Usually, the orbits and motion of a spiral galaxy can be expressed with Figure 1.

From Figure 1, we know, as the galaxy is moving along the red arrow, the stars in the galaxy are orbiting or rotating around the center of the galaxy along the black arrow. Now, it is known that, at the center of the Milky Way, it is the Sgr A*. Therefore, as studied in [12], a moving galaxy is just as a moving stellar system which is moving as one single unit; the directions of the orbits in it cannot affect the motion of the whole system. So, we have the conclusions for the Sgr A*:

1)

Sgr A* is the center body of the Milky Way.

2)

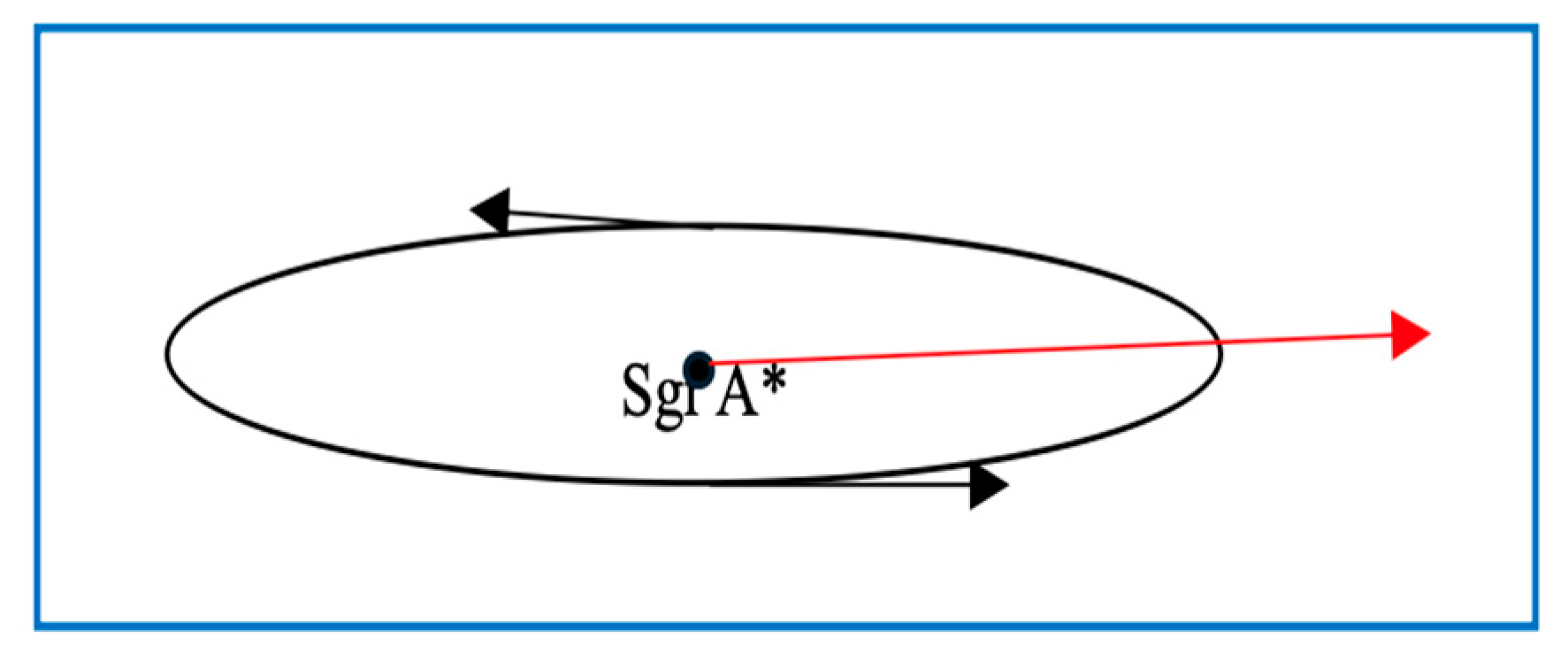
Because the directions of the orbits of many stars are contrary to that of the motion of the galaxy, it can be concluded that it is the Sgr A* that makes the whole galaxy moved along the red arrow, just as the solar system is moved by the motion of the Sun.[12]

3)

It is emphasized that the orbits in the Milky Way are stable and are dominated by the Sgr A*. The galaxy is with a radius about 100,000 light years, if the orbit of every star or stellar cluster was with a little shift, the motion of the galaxy should have become chaotic.

4)

The mass of the Sgr A* need be very large. A small mass cannot make the whole galaxy moved and make the orbits with the radius about 100,000 light years in the galaxy stable.

2.2. Misled Theories of Gravity

In understanding the orbits in a galaxy, the Newtonian theory of orbit perturbation was misled by two factors.

First, the Newtonian theory of gravity was misunderstood by the Poincaré’s equation for Three-body problem. For the convenience of the readers, we copy our previous sentence here: [12]

Newton established the theory of orbit in 1660s. But, Newton’s theory has not been completely. understood till now. As soon as comparing Poincaré’s equation of Three-body problem with Newtonian orbital perturbation theory, we shall know what is the problem in current understanding about Newtonian theory of gravity. The Sun-Earth-Moon system is the oldest Three-Body problem. It is clear, the orbits about it was well resolved by Newton. But, there is a famous old problems: calculating with$F=GMm/R^2$, the attractive force of the Sun on the Moon is almost 2.2 times that of the Earth, but the orbit of the Moon around the Earth cannot be broken off by the Sun. It is clear, as Poincaré’s equation for Three-body problem is applied on the solar system, the orbits in it should be broken off in a short time. We think, this is the crucial evidence to show that the Poincaré’s equation for Three-body problem is wrong. And, the triple star system and multiple star systems, including Six-star system, [22,23] were observed. The orbit in these systems are stable and certain.

The Poincaré’s equation for Three-body problem is very strange. First, no orbit of the celestial body is chaotic. So, Poincaré’s equation cannot be related with any real orbit. Second, the orbits of the typical Three-body system, such as the Sun-Earth-Moon system and Sun-Pluto-Charon system, are stable. Poincaré’s equation is invalid to understand these orbits. Third, Poincaré’s equation is invalid to design an artificial orbit. It is very clear, the Poincaré’s equation is nonsense in understanding any real orbit. Additionally, the relationship between the Poincaré’s equation and other theory is very weak. If there was not Poincaré’s equation, the celestial dynamics could not be affected. But, very unfortunately, Poincaré’s equation is the mainstream understanding about Newtonian theory of gravity. It results in that, the current theory of orbit about the galaxy is questioned.

Second, the most importantly, at the time the galactic rotation curve was formulated, the Sgr A* had not been confirmed.[3,4] The center body for the orbit in the Milky Way had not been known, the Newtonian theory of orbit perturbation cannot be considered to understand the orbit in the Milky Way. In this case, physicists have to use the Poisson equation to calculate the orbits in the galaxy. It is clear, this is inapt and unwarranted for that the Sgr A* is the center body that the whole galaxy is rotating around, which determines the orbits in the galaxy and the motion of the whole galaxy.

Although now the Poisson equation is still prevailing in studying the orbits in the galaxy, it is questioned theoretically and observationally.

Here, it is emphasized that, it was well observed there are many stellar clusters in a galaxy. Therefore, the orbits in a galaxy is complicated. Usually, the orbits of a stellar cluster can be described with Figure 2. As a center body B (black hole) of a cluster is orbiting around the Sgr A*, there are a lot of stars are orbiting around B, which results in that the orbits of the stars are very complicated. As shown in Figure 1, the direction of the orbital velocity of the stars a’ is contrary to that of b’; the velocity of a and b are $v_a=\sqrt{M_{SgrA*}/R}+\sqrt{M_{SgrA*}/(R+r)}$ and $v_b=\sqrt{M_{SgrA*}/(R+r)}$, respectively; and the velocity of a’ and b’ are $v_{a\text{'}}=\sqrt{M_{SgrA*}/R}-\sqrt{M_{SgrA*}/(R+r)}$ and $v_{b\text{'}}=\sqrt{M_{SgrA*}/(R-r)}$, respectively.

Therefore, here, it is emphasized that, as soon as the orbits in a stellar cluster is studied, it shall be known at once that lots of stars have not orbit around the Sgr A*. And, the rotation curve of these stars around the Sgr A* is with the shape between the two kinds of lines described in the Figure 1 of [12]. The shapes of the lines are very different. So, a galactic rotation curve is made up of two different kinds of lines: First, it is the orbits around the Sgr A*. Second, it is the orbits of the stars in the cluster around the center body of the cluster; which is not with the orbit around the Sgr A* although it is rotating around the Sgr A*.

Therefore, it need be noted that an orbit is basically determined with G${\displaystyle \frac{Mm}{R^2}}=m{\displaystyle \frac{v^2}{R}}$, and, an orbit is usually an oval. It need be distinguished from the rotation curve formed with the second kind of line. The second kind of line can be generally observed. And, we think, the observation in [28] is the second kind of line, instead of a kind of orbit. It is with many different shapes. So, the second kind of line is generally confused as the orbit around the Sgr A*. So, how to understand some of observed lines in the bar need be further investigated.

From Figure 2 we know, there are these problems for the Poisson equation. First, as shown in Figure 1, we know, as B is orbiting around the Sgr A*, the orbit is only determined with the force along the straight line connected with the Sgr A* and B. From the initial knowledge of mechanics, we know, a force is with a direction. The direction of the force of the stars which are not on the line SgrA*B is not along the straight line. Therefore, the masses of these stars cannot be simply added to that of the Sgr A*. So, the Poisson equation violated the initial knowledge of mechanics. Only for this reason, it is certainly known that the Poisson equation is invalid.

Second, in the Poisson equation, the bodies out of the orbit cannot have action on the orbit. This is groundless. It is clear, these bodies certainly have action on the orbit. In Newtonian theory of orbit perturbation, the action of them is described in Eq.(1) with $g_{perturb}=G{\displaystyle \frac{m_i}{r_i^3}}\mathit{R}$. For precise orbit, this action need be considered.

Third, in Figure 2, the orbits in a galaxy is complicated. In a galaxy, a lot of stars cannot have orbits around the Sgr A* (instead, they have orbits around a other center body); while the Poisson equation only can describe such a kind of orbits that is orbiting around the Sgr A*.

Forth, the Poisson equation is invalid to explain why there are the orbits in a stellar cluster which cannot be affected by the sum of the masses enclosed in a sphere, such as that the orbits in the green circle cannot be affected by the masses out off the green circle.

2.3. The Mass of Sgr A* and the Galactic Rotation Curve

Now, it is commonly agreed that the mass of the Sgr A* is about $4\times {10}^6{M}_{Sun}$. We know, the mass of the Sgr A* is first obtained with the orbit of the S-star S02. It is well observed that the period of the orbit of S02 is almost 16 years, with the orbits of a dozen of other S-stars, the mass of $4\times {10}^6{M}_{Sun}$ is obtained. But, we think, the mass of $4\times {10}^6{M}_{Sun}$ should be such a conclusion that was affected by current thoughts and theory about the orbit in a galaxy, including the Poisson equation and the galactic rotation curve. It is clear, after the Sgr A* had been discovered, the galactic rotation curve need be revised and the sum of the mass enclosed in the sphere with same radius need be changed. But, both of them have not be revised till now. Now, it is required that the sum of the mass enclosed in a sphere cannot be contradicted with the current galactic rotation curve. It should result in that the mass of the Sgr A* cannot be right measured.

It is important, because of the advance of the technology, in recent, it was observed that the circular velocity curve of the Milky Way from 5 to 30 kpc is with a Keplerian decline.[21,22,23,24,25,26,27] We know, the Keplerian decline is correspondent to that, in $v=\sqrt{M/r}$, M is a constant, rather than that M(r) is a function of the radius, r, of the sphere. Therefore, the observations in [21,22,23,24,25,26,27] should be the evidence to that the orbits in the galaxy is fundamentally determined with the mass of the Sgr A*. It was presented that the observed circular velocity curve of the Milky Way [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] is highly accordant with that predicted with that the mass of the Sgr A* is $M_{SgrA*}~1.8\times {10}^{11}{M}_{Sun}$.[4]

2.4. The Orbits of the S-Stars and the Mass of Sgr A*

Although the mass of the Sgr A* can be measured directly from the orbits of the S-stars, the structure in the center region of the galaxy is very complicated and the distance from the Sgr A* is very large, it is very difficult to have an orbit of the S-stars with accurate and precise radius and velocity. Usually, the period of an orbit can be more easily and accurately observed. Mainly from the observed period or the acceleration of the orbit and the mass of the Sgr A*, an orbit of the S-stars is usually obtained. Therefore, currently, the mass of the Sgr A* is usually taken as one of the conditions to the orbit of the S-stars, rather than that the mass of the Sgr A* is known from the orbits of the S-stars.

2.5. Newtonian Theory of Orbit and Galactic Dynamics

The Newtonian theory of orbit perturbation with Hill sphere was well applied in the solar system and other stellar systems and in designing the interstellar orbit while it has not been generalized to understand the orbits in a galaxy. The reason is that, as pointed out in the above, the Sgr A* was confirmed after 2000.[1,2] Before the Sgr A* had been discovered, the center body in the Milky Way cannot be known, the orbits in the galaxy cannot be right understood and cannot be described with the Newtonian theory of orbit perturbation.

Therefore, new observation is important to the development of galactic dynamics. And, now, it is the time to develop a complete galactic dynamics, including to generalize the Newtonian theory to the galaxy. Because it is very difficult to have a complete observed image about the whole galaxy, there are many problems for understanding the galaxy, such as that how and why there are the bar and spiral arms in many galaxies. It seems too early to talk about the Modified Gravity and other conclusions, such as dark matter, before there are many unknown problems with a uncomplete galactic dynamics.

We think, a complete galactic dynamics need be valid to understand two main subjects about a galaxy: first, the structure of the galaxy, such as that how and why there are the bar and spiral arms in many galaxies. Second, the orbit and motion of the galaxy. Fundamentally, it need be valid to understand the problems in the Figure 1 and Figure 2: Why the whole galaxy can move along one direction as the directions of the orbits of the stars are different? How do the orbits in a stellar cluster formed? Why the orbits with a radius of 100,000 light year is stable?

3. Conclusion

1)

The discovery of the Sgr A* determines two different times in understanding the Milky Way. Before the Sgr A* had been discovered, the center mass for the orbits in the Milky Way cannot be known, the understanding about the orbits need be improved; after the Sgr A* has been discovered, it is known that all other bodies are orbiting or rotating around it; which is the fundamental to the development of galactic dynamics.

2)

We studied the action of the Sgr A* on the orbits in the solar system and in the ω Centauri. We found, the Newtonian theory of orbit perturbation and the Hill sphere are needed to understand the orbit in a galaxy. Therefore, we need to return to the Newtonian theory of gravity by excluding the wrong theories, such as the Poincaré’s equation for Three-body problem and the Poisson equation.

3)

According to Newtonian theory of orbit perturbation, from Eq.(1), it is easy to know that the mass of the Sgr A* should be $M_{SgrA*}~1.8\times {10}^{11}{M}_{Sun}$; which is highly consistent with that known from the Hill sphere. And, the recent observed circular velocity curve of the Milky Way [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27] should be an evidence for it. It is imaginable that the mass of the center (Sgr A*) of the Milky Way need be large enough to make the orbits in the radius about $1\times {10}^5$ light years stable and to make the whole galaxy moved stably.

4)

In every stellar cluster, there should be a center body (black hole or other massive body) at the center of the cluster. The mass of the center body can be measured from two ways: 1) directly calculated from any one of the orbits in the cluster with Eq.(1); 2) calculated from the radius of the cluster and the mass of the Sgr A* with the Hill sphere Eq.(2).