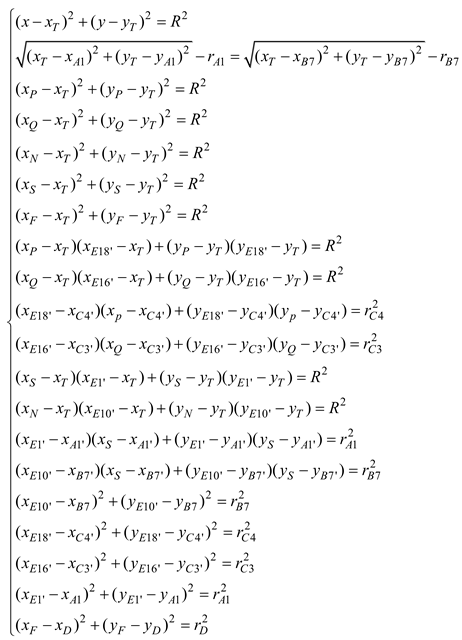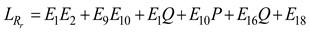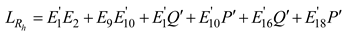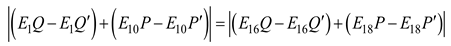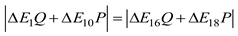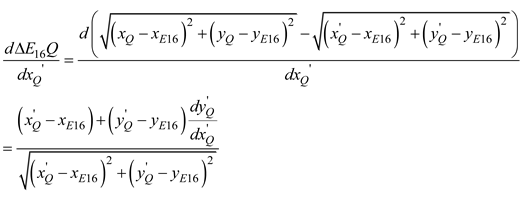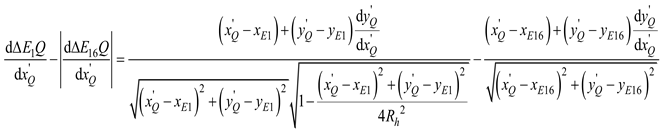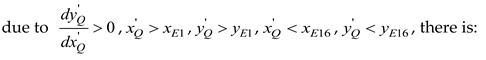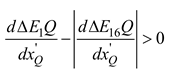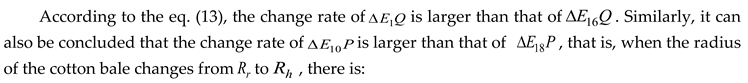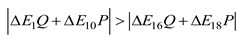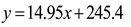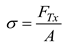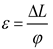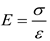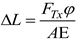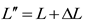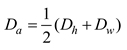1. Introduction
Cotton, a crucial cash crop, plays a significant role in China’s economy and the livelihoods of its people [
1,
2,
3]. China, along with India and the United States, dominates the global cotton market. According to the statistics, China’s total cotton production in 2023 reached 5.618 million tons, ranking first in the world. With the rapid development of the cotton industry and continuous advancements in mechanization, cotton picker has emerged and undergone constant improvements. Among these, packing cotton picker has become the mainstream cotton-picking equipment in China due to their advantages of integrated and packing capabilities, as well as non-stop unloading [
4,
5].
Precision packing is an inevitable development trend, by analogy from other agricultural machinery, such as precision seeding [
6,
7], precision irrigation [
8,
9], precision fertilization [
10], precision pesticide application [
11], etc. Accurate detection of the cotton bale's dimension during the packing process is the first step toward achieving this.
The dimension of a cotton bale, primarily referring to its diameter, is a critical parameter in the packing process of packing cotton picker, as it determines whether the packing is successfully completed. Leading domestic and international packing cotton picker manufacturers currently use angle sensor detection signal values, which are converted into the cotton bale diameter, to measure the bale's dimension [
12,
13,
14,
15]. However, these methods merely establish a direct correlation between the angle sensor signal and the cotton bale dimension without accounting for the deviation caused by changes in packing belt length under varying cotton bale densities. As a result, the accuracy of cotton bale dimension detection is compromised. Besides these, there are few related reports.
This study aimed to propose a precise geometry-based method for determining the dimension of cotton bale in packing cotton picker, improving measurement accuracy to ensure the production of more uniform cotton bales.
2. Materials and Methods
2.1. Establishment of Mathmatical Model of Packing Process
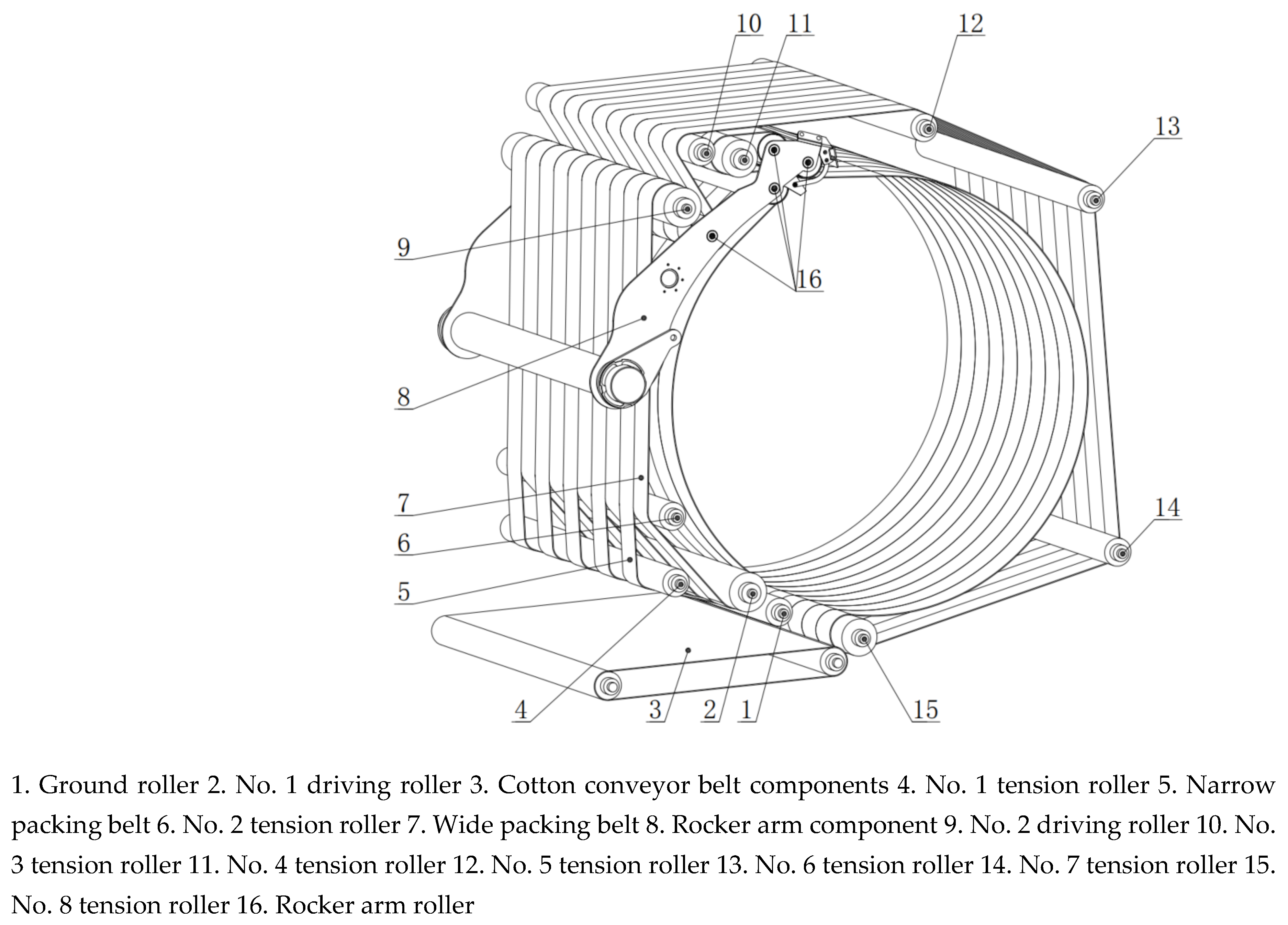
The packing device of the packing cotton picker serves as the actuator for cotton bale rolling and molding. The packing device primarily consists of the cotton conveyor belt assembly, drive roller, tensioning roller, rocker arm component, rocker arm roller, and packing belt (
Figure 1). The seed cotton, collected at the front of the packing cotton picker, is transported to the rear of the machine and enters the cavity formed by the packing belt through the cotton conveyor belt components. Driven by the drive roller, the packing belt circulates, continuously rolling and compressing the seed cotton within the cavity, ultimately forming a compact cotton bale with a specific density and diameter.
Because seed cotton is a viscoelastic material and the packing belt is elastic, the interaction during the packing process is complex, necessitating simplification. Before establishing the mathematical model of the packaging device, the following assumptions are necessary:
Cylindrical Shape with Uniform Mass Distribution: The cotton bale is assumed to have a cylindrical shape with uniform mass distribution. Throughout the packing process, as seed cotton is continuously fed, the rotating cotton bale becomes progressively filled and rounded, achieving a consistent compaction density. This continuous rolling ensures uniformity across all parts, effectively treating the cotton bale as a cylindrical object with uniform mass distribution.
Ignoring Elastic Deformation of the Packing Belt: The packing belt's elastic properties cause its tension to increase with the weight of the cotton bale, resulting in slight changes in belt length. However, these length variations are minimal within a certain operational range, exerting negligible influence on the analysis and calculation of the cotton bale's dimensions. Therefore, for the purposes of this analysis, the elastic deformation of the packing belt can be disregarded.
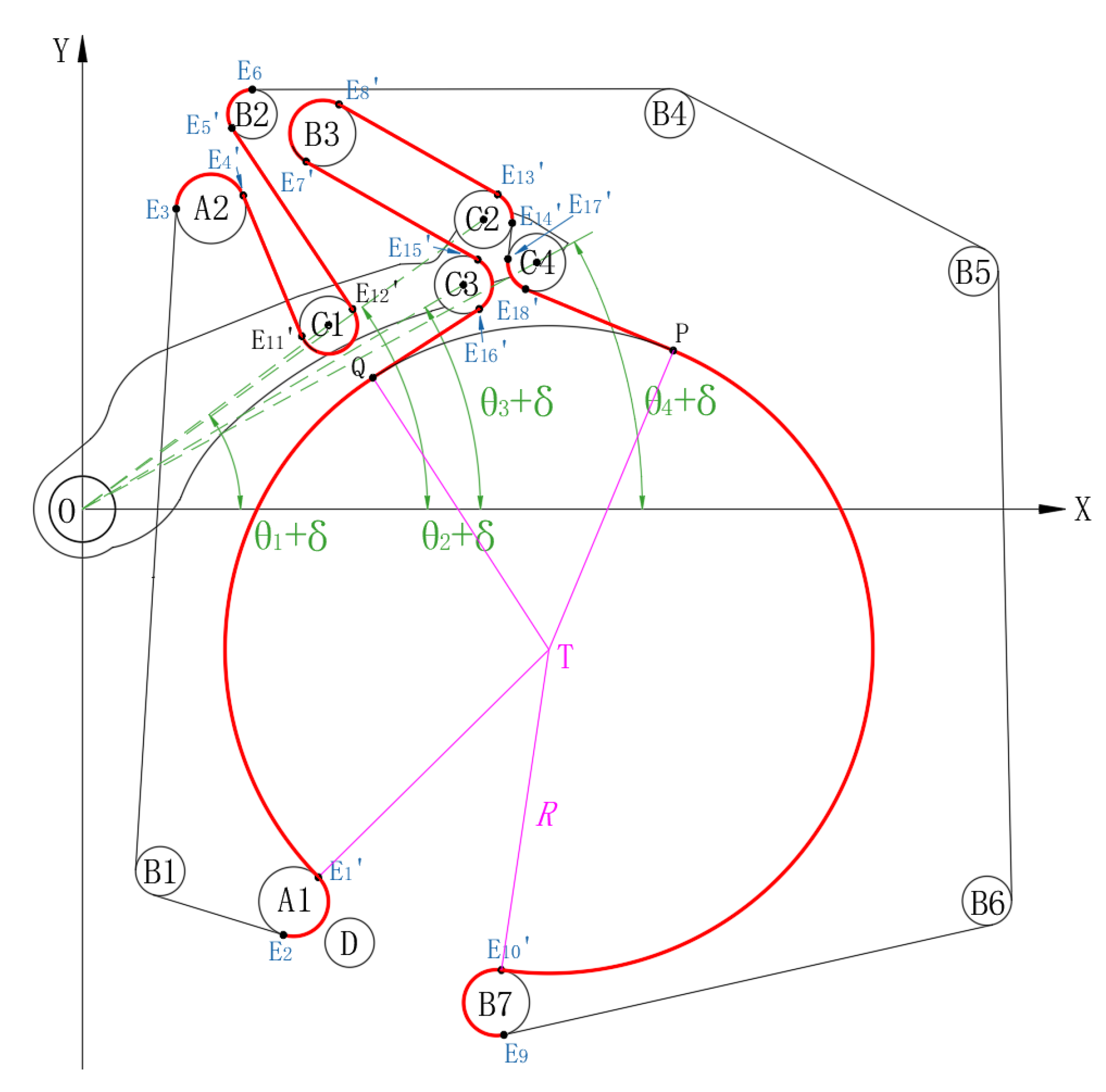
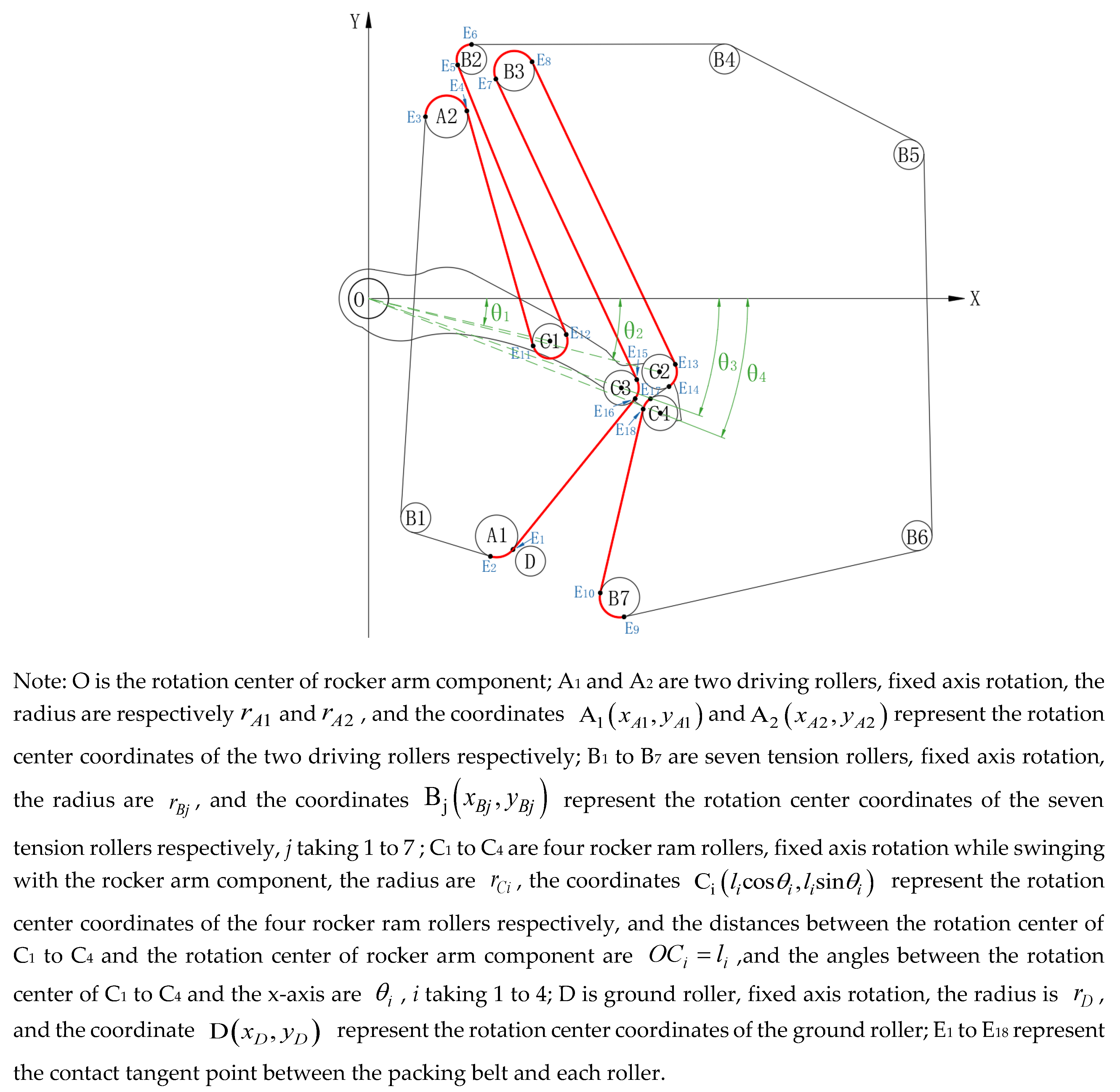
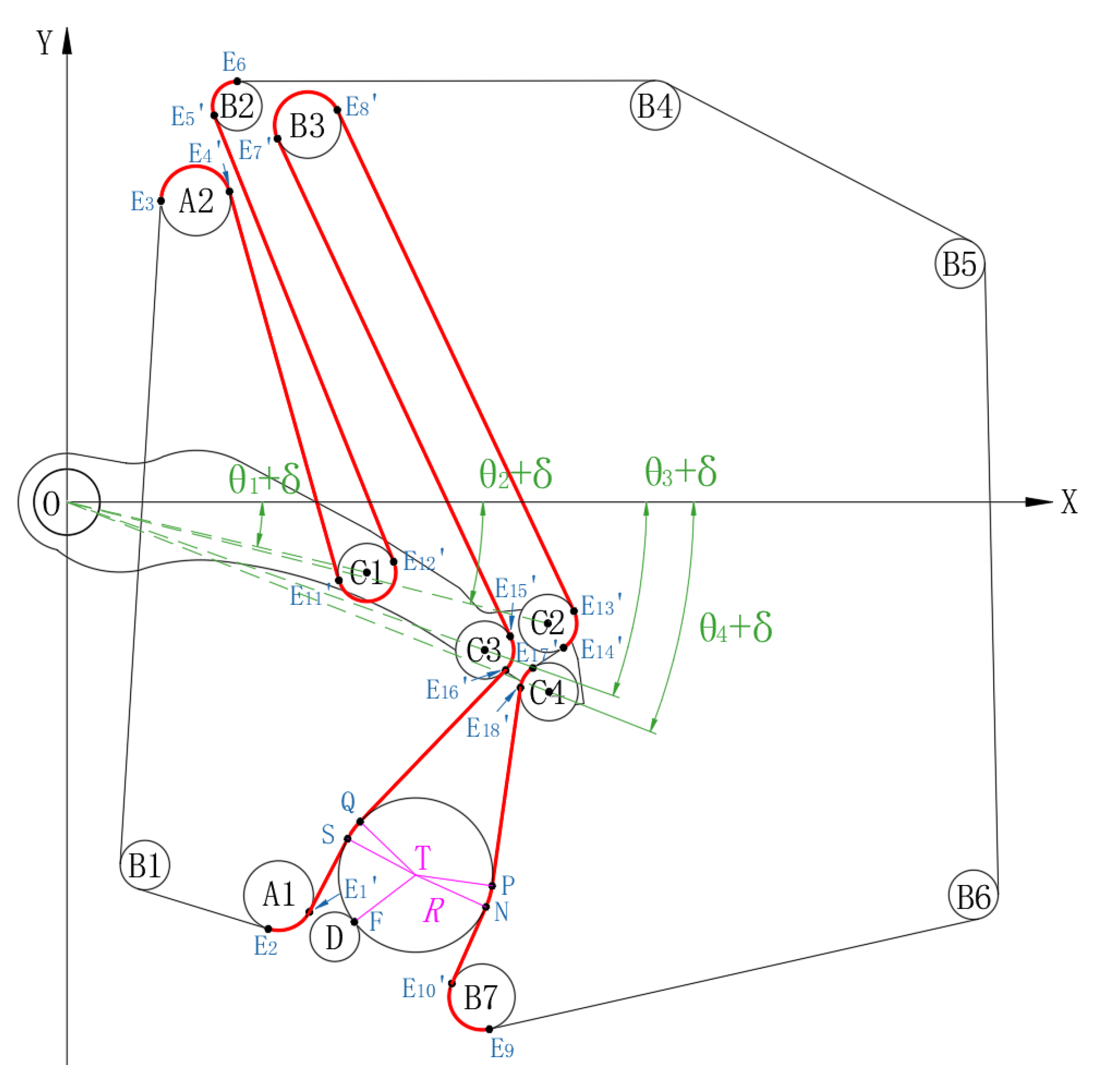
Based on the above assumptions, the analysis is conducted under the condition that the total length of the packing belt remains constant throughout the packing process, and the continuous seed cotton feeding process is discretized. A plane coordinate system is established with the rotation center of the rocker arm component as the origin. Since the length of the packing belt wrapped around the rollers fixed at each axis does not change, the calculation is simplified by only considering the length variation of the packing belt between the moving shaft rollers. As shown in
Figure 1, the packing belt alternates between wide and narrow segments. Calculating the lengths of these two segments separately would complicate the process. However, because the winding patterns of the two belts differ only at the No. 1 and No. 2 tension rollers—segments where the belt length remains unchanged—the No. 2 tension roller can be omitted for simplification. The initial-state mathematical model of the packing device (
Figure 2), which line with red color is the variable segment packing belt involved in the calculation.
In the initial state, the total length of the variable segment packing belt
L can be expressed as (
indicating the arc length):
During the operation of the packing device, the process is
divided into two stages based on the dimension and positional relationship of
the cotton bale. In the first stage, the diameter of the cotton bale is small. At
this point, the cotton bale is only tangent to the roller D, and small sections
of packing belts appear on both the left and right sides. When the rocker ram
component turns
δ angle
counterclockwise, the first-stage mathematical model of the packing device (
Figure 3) identifies the tangent contact points
of the cotton bale and packing belt as N, P, Q, and S, respectively. The tangent contact point between the cotton
bale and roller D is denoted as F. The center coordinates of the rollers C
1
to C
4 can be expressed as
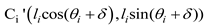
, and the contact
tangent points and arc lengths of the packing belt at each roller can be
determined using geometric relationships.
At this stage, the total length of the variable segment packing belt
L’ at this time can be further expressed (
x’ indicating changes in coordinate positions):


Figure 4.
The second stage mathematical model of packing device.
Figure 4.
The second stage mathematical model of packing device.
Using the same calculation method as in the first stage, the relationship between the dimensions of the cotton bale and the angle of the rocker arm component in the second stage can be similarly determined. At this stage, the overall relationship between the rotation angle of the rocker arm component and the dimension of the cotton bale throughout the entire packing process is established. Consequently, the dimension of the cotton bale can be calculated by detecting the rotation angle of the rocker arm component.
2.2. Deterministic Verification of Cotton Bale Dimension
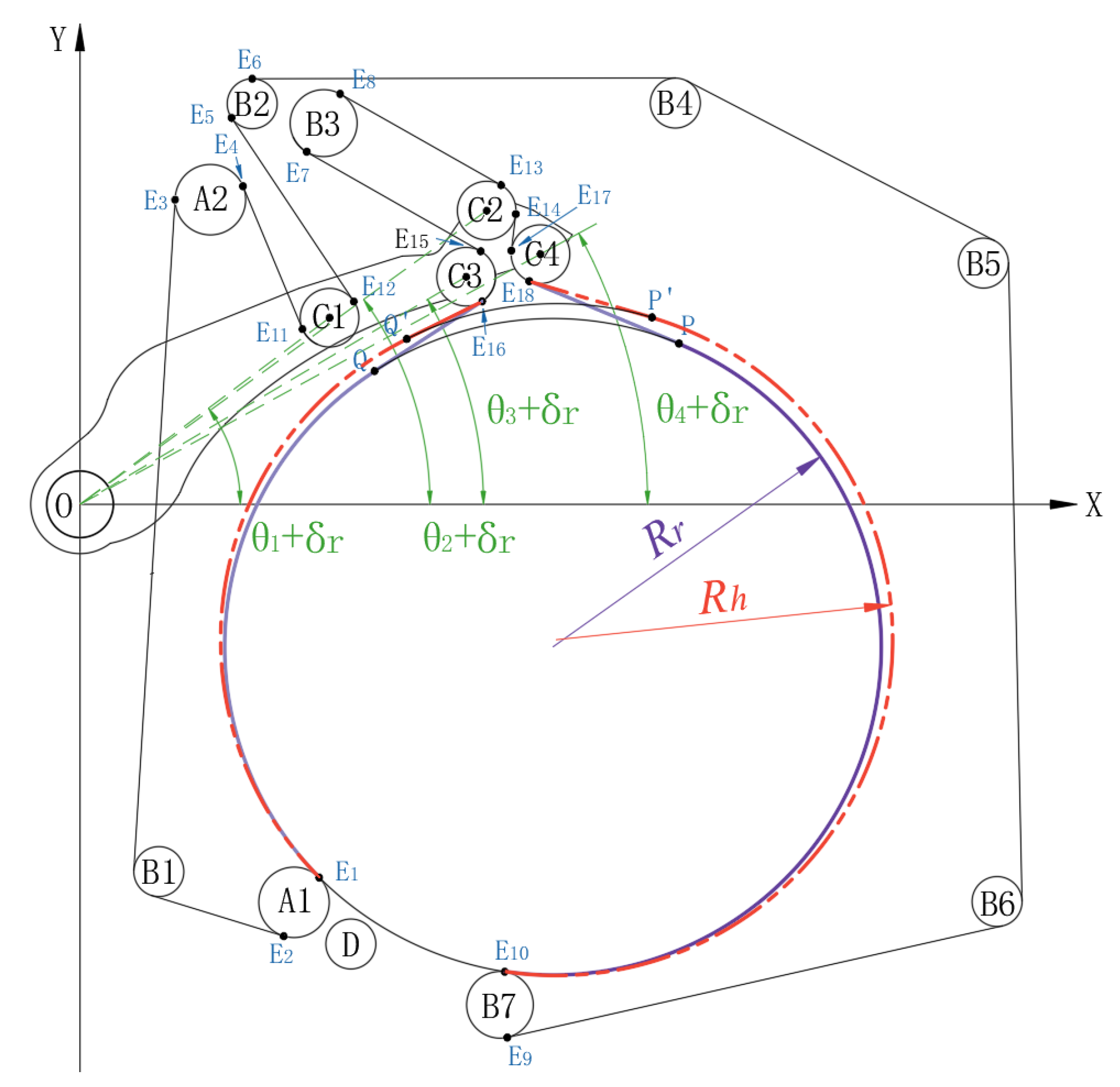
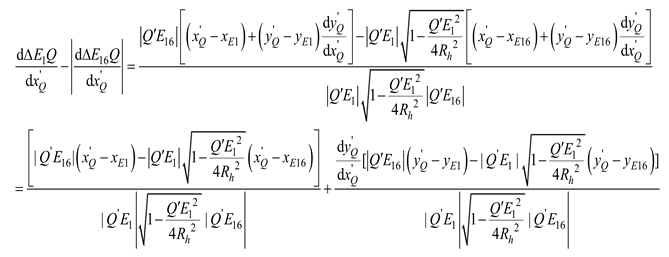
To ensure that during the entire packing process, a unique radius of the cotton bale corresponds to the same total length of the variable segment packing belt and the angle of the rocker arm component, the issue of uncertainty due to multiple solutions must be eliminated. Taking the second stage as an example, the certainty of the cotton bale's dimension is demonstrated.

In the same way, the changed length of the packing belts can be written when the corresponding radius is
Rh:

Figure 5.
The assumption of the same rotation angle corresponds to different bale dimension.
Figure 5.
The assumption of the same rotation angle corresponds to different bale dimension.
And then, eq. (7) can be further written as:

The analysis reveals that eq. (14) and eq. (8) are contradictory, rendering the hypothesis invalid. The first stage can be analyzed using the same method. Ultimately, it can be concluded that the dimension of the cotton bale in the packing process is deterministic when the length of the packing belt is constant. That is, the angle of the rocker arm component has a one-to-one correspondence with the dimension of the cotton bale, which further demonstrates the feasibility of calculating the cotton bale's dimension by detecting the rotation angle of the rocker arm component.
2.3. Calculation Example
This paper takes the packing device of 4MZD-6 packing cotton picker as an example and obtains the position and size parameters of each roller (
Table 1). The theoretical maximum rotation angle of the rocker arm component is 65°.
After obtaining the above parameters, the developed program is used for calculation. By inputting different rotation angles of the rocker arm component, the corresponding geometric parameters of the cotton bales can be determined (
Table 2).
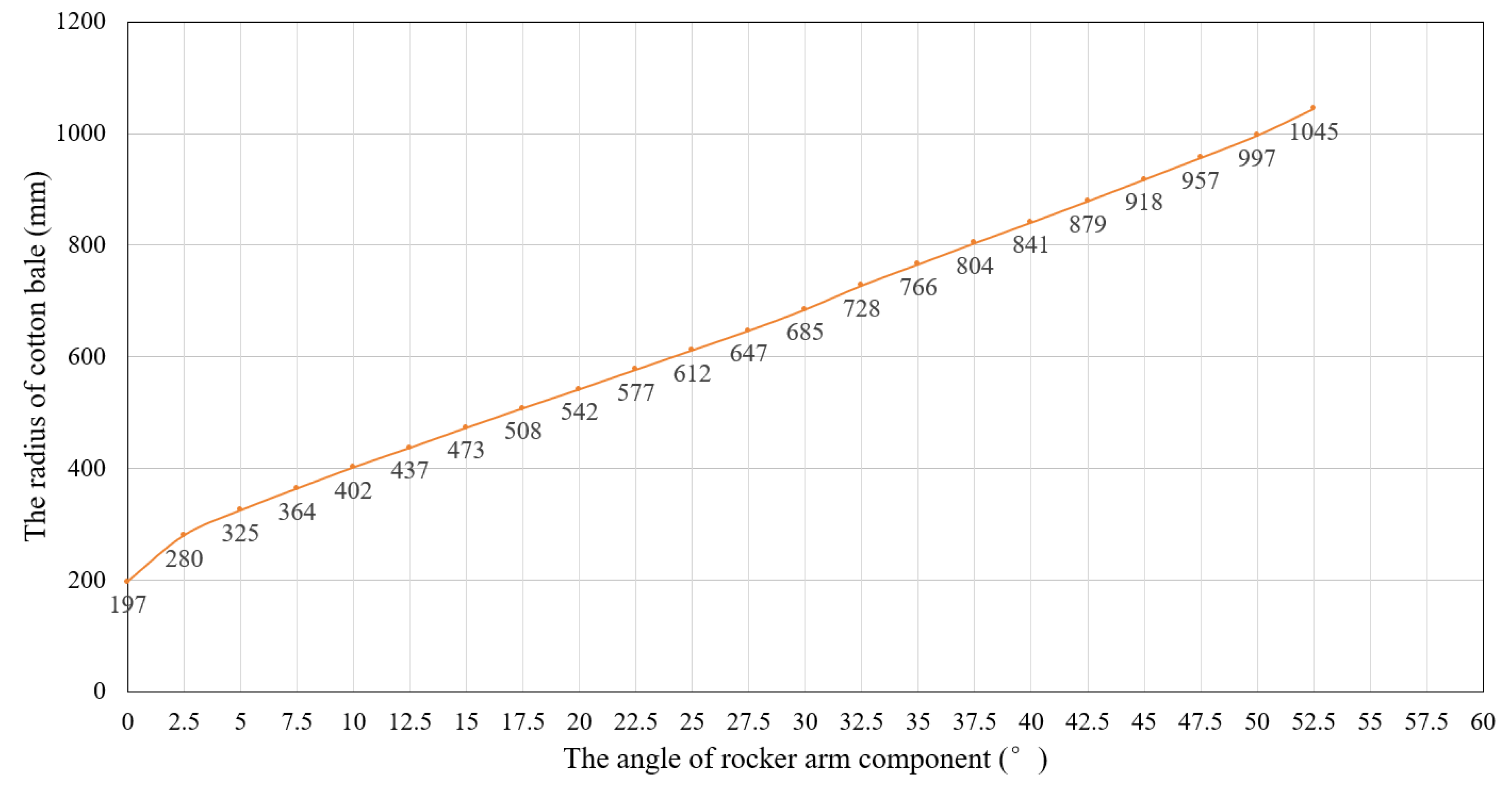
When the rotation angle of the rocker arm component exceeds a certain value 55°, the program fails to provide a solution. This is because, as the dimension of the cotton bale continues to increase, changes in the length of the packing belt become significant and cannot be ignored. To address this, a fitting method is employed to calculate the radius of the bale when the rotation angle exceeds this threshold 55°. The relationship between the rotation angle of the rocker arm component and the radius of the cotton bale is illustrated (
Figure 6).
It can be observed from
Figure 6 that, except for specific outlier points, the rotation angle of the rocker arm component and the radius of the cotton bale exhibit a strong linear correlation throughout the entire packaging process. Therefore, linear fitting is applied in this paper. To improve the accuracy of the bale radius calculation, linear fitting is performed
R2 = 0.9994 after removing the identified outlier point 0°. The resulting fitting function is:
Using eq. (15), the geometric parameters of the bales corresponding to the different rotation angles of the rocker arm component can be obtained (
Table 3).
Based on the geometric structure design, the motion range of the rocker arm component, and the actual verification of the packaging device of the 4MZD-6 packing cotton picker, the maximum packing diameter is approximately 2.4 meters. This result is consistent with the analysis and calculation results presented in this paper. Therefore, the correctness of the mathematical model relating the angle of the rocker arm component to the size of the cotton bale is preliminarily validated.
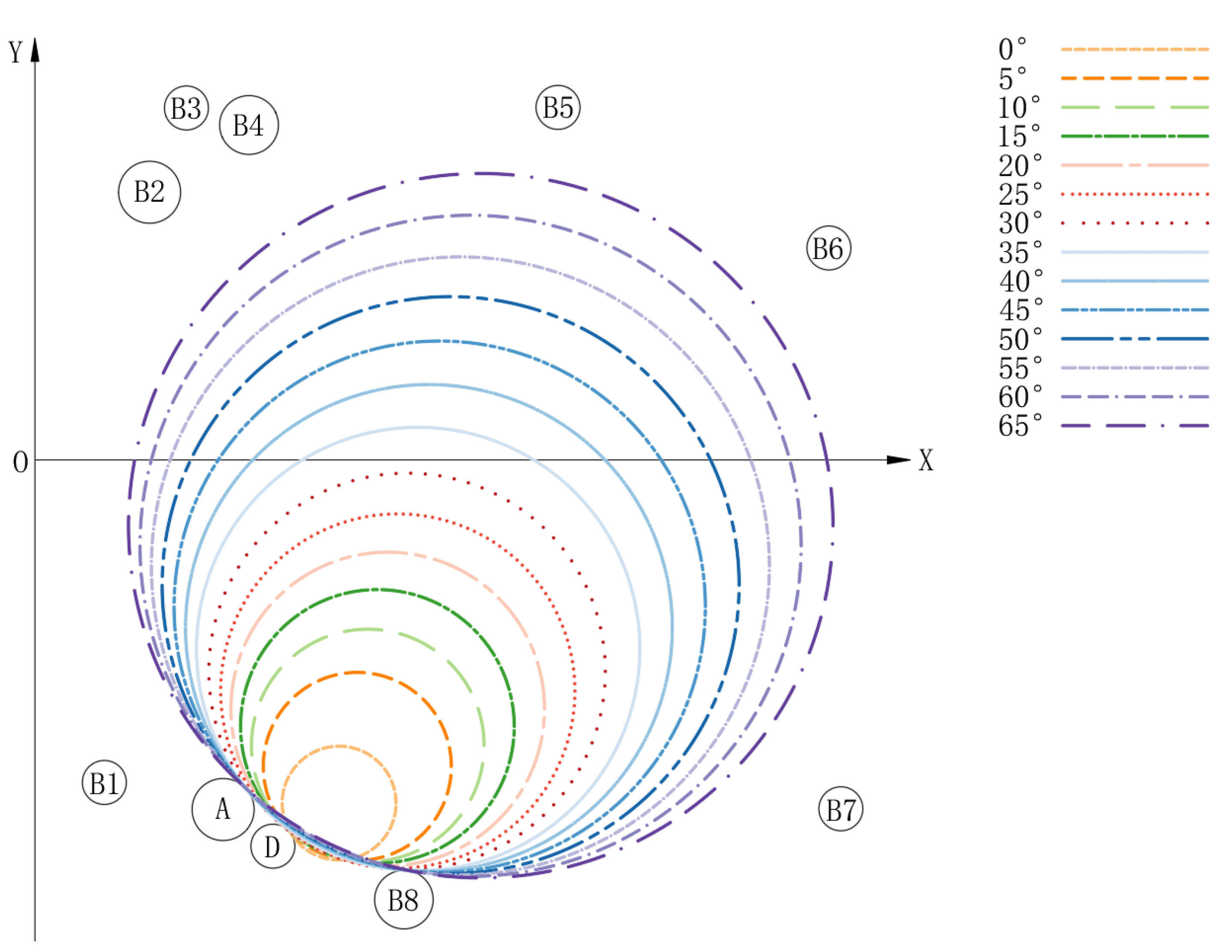
The geometric shape of the cotton bales corresponding to different rotation angles of the rocker arm component (
Figure 7), which further verifies the correctness, rationality, and reliability of the analysis results.
2.4. Theoretical Modification
In the above analysis, the elastic deformation of the packing belt is neglected, which causes the software to fail when solving for the dimensions of the cotton bale as the rotation angle of the rocker arm component exceeds 55°. This indicates that, with the increase in the dimension and weight of the cotton bale, the elastic deformation of the packing belt becomes significant due to the continuous increase in tension force. Therefore, when the dimension and weight of the cotton bale are large, the elastic deformation of the packing belt must be considered, and the total length of the variable segment packing belt should be corrected to achieve more accurate results. Specifically, the tension force of the packing belt can be temporarily ignored in the first stage of the packaging process but must be accounted for in the second stage.
For the second stage of packing process, under a given rotation angle δx of the rocker arm component and without considering the elastic sliding of the packaging belt, it is approximately assumed that the tension of each part of the packing belt is FTx. At this stage, the stress in the packing belt can be expressed as:
in which:
σ - the stress of the packing belt.
FTx - the tension of packing belt.
A - the cross-sectional area of the packing belt.
Further, the strain of the packing belt can be obtained as:
in which:
ε- the strain of packing belt.
ΔL - the variation of the total length of the variable segment packing belt.
φ - the total length of the variable segment packaging belt in the initial state.
The relationship between stress and strain can be expressed as:
in which:
E - the elastic modulus of packing belt.
Combining eq. (16), eq. (17) and eq. (18) can be further written as:
Further, the total length of the variable segment packing belt considering the elastic deformation is:
in which:
L’’ - the total length of variable segment packing belt considering elastic deformation.
Using the total length of the modified variable segment packing belts, a more accurate cotton bag dimension can be calculated, which will be further verified in the experiment.
3. Results and Discussion
3.1. Field Test
To further validate the proposed geometry-based method for determining the dimensions of the cotton bale, a field test was conducted. The test equipment used was the 4MZD-6 packing cotton picker, jointly developed in collaboration with the enterprise, as shown in
Figure 8. To prevent damage to the cotton bales during transportation due to excessive dimensions, the packing cotton picker typically does not operate at the maximum theoretical diameter. Specifically, the rotation angle of the rocker arm component does not reach 65°; instead, the packing process is considered complete when the angle reaches 60°.
The test site was the Shaya county, Xinjiang, where Xinluzhong 78 cotton variety was used for testing. Due to the fixed length of the coating used in the packing cotton picker, minimizing waste requires that the cotton bale size not be excessively small. During the test, the rocker arm component's angle ranged from a minimum of 45° to 60° in increments of 5°, with three repeated packing tests conducted. Each test result was taken as the measured value, which was then compared with the theoretical value calculated using this method. The measurement diagram of the cotton bale diameter is depicted in
Figure 9, and the actual diameter of the cotton bale is calculated using the following equation:
in which:
Da - the actual diameter of cotton bale.
Dh - height direction of the cotton diameter.
Dw - width direction of the cotton diameter.
3.2. Analysis of Test Results
The results of theoretical calculation and actual measurement of cotton bale diameter are shown in
Table 4.
As shown in
Table 4, with the increase in the rotation angle of the rocker arm component, both the absolute error and relative error exhibit an increasing trend. In general, the absolute error in the cotton bale diameter can be kept within 50 mm, while the relative error remains within 2%. Therefore, the calculation accuracy for determining the cotton bale's dimension is generally satisfactory.
3.3. Discussion
Through detailed analysis, it can be concluded that the errors in the geometry-based cotton bale dimension calculation method proposed in this paper stem from the following factors:
The method assumes the cotton bale is a perfect cylinder with uniform mass distribution. However, the cotton bale is a quasi-cylindrical shape because of gravity, and its mass distribution is not perfectly uniform. This discrepancy leads to unavoidable errors when calculating the total length of the variable segment packing belts.
When using a tension sensor to correct the total length of the variable segment packing belts during the packing process, the elastic sliding between the packing belt and the contact roller causes different tension values on each side, like a belt drive system. Since only one tension value is measured instead of the entire tension distribution, this introduces an additional source of error.
Rounding errors in numerical calculations and human errors in measuring the cotton bale dimensions are also significant contributors to the overall error.
In summary, due to the complex interactions in the packaging process, the simplified calculation method inevitably introduces errors. However, further investigation into the relationship between the theoretical calculation and actual measurements using the method proposed in this paper could help refine the model. It is feasible to reduce these errors by introducing correction coefficients or correction functions.
4. Conclusions
The geometry-based method for determining the cotton bale dimensions in the packing cotton picker, as presented in this paper, is generally satisfactory. For measuring the diameter of the bale, the absolute error can be kept within 50 mm, and the relative error can be controlled within 2%. The next step is to further explore the relationship between the theoretical calculation and actual measurements, which will help reduce the error and provide a theoretical foundation for precise control of the cotton bale weight in the packing cotton picker.
Author Contributions
Conceptualization, Q.L. and S.L.; methodology, Q.L.; software, S.L.; validation, Q.L., S.L. and P.L.; formal analysis, P.L.; investigation, Q.L., S.L. and P.L.; resources, X.F.; data curation, Q.L. and X.F.; writing—original draft preparation, Q.L., S.L.; writing—review and editing, Q.L. and P.L.; visualization, Q.L. and S.L.; supervision, X.F.; project administration, X.F.; funding acquisition, X.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key R & D Program of Shandong Province, 2022CXGC020705.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Guo WJ, Feng Q. Cotton leaf disease detection based on improved YOLO. Agricultural Research in the Arid Areas. 2024, 42(06): 195-205. (in Chinese).
- Li Z, Li L, Wei XW, Liu Y, Li LL, Lu ZB, Song YY, Wang GF, Men XY. Comparison of the ecological service value of different “green” and efficient cotton planting modes. Chinese Journal of Applied Entomology. 2024, 61(4):893-901. (in Chinese).
- Liu WJ, Fan YS, Dong YQ, Qu T, Zhu K, Liu YC, Wei F. Analysis and suggestions on the current situation of cotton production in China. China Seed Industry. 2022, 22(1):21-25. (in Chinese).
- Bian XL, Mamtimin·GN, Nijat·YSP. Design and Test on Hydraulic System of Cotton-picking Machine Packing Cotton Box. Journal of Agriculture Mechanization Research. 2022, 44(12):77-82. (in Chinese).
- Li H, Lei QS, Feng XY, Li XS, Wang YG, Li ZT, Li HK. Lightweight design of key parts of packaging mechanism of packaging cotton picker. Agricultural Engineering. 2024, 14(10):89-95. (in Chinese).
- Jiang XM, Zhang J, Liu SY, Fu LL, Huang DY. Development and Evaluation of a Universal Seed Discharger for Precision Planting in Corn-Soybean Cropping System. Processes. 2024, 12: 1595.
- Sun WS, Yi SJ, Qi HL, Wang S, Li YF, Dai ZB. Design and Experiment of Twin Discs Intertwined Air-pressure High-speed Precision Seed-metering Device for Maize Delta-row Dense Plantings. Transactions of the Chinese Society for Agricultural Machinery. 2024, 48(12): 48-57. (in Chinese).
- Bukhari M, Athar SO, Ullah M, Aman MN. A Fuzzy-Logic-Based Smart Irrigation Controller for Precision Agriculture. IEEE Internet of Things Journal. 2024, 11(22): 37257-37268.
- Shan YC, Zhang LX, Wang H, Du CC, Ma Y, Ma X, Wang WD. Design of Control System of Cotton Submembrane Precise Irrigation and Fertilization Based on PLC. Journal of Agricultural Mechanization Research. 2022, 44(10): 172-175+180. (in Chinese).
- Munir A, Salah MA, Ali M, Ali B, Saleem MH, Samarasinghe, KGBA, De Silva SIS, Ercisli S, Iqbal N, Anas M. Advancing Agriculture: Harnessing Smart Nanoparticles for Precision Fertilization. Materials Science, Biomaterials. 2024, 14(4): 3846-3863.
- Han L, Wang ZC, He XK. Development of an energy-saving PWM driving method for precision pesticide application using adjustable frequency and characterization of spray. Computers and Electronics in Agriculture. 2024, 217: 108634.
- Yang X. Developing and test of 4MZD-6 cotton picking baler. Xinjiang Agricultural Mechanization. 2023, 23(04):22-24. (in Chinese).
- Ye H. Cotton picker market trend analysis. Jiangsu Agricultural Mechanization. 2022, 22(03):51-52. (in Chinese).
- Yang J. Domestic cotton picker straight waist. China Agricultural Machinery Equipment. 2021, 21(12):13-14. (in Chinese).
- Lei ZH, Jiang ZC, Zheng HX, Wang QT. Development status and detection of cotton picker in China. Farm Machinery. 2021, 21(12):52-53+55. (in Chinese).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
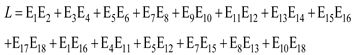
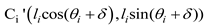 , and the contact
tangent points and arc lengths of the packing belt at each roller can be
determined using geometric relationships.
, and the contact
tangent points and arc lengths of the packing belt at each roller can be
determined using geometric relationships.