Theoretical and Numerical Research on High-Speed Small Refrigeration Twin-Screw Compressor

1. Introduction

Twin-screw compressors are characterized by high operational reliability, superior efficiency, excellent dynamic balance, low vibration and noise levels, compact and energy-efficient designs, and user-friendly operation. These advantages have led to their extensive application in traditional industries such as mechanical manufacturing, petrochemical processing, and refrigeration systems, while their use is progressively expanding into advanced technology sectors [1,2]. The capability of screw refrigeration compressors for high-speed design enables significant miniaturization and weight reduction, making them an effective solution for enhancing the performance of small-to-medium sized chillers and achieving efficient, reliable airborne cooling systems.

High-speed operation of screw compressors enables reduced volume and weight for equivalent cooling capacity while significantly decreasing internal leakage through clearances, thereby improving overall efficiency [3]. The optimal clearance distribution in screw compressors can be determined through thermodynamic modeling, CFD simulations, or experimental validation [4,5,6,7,8]. Wu Huagen et al. [6] demonstrated through theoretical analysis and experimental studies that the meshing clearance has a substantially greater impact on performance than the discharge end clearance, with each 0.01 mm increase reducing volumetric efficiency by 0.4% and 0.13%, respectively. Rane et al. [7] employed a bidirectional coupling approach using ANSYS CFX for fluid dynamics and ANSYS Mechanical for structural analysis to determine variations in leakage clearance dimensions, enabling accurate performance calculations in their CFD model. By optimizing the compressor's radial clearance to appropriate values, they achieved significant performance improvements, including an 8.2% increase in volumetric efficiency, a 2.5% reduction in indicated power, and a 5.5% enhancement in adiabatic efficiency. Petrescu et al. [8] experimentally confirmed these clearance effects while noting that increased rotational speed can mitigate their negative impacts.

High rotational speeds in screw compressors generate substantial airflow pulsations and high-frequency noise, as intermittent flow patterns create pressure oscillations that result in structural vibrations and acoustic challenges. These issues can be effectively mitigated through advanced muffler designs or optimized oil supply configurations [9,10,11,12,13,14]. Zhou Minglong et al. [13] conducted comprehensive research on the generation mechanisms and suppression methods for vibration and noise in screw refrigeration compressors, proposing a perforated tube muffler through combined simulation and experimental approaches. This solution achieved over 60% reduction in airflow pulsation amplitude, more than 3 dB(A) noise reduction at the compressor, and over 8 dB(A) noise reduction in system piping when implemented in actual systems. Yang et al. [14] experimentally investigated oil supply parameter variations in operational compressor units, developing a noise reduction strategy through optimized oil supply configurations while maintaining constant oil flow rates.

High-speed operation of screw rotors introduces additional challenges beyond clearance and airflow pulsation effects, including insufficient heat dissipation and reduced motor efficiency [15,16]. Liu Mingkun et al. [15] discovered that the compressor's working chamber walls undergo irregular thermal deformation at high temperatures, with lateral outward expansion and inward deformation at the tip points. Increasing cooling water flow in water-cooled casings effectively reduces average clearances, enhances discharge capacity, and minimizes tip deformation, thereby improving operational conditions under extreme scenarios. Wagner et al. [16] developed a high-speed miniaturized airborne screw refrigeration compressor with a maximum cooling capacity of 47 kW using R134a refrigerant, designed for 15000-25800 rpm operation. Experimental tests revealed stable compressor efficiency within the 15000-19000 rpm range, as motor efficiency reduction in the field-weakening control region offset the efficiency gains from increased rotor speed.

Current research lacks comprehensive theoretical frameworks and experimental validation for high-speed miniaturization of small screw compressors. To explore this potential in refrigeration screw compressors, this study designs rotors with varying rated speeds at constant displacement, employing normalization methods for geometric analysis and exergy analysis for power loss characterization, while developing a CFD model to analyze gas force variations across speeds. Furthermore, it investigates how lobe number and wrap angle impact thermodynamic performance.

2. Structural Comparison

To investigate the high-speed performance of miniaturized screw compressors, this study designed screw rotors with identical theoretical volumetric displacements but varying rated speeds.

2.1. Rotor and Ports Profile

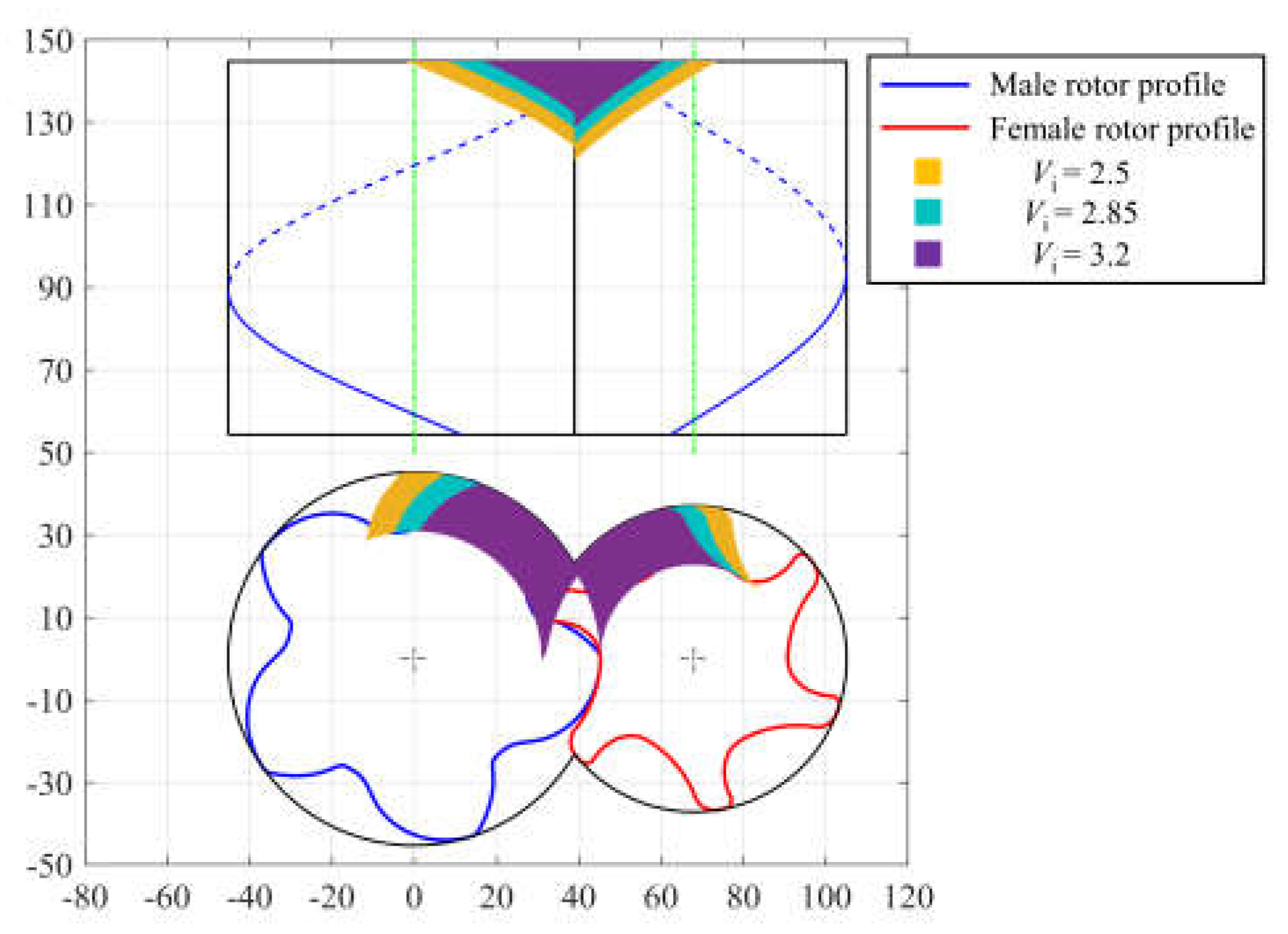
The rotor of the screw compressor is designed with a multi-arc asymmetric rotor profile, and the geometric parameters of which are outlined in Table 1. The compressor exhibits a theoretical displacement of 51.8 m³/h at 3000 rpm. The configuration of the suction and discharge ports is determined by the screw rotor profile and wrap angle, enabling the accommodation of diverse bulit-in volume ratios (V_i). The compressor's theoretical profile along with the arrangement of the suction and discharge ports is provided in Figure 1.

2.2. Component Structure and Size

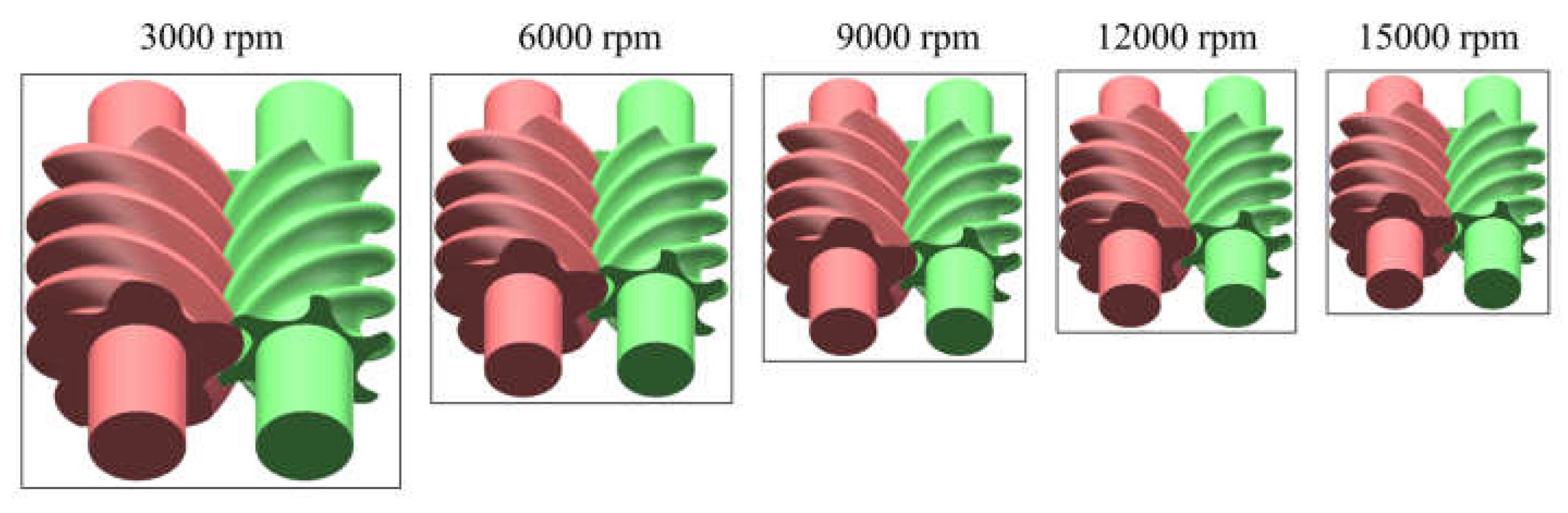
The screw rotor is optimized for high-speed operation while maintaining constant theoretical capacity and built-in volume ratio of the compressor. The theoretical displacement demonstrates a linear proportionality with rotational speed, while exhibiting a cubic functional relationship with rotor length. As rotational speed increases, the compressor's geometric dimensions undergo significant reduction, achieving enhanced compactness and weight. Notably, the length reduction rate demonstrates a diminishing trend with the increase of rotational speed. 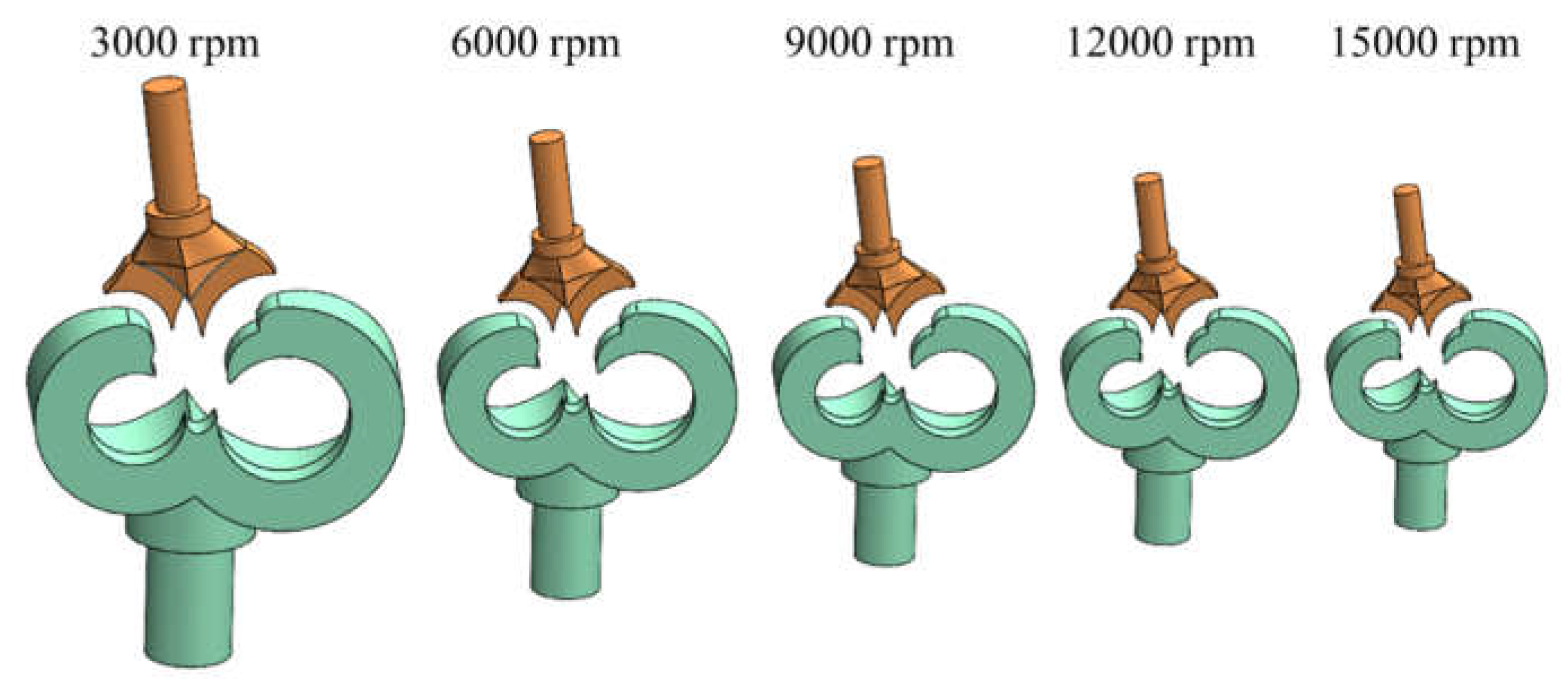Figure 2 presents a comparative analysis of rotor configurations maintaining equivalent theoretical displacement at 3000, 6000, 9000, 12000, and 15000 rpm. With increasing rotational speed, the suction and discharge flow domains of the screw compressor exhibit a progressive reduction. Figure 3 provides a detailed representation of the specific variations in the suction and discharge flow domains at different rotational speeds.

Table 2. Comparison of screw rotor structure with different rated speeds.

Parameters	3000rpm	6000rpm	9000rpm	12000rpm	15000rpm
diameter of male rotor /mm	90.5000	71.8299	62.7492	57.0114	52.9247
diameter of the female rotor /mm	74.1818	58.8781	51.4348	46.7316	43.3818
length of the rotor /mm	90.5000	71.8299	62.7492	57.0114	52.9247
center distance /mm	68.0000	53.9716	47.1486	42.8373	39.7666
rotor weight /kg	5.6492	2.8247	1.8831	1.4123	1.1299

Table 2. Comparison of screw rotor structure with different rated speeds.

Parameters	3000rpm	6000rpm	9000rpm	12000rpm	15000rpm
diameter of male rotor /mm	90.5000	71.8299	62.7492	57.0114	52.9247
diameter of the female rotor /mm	74.1818	58.8781	51.4348	46.7316	43.3818
length of the rotor /mm	90.5000	71.8299	62.7492	57.0114	52.9247
center distance /mm	68.0000	53.9716	47.1486	42.8373	39.7666
rotor weight /kg	5.6492	2.8247	1.8831	1.4123	1.1299

3. Theoretical Model

The geometric and thermodynamic models of the screw compressor are systematically established. The geometric characteristics of the compressor are analyzed using a normalized methodology, while the power loss is evaluated through an exergy analysis model.

3.1. Geometric Property Model

The normalized working chamber volume serves as a critical evaluation criterion for assessing the geometric performance of screw compressors. This dimensionless parameter enables systematic comparison of volumetric efficiency across different compressor configurations, independent of absolute dimensional constraints.

$$V_{\mathrm{s}\mathrm{N}}=V/V_{\mathrm{suc}}$$

(1)

To quantitatively assess energy dissipation associated with suction and discharge processes in screw machinery, we assume that the total energy loss originates exclusively from the additional kinetic energy component within the flow field. The corresponding energy dissipation is determined by employing the following governing equation:

$$P_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}={\displaystyle \frac{m{v}^2}{2}}$$

(2)

To quantify the energy dissipation associated with suction-discharge processes, the functional dependence of power loss on volumetric variations is derived from the normalized chamber volume $V_{\mathrm{s}\mathrm{N}}$, expressed as:

$${\displaystyle \frac{\mathrm{d}{P}_{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}}{\mathrm{d}{V}_{\mathrm{sN}}}}={\displaystyle \frac{\mathrm{d}m}{\mathrm{d}V}}{\displaystyle \frac{v^2}{2}}{V}_{\mathrm{suc}}=\rho {\displaystyle \frac{v^2}{2}}{V}_{\mathrm{suc}}$$

(3)

The relative leakage quantity is defined as the dimensionless ratio between the leakage mass flow rate and the theoretical intake mass flow rate. Consequently, the differential relationship between the relative leakage quantity and the relative volumetric variation can be expressed through the following derivative formulation:

$${\displaystyle \frac{\mathrm{d}{\eta }_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}{V}_{\mathrm{sN}}}}={\displaystyle \frac{\mathrm{d}\frac{m_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{m_{\mathrm{s}\mathrm{u}\mathrm{c}}}}{\mathrm{d}{V}_{\mathrm{sN}}}}={\displaystyle \frac{\mathrm{d}{m}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}V}}{\displaystyle \frac{V_{\mathrm{s}\mathrm{u}\mathrm{c}}}{m_{\mathrm{s}\mathrm{u}\mathrm{c}}}}={\displaystyle \frac{\mathrm{d}{m}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}V}}{\displaystyle \frac{1}{{\rho }_{\mathrm{s}\mathrm{u}\mathrm{c}}}}={\displaystyle \frac{\mathrm{d}{m}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}t}}{\displaystyle \frac{\mathrm{d}t}{\mathrm{d}V}}{\displaystyle \frac{1}{{\rho }_{\mathrm{s}\mathrm{u}\mathrm{c}}}}={\displaystyle \frac{\mathrm{d}{m}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}t}}{\displaystyle \frac{\mathrm{d}\phi }{\mathrm{d}V}}{\displaystyle \frac{1}{\omega {\rho }_{\mathrm{s}\mathrm{u}\mathrm{c}}}}$$

(4)

To quantitatively evaluate the exergy loss induced by leakage processes, an exergy analysis model is employed to assess the thermodynamic irreversibility associated with fluid leakage phenomena.

$$P_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}=m_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}\left(Ex\left(p_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}},T_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}\right)-Ex(p_{\mathrm{l}\mathrm{o}\mathrm{w}},T_{\mathrm{l}\mathrm{o}\mathrm{w}})\right)$$

(5)

The differential governing equation describing the relationship between exergy loss induced by leakage processes and volumetric variation is mathematically formulated through the following derivation:

$${\displaystyle \frac{\mathrm{d}{P}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}{V}_{\mathrm{sN}}}}={\displaystyle \frac{\mathrm{d}{m}_{\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{k}}}{\mathrm{d}t}}\left(Ex\left(p_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}},T_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}\right)-Ex(p_{\mathrm{l}\mathrm{o}\mathrm{w}},T_{\mathrm{l}\mathrm{o}\mathrm{w}})\right){\displaystyle \frac{\mathrm{d}\phi }{\mathrm{d}V}}{\displaystyle \frac{V_{\mathrm{s}\mathrm{u}\mathrm{c}}}{\omega }}$$

(6)

3.2. Thermodynamic Model

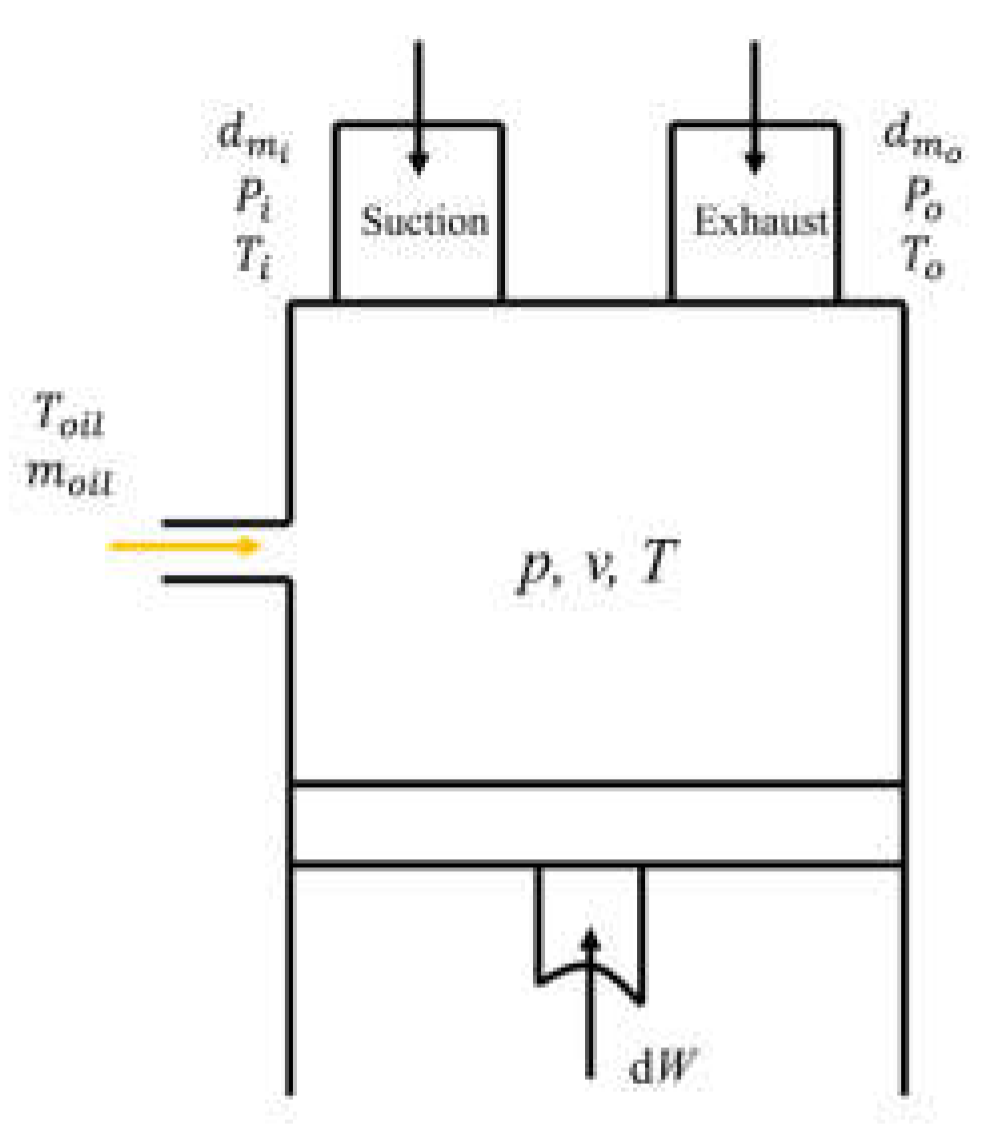
The dynamic model of the screw compressor working process is developed based on variable-mass thermodynamics, incorporating the following fundamental assumptions:

1) Steady-state pressure conditions at suction and discharge ports.

2) Complete thermal equilibrium between refrigerant and lubricant.

3) The gas within the working chamber maintains uniform temperature and pressure distributions.

4) Adiabatic boundary condition at chamber walls.

Figure 4 presents a schematic representation of the control volume configuration.

Based on the first law of thermodynamics and the established hypotheses, the governing energy equation for the control volume is derived as follows:

$$m{\displaystyle \frac{du}{d\phi }}+u{\displaystyle \frac{dm}{d\phi }}=\sum {\displaystyle \frac{d{m}_i}{d\phi }}\left(h_i+{\displaystyle \frac{{v_i}^2}{2}}\right)-\sum {\displaystyle \frac{d{m}_o}{d\phi }}\left(h_o+{\displaystyle \frac{{v_o}^2}{2}}\right)-{\displaystyle \frac{dQ}{d\phi }}-p{\displaystyle \frac{d{V}_{\mathrm{s}\mathrm{N}}}{d\phi }}$$

(7)

Mass conservation equation:

$${\displaystyle \frac{dm}{d\phi }}={\displaystyle \frac{d{m}_i}{d\phi }}-{\displaystyle \frac{d{m}_o}{d\phi }}$$

(8)

The leakage flow model employs the Lin two-phase nozzle model without considering geometric boundary effects of leakage channels. For suction and discharge flows, a modified Lin two-phase nozzle model with upstream and downstream area corrections is implemented. Thermodynamic properties are determined using the NIST REFPROP database, while the governing differential equations are numerically solved through the Backward Differentiation Formula (BDF) method. The design condition parameters are specified in Table 3.

The volumetric efficiency is defined as the ratio of actual intake mass flow rate to theoretical intake mass flow rate:

$${\eta }_V={\displaystyle \frac{m_{\mathrm{a}\mathrm{c}}}{m_{\mathrm{t}\mathrm{h}}}}$$

(9)

The adiabatic efficiency is calculated by the following formula:

$${\eta }_{\mathrm{a}\mathrm{d}}={\displaystyle \frac{m_{\mathrm{a}\mathrm{c}}∆h_{\mathrm{s}}}{P_{\mathrm{i}\mathrm{n}\mathrm{d}}}}$$

(10)

4. Numerical Model

4.1. Control Volume and Grids of the Fluid Domain

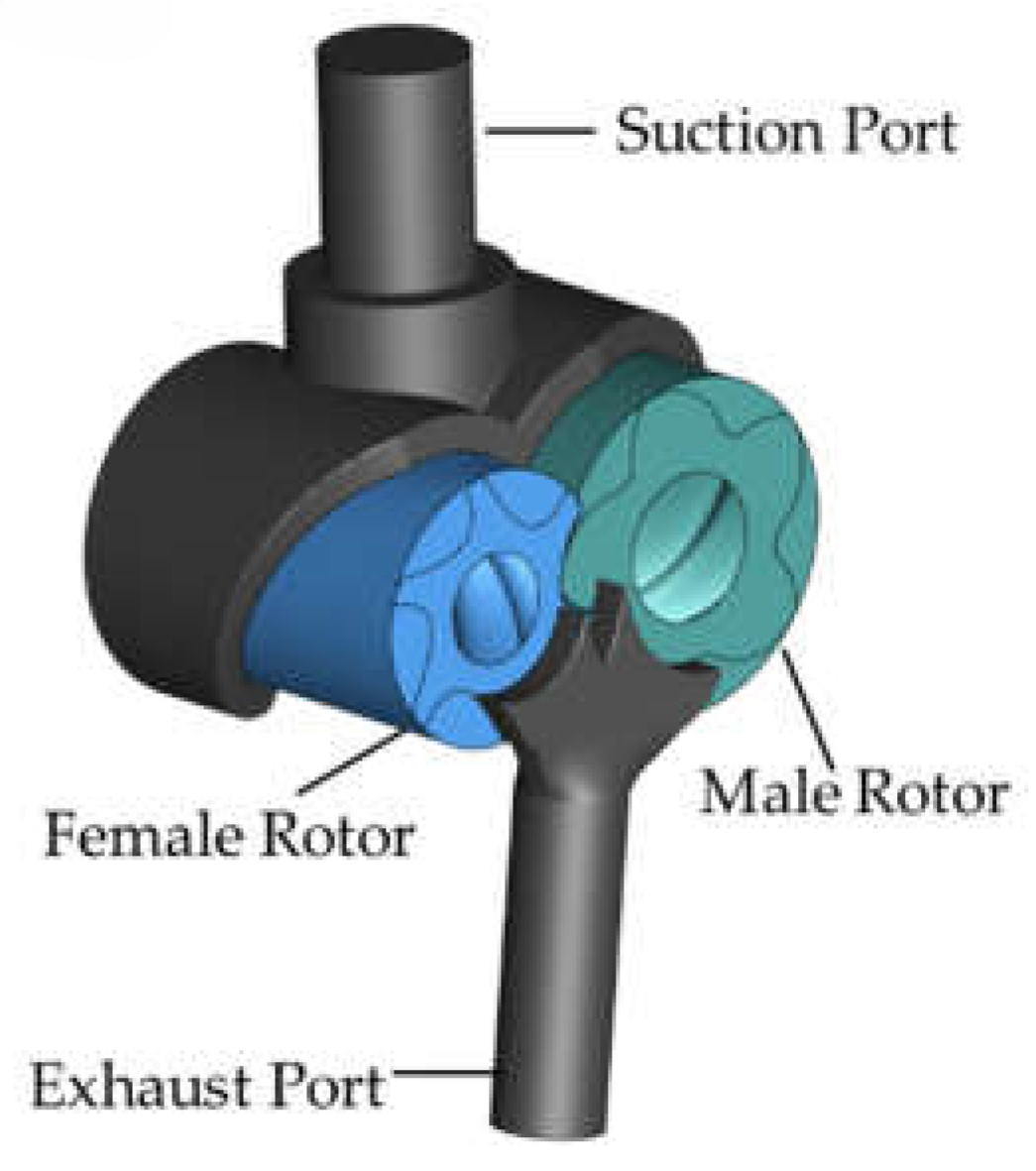
The CFD domain comprises the main and gate rotor fluid regions along with the suction and discharge port. The numerical model incorporates critical geometric clearances, including tip, inter-lobe meshing, and axial end clearances. Figure 5 illustrates the complete control volume configuration with detailed boundary definitions.

The fluid dynamics within the computational domain are governed by the fundamental conservation laws of mass, momentum, and energy. The turbulence characteristics are modeled using the Shear Stress Transport (SST) k-ω formulation, which effectively combines the advantages of the k-ω model's near-wall resolution with the k-ε model's far-field performance. The total energy model is employed to simulate thermal energy transport, providing a comprehensive approach for accurate heat transfer prediction in high-speed compressible flows.

The thermodynamic properties of refrigerant R410A are determined using the Redlich-Kwong (RK) equation of state. The analysis assumes negligible influence of lubricating oil throughout the computational domain. The operational boundary conditions, including inlet/outlet pressure and temperature parameters, are specified in Table 3.

4.2. Independence Verification

The stationary domain, encompassing suction and discharge ports, is meshed using ANSYS Meshing with tetrahedral-dominated elements, incorporating boundary layer refinement and interface densification for enhanced accuracy. For the rotating domain, TwinMesh generates high-quality structured grids through a systematic process: first creating a 2D cross-sectional mesh via node mapping between the screw rotor profile and casing contour, then developing the 3D mesh through axial interpolation while maintaining rotational periodicity. This meshing approach ensures optimal grid resolution for both stationary and rotating components. Figure 6 illustrates the detailed rotating domain grid of the screw compressor.

A grid independence study was conducted using the 3000 rpm rotor domain mesh. The investigation systematically varied the radial, circumferential, and axial node counts while monitoring changes in intake mass flow rate and gas power output. The comparative results for different grid configurations are presented in Table 4. Analysis revealed that radial and axial node distributions exhibited significant influence on solution accuracy within the screw rotor domain. Based on the convergence criteria, Configuration 7 was selected as the optimal mesh configuration for the 3000 rpm rotor simulation. For other rated rotor configurations, the mesh parameters were determined through geometric scaling based on the ratio of cylinder diameter and rotor length relative to the 3000 rpm reference configuration.

The computational grids is generated using TwinMesh, where the temporal resolution is intrinsically linked to the angular step size of the cross-sectional mesh. For the current simulation, an angular resolution of 1° is implemented, corresponding to the generation of a complete structured mesh and subsequent iterative computation at each degree of rotor rotation until the convergence criteria are satisfied. This 1° angular step size is consistently maintained across all rotor speed configurations to ensure temporal resolution uniformity.

5. Results and Analysis

5.1. Difference of Leakage Characteristic

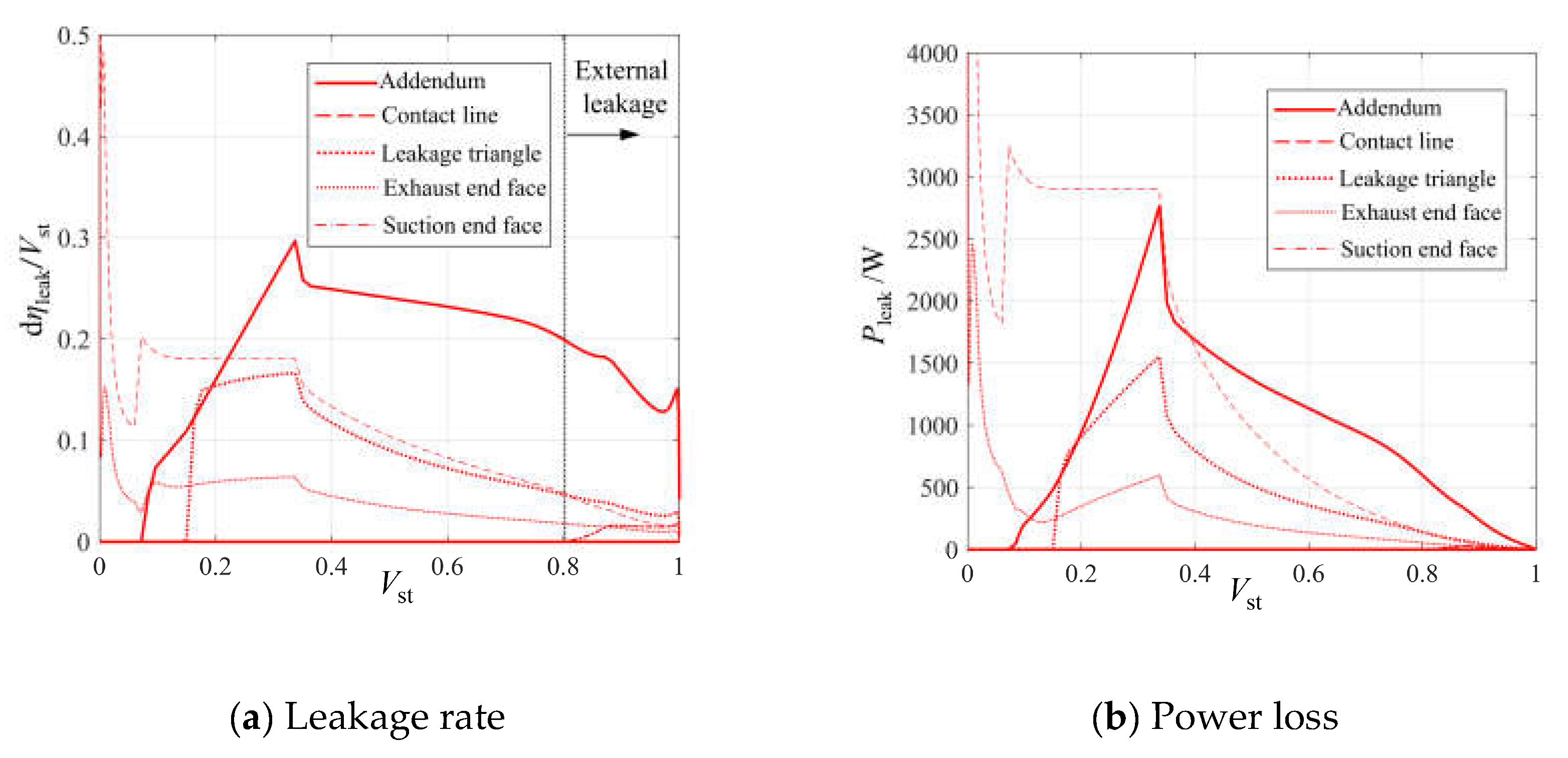
The investigated screw compressor configuration features a main rotor with five teeth, establishing a 72° rotational periodicity. A leakage state transition occurs at 72° post suction completion, where the leakage mechanisms through both the tooth tip and triangular channels undergo a fundamental transformation from external to internal leakage. Figure 7 illustrates the leakage power loss and leakage rate characteristics of the screw compressor operating at 3000 rpm. The analysis reveals a distinct hierarchy of leakage flow magnitudes through various pathways under identical clearance conditions: tooth tip leakage (dominant), contact line leakage (secondary), leakage triangle flow (tertiary), discharge end leakage, and suction end leakage (minimal).

The energy loss hierarchy induced by leakage pathways is established as follows: contact line leakage (primary) > tooth tip leakage (secondary) > leakage triangular flow (tertiary) > discharge end leakage > suction end leakage (minimal). The contact line leakage exhibits greater energy loss than the tooth tip leakage due to its persistent external leakage. This results in higher pressure differentials, causing increased specific energy loss compared to the tooth tip leakage.

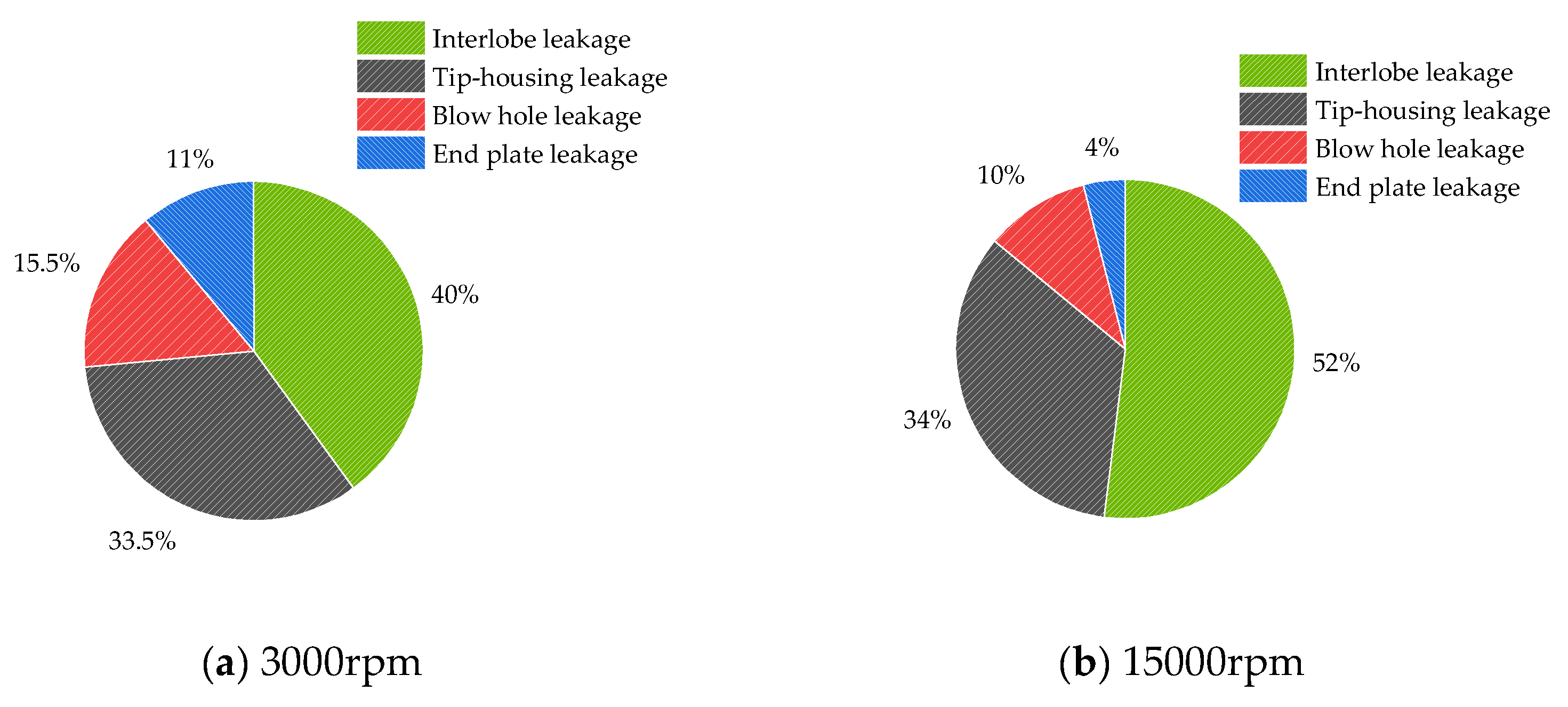
Figure 8 presents a comparative analysis of leakage characteristics for rotors operating at different rated speeds while maintaining constant displacement capacity. The results demonstrate that despite the reduction in rotor dimensions with increasing rotational speed, contact line leakage remains the dominant contributor to overall leakage losses.

5.2. Performance of Different Rotors at Rated Rotational Speed

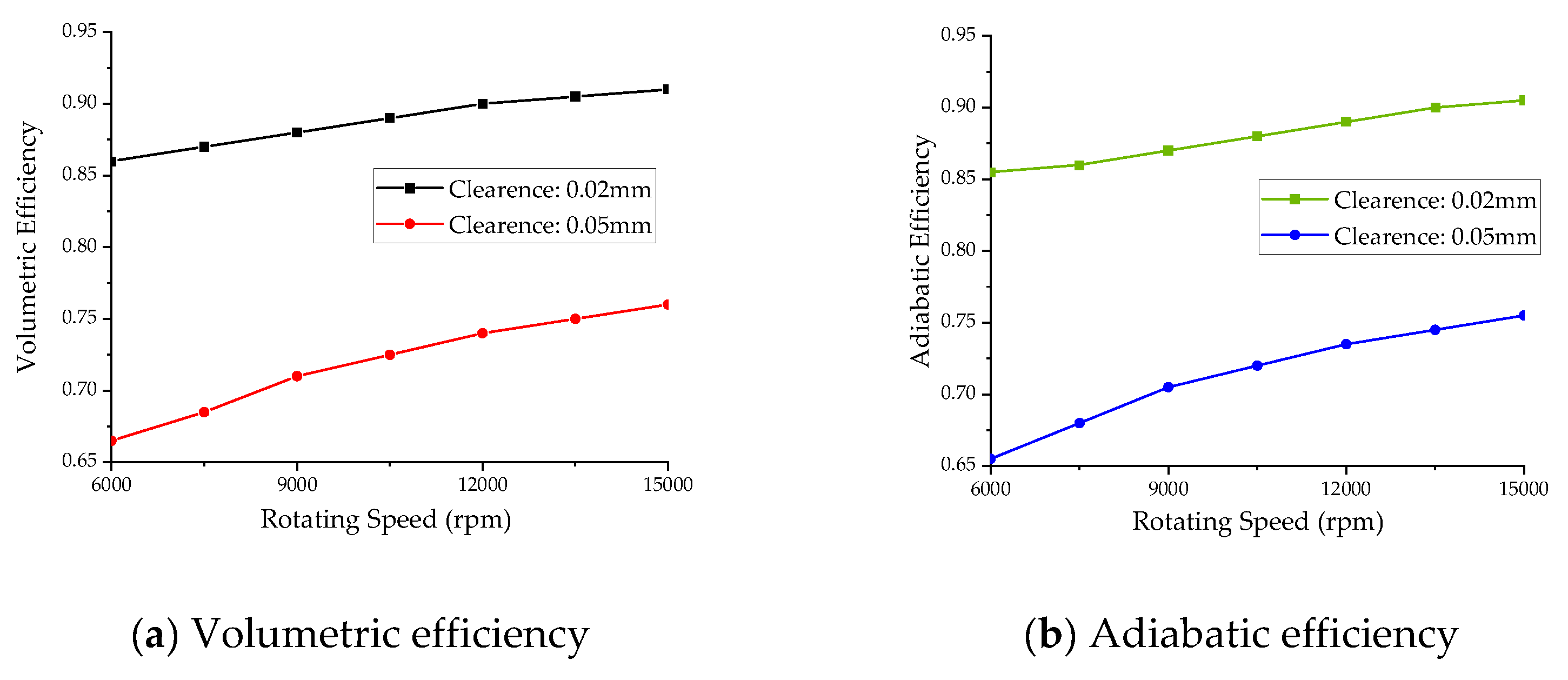
Figure 9 demonstrates the variation in volumetric efficiency across different tated rotational speeds for the screw compressor. At lower speeds, the compressor exhibits reduced volumetric efficiency, which shows significant improvement as speed increases from low to high ranges. While the efficiency continues to rise into ultra-high speed regimes, the rate of increase diminishes considerably. Specifically, when the rotational speed is elevated from 6000 rpm to 9000 rpm, 12000 rpm, and 15000 rpm, the volumetric efficiency increases by 5.07%, 3.45%, and 1.33%, respectively, indicating a nonlinear relationship between speed and efficiency. The adiabatic efficiency of different rotors exhibits an similar trend with increasing rated rotational speed.

For screw rotors with identical displacement capacities, operating at ultra-high rotational speeds presents limited improvements in volumetric and adiabatic efficiencies, while introducing significant challenges in rotor dynamics and operational stability. The clearance dimensions, which are intrinsically linked to manufacturing precision and assembly tolerances, cannot be reduced without compromising mechanical reliability.

5.3. Gas Force of Different Rotors at Rated Rotational Speed

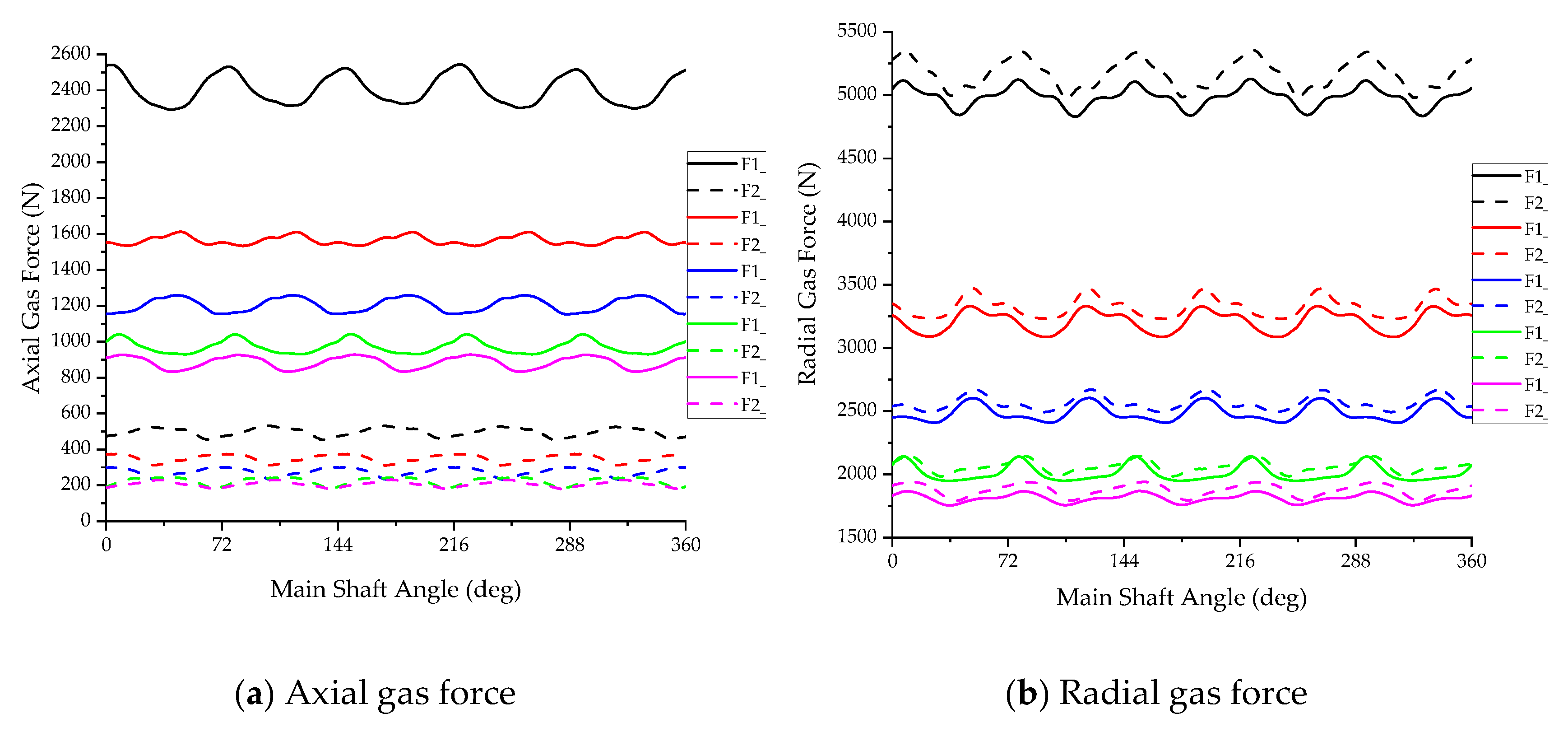
A CFD model was employed to analyze the gas forces acting on rotors with different rated speeds under identical operating conditions. Figure 10 illustrates the axial and radial gas forces exerted on each rotor configuration across various rotational speeds. The results demonstrate a significant reduction in both axial and radial gas forces with increasing speed while maintaining constant theoretical displacement. Notably, the main rotor experiences substantially higher axial forces compared to the gate rotor, whereas the gate rotor exhibits greater radial forces than the main rotor.

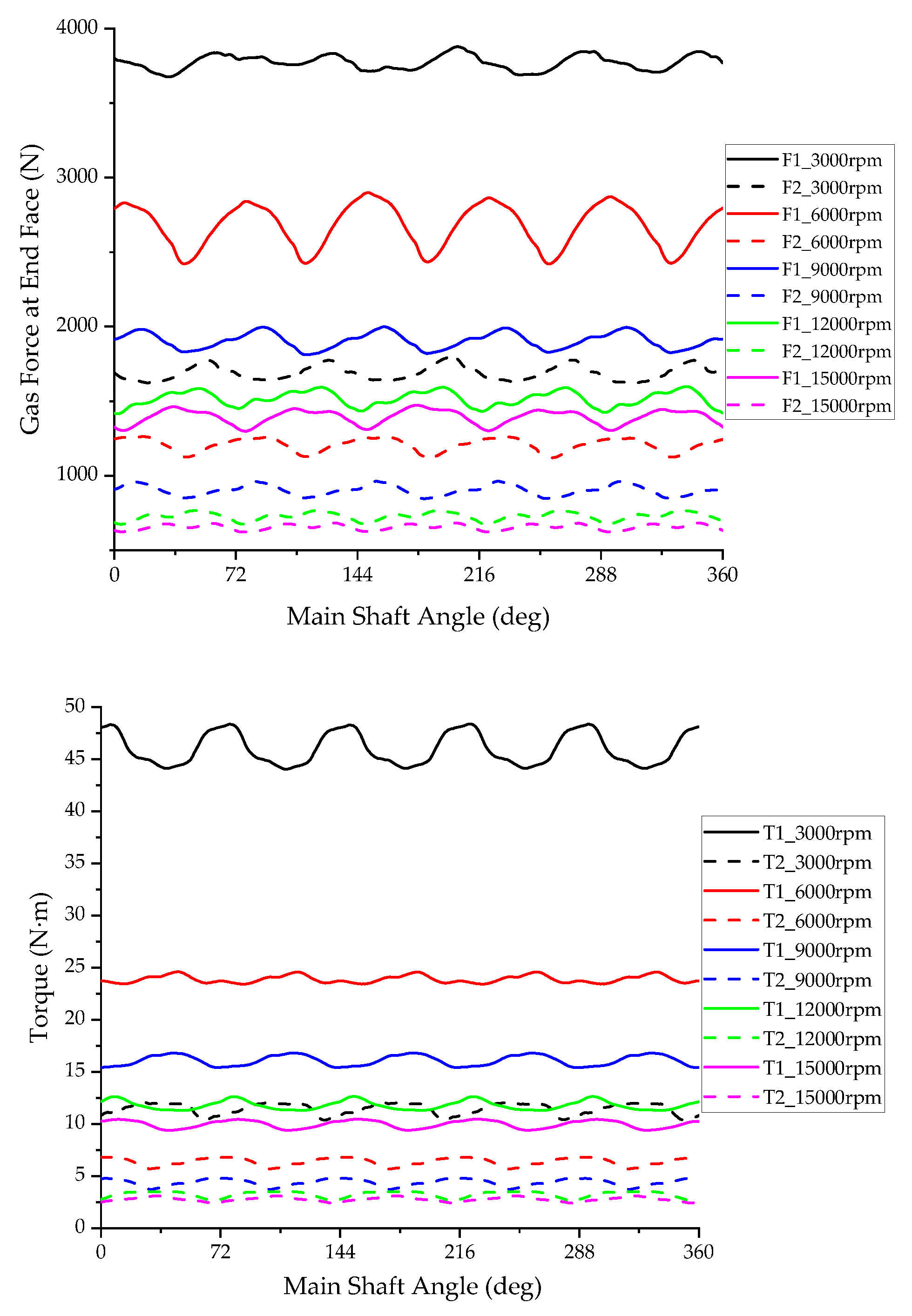
Figure 11 illustrates the variation of end-face gas forces and the resulting torque acting on the rotors. The analysis reveals that with increasing rated speed at constant displacement, the gas forces acting on the rotors decrease significantly. Notably, the main rotor experiences substantially higher axial gas forces compared to the gate rotor, necessitating differentiated bearing selection based on their distinct load characteristics. Concurrently, the torque demonstrates a marked reduction with increasing speed, accompanied by decreased amplitude of torque fluctuations.

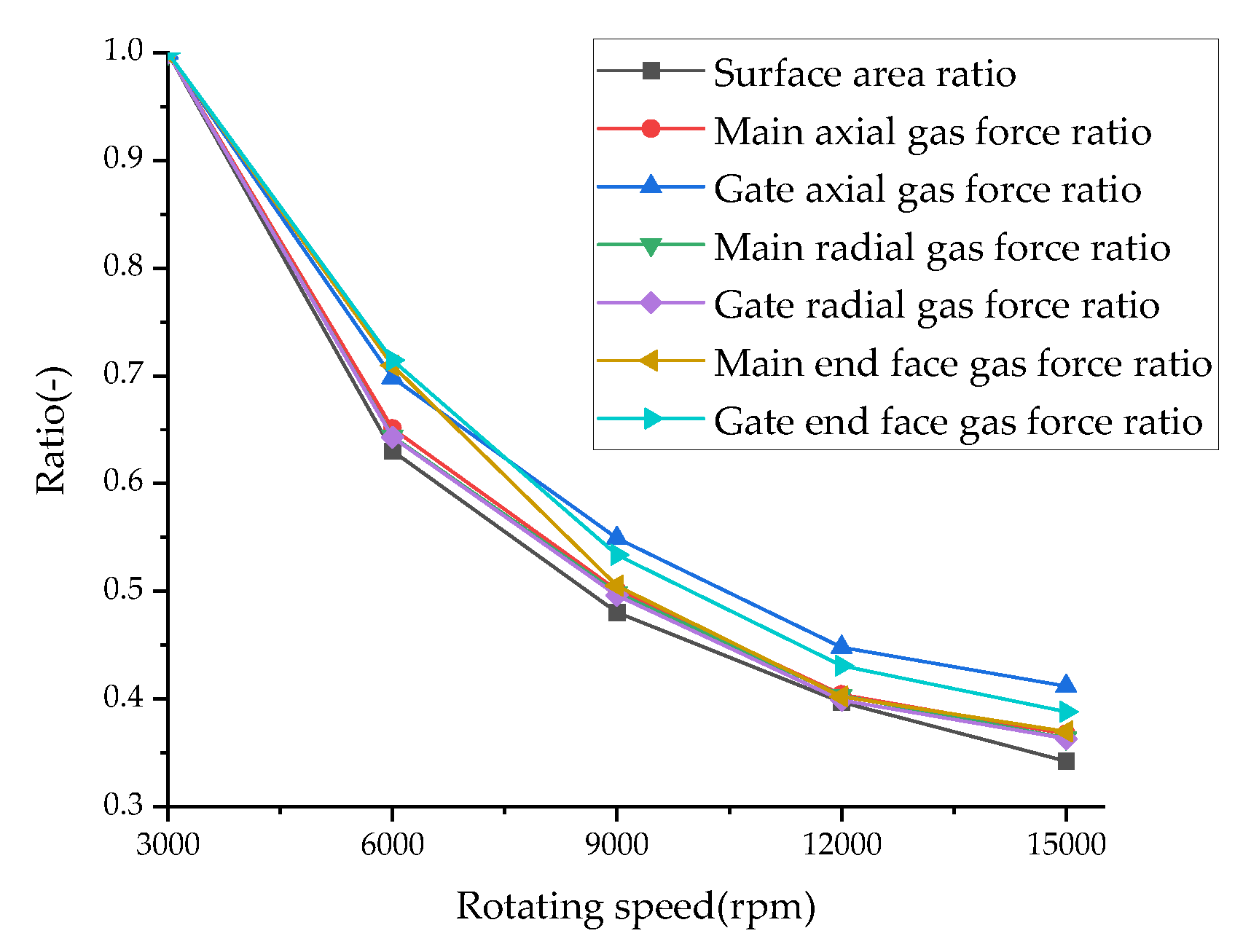
Using the axial, radial, and end-face gas forces acting on the 3000 rpm rated rotor as reference values, the force ratios at other rotational speeds were compared relative to the 3000 rpm baseline. The analysis reveals that, with the exception of the gate rotor's axial and end-face gas forces, the force ratios exhibit consistent trends with the corresponding surface area ratios relative to the 3000 rpm configuration. This finding highlights the need for special consideration of force distribution on the gate rotor during the design process, particularly for its axial and end-face loading characteristics.

Figure 10. Axial and radial gas forces on the main and gate rotors at different rated speeds.

Figure 10. Axial and radial gas forces on the main and gate rotors at different rated speeds.

Figure 11. The End gas forces on the main and gate rotors at different rated speeds.

Figure 11. The End gas forces on the main and gate rotors at different rated speeds.

Figure 12. Variation of rotor gas force ratios across different rotational speeds.

Figure 12. Variation of rotor gas force ratios across different rotational speeds.

5.4. The Effect of Rotor Configuration and Wrap Angle

The analysis demonstrates that leakage losses remain the predominant loss mechanism in high-speed small screw compressor design. While increasing rotational speed can decrease leakage, this approach against rotor stability and reduced motor efficiency at elevated speeds. For compressors with identical external dimensions, leakage reduction strategies extend beyond clearance minimization to include decreasing leakage path length through optimized lobe configuration. Specifically, reducing the number of rotor lobes improves the area utilization coefficient while decreasing the leakage proportion, thereby enhancing overall performance.

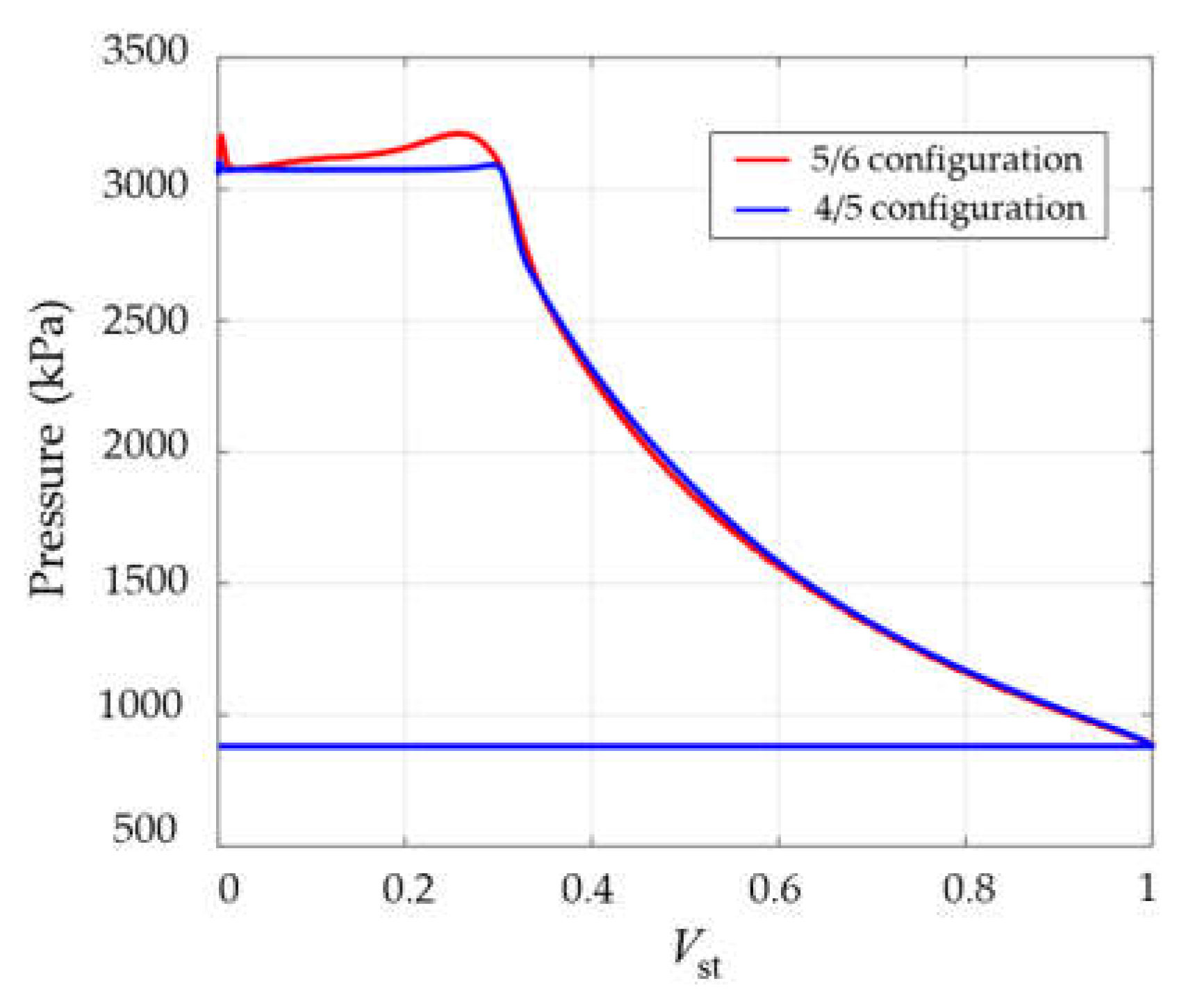
Based on these principles, a 12000 rpm rated speed was selected, and the rotor geometry was optimized to minimize leakage area. This optimization resulted in a novel 4/5 lobe rotor profile. Under conditions of constant theoretical displacement and built-in volume ratio, Figure 13 illustrates the pressure variation with respect to normalized volume for both 4/5 and 5/6 lobe configurations at design operating conditions. During the compression and discharge processes, the 4/5 lobe configuration demonstrates significantly reduced over-compression phenomena compared to the 5/6 lobe, accompanied by lower discharge pressure fluctuations. These characteristics contribute to enhanced energy efficiency and reduced power consumption.

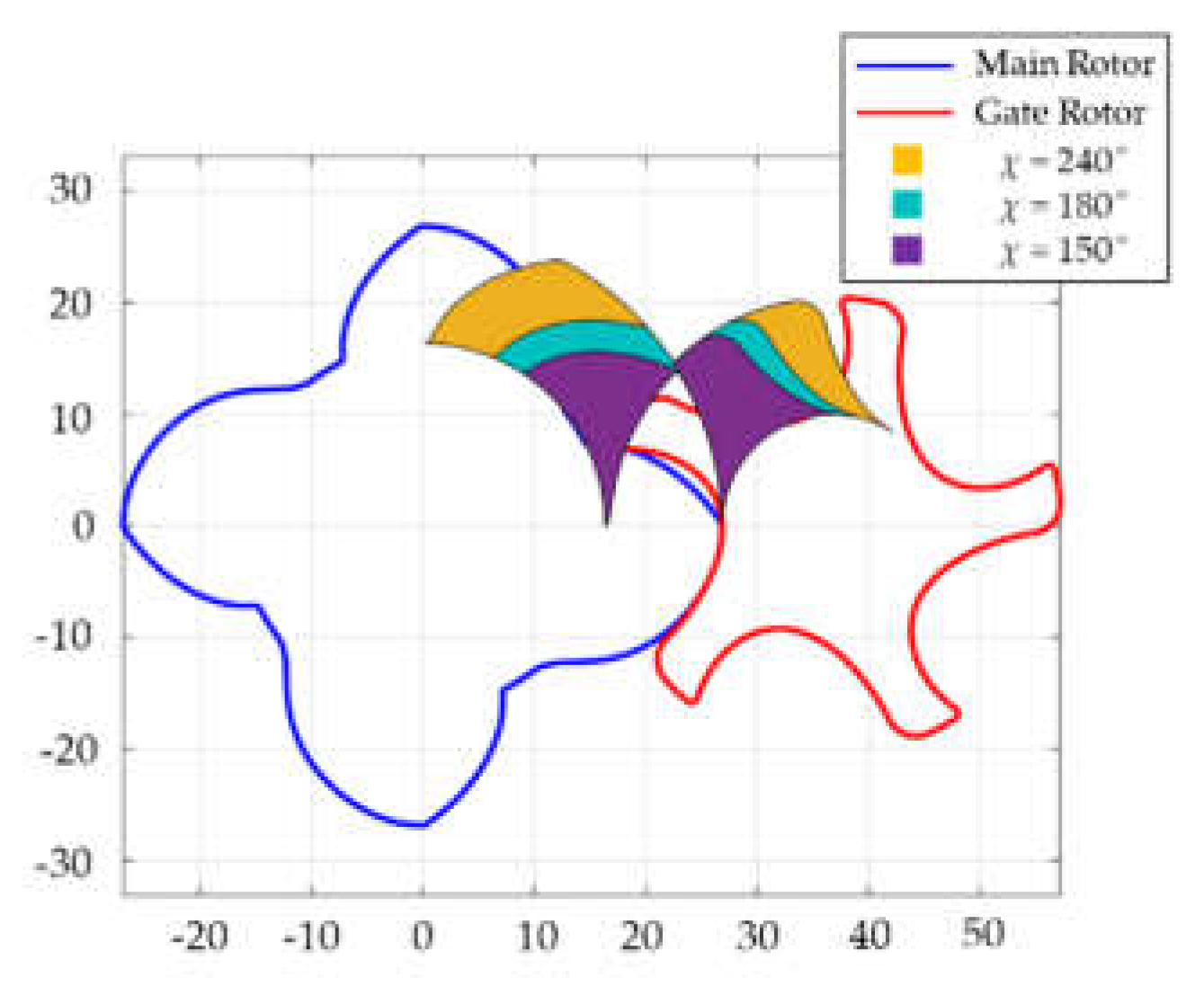
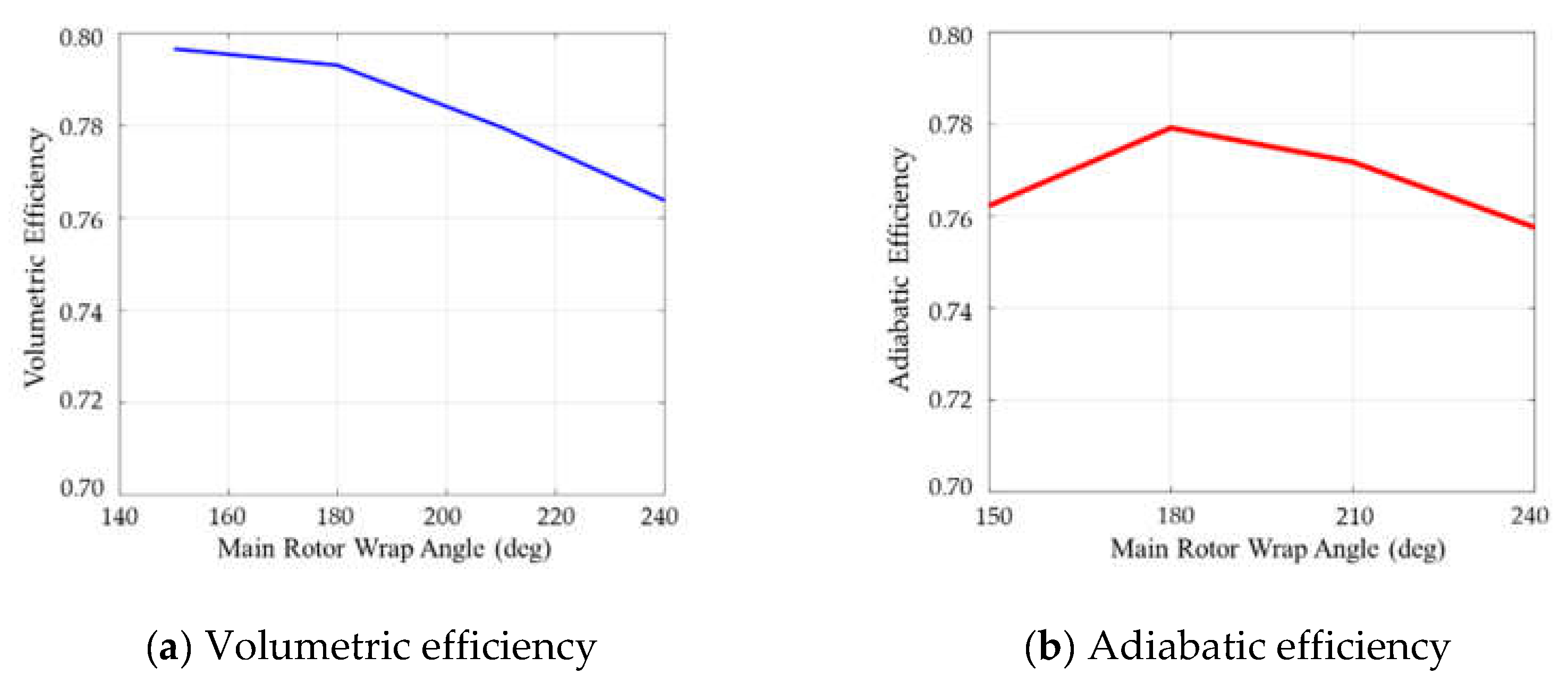
The variation of wrap angle serves as an effective parameter for optimizing the balance between leakage losses and discharge resistance. Figure 14 presents the discharge port configurations for screw rotors with different wrap angles at a constant built-in volume ratio of 2.8. Utilizing the thermodynamic performance prediction model, Figure 15 illustrates the impact of wrap angle on efficiency.

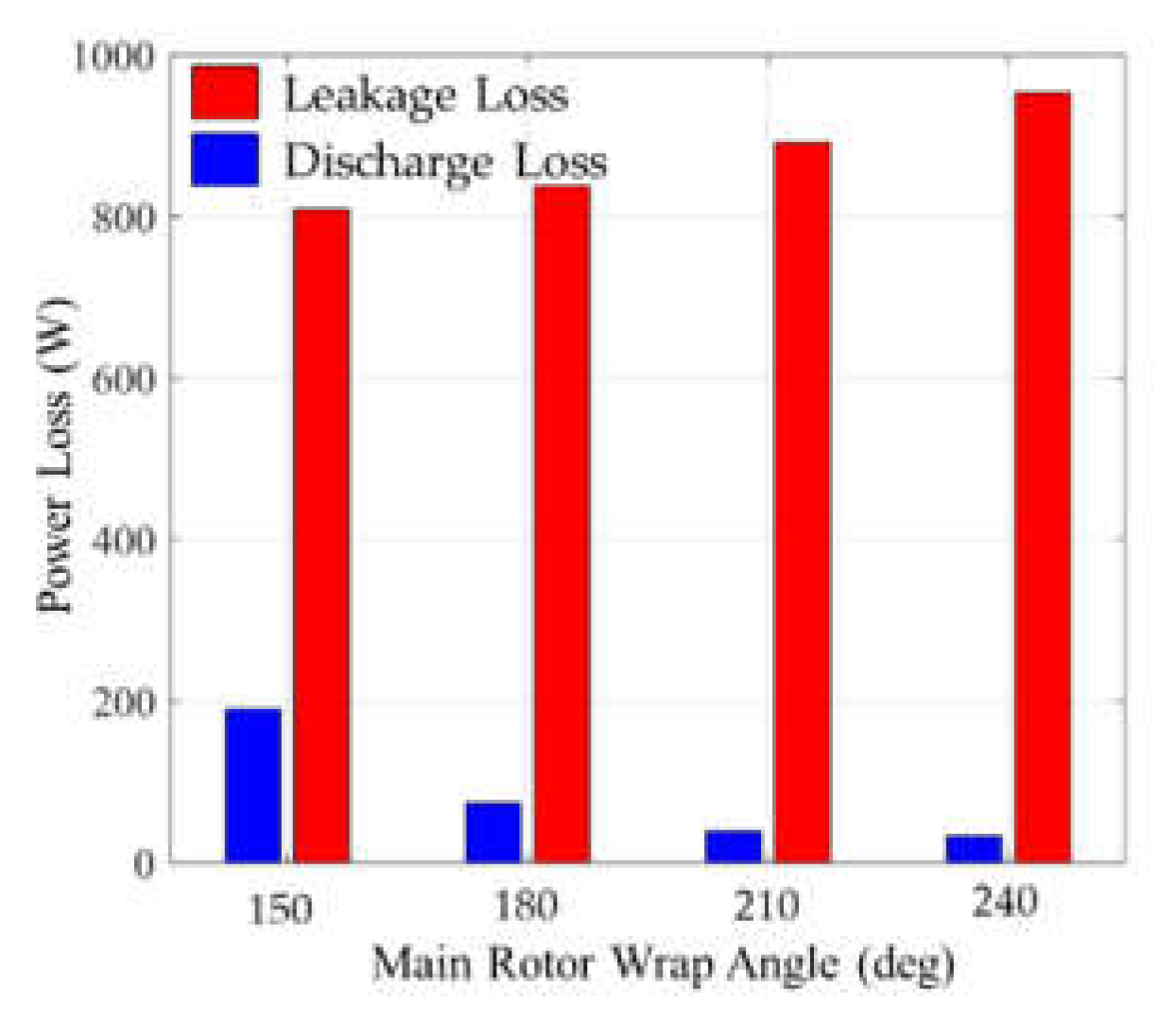
The analysis reveals that volumetric efficiency decreases with increasing wrap angle due to extended contact line length. In contrast, adiabatic efficiency demonstrates a non-monotonic relationship with wrap angle. At lower wrap angles, the reduced discharge port area leads to increased discharge power losses. Conversely, higher wrap angles exhibit diminished discharge power losses but are accompanied by elevated leakage losses. This trade-off relationship results in an optimal wrap angle that maximizes adiabatic efficiency by balancing these competing loss mechanisms. Figure 16 illustrates the variation of power losses across different wrap angles, quantitatively demonstrating this efficiency optimization phenomenon.

6. Conclusions

This study investigates the high-speed miniaturization potential of refrigeration screw compressors by designing rotors with varying rated speeds at constant displacement. A comprehensive analysis framework was developed, integrating geometric characterization, thermodynamic modeling, and CFD-based force analysis. The performance characteristics under miniaturized high-speed conditions were systematically compared, leading to the following conclusions:

While tooth tip leakage represents the largest volumetric leakage flow in screw compressors, the contact line leakage contributes most significantly to power losses due to the huge pressure differential across the contact line. When the rated speed increases to 15000 rpm, contact line leakage remains the dominant source of power loss, with its relative contribution showing a marked increase.

At constant rated speeds, reducing leakage clearances significantly improves both volumetric and adiabatic efficiencies. As rated speed increases and rotor dimensions decrease, the gas forces acting on the rotors decrease significantly, generally correlating with the reduction in force-bearing areas. However, the gate rotor experiences higher-than-ideal axial and end-face gas forces. Under ultra-high-speed conditions, the efficiency gains from further speed increases become negligible.

For screw compressors with identical cylinder dimensions, reducing the number of lobes increases the area utilization coefficient while enabling leakage reduction through optimized profile design. Larger wrap angles, at constant theoretical displacement and rotor profiles, extend contact line length and increase discharge port area, leading to reduced volumetric efficiency. This creates a trade-off between increased leakage losses and decreased discharge losses, resulting in an optimal wrap angle that maximizes adiabatic efficiency.