Dynamically Tunable Singular States Through Air-Slit Control in Asymmetric Resonant Metamaterials

1. Introduction

Metamaterials and metasurfaces have been widely recognized as transformative platforms for controlling electromagnetic waves [1,2,3]. These advanced materials utilize subwavelength structures to achieve remarkable electromagnetic properties, such as negative refraction, flat lensing and perfect light absorption and [4,5,6]. By engineering their composition at the nanoscale, these systems enable accurate control over the amplitude, phase, and polarization of light [7]. Depending on their dimensionality (i.e., 1D, 2D or 3D), these periodic structures provide compact solutions for manipulating light-matter interactions [8,9,10].

The realization of such advanced materials relies on several physical concepts such as effective medium theory (EMT) [11], lattice resonances [12], particle scattering resonances [13], and surface plasmon effects [14]. EMT uses macroscopic effects from complex subwavelength interactions, which generates extraordinary properties such as negative refractive indices or anisotropic behavior [11,15]. Lattice resonances, namely guided-mode resonances (GMRs), arise from the coupling of guided resonances with diffracted waves in periodic arrays [16,17]. These periodic structures exhibit diverse spectral responses with high quality factor (high-Q) resonances, which enable them highly desirable for wavelength-selective photonic devices [18]. Additionally, particle scattering resonances driven by electric or magnetic dipoles in individual structures facilitate strong light-matter interactions and related phenomena [13,19].

Recently, among various mechanisms, the concept of bound state in the continuum (BIC) has attracted significant attention in metasurface research, which are non-radiative states embedded within resonance modes under perfect symmetry condition [20,21]. By controlling symmetrical breaking such as off-normal incidence or structural asymmetry, BICs can transition into radiative modes known as quasi-BICs, which shows a great potential for innovative devices including narrowband filtering, optical switching, and biosensing [22,23,24]. Recent advancements have revealed a new type of resonance in photonic lattices (PLs), where strong resonances radiate immediately at isolated spectral positions from adjacent bands when symmetry is broken. This phenomenon, known as the singular state, represents the realization of quasi-BIC and is explained through asymmetric guided-mode resonances (aGMRs) [25].

In this work, we present a novel method for dynamically tuning singular states by employing PLs with air-slit-based structural modifications. This approach enables effective control over resonance positions and dual functionalities, including narrowband reflection and notch filtering. Furthermore, the introduction of multiple air-slits demonstrates that increasing asymmetry significantly enhances spectral tunability by inducing multiple folding behavior in the resonance bands. These tunable singular states show great potential for designing multifunctional photonic devices.

2. Air Slit Induced Singular States

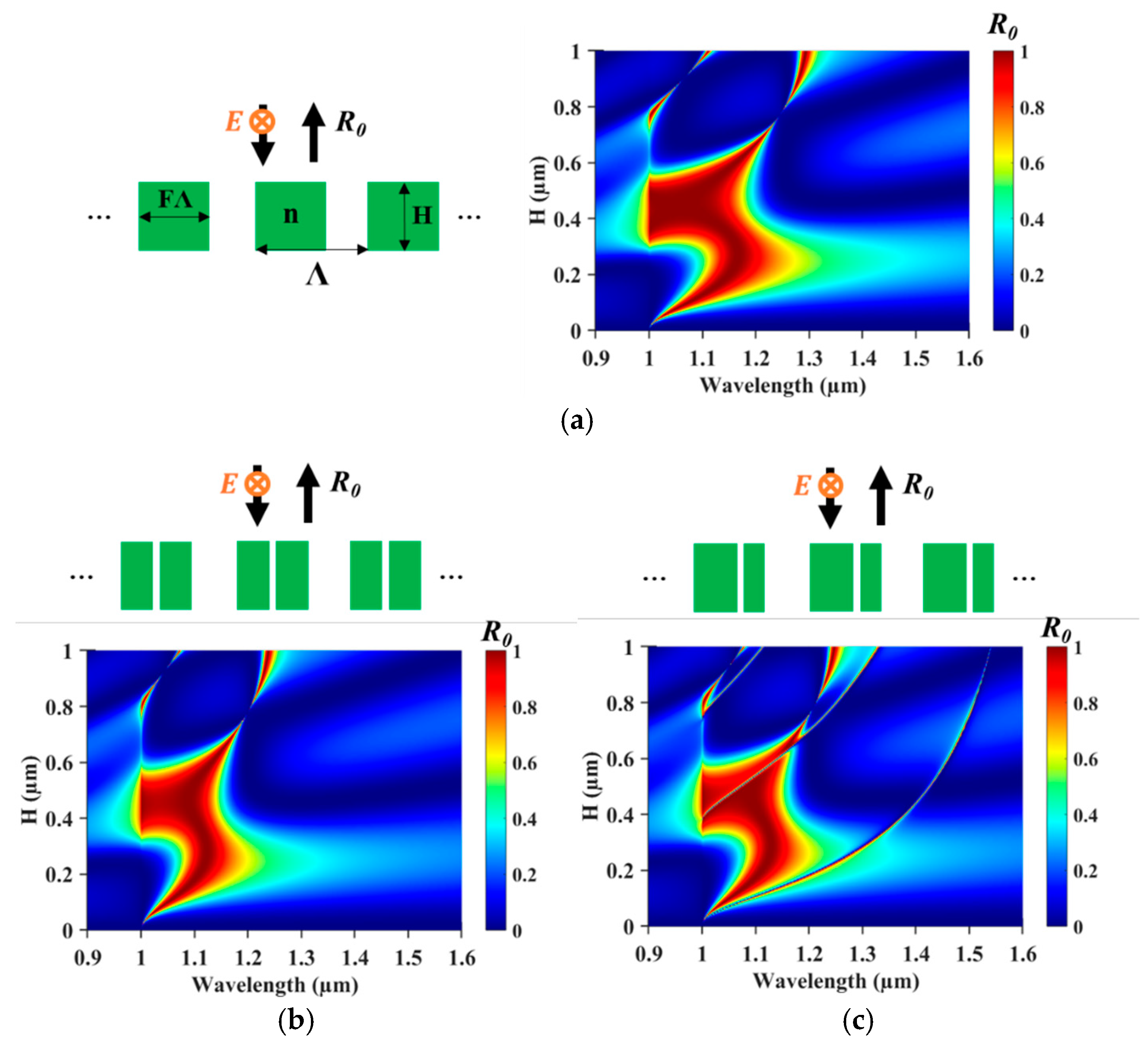
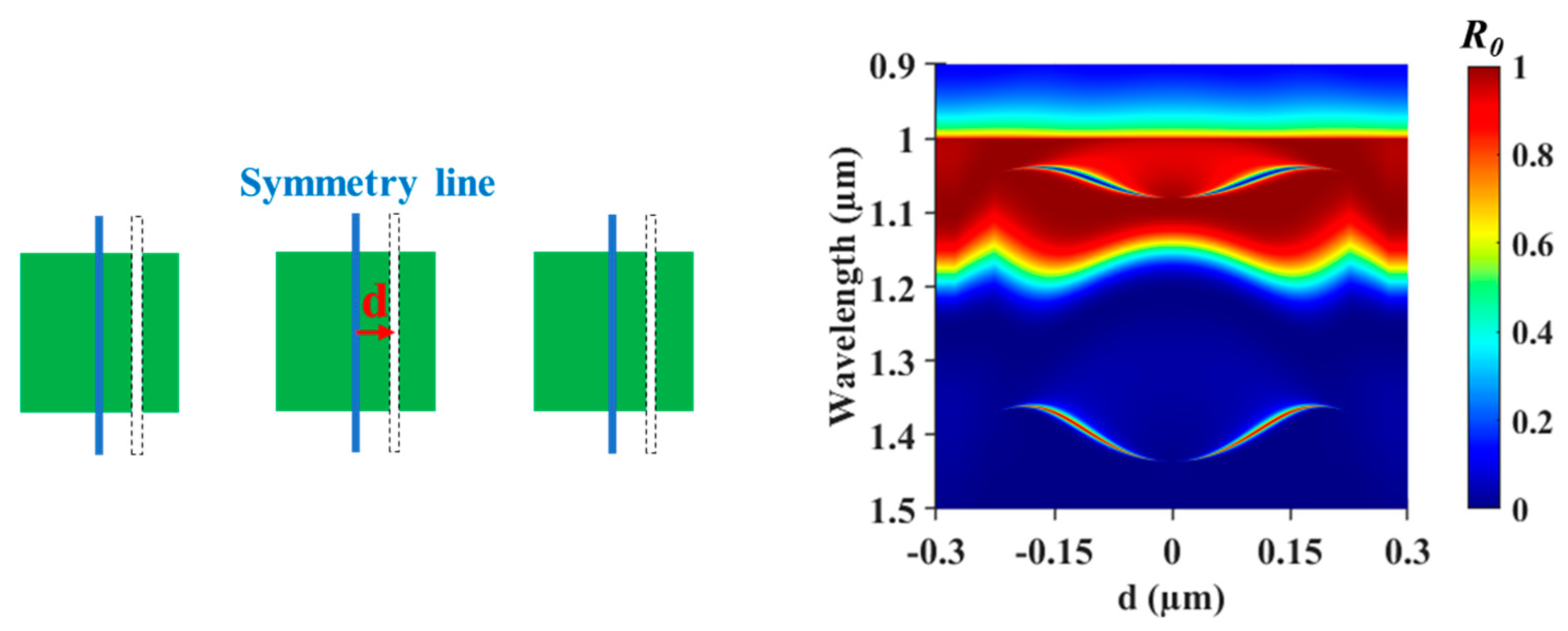
To investigate tunable singular states, we broke the symmetry of a simple one-dimensional (1D) photonic lattice (PL) by incorporating an air-slit. Figure 1a illustrates the 1D resonant structure, defined by grating parameters such as period (Λ), fill factor (F), and grating height (H) with refractive index (n). Continuing the study of singular states, we employed the previous design of the 1D PL [26] where the grating parameter set is {$\Lambda$ = 1 µm, $F$ = 0.5, $H$ = 0.5 µm} with a lossless material ($n$ = 2). In this study, we characterized the zeroth-order reflectance ($R_0$) using the rigorous coupled-wave analysis (RCWA) [27] method implemented in commercial software [28]. The analysis is performed with TE-polarized light (electric field parallel to the grating grooves) illuminating the 1D PL at normal incidence in the air ($n_{air}$ = 1). As shown in calculated $R_0$ map of Figure 1a, wideband perfect reflection is observed in the spectral region due to the resonant radiation, which has been understood by the guided mode resonance (GMR) phenomenon [16]. As the height ($H$) increases, additional resonance bands are generated by excitation of higher GMR modes. Figure 1b presents the case where an air-slit with a width of 0.05 µm is introduced at the center of the grating, preserving the structural symmetry. The $R_0$ map shows resonance bands like those observed without the air-slit (i.e., Figure 1a) but only a slight narrowing observed. This narrowing can be attributed to the effective refractive index reduction due to the presence of air. In contrast, the resonance band is significantly changed when the symmetry is broken by shifting the air-slit. Figure 1c shows the $R_0$ map of the 1D PL with air slit displaced 0.05 µm from the center. The asymmetry of the 1D PL leads to the formation of a sharp band, which can be interpreted as an off-BIC (bound state in continuum) [20] or asymmetric GMR [25]. Observed in the asymmetric system, these resonance bands can be classified as asymmetric guided-mode resonance (aGMR) modes owing to their origin in asymmetric excitation of GMR modes. Notably, shown in the $R_0$ map, the fundamental aGMR mode manifests as a singular state, distinctly separated from the other resonance bands. This singular state will be shown to be tunable through manipulation of the air slit.

3. Interpretation of Singular States

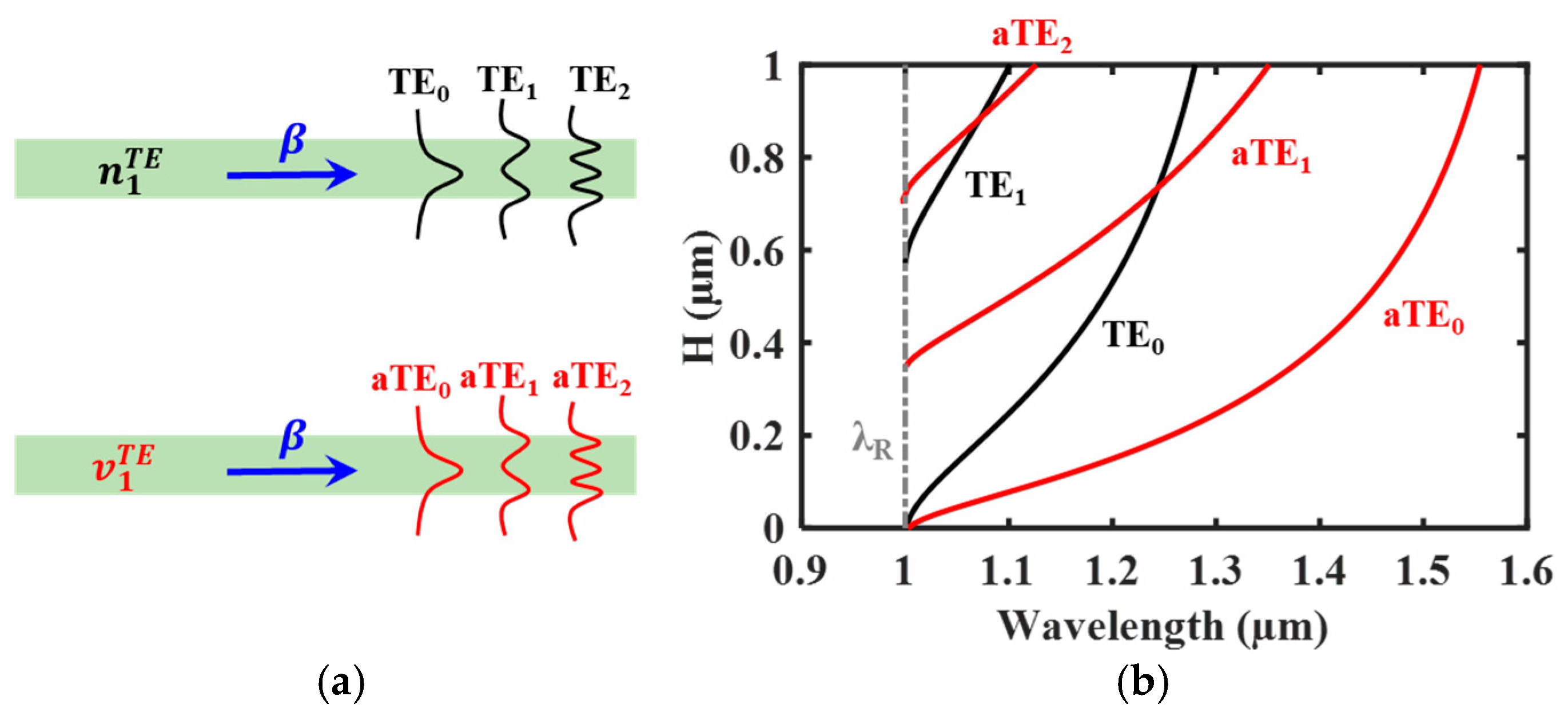
Singular states can be interpreted by analyzing the slab waveguide modes of an equivalent 1D PL. As depicted in Figure 2a, the 1D PL can be approximated as a slab waveguide where electromagnetic fields are confined through the coupling of diffracted waves to a propagation constant ($\beta$). For this equivalent slab waveguide, the 1D grating layer is homogenized using effective medium theory (EMT) with the Rytov’s formalism [29]. The effective refractive indices ($n_m^{TE}$ and $v_m^{TE}$) are determined by the mth order solutions from the following equations [29,30]:

$${\displaystyle \frac{\sqrt{n^2-{(n_m^{TE} )}^2} }{\sqrt{1-{(n_m^{TE} )}^2 }}}={\displaystyle \frac{tan\left\{\frac{\pi \Lambda }{\lambda }(1-F)\sqrt{1-{(n_m^{TE} )}^2 }\right\}}{tan\left\{\frac{\pi \Lambda }{\lambda }F \sqrt{n^2-{(n_m^{TE} )}^2 }\right\}}} (\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}),$$

(1)

$${\displaystyle \frac{\sqrt{n^2-{(v_m^{TE} )}^2} }{\sqrt{1-{(v_m^{TE} )}^2 }}}={\displaystyle \frac{tan\left\{\frac{\pi \Lambda }{\lambda }F \sqrt{n^2-{(n_m^{TE} )}^2 }\right\}}{tan[\frac{\pi \Lambda }{\lambda }(1-F)\sqrt{1-{(v_m^{TE} )}^2 }]}} (\mathrm{a}\mathrm{s}\mathrm{y}\mathrm{m}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}).$$

(2)

Here, the $n_m^{TE}$ and $v_m^{TE}$ represent the symmetric and asymmetric field EMT solutions from each equation (1) and (2). Considering the first diffraction waves, we apply the first solution $n_1^{TE}$ and $v_1^{TE}$ for slab waveguide analysis. The eigenvalue problem of the lth TE mode of slab waveguide can be expressed as [25,31]:

$$tan\left\{q_1{\displaystyle \frac{H}{2}}-l{\displaystyle \frac{\pi }{2}}\right\}={\displaystyle \frac{\sqrt{{\left(\beta \right)}^2-{\left(k_0\right)}^2}}{q_1}} l=\mathrm{0,1},\dots ,$$

(3)

where the $q_1$ and $k_0$ are vertical propagation vectors of first-order diffracted waves and propagation constant ($2\pi /\lambda$) in vacuum, respectively. Based on the different EMT solutions ($n_1^{TE}$ and $v_1^{TE}$), the $q_1$ is given by $n_1^{TE}{k}_0$ or $v_1^{TE}{k}_0$. The $\beta$ represents the propagation constant of the guided mode, assuming coupled from the first-order grating vector ($K=2\pi /\mathsf{\Lambda }$). Consequently, the lth TE guided modes (${TE}_l$ or $a{TE}_l$) are obtained as eigen-solutions using symmetric and asymmetric effective refractive indices. Figure 2b displays the calculated ${TE}_l$ or $a{TE}_l$ modes, which matches the resonance bands observed in the asymmetric air slit 1D PL in Figure 1c. Indeed, the singular state originates from the $a{TE}_0$, indicating the fundamental guided mode of asymmetric EMT slab coupled by first-order diffracted waves.

4. Analysis of Air Slit-Induced Singular States

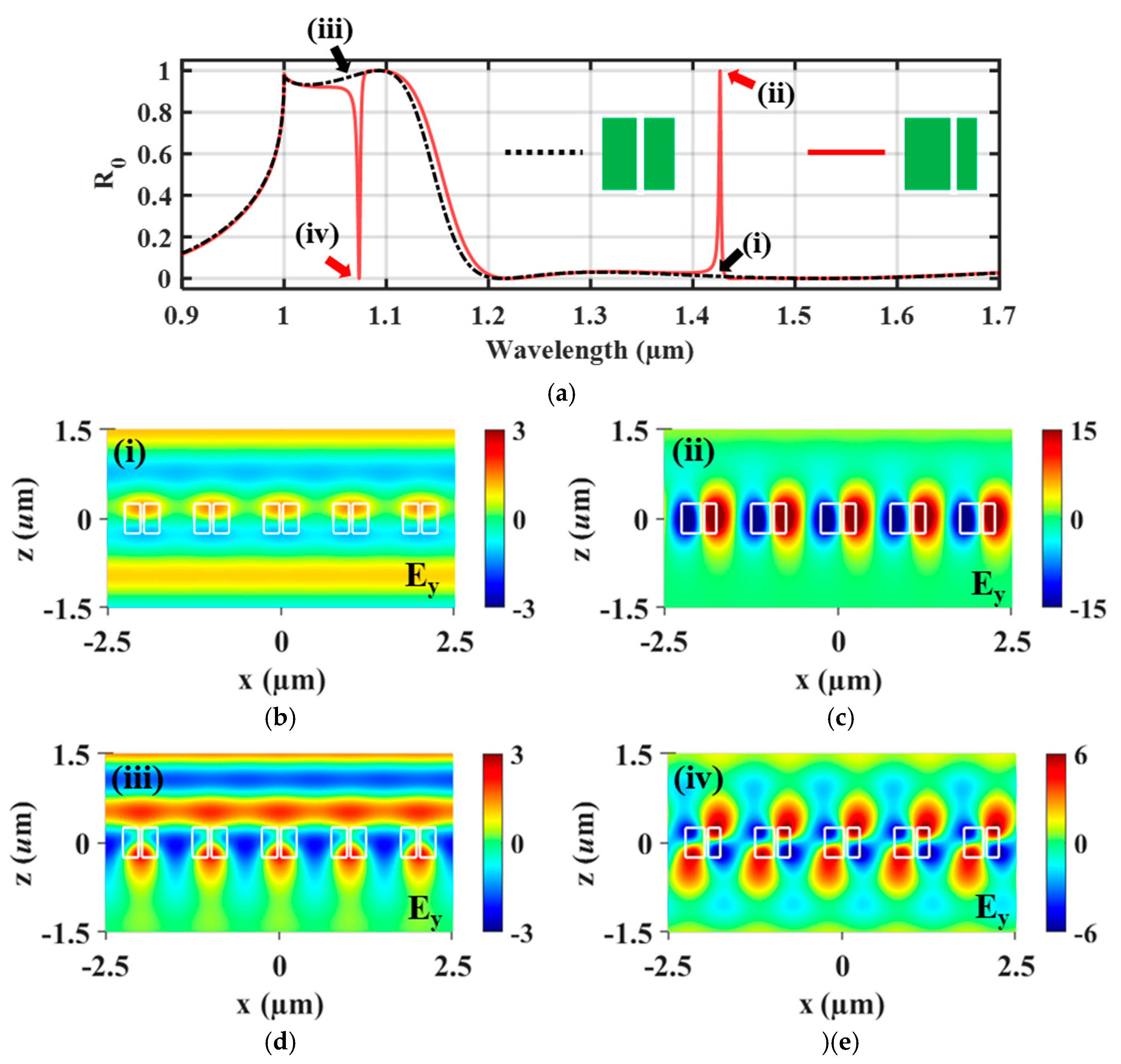
To characterize the ${aTE}_0$ mode of the singular state, we analyze the electric field profiles at specific points on the $R_0$ spectra of both the symmetric and asymmetric air-slit 1D PLs, as depicted in Figure 2b and Figure 2c. Figure 3a shows these points (i)-(iv) on the $R_0$ spectra for the air slit 1D PLs. In contrast to point (i) on the spectrum of the symmetric air-slit 1D PL (black dash line), the point (ii) on the asymmetric air-slit 1D PL (red solid line) spectrum exhibits a sharp resonance peak at λ=1.4266 µm, associated with a singular state. In shorter wavelength region, the point (iii) corresponds high reflection while point (iv) shows a sharp dip at $\lambda$=1.0734 µm. The electric field distributions ($E_y$, as out of plane) corresponding to these points are presented in Figure 3b to 3e. As shown in Figure 3b, the light propagates through the 1D PL without resonance. In Figure 3c, however, the light is strongly confined to the lattice with asymmetric air-slit. This $E_y$ profile represents the singular state, formed by the fundamental guided modes (i.e., ${aTE}_0$). In Figure 3d, the light is highly reflected from the symmetric air-slit 1D PL. Conversely, in Figure 3e, it passes through in the asymmetric air-slit 1D PL due to interaction with enhanced $E_y$ field, forming the first guided modes (i.e., ${aTE}_1$).

5. Tunable Singular States by Asymmetric Air-Slit 1D Lattice

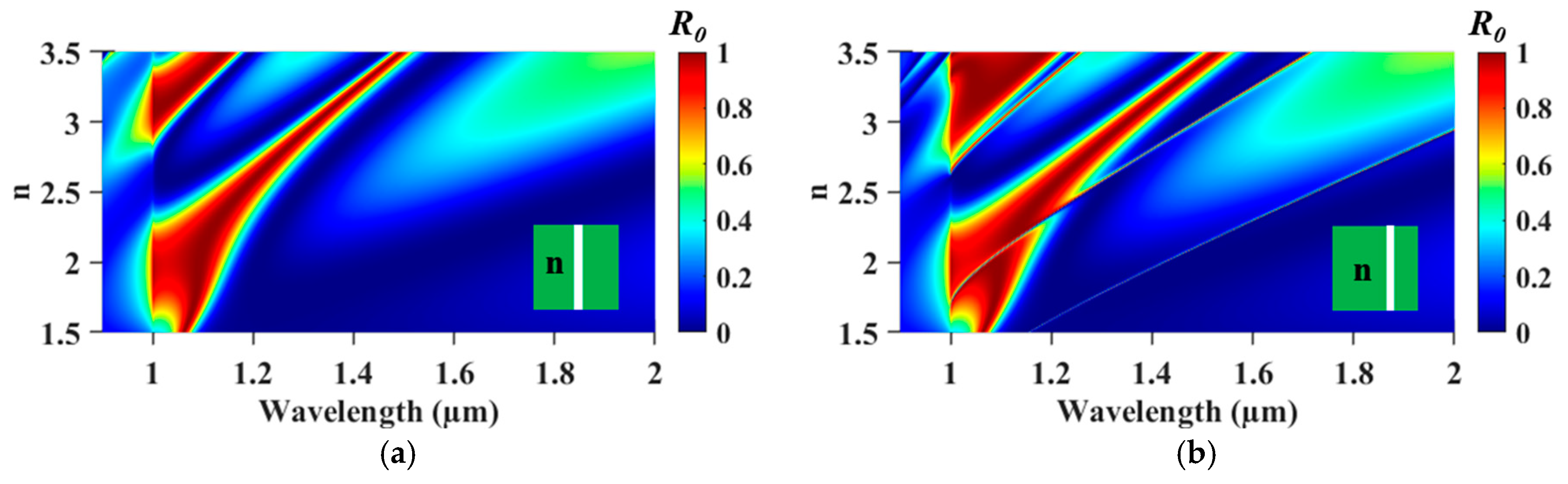
Prior to designing tunable singular states, we examine the refractive index ($n$) effects on the singular state in the asymmetric air-slit 1D PL. Figure 4a presents the $R_0$ map for the symmetric air-slit 1D PL where the spectral response is calculated by varying the $n$ from 1.5 to 3.5. As observed, two resonance bands shift toward longer wavelengths as $n$ increases. This red shift is a characteristic behavior of GMRs as higher $n$ increases a propagation constant of guided mode. Figure 4b shows the corresponding $R_0$ map for the asymmetric air-slit case under the same refractive index variations. As expected, sharp resonance bands appear and exhibit a red shift. Notably, the singular state becomes increasingly isolated from the other resonance bands for higher refractive index material as silicon nitride (Si₃N₄, n ≈ 2) and silicon (Si, n ≈ 3.5).

The aGMR enables the generation of tunable singular state by varying asymmetry of the air-slit 1D PL. Figure 5 shows the tunable singular state in an air-slit 1D PL based on a dielectric material ($n$=2), where the grating parameter set is {$\Lambda$ = 1 µm, $F$ = 0.5, $H$ = 0.5 µm}. As illustrated in the schematic of Figure 5, a single air-slit with a width of 0.05 µm is displaced by a distance $d$ from the symmetric line. In the $R_0$ map of the asymmetric air-slit 1D PL, two sharp resonances are observed due to the aGMRs. The lower peak corresponds to the ${aTE}_0$ mode, while the upper dip represents the ${aTE}_1$ mode. These modes arise from the interference between leaky waveguide modes and background radiation, as a phenomenon characteristic of Fano resonances [32]. At the low reflection region, the $R_0$ peak can be used as a notch filter. In contrast, the $R_0$ dip around the high reflection band for band pass filter. When the $d$ gradually increases from zero to $\pm$0.15 µm, these dual functionalities can be simultaneously tuned by varying the $d$.

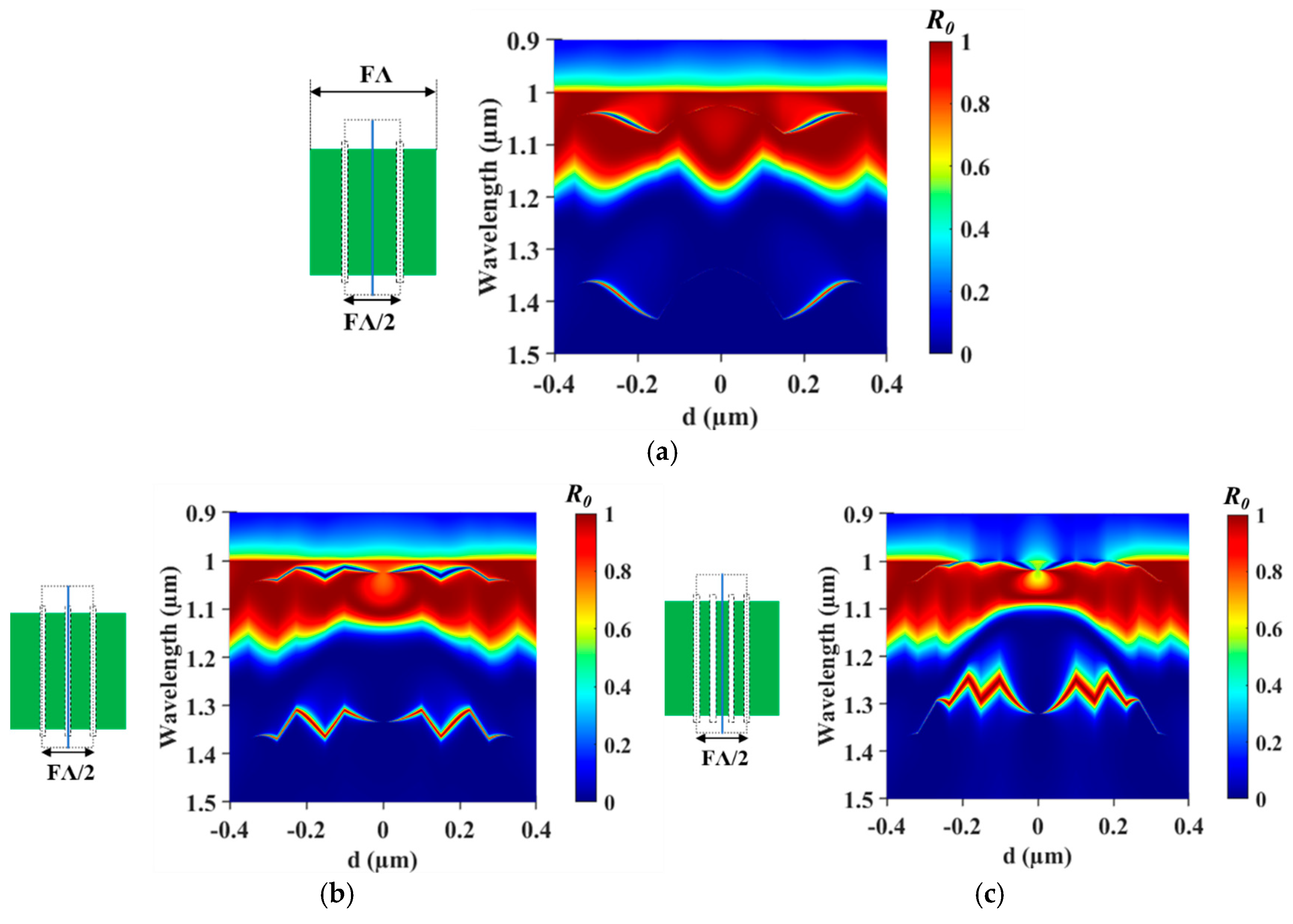
This dual functionality becomes even more dynamic with the introduction of multiple air-slits. As shown in the schematic of Figure 6a, two air-slits are aligned with a pitch width of $F\Lambda /2$=0.25 μm. By varying the displacement $d$ from zero to $\pm$0.35 μm, as seen in $R_0$ map of Figure 6b, the two sharp aGMRs are rapidly tuned. This behavior corresponds to the one-fold radiation observed in the single air-slit case of Figure 5. Using triple and quadruple air-slits, the aGMRs exhibit even faster tuning due to two- and three-fold radiation effects as presented in Figure 6c and Figure 6d. Herein, the triple and quadruple air-slits are equally distributed within the same pitch width ($F\Lambda /2$=0.25 μm). These additional slits introduce more degrees of asymmetry, thus leading to more change of the spectral position of the aGMRs. Meanwhile, these resonances shift toward shorter wavelengths (blue-shift) as the number of air-slits increases because the effective refractive index is reduced by more air gaps. This ability to dynamically tune singular states by simply adjusting the multiple air-slit promise for applications in metamaterials and metasurfaces.

6. Conclusions

In conclusion, the asymmetric guided-mode resonance (aGMR) mechanism enables the radiation of tunable singular states by varying the structural asymmetry of photonic lattices (PLs) through air-slits. Our analysis demonstrates that the air-slit induced singular state can effectively control the spectra position of strong resonance interfering with background radiation. Through systematic investigation, we have shown that the refractive index plays a critical role in determining the spectral position and isolation of singular states. Dielectric materials such as silicon nitride (Si₃N₄) and silicon (Si) are proper for realizing tunable singular states due to their high refractive indices and compatible fabrication technologies. Furthermore, the multiple air-slits significantly enhance the tunability of singular states, which enables dynamic control over resonance positions through multiple folding behavior of resonances. By displacing the air-slits, dual functionalities (i.e., narrowband band pass filter and notch filtering) are achieved. It expects to be useful for versatile metasurface and metamaterial applications in optical filters, switches and photonic devices. Despite potential fabrication challenges such as precise air-slit alignment and symmetry control, these structures are feasible with advanced nanofabrication techniques. The proposed concepts are extendable to other spectral regions and polarization-independent designs by 2D metastructures. This work will be useful for developing highly tunable optical devices for photonic applications.