Outage Probability Analysis of Relay Communication Systems for Semantic Transmission

1. Introduction

Traditional communication systems mainly focus on how to efficiently transmit symbol streams, while semantic communication emphasizes how to encode information so that the receiver can accurately understand the transmitted content. To achieve this effectively, researchers have utilized technologies like deep learning to design semantic encoders and decoders. For instance, neural networks are used to replace traditional modems, optimizing the expression of information during transmission. Deep Neural Networks (DNN), Convolutional Neural Networks (CNN), and Transformer models have all been applied to semantic communication, enhancing the system’s intelligence. [1] proposed a deep learning-based semantic communication system called DeepSC, which is used for text transmission and outperforms traditional communication systems under low signal-to-noise ratio conditions.

In semantic communication, resource allocation (such as bandwidth, power, time, etc.) has become a critical issue. How to allocate limited communication resources based on the semantic importance of the information, avoid unnecessary data transmission, and ensure the integrity and accuracy of the information is one of the key directions of current research. [2] focuses on the resource allocation problem in text-based semantic communication, where the concept of Semantic Spectral Efficiency (S-SE) is introduced for the first time. By optimizing channel allocation and the number of semantic symbols transmitted, a resource allocation model is proposed to improve the efficiency of semantic communication.

[3] proposed a lightweight, distributed semantic communication system based on deep learning, called L-DeepSC, for low-complexity text transmission. In this system, data transmission from IoT devices to the cloud/edge is performed at the semantic level to improve transmission efficiency.

Semantic communication, as a new paradigm for next-generation networks, significantly reduces bandwidth requirements and improves communication efficiency by extracting the core semantic information from data and transmitting only the relevant content, even under low signal-to-noise ratio conditions. However, relying solely on semantic communication may face challenges in scenarios with high real-time requirements or strict data integrity demands. Therefore, combining the stability of traditional communication with the efficiency of semantic communication to form a hybrid communication architecture can not only meet the needs of different application scenarios but also provide new ideas and directions for the development of next-generation communication networks. [4] studied a heterogeneous communication framework that supports the coexistence of semantic communication and traditional bit-based communication. By proposing a Semi-NOMA (Semi-Non-Orthogonal Multiple Access) scheme, it enables flexible and efficient transmission of both semantic and bit streams. When compared with Orthogonal Multiple Access (OMA) and Non-Orthogonal Multiple Access (NOMA), it was shown that Semi-NOMA offers advantages in terms of semantic and bit rate, as well as power utilization efficiency.

Introducing relays into semantic communication systems is a highly promising innovation. The addition of relay nodes can effectively extend the communication coverage, compensating for the limitations of traditional direct communication in long-distance transmission or signal-blocked scenarios. A relay can receive semantic information from the source node and, leveraging its powerful signal processing and forwarding capabilities, analyze, optimize, and regenerate the semantic content. This ensures that the integrity and accuracy of the semantic information are maintained or even improved during transmission to the destination node. For example, in complex urban environments where tall buildings may cause signal blockage and attenuation, a relay can receive, process, and retransmit the semantic information at appropriate locations, overcoming obstacles and ensuring stable communication. Additionally, the relay can intelligently adjust its forwarding strategy based on network conditions and the destination node’s requirements, compressing or expanding the semantic information as needed, thereby improving overall communication efficiency and quality. This lays a solid foundation for the widespread application of semantic communication in more complex scenarios and significantly drives the advancement of semantic communication technology towards greater maturity and reliability.

[5] proposed a semantic relay (SemRelay) framework to address the issues of limited resources in mobile devices and insufficient research in collaborative communication within semantic communication systems. By integrating deep learning techniques on edge devices, it achieves efficient text semantic communication and significantly improves spectrum efficiency and semantic transmission performance in multi-user scenarios through joint optimization of relay power and bandwidth allocation.

[6] proposed a SemRelay-assisted base station system for transmitting text to mobile devices to solve the problem of resource-constrained mobile devices being unable to deploy deep learning-based semantic encoders and decoders. By jointly optimizing relay positions and bandwidth allocation to maximize effective bit rate, the proposed algorithm, which uses a penalty-based approach, yields numerical results showing near-optimal performance, with SemRelay outperforming traditional decode-and-forward relays in terms of rate performance.

Building on this, [7] addressed the problem of deploying deep learning semantic encoders and decoders for multiple mobile users. [8] developed a novel intelligent relay-assisted semantic communication system, combining traditional deep learning methods with intelligent semantic relays. By restoring the meaning of sentences, the system minimizes semantic errors and addresses issues caused by channel variations, applicable in scenarios of deteriorating wireless channels or mismatched knowledge backgrounds between the transmitter and receiver.

[9] proposed a wireless relay channel semantic communication scheme based on autoencoders (AESC), which encodes and decodes sentences from the semantic dimension. The autoencoder module enhances the system’s robustness against noise. Additionally, a novel semantic forwarding (SF) mode was designed for relay nodes to forward semantic information at the semantic level, especially in cases where the source and destination nodes do not share common knowledge.

[10] studied semantic communication in multi-hop relay networks to achieve reliable information transmission over long distances or under high path-loss attenuation conditions.

Semantic communication, by focusing on transmitting the core meaning of the source, has the potential to significantly reduce network traffic, effectively alleviating the problem of spectrum resource scarcity. Specifically, for different types of transmission sources such as text [1,11], images [12,13], speech [14], and video [15], researchers have proposed various semantic communication systems that significantly enhance the reliability of semantic transmission.

Full-duplex communication technology, which allows communication nodes to transmit and receive simultaneously, has been regarded as highly promising when combined with semantic communication. In this mode, researchers aim to optimize resource allocation, interference management, and other issues in full-duplex communication using deep learning techniques to improve the efficiency of semantic communication. [16] proposed a novel in-band full-duplex (IBFD) paradigm called Semantic Division Duplex (SDD), using semantic communication to address the reliable source reconstruction problem in traditional IBFD systems.

Semantic communication has shown immense application potential in fields such as intelligent transportation, the Internet of Things (IoT), and smart healthcare. For example, in autonomous driving, communication between vehicles no longer involves transmitting all sensor data but instead transmits semantic information relevant to current driving decisions, thereby improving system efficiency and reducing network load. [17] proposed a unified multi-user semantic communication system for multimodal data transmission, multi-user collaboration, and multi-task execution in edge-intelligent autonomous driving systems to address communication challenges in autonomous driving.

In this paper, we focus on relay semantic communication systems and deeply investigate their performance under different conditions, particularly the outage probability, which is a critical metric. The outage probability directly reflects the likelihood that the communication system fails to meet the predetermined communication quality requirements during transmission, making it essential for evaluating the system’s reliability and stability.

We consider various scenarios, including those where semantic transmission occurs between the source node (S) and the relay node (R), as well as between the relay node and the destination node (D), with the destination node having either the same or different background knowledge (BK) as the source node. We also explore scenarios where the relay performs a function similar to traditional amplify-and-forward (AF) due to signal loss caused by long-distance transmission, and hybrid transmission scenarios where the source node and the relay node use semantic transmission, while the relay node and the destination node perform bit transmission. Through modeling and analyzing these different scenarios, we derive the corresponding communication capacity and outage probability expressions, providing a theoretical foundation for comprehensively understanding the performance of relay semantic communication systems.

The paper is organized as follows: Section 2 establishes the system model. Section 3 deals with the outage probability performance of the proposed relay selection strategy, providing both exact and high signal-to-noise ratio approximations. Section 4 presents the simulation and analysis results, while Section 5 summarizes the paper and provides our conclusions.

Notation: ${\mathbb{C}}^{m\times n}$ and ${\mathbb{R}}^{m\times n}$ represent sets of complex matrices and real matrices of size $m\times n$, respectively. Boldface variables represent matrices or vectors. $\mathcal{C}$ denotes that a variable follows a circularly symmetric complex Gaussian distribution with mean $\mu$ and covariance $\Sigma$.

2. System Model

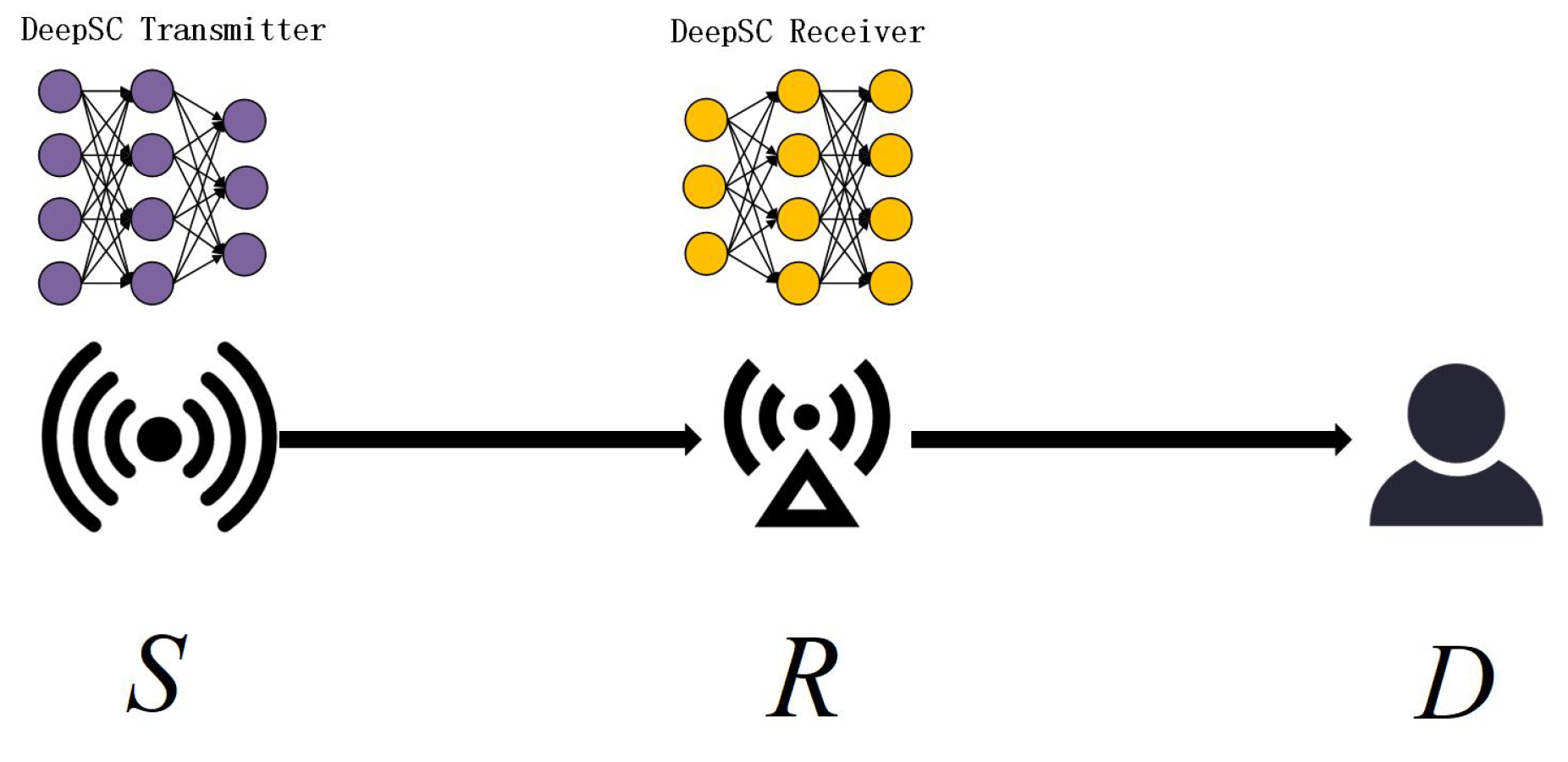
We consider a three - point two - line communication transmission model, as shown in Figure 1, which includes the source node (S), the relay node (R), and the destination node (D), with no direct link. The relay operates in half - duplex mode and uses DeepSC as the communication transmission model. Semantic and channel encoders and decoders are deployed at both the source node (S) and the relay node (R), where the semantics of the text can be effectively extracted through the Transformer model. It is assumed that the DeepSC transceivers are trained at a base station or cloud platform.

In this model, the source node (S) inputs a sentence $s=[w_1,w_2,\dots ,w_L]$, where $w_L$ represents the L-th word in the sentence. The DeepSC transmitter consists of two parts: the semantic encoder and the channel encoder, which are responsible for extracting semantic information from s and ensuring its successful transmission over the physical channel. The sentence is input into the DeepSC transmitter and mapped into a semantic symbol vector $X_n=[x_1,x_2,\dots ,x_{KL}]$, where $X_n\in {\mathbb{R}}^{KL\times 1}$, and $KL$ is the length of the semantic symbol vector after transforming the sentence. We note that the length of $X_n$ changes with L, allowing more effective extraction of semantic information from sentences of varying lengths. In this model, K represents the average number of semantic symbols used for each word, and each semantic symbol can be directly transmitted over the communication medium.

The encoded symbol stream can be expressed as:

$$x=C_{\alpha }\left(S_{\beta }\left(s\right)\right)$$

(1)

where $x\in {\mathbb{C}}^{M\times 1}$, $S_{\beta }$ is the semantic encoder network with parameter set $\beta$, and $C_{\alpha }(·)$ is the channel encoder with parameter set $\alpha$.

At the relay node (R), the received signal is:

$$y_R=h_{SR}{x}_S+n_{SR}$$

(2)

where $y_R\in {\mathbb{C}}^{M\times 1}$, h represents the Rayleigh fading channel, which follows a $\mathcal{CN}(0,1)$ distribution, and $n\sim \mathcal{CN}(0,{\sigma }_n^2)$. The decoded signal can be expressed as:

$$\widehat{s}=S_{\chi }^{-1}\left(C_{\delta }^{-1}\left(y\right)\right)$$

(3)

where $\widehat{s}$ is the recovered sentence, $C_{\delta }^{-1}(·)$ is the channel decoder with parameter set $\delta$, and $S_{\chi }^{-1}(·)$ is the semantic decoder network with parameter set $\chi$.

At the destination node (D), depending on D’s computational power, either bit transmission or semantic transmission is employed. Specifically, if D has sufficient computational power to decode the semantic stream, semantic transmission is used over the $RD$ link. If D lacks sufficient computational power, traditional bit transmission is used.

Both the $SR$ link and $RD$ link employ Rayleigh fading channel transmission models. In a Rayleigh fading channel, $|h_{SR}{|}^2$ follows an exponential distribution with parameter ${\displaystyle \frac{1}{{\sigma }^2}}$, that is:

$$f_{{\left|h\right|}^2}\left(z\right)={\displaystyle \frac{1}{{\sigma }^2}}{e}^{-{\displaystyle \frac{z}{{\sigma }^2}}},z\ge 0.$$

(4)

For ${\gamma }_{SR}$, its expression is:

$${\gamma }_{SR}={\displaystyle \frac{P_S{\left|h_{SR}\right|}^2}{W{N}_S}},$$

(5)

where $P_S$ is the transmit power, and $W{N}_S$ is the noise power. ${\gamma }_{SR}$ is a linear transformation of $|h_{SR}{|}^2$, which is:

$${\gamma }_{SR}={\displaystyle \frac{P_S}{W{N}_S}}{\left|h_{SR}\right|}^2.$$

(6)

It can be derived that ${\gamma }_{SR}$ follows an exponential distribution with parameter ${\lambda }_{SR}$, whose probability density function is:

$$f_{{\gamma }_{SR}}\left(y\right)={\lambda }_{SR}{e}^{-{\lambda }_{SR}y},y\ge 0,$$

(7)

where:

$${\lambda }_{SR}={\displaystyle \frac{W{N}_S}{P_S{\sigma }^2}}.$$

(8)

Similarly, we can derive the following for the $RD$ link: In a Rayleigh fading channel, $|h_{RD}{|}^2$ also follows an exponential distribution with parameter ${\displaystyle \frac{1}{{\sigma }^2}}$, that is:

$$f_{|h_{RD}{|}^2}\left(z\right)={\displaystyle \frac{1}{{\sigma }^2}}{e}^{-{\displaystyle \frac{z}{{\sigma }^2}}},z\ge 0.$$

(9)

For ${\gamma }_{RD}$, its expression is:

$${\gamma }_{RD}={\displaystyle \frac{P_R{\left|h_{RD}\right|}^2}{W{N}_R}},$$

(10)

where $P_R$ is the transmit power and $W{N}_R$ is the noise power. ${\gamma }_{RD}$ is a linear transformation of $|h_{RD}{|}^2$, which is:

$${\gamma }_{RD}={\displaystyle \frac{P_R}{W{N}_R}}{\left|h_{RD}\right|}^2.$$

(11)

It can be derived that ${\gamma }_{RD}$ follows an exponential distribution with parameter ${\lambda }_{RD}$, whose probability density function is:

$$f_{{\gamma }_{RD}}\left(y\right)={\lambda }_{RD}{e}^{-{\lambda }_{RD}y},y\ge 0,$$

(12)

where:

$${\lambda }_{RD}={\displaystyle \frac{W{N}_R}{P_R{\sigma }^2}}.$$

(13)

Based on the computational power of the destination node (D) and whether the channel conditions meet the requirements for semantic transmission, the channel transmission strategy can be divided into the following four cases:

• $SR$ and $RD$ links both perform semantic transmission, and S and D have the same background knowledge ($BK$): In this case, the destination node (D) has sufficient storage and computational resources to decode the transmitted semantic information. Additionally, its semantic encoding logic is consistent with that of the source node (S), meaning that S and D share the same background knowledge ($BK$). The relay node (R) functions similarly to a traditional decode - and - forward ($DF$) relay, responsible for decoding and re - encoding data at the semantic level to ensure the integrity and efficient transmission of the semantic information.
• $SR$ and $RD$ links both perform semantic transmission, but S and D have different background knowledge ($BK$): In this case, the destination node (D) also has sufficient computational resources to decode semantic information, but its background knowledge is not the same as the source node (S). This mismatch in background knowledge may lead to deviations in the expression and understanding of the semantic information. Therefore, the relay node (R) needs to perform additional tasks, such as converting and adapting the semantic information to ensure that the destination node can correctly interpret the received semantic information.
• $SR$ and $RD$ links both perform semantic transmission, and S and D have the same background knowledge ($BK$), but signal degradation prevents D from decoding: In this case, although the destination node (D) has sufficient computational resources and shares the same background knowledge as the source node (S), the signal suffers significant degradation due to the long distance and poor channel quality, preventing D from correctly decoding the semantic information. As a result, the relay node (R) needs to operate like a traditional amplify - and - forward ($AF$) relay, amplifying and forwarding the signal. In this scenario, the system’s channel capacity is equivalent to that of a two - hop $AF$ relay.
• $SR$ link performs semantic transmission, $RD$ link performs bit transmission: In this case, the source node (S) and the relay node (R) use semantic transmission, but the relay node (R) and the destination node (D) only perform bit transmission. This model is applicable when the destination node (D) has limited computational resources. The relay node needs to decode the semantic information and re - encode it into a bit stream for transmission to the destination node. In this situation, the transmission performance of the $RD$ link is determined by the channel capacity for bit transmission.

In summary, these four cases demonstrate the optimization strategies for transmission under different system conditions. By combining semantic transmission with traditional transmission methods, these strategies address various limitations, such as background knowledge matching, channel quality, and computational resources, providing a theoretical basis and practical guidance for efficient semantic transmission in relay communication systems.

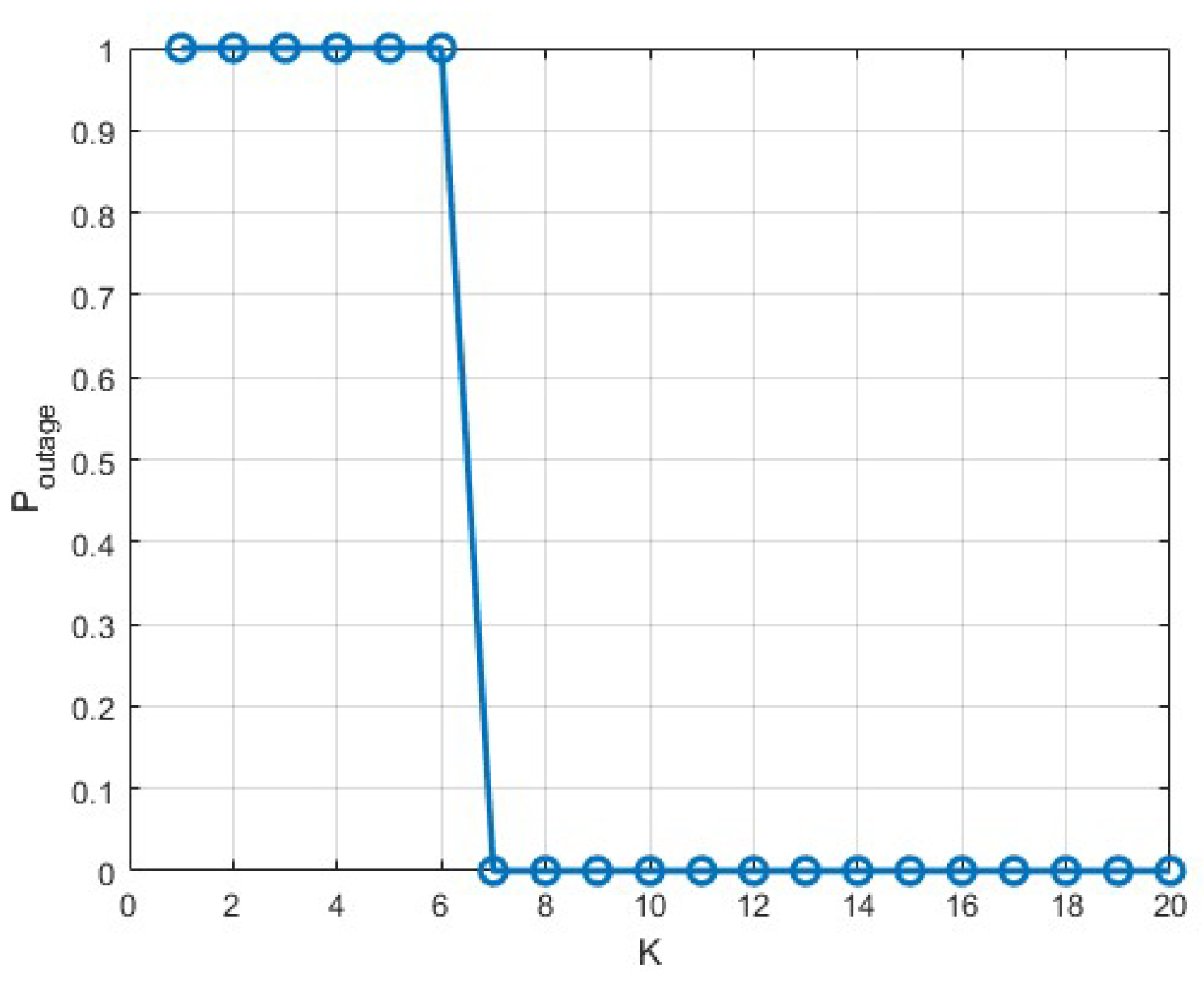
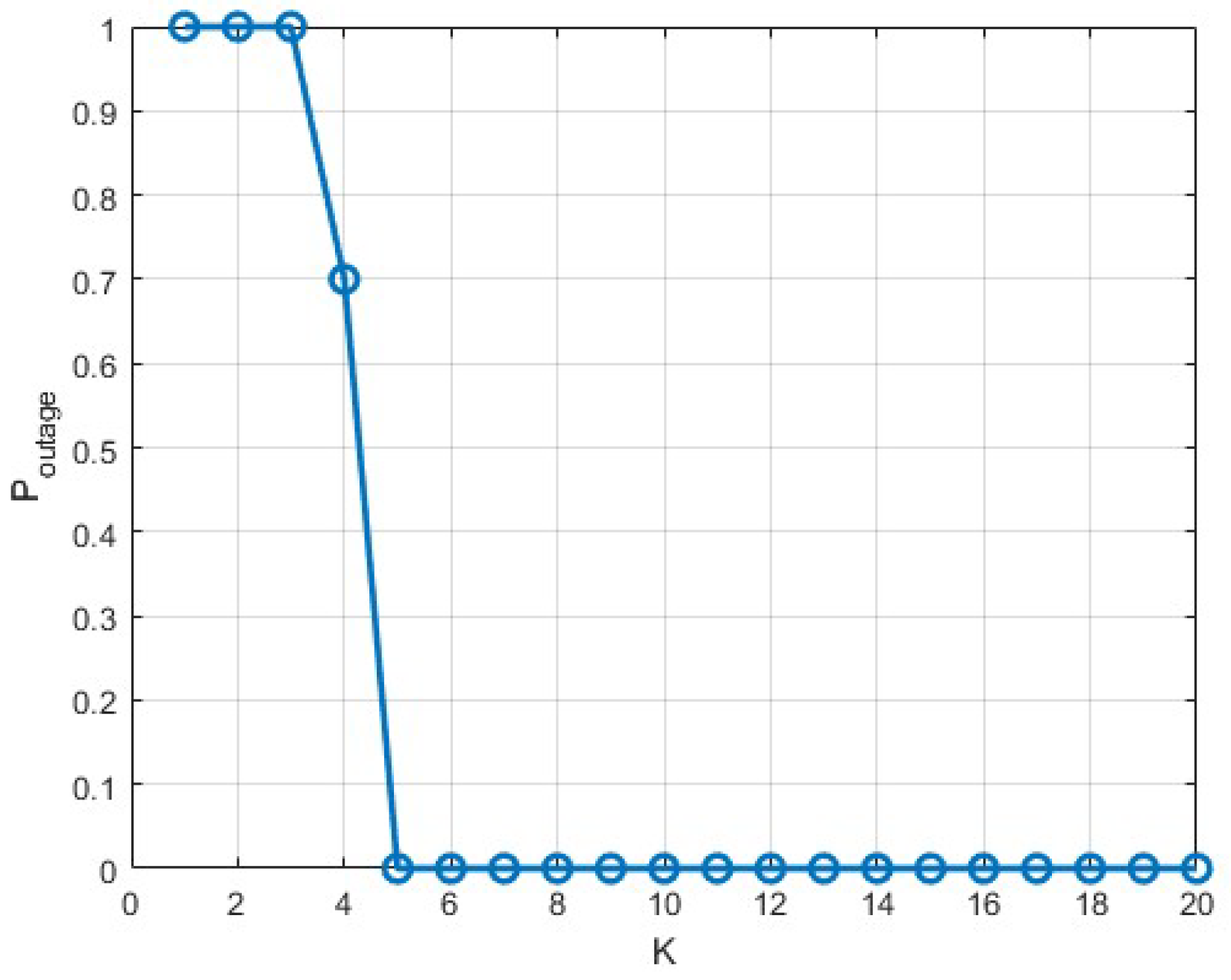
3. Performance Analysis

To evaluate the performance of semantic communication in text transmission, this paper uses semantic similarity as the primary performance metric. Specifically, the semantic similarity $\xi$ is defined as:

$$\xi ={\displaystyle \frac{B\left(s\right)B{\left(s\right)}^T}{\parallel B\left(s\right)\parallel \parallel B\left(s\right)\parallel }}$$

(14)

where $B(·)$ represents the bidirectional encoder representations from Transformers (BERT) model, which has made significant improvements in state - of - the - art sentence embedding methods. The pre - trained Sentence - BERT model is used. Unlike other semantic evaluation metrics like BLEU, the BERT similarity can more accurately measure the semantic distance between two sentences. Notably, the range of semantic similarity values is $0\le \xi \le 1$, where $\xi =1$ indicates that the two sentences are identical, and $\xi =0$ means they have no similarity.

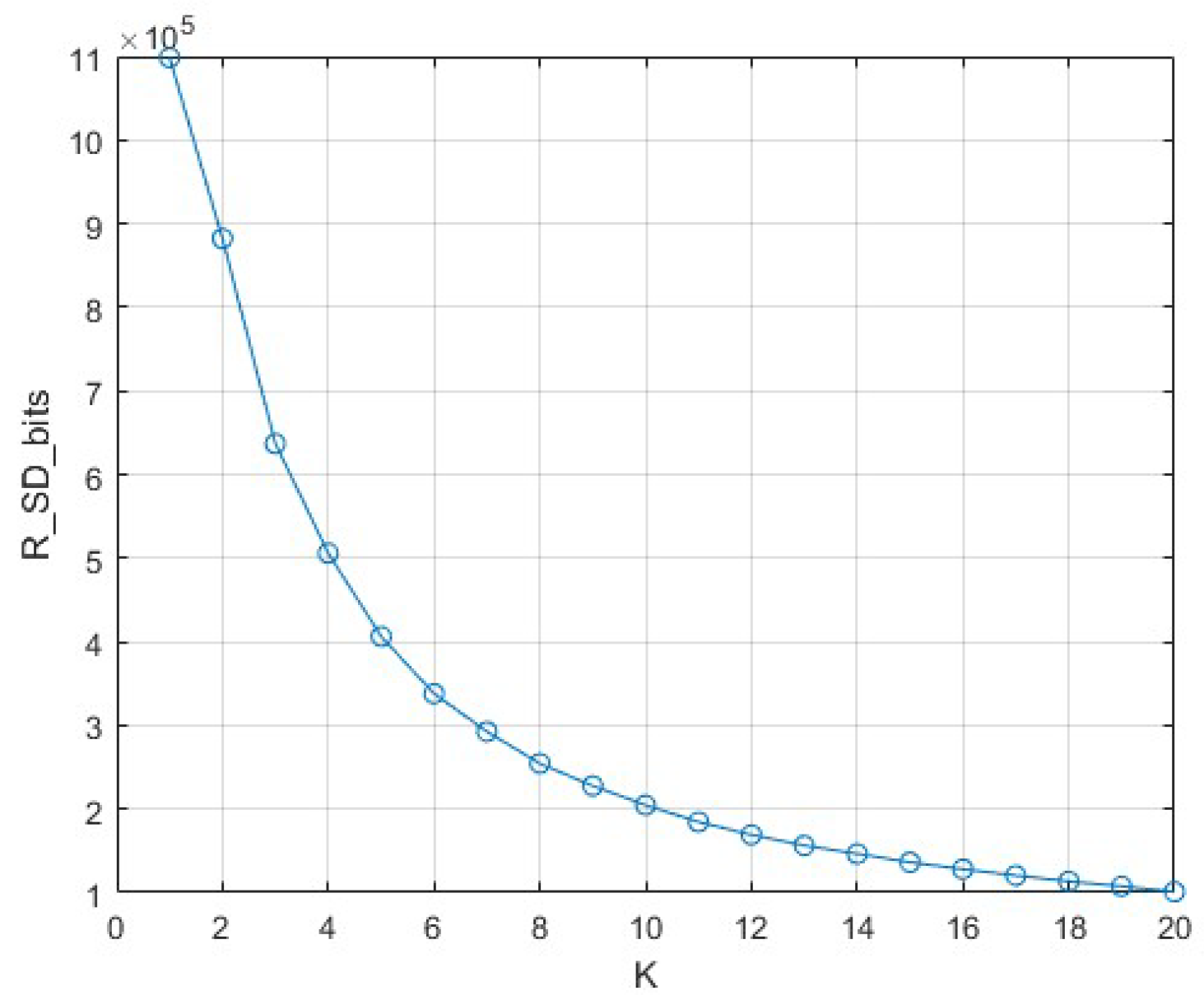
Based on semantic similarity, a new performance metric called semantic rate is introduced in literature [2] to measure the semantic information transmission rate achieved by DeepSC. Let I represent the semantic units (suts), i.e., the average amount of semantic information contained in a sentence s. Therefore, the semantic information for each semantic symbol can be expressed as ${\displaystyle \frac{I}{KL}}$ (units: suts/symbol). Recall that the symbol rate is equal to the transmission bandwidth W. Thus, the effective semantic rate (units: suts/s) can be expressed as:

$$S=W·{\displaystyle \frac{I}{KL}}·\xi (K,\gamma )$$

(15)

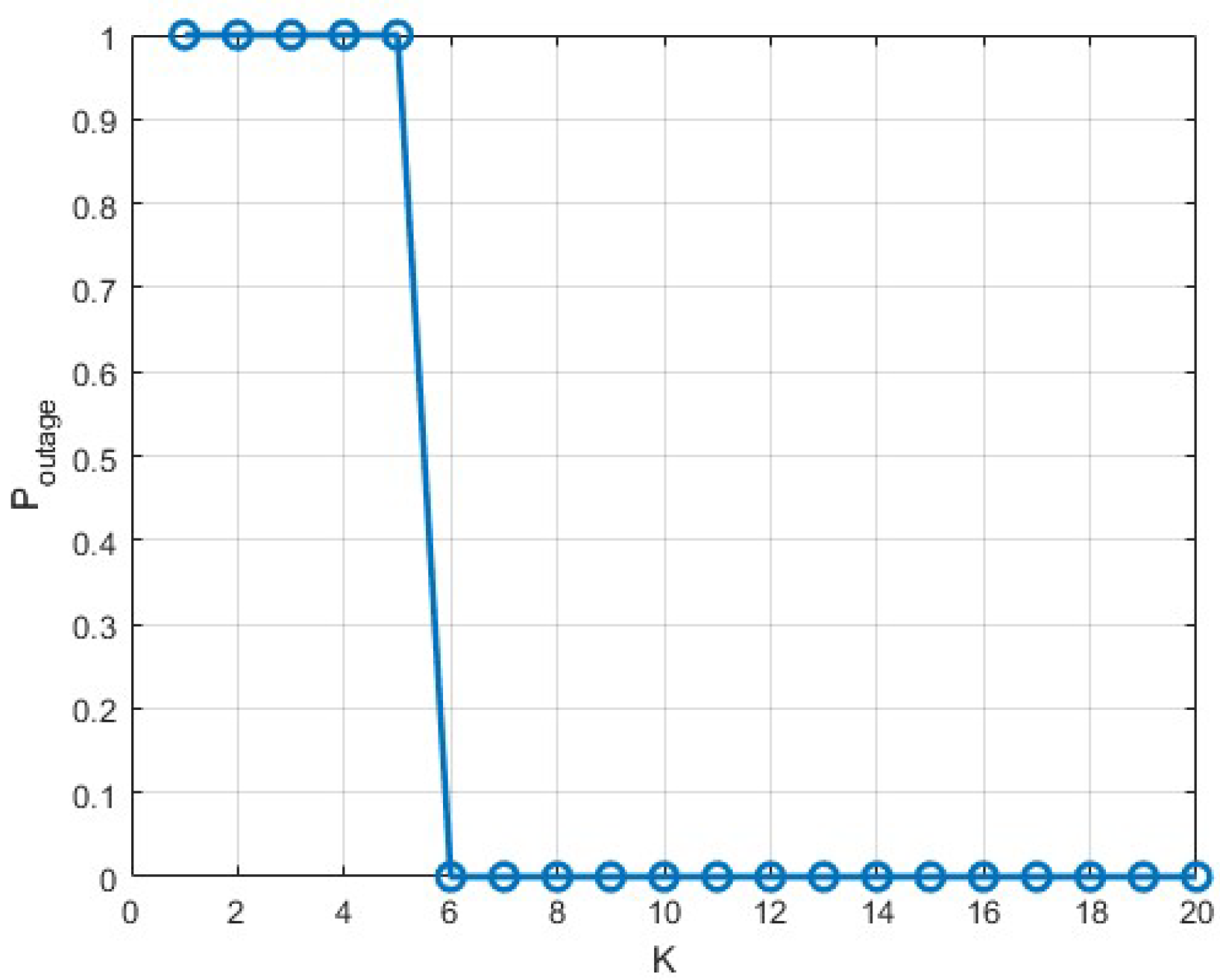
where $ϵ$ is a function dependent on the specific semantic communication system and physical channel conditions. The value of $ϵ(K,\gamma )$ can be obtained by running the DeepSC tool, with the mapping relationship shown in Figure 2. Semantic similarity has been proven to be a function of received signal - to - noise ratio (SNR) $\gamma$ and K. For any given K, the semantic similarity function $ϵ\in [0,1]$ typically follows an "S" curve as SNR changes. Therefore, a generalized logistic regression method can be used to approximate it as a sigmoid function, expressed as:

$$\xi =a_1+{\displaystyle \frac{a_2}{1+e^{-(c_1\gamma +c_2)}}}$$

(16)

where $a_1$, $a_2$, $c_1$, and $c_2$ are constant coefficients dependent on K.

Based on this, the channel capacity formulas for four scenarios can be derived: Based on this, the channel capacity formulas for the four cases can be derived:

3.0.1. Semantic Transmission in Both SR and RD Links, with S and D Having the Same Background Knowledge (BK) 

At this point, the semantic rate (suts/s) of the SR link can be represented as:

$$R_{SR}^{\mathrm{sem}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{W}{KL}}\xi (K,{\gamma }_{SR})$$

(17)

where W is the channel bandwidth, I is the average amount of semantic information per sentence, measured in semantic units (suts), K is the average number of semantic symbols per word in the original sentence, L is the number of words in the sentence, and $ϵ(K,{\gamma }_{SR})$ is the semantic similarity.

The bit rate for transmission is:

$$R_{SR}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{SR}^{\mathrm{sem}}}{I/L}}={\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{K}}\xi (K,{\gamma }_{SR})$$

(18)

where $\mu$ is the conversion factor for encoding the source information into bits, indicating the average number of bits per word.

The capacity of the RD link is:

$$C_{RD}^{\mathrm{bit}}={\displaystyle \frac{1}{2}}W{log}_2\left(1+{\displaystyle \frac{P_{R}g{\left|h_{RD}\right|}^2}{N_D}}\right)$$

(19)

where the bit stream includes encoded semantic symbols, and $r_c$ represents the average number of bits per semantic symbol using the traditional joint encoder. Thus, the effective semantic symbol rate on the RD link is:

$$R_{RD}^{\mathrm{sem}}={\displaystyle \frac{C_{RD}^{\mathrm{bit}}I}{r_{c}KL}}$$

(20)

The effective semantic bit rate on the SR link is:

$$R_{RD}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{RD}^{\mathrm{sem}}}{I/L}}=\mu {\displaystyle \frac{C_{RD}^{\mathrm{bit}}}{r_{c}K}}={\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{r_{c}K}}{log}_2\left(1+{\displaystyle \frac{P_{R}g{\left|h_{RD}\right|}^2}{N_D}}\right)$$

(21)

Assuming the predefined channel capacity is C, the signal - to - noise ratio (SNR) threshold is ${\gamma }_{\mathrm{th}}$, and the outage probability is:

$$P_{\mathrm{out}}\left(R\right)=P_r(R_{SD}^{\mathrm{bit}}<C)=1-P_r(R_{SD}^{\mathrm{bit}}>C)=1-P_r(min\{R_{SR}^{\mathrm{bit}},R_{RD}^{\mathrm{bit}}\}>C)$$

(22)

Based on $R_{SR}^{\mathrm{bit}}>C$, we can derive:

$${\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{K}}\xi (K,{\gamma }_{SR})>C\Rightarrow \xi >{\displaystyle \frac{2CK}{\mu W}}$$

(23)

Substituting:

$$\xi (K,{\gamma }_{SR})=a_1+{\displaystyle \frac{a_2}{1+e^{-(c_1{\gamma }_{SR}+c_2)}}}$$

(24)

where $\xi \in [0,1]$, we can obtain:

$${\gamma }_{SR}>{\displaystyle \frac{-ln\left(\frac{a_2}{\frac{2CK}{\mu W}-a_1}-1\right)-c_2}{c_1}}$$

(25)

The SR link follows a Rayleigh channel model, so the probability $P_r(R_{SR}^{\mathrm{bit}}>C)$ is:

$$P_r(R_{SR}^{\mathrm{bit}}>C)=1-F_{{\gamma }_{SR}}\left({\displaystyle \frac{-ln\left(\frac{a_2}{\frac{2CK}{\mu W}-a_1}-1\right)-c_2}{c_1}}\right)$$

(26)

Using the CDF for the Rayleigh distribution, this becomes:

$$P_r(R_{SR}^{\mathrm{bit}}>C)=e^{-{\lambda }_{SR}\left({\displaystyle \frac{-ln\left(\frac{a_2}{\frac{2CK}{\mu W}-a_1}-1\right)-c_2}{c_1}}\right)}$$

(27)

Similarly, for $R_{RD}^{\mathrm{bit}}>C$, we get:

$${\gamma }_{RD}>2^{{\displaystyle \frac{2r_{c}KC}{\mu W}}}-1$$

(28)

and the probability:

$$P_r({\gamma }_{RD}>2^{{\displaystyle \frac{2r_{c}KC}{\mu W}}}-1)=e^{-{\lambda }_{RD}(2^{{\displaystyle \frac{2r_{c}KC}{\mu W}}}-1)}$$

(29)

Hence, the outage probability is:

$$P_r(R_{SD}^{\mathrm{bit}}<C)=1-e^{{\displaystyle \frac{ln\left(\frac{a_2}{\frac{2CK}{\mu W}-1}-1\right)+c_2}{c_1}}}\times e^{-{\lambda }_{RD}(2^{{\displaystyle \frac{2r_{c}KC}{\mu W}}}-1)}$$

(30)

3.0.2. Semantic Transmission in Both SR and RD Links, but S and D Have Different Background Knowledge (BK) 

For the SR link, the effective semantic rate is:

$$R_{SR}^{\mathrm{sem}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{W}{KL}}ϵ(K,{\gamma }_{SR})$$

(31)

which can be converted to the bit transmission rate:

$$R_{SR}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{SR}^{\mathrm{sem}}}{I/L}}={\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{K}}\xi (K,{\gamma }_{SR})$$

(32)

For the RD link, the effective semantic rate is:

$$R_{RD}^{\mathrm{sem}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{W}{KL}}ϵ(K,{\gamma }_{RD})$$

(33)

and the bit transmission rate is:

$$R_{RD}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{RD}^{\mathrm{sem}}}{I/L}}={\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{K}}\xi (K,{\gamma }_{RD})$$

(34)

The overall communication capacity is determined by the minimum value of the two links:

$$R_{SD}^{\mathrm{bit}}=min\{R_{SR}^{\mathrm{bit}},R_{RD}^{\mathrm{bit}}\}$$

(35)

Thus, the outage probability can be expressed as:

$$\begin{array}{c}{P}_{\mathrm{out}}\left(R\right)=P_r(R_{SD}^{\mathrm{bit}}<C)=1-P_r(R_{SD}^{\mathrm{bit}}>C)\hfill \\ \hfill =1-P_r\left(min\{R_{SR}^{\mathrm{bit}},R_{RD}^{\mathrm{bit}}\}>C\right)\end{array}$$

(36)

Using the probability properties, we get:

$$P_{\mathrm{out}}\left(R\right)=1-P_r(R_{SR}^{\mathrm{bit}}>C)·P_r(R_{RD}^{\mathrm{bit}}>C)$$

(37)

Substituting the expressions for $R_{SR}^{\mathrm{bit}}$ and $R_{RD}^{\mathrm{bit}}$, we have:

$$\begin{array}{c}{P}_{\mathrm{out}}\left(R\right)=1-P_r\left({\gamma }_{SR}>{\displaystyle \frac{-ln\left(\frac{a_2}{\frac{2CK}{\mu W}-1}-1\right)-c_2}{c_1}}\right)\hfill \\ \hfill ·P_r\left({\gamma }_{RD}>{\displaystyle \frac{-ln\left(\frac{a_2}{\frac{2CK}{\mu W}-1}-1\right)-c_2}{c_1}}\right)\end{array}$$

(38)

3.0.3. Semantic Transmission in Both SR and RD Links, with S and D Having the Same Background Knowledge (BK), but Signal Degradation Causes D to Fail to Decode 

In a two - hop relay communication system, the channel capacity is:

$$C_{SD}^{\mathrm{bit}}={\displaystyle \frac{1}{2}}W{log}_2\left(1+{\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{1+{\gamma }_{SR}+{\gamma }_{RD}}}\right)$$

(39)

The semantic channel capacity is derived as:

$$R_{SD}^{\mathrm{sem}}={\displaystyle \frac{C_{SD}^{\mathrm{bit}}}{r_c}}·{\displaystyle \frac{I}{KL}}$$

(40)

The bit rate for transmission is:

$$R_{SD}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{SD}^{\mathrm{sem}}}{I/L}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{W\mu }{K{r}_c}}{log}_2\left(1+{\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{1+{\gamma }_{SR}+{\gamma }_{RD}}}\right)$$

(41)

Based on this, the outage probability is:

$$P_{\mathrm{out}}\left(R\right)=P_r(R_{SD}^{\mathrm{bit}}<C)=1-P_r(R_{SD}^{\mathrm{bit}}>C)$$

(42)

Substituting the expression for $R_{SD}^{\mathrm{bit}}$, we get:

$$P_{\mathrm{out}}\left(R\right)=1-P_r\left({\displaystyle \frac{1}{2}}{\displaystyle \frac{W\mu }{K{r}_c}}{log}_2\left(1+{\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{1+{\gamma }_{SR}+{\gamma }_{RD}}}\right)>C\right)$$

(43)

Let $M=2^{{\displaystyle \frac{2K{r}_{c}C}{W\mu }}}-1$, and simplify:

$$P_{\mathrm{out}}\left(R\right)=1-P_r\left({\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{1+{\gamma }_{SR}+{\gamma }_{RD}}}>M\right)$$

(44)

Under high SNR conditions, where ${\gamma }_{SR}\gg 1$ and ${\gamma }_{RD}\gg 1$, we can approximate:

$${\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{1+{\gamma }_{SR}+{\gamma }_{RD}}}\approx {\displaystyle \frac{{\gamma }_{SR}·{\gamma }_{RD}}{{\gamma }_{SR}+{\gamma }_{RD}}}$$

(45)

and the final expression for the outage probability involves integrating the joint probability of two independent exponential random variables:

$$P_{\mathrm{out}}\left(R\right)=1-{\int }_0^{\infty }{\int }_0^{{\displaystyle \frac{1}{M-u}}}{\lambda }_{SR}{e}^{-{\displaystyle \frac{{\lambda }_{SR}}{u}}}·{\lambda }_{RD}{e}^{-{\displaystyle \frac{{\lambda }_{RD}}{v}}}{\displaystyle \frac{1}{u^2}}{\displaystyle \frac{1}{v^2}}dvdu$$

(46)

3.0.4. Semantic Transmission on the SR Link and Bit Transmission on the RD Link 

In this case, the effective semantic rate for the SR link is:

$$R_{SR}^{\mathrm{sem}}={\displaystyle \frac{1}{2}}{\displaystyle \frac{W}{KL}}ϵ(K,{\gamma }_{SR})$$

(47)

and the bit rate is:

$$R_{SR}^{\mathrm{bit}}=\mu {\displaystyle \frac{R_{SR}^{\mathrm{sem}}}{I/L}}={\displaystyle \frac{1}{2}}\mu {\displaystyle \frac{W}{K}}\xi (K,{\gamma }_{SR})$$

(48)

For the RD link, the bit transmission rate is:

$$R_{RD}^{\mathrm{bit}}={\displaystyle \frac{1}{2}}W{log}_2\left(1+{\displaystyle \frac{P_R{\left|h_{RD}\right|}^2}{W{N}_R}}\right)$$

(49)

The overall communication capacity is:

$$R_{SD}^{\mathrm{bit}}=min\{R_{SR}^{\mathrm{bit}},R_{RD}^{\mathrm{bit}}\}$$

(50)

The outage probability is:

$$P_{\mathrm{out}}\left(R\right)=P_r(R_{SD}^{\mathrm{bit}}<C)$$

(51)

Simplifying:

$$P_{\mathrm{out}}\left(R\right)=1-P_r(R_{SD}^{\mathrm{bit}}>C)=1-P_r(min\{R_{SR}^{\mathrm{bit}},R_{RD}^{\mathrm{bit}}\}>C)$$

(52)

The probabilities for the SR and RD links are derived as:

$$P_r(R_{SR}^{\mathrm{bit}}>C)=e^{{\displaystyle \frac{ln\left(\frac{a_2}{\frac{2CK}{\mu W}-1}-1\right)+c_2}{c_1}}}$$

(53)

and:

$$P_r(R_{RD}^{\mathrm{bit}}>C)=e^{-{\lambda }_{RD}(2^{{\displaystyle \frac{2C}{W}}}-1)}$$

(54)

The final outage probability is:

$$P_{\mathrm{out}}\left(R\right)=1-e^{{\displaystyle \frac{ln\left(\frac{a_2}{\frac{2CK}{\mu W}-1}-1\right)+c_2}{c_1}}-{\lambda }_{RD}(2^{{\displaystyle \frac{2C}{W}}}-1)}$$

(55)

4. Simulation and Results

This section presents the theoretical analysis of outage probability for the four proposed semantic communication systems and verifies it through Monte Carlo simulations. The experimental parameters are shown in Table 1. In this simulation, the outage probability for four relay - based semantic communication models is tested under different values of K and transmit power of the source.

4.1. First Case

In the BD channel, bit transmission is performed, so the SD link’s channel capacity is actually determined by the SR link. Since the signal - to - noise ratio (SNR) ${\gamma }_{SR}$ is much greater than 1, no matter how the transmit powers of S and R are changed, $\epsilon (K,{\gamma }_{RD})$ is approximately equal to 1, meaning the outage probability can be approximated to 0. The SD link’s channel capacity decreases as K increases.As shown in Figure 2.

4.2. Second Case

By adjusting the transmit power P of S and R, the semantic similarity $\xi$ between the SR and RD links can be modified, thereby altering the channel capacity of the SD and RD links. As the value of P increases, the SNR of the link increases. At this point, the SD link’s channel capacity is determined by the link with the lower SNR. When K exceeds 6, the outage probability decreases and approaches 0.As shown in Figure 3.

4.3. Third Case

In this case, the outage probability decreases as K increases. Since the relay performs an amplify - and - forward (AF) function, this case is consistent with a traditional three - node communication model. The outage probability decreases as the SNR increases.As shown in Figure 4.

4.4. Fourth Case

In this case, the outage probability decreases as K increases.As shown in Figure 5.

5. Conclusion

This paper provides an in - depth study of the outage probability performance in relay - based semantic communication systems and proposes four transmission strategies under different background knowledge, computational capabilities, and channel conditions. By establishing a three - node communication model, the channel capacity and outage probability expressions for each scenario were derived and verified through Monte Carlo simulations. The research findings indicate that:

• The effectiveness of semantic transmission is influenced by the degree of background knowledge matching. When the background knowledge (BK) of the source node (S) and the destination node (D) is consistent, the semantic transmission performance of the communication system is optimal.
• Relay nodes play a crucial role in semantic conversion and adaptation, particularly when background knowledge does not match. Relay nodes can optimize semantic information transmission, improving the accuracy of semantic decoding.
• Channel conditions have a significant impact on the success rate of semantic transmission. When channel quality is poor, the relay node needs to use an amplify - and - forward (AF) strategy to enhance the signal, thereby reducing the outage probability.
• Hybrid strategies of semantic and bit transmission are suitable for scenarios with limited computational resources. When the computational power of the destination node is insufficient, performing semantic decoding at the relay node and converting it to bit streams can enhance the overall transmission reliability.

The theoretical analysis and simulation results in this study provide new insights for optimizing relay strategies in semantic communication systems and are of significant importance for improving the stability and reliability of future intelligent communication systems. Future research can further consider full - duplex relay modes and joint optimization of resource allocation to further enhance the performance of semantic communication systems.