Submitted:
15 March 2025
Posted:
18 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Bianchi Type Metric and Field Equations
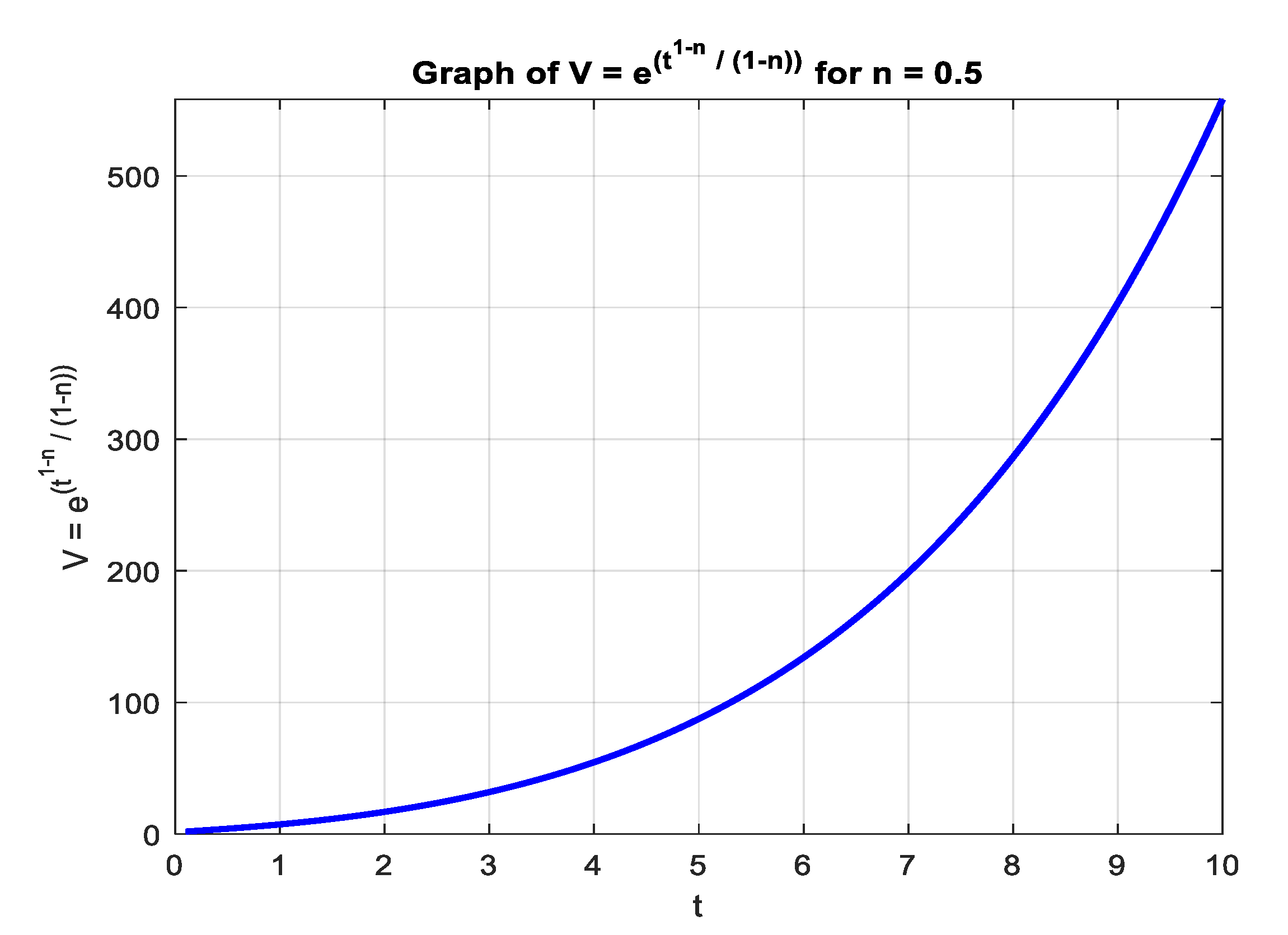
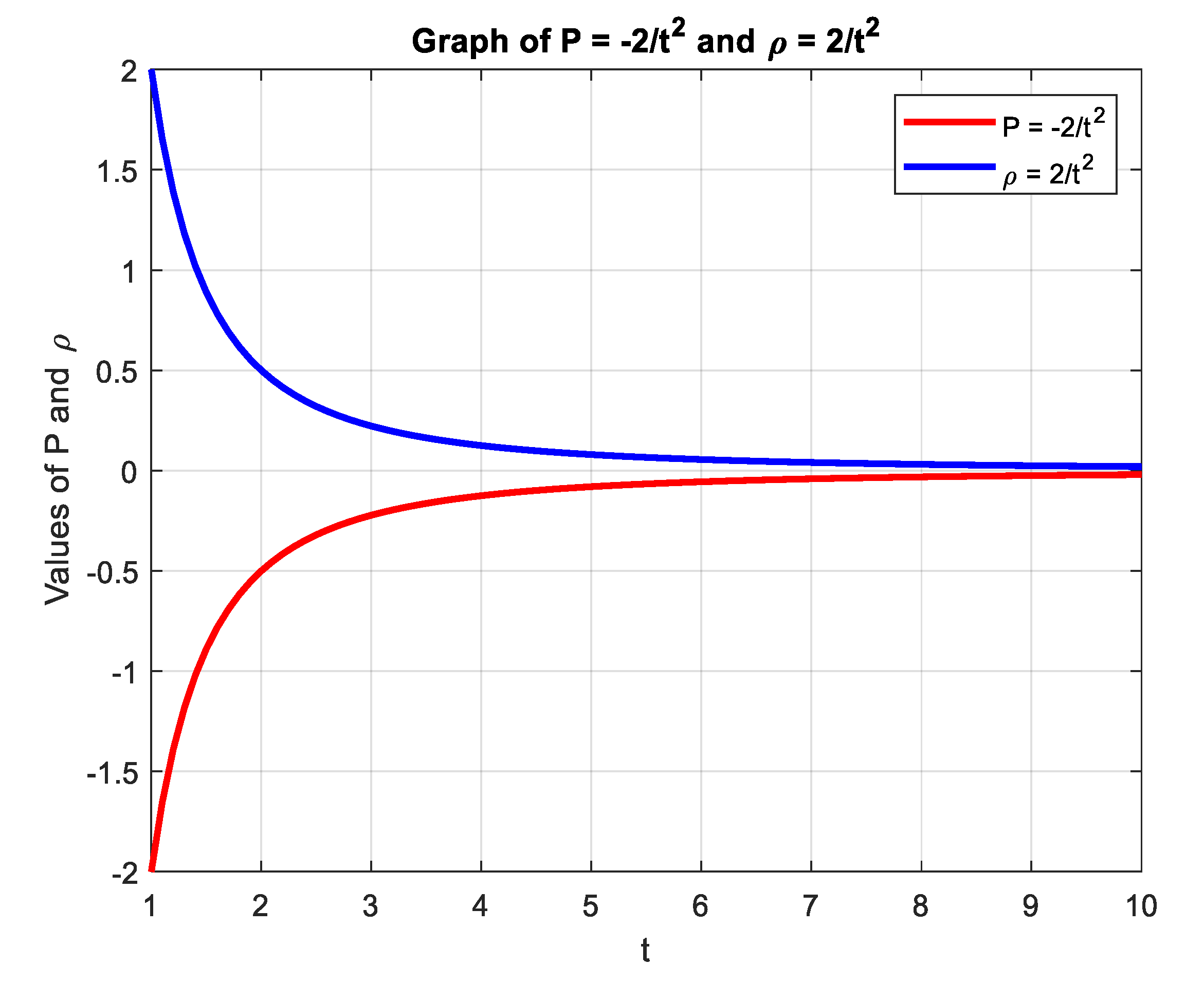
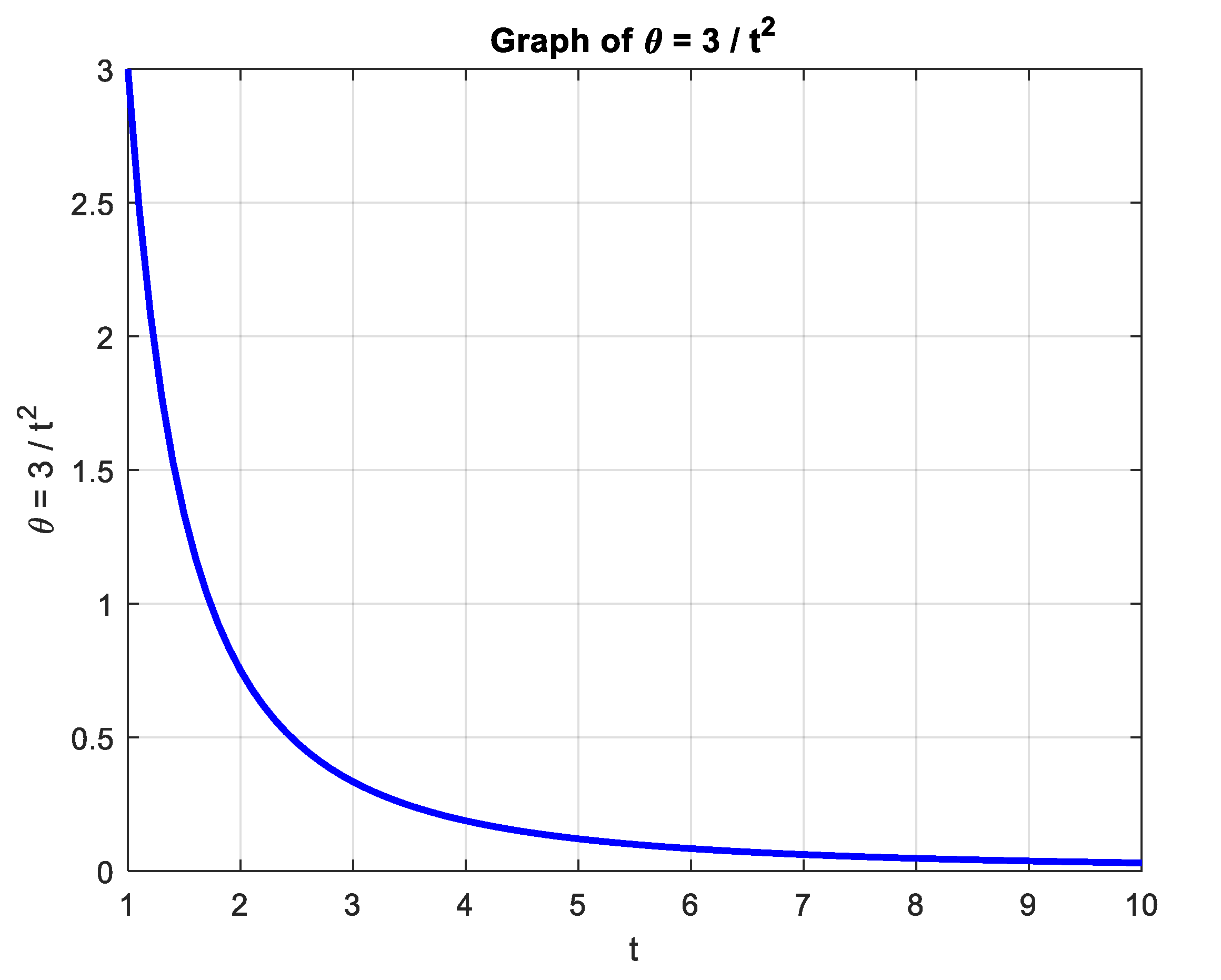
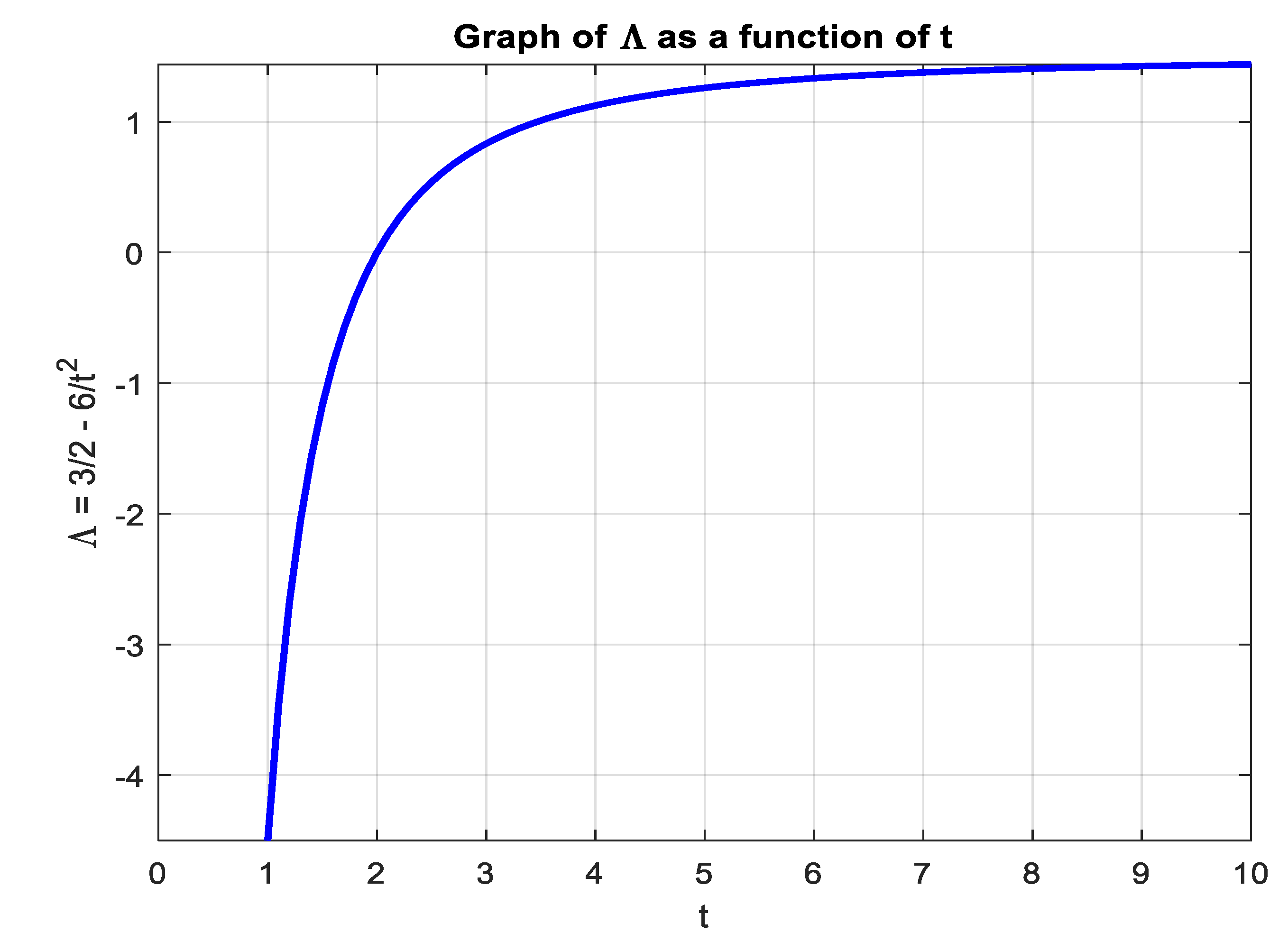
3. Results
References
- Lyra, G. über-eine Modifikation der Riemannschen Geometrie. Mathematische Zeitschrift 1951 54, 52–64.
- Rahaman, F; Bera, J. Higher dimensional cosmological model in Lyra geometry. Int. J. Mod. Phys. 2001, 10, 729. [Google Scholar] [CrossRef]
- Rahaman, F.; Chakraborty, S.; Bera,J. Inhomogeneous cosmological model in Lyra geometry. Int. J. Mod. Phys. 2002, 11, 1501. [Google Scholar]
- Baro,J. ; Singh,P. K. ; Singh,T. A. Higher Dimensional LRS Bianchi Type-I String Cosmological Model with Bulk Viscosity in Relativity. Indian J. Sci. Tech.
- Mohanty,G. ; Mahanta, K. L.;. Sahoo, R. R. Non-Existence of Five Dimensional Perfect Fluid Cosmological Model in Lyra Manifold. Astrophys. Space Sci. 2006 306, 269.
- Mohanty,G. ;. Mahanta, K. L,; Bishi,B. K. Five Dimensional Cosmological Models in Lyra Geometry with Time Dependent Displacement Field Astrophys. Space Sci. 2007, 310, 273.
- Mohanty,G.; Mahanta, K. L. Five-Dimensional Axially Symmetric String Cosmological Model in Lyra Manifold. Astrophys. Space Sci.
- Singh, P. K.; Mollah, M. R. R. Higher dimensional LRS Bianchi type-I Cosmological model universe Interacting with perfect fluid in Lyra Geometry The African Rev. Phys. 2016, 11, 33. [Google Scholar]
- B. P. Brahma and M. Dewri, Role of f(R,T) Gravity in Bianchi Type-V Dark Energy Model with Electromagnetic Field based on Lyra Geometry J. Sci. Res. 2022, 14, 721.
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. Scenario of two-fluid dark energy models in Bianchi type-III Universe. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850189. [Google Scholar]
- Tiwari, R.; Beesham, A.; Shukla, B. Cosmological models with viscous fluid and variable deceleration parameter. Eur. Phys. J. Plus 2017, 132, 20. [Google Scholar]
- Tiwari, R.; Beesham, A.; Shukla, B. Behaviour of the cosmological model with variable deceleration parameter. Eur. Phys. J. Plus 2016, 131, 1–9. [Google Scholar]
- Tiwari, R.K.; Beesham, A.; Shukla, B.K. FLRW Cosmological Models with Dynamic Cosmological Term in Modified Gravity. Universe 2021, 7, 319. [Google Scholar] [CrossRef]
- Khan, R.A.A.; Tiwari, R.K.; Bharali, J.; Bouali, A.; Yildiz, G.D.A.; Güdekli, E. Hyperbolic Scenario of Accelerating Universe in Modified Gravity. Symmetry 2023, 15, 1238. [Google Scholar] [CrossRef]
- Berman, M.S.; de Mello Gomide, F. Cosmological models with constant deceleration parameter. Gen. Relativ. Gravit. 1988, 20, 191–198. [Google Scholar]
- Akarsu, Ö.; Dereli, T. Cosmological models with linearly varying deceleration parameter. Int. J. Theor. Phys. 2012, 51, 612–621. [Google Scholar]
- Bolotin, Y.L.; Cherkaskiy, V.; Lemets, O.; Yerokhin, D.; Zazunov, L. Cosmology in terms of the deceleration parameter. Part I. arXiv 2015, arXiv:1502.00811. [Google Scholar]
- Bouali, A.; Chaudhary, H.; Debnath, U.; Sardar, A.; Mustafa, G. Data Analysis of three parameter models of deceleration parameter in FRW Universe. arXiv 2023, arXiv:2304.13137. [Google Scholar]
- Starobinsky, A.A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Kerner, R. Cosmology without singularity and nonlinear gravitational Lagrangians. Gen. Relativ. Gravit. 1982, 14, 453–469. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F (R) theory to Lorentz non-invariant models. Phys. Rep. 2011, 505, 59–144. [Google Scholar]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Modified gravity theories on a nutshell: Inflation, bounce and late-time evolution. Phys. Rep. 2017, 692, 1–104. [Google Scholar]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Linder, E.V. Einstein’s Other Gravity and the Acceleration of the Universe. Phys. Rev. D 2010, 81, 127301. [Google Scholar] [CrossRef]
- Bamba, K.; Geng, C.Q. Thermodynamics of cosmological horizons in f (T) gravity. J. Cosmol. Astropart. Phys. 2011, 2011, 008. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. Finite-time future singularities in modified Gauss–Bonnet and (R, G) gravity and singularity avoidance. Eur. Phys. J. C 2010, 67, 295–310. [Google Scholar] [CrossRef]
- deS.Silva, M.V.; Rodrigues, M.E. deS.Silva, M.V.; Rodrigues, M.E. Regular black holes in f (G) gravity. Eur. Phys. J. C.
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f (R, T) gravity. Phys. Rev. D 2011, 84, 024020. [Google Scholar] [CrossRef]
- Brans, C.; Dicke, R.H. Mach’s principle and a relativistic theory of gravitation. Phys. Rev. 1961, 124, 925. [Google Scholar] [CrossRef]
- Saez, D.; Ballester, V. A simple coupling with cosmological implications. Phys. Lett. A 1986, 113, 467–470. [Google Scholar] [CrossRef]
- Duff, M.J. Kaluza-Klein theory in perspective. In Proceedings of the Symposium: The Oskar Klein Centenary; World Scientific: Singapore, 1994; pp. 22–35. [Google Scholar]
- Porlawski, N.J. Interacting dark energy in f(R) gravity. Arxiv 8031.
- Ahmed, N. ; Pradhan,A. Bianchi Type-V cosmology in f(R,T) gravity with Λ(T). arxiv, 3000. [Google Scholar]
- Magnano, G. Are there metric theories of gravity other than General Relativity? arxiv 1995, 9511027. [Google Scholar]
- Porlawski, N.J. A Lagrangian description of interacting dark energy Class Quantum Grav. 2006, 23, 2011.
- Sen, D.K. A static cosmological model. Z.Phys. 1957, 149, 311. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



