High-Spatial-Resolution High-Accuracy OFDR Distributed Sensors Based on Seamless fs-WFBG Array

1. Introduction

Optical frequency domain reflectometry (OFDR) originates from frequency-modulated continuous wave (FMCW) technology[1]. Due to its unique advantage of high spatial resolution, OFDR has been widely applied in fields such as wing deformation monitoring[2] and 3D shape sensing[3]. In 1998, Froggatt et al. proposed treating Rayleigh backscattering in optical fibers as weak fiber Bragg grating (WFBG) and achieved wavelength demodulation by measuring the spectral offset of Rayleigh backscattering[4]. However, there is a trade-off between the sensing spatial resolution and sensing accuracy in OFDR[5]. Furthermore, random optical noise in the weak Rayleigh backscattering signal further limits performance metrics of OFDR, including spatial resolution and sensing accuracy[6].

To enhance the performance metrics of optical frequency domain reflectometry (OFDR), researchers have introduced WFBG arrays into the fiber under test (FUT) to amplify Rayleigh backscattering signals. In 2021, Xu et al. employed femtosecond laser point-by-point (PDP) technology to fabricate a WFBG array with a grating spacing of 9 mm, achieving a sensing spatial resolution of 10 mm[7]. In 2022, Zhong et al. utilized femtosecond laser point-by-point inscription technology to create a WFBG array with a grating spacing of 509 μm in a single-mode fiber, achieving a sensing spatial resolution of 979 μm[8]. In 2023, Fu et al. fabricated a WFBG array with a grating length of 1 mm and a grating spacing of 4 mm using femtosecond laser technology, achieving a sensing spatial resolution of 5 mm[9]. In 2024, Chen et al. used a drawing tower grating writing technique to fabricate a WFBG array with a grating length of 9 mm and a grating spacing of 1 mm, and by applying a sliding window to extract partial grating signals, they achieved a sensing spatial resolution of 1.28 mm and a wavelength demodulation accuracy of ±4 pm[10]. Although the aforementioned methods can effectively enhance the performance of OFDR, the size of the sliding window and the effective WFBG signals captured by the sliding window are constrained by the grating spacing, thereby limiting the sensing spatial resolution and accuracy of OFDR. Currently, there is no effective solution to address the limitations imposed by grating spacing on sensing spatial resolution and accuracy.

In this paper, we propose a novel high-spatial-resolution high-accuracy OFDR distributed sensors based on seamless femtosecond WFBG (fs-WFBG) array. The scheme utilizes femtosecond laser PDP technology to inscribe a 5 cm long seamless weak fiber grating array in a polyimide fiber, consisting of ten 5 mm long weak gratings. By employing a traditional windowed cross-correlation demodulation algorithm, a sensing spatial resolution of 533 μm and a wavelength demodulation accuracy of ±2.23 pm were achieved, effectively alleviating the trade-off between sensing spatial resolution and accuracy of OFDR. The following sections detail the experimental configuration and validate the effectiveness of the proposed method through experiments.

2. Experimental Configuration

2.1. Experimental Setup for Seamless fs-WFBG Array

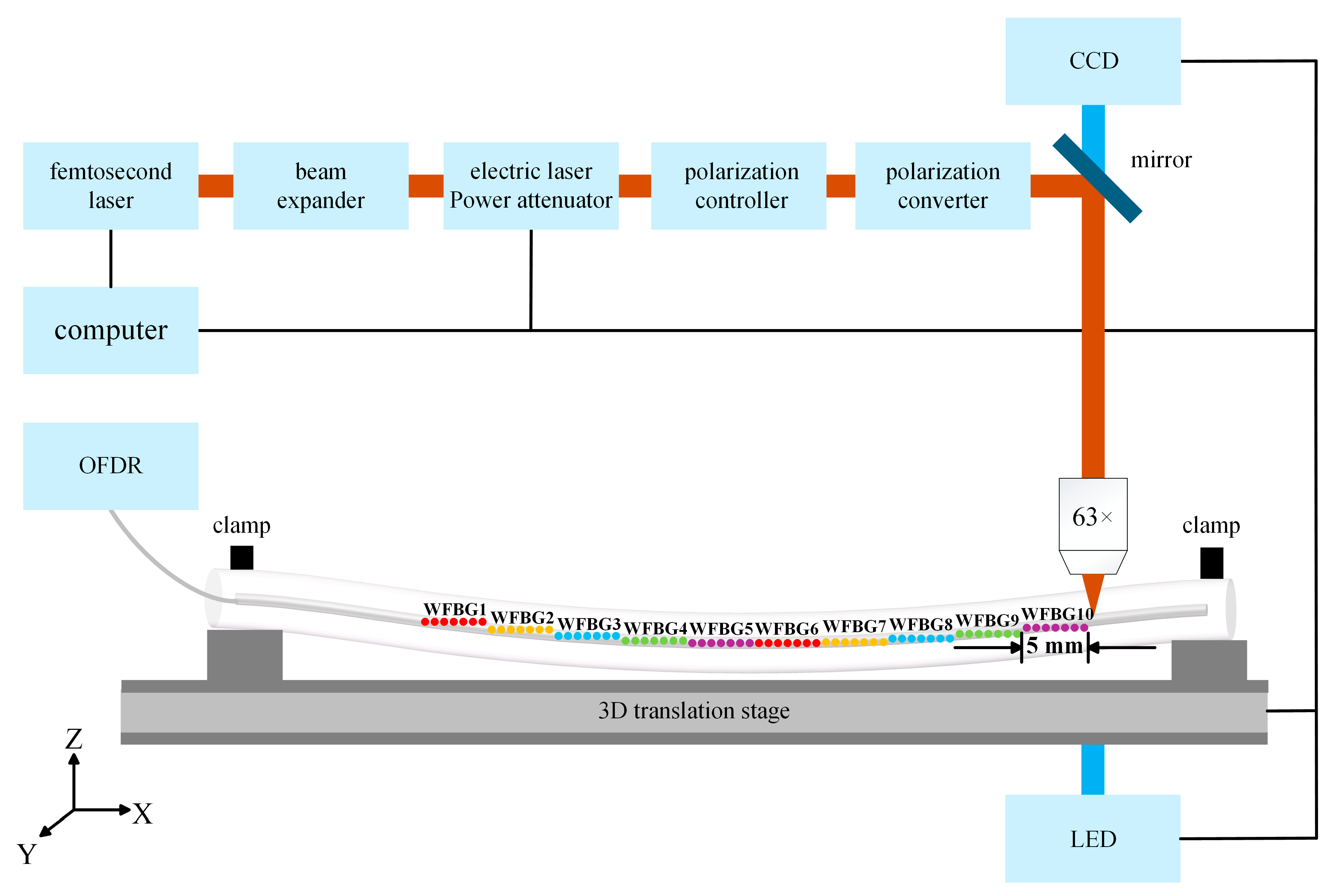
Figure 1 illustrates the schematic diagram of the femtosecond laser micro-nano fabrication inscription system. The system employs a femtosecond laser (Light Conversion, Carbide) as the light source, with a pulse width of 220 fs, a central wavelength of 1030 nm, a maximum pulse energy of 83 μJ, and an adjustable repetition rate range of 0–1 MHz. The output power of the laser pulses is regulated in real-time using an electric laser power attenuator. The laser beam passes through a reflector, a polarization controller, and a polarization converter before being focused onto the polyimide fiber core (YOFC, HT1510-B) via a 63× objective lens (numerical aperture NA = 1.4). The fiber is fixed on a 3D translation stage using two holders and immersed in index-matching oil (Cargille, n = 1.4587) to eliminate astigmatism and positional distortion caused by the cylindrical fiber. During the inscription of WFBGs, the fiber is moved by a computer-controlled three-axis translation stage. The real-time monitoring of the fiber core's microscopic image is achieved using a CCD camera and an LED light source, ensuring precise alignment of the fiber core center. Due to the curvature of the fiber, the focus point of the femtosecond laser gradually deviates from the center of the fiber core during the inscription of WFBG. Therefore, after completing the inscription of each WFBG, it is necessary to recalibrate the depth of the fiber core to ensure precise alignment with the center of the fiber core.

The inscription process of the seamless fs-WFBG array involves four main steps: Step 1, a section of polyimide fiber is fixed on a three-axis displacement stage using clamps, with one end connected to an OFDR; Step 2, the position of the fiber in the CCD field of view is used to adjust the three-axis translation stage, ensuring precise alignment of the laser beam focus with the center of the fiber core; Step 3, the displacement stage moves the polyimide fiber along the x-axis at a speed of 0.032 mm/s for a distance of 5 mm, while the femtosecond laser PbP inscription technique creates refractive index modulation points along the fiber axis, thereby fabricating a WFBG, where the distance moved by the displacement stage corresponds to the length of the WFBG; Step 4, the second WFBG is fabricated by repeating Steps 2 and 3, ensuring no grating spacing between adjacent WFBGs, and the third to tenth WFBGs are fabricated through the same process. Ultimately, a Seamless fs-WFBG array is successfully fabricated using the femtosecond laser point-by-point inscription technique.

2.2. OFDR-Based Wavelength Demodulation

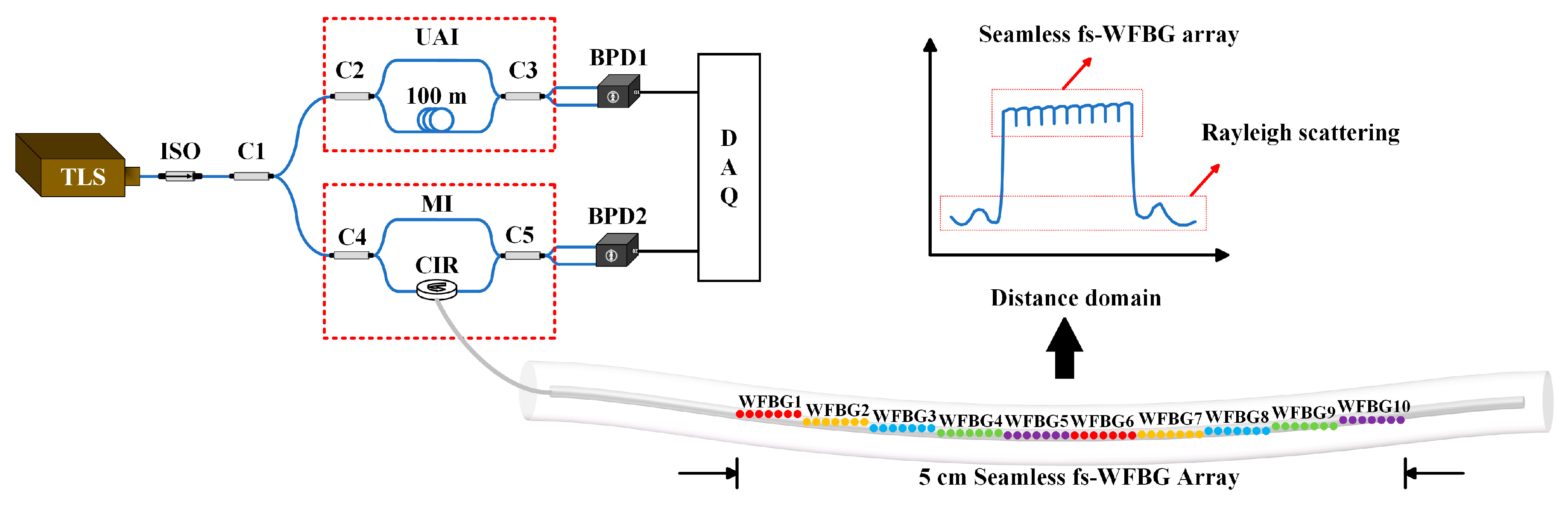
In an OFDR system[11,12,13], a main interferometer (MI) and an unbalanced auxiliary interferometer (UAI) are typically included, as shown in Figure 2. The MI is used to generate the beat signal between the Rayleigh backscattering signal and the reference signal, while the UAI is employed to compensate for the nonlinear frequency sweeping (NFS) of the laser[14,15]. Owing to the higher reflectivity of WFBG compared to Rayleigh scattering, the reflected light intensity of WFBG in the distance-domain signal of OFDR is significantly stronger than that of Rayleigh scattering. During the femtosecond laser inscription of WFBG, the focus point of the femtosecond laser gradually deviates from the center of the fiber core, leading to variations in the reflected light intensity between adjacent WFBG.

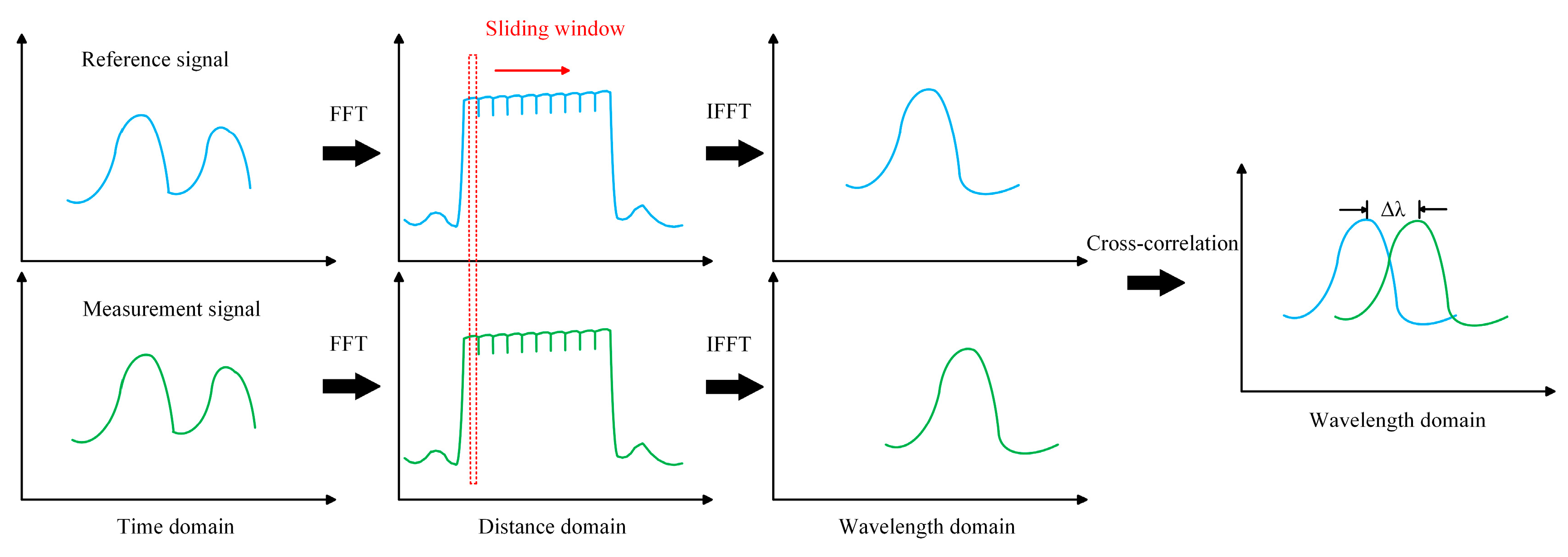
After obtaining the MI beat signal sampled by compensatiing for the NFS, the wavelength offset is demodulated using a traditional windowed cross-correlation demodulation algorithm, as illustrated in Figure 3. First, a reference signal and a test signal are transformed into the distance-domain signal by fast Fourier transform (FFT). Then, a sliding window is applied to extract the distance-domain signals of partial WFBG, followed by inverse fast Fourier transform (IFFT) to obtain the wavelength-domain signals. Since a seamless fs-WFBG array is used, the size of the sliding window does not need to account for the length of the WFBG. Finally, the wavelength offset is obtained by performing a cross-correlation operation on the two wavelength-domain signals.

3. Experiment Result and Discussion

The seamless fs-WFBG array is located between 3.787 m and 3.837 m along the fiber. A conventional OFDR system was also established for high-spatial-resolution high-accuracy distributed sensing, as shown in Figure 2. In this optical setup, a tunable laser source (TLS, Santec TSL-770) generates a frequency-modulated continuous wave with a wavelength scanning range from 1540 nm to 1560 nm, a scanning rate of 20 nm/s, and an output optical power of 6 dBm. Then the spatial resolution, i.e., ∆z, could be calculated as 41 µm based on the equation ∆z = c/2n∆F, where c, n, and ∆F are the light velocity in a vacuum, refractive index of the medium, and sweeping range of TLS; The frequency-modulated continuous wave first passes through an isolator (ISO) to protect the tunable laser from back reflections. The continuous wave is then split by a 99/1 coupler (C1) into two paths: (1) 99% of the light enters the main interferometer (MI) and is further divided by a 99/1 coupler (C4). Here, 99% of the light passes through a circulator (CIR) into the fiber under test, generating a reflected signal at the spacing-free WFBG. The reflected signal is directed back by the CIR and interferes with the remaining 1% reference light at a 50/50 coupler (C5) to produce a beat signal. (2) The other 1% of the light enters an unbalanced auxiliary interferometer (UAI) through a 50/50 coupler (C2), and after passing through a 100-meter delay fiber, generates a beat signal at a 50/50 coupler (C3). The beat signal from the UAI is detected by a balanced photodetector (BPD1) and serves as an external clock for the data acquisition card (DAQ), triggering the DAQ to collect the beat signal from the main interferometer detected by BPD2. After obtaining the beat signal from the MI, a windowed cross-correlation demodulation algorithm is employed to calculate the spectral wavelength offset. The sliding window N is set to 13 points, and based on the formula ∆x = N∆z, the spatial resolution of the OFDR system is determined to be 533 μm.

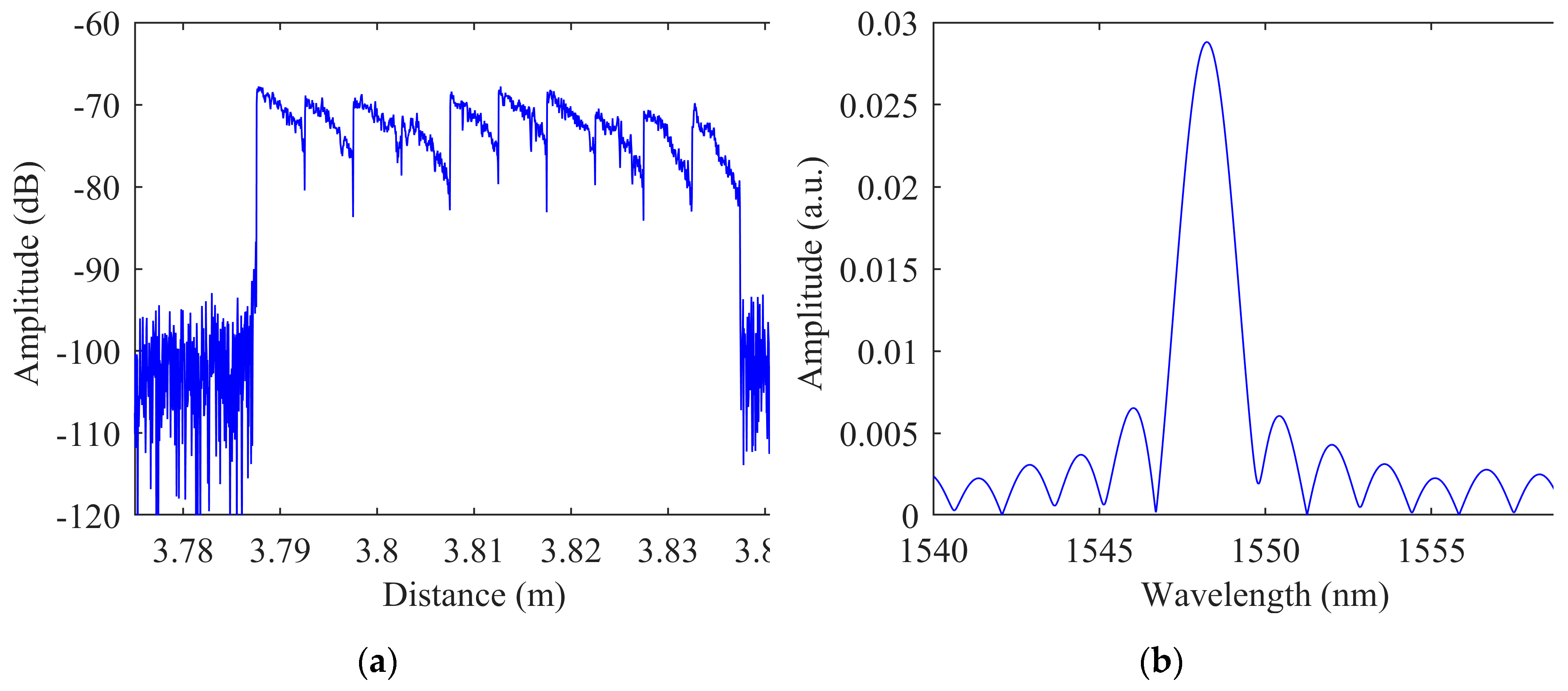
The distance-domain signal of OFDR based on the seamless fs-WFBG array was acquired, as shown in Figure 4(a). The measured WFBG length of 5 cm precisely matches the actual length of the femtosecond laser-inscribed seamless fs-WFBG array. Subsequently, an 533-μm sliding window was applied to extract a segment of the distance-domain signal, which was then processed through inverse Fast Fourier Transform (IFFT) to obtain the wavelength-domain signal of OFDR. The resulting signal exhibits a Gaussian-distributed envelope with a central wavelength of 1548 nm, as illustrated in Figure 4 (b).

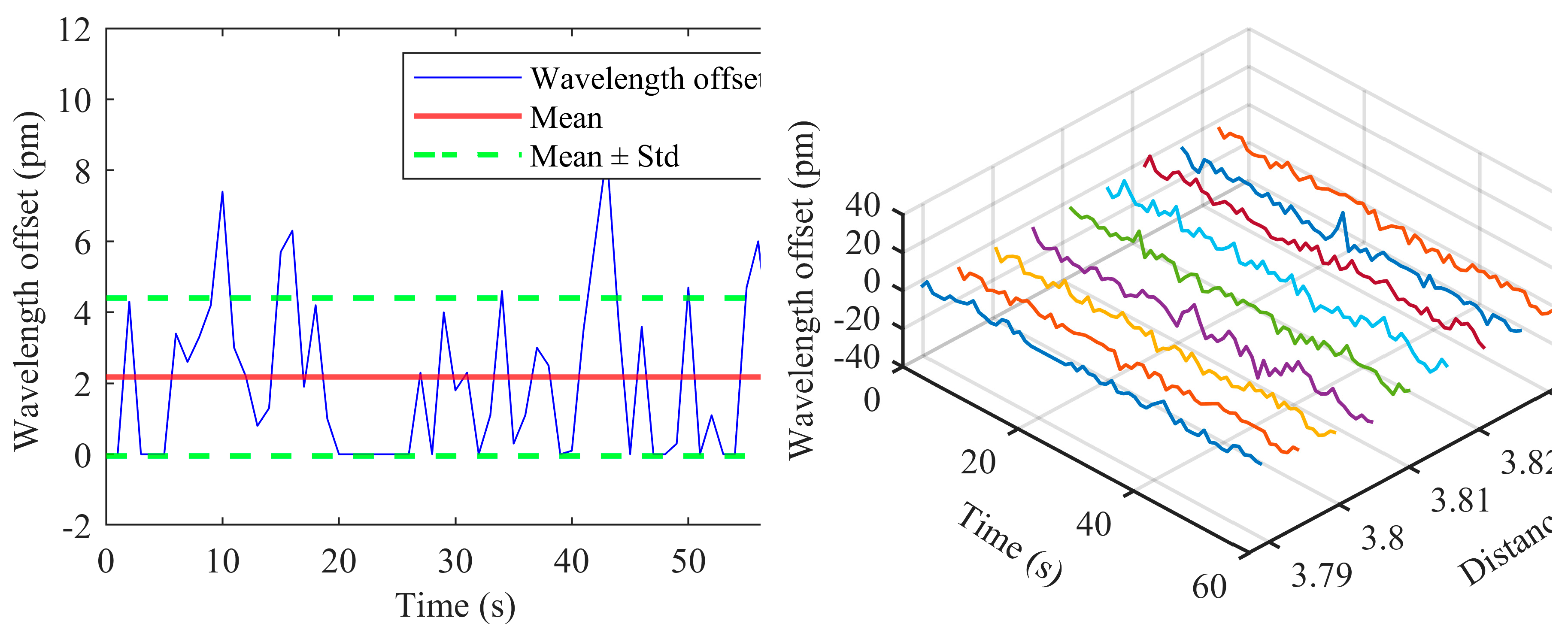
Subsequently, the MI beat signal was used as reference data, while subsequently collected signals served as measurement data. The wavelength offset between measurement and reference data was calculated using the windowed cross-correlation demodulation algorithm. Within the 5-cm-long spacing-free weak fiber Bragg grating array, an 533-μm sliding window generated 91 sensing channels. Figure 5(a) presents the wavelength offset of the first sensing channel over a 60-second period, showing a mean value of 2.18 pm with a standard deviation of ±2.23 pm. Additionally, Figure 5(b) displays the wavelength offset results of sensing channels 1, 11, 21, 31, 41, 51, 61, 71, 81, and 91 over the same 60-second duration.

Table 1 summarizes the sensing spatial resolution and accuracy achieved by OFDR systems using WFBG arrays with different grating spacings. Notably, in previous studies, the sensing spatial resolution and accuracy of OFDR systems based on WFBG arrays were limited by the grating spacing, specifically manifested in the constraints on the size of the sliding window and the effective WFBG signals captured by the sliding window. In contrast, the seamless fs-WFBG array proposed in this study successfully achieved a sensing spatial resolution of 533 μm and a sensing accuracy of ±2.23 pm. This innovative solution effectively alleviates the trade-off between sensing spatial resolution and accuracy, demonstrating significant technical advantages.

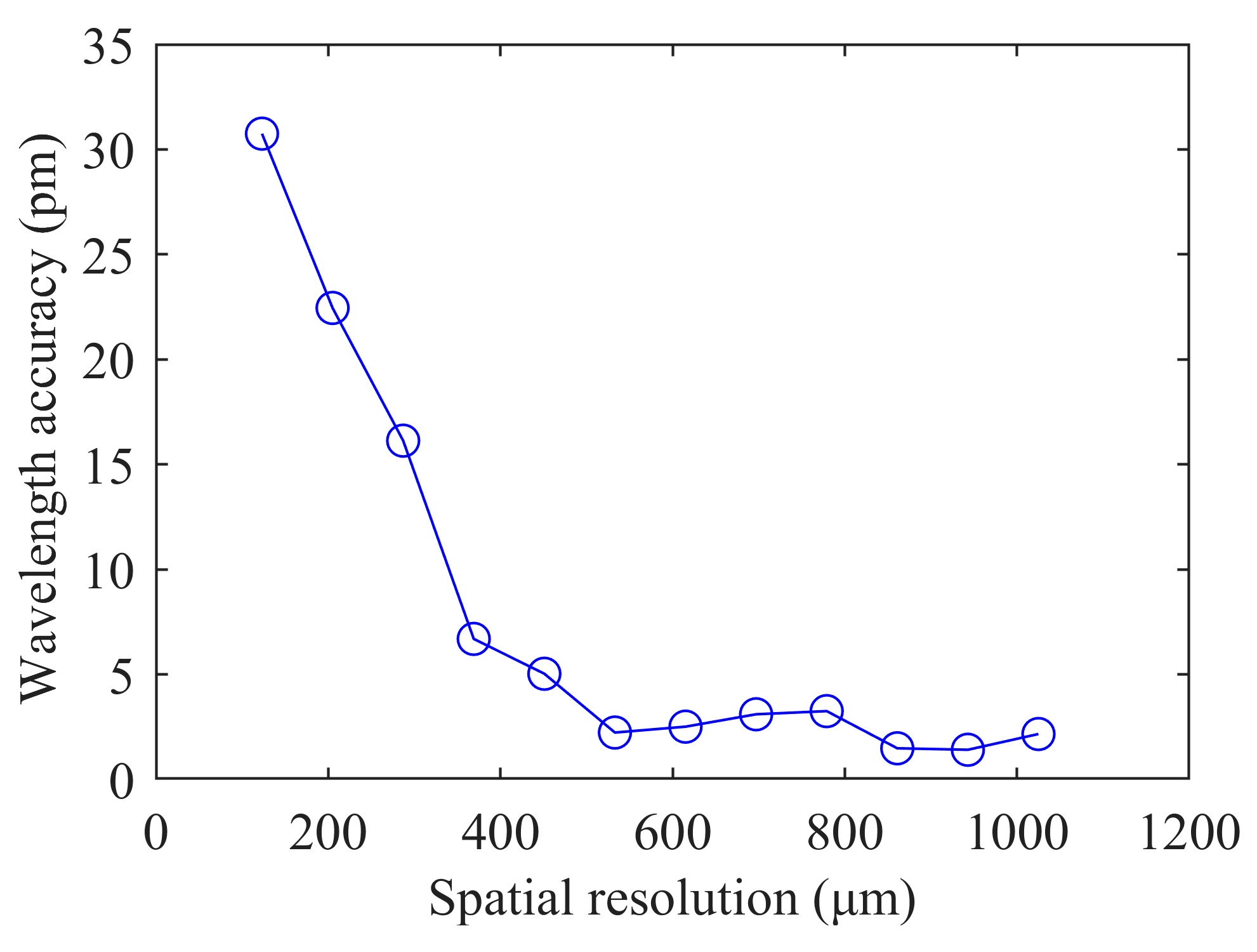
In addition, we tested the sensing accuracy at different sensing spatial resolutions, as shown in Figure 6. The experimental results reveal that as the sensing spatial resolution increases, the sensing accuracy gradually decreases. When the sensing spatial resolution is 123 μm, the sensing accuracy is ±30.75 pm; when the sensing spatial resolution is reduced to 533 μm, the sensing accuracy improves to ±2.23 pm. This trend indicates a trade-off relationship between sensing spatial resolution and accuracy. However, when the sensing spatial resolution is further reduced, the sensing accuracy does not significantly improve, which may be attributed to the influence of system noise and environmental noise.

4. Conclusions

In conclusion, we have proposed and experimentally validated a high-spatial-resolution high-accuracy OFDR method based on seamless fs-WFBG array. To alleviate the trade-off between sensing spatial resolution and accuracy of OFDR, we successfully fabricated a 5-cm-long seamless fs-WFBG array in polyimide fiber using femtosecond laser PbP inscription technique, which consists of ten continuously arranged 5-mm-long WFBG units. Experimental results demonstrate that this method could achieve a sensing spatial resolution of 533 μm and a wavelength demodulation accuracy of ±2.23 pm, providing a novel technical solution for distributed OFDR sensing.