Study on the Support Pressure of Tunnel Face for the Construction of Pipe-Jacking Across Thin Overburden River Channel Based on Mud-Water Balance

1. Introduction

Control the tunnel face support pressure and the soil layer groundwater pressure and soil pressure in a balanced state, which is the key to ensure the smooth jacking construction of mud-water balanced pipe-jacking and reduce the impact of disturbance on the surrounding soil. In pipe-jacking project, if the tunnel face support pressure is not properly controlled, it will trigger the tunnel face instability problem. When the support pressure of tunnel face is too small, the front soil unloading and a large amount of soil influx into the mud and water silo, which will cause over excavation, surface subsidence, and obstruction of pipe-jacking; When the support pressure on the tunnel face is too high, the soil in front is compressed due to loading, causing uplift and damage in a certain area of the surface[1]. Therefore, in order to avoid problems such as surface subsidence with too much support pressure or uplift damage with too little support pressure, reasonable and accurate control of support pressure on the tunnel face is the key to mud-water balanced pipe-jacking construction[2].

The research about ultimate support pressure is currently using indoor physical model test, stability coefficient method, limit analysis method, limit equilibrium method and numerical calculation[3,4]. Physical model tests are costly and difficult to generalize to complex real-world projects[5,6,7]. The stability coefficient method was first proposed by Broms[8], who in 1967 established a mathematical relationship between the support force and the surface load, soil gravity, overburden burial depth, and clay undrained strength, and defined the ratio of each parameter as the stability coefficient N. Based on a large amount of surface settlement data, Peck[9] proposed that N=5 to 7 will lead to the destabilization of the excavation surface and induce surface collapse, and explored the relationship between the stability coefficients and the overburden burial depth, the unsupported length, and the variation of settlement. However, it was found in practice that the prediction error of the stability coefficient method was large, and it was very easy to misjudge the unstable condition as stable condition. At the same time, the stabilization coefficient method can only be applied to clay formations (i.e., cohesion ≠ 0), and cannot be applied in sandy soil formations. Although the stabilization factor method had received a series of improvements to diversify the form of expression, one point that was never taken into account was that the effect of permeability on the excavated surface was suitable for calculations in groundwater-free construction conditions. In addition, the arc effect overestimated the destructive power. The limit analysis[10,11,12,13] method is based on the kinematic permissive velocity field and the static permissive stress field. It establishes the equilibrium conditions and damage conditions in the critical state of the soil body and deduces the excavation surface support force based on the principle of virtual work[14].

Limit equilibrium method[15,16] assumes that the soil body damage in front of the excavation produces a sliding body, and analyses the equilibrium of forces in the soil body at the moment of damage to find the solution of the problem. Then the complex static indeterminate problem of soil damage is transformed into a simpler static deterministic solvable problem. The theory of the limit equilibrium method[17,18,19,20] is rigorous, the mechanical mechanism is clear, and the calculation formula is concise and refined. After decades of improvement and enhancement, it has been developed to a fairly perfect degree by now and is widely used in practical engineering[21,22]. Based on the two-dimensional limit equilibrium model and silo theory[23], Horn[24] et al. established a three-dimensional wedge-shaped model for the stability of the tunnel face. This model can determine the magnitude of the ultimate support pressure; R. P. Chen[25] considered the effects of prism height and soil arching. Then he proposed an improved three-dimensional wedge-shaped prism model and an analytical formula for the lateral stress ratio between the prism and adjacent soil that reflects the arching effect of the soil; P. Perazzell[26] introduced the supporting force of a single anchor in a wedge limit equilibrium model and proposed a limit equilibrium method for analyzing the stability of the tunnel face of reinforced tunnels in purely cohesive soils without draining shear strength; Based on four typical pipe-slurry-soil contact modes, Weizheng Liu[27] proposed a calculation method for the jacking force of each pipe section considering the jacking resistance at the excavation surface and the lateral friction resistance around the pipe. And the reliability of the calculation method was verified by comparing with the model test results and engineering example data.

Numerous scholars have carried out a lot of research on the stability of tunnel face of pipe-jacking, and the results are more fruitful. However, some aspects are yet to be further deepened. Existing tunnel face support pressure calculations are analysed based on plane strain[28], and the front earth pressure is simplified into a rectangular distribution calculation. This differs from the trapezoidal distribution of soil pressure in front of the actual tunnel face[29]. Moreover, the above study only focuses on a single pipe-jacking, but nowadays double-row or even triple-row pipe-jacking has been widely used in engineering practice[30]. In addition, passive damage to the soil in front of the pipe-jacking is more common in actual pipe-jacking projects. If the thickness of the overlying soil layer is not large and the construction of the pipe-jacking crossing river channel is carried out, active damage to the soil in front of the pipe-jacking must be considered. Therefore, in this paper, based on the mud-water balance and considering the conditions of pipe-jacking through the river channel, thin overburden of the river, and multi-line construction with small clearances, the support pressure of the tunnel face was characterized. The research can provide theoretical basis, and practical guidance for the construction of pipe-jacking under similar engineering conditions, which is of great practical significance.

2. Theoretical Analysis of Tunnel Face Support Pressure

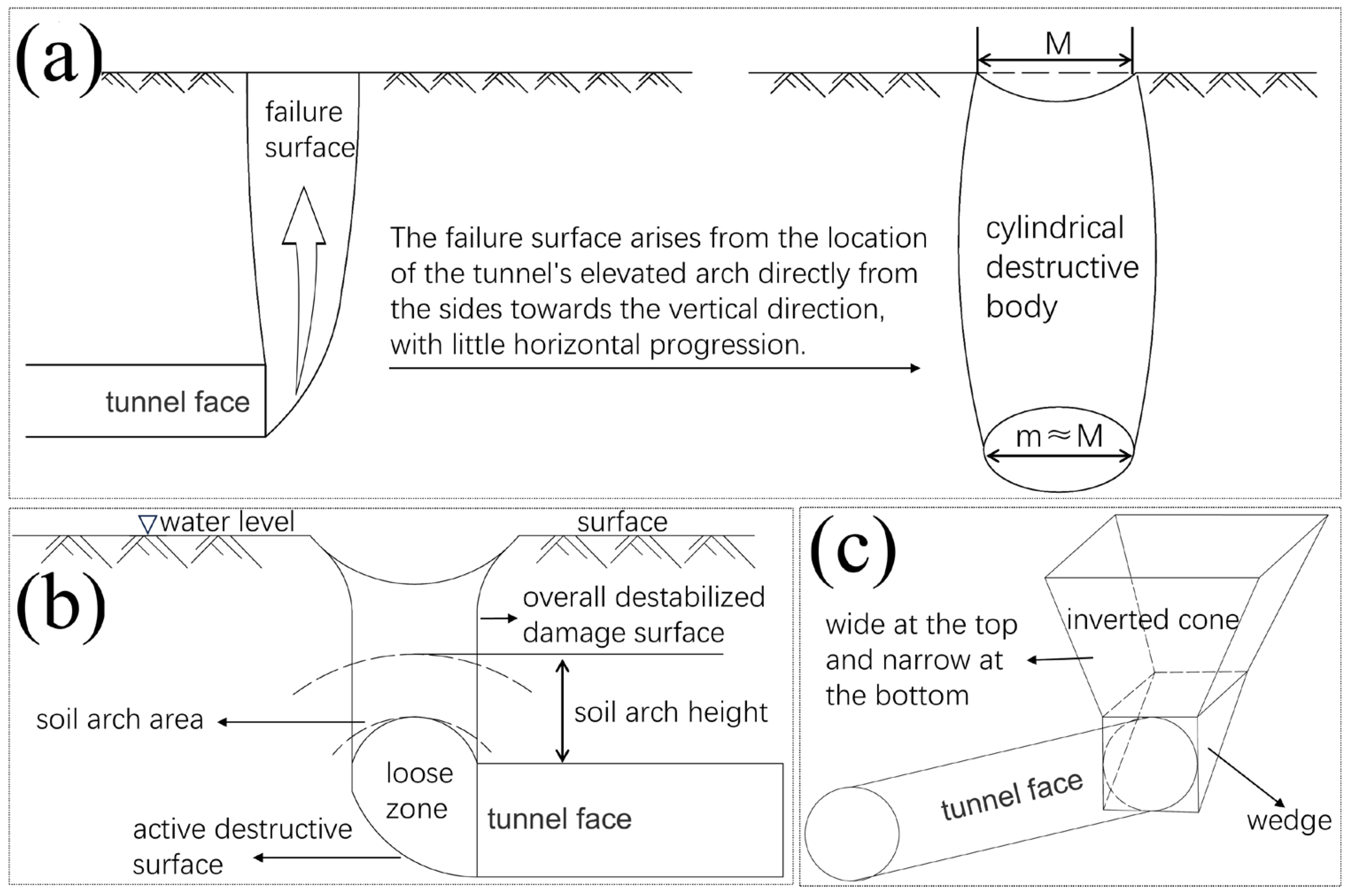
2.1. Mechanism of Support Pressure on the Tunnel Face of the Pipe-Jacking

The mud-water balance theory is a pipe-jacking theory that balances the soil pressure and groundwater pressure in the soil layer where the tunneling machine is located by using the pressure inside the mud compartment of the tunneling machine (i.e., the support pressure on the tunnel face). Theoretically, when the support pressure of the tunnel face is in balance with the soil and water pressure in front of it, the effect of pipe-jacking construction on the deformation of the stratum in front of the tunnel face will not occur.

When the support pressure of the tunnel face is less than the soil and water pressure in front of it, the stratum in front of the tunnel face moves towards the tunnel. The interaction between the soils has a tendency to inhibit the sliding of the soils and the shear resistance increases; When the support force of the tunnel face decreases to a certain critical point, the displacement of the tunnel face suddenly increases sharply, and the tunnel face undergoes active damage. Established research results show that the damage pattern is manifested as a chimney-like shear zone[31,32] when active damage occurs on the tunnel surface of shallow buried pipe-jacking in sandy soil layers. The damage surface arises from the location of the tunnel’s elevated arch directly from the sides toward the vertical direction, almost not toward the horizontal. The damage body is in the shape of a column with a small difference in width between the top and bottom (as shown in Figure 1 (a)). When the water level is above the surface, the upper strata in front of the tunnel face undergoes overall damage and slides downward to the surface[33], as depicted in Figure 1(b).

When the support pressure of the tunnel face is greater than the resistance, the soil body in front of the tunnel face shows an upward sliding displacement tendency. The interaction between soil grains inhibits the sliding tendency of the soil body and the shear resistance increases; When reaching the support pressure increases to a critical point, the displacement of the tunnel face suddenly increases sharply, and the tunnel face of pipe-jacking undergoes passive damage. Existing research results show that: when the tunnel surface of shallow buried pipe-jacking in sandy soil layer is passively damaged, the shape of the damaged area of the formation in front is similar to an inverted cone which is wide at the top and narrow at the bottom with a certain angle of inclination[34](as seen in Figure 1(c)).

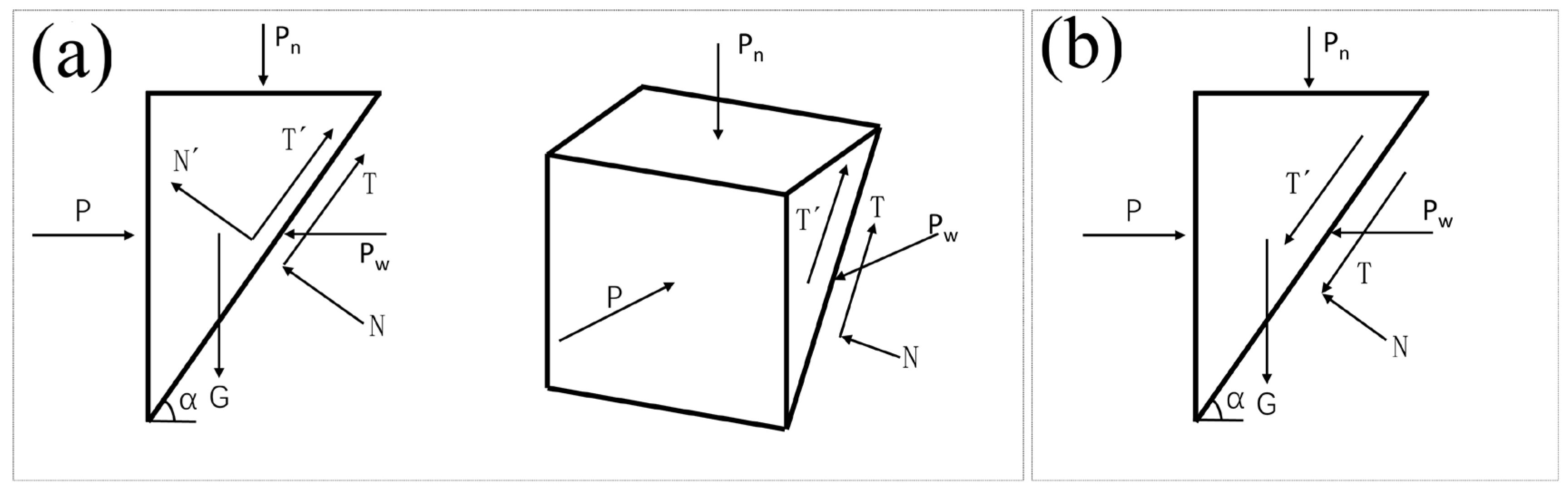
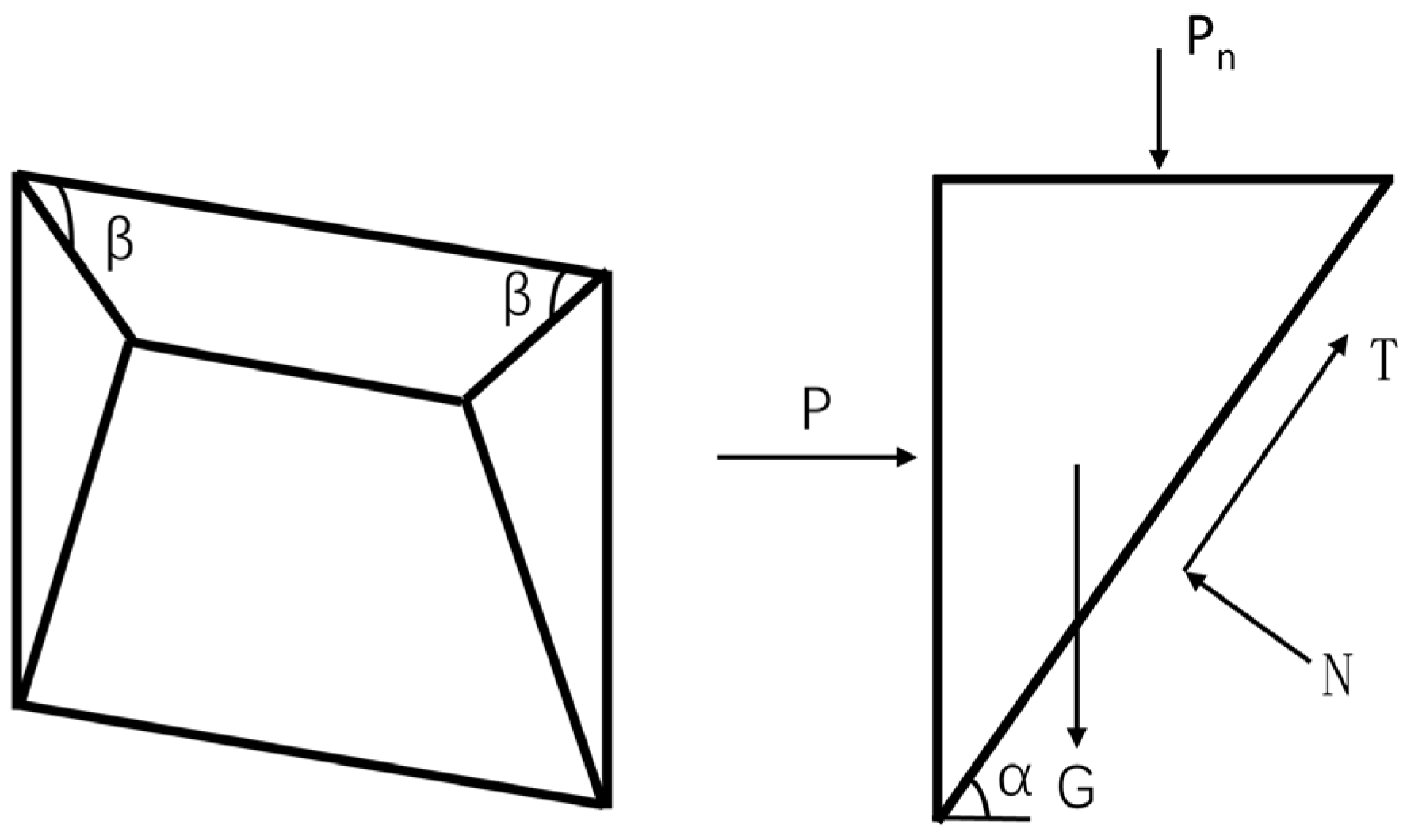
2.2. Theoretical Calculation Principle of Tunnel Face Support Pressure

For river crossing pipe-jacking projects with significant features such as small thickness of overburden and water level above the surface, the analytical model for calculating the support pressure at the tunnel face was made with the following assumptions:

1)The project site strata were homogeneous, continuous, and isotropic. Tunnel face damage was caused by sliding within the strata soil body. The soil on the sliding surface obeyed the Mohr-Coulomb damage criterion.

2)The support pressure on the tunnel face was uniformly distributed. Its vertical variation and the effect of seepage from the ground at the tunnel face were not considered.

3)The circular tunnel face of the pipe-jacking was simplified to a retaining wall of equal area and no thickness.

4)When the tunnel face of pipe-jacking was damaged, there was a wedge-shaped block in front. The effect of friction on the contact surface of the wedge block was neglected; the wedge block would not undergo internal deformation and the static equilibrium condition was satisfied.

The force on the wedge-shaped block in front of the tunnel face of the pipe-jacking was as shown in Figure 2(a). The meaning of each parameter in the figure was as follows: P was the support pressure of the tunnel face; P_w was the hydrostatic pressure exerted on the tunnel face; P_n was the vertical force acting on the top of the wedge block; G was the self-weight of the wedge block; T and N were the frictional force (upward in the direction of active damage and downward in the direction of passive damage) and the normal stress on the diagonal section of the wedge block, respectively; T’ and N’ respectively represented the frictional resistance (active failure direction upward, passive failure direction downward) and normal force on the sliding surfaces on both sides of the wedge-shaped block.

The force characteristic of the wedge-shaped block was analyzed by taking the example of passive damage occurring on the tunnel face of the pipe-jacking. Equations (1) and (2) can be obtained from the conditions of equilibrium of forces in the horizontal and vertical directions, respectively.

$\begin{array}{c}P=T\cos \mathsf{\alpha }+2{\mathrm{T}}^{\mathrm{\text{'}}}+N\sin \mathsf{\alpha }+{\mathrm{P}}_{\mathrm{W}}\left(1\right)\end{array}$

$\begin{array}{c}{\mathrm{P}}_{\mathrm{n}}+G=N\cos \mathsf{\alpha }-T\sin \mathsf{\alpha }+2{\mathrm{T}}^{\mathrm{\text{'}}}\sin \mathsf{\alpha }\left(2\right)\end{array}$

Equation (3) can be obtained from the relationship between the friction force T and the normal force N on the sliding surface of the block.

$\begin{array}{c}T={\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{\sin \mathsf{\alpha }}}+N\tan \mathsf{\phi }\left(3\right)\end{array}$

Where: c was the soil cohesion, kPa; $\mathsf{\alpha }$ was the angle of inclination of the sliding block, °, $\mathsf{\alpha }=45°+{\displaystyle \frac{\mathsf{\phi }}{2}}$; $\mathsf{\phi }$ was the angle of internal friction of the soil, °; $\mathrm{G}$ was the self-weight of the wedge block, $\mathrm{G}={\displaystyle \frac{{\mathrm{B}}^3{\mathsf{\gamma }}_{\mathrm{s}}}{2\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\alpha }}}$, kN; ${\mathsf{\gamma }}_{\mathrm{s}}$ was volumetric weight of soil, kN/m³.

Equation (4) can be obtained by combining equations (1) to (3) and simplifying.

$\begin{array}{c}P={\displaystyle \frac{\sin \mathsf{\alpha }-\tan \mathsf{\phi }\cos \mathsf{\alpha }}{\cos \mathsf{\alpha }+\tan \mathsf{\phi }\sin \mathsf{\alpha }}}\left({\mathrm{P}}_{\mathrm{n}}+\mathrm{G}\right)-\left({\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}+2{\mathrm{T}}^{\mathrm{\text{'}}}\right)\left({\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }}{\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }+\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}\sin \mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{P}}_{\mathrm{W}}\left(4\right)\end{array}$

Where: ${\mathrm{P}}_{\mathrm{w}}$ was the hydrostatic pressure, kN, ${\mathrm{P}}_{\mathrm{w}}={\mathrm{B}}^2({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}){\mathsf{\gamma }}_{\mathrm{w}}$; ${\mathsf{\gamma }}_{\mathrm{w}}$ was volumetric weight of water, kN/m³; ${\mathrm{H}}_{\mathrm{u}}$ was the distance from the top of the pipe-jacking to the underground-water level line, m; D was the outer diameter of the digging machine, m; ${\mathrm{T}}^{\mathrm{\text{'}}}$ was the sliding friction force of the sliding surfaces on both sides of the wedge-shaped block, kN, ${\mathrm{T}}^{\mathrm{\text{'}}}={\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2}{2\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\alpha }}}+\mathrm{k}{\mathsf{\gamma }}_{\mathrm{s}}{(\mathrm{C}+\mathrm{D}/3)}^3\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }$; $\mathrm{k}$ was the coefficient of lateral pressure of the soil, $\mathrm{k}=1-\sin \mathsf{\phi }$; $\mathrm{C}$ was the length of wedge block, m.

${\mathrm{P}}_{\mathrm{n}}$ was the vertical force on the top of the wedge block. Due to the small thickness of the pipe-jacking overburden, ${\mathrm{P}}_{\mathrm{n}}$ was taken as the self-weight of the overlying soil according to the soil column theory. That was to say: ${\mathrm{P}}_{\mathrm{n}}={\mathrm{B}}^2{\mathrm{H}}_{\mathrm{s}}{\mathsf{\gamma }}_{\mathrm{s}}\mathrm{c}\mathrm{o}\mathrm{t}\mathsf{\alpha }$. ${\mathrm{H}}_{\mathrm{s}}$ was the thickness of the overburden.

Each of the above parameters was brought into Equation (4) and simplified. The general mathematical equation for the tunnel face support pressure $\mathrm{P}$ can then be obtained as shown in equation (5).

$\begin{array}{c}{\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}=\epsilon {\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{s}}\cos \mathsf{\alpha }+{\displaystyle \frac{\mathrm{B}}{2\tan \mathsf{\phi }}}\right)-\left[{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(1-\cos \mathsf{\alpha }\right)}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}+2{\mathsf{\gamma }}_{\mathrm{s}}\tan \mathsf{\phi }\left(1-\sin \mathsf{\phi }\right){\left(\mathrm{C}+{\displaystyle \frac{\mathrm{D}}{3}}\right)}^3\right]\\ \left(\mathsf{\epsilon sin}\mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}\right){\mathsf{\gamma }}_{\mathrm{w}}\left(5\right)\end{array}$

Where: $\epsilon ={\displaystyle \frac{\sin \alpha —\tan \phi \cos \alpha }{\cos \alpha +\tan \phi \sin \alpha }}$. Other symbols had the same meaning as above.

The slider inclination $\mathsf{\alpha }$ angle in Equation (5) was considered as an unknown quantity. The lowest value of the support pressure of tunnel face $\mathrm{P}$, which was the lower limit of the support force ${\mathrm{P}}_{\mathrm{m}\mathrm{i}\mathrm{n}}$ on the tunnel face of the pipe-jacking, was obtained through the optimization search.

The horizontal unloading arch effect needed to be taken into account when active damage occurred (the support pressure at the tunnel face was less than the soil and water pressure in front of it). The wedge in front of the tunnel face adopted a trapezoidal wedge, and the angle between the balance arch and the tunnel face was assumed to be 50°[35]. The contact surface between the sliding soil and the horizontal unloading arch (the side of the original wedge model and the trapezoidal wedge) was assumed to be unstressed, as shown in Figure 3.

Based on the above assumptions:

$\begin{array}{c}P={\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }}{\mathrm{c}\mathrm{o}\mathrm{s}\mathsf{\alpha }+\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }}}\left({\mathrm{P}}_{\mathrm{n}}+\mathrm{G}\right)-{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(\tan \mathsf{\beta }-1\right)}{\sin \mathsf{\alpha }\tan \mathsf{\beta }}}\left({\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }-\mathrm{t}\mathrm{a}\mathrm{n}\mathsf{\phi }\cos \mathsf{\alpha }\mathsf{\alpha }}{\cos \mathsf{\alpha }+\tan \mathsf{\phi }\sin \mathsf{\alpha }}}\sin \mathsf{\alpha }+\cos \mathsf{\alpha }\right)+{\mathrm{P}}_{\mathrm{W}}\left(6\right)\end{array}$

According to the overall force balance of the trapezoidal wedge, the upper limit of the support pressure (maximum support pressure, ${\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}$) of the tunnel face can be obtained as:

$\begin{array}{c}{\mathrm{P}}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\epsilon {\mathsf{\gamma }}_{\mathrm{s}}{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{s}}\cot \mathsf{\alpha }+{\displaystyle \frac{\mathrm{B}}{2\tan \mathsf{\phi }}}\right)+{\mathrm{B}}^2\left({\mathrm{H}}_{\mathrm{u}}+0.5\mathrm{D}\right){\mathsf{\gamma }}_{\mathrm{w}}-{\displaystyle \frac{\mathrm{c}{\mathrm{B}}^2\left(\tan \mathsf{\beta }-1\right)}{\mathrm{s}\mathrm{i}\mathrm{n}\mathsf{\alpha }\tan \mathsf{\beta }}}\left(\mathsf{\epsilon sin}\mathsf{\alpha }+\cos \mathsf{\alpha }\right)\left(7\right)\end{array}$

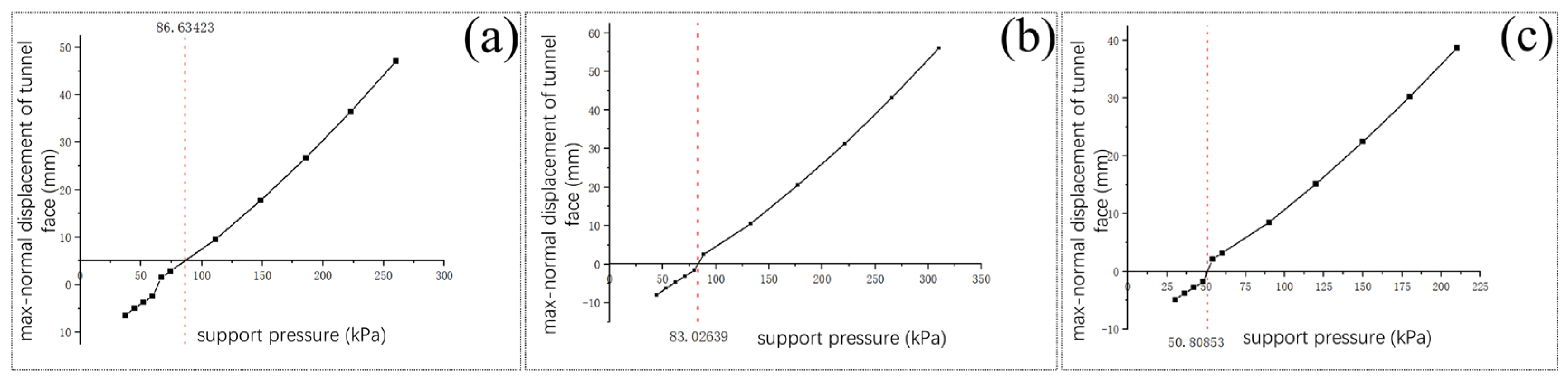
2.3. Calculation and Analysis of the Optimal Value of Support Pressure

Mud-water balanced pipe-jacking construction was to use the balancing medium, such as mud and water, to obtain a certain pressure in the working silo, which was in order to balance the pressure of unground-water and soil layer in front of the tunnel face. The sum of soil and water pressures in the soil above the front of the pipe-jacking machine was assumed to be ${\mathrm{P}}_1$. The corresponding tunnel face support pressure was ${\mathrm{P}}_2$; The sum of soil and water pressures in the bottom soil at the front of the pipe-jacking machine was assumed to be ${\mathrm{P}}_3$. The corresponding tunnel face support pressure was ${\mathrm{P}}_4$, as illustrated in Figure 4. Theoretically, the condition that the mud-water balanced jacking tunnel face was in equilibrium was ${\mathrm{P}}_1$=${\mathrm{P}}_2$ and ${\mathrm{P}}_3$=${\mathrm{P}}_4$.

In order to simplify the analysis and to highlight the main contradictions of the problem, the following assumptions were made: 1) The tunnel face support pressure and resistance were trapezoidal in distribution and the point of action was located at the center of gravity of the trapezoidal area; 2) The stratum in front of the pipe-jacking tunnel face was a semi-infinite body of homogeneous isotropy; 3) The influence of the top pipe digging speed and the friction action between the cutter and the tunnel face were not considered.

Based on the above assumptions, the tunnel face support pressure calculation model can be constructed, as shown in Figure 2(b). The static soil pressure at the point of action of the ground pressure at the tunnel face was used as a datum. Soil and water sub-calculation was adopted and the calculation of the optimal value of the tunnel face support pressure can be obtained as shown in Equations (8) and (9).

$\begin{array}{c}{\mathrm{P}}_{\mathrm{o}1}={[\mathrm{K}}_0{\mathsf{\gamma }}_s\left({\mathrm{H}}_{\mathrm{a}}+{\mathrm{H}}_{\mathrm{w}}\right)+{\mathsf{\gamma }}_{\mathrm{w}}{\mathrm{H}}_{\mathrm{w}}]\pi {\mathrm{D}}^2/4\left(8\right)\end{array}$

$\begin{array}{c}{\mathrm{P}}_{\mathrm{o}2}=[{\mathrm{K}}_0{\mathsf{\gamma }}_s\left({\mathrm{H}}_{\mathrm{b}}+{\mathrm{H}}_{\mathrm{c}}\right)+{\mathsf{\gamma }}_{\mathrm{w}}{\mathrm{H}}_{\mathrm{r}}]\pi {\mathrm{D}}^2/4\left(9\right)\end{array}$

Where: ${\mathrm{P}}_{\mathrm{o}1}$ was the optimal support pressure for the tunnel face in the area without river water influence, kPa; ${\mathrm{P}}_{\mathrm{o}2}$ was the optimal support pressure for the tunnel face in the area with river water influence, kPa; ${\mathrm{K}}_0$ was the static earth pressure coefficient; ${\mathsf{\gamma }}_{\mathrm{w}}$ was the volumetric weight of water, kN/m³; ${\mathrm{H}}_{\mathrm{a}}$ was the distance from the underground-water level to the ground surface, m; ${\mathrm{H}}_{\mathrm{b}}$ was the depth of burial of the pipe-jacking, m; ${\mathrm{H}}_{\mathrm{c}}$ was the distance from the point of ground pressure action on the tunnel face of the pipe-jacking to the top axis of the digging machine (which took the value of 2/3D), m; ${\mathrm{H}}_{\mathrm{r}}$ was the river depth, m; ${\mathrm{H}}_{\mathrm{w}}$ was the distance from the point of soil pressure action to the underground-water level, m.

3. Numerical Simulation and Analysis of Support Pressure on Tunnel Face

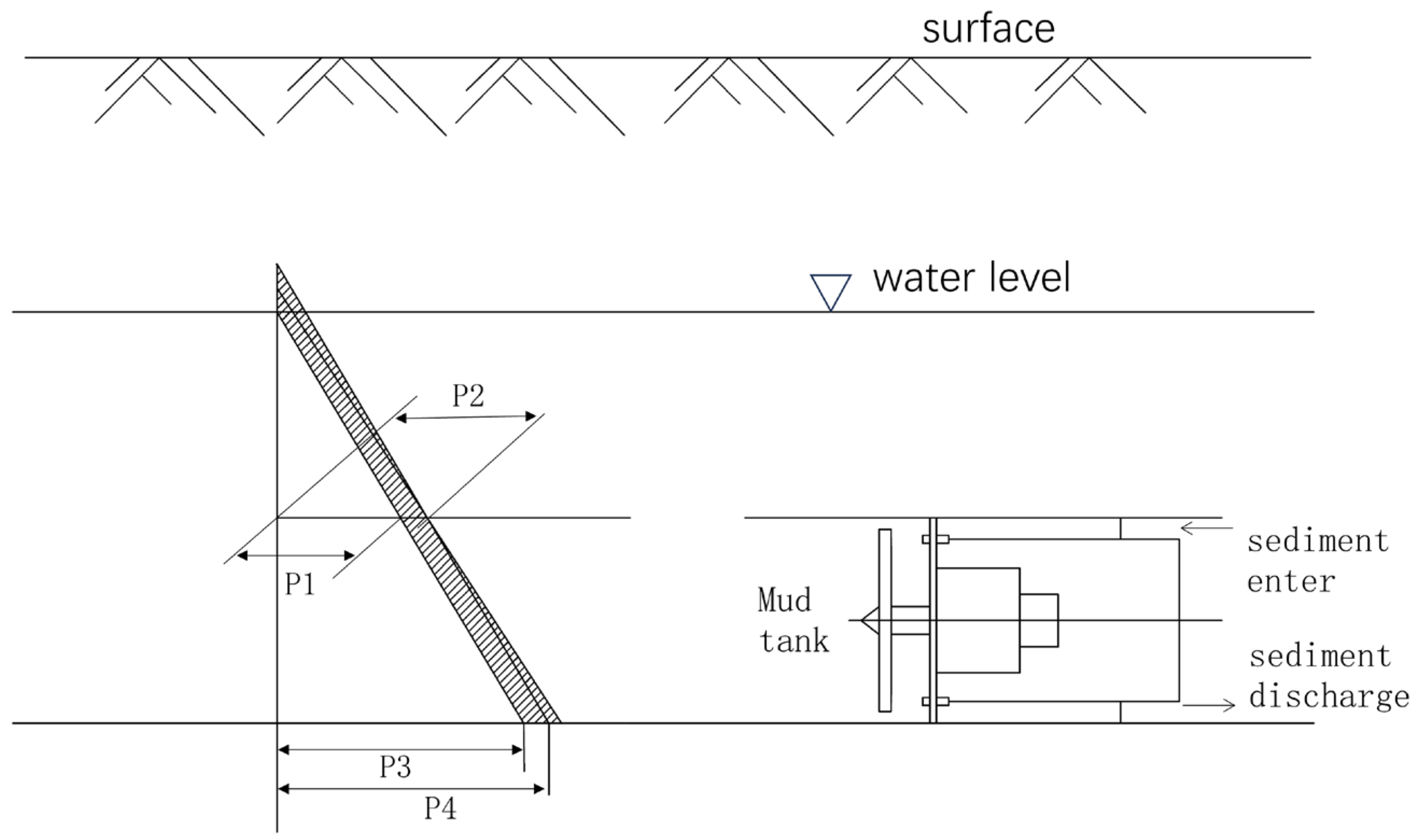
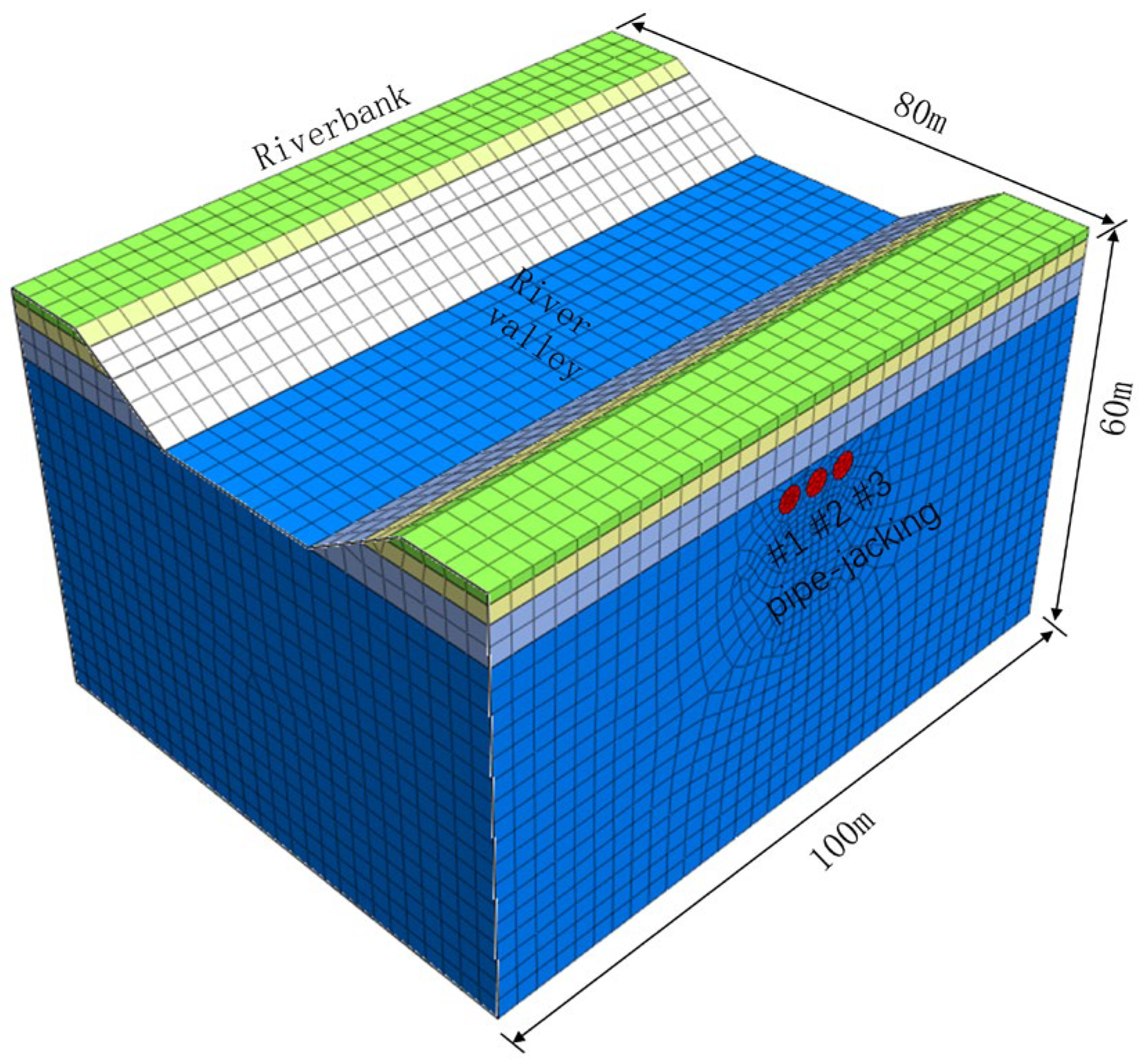
3.1. Simulation Model and Basic Assumptions

The numerical simulations were carried out in close connection with the actual situation of the relying projects. The length, width and height of the numerical simulation model were taken as 100m×80m×60m, as seen in Figure 5. The bottom surface of the model was constrained with vertical and horizontal displacements, while the top surface was free. The pipe-jacking was constructed using three circular reinforced concrete pipes with an internal diameter of 3.0m and an external diameter of 3.6m. The spacing between two neighboring pipes was 2.8m, and the length of pipe-jacking excavation was 80m. The reinforced concrete pipe sheet was considered as an elastic material with a thickness of 0.3m. The pipe-jacking machine casing was made of steel, which was also considered to be an elastic material. The values of the calculated parameters were taken as shown in Table 1. The material properties of the strata and pipe joints were used as 3D cell entities. Partial components were meshed by geometric partitioning and then expanded with a 2D mesh. The pipe perimeter grid was 0.5m. The model boundary calculation cell grid was set to 1.0 m in both longitudinal and transverse directions. The pipe-jacking machine shield shell was modeled elastically and its material property was belonged to 2D plate cells, which were meshed by analyzing the outer surface of the iso-surrogate layer. The values of the stratigraphic parameters were taken as shown in Table 2.

The pipe-jacking construction formed a boundary inside the formation and changed the original stress field of the formation, which led to a series of complex physical and mechanical effects in the formation around the construction area. This was not only related to the physical properties of the formation, but also closely related to the construction method, construction process and related construction parameters. When using numerical software for three-dimensional calculation of multi-line parallel pipe-jacking construction, it was difficult to take all the factors of pipe-jacking construction into account to reflect the construction process completely and realistically. Therefore, the mechanical behavior related to pipe-jacking construction was appropriately simplified when performing numerical simulations. This can make it not only meet the requirements of the software for calculation, but also make the numerical calculation results better reflect the construction process and reveal the regularity of the construction impact. Based on the actual situation of the relying project, the numerical simulation had the following assumptions:

1) Each stratum was assumed to be ideally elastoplastic; The numerical simulation model only considered the soil settlement caused by self-weight and pipe-jacking construction, and ignored the effects of underground-water as well as consolidation settlement of the soil;

2) It was assumed that the soil pressure was considered as a circular distributed load acting on the tunnel face; It was assumed that the gap grouting units around the perimeter of the pipe were distributed in equal thicknesses along the radial direction of the pipe sheet (the modulus of elasticity was taken as 1/50 of the in-situ stratigraphic unit, and the thickness of the grouted iso-surrogate layer was 2cm.); Friction between the pipe and soil was achieved by setting a coefficient of friction on the contact surface(the friction between the pipe and soil was a certain value and was uniformly distributed along the pipe-jacking direction.); The model was assumed to ignore the effect of grouting pressure on the construction process and the joints between pipe joints; The jacking pressure was taken from the lateral static soil pressure at the center point of the pipe’s tunnel face, and its value was taken as 88.5kPa; The friction between the pipe and soil was taken as 3.5kPa.

The previous study[36] by our team used strength reduction and numerical simulation methods. This study analyzed in detail the stability of the surrounding strata unloaded by pipe-jacking construction under different water depths, overburden thicknesses and clearances. The surrounding strata were divided into the mutual influence nonself-stability zone, the mutual influence self-stability zone, and the no mutual influence self-stability zone. The assumptions of the numerical simulation and the specific simulated construction conditions in this paper were consistent with those of [36], so they were not described in detail.

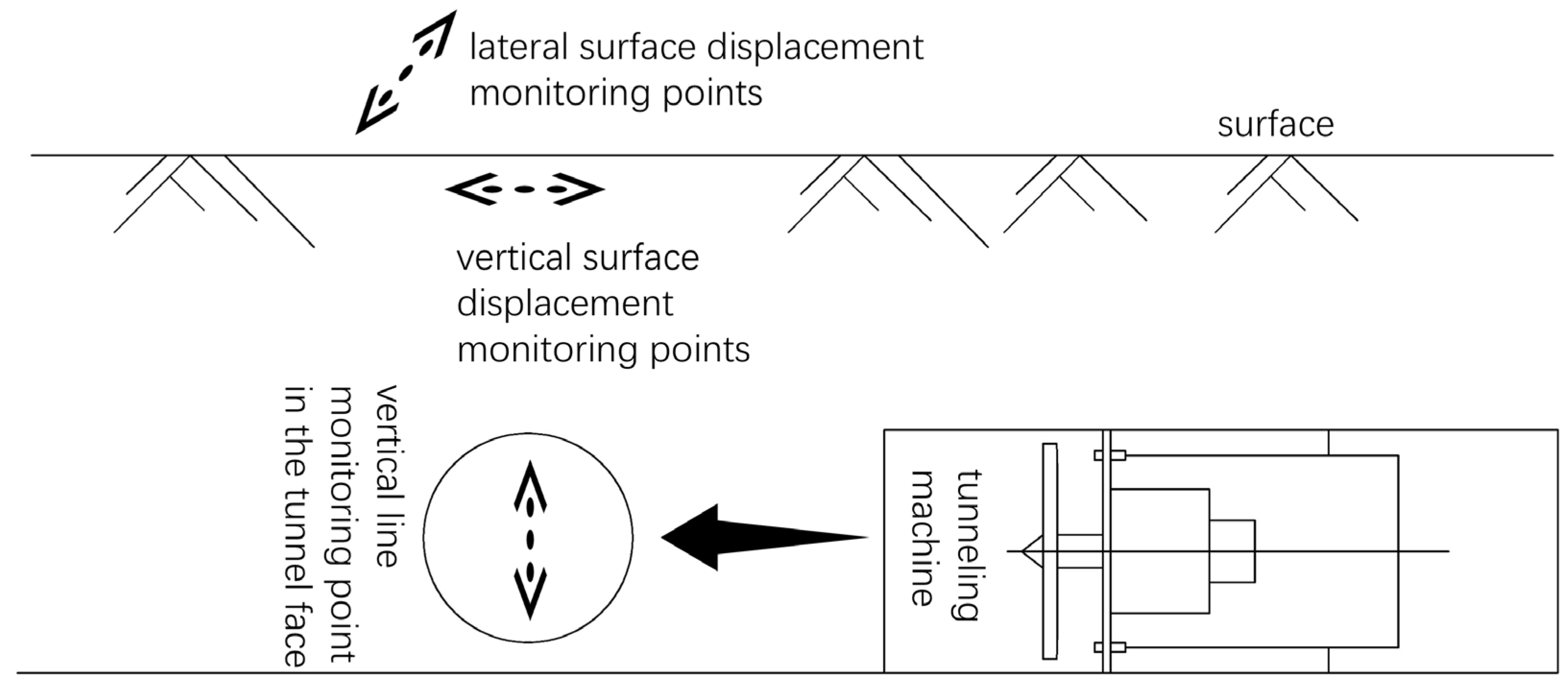
3.2. Simulation Conditions and Implementation Steps

Numerical simulations were directed at analyzing the river bottom cross section. In order to investigate the effect of overburden thickness on the support pressure, the river bottom section conditions were categorized into three conditions: The overburden thickness of 3m was considered as Case Ⅰ, the overburden thickness of 2m was considered as Case Ⅱ, and the overburden thickness of 1m was considered as Case Ⅲ. The theoretical values of the tunnel face support pressures calculated were applied, as shown in Table 3.

To explore the variation characteristics of the support pressure in the tunnel face, the support pressure ratio coefficient $\mathsf{\lambda }$ of the tunnel face was adopted, as demonstrated in equation (10).

$\begin{array}{c}\lambda ={\displaystyle \frac{{\mathsf{\sigma }}_{\mathrm{s}}}{{\mathsf{\sigma }}_0}}\left(10\right)\end{array}$

Where:$\mathsf{\lambda }$ is the support ratio of the support pressure at the tunnel face of the pipe-jacking; ${\mathsf{\sigma }}_{\mathrm{s}}$ was the support pressure at the center point of the pipe-jacking tunnel face, kPa; ${\mathsf{\sigma }}_0$ was the soil and water pressure at the center point of the pipe-jacking tunnel face, kPa.

Displacement monitoring points were arranged on the center vertical line of the tunnel face, on the ground surface along the lateral and vertical line, as depicted in Figure 6.

Mud-water balancing pipe construction was a step-by-step process. To simulate dynamic construction that matched reality, step-by-step excavation was used. The effect of the jacking force on the disturbance of the soil in front of the tunnel face was considered. The numerical simulation calculation process was as follows:

1) The basic numerical model was established. Material properties were assigned and corresponding displacement boundary conditions were imposed. Ground stress equilibrium calculations were performed under initial stress conditions, which were designed to simulate the initial ground stress state;

2) Support pressure equal to the resistance applied in front of the tunnel face was set. The next step was to simulate the disturbance caused by the jacking to the strata ahead until steady state was reached;

3) The pipe-jacking will be excavated to the bottom of the river channel according on actuality construction. The soil was removed and the pipe support structure was activated. At the same time, an excavation process can be completed by setting up a support pressure applied on the tunnel face;

4) The overall deformation of the tunnel face and the displacement changes at the corresponding monitoring points were observed and recorded;

5) According to the support pressure ratio $\mathsf{\lambda }$, the magnitude of the mud-water pressure applied at the center point of the tunnel face was altered. Re-excavation calculations were carried out and the overall deformation of the tunnel face as well as the displacement changes at the corresponding monitoring points were observed and recorded.

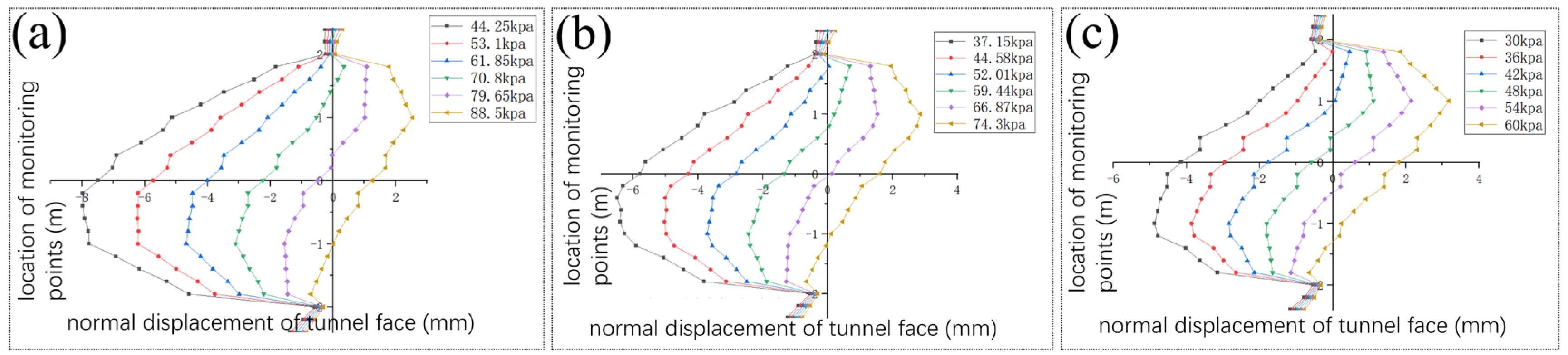
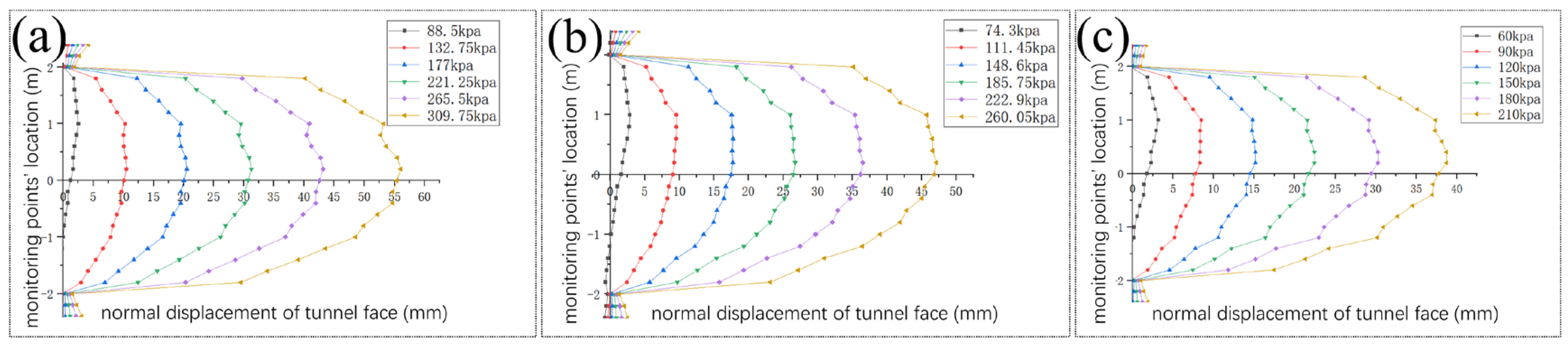
3.3. Analysis of Calculation Results

For investigating the effect of overburden thickness on the support pressure at the tunnel face under the river, the support ratio $\mathsf{\lambda }$ was taken as 0.5, 0.6, 0.7 0.8, 0.9, 1.0 and 1.5, 2.0, 2.5, 3.0, 3.5 in that order. The total of 11 working conditions was shown in Table 4.

As can be seen in Figure 7: when the river overburden was 3m, the applied pressure was obtained from the calculation of the theoretical tunnel surface support pressure decreasing, the normal displacement of the tunnel face gradually increased. When $\mathsf{\lambda }$=1.0~0.9, the tunnel face was slightly concave towards the soil. The displacement change was not significant and can be considered to satisfy the equilibrium stabilization requirements. As the support pressure continued to decrease to the active soil pressure ($\mathsf{\lambda }$ changed from 0.9~0.6), the tunnel face displacement showed an approximately linear increasing trend with decreasing support pressure. The tunnel face gradually bulged towards the digging machine and the surrounding soil slipped and failed. When the river channel overburden was 2m and when the river channel overburden was 1m, the trend was the same as when the river channel overburden was 3m. However, as the thickness of the overburden decreases, the displacement of the soil monitoring points caused by the active support pressure continued to increase. When ${\mathrm{H}}_s$=3m, the maximum normal displacement of the tunnel face was -8mm; When ${\mathrm{H}}_s$=2m, the maximum normal displacement of the tunnel face was -6.5mm; When ${\mathrm{H}}_s$=1m, the maximum normal displacement of the tunnel face was -5mm.

As seen in Figure 8: When the river overburden was 3m, the support pressure exerted on the tunnel face increased from static soil pressure to passive soil pressure. The trend was the same as when the river channel overburden was 2m and when the river channel overburden was 1m. The displacement of the tunnel face along the soil direction was increasing. However, as the thickness of the overburden decreased, the displacement of the soil monitoring points caused by the passive support pressure continued to decrease. When ${\mathrm{H}}_s$=3m, the maximum normal displacement of the tunnel face was 56mm; When ${\mathrm{H}}_s$=2m, the maximum normal displacement of the tunnel face was 47mm; When ${\mathrm{H}}_s$=1m, the maximum normal displacement of the tunnel face was 38mm.

As illustrated in Figure 9: according to the calculation results, the calculated ultimate support force was 86.63kPa when the river channel overburden was 3m (86.63kPa multiplied by the area of the tunnel surface πD²/4 was 881.786kN); The calculated ultimate support force was 83.03kPa when the river channel overburden was 2m (83.03kPa multiplied by the area of the tunnel surface πD²/4 was 845.142kN); The calculated ultimate support force was 50.81kPa when the river channel overburden was 1m (50.81kPa multiplied by the area of the tunnel surface πD²/4 was 517.183kN). This support force can control the position of the tunnel face to keep in the best condition. Based on the above results, it can be seen that when the thickness of the channel overburden was decreasing, the support force of the excavation surface to reach the optimal stabilization state was decreasing. From Figure 9, it can be seen that the optimal support force was taken in the interval of $\mathsf{\lambda }$=1.0~1.5 when ${\mathrm{H}}_s$=3m; The optimal support force was taken in the interval of $\mathsf{\lambda }$=0.9~1.0 when ${\mathrm{H}}_s$=2m; The optimal support force was taken in the interval of $\mathsf{\lambda }$=0.8~0.9 when ${\mathrm{H}}_s$=1m. This would indicate that when the overburden thickness was small, the support pressure would need to be set at a reduced support ratio; The support ratio would need to be increased when the overburden thickness was thick.

4. Engineering Case Study

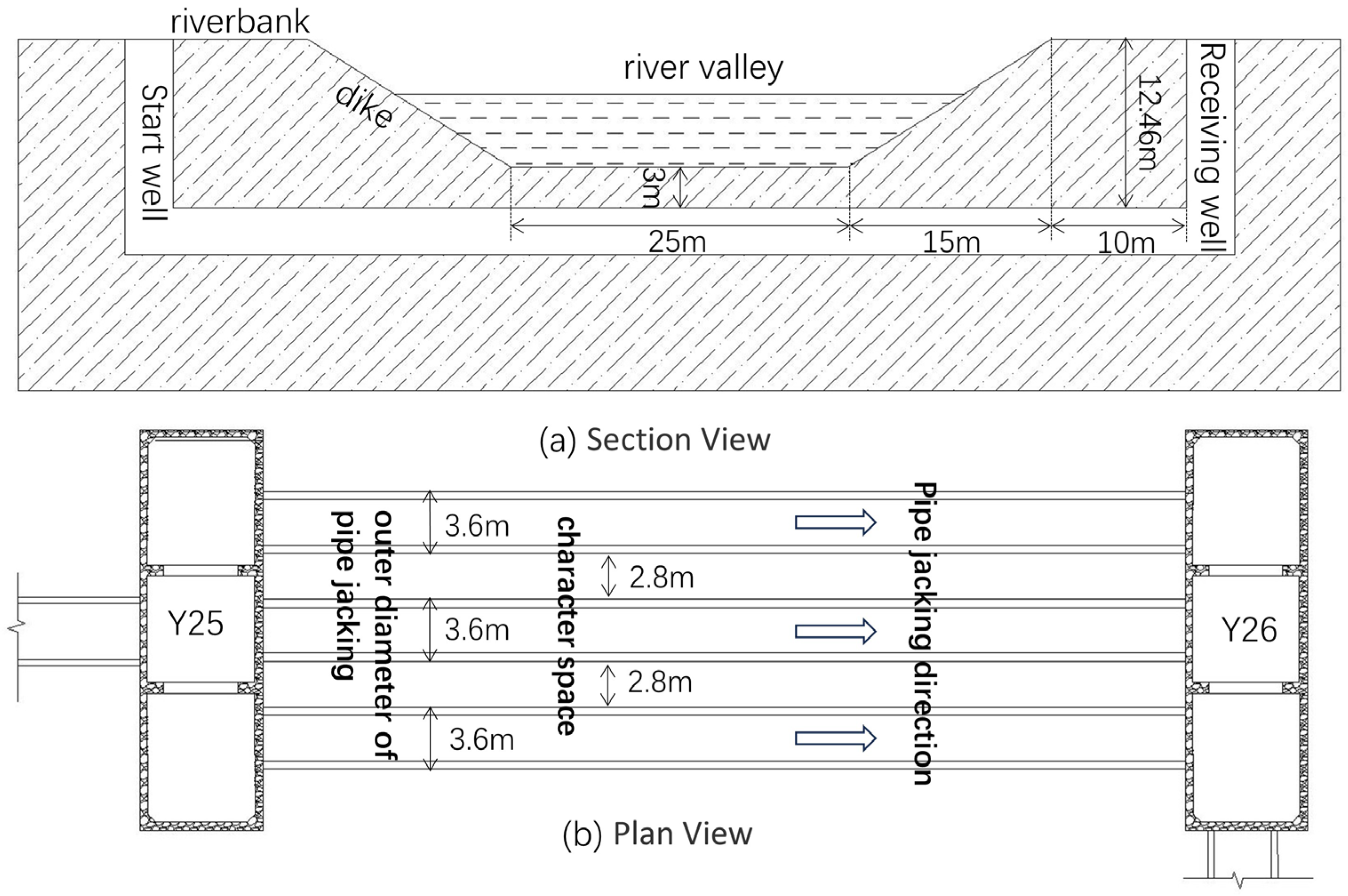
4.1. Engineering Background

The project of pipe-jacking across the Chu River channel was located in Shuangdun Town, Changfeng County, Hefei City, Anhui Province. The project site belonged to the Jianghuai undulating plain landform, with a micro landform of hills and valleys. The geotectonic location of the region belonged to the southern edge of the North China Plateau, and the secondary tectonic unit belonged to the Hefei Basin. The stratigraphic distribution from top to bottom was as follows: Filling soil, 0.5 to 1.5m thick; Silty chalky clay, 1.2 to 2.7m thick; Clay, 5.9 to 7.5m thick; Silty clay, 4.8 to 6.0m thick; Strongly weathered mudstone, 1.7 to 2.6m thick. The physical and mechanical parameters of each stratigraphic layer were shown in Table 2.

The project of Y25-Y26 working well crossing Chu River channel adopted mud-water balance mechanical pipe-jacking construction. The pipe-jacking crossed the stratum of silty clay, and the thickness of the pipe-jacking cover layer was 3.0m. The width of the river valley in the section where the pipeline crosses was 55m, the width of the river bed was 25m, the height of the river bank was 9.46m, and the average depth of the river water in the dry season was about 3.0m. The pipe-jacking was composed of three circular reinforced concrete pipes with an internal diameter of 3.0m and an external diameter of 3.6m. The sandwich width of two adjacent pipes was 2.8m. The project had remarkable features such as high environmental requirements, small thickness of overburden, and large diameter of pipe-jacking. Controlling the stability of the pipe-jacking tunnel surface was the priority of engineering control. The section and plan view of the portion where the pipe-jacking crossed the river were shown in Figure 10.

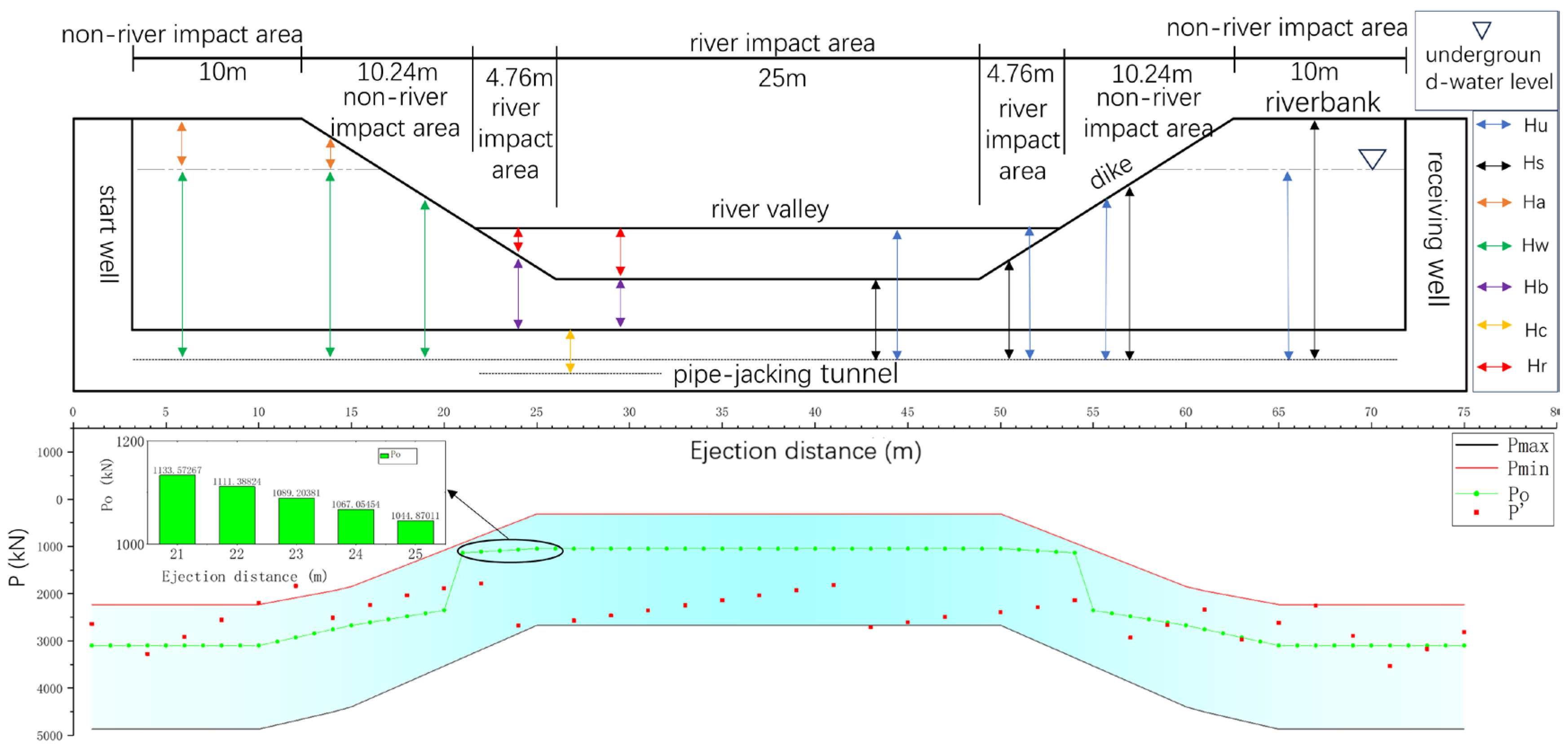
4.2. Comparative Analysis of Engineering Effect and Discussion

Combined with the project of Y25-Y26 pipe-jacking construction crossing Chu River channel in Hefei North City, and according to the theoretical formulas (5), (7), (8) and (9), the upper limit value P_max, lower limit value P_min, and optimal value P_o, of the support pressure of the tunnel face under different jacking distances were calculated, as shown in Table 5. Table 6 presented the measured values of the tunnel face support pressures obtained by testing during the jacking process of the project. Since the upper limit, lower limit and optimal values of the support pressure on the tunnel face during the jacking distance of the pipe-jacking from 50m to 75m were the same as those for the jacking distance from 25m to 1m, they were not shown in detail in Table 5. For more direct and graphic depiction of the variation of different support pressure values at different jacking distances, we combined a simple model of the project to produce pictures corresponding to Table 5 and Table 6, as shown in Figure 11.

In Figure 11, according to the principle of optimal value calculation, the jacking area was divided into non-river impact area (from 0m-20.24m and from 54.76-75m) and river impact area (from 20.24m-54.76m). The underground-water level was -3m from the surface of the riverbank. The construction stratum was located in a silty clay layer and ${\mathrm{K}}_0$ was the static soil pressure coefficient taken as 0.7. The heights described by H_a, H_b, H_c, H_r, H_s, H_u, H_w in the above equation were also given in the upper part of Figure 11. The dimension of the simple model of the project in the upper half of Figure 11 was kept the same as the length of the jacking in the bottom half of the figure. The bottom half of Figure 11 described the upper limit value P_max, the lower limit value P_min, the optimal value P_o, and the measured value P’ of the support pressure in the tunnel face for different jacking distances. A partial enlargement of the optimum value during the jacking distance from 20.24m to 25m was also given.

The change rules of upper limit value P_max, lower limit value P_min and optimal value P_o of palm face support pressure were basically the same: the jacking distance from 0m-10m (non-river impact area), the value of the support pressure was constant in size, respectively 4868.249kN, 2230.598kN, 3098.977kN; The value of the support pressure decreased for jacking distances from 10m to 25m; The jacking distance from 25m to 50m (river impact area), the value of the support pressure was also constant, respectively 2669.977kN, 309.910kN and 1044.870kN. But there were some differences between the three: when the jacking distance of the pipe-jacking exceeded the intersection of the underground-water level line and dike line, the decrease rate of the upper limit value of the support pressure P_max and the lower limit value P_min increased, while the optimal value P_o did not change significantly. When the jacking distance of the pipe-jacking was greater than 20.24m (form non-river impact area into river impact area), the optimal value of the palm face support pressure, P_o, changed abruptly with decreasing from 2351.527kN to 1133.573kN, while there was no significant change in the upper limit value, P_max, and the lower limit value, P_min. In the process of pipe jacking distance from 20.24m to 25m, the rate of decrease of the optimal value P_o showed a linear decreasing law. Each decrement was approximately 22.5kN, which was reflected in the partial enlargement in the upper left corner of the bottom half of the graph in Figure 11. The overburden thickness was 3m during the jacking distance from 25m to 50m. In section 3.3 the numerical simulation calculated the ultimate support pressure as 881.786kN, while the optimal value of the support pressure at the palm face was 1044.87kN. Such results were relatively similar. It can be seen in Figure 11 that the measured value of the palm face support pressure, P’, fluctuated between 1700kN and 3600kN. The measured value P’ basically lied between the upper limit value P_max and the lower limit value P_min, and was most similar to the optimal value P_o in the non-river impact area and to the upper limit value Pmax in the river impact area.

The measured value of the support pressure P’ on the palm face of the was between the upper limit value P_max and the lower limit value P_min, which can ensure that the pipe-jacking jacking construction will not have active and passive damage. This would be more economical and reasonable if the measured value of the palm face support pressure P’ was close to the optimum value P_o. During the mud-water balanced pipe-jacking construction, the jacking machine adopted a mud-water balancing device to ensure the balance of water and soil pressure on the palm face. Theoretically, if the palm face support pressure and the resistance were kept in equilibrium during the jacking construction process, the impact of the pipe-jacking frontal propulsion on the deformation of the stratum would not be generated. However, in the actual jacking construction process, due to the complexity of geological conditions, limitations of mechanical equipment and other factors, it is difficult to always maintain a balanced state between the support pressure and resistance of the palm face in pipe jacking construction. Therefore, the support pressure at the palm face can be set within a reasonable range between the upper limit value P_max and the lower limit value P_min.

5. Conclusions

The support pressure at the palm face during mud-water balance pipe jacking construction was an important construction control parameter. If the support pressure was not set properly, it would cause stratum displacement or palm face collapse, which would bring great safety hazards to the pipe-jacking construction. In this paper, the support pressure on the palm face of pipe--jacking construction under the conditions of thin overburden, mud-water balance, and crossing the river channel was studied in depth, and the following conclusions were obtained:

(1) The damage mechanism of the palm face of the pipe-jacking under the conditions of thin overburden, mud-water equilibrium, and crossing the river was undertaken. Mathematical expressions for the lower and upper limit values of the palm face support pressure, P_min and P_max, were derived from the passive and active damages occurring at the palm face of the pipe tunnel in conjunction with the limit equilibrium method. The jacking area was divided into non-river impact area and river impact area. The mathematical expressions for the optimal values of the support pressures P_o1 and P_o2 for the two areas were also given separately.

(2) By relying project Y25-Y26 pipe-jacking crossing the Chu River in Hefei North City and through numerical simulation, the displacement and ultimate support pressure of the palm face under different river overburden and different support ratios were discussed: as the thickness of the overburden decreased, the displacement of the soil monitoring points caused by the active support pressure continued to increased while the displacement caused by the passive support pressure continued to decrease. When large-diameter pipe-jacking crossed the river channel, if the overburden thickness was small the setting of the support pressure needed to reduce the support ratio, while the support ratio would need to be increased if the overburden thickness was large. The optimal support force was taken in the interval of $\mathsf{\lambda }$=1.0~1.5 when ${\mathrm{H}}_s$=3m; The optimal support force was taken in the interval of $\mathsf{\lambda }$=0.9~1.0 when ${\mathrm{H}}_s$=2m; The optimal support force was taken in the interval of $\mathsf{\lambda }$=0.8~0.9 when ${\mathrm{H}}_s$=1m.

(3) During the construction of pipe-jacking crossing the thin-covered river channel, the theoretically calculated upper limit value of the support pressure P_max, lower limit value P_min, optimal value P_o, and the numerical simulation calculated limit values were 2669.977kN, 309.910kN, 1044.870kN, and 881.786kN, respectively. The measured value during pipe-jacking construction fluctuated between the upper limit value P_max and the lower limit value P_min. It was more similar to the optimal value P_o in the non-river impact area and more similar to the upper limit value P_max in the river impact area. For overcoming the complexity of geological conditions, limitations of mechanical equipment and other factors to ensure the stability of the palm face without damage, it would be necessary to set the palm face support pressure in a reasonable range between the upper limit value P_max and the lower limit value P_min, and it suggested to adopt the optimal value P_o.