1. Introduction
Pattaya, Thailand is one of the most popular destinations for many people. Its economy is dependent on both tourism and business. Its beautiful beach, temple, museums, botanic garden, and nightlife activities attract Thai and foreign tourists to visit repeatedly. Pattaya is a part of the Eastern Economic Corridor (EEC), a major economic development zone in Thailand. The EEC is expected to bring about foreign investment and create several jobs. Accordingly, Pattaya’s economy is bustling, and the demand for accommodation is high.
Renting a condominium in Pattaya is an interesting alternative for many people. On the demand side, the tourists who come to visit the city for a short period, the workers who receive companies’ accommodation allowance or have not decided to permanently settle down, etc. should prefer renting the condominium. On the supply side, many investors find that the investment in real property in Pattaya is interesting as they can rent the property and wait for gain from price appreciation as suggested by the Sing (2001)’s study. Real Estate Information Center (2024) reports that in the first quarter of 2024, 36,471 units of condominiums in Pattaya have been sold and 4,493 units of new condominium have been offered. Pattaya’s total supply for condominium from 2011 to the first quarter of 2024 totals 112,671 units.
Knowing appropriate rental prices is crucial for investors, tenants, developers, and policymakers. For instance, investors can avoid loss by setting rental prices that are too low. Tenants would not have to pay too expensive price. Developers could use the price data to set the selling price and analyze the feasibility for the condominium project. Policymakers can use the price data to set a fair tax rate or optimize land use via zoning.
However, traditional valuation methods, such as regression pricing models, often have limitations in capturing complex and nonlinear relationships in real estate markets [
1,
2]. This has prompted the adoption of advanced techniques like Artificial Neural Network (ANN) for more accurate and reliable predictions. ANN can manage intricate dependencies and interactions between multiple variables, offering a more precise understanding of price determinants [
3,
4,
5].
This research aims to explore the factors affecting condominium pricing in Pattaya, Chonburi province in Thailand using ANN. The study seeks to identify the key determinants of condominium prices that are accessible to most people. They include distance to the beach, property size, building age, number of bedrooms, number of bathrooms, floor level, duplex or ordinary condominium, and sea view. The comparison of the results from ANN with the regression model can highlight the advantages of ANN in analyzing the complex relationship in real estate pricing. Understanding these factors and their interactions will provide valuable insights into the Thai condominium market, enabling more accurate price predictions and offering practical contributions to market participants.
In the following sections, we will review the relevant literature on rental price prediction models, describe the methodology employed in this study, present the results of the ANN model, and discuss the implications of the findings for the real estate market in Pattaya.
2. Literature Reviews
The prediction of rental prices in real estate markets has been a topic of significant research interest for decades. As property markets evolve, particularly in dynamic regions like Pattaya, Thailand, the need for more sophisticated and accurate predictive models has become apparent. This chapter reviews the relevant literature on rental price prediction, with a focus on traditional and contemporary approaches, including the use of Artificial Neural Network (ANN). The review begins by exploring the studied factors affecting property price and rental price. Next, the conventional methods for rental price prediction, followed by a discussion of machine learning applications in real estate and concludes with the specific use of ANN for price prediction. Then, the last section is the review of previous studies relating to the factors affecting the residential property price and rental price.
2.1. Determinants of Property Price and Rental Price
Numerous studies have examined the factors that influence rental prices across various cities and regions. In Guangzhou, China, key determinants of rental prices include the administrative district, rental type, house size, and floor level [
6]. Similarly, in Madrid, Spain, apartment size and capacity play a significant role in shaping short-term rental price [
7].
In Istanbul, Turkey, tenants prioritize factors such as green spaces, scenic views, access to facilities, neighborhood relationships, and proximity to shopping centers when evaluating rental property values [
8]. A broader study by Sirmans (1991) [
9] identifies property age, amenities, services, physical attributes, and location as the main drivers of rental prices. Additionally, duplex units, which provide more space and unique layouts, tend to command higher rental rates. In contrast, in Japan, rental prices decrease as buildings age [
10].
The number of bedrooms and bathrooms is also positively associated with short-term rental prices, as these features enhance tenant comfort and convenience [
7] . A study in Pune, India, highlights that floor area and the number of rooms significantly impact rental prices. However, properties located near employment hubs, schools, colleges, and transportation networks tend to have lower rental values due to increased congestion and noise levels [
11].
In the Accra Metropolitan Area of Ghana, research has found that rental prices are primarily influenced by location, the availability of amenities and facilities, and the number of bedrooms [
12].
Collectively, these studies demonstrate that rental prices are shaped by a combination of property attributes, location, and access to amenities, although the specific influence of each factor varies across different markets.
2.2. Traditional Approaches to Real Estate Price and Rental Price Prediction
The traditional statistical methods such as hedonic pricing models, autoregressive integrated moving averages, and multiple linear regression (MLR) have been applied to predict the rental price of real estate. The prediction factors include a set of measurable attributes including property size, location, and number of rooms. The different methods are listed below:
2.2.1. Hedonic Pricing Models
The hedonic pricing model by Rosen (1974) [
13] is one of the most applied approaches in real estate price estimation. The price of a property can be estimated by summing its individual characteristics. The rental price is affected by independent variables such as floor level, age of building, and accessibility to public transportation. This approach has a limitation in terms of linear relationships of variables required.
2.2.2. Time Series or Autoregressive Integrated Moving Averages (ARIMA)
ARIMA is the model that Box and Jenkins (1970) [
14] initiated to apply the time series data in the forecasting approach. It is considered a foundation in time series modeling. To predict the rental price, the historical rental price data is used to capture trend and seasonality.
2.3. Machine Learning Approach
Machine Learning has a better ability to deal with nonlinear relationships of variables and manage large datasets than traditional modeling. These are some examples of the machine learning approach.
2.3.1. Support Vector Machines (SVMs)
It is applied for classification and regression tasks. This is a model of a supervised machine-learning algorithm used for classification, regression, and outlier detection tasks [
15]. SVMs can deal with non-linear relationships by transforming the data into higher dimensions using kernel functions such as polynomial, and radial basis functions. However, this method has limitations in terms of interpretation difficulty for higher dimensions data, less efficiency for large datasets, and careful selection of hyperparameters.
2.3.2. Gradient Boosting Machines (GBMs)
Gradient Boosting Machines (GBMs) are a sophisticated ensemble learning technique designed to build predictive models incrementally. By combining the outputs of multiple weak learners, typically decision trees, GBMs iteratively reduce prediction errors. At each step, the algorithm focuses on addressing the residual errors from prior iterations, enabling it to effectively model complex, non-linear relationships between variables [
16]. This approach has some limitations including the slow training of machine learning especially in large datasets and careful tuning of hyperparameter [
16,
17].
Although these machine learning models provide greater accuracy compared to traditional approaches, their effectiveness relies significantly on the quality of the data and the choice of features. Additionally, they may face challenges in handling the intricate, nonlinear relationships often observed in real estate markets. As a result, there has been a growing shift toward the adoption of more advanced models, such as Artificial Neural Networks (ANN) .
2.4. Artificial Neural Networks (ANN)
An Artificial Neural Networks (ANN) are inspired by the biological neural networks in the animal brain to develop computational models. It is the model to simulate the way humans learn by interpreting patterns and features in data. ANN have the capabilities to model complex relationships between inputs and outputs, thus they are widely applied to various activities for instance natural language processing, image recognition, and predictive modeling [
18,
19].
Artificial Neural Networks (ANN) have garnered considerable attention in predictive modeling due to their capacity to capture complex, nonlinear relationships and learn from large datasets. ANN are inspired by the human brain's neural architecture and consist of interconnected nodes (neurons) organized in layers, allowing them to process input data and produce highly accurate predictions [
20].
Artificial Neural Networks (ANN) are composed of interconnected components that work collaboratively to process and interpret data. Neurons, or nodes, serve as the basic units of the network, responsible for receiving, processing, and transmitting information. These neurons are structured into layers, beginning with the input layer, which accepts the raw data, followed by one or more hidden layers where computations and pattern recognition take place, and concluding with the output layer that provides the final predictions or outcomes. Weights and biases are adjustable parameters that optimize the model by minimizing errors during training. Activation functions are employed to introduce non-linear transformations, which allow the network to model complex relationships and learn intricate patterns in the data. These elements collectively make ANN versatile and powerful tools in various domains, including predictive modeling, natural language processing, and image recognition [
20,
21,
22].
The primary advantage of ANN lies in their ability to model complex, nonlinear interactions between independent variables and the dependent variable (Lecun et al., 2015). This makes them particularly well-suited for rental price prediction in dynamic markets like Pattaya, where various factors interact in unpredictable ways. Unlike traditional linear models, ANN do not require explicit specification of the relationship between variables, allowing the model to automatically learn these relationships from the data. ANN also can be adapted to various data types [
23,
24,
25].
While ANN provide excellent predictive performance, they are not without challenges. One of the main drawbacks is their "black box" nature, which makes it difficult to interpret how the model arrives at its predictions. This lack of interpretability can be problematic in the real estate industry, where stakeholders may require transparent models for decision-making. Additionally, ANN require large amounts of data and are computationally intensive, which can be a barrier in markets where high-quality data is limited [
26,
27,
28].
2.5. Application of ANN in Real Estate Price and Rental Price Prediction
Borst (1991) [
29] was one of the pioneers to demonstrate that ANN has reliability in predicting property values. McGreal et al. (1998) [
30] identified the superior predictive accuracy of ANN in predicting property sales data compared to the traditional valuation methods. ANN outperform multiple regression analysis in predicting housing prices especially in capturing non-linear relationships among variables [
27,
31].
Selim (2009) [
32] used an ANN to predict housing prices in Istanbul, Turkey, showing that the ANN model outperformed traditional regression models in accuracy. Similarly, ANN models was applied to real estate price prediction in Taiwan, with promising results (Lin,2011) [
33]. In both cases, the ANN's ability to capture nonlinear patterns in the data was a key factor in its superior performance.Several studies have demonstrated the effectiveness of ANN in real estate price prediction, ANN have also been increasingly employed in real estate markets for predicting rental prices, owing to their capacity to process large datasets and capture complex relationships between variables. While their application to rental price prediction is still an emerging area, several notable studies have demonstrated the effectiveness of ANN in this domain [
25,
34,
35].
The application of neural networks for pricing prediction in the Australian market identified location and size as the most influential factors on condominium prices [
36] (Peterson and Flanagan, 2009). ANN also can be combined with fundamental forecast to understand the housing price trends [
37]. The study of properties price in Hong Kong identified that three most important variables include interest rate, unemployment, and household size. The study also confirmed the outperformance of ANN over SVM and ARIMA [
38].
The estimation of residential property rental prices in Australia utilized factors including location, number of bedrooms, age of the building, and proximity to public transport using the ANN model [
39]. The study of the housing rental price in Taipei used by the size, number of floors, pet-friendly allowance, and permissibility of restaurant operation. The employing of ANN provides effective estimation of rental price with reliability and accuracy [
40].
Mohd Tahir et al. (2019) [
35] explored the residential rental price in Malaysia using ANN model by incorporating property features such as size, type of property, location, and surrounding infrastructure as the predictors. The study pointed out the benefit of ANN over the multiple regression models in terms of prediction accuracy and also flexibility in processing various input data. The study in Japan compared the accuracy of Deep Neural Networks (DNN) and Kringing methods to set apartment rent prices in Japan. The results confirm the effectiveness of DNNs as a rental prediction tool [
41] .
ANN model was also studied in short-term rentals prediction such as Airbnb. The study of [
42] Liu (2021) used independent variables including user ratings, number of reviews, location, size, and seasonal demand trends. The results indicated the ability of ANN to capture the fluctuations in rental demand, to incorporate with non-traditional variables such as customers’ reviews.
The previous studies of real estate prices and rental price predictions using ANN highlight the effectiveness and superiority of ANN over other techniques especially with a non-linear relationship between predictors and rental prices, and with large datasets.
3. Methodology
3.1. Data Collection
This study’s population is condominiums for rent in Pattaya. A sample of the condominiums is randomly gathered from FazWaz’s website, one of Thailand’s leading platforms serving as a marketplace for real estate in Thailand and ranked in the top 5 real estate agents in Thailand [
43]. The data collected on June 15, 2023, a snapshot of 1050 condominiums for rent available on that date. The incomplete data set was removed, and 983 condominium data was left for the study.
3.1. Variables
The dependent variable for the study is the rental price per square meter (RENT). The key independent variables are applied from previous studies including age of building [
6,
7], number of bedroom and bathroom [
8,
12], distance from the beach [
11,
12], floor level [
6,
10], type of room [
6,
10], and sea view [
8]. The list of independent variables are as shown in
Table 1.
The study compared the effectiveness of forecasting using ANN with the forecasting using multiple regression analysis. The results will ensure whether the ANN should be suggested as the tool to predict the appropriate rental price for condominiums in Pattaya.
The descriptive statistics are calculated to provide information of the distribution of the data studied before the examinations of multiple regression and ANN are proceeded.
3.2. Multiple Regression Analysis
Multiple regression is used as the traditional technique for prediction precision comparison with the artificial neural network. Additionally, the analysis allows the study to find out the impact of predictors which are not exhibited by the ANN. This study applies the Stepwise technique on the multiple regression analysis since this method could select only statistically significant independent variable into the model. This technique also lowers the multicollinearity and model’s overfitting problem since the redundant variables that have no unique information will not be counted..
The influence of the independent variables on the rental price could be exhibited as follows:
where, β
0 is constants in equation, β
1 to β
8 are beta coefficients showing the impact of each independent variable, and e is the error term. However, only statistically significant factors will be left after the selection by Stepwise technique.
3.3. Artificial Neural Network Analysis
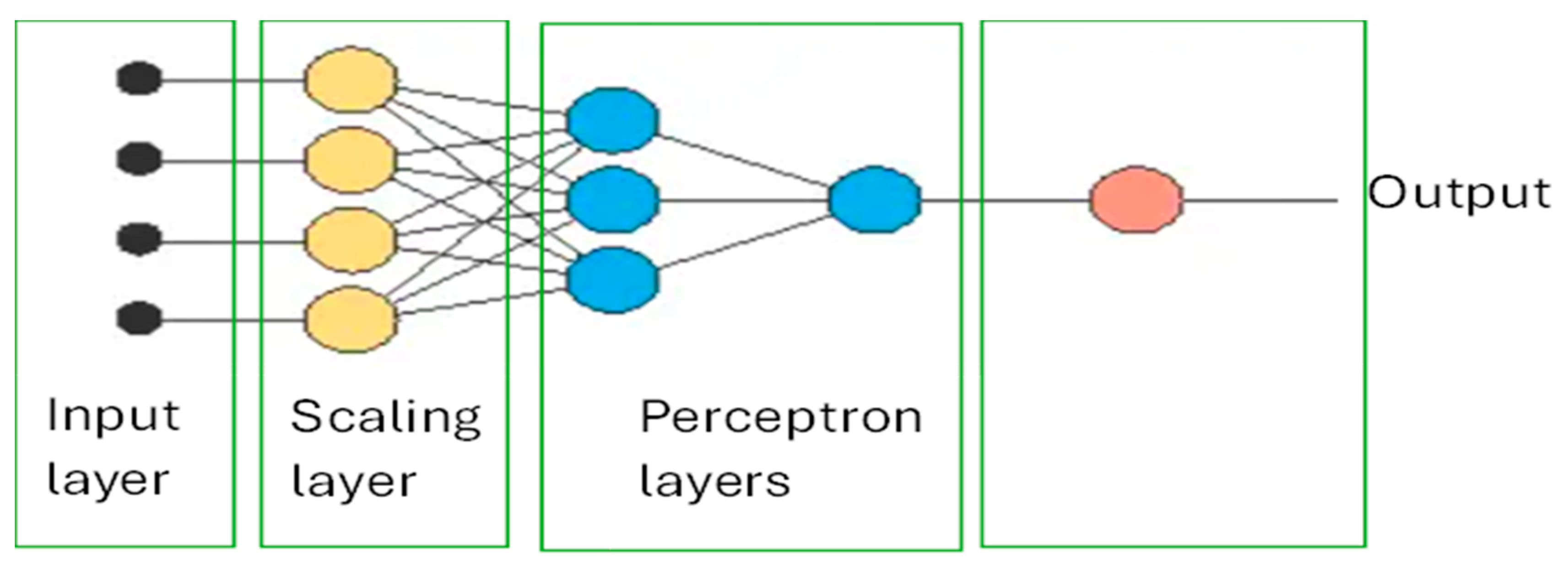
This research uses Neural Designer software to discover the appropriate rental prices of condominiums. The software provides a neural network for function approximation with multiple layers including a scaling layer, perceptron layers, an unscaling layer and a bounding layer. These layers are organized in a network architecture as presented in
Figure 1.
The independent variables’ data are fed in the input layer and undergo transformation at different layers. The scaling layer was used to make the independent variables’ values with different scales comparable before moving into perception layers for training. At the unscaling layer the calculated output will be unscaled back to the original units.
The Neural Design software would discover the optimal network architecture for the model with the training strategy’s algorithm that allows for the minimum error.
To find the model by the ANN, the input variables’ data, Xi, from each node will be weighed by the weights, Wi, and added by the bias, b, to create a weighted sum as follows:
Then, the weighted sum will be transformed through the activation function in hidden layers as follows
The weights and bias will be adjusted to generate the predicted values with minimum errors. Hyperbolic tangent activation, Rectified linear (ReLU) activation, Linear activation, and Logistic activation are the most used activation functions in the software. The Quasi-Newton Method, an optimization algorithm, is used to train the neural networks to advance the model’s accuracy.
This study splits the data into 3 sets with the average of the proportion range as suggested by (Buhl, 2023) [
44] as follows; 80% is under training set, 10% is selection set, and 10% is testing datasets. The high proportion of training data helps in capturing the variability of the data. The training set is used for the construction of several models during model design. To ensure that the model created of the training dataset is practical for the new data, the selection dataset is used to validate and improve the model. Then, the testing dataset will be used to evaluate the effectiveness of the model using for the unseen data.
4. Result
4.1. Descriptive Analysis
The descriptive statistics of all variables from the sample-set of 983 condominium in Pattaya, Thailand are summarized in
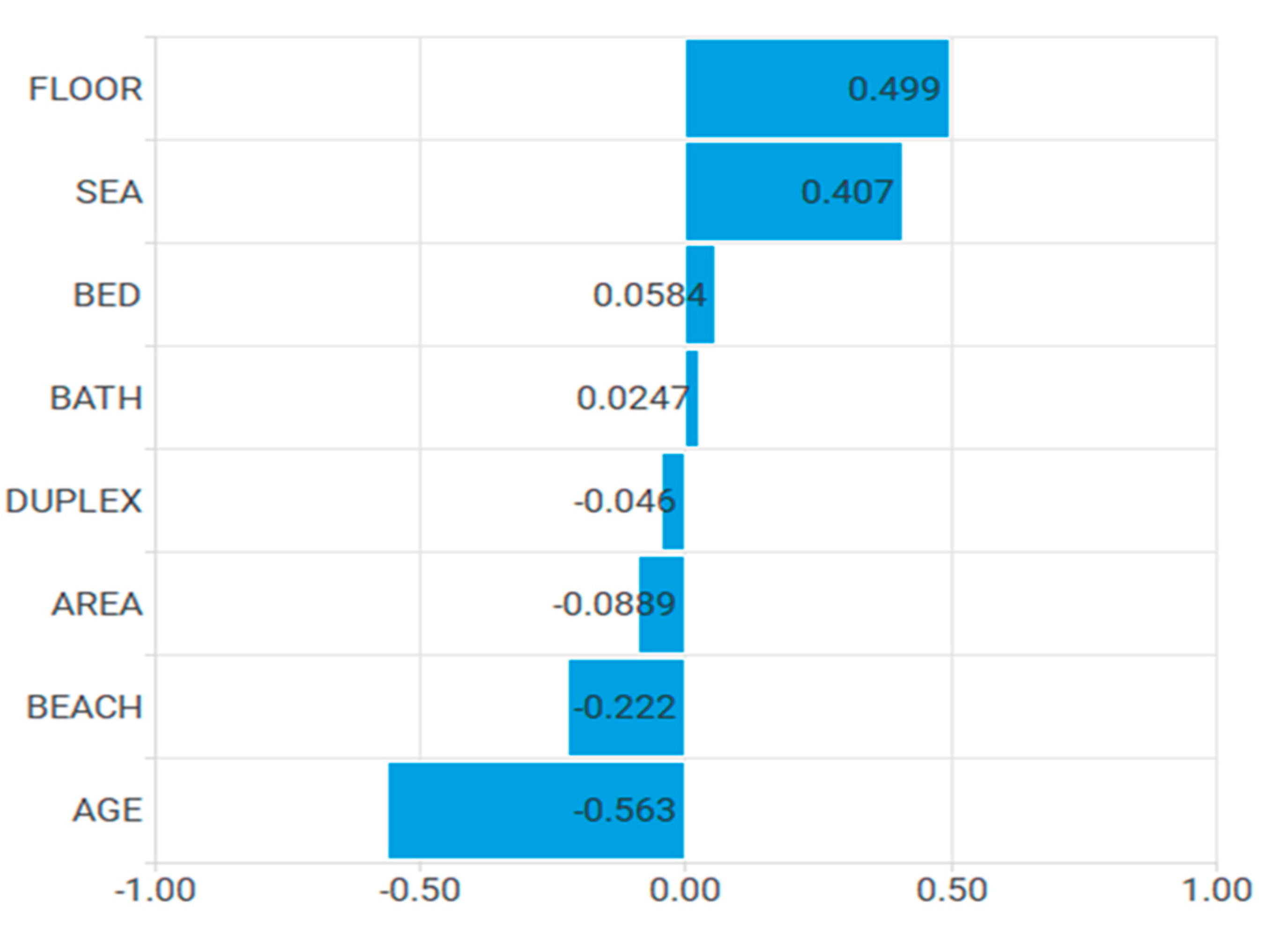
Table 2. The correlation coefficients between 8 independent variables and rental price are exhibited in
Figure 2. Half of them are positively correlated with the price (FLOOR at 0.499, SEA at 0.407, BED at 0.0584, BATH at 0.0247) Another half are negatively correlated to the price (AGE at -0.563, BEACH at -0.222, AREA at -0.089, DUPLEX at -0.046). The high coefficient value indicated that the high chance that the independent variable would statistically significantly affect the dependent variable.
4.2. Multiple Regression Analysis
Table 3 reports that there are five determinants which statistically significantly impact the rental price. Condominium’s age (AGE) and distance from beach (BEACH) have a negative effect on the rental price while numbers of bedrooms (BED), floor level (FLOOR), and sea view (SEA) have positive impact. The explanatory variables could explain 43.44% of the rental price. Durbin-Watson statistics reported that there is no serial correlation (1.5<DW<2.5).
4.3. ANN Analysis
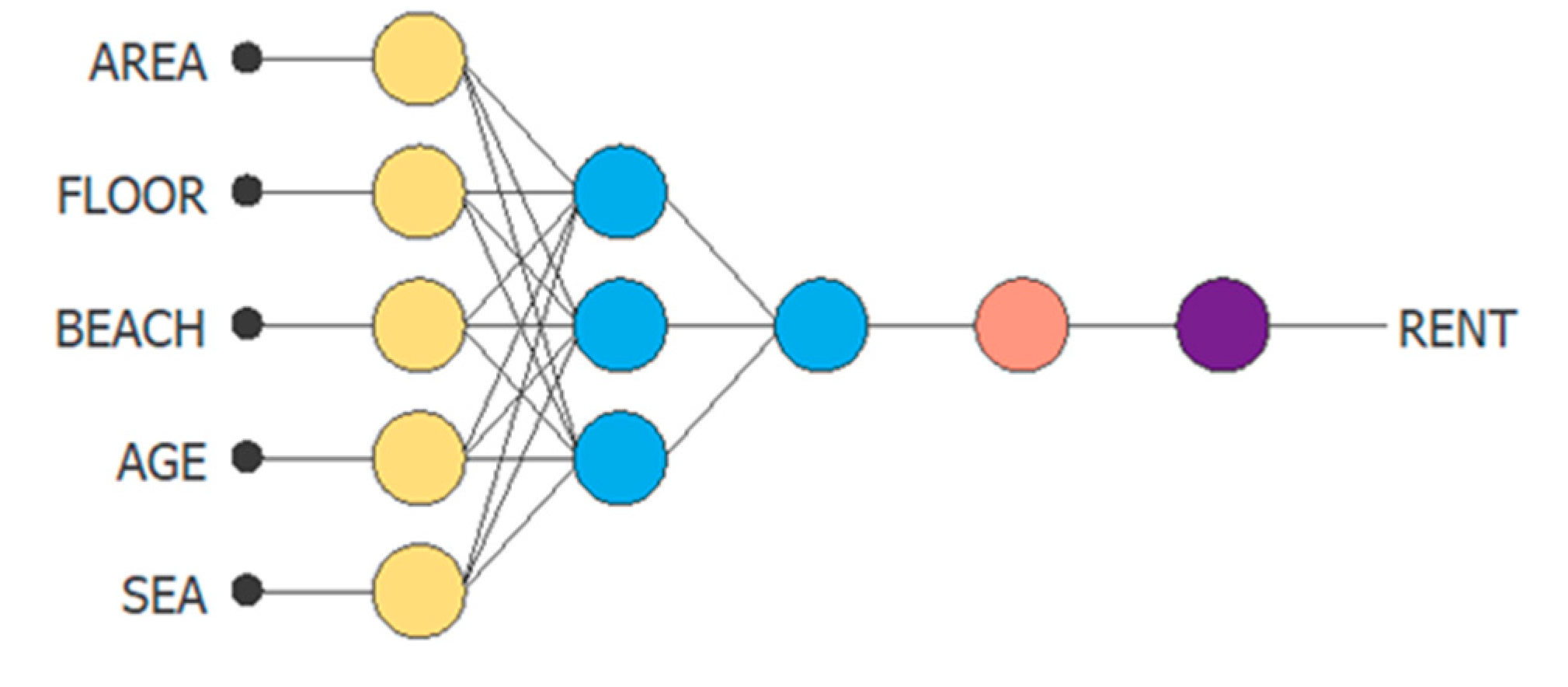
To find the optimal model, the ANN performs neurons and input selection and generates optimal architecture as shown in
Figure 3. The selected independent variables for rental price (RENT) prediction include five variables as follows: the area of the condominium (AREA), the condominium’s floor level (FLOOR), distance from the condominium to the beach (BEACH), the age of condominium’s building (AGE), and the sea view (SEA). Most of these independent variables are statistically significant in regression analysis, except AREA. The ANN’s algorithm might be able to discover the non-linear relation between the AREA variable and rental price. In addition, the number of bedrooms variable is not counted in the ANN’s architecture.
ANN’s Model
The ANN discovered the model for the rental price prediction as follows:
scaled_AREA = (AREA-59.01279831)/36.9076004
scaled_FLOOR = (FLOOR-12.85960007)/10.91930008
scaled_BEACH = (BEACH-1.305299997)/0.784035027
scaled_AGE = (AGE-10.85659981)/7.441609859
scaled_SEA = SEA*(1+1)/(1-(0))-0*(1+1)/(1-0)-1
perceptron_layer_1_output_0 = tanh( 2.88003 + (scaled_AREA*0.30624) + (scaled_FLOOR*-0.165295) + (scaled_BEACH*0.694656) + (scaled_AGE*2.50522) + (scaled_SEA*-0.165819) )
perceptron_layer_1_output_1 = tanh( -1.65673 + (scaled_AREA*0.716831) + (scaled_FLOOR*-0.199917) + (scaled_BEACH*0.515554) + (scaled_AGE*0.0497823) + (scaled_SEA*-0.243526) )
perceptron_layer_1_output_2 = tanh( 0.475768 + (scaled_AREA*-0.43637) + (scaled_FLOOR*-0.311676) + (scaled_BEACH*-0.190266) + (scaled_AGE*0.478451) + (scaled_SEA*-0.159676) )
perceptron_layer_2_output_0 = ( 0.518451 + (perceptron_layer_1_output_0*-0.92347) + (perceptron_layer_1_output_1*-0.620771) + (perceptron_layer_1_output_2*-0.890531) )
unscaling_layer_output_0=perceptron_layer_2_output_0*197.9170074+472.1080017
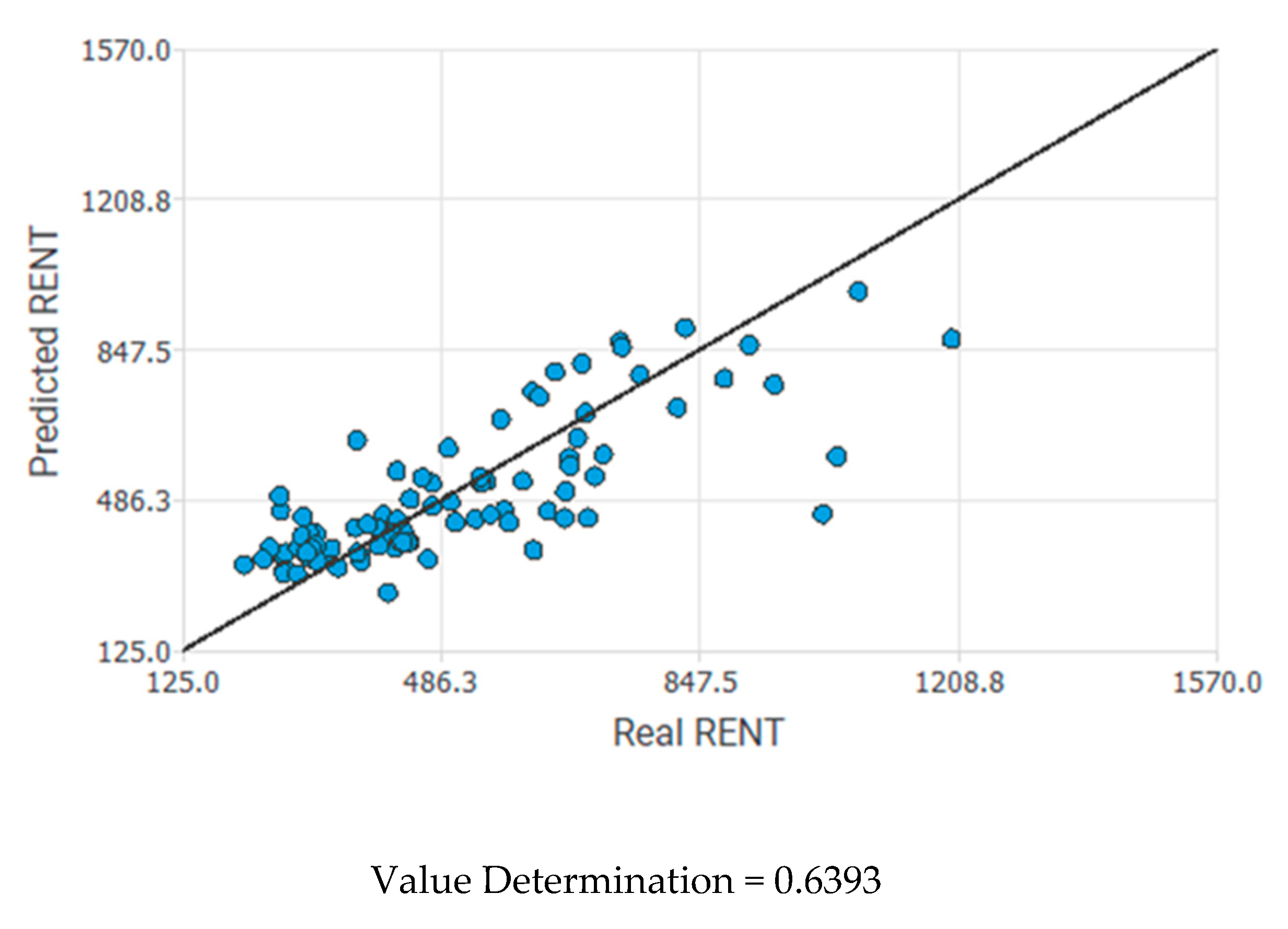
Figure 4 shows the precision of the predicted rental price. At the 45 degree line, the predicted and the real rental prices are the same. The value determination evidences that the explanatory power was improved with the ANN’s algorithm. The rental price could be explained by the selected independent variable of 63.93%, which is better than the traditional multiple regression model whose selected variables could explain the rental price by 43.32% according to its adjusted R-Squared value. However, the ANN’s prediction for the rental price might not be effective as the ordered pair are widely diverse from the line.
Value Determination = 0.6393
The errors of the ANN’s model for training, selection, and testing set are measured in sum squared error or sum squared residual to compare with the multiple regression model. The results in
Table 4 show that ANN model’s total sum squared error is much less than the multiple regression model.
5. Discussion
This study applies multiple regression analysis and ANN to determine the condominium rental price in Pattaya, Thailand by incorporating different independent variables including distance to the beach, property size, building age, number of bedrooms, number of bathrooms, floor level, duplex or ordinary condominium, and sea view. The determinants are applied from different previous studies
The ANN model provides an accurate and adaptive estimation of condominium rental prices in Pattaya, Thailand which confirms the results of price and rental price estimation in previous studies [
23,
26,
28,
29,
32]. The model has lower Sum Square Error (SSE) values than the traditional model which confirms the prediction capacity to ANNs and their outperformance in the regression analysis. ANNs can deal with the non-linear relationships between variables used in the analysis like room view. These affirm the capacity and accuracy of ANN in rental price prediction which are conformity of other studies [
20,
22,
23,
31,
34,
36,
39]
The regression model provides a better understanding of the influence and weight of dependent variables on the rental price. ANNs are more utilized in terms of precision of prediction. Thus, the combination of these methods benefits the stakeholders with better estimation accuracy and application in the market dynamics [
33]. However, the independent variable reasoning is still important to avoid overfitting the model from untrue relationships.
The results of this study apply to different stakeholders. Real estate investors can use ANNs to receive appropriate and market-competitive rental prices to optimize returns and minimize the risk of overpricing or underpricing of rental prices. ANNs are the analysis tool for investors to predict areas where future price appreciation is in the forecast, and to assess the risks associated with different types of condominiums, then they can manage their portfolio investment.
The accuracy estimation also supports policymakers in monitoring dynamics in the real estate sector, establishing benchmarks for condominium rental prices, and protecting people from overpricing. Policymakers can allocate resources and infrastructure to property areas with potentially high prices.
Real estate developers can understand the drivers of rental prices such as distance to the beach, room area, and view from the ANN model thus they can add value to their projects and design property projects to meet consumer preferences.
In conclusion, the ANN model is applicable to stakeholders to transition from intuition-based decision-making to data-driven decision-making. This promotes market transparency and efficiency in real estate markets. ANN is a well-established method for setting rental prices, especially in fast-growing and dynamic real estate markets like Pattaya.
This study has limitations in terms of excluding the macroeconomic variables such as the inflation rates, economic growth, interest rates, and unemployment rates. The future research should be conducted in different major areas in Thailand such as Bangkok, and Chiangmai. Smart city data including pollution level, traffic situation, or public transport may be incorporated into the study. Additionally, data is still key success of ANN’s prediction because the ANN uses data for training and learning relationships. Small data or old data might not represent the correct pattern of relationship. The rapid change in relationship structure, for example, the drop of tourist numbers during pandemic crisis, could make the model which was created from old data outdated and could not be appropriate for use. Those who would like to use ANN for rental prediction should keep updating the data and rerun to find the updated model for accurate prediction.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
Table 1: Independent variables for the study;
Table 2. Descriptive Statistics;
Table 3: Regression Results;
Table 4: Comparison between ANN’s and Multiple Regression’s sum squared error
Figure 1: ANN’s architecture;
Figure 2: Pearson Correlation between 8 Independent Variables and Rental Price;
Figure 3:ANN’s architecture;
Figure 4: Graph Shows the Precision of Predicted Rental Price.
Author Contributions
methodology, J.B.; software, J.B.; validation, J.B.; formal analysis, J.B.; investigation, J.B. and M.L.; resources, J.B. and M.L.; data curation, J.B.; writing—original draft preparation, M.L.; writing—review and editing, J.B. and M.L.; All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available upon request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Robey, S.L.; McKnight, M.A.; Price, M.R.; Coleman, R.N. Considerations for a Regression-Based Real Estate Valuation and Appraisal Model: A Pilot Study. Account. Finance Res. 2019, 8, 99. [Google Scholar] [CrossRef]
- Benjamin, J.; Guttery, R.; Sirmans, C. Mass Appraisal: An Introduction to Multiple Regression Analysis for Real Estate Valuation. J. Real Estate Pract. Educ. 2004, 7, 65–77. [Google Scholar] [CrossRef]
- Artificial Neural Networks for Predicting Real Estate Prices Available online:. Available online: https://www.researchgate.net/publication/282158904_Artificial_neural_networks_for_predicting_real_estate_prices (accessed on 31 January 2025).
- Mostofi, F.; Toğan, V.; Başağa, H.B. Real-Estate Price Prediction with Deep Neural Network and Principal Component Analysis. Organ. Technol. Manag. Constr. Int. J. 2022, 14, 2741–2759. [Google Scholar] [CrossRef]
- Tin, T.T.; Wei, C.J.; Min, O.T.; Feng, B.Z.; Xian, T.C. Real Estate Price Forecasting Utilizing Recurrent Neural Networks Incorporating Genetic Algorithms. Int. J. Innov. Res. Sci. Stud. 2024, 7, 1216–1226. [Google Scholar] [CrossRef]
- Mao, X. Research on the Influencing Factors of Rental House Prices. Trans. Econ. Bus. Manag. Res. 2024, 10, 146–151. [Google Scholar] [CrossRef]
- de Jaureguizar Cervera, D.; Pérez-Bustamante Yábar, D.C.; de Esteban Curiel, J. Factors Affecting Short-Term Rental First Price: A Revenue Management Model. Front. Psychol. 2022, 13. [Google Scholar] [CrossRef]
- Dökmeci, V.; Yavas, A. External Factors, Housing Values And Rents: Evidence From Survey Data.
- Sirmans, G.S.; Benjamin, J. Determinants of Market Rent. J. Real Estate Res. 1991, 6, 357–379. [Google Scholar] [CrossRef]
- Yoshida, J.; Sugiura, A. The Effects of Multiple Green Factors on Condominium Prices. J. Real Estate Finance Econ. 2015, 50, 412–437. [Google Scholar] [CrossRef]
- Singla, H.K.; Bendigiri, P. Factors Affecting Rentals of Residential Apartments in Pune, India: An Empirical Investigation. Int. J. Hous. Mark. Anal. 2019, 12, 1028–1054. [Google Scholar] [CrossRef]
- Factors Determining Residential Rental Prices | Asian Economic and Financial Review Available online:. Available online: https://archive.aessweb.com/index.php/5002/article/view/970 (accessed on 30 January 2025).
- Rosen, S. Hedonic Prices and Implicit Markets: Product Differentiation in Pure Competition. J. Polit. Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Box, G. Box and Jenkins: Time Series Analysis, Forecasting and Control. In A Very British Affair; Palgrave Macmillan UK: London, 2013; pp. 161–215. ISBN 978-1-349-35027-8. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29. [Google Scholar] [CrossRef]
- Natekin, A.; Knoll, A. Gradient Boosting Machines, a Tutorial. Front. Neurorobotics 2013, 7. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Xu, P.; Wang, J.; Jiang, Y.; Gong, X. Applications of Artificial Intelligence and Machine Learning in Image Processing. Front. Mater. 2024, 11, 1431179. [Google Scholar] [CrossRef]
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press. Available at: Https://Www.Deeplearningbook.Org -. (accessed on 28 June 2024).
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Nielsen, A. Neural Networks and Deep Learning 2015.
- Chaudhuri, T.D.; Ghosh, I. Artificial Neural Network and Time Series Modeling Based Approach to Forecasting the Exchange Rate in a Multivariate Framework 2016.
- Chao, C.-H. Training a Neural Network to Predict House Rents Using Artifical Intelligence and Deep Learning. In Proceedings of the 2023 IEEE International Conference on Image Processing and Computer Applications (ICIPCA); IEEE: Changchun, China, August 11, 2023; pp. 1011–1015. [Google Scholar]
- Chen, W.; Farag, S.; Butt, U.; Al-Khateeb, H. Leveraging Machine Learning for Sophisticated Rental Value Predictions: A Case Study from Munich, Germany. Appl. Sci. 2024, 14, 9528. [Google Scholar] [CrossRef]
- Kumar Mally, P. Data and Algorithms: Reviewing the Role of Machine Learning in the Real Estate Sector. Int. J. Comput. Trends Technol. 2023, 71, 55–64. [Google Scholar] [CrossRef]
- Neves, F.T.; De Castro Neto, M.; Aparicio, M. The Impacts of Open Data Initiatives on Smart Cities: A Framework for Evaluation and Monitoring. Cities 2020, 106, 102860. [Google Scholar] [CrossRef]
- Fan, F.-L.; Xiong, J.; Li, M.; Wang, G. On Interpretability of Artificial Neural Networks: A Survey. IEEE Trans. Radiat. Plasma Med. Sci. 2021, 5, 741–760. [Google Scholar] [CrossRef]
- Borst, R.A. Artificial Neural Networks: The next Modelling/Calibration Technology for the Assessment Community. Prop. Tax J. 1991, 10, 69–94. [Google Scholar]
- McGreal, S.; Adair, A.; McBurney, D.; Patterson, D. Neural Networks: The Prediction of Residential Values. J. Prop. Valuat. Invest. 1998, 16, 57–70. [Google Scholar] [CrossRef]
- Truong, Q.; Nguyen, M.; Dang, H.; Mei, B. Housing Price Prediction via Improved Machine Learning Techniques. Procedia Comput. Sci. 2020, 174, 433–442. [Google Scholar] [CrossRef]
- Selim, H. Determinants of House Prices in Turkey: Hedonic Regression versus Artificial Neural Network. Expert Syst. Appl. 2009, 36, 2843–2852. [Google Scholar] [CrossRef]
- Lin, H.; Chen, K. Predicting Price of Taiwan Real Estates by Neural Networks and Support Vector Regression. In Proceedings of the Proc. of the 15th WSEAS Int. Conf. on Syst; 2011; pp. 220–225. [Google Scholar]
- Ja’afar, N.S.; Mohamad, J.; Ismail, S. MACHINE LEARNING FOR PROPERTY PRICE PREDICTION AND PRICE VALUATION: A SYSTEMATIC LITERATURE REVIEW. Plan. Malays. 2021, 19. [Google Scholar] [CrossRef]
- Mohd, T.; Masrom, S.; Johari, N. Machine Learning Housing Price Prediction in Petaling Jaya, Selangor, Malaysia. Int J Recent Technol Eng 2019, 8, 542–546. [Google Scholar]
- Peterson, S.; Flanagan, A. Neural Network Hedonic Pricing Models in Mass Real Estate Appraisal. J. Real Estate Res. 2009, 31, 147–164. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Y. Residential Housing Price Index Forecasting via Neural Networks. Neural Comput. Appl. 2022, 34, 14763–14776. [Google Scholar] [CrossRef]
- Abidoye, R.B.; Chan, A.P.C.; Abidoye, F.A.; Oshodi, O.S. Predicting Property Price Index Using Artificial Intelligence Techniques: Evidence from Hong Kong. Int. J. Hous. Mark. Anal. 2019, 12, 1072–1092. [Google Scholar] [CrossRef]
- Nguyen, N.; Cripps, A. Predicting Housing Value: A Comparison of Multiple Regression Analysis and Artificial Neural Networks. J. Real Estate Res. 2001, 22, 313–336. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, H.-M.; Chao, C.-H.; Wei, S.; Yang, C.-F. Training a Neural Network to Predict House Rents Using Artificial Intelligence and Deep Learning. Sens. Mater. 2023, 35, 4671. [Google Scholar] [CrossRef]
- Seya, H.; Shiroi, D. A Comparison of Apartment Rent Price Prediction Using a Large Dataset: Kriging versus DNN 2019.
- Liu, P. Airbnb Price Prediction with Sentiment Classification. 2021.
- Top 5 Real Estate Agents in Thailand. Available online: https://www.investasian.com/property-investment/real-estate-agents-thailand/ (accessed on 31 January 2025).
- How to Split Machine Learning Datasets: Training, Validation, & Test Sets Available online:. Available online: https://encord.com/blog/train-val-test-split/ (accessed on 31 January 2025).
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).