Review of Advanced Optimal Power Flow Techniques for Multi-Energy Systems with High Renewable Penetration

1. Introduction

1.1. Background and Motivation

The urgent global transition towards sustainable energy systems is propelled by escalating concerns over climate change and the increasing demand for energy security. As shown in Fig. 1, Integrated Energy Systems (IESs), which synergistically combine electricity, heat, and natural gas networks, offer a holistic solution poised to substantially enhance energy efficiency, minimize carbon footprints, and bolster system reliability [1,2,3]. Such systems embody the integration of various energy vectors, thereby facilitating a more resilient energy infrastructure capable of accommodating diverse energy demands efficiently. However, the incorporation of high shares of variable Renewable Energy Sources (RES), such as solar and wind power, introduces significant complexities. These energy sources are inherently intermittent, with production levels that can fluctuate drastically due to environmental conditions, thereby posing substantial challenges in energy consistency and reliability. The variability of these sources often leads to system imbalances and can precipitate operational inefficiencies, making the management of energy flows across interconnected networks increasingly complex [4].

Figure 1. Structure of an integrated energy system.

Figure 1. Structure of an integrated energy system.

Optimal Power Flow (OPF), a pivotal tool in modern power systems management, plays a critical role in navigating these complexities. OPF is essential for the strategic routing of energy in a manner that maximizes efficiency while adhering to system constraints and maintaining stability [5,6]. However, as the energy landscape evolves and the share of RES grows, the traditional methodologies of OPF must also adapt. Modern OPF solutions must effectively address the uncertainties introduced by renewable integrations, such as forecasting errors, sudden changes in generation capacity, and the integration of energy storage systems.

To tackle these challenges, advanced OPF techniques are increasingly employing sophisticated algorithms that incorporate real-time data, probabilistic forecasting, and machine learning models to enhance predictive accuracy and operational resilience [7,8,9]. These developments signify a paradigm shift in how energy systems are optimized, moving from static, deterministic models to dynamic, adaptive systems capable of responding to fluctuations in real-time. Moreover, the integration of digital technologies such as the Internet of Things (IoT) and smart grid capabilities into IES can further optimize energy management. These technologies enable enhanced monitoring, control, and predictive maintenance, which are crucial for the effective integration of diverse energy resources and ensuring the reliability of energy supply. As the deployment of RES continues to escalate, the role of OPF in facilitating efficient, reliable, and sustainable energy systems becomes ever more critical [10]. Addressing these multifaceted challenges requires a holistic approach to system design and operation, one that leverages both technological innovations and coordinated policy frameworks aimed at supporting the seamless integration of renewable energies into the global energy mix.

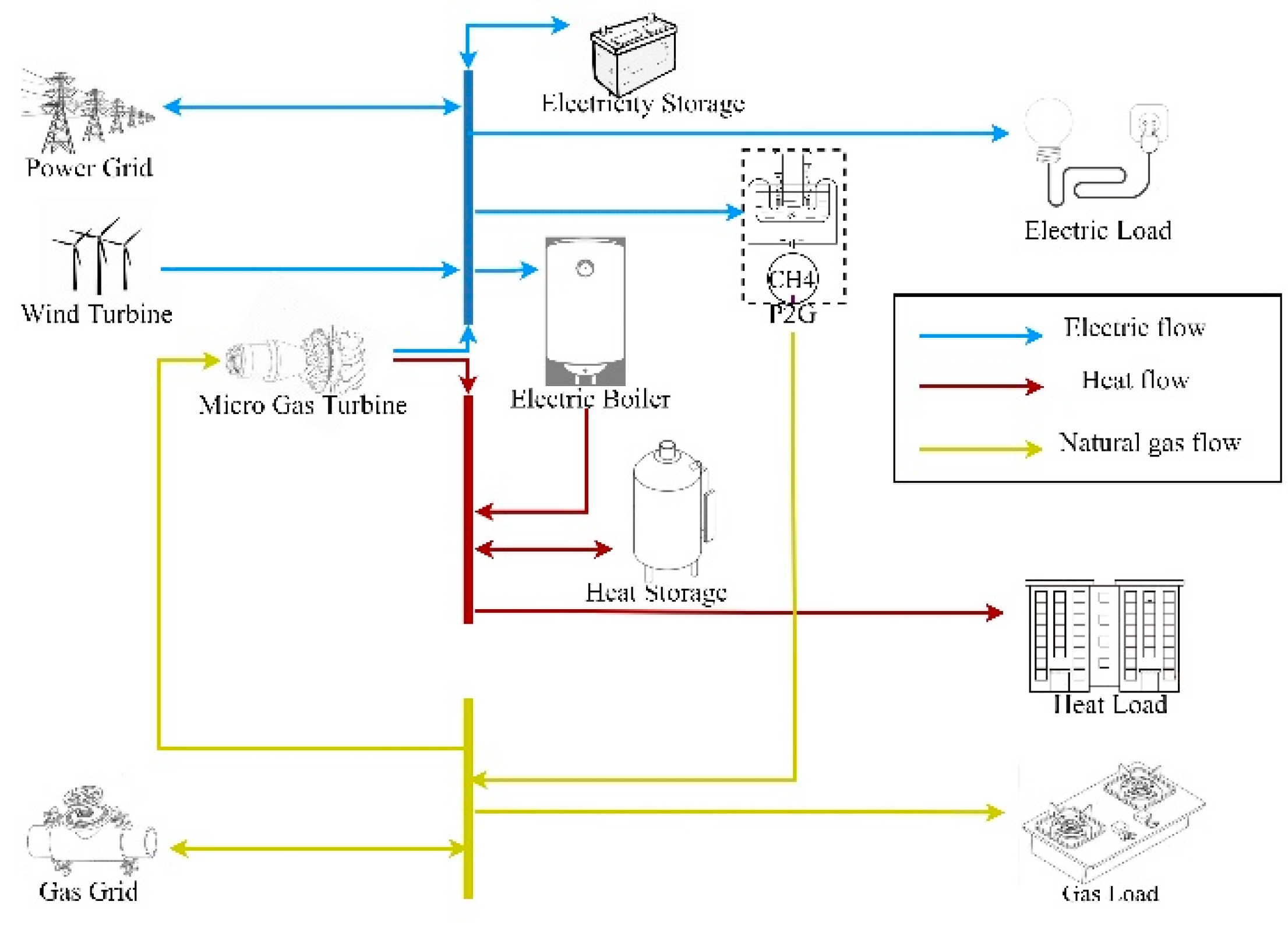
1.2. Objectives and Scope

The primary objective of this paper is to explore and articulate the advancements in OPF methodologies within IESs that incorporate high penetrations of RES. Given the increasing complexity and multidisciplinary nature of modern energy systems, this review seeks to synthesize current research trends, identify gaps in existing methodologies, and highlight opportunities for future research. Specifically, the paper aims to:

• Provide a comprehensive overview of OPF challenges and solutions in the context of multi-energy systems.
• Analyze the impact of renewable energy integration on the stability, efficiency, and sustainability of IES.
• Evaluate the role of emerging technologies like machine learning, blockchain, and quantum computing in enhancing OPF applications.

1.3. Methodology

This review employs a systematic literature review methodology, examining a wide range of sources, including peer-reviewed journal articles, conference proceedings, and industry reports. The selection criteria for literature include relevance to OPF in IES, focus on renewable integration, and the incorporation of innovative computational technologies. This approach ensures a thorough examination of the state-of-the-art, facilitating a nuanced understanding of the current landscape and future directions in OPF research.

1.4. Contributions of this Paper

This paper provides significant contributions by establishing a holistic framework for OPF tailored for IES with high renewable energy integration. It evaluates cutting-edge technologies such as machine learning, quantum computing, and blockchain for their potential to enhance OPF's accuracy and efficiency. By identifying crucial research gaps, it outlines a strategic roadmap for future investigation and suggests necessary policy adaptations to support technological transitions in energy system management. Through an interdisciplinary approach that includes quantitative and qualitative analyses, this review illustrates practical applications and underscores the need for robust, adaptable OPF solutions that can dynamically respond to renewable energy variability, enhancing system resilience and operational efficiency.

2. OPF of IESs

2.1. Definition and Importance of OPF in IES

The OPF problem is a central task in power systems, focusing on determining the most cost-effective and efficient operating conditions for electricity generation, transmission, and distribution [11,12]. OPF aims to optimize system performance by minimizing costs while meeting all operational constraints, such as voltage limits, generation limits, and line capacities. Traditionally, OPF has been applied to electricity systems, where the objective is to balance generation with demand, maintain system stability, and ensure efficient power distribution. However, when extended to IES—which involve the coordination of multiple energy carriers like electricity, gas, and heat—the complexity of the OPF problem increases significantly. In IES, the optimization task must account for not just electricity, but also the generation, storage, and distribution of gas and heat, which often operate on different timescales and have distinct technical and economic characteristics [13,14,15].

In renewable-integrated IES, OPF becomes even more critical. The variability and intermittency of RES, such as wind and solar power, create additional challenges for system operators [16,17,18,19]. Unlike conventional energy sources, RES cannot always be predicted with certainty, and their output can fluctuate due to weather conditions, time of day, or seasonal variations. OPF models in renewable-integrated IES must adapt to these uncertainties by incorporating forecasting models, probabilistic approaches, and real-time data to ensure that energy generation and distribution remain reliable and efficient. The role of OPF in renewable-integrated IES extends beyond just minimizing operational costs; it also plays an essential role in ensuring system resilience. By dynamically adjusting the flow of energy between multiple carriers, OPF can help mitigate the risks associated with fluctuating renewable generation, prevent system imbalances, and enhance the overall stability of the energy system. This is particularly important as the share of renewable energy continues to rise globally, challenging the traditional reliability of energy systems. Moreover, OPF is integral to promoting sustainable practices in IES [20]. By optimizing the operation of renewable energy resources, energy storage systems, and flexible demand response, OPF can facilitate the integration of more RES into the grid, thereby reducing reliance on fossil fuels and minimizing the carbon footprint of energy systems. The optimization process ensures that each energy carrier—electricity, gas, and heat—supports the others in a way that maximizes the efficiency and sustainability of the overall system.

In essence, OPF in IES involves making critical decisions about energy production, distribution, and storage that ensure each energy carrier is used optimally [21,22,23]. The goal is to provide a reliable, cost-effective, and environmentally sustainable energy supply that meets the demands of modern, integrated energy networks. As the energy landscape evolves with the increasing adoption of RES and the need for multi-sector coordination, the role of OPF becomes even more pivotal in shaping the future of energy systems [24].

2.2. OPF Problem Formulation in IESs

The mathematical formulation of the OPF problem for IESs involves minimizing the total operational cost across multiple energy carriers while satisfying various technical, operational, and environmental constraints [25,26,27]. The objective function accounts for the generation costs associated with electricity, gas, and thermal energy. In IES, the problem is more complex than traditional OPF due to the interconnections between different energy carriers and the need to balance their interactions [28].

The IES OPF problem can be represented in a non-linear structure as follows:

$$\left\{\begin{array}{c}\mathit{min}f\left(P,F,\nu \right)\\ s.t.\mathit{L}-c\mathit{P}=0\\ G_{\alpha }\left(\mathit{P}\right)=0\\ \underset{\_}{P}⩽\mathit{P}⩽\overline{P}\end{array}\right.$$

(1)

where F is the vector of different energy flows；v represents the scheduling factors；$G_{\alpha }\left(\mathit{P}\right)=0$ is the related equal constraints of the IES OPF problem；$\underset{\_}{P}$ and $\overline{P}$ are respectively the upper and lower vectors of the input energy vector. This paper aims to minimize the total energy cost as the objective, and the feasible domain of this optimization problem is defined by some practical equal and unequal constraints. During the optimization process, flow equations related to EH and the energy network must be satisfied as equal constraints.

3. Challenges in OPF for Renewable-Integrated IESs

The integration of renewable energy into IESs presents several critical challenges that must be addressed to ensure the stable and efficient operation of these systems. Below, we will analyze the key issues that impact OPF in renewable-integrated IES.

3.1. Uncertainty and Variability of Renewable Resources

One of the primary challenges in renewable-integrated OPF is the uncertainty and variability of renewable resources, particularly solar and wind power [29,30,31]. These resources exhibit inherently unpredictable generation patterns due to factors like weather, time of day, and seasonal variations. The variability of renewable generation complicates the scheduling and dispatching of power, as system operators must account for potential deviations from forecasted production levels.

To effectively manage uncertainty, multiple methods have been proposed, such as probabilistic forecasting, scenario-based optimization, and stochastic modeling. These approaches aim to quantify the uncertainty in renewable generation and provide a framework for incorporating it into the OPF formulation. Scenario-based methods, in particular, allow for the modeling of various possible future states of the system, enhancing the robustness of OPF solutions by preparing for different outcomes. However, these methods significantly increase the computational complexity of the problem, particularly for large-scale systems [32,33,34].

The challenge is to develop robust OPF models that can handle these uncertainties while minimizing the computational burden. Advanced techniques, such as machine learning for renewable energy prediction, may be leveraged to improve forecasting accuracy and reduce uncertainty in real-time decision-making.

3.2. Computational Complexity and Scalability

The OPF problem becomes particularly complex when applied to IES, as the optimization problem involves multiple interconnected energy carriers—electricity, gas, and heat. This multi-energy coupling introduces nonlinearities, non-convexities, and increased dimensionality, which significantly elevate the computational complexity of the problem [35]. As IES scale up, the number of nodes and interconnections increases, which further exacerbates the difficulty in solving the OPF problem in a computationally feasible manner.

To address this, various optimization techniques, including decomposition methods, distributed optimization, and heuristic algorithms, have been proposed to handle large-scale OPF problems [36,37,38,39]. These methods aim to break the OPF problem into smaller, more manageable subproblems, allowing for parallel computation and reducing the overall computational load. Despite these advances, scalability remains a key challenge, particularly for real-time applications in large-scale systems.

Another approach to tackling this issue is the use of quantum computing, which holds the potential to revolutionize the field of optimization by solving complex problems much faster than classical computers [40,41]. Although quantum computing is still in its infancy, its potential to address large-scale, non-convex optimization problems in OPF cannot be overlooked.

3.3. Coordination Challenges in Multi-Energy Coupling

IES involve the coordination of multiple energy carriers—electricity, gas, and heat—which each have distinct operational dynamics, timescales, and control mechanisms. Effective multi-energy coupling is crucial for the optimal functioning of these systems, as poor coordination between the energy sectors can lead to inefficiencies, increased operational costs, and even system instability.

For instance, gas and electricity networks are often interconnected through Combined Heat and Power (CHP) systems [42], and coordinating the operation of these systems requires a detailed understanding of both energy supply and demand patterns. Furthermore, heat networks typically operate at different timescales than electricity systems, which complicates real-time dispatch and optimization.

The OPF formulation must, therefore, incorporate interdependencies between electricity, gas, and heat systems [43,44,45]. This requires sophisticated multi-level decision-making strategies that optimize the operation of all interconnected networks simultaneously. Additionally, real-time data exchange and robust communication infrastructure are essential for ensuring the smooth coordination of operations across different energy carriers.

3.4. Stability and Security Risks

The integration of renewable energy into IES introduces additional risks related to system stability and security [46,47]. High levels of renewable penetration can cause rapid power fluctuations due to the intermittent nature of wind and solar energy, which can impact voltage stability and transient stability in power grids [48]. Moreover, the unpredictability of renewable generation can lead to energy imbalances, resulting in voltage deviations, system oscillations, or even blackouts [49,50,51].

In addition to physical instability, the increasing digitization of energy systems introduces cybersecurity risks [52,53,54]. Cyber-attacks, such as false data injection (FDI) attacks, can compromise the integrity of OPF solutions and disrupt grid operations [55,56,57,58]. The OPF formulation must, therefore, integrate cybersecurity measures to detect, mitigate, and prevent such attacks. For example, the incorporation of robust optimization and data-driven attack detection methods, such as federated learning and deep learning techniques, can help improve system resilience against cyber threats [59].

Given these challenges, OPF models must be designed not only to optimize energy flows but also to enhance system robustness and security. Resilient OPF frameworks that integrate both physical disturbances and cyber threats are essential for maintaining the stability and reliability of renewable-integrated IES [60].

4. Strategies and Solutions for OPF Under Renewable Energy Integration

In this section, we examine the strategies and solutions developed to tackle the key challenges in OPF for renewable-integrated IES. These solutions aim to enhance the efficiency, scalability, and resilience of IES while optimizing the integration of RES. The increasing variability of RES and the need for effective multi-energy carrier coordination in IES require innovative approaches to optimize energy flows, reduce operational costs, and improve system reliability.

4.1. Advanced Modeling and Forecasting Techniques

Effective management of renewable energy integration requires accurate forecasting of renewable generation, which is inherently uncertain [61,62,63]. Traditional forecasting methods, such as statistical time series analysis, have been widely used, but these methods often struggle with the high volatility and complexity of renewable resources. To address this, advanced techniques such as machine learning and deep learning are being increasingly employed [64].

For instance, artificial neural networks (ANNs), support vector regression (SVR), and deep learning models like Long Short-Term Memory (LSTM) networks are capable of capturing complex patterns in renewable generation data [65,66,67]. These models can improve the accuracy of short-term forecasting, which is critical for operational decision-making in renewable-integrated systems. In addition, probabilistic forecasting models, which quantify uncertainty in renewable generation, provide a more comprehensive approach to managing the unpredictability of RES [68,69].

To further enhance the forecasting process, scenario generation techniques such as stochastic optimization and robust optimization have been applied [70]. These methods allow for the creation of multiple future scenarios based on probabilistic distributions, which are then incorporated into the OPF model to improve decision-making under uncertainty [71,72,73].

4.2. Optimization Methods for OPF Problems

The OPF problem for renewable-integrated IESs is inherently complex due to the interactions between multiple energy carriers (electricity, gas, heat) and the need to optimize their flows while considering the unpredictability of renewable resources [74]. To address this, a variety of optimization methods have been developed, ranging from classical optimization techniques to more modern, heuristic approaches [75,76,77].

4.2.1. Classical Optimization Methods

Classical optimization techniques, such as Linear Programming (LP), Nonlinear Programming (NLP), Mixed-Integer Linear Programming (MILP), and Mixed-Integer Nonlinear Programming (MINLP), have long been used in OPF [78,79]. These methods are well-suited for modeling simpler systems or systems with relatively predictable behavior. For example, LP and MILP are particularly useful when the system can be approximated as linear or with linear constraints. These methods are computationally less expensive and can efficiently solve smaller, simpler OPF problems [80,81].

However, when integrating RES, which are inherently non-linear, more complex methods like NLP and MINLP become necessary. These methods allow for the modeling of the non-linearities introduced by RES and other factors like energy storage and hybrid systems, which are common in IES [82,83,84]. While these methods are more accurate in capturing the complexities of renewable energy systems, they are computationally more intensive and require more sophisticated algorithms to solve.

4.2.2. Heuristic and Metaheuristic Algorithms

Given the complexities and non-convexities of OPF problems in renewable-integrated IES, heuristic and metaheuristic algorithms have gained traction [85,86,87]. These algorithms, such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), Differential Evolution (DE), and Ant Colony Optimization (ACO), are well-suited for large-scale, non-convex OPF problems where traditional optimization methods may struggle [88,89].

Heuristic and metaheuristic algorithms do not rely on gradient-based methods and can explore a broader solution space, making them more effective at finding globally optimal or near-optimal solutions in highly complex systems [90,91,92]. These methods are particularly valuable for solving large-scale OPF problems that involve many variables and constraints, such as those encountered in IESs with high renewable energy penetration [93].

For example, GA and PSO are popular for their ability to handle large, non-linear problems by simulating natural processes (evolution and swarm behavior) to optimize the solution [94,95]. They are particularly effective for OPF problems in systems with multiple energy carriers, where traditional methods might fail due to the high dimensionality of the problem.

4.2.3. Decomposition and Distributed Optimization Algorithms

As IESs continue to grow in size and complexity, solving OPF problems in large-scale systems becomes increasingly difficult due to the computational burden [96,97,98]. One promising approach to managing this complexity is the use of decomposition methods and distributed optimization techniques. These methods aim to break the overall OPF problem into smaller, more manageable subproblems that can be solved independently or in parallel.

Techniques like the Alternating Direction Method of Multipliers (ADMM), Benders Decomposition, and Distributed Gradient Methods are commonly used for OPF in IESs. These methods enable the OPF problem to be decomposed into smaller parts based on system topology, such as individual energy carriers or local subsystems. This decomposition allows for parallel computation, significantly improving scalability and reducing computational time [99,100,101].

For example, ADMM is effective in solving large-scale, multi-party optimization problems, where each party (e.g., electricity, gas, and heat networks) can optimize its local objective function while coordinating with the other networks to achieve a global solution. By solving these subproblems concurrently, decomposition methods enhance the efficiency of OPF solutions, especially in real-time applications [102].

4.3. Hybrid Approaches

Given the diverse nature of IESs and the challenges associated with renewable energy integration, hybrid optimization methods are becoming increasingly popular [103,104,105]. These approaches combine the strengths of classical optimization, heuristic algorithms, and machine learning techniques to tackle the complex, multi-dimensional nature of OPF in IESs [106,107]. For instance, hybrid models may use machine learning for accurate forecasting and then apply optimization algorithms (e.g., PSO or GA) to solve the OPF problem under uncertain conditions.

Additionally, hybrid models may also integrate digital twin technology, which creates virtual replicas of physical systems to simulate and optimize energy flows in real time. By combining various optimization techniques with digital twins, energy systems can be continuously monitored, and operational decisions can be dynamically adjusted based on the current system state [108,109,110].

5. Innovative Trends and Emerging Technologies

As the demand for renewable energy integration continues to grow, innovative technologies are emerging to enhance OPF methodologies. These technologies aim to improve efficiency, scalability, resilience, and optimization of renewable energy systems, enabling them to cope with the complexities introduced by high penetration of RES in IES.

5.1. Machine Learning-Driven OPF

Machine learning techniques, particularly reinforcement learning, are increasingly being applied to OPF problems due to their ability to adapt to dynamic environments and make real-time decisions [111,112,113]. RL algorithms allow OPF models to continuously learn optimal dispatch strategies from historical data, which can then be refined based on real-time feedback. This continuous learning and adaptation make RL well-suited for managing renewable energy systems that experience frequent fluctuations.

In addition to RL, federated learning—a form of collaborative machine learning that trains models without sharing sensitive data [114,115]—has gained attention in OPF research, especially in scenarios involving multiple stakeholders or geographically distributed systems. This technique enables the development of global models for energy optimization while ensuring data privacy and security, which is crucial in sensitive energy market environments [116,117].

Additionally, deep generative models, such as Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), are being utilized to generate scenarios for renewable generation forecasting. These models, which capture the probabilistic nature of RES, provide more accurate and reliable predictions of renewable generation, thereby improving the performance of OPF solutions. By modeling uncertainty and incorporating probabilistic distributions, these techniques enhance the robustness of OPF models and contribute to better decision-making under uncertainty [118,119,120].

5.2. Quantum Computing for OPF Problems

Quantum computing is ushering in a new era for solving optimization problems, offering unprecedented speed and computational efficiency for problems that are currently intractable with classical methods [121,122,123]. OPF problems, particularly in large-scale, non-convex multi-energy systems, are inherently complex and involve high dimensionality, making them ideal candidates for quantum optimization techniques.

Quantum computing can significantly reduce the time required to solve OPF problems by leveraging techniques such as quantum annealing and quantum-inspired algorithms [124]. These quantum-based approaches can explore large, non-convex search spaces more efficiently than traditional optimization methods, providing a breakthrough for real-time optimization of large, complex systems [125]. Early research indicates that quantum optimization may outperform classical algorithms, particularly in large-scale IES with high renewable energy penetration.

Despite the potential of quantum computing, its application to OPF remains in the developmental stages. Key challenges include hardware limitations, algorithmic design, and the need for specialized quantum programming expertise. However, the promise of quantum computing to revolutionize the optimization of renewable-integrated IES is significant, particularly as quantum hardware and algorithms continue to advance.

5.3. Digital Twin Technologies for IES OPF

Digital twin technology involves creating a virtual replica of a physical system, allowing real-time simulation, monitoring, and optimization of system behavior. In the context of IES, digital twins are increasingly integrated with OPF methodologies to improve decision-making and optimize energy flows. By simulating the behavior of interconnected energy carriers—electricity, gas, and heat—digital twins provide operators with valuable insights into system performance and potential failure modes under different conditions [126].

Integrating digital twin models with OPF enables continuous monitoring and optimization of energy flows, improving system resilience and stability. Additionally, digital twins facilitate predictive maintenance and scenario testing, allowing for more accurate forecasting of renewable generation and demand. By simulating various operational scenarios, digital twins can help identify potential bottlenecks, optimize resource allocation, and mitigate risks in real-time. Moreover, digital twin technology enhances the management of renewable energy integration by predicting the impacts of variability on system stability [127]. It opens new possibilities for simulating large-scale systems with high renewable penetration and testing new operational strategies in a controlled virtual environment, helping operators refine their OPF solutions and prepare for future challenges.

5.4. Blockchain-Enabled Energy Trading and OPF

Blockchain technology, known for its transparency, security, and decentralization, is poised to transform the energy sector, particularly in enabling peer-to-peer (P2P) energy trading and enhancing the transparency of transactions [128]. In IES, blockchain can enable secure and decentralized energy trading between consumers, prosumers, and utilities, making it particularly beneficial in systems with a high penetration of distributed generation.

When integrated with OPF models, blockchain provides a secure, immutable ledger for tracking energy generation, consumption, and trading. This ensures that all transactions are transparent, verifiable, and tamper-proof, reducing transaction costs and enhancing market efficiency. Blockchain can also improve coordination in demand response (DR) and distributed energy resources (DER) management, facilitating real-time settlement and ensuring that all participants in the energy system are compensated fairly.

Moreover, blockchain can support the integration of flexible energy storage systems and electric vehicles (EVs) [129], enabling users to buy and sell energy as needed, enhancing system flexibility. This decentralized approach aligns with the principles of smart grids, where energy is managed more efficiently, and OPF solutions are optimized. Blockchain's secure and transparent nature also fosters trust among stakeholders, crucial for the future of decentralized energy markets [130].

5.5. Resilience-Oriented OPF Frameworks

As renewable energy systems become more integrated, the frequency of extreme weather events, cyber-attacks, and other disruptions increases, making resilience a critical aspect of modern OPF frameworks [131]. A resilience-oriented OPF framework explicitly incorporates system robustness, disaster preparedness, and rapid recovery capabilities into the optimization process. This approach ensures that energy systems can continue to function effectively despite physical or cyber disruptions.

Resilience-oriented OPF frameworks model potential disruptions, such as natural disasters or cyber-attacks, and develop strategies to minimize their impact on system performance. These frameworks can integrate disaster response measures, including load shedding, backup generation, and recovery protocols, directly into the OPF optimization process. This ensures that, even in the event of disruptions, the system can recover quickly while maintaining energy security [132].

Additionally, adaptive cybersecurity measures are being incorporated into OPF models to detect and mitigate cyber threats in real-time. For example, reinforcement learning-based defense strategies can be used to dynamically adapt to emerging threats and ensure that OPF solutions remain secure and resilient against evolving cyber risks. This proactive approach to cybersecurity and physical system stability enhances the overall robustness of renewable-integrated IES, making them more resilient to unexpected disruptions.

6. Case Studies and Application Scenarios

In this section, we present case studies and application scenarios that demonstrate the practical application of OPF strategies in renewable-integrated IES. These case studies provide valuable insights into the effectiveness of OPF methodologies and highlight both the benefits and challenges of integrating renewable energy into energy systems at various scales.

6.1. Industrial-Scale IES Case Studies

The practical application of OPF strategies at industrial scales has been successfully demonstrated in several large-scale renewable-integrated IES. These case studies showcase the benefits of optimizing energy flows across multiple energy carriers—electricity, heat, and gas—while incorporating renewable energy resources [133].

For instance, Denmark has become a leader in utilizing CHP plants alongside wind energy. These plants are optimized using OPF strategies to ensure that both power and heat generation are balanced, maximizing energy efficiency while minimizing environmental impact. The integration of renewable energy sources, such as wind power, to drive CHP plants has led to significant reductions in fossil fuel dependency and enhanced the sustainability of Denmark's energy grid. OPF ensures that renewable generation is used optimally for both electricity and heat, which reduces waste and operational costs while maintaining energy security.

In China, large-scale multi-energy industrial parks have demonstrated the successful integration of solar, wind, and thermal energy with traditional gas and electricity networks. By utilizing advanced OPF strategies, these industrial parks have optimized energy flows, reducing reliance on conventional energy sources and significantly improving operational efficiency. These parks have not only resulted in substantial economic savings but have also enhanced energy reliability by coordinating the use of different energy carriers. This case highlights the potential of OPF to improve the stability and flexibility of IES while integrating high levels of renewable energy [134,135].

These case studies underscore the importance of developing robust OPF solutions capable of integrating renewable energy in complex, large-scale IES. They demonstrate that renewable energy, when managed with advanced OPF methodologies, can provide significant economic, environmental, and operational benefits. The ability to coordinate multiple energy carriers and renewable resources is essential for creating a sustainable energy future.

6.2. Urban and Community-Level Renewable-Integrated IES

At the urban and community level, the integration of renewable energy into localized energy systems has been increasingly facilitated by microgrids [136]. Microgrids, typically consisting of renewable generation (solar, wind, biomass), energy storage, and demand-side management (DSM) technologies, offer a flexible and scalable solution for energy management. OPF techniques are employed to ensure that energy flows are efficiently coordinated between these components, optimizing the overall operation of the microgrid.

For example, several microgrid projects in Germany and the United States have demonstrated the effectiveness of OPF in balancing renewable generation with energy storage and demand response. These projects have achieved near-zero carbon emissions by utilizing locally sourced renewable energy and optimizing energy usage through advanced OPF strategies. By incorporating energy storage systems and DSM technologies, these microgrids have also enhanced energy reliability and reduced the dependence on external energy sources, allowing them to operate autonomously while maintaining grid stability.

The success of these projects illustrates the growing potential of decentralized energy systems that rely on renewable resources. Microgrids can improve the resilience of energy systems by ensuring that local energy needs are met even during disruptions to the central grid. Furthermore, the use of OPF ensures that renewable energy is efficiently distributed within the microgrid, optimizing energy storage and reducing operational costs. As cities and communities transition towards more sustainable energy solutions, OPF will be crucial for maintaining the efficiency, reliability, and resilience of these systems [137].

6.3. Comparative Analysis of Different OPF Methodologies

The OPF problem in renewable-integrated IES is inherently complex, and selecting the most suitable optimization methodology depends on system characteristics, computational resources, and the level of renewable energy integration [138,139]. In this section, we provide a comparative analysis of various OPF methodologies, focusing on their strengths, limitations, and applicability to different system configurations.

• Deterministic Methods: Classical deterministic methods such as Linear Programming (LP) and Nonlinear Programming (NLP) are widely used in OPF for traditional energy systems. These methods are particularly effective when renewable generation is predictable and stable. LP and MILP are useful for solving simpler, linearized models of OPF, while NLP and MINLP can handle non-linearities in more complex systems. However, these methods struggle with high uncertainty and nonlinearity, which are common in renewable-integrated systems.
• Stochastic and Robust Optimization: Stochastic optimization and robust optimization have proven to be effective in managing uncertainty in renewable generation. These methods excel in environments where there is substantial renewable uncertainty, such as wind and solar power, providing more reliable solutions by considering multiple possible future states of the system. Stochastic methods incorporate probabilistic distributions into the OPF model, allowing for better risk management and more reliable decision-making. However, the trade-off is that these methods come with significantly increased computational complexity, especially in large-scale systems, which can be a limitation in real-time applications. Robust optimization focuses on ensuring that solutions are feasible and efficient under a range of uncertain conditions, making it a valuable approach for optimizing energy systems with high levels of renewable energy. These methods allow OPF models to handle uncertainty more effectively but also require more computational resources and may result in suboptimal solutions under ideal conditions.
• Emerging Machine Learning Methods: Emerging machine learning techniques, particularly reinforcement learning and federated learning, are gaining attention due to their ability to adapt in real-time to dynamic environments. RL algorithms are particularly useful for systems with high uncertainty, as they can continuously learn and optimize the system's operation based on historical data and real-time feedback. These methods enable OPF models to continuously improve decision-making, adapting to changing system conditions without the need for explicit programming. Federated learning allows for collaborative model training across multiple stakeholders without sharing sensitive data, making it particularly valuable in scenarios involving multiple entities, such as in smart grid systems with various operators. These methods offer significant advantages in real-time optimization and adaptability but require substantial computational resources and large datasets for training.

Selecting the appropriate OPF methodology depends on several factors, including the complexity of the system, the level of renewable energy integration, and the computational resources available. While classical methods like LP and NLP are suitable for simpler, stable systems, stochastic and robust optimization methods are better equipped to handle uncertainty. Emerging machine learning techniques, such as RL and federated learning, offer real-time adaptability and are particularly useful for systems with high uncertainty and complex, dynamic behaviors. The continued development and integration of these advanced optimization techniques will be crucial for improving the efficiency and resilience of renewable-integrated IES in the future.

7. Discussion and Future Directions

This section provides a comprehensive overview of the progress made in OPF strategies for renewable-integrated IES, critically evaluates existing methodologies, and suggests key directions for future research.

7.1. Summary of Current Progress and Remaining Challenges

Substantial progress has been made in advancing OPF strategies for renewable-integrated IES, driven by innovations in modeling techniques, optimization algorithms, and the coordination of multi-energy systems. These developments have been pivotal in addressing some of the operational challenges associated with integrating renewable energy sources such as wind and solar power [140]. Key achievements include:

• The development of probabilistic forecasting models to handle uncertainty in renewable generation, improving the robustness of OPF solutions.
• The application of multi-energy optimization, allowing the simultaneous coordination of electricity, gas, and heat networks to enhance system efficiency and reduce operational costs.
• The use of machine learning and deep learning methods to improve decision-making and real-time optimization in complex and dynamic environments.

However, despite these advancements, significant challenges remain [141]. The integration of RES into IES continues to present difficulties in the following areas:

• Managing uncertainty: While various forecasting techniques have been developed, the unpredictability of renewable energy generation remains a key challenge, particularly when dealing with large-scale systems.
• Improving computational efficiency: As systems grow in complexity, the computational burden of OPF increases, especially for real-time applications. Solutions that balance optimization accuracy with computational feasibility are still a work in progress.
• Coordinating multi-energy networks: The interaction between electricity, gas, and heat systems requires intricate coordination to avoid inefficiencies and instability. Ensuring seamless communication and optimization across energy carriers remains a significant challenge.
• System stability and cybersecurity: The increasing reliance on digital technologies introduces cybersecurity risks, including potential cyber-attacks on critical infrastructure. Enhancing the stability and security of OPF solutions in the face of these risks is a major concern.

7.2. Critical Assessment of Different Methodologies

While traditional optimization methods such as LP, NLP, and MILP have provided well-established solutions to OPF problems, they struggle to handle the inherent complexity and uncertainty of renewable-integrated systems [142]. These classical methods excel in simpler, more predictable systems but become less effective when addressing the non-linearity and volatility introduced by renewable energy generation.

Emerging methods, such as stochastic optimization, robust optimization, and machine learning-based approaches, offer more flexibility and adaptability in managing uncertainty. These methods can more effectively handle the variability of RES by incorporating probabilistic models, enabling OPF to adapt in real time to changing conditions. However, these approaches often require substantial computational resources, which poses challenges for large-scale or real-time applications.

Machine learning techniques, particularly reinforcement learning, show promise in enabling real-time optimization of OPF by continuously learning from operational data and adjusting the system's control strategies. Despite their advantages, these methods are still developing and need substantial data for training, which can be resource-intensive [143].

In summary, while classical optimization methods remain essential in many applications, machine learning and stochastic optimization methodologies are emerging as more suitable solutions for dynamic and uncertain environments. However, computational efficiency and data requirements for these methods need to be addressed before they can be widely applied in large-scale systems.

7.3. Future Research Opportunities and Open Questions

Future research should focus on several critical areas to advance OPF for renewable-integrated IES:

1)

Cybersecurity Integration: As energy systems become more interconnected and reliant on digital technologies, cybersecurity becomes an essential aspect of OPF. Research should focus on developing OPF models that can withstand cyber-attacks in real-time. This could involve integrating cybersecurity measures into OPF formulations, such as using reinforcement learning-based defense strategies to detect and mitigate cyber threats as they arise.

2)

Quantum Computing: Quantum computing holds significant promise for addressing the computational challenges of OPF, particularly for large-scale, non-convex problems in IES. Future research should explore the potential of quantum computing for solving OPF problems more efficiently, enabling faster decision-making and improved scalability, especially in systems with high renewable energy penetration. Quantum annealing and quantum-inspired algorithms could revolutionize the optimization process for complex multi-energy systems.

3)

Real-time OPF Implementation: One of the most pressing challenges is enhancing OPF algorithms to support real-time decision-making. Future research should focus on improving the computational efficiency of OPF models to reduce the time required for optimization without sacrificing solution quality. This includes the development of more efficient algorithms, better integration of real-time data, and leveraging advanced computing technologies like cloud computing and distributed optimization.

4)

Advanced Forecasting and Scenario Generation: The ability to predict renewable energy generation with greater accuracy is critical for improving OPF performance. Research into more advanced forecasting techniques, such as hybrid machine learning models and probabilistic forecasting, could improve the accuracy of renewable generation predictions. Additionally, enhancing scenario generation methods, such as incorporating stochastic optimization and adaptive scenario-based models, would provide more reliable input for OPF models, allowing them to respond more effectively to varying system conditions.

5)

Hybrid Optimization Approaches: As renewable-integrated systems become more complex, hybrid optimization approaches that combine the strengths of different methodologies will likely play a key role. For example, combining machine learning for forecasting with stochastic optimization for decision-making could create more resilient and adaptive OPF models. Additionally, the integration of digital twins and blockchain into OPF frameworks presents opportunities to improve real-time monitoring, predictive analytics, and secure energy transactions.

Addressing these open questions will be crucial for enhancing the resilience, efficiency, and sustainability of renewable-integrated IES [144]. By continuing to develop and refine OPF strategies, integrating emerging technologies, and addressing current challenges, we can create more adaptive, secure, and efficient energy systems capable of supporting the global transition to renewable energy [145].

8. Conclusions

This review analyzes OPF techniques tailored for renewable-integrated integrated energy systems, focusing on challenges such as uncertainty management, computational complexity, and multi-energy network coordination. Progress in forecasting, probabilistic models, and machine learning has improved renewable generation prediction and uncertainty management. Multi-energy optimization strategies have enhanced the coordination of electricity, gas, and heat networks, improving efficiency and reducing costs. Emerging technologies like machine learning, quantum computing, and blockchain show potential for transforming OPF methodologies, though challenges remain regarding computational resources, real-time applicability, and integration. Future research should focus on cybersecurity, real-time OPF implementation, quantum computing, and hybrid optimization approaches to tackle IES complexities. Advancing these technologies will help create smarter, more resilient, and sustainable energy systems, driving the global transition to renewable energy.