A New Frailty Model Based Archimedean Bivariate Copula That Models Only Positive Dependency

1. Methodology of Derivation

This copula depends on the frailty method for generating the copula. Assuming two individuals have survival time distributed as exponential $T_1$ and $T_2$. They have exponential baseline hazard function with ${\lambda }_1={\lambda }_2=1$. The survival function is shown in equation (1) and the hazard function in equation (2)

$$S\left(t\right)=Prob\left(T>t\right)=1-F\left(t\right)$$

(1)

$$h\left(t\right)=-{\displaystyle \frac{\mathsf{\partial }\ln S\left(t\right)}{\mathsf{\partial }t}}={\displaystyle \frac{F\left(t\right)}{S\left(t\right)}}$$

(2)

The Cox proportional hazard model uses the hazard function as shown in equation (3)

$$\left(t,Z\right)=e^{\beta Z}b\left(t\right)$$

(3)

where the Z are the explanatory variables in survival analysis and b(t) is the baseline hazard function. And B is the vector of regression coefficients. It is proportional because all information is contained in the multiplicative factor $\gamma =e^{BZ}$, this is called the frailty model when some explanatory variables (Z) and hence the factor $\gamma$ are unobserved. And the factor $\gamma$ is called the frailty parameter. Integrating and exponentiating the negative hazard

$\lambda =e^{{\beta }_0+{\beta }_1{Z}_1+{\beta }_2{Z}_2}=e^{{\beta }_0}{e}^{{\beta }_1{Z}_1+{\beta }_2{Z}_2}={\lambda }_0{e}^{{\beta }_1{Z}_1+{\beta }_2{Z}_2}$ for 2 explanatory variables for example

$$\begin{gathered} S\left(t|\gamma \right)=exp\left(-{\int }_0^t-{\displaystyle \frac{\mathsf{\partial }\ln S\left(t\right)}{\mathsf{\partial }t}}\right)dt=exp\left(-{\int }_0^{t}h\left(t\right)\right)dt=exp\left(-{\int }_0^t\lambda \right)dt \\ exp\left(-{\int }_0^t{e}^{{\beta }_0+{\beta }_1{Z}_1+{\beta }_2{Z}_2}\right)dt=exp\left(-{\int }_0^t{e}^{{\beta }_0\gamma }\right)dt=exp\left(-\gamma {\int }_0^t{e}^{{\beta }_0}\right)dt \\ {e}^{\left(-\gamma {\int }_0^t{e}^{{\beta }_0}dt\right)}={\left[e^{\left(-{\int }_0^t{\lambda }_{0}dt\right)}\right]}^{\gamma }={\left[e^{-t{\lambda }_0}\right]}^{\gamma }where{e}^{{\beta }_0}={\lambda }_{0}assume{\lambda }_0=1 \\ {\left[B\left(t\right)\right]}^{\gamma }whereB\left(t\right)isthebaselinehazard,\mathrm{to}\mathrm{sum}\mathrm{up} \\ {\left[e^{-t{\lambda }_0}\right]}^{\gamma }={\left[e^{-S_{0\left(t\right)}}\right]}^{\gamma }=e^{-t\gamma }=S\left(t|\gamma \right) \end{gathered}$$

The marginal distribution for a single life time T is obtained by taking expectation over the potential values of $\gamma$ that is $E\left(e^{-t\gamma }\right)$, assuming the $f\left(\gamma \right)$ is the PDF of the frailty variable so

$$E\left(e^{-t\gamma }\right)={\int }_0^{\infty }{e}^{-t\gamma }f\left(\gamma \right)d\gamma$$

Let y be a random variable distributed as Median Based Unit Rayleigh (BMUR) (Attia, M.I., 2024), transform this variable to be defined on the interval from zero to infinity as shown below. The PDF of the Median Based Unit Rayleigh (MBUR) is shown in equation (4)

$${\displaystyle \frac{6}{{\alpha }^2}}\left[1-y^{{\displaystyle \frac{1}{{\alpha }^2}}}\right]y^{\left({\displaystyle \frac{2}{{\alpha }^2}}-1\right)},0<y<1,\alpha >0$$

(4)

The following transformation will be applied to the above PDF:

Let $w=-\ln {\left(y\right)}^{{\displaystyle \frac{1}{{\alpha }^2}}}\to w={\displaystyle \frac{-\ln y}{{\alpha }^2}}\to -w{\alpha }^2=\ln y\to y=e^{-{\alpha }^{2}w}$

The Jacobian is shown in equation (5) $dy=e^{-{\alpha }^{2}w}\left(-{\alpha }^2\right)dw\dots \dots \dots \dots \dots \dots \dots \dots ..\left(5\right)$

Replace the transformation of equation (5) into equation (4) as shown in equation (6):

$$\begin{gathered} {\int }_0^{\mathrm{\infty }}{\displaystyle \frac{6}{{\alpha }^2}}\left[1-{\left(e^{-{\alpha }^{2}w}\right)}^{{\displaystyle \frac{1}{{\alpha }^2}}}\right]{\left(e^{-{\alpha }^{2}w}\right)}^{\left({\displaystyle \frac{2}{{\alpha }^2}}\right)}{\left(e^{-{\alpha }^{2}w}\right)}^{-1}\left({\alpha }^2\right)e^{-{\alpha }^{2}w}dw\dots \dots \dots \dots \dots \dots \dots \\ {\int }_0^{\mathrm{\infty }}6\left[1-e^{-{\displaystyle \frac{{\alpha }^{2}w}{{\alpha }^2}}}\right]e^{-{\displaystyle \frac{2{\alpha }^{2}w}{{\alpha }^2}}}dw \end{gathered}$$

(6.A)

$$f_W\left(w\right)=6\left[1-e^{-w}\right]e^{-2w}\dots$$

(6.B)

Now this w is the frailty variable$\gamma$ which is distributed as unbounded MBUR defined on the interval $\left(0,\infty \right)$. Now take the conditional expectation of the survival function of the time distributed as exponential random variable with hazard rate equal one (scale parameter or lambda=1) given the frailty variable as shown in equation (7)

$$\begin{gathered} E\left(e^{-t\gamma }\right)={\int }_0^{\mathrm{\infty }}{e}^{-t\gamma }f\left(\gamma \right)d\gamma \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \\ ={\int }_0^{\mathrm{\infty }}\left(e^{-t\gamma }\right)6\left[1-e^{-\gamma }\right]e^{-2\gamma }d\gamma =6{\int }_0^{\mathrm{\infty }}{e}^{-\gamma \left(t+2\right)}d\gamma -6{\int }_0^{\mathrm{\infty }}{e}^{-\gamma \left(t+3\right)}d\gamma \\ =6{\left.\left[{\displaystyle \frac{e^{-\gamma \left(t+2\right)}}{-\left(t+2\right)}}\right]\right|}_0^{\mathrm{\infty }}-6{\left.\left[{\displaystyle \frac{e^{-\gamma \left(t+3\right)}}{-\left(t+3\right)}}\right]\right|}_0^{\mathrm{\infty }}=6\left[\left({\displaystyle \frac{1}{t+2}}\right)-\left({\displaystyle \frac{1}{t+3}}\right)\right] \\ E\left(e^{-t\gamma }\right)=E\left(S\left(t\right|\gamma \right))={\displaystyle \frac{6}{\left(t+2\right)\left(t+3\right)}}={\displaystyle \frac{6}{t^2+5t+6}} \end{gathered}$$

(7)

We can think of this expectation as a function of the frailty variable, it is averaging the probability to survive beyond specific time given that frailty. It is the expectation of a function of the frailty not the variable frailty itself so this function which is the baseline survival function should be multiplied by the PDF of the frailty variable. This way the frailty variable is integrated out. So this expectation is considered as the joint CDF of the two random variables T1 and T2. How to get this time? By inverting this expectation as shown in equation (8). Let us call this expectation u then solving second degree polynomial to get its root.

$$\begin{gathered} \left(u={\displaystyle \frac{6}{t^2+5t+6}}\right)\to \left({\displaystyle \frac{6}{u}}=t^2+5t+6\right)\to \left(t^2+5t+6-{\displaystyle \frac{6}{u}}=0\right) \\ t={\displaystyle \frac{-5+\sqrt{25-4\left(1\right)\left(6\right)\left(1-\frac{1}{u}\right)}}{2}}={\displaystyle \frac{-5+\sqrt{25-24\left(1-\frac{1}{u}\right)}}{2}} \\ t={\displaystyle \frac{\left(-5+\sqrt{\left(25-24+\frac{24}{u}\right)}\right)}{2}}={\displaystyle \frac{\left(-5+\sqrt{\left(1+\frac{24}{u}\right)}\right)}{2}}\dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \dots \end{gathered}$$

(8)

2. The Generator

In previous work by Iman M. Attia (Attia, 2025), the generator obtained by this method (modeling the frailty variable) yielded a Kendall tau measure that is fixed. As shown here the same method with different re-parameterization yielded a generator with no dependency parameter; therefore, the author did some manipulations to enhance the Kendall tau measures. The author added dependency parameter and remove the denominator as shown in the following equation (9), $u$ is the marginal CDF.

$$t=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}},0<u<1$$

(9)

This (t) is the generator and (u) is the inverse generator. So the time (t) is a function of (u)

Preposition 1

: the generator shown in equation (9), $t=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}$ can be considered as a generator for this new Archimedean copula.

Proof 

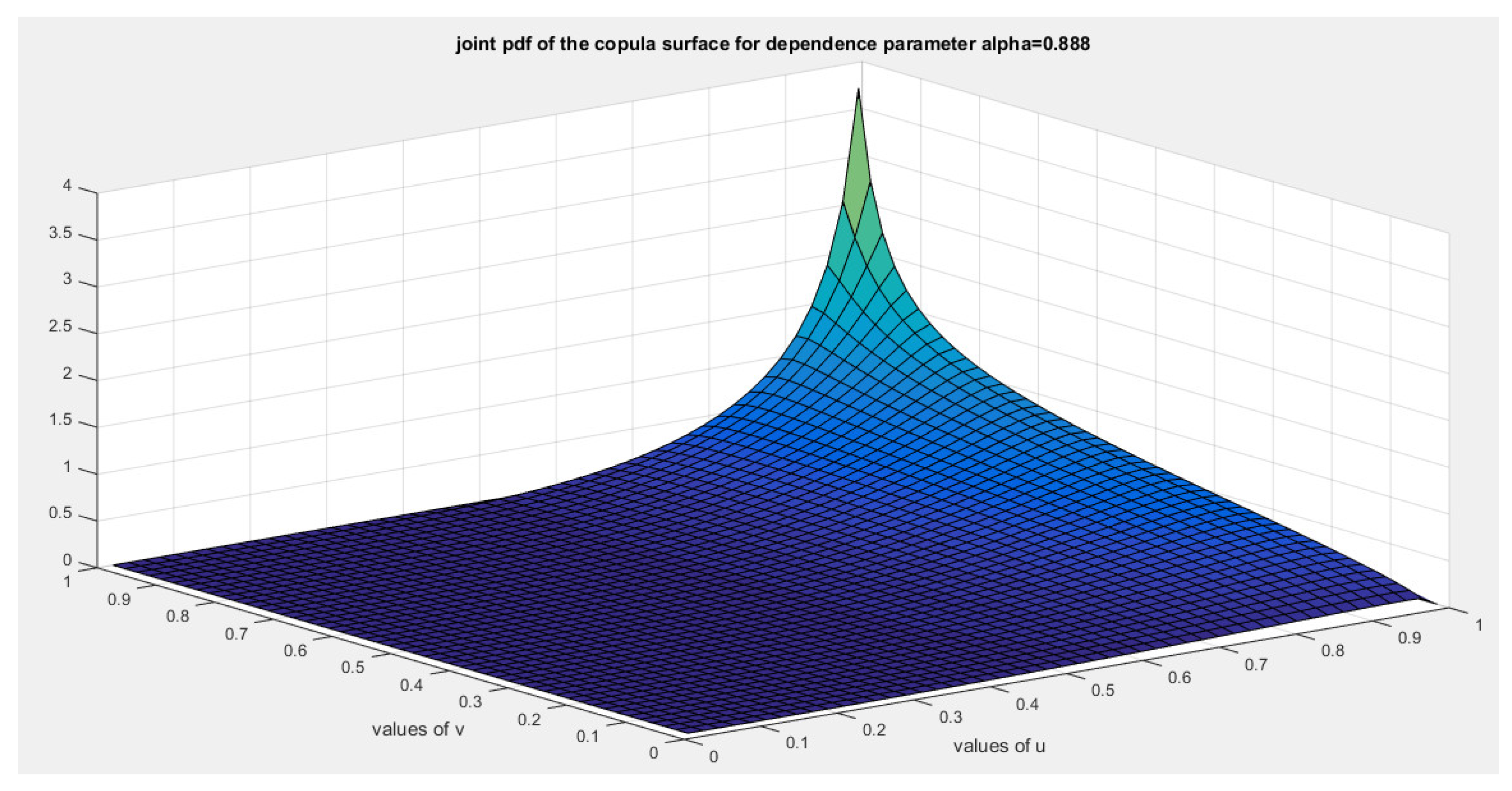
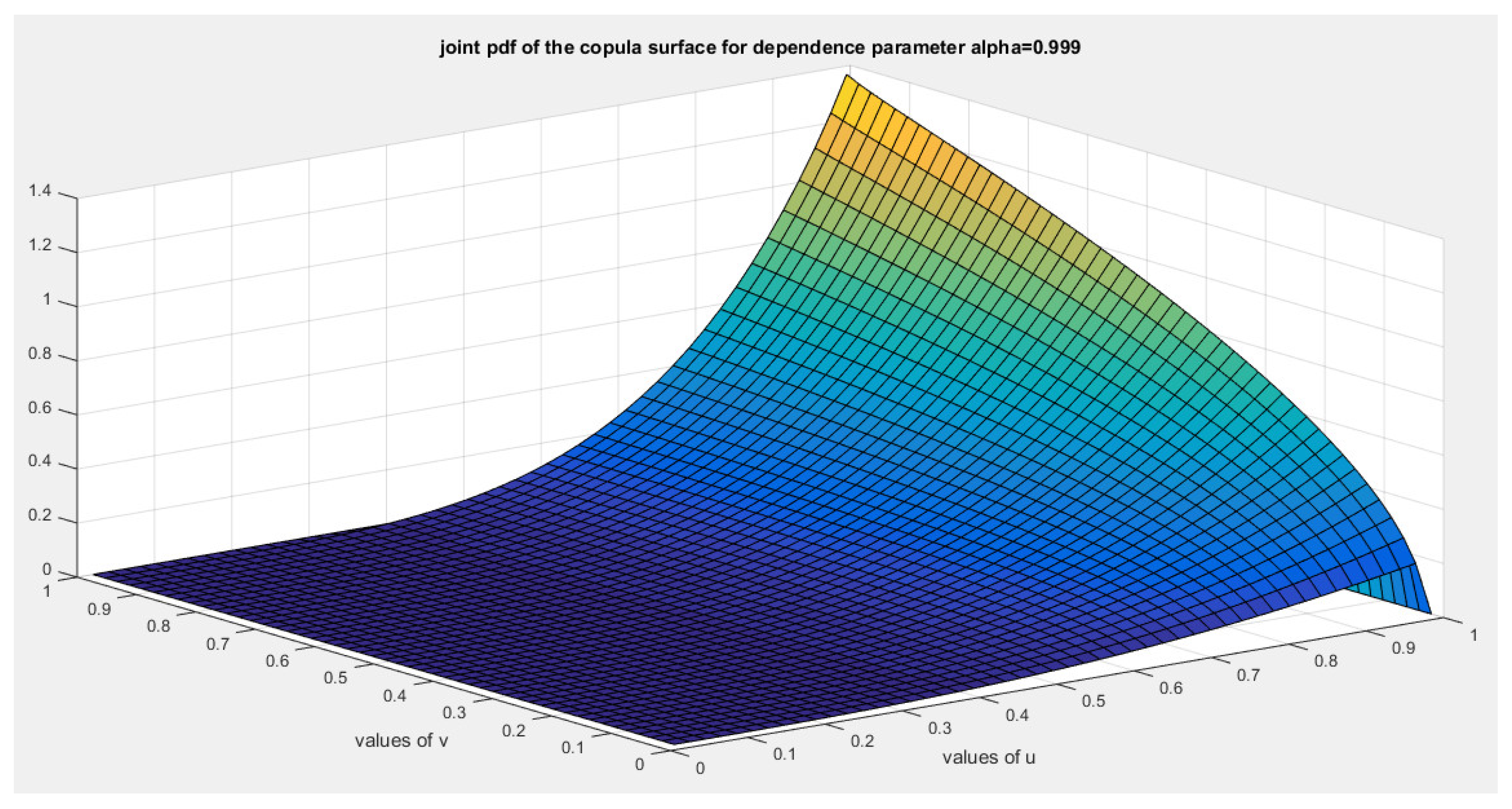
: The generator fulfills the sufficient conditions of a generator.

1)

$\phi \left(0\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{\left(0\right)}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}=\infty$

2)

$\phi \left(1\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{\left(1\right)}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}=0$

3)

${\phi }^{\text{'}}\left(u\right)={\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-0.5}\left({\displaystyle \frac{-12}{u^2}}\right)<0$

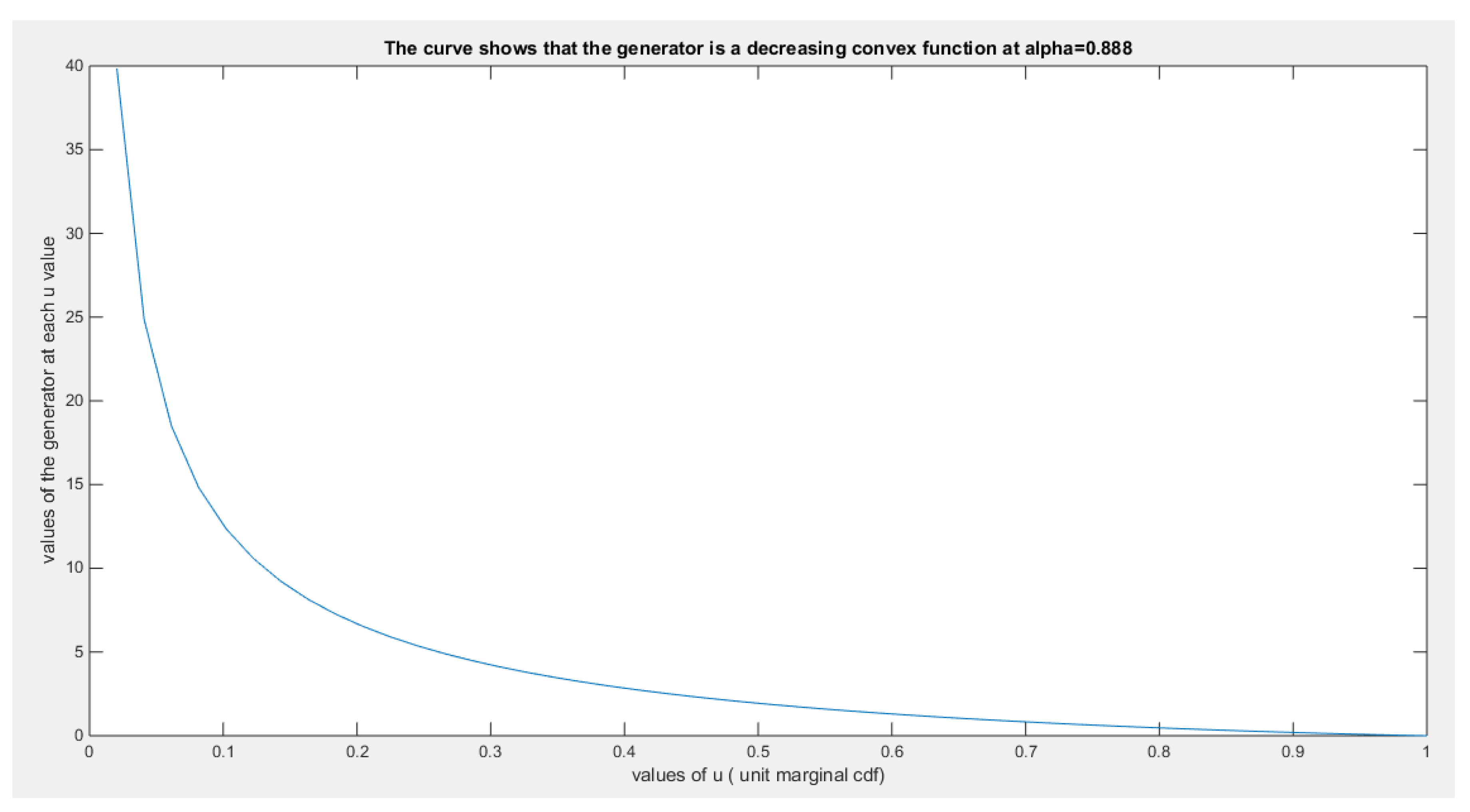
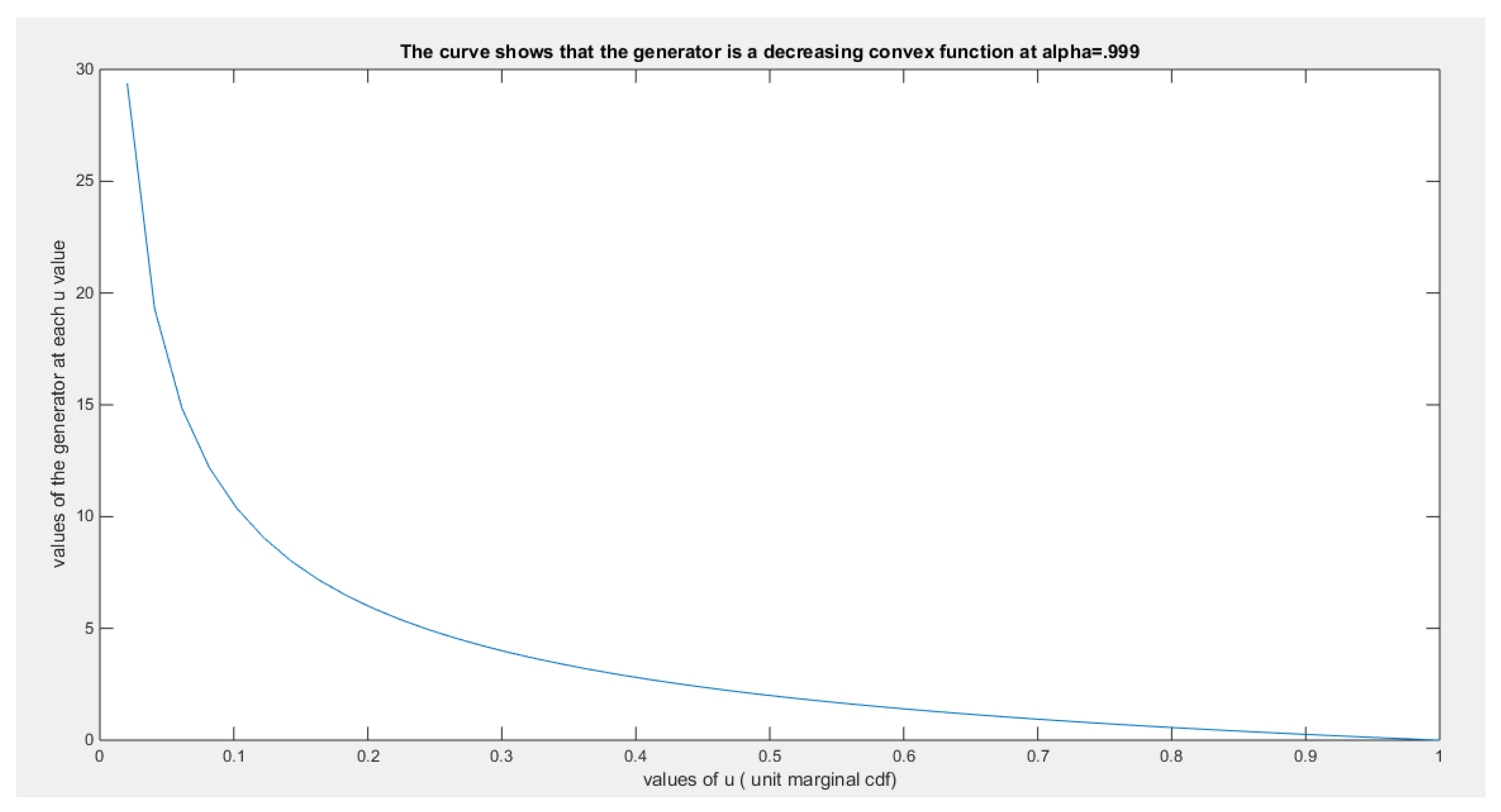
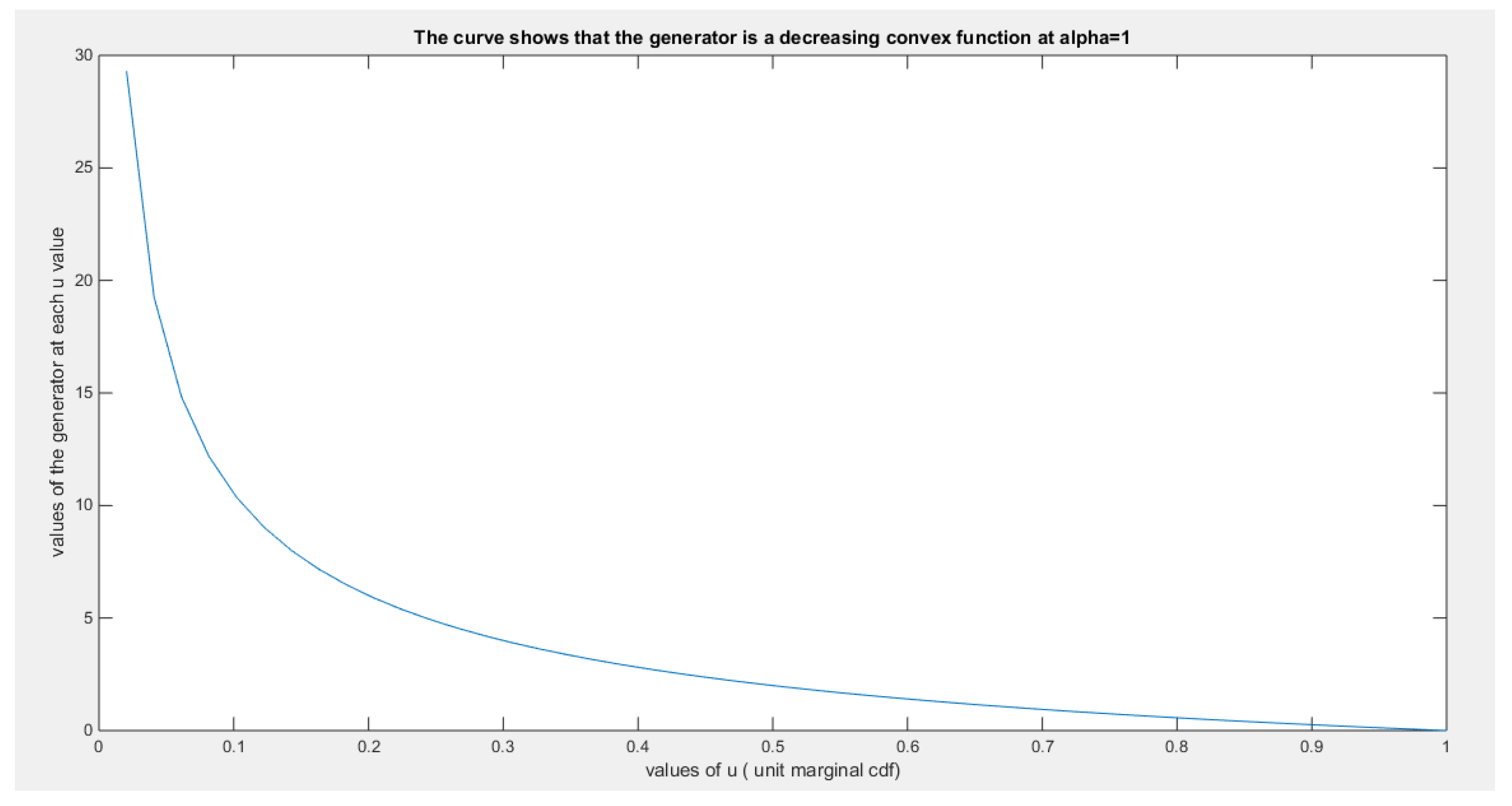
This ensures that the generator is a decreasing function in u.

4)

${\phi }^{\text{'}\text{'}}\left(u\right)=\left({\displaystyle \frac{1}{\theta }}-1\right){\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-2}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-1}{\left({\displaystyle \frac{-12}{u^2}}\right)}^2+$${\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left({\displaystyle \frac{-1}{2}}\right){\left(1+{\displaystyle \frac{24}{u}}\right)}^{-1.5}{\left({\displaystyle \frac{-12}{u^2}}\right)}^2+$${\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-0.5}\left({\displaystyle \frac{24}{u^3}}\right)>0$

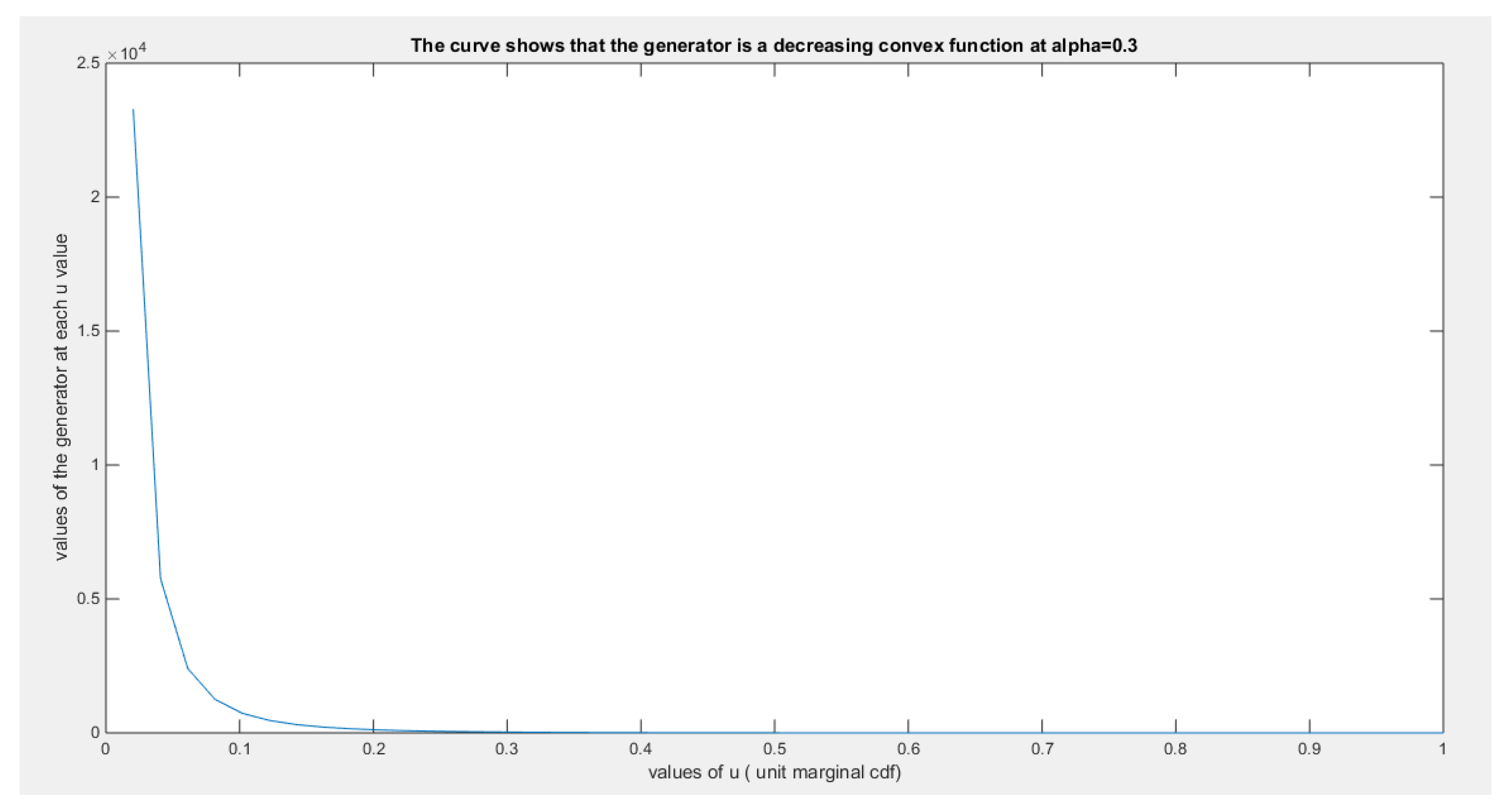
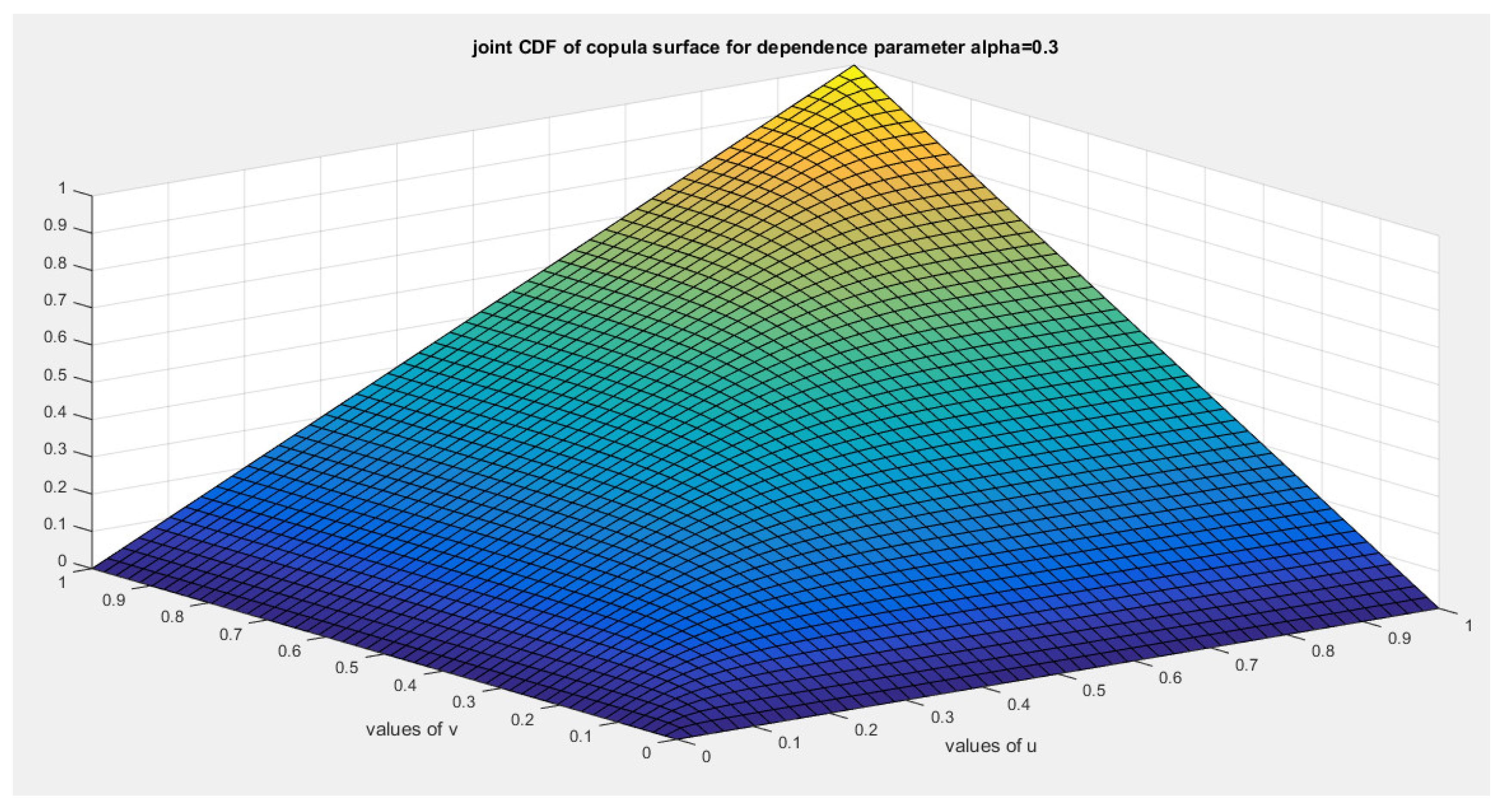
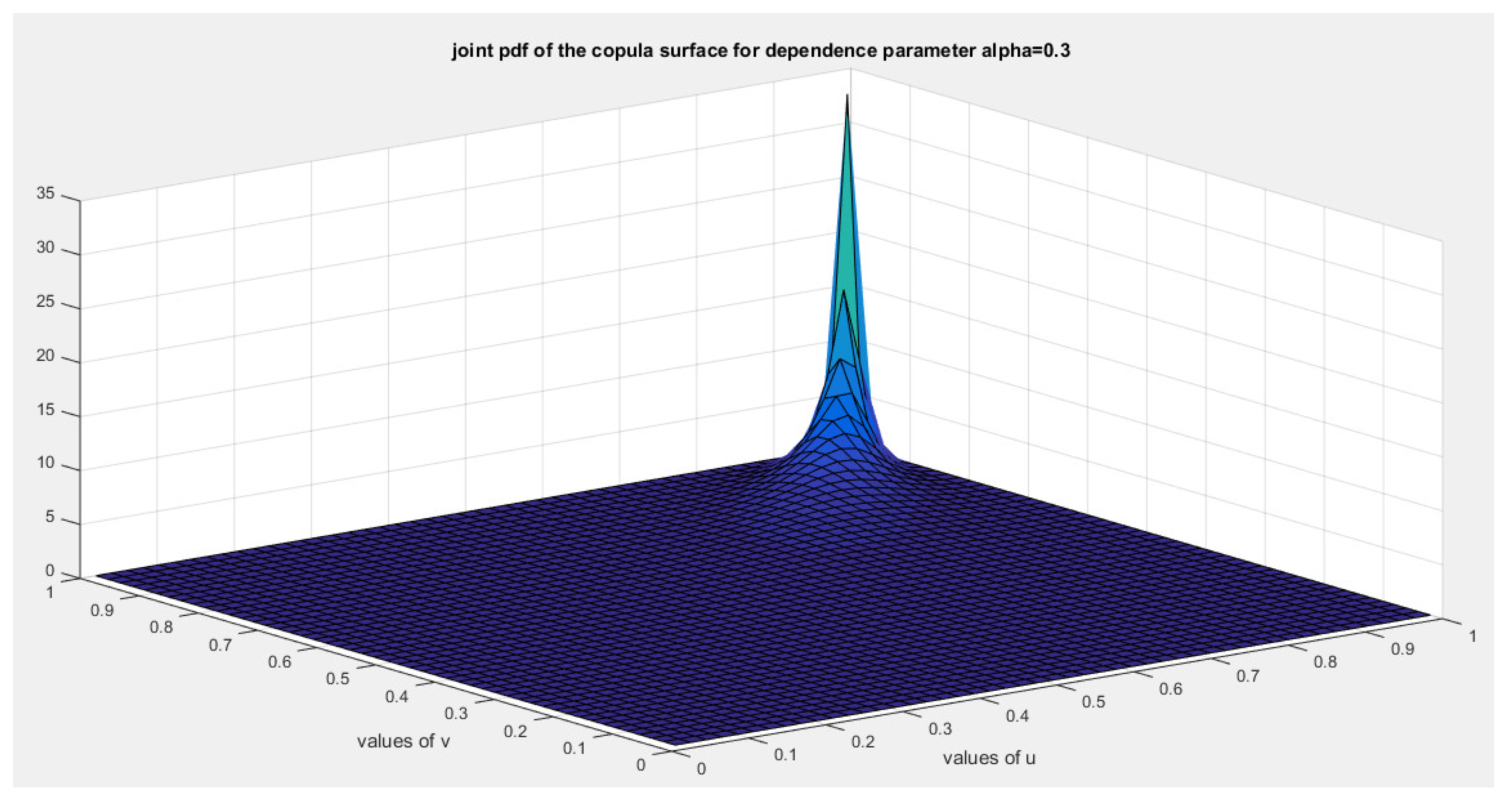
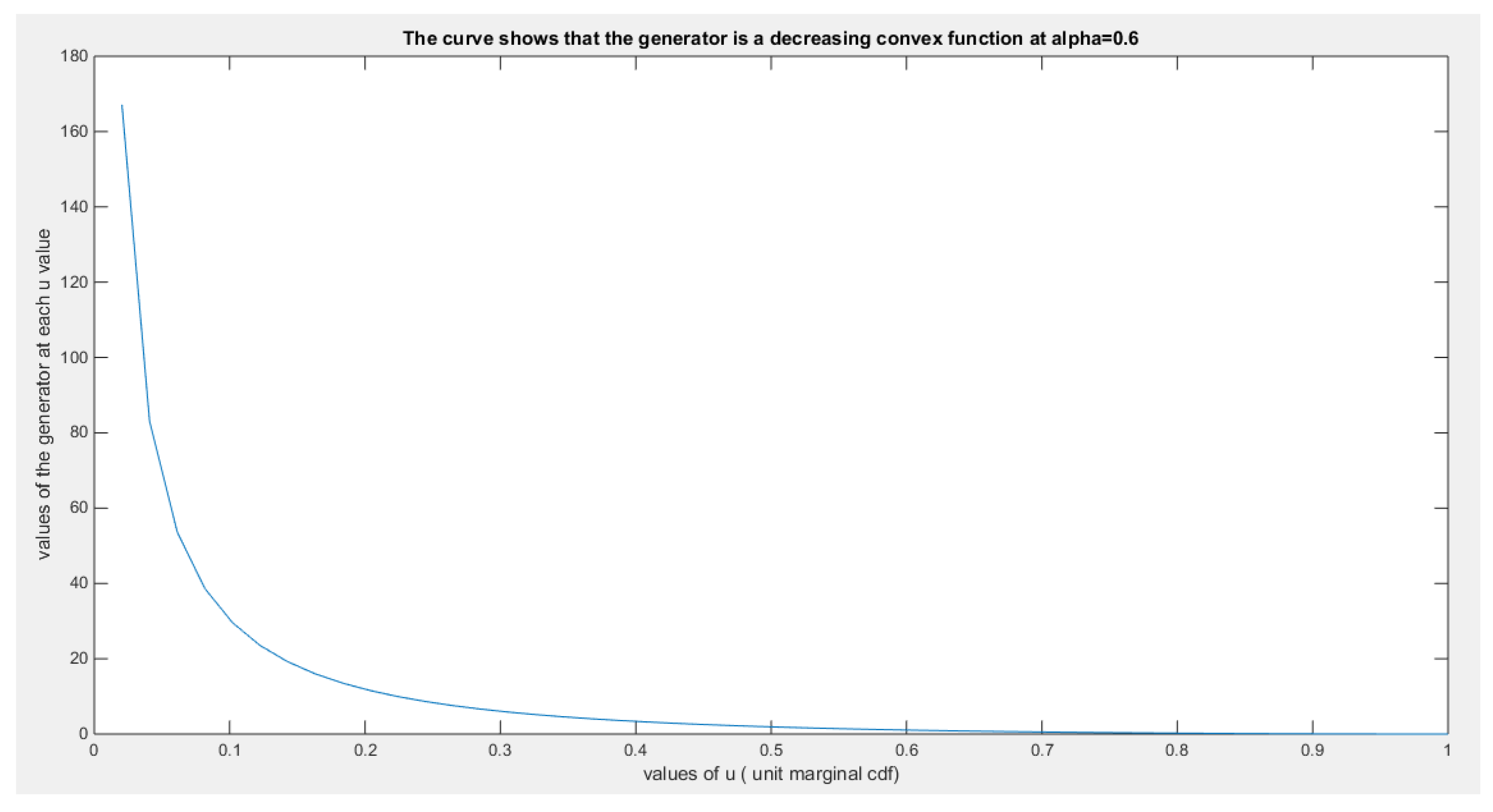
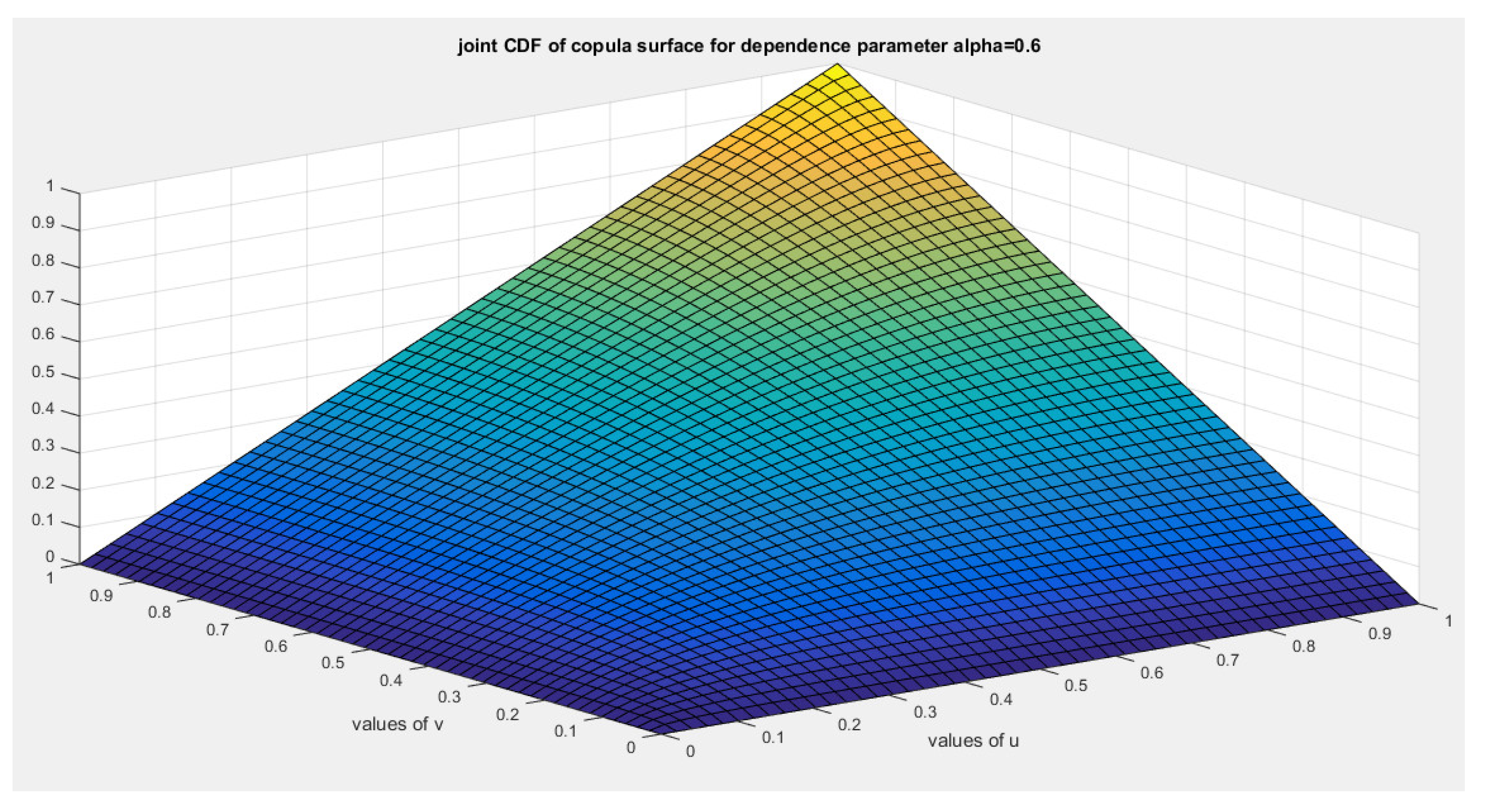
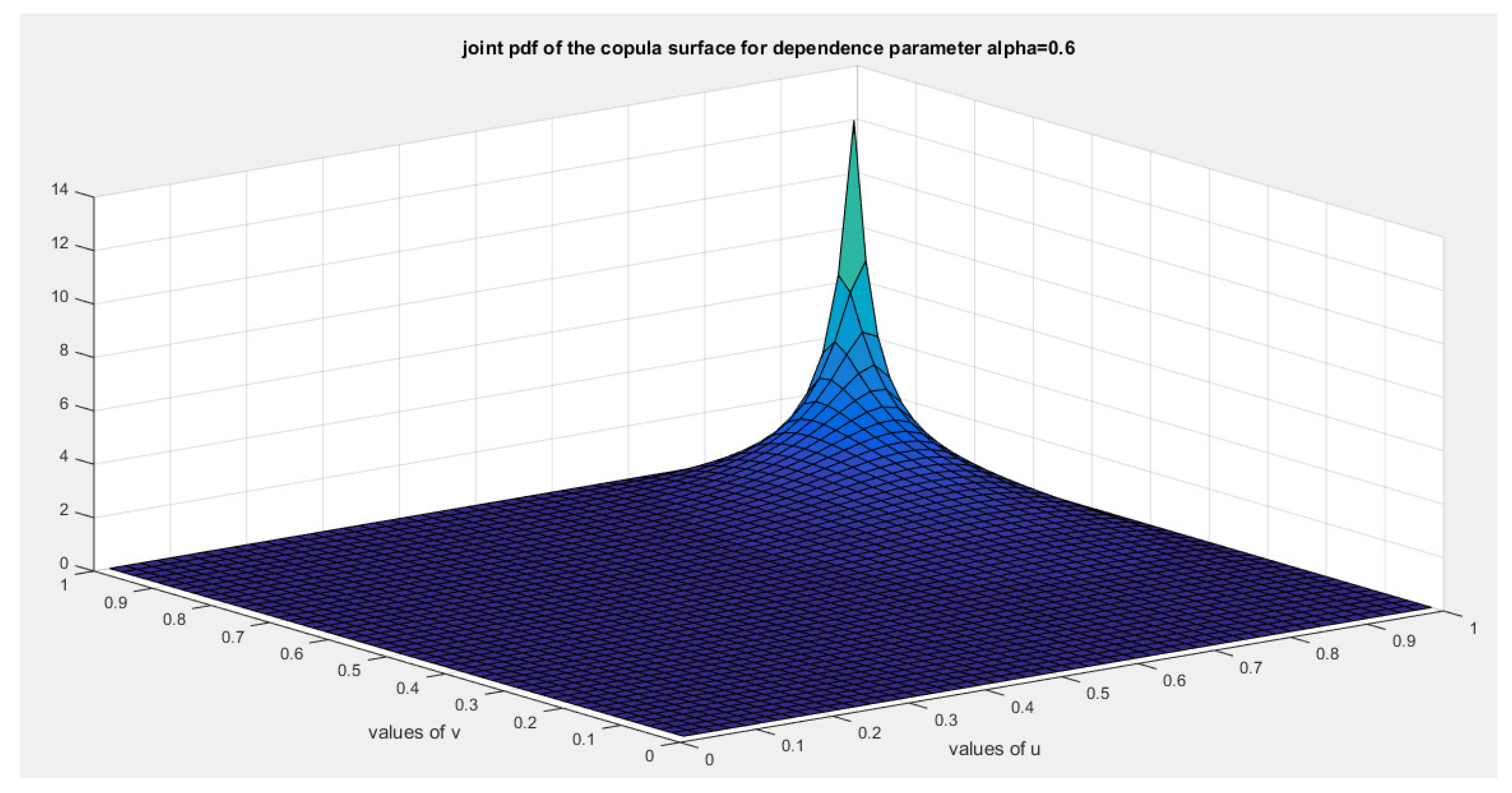
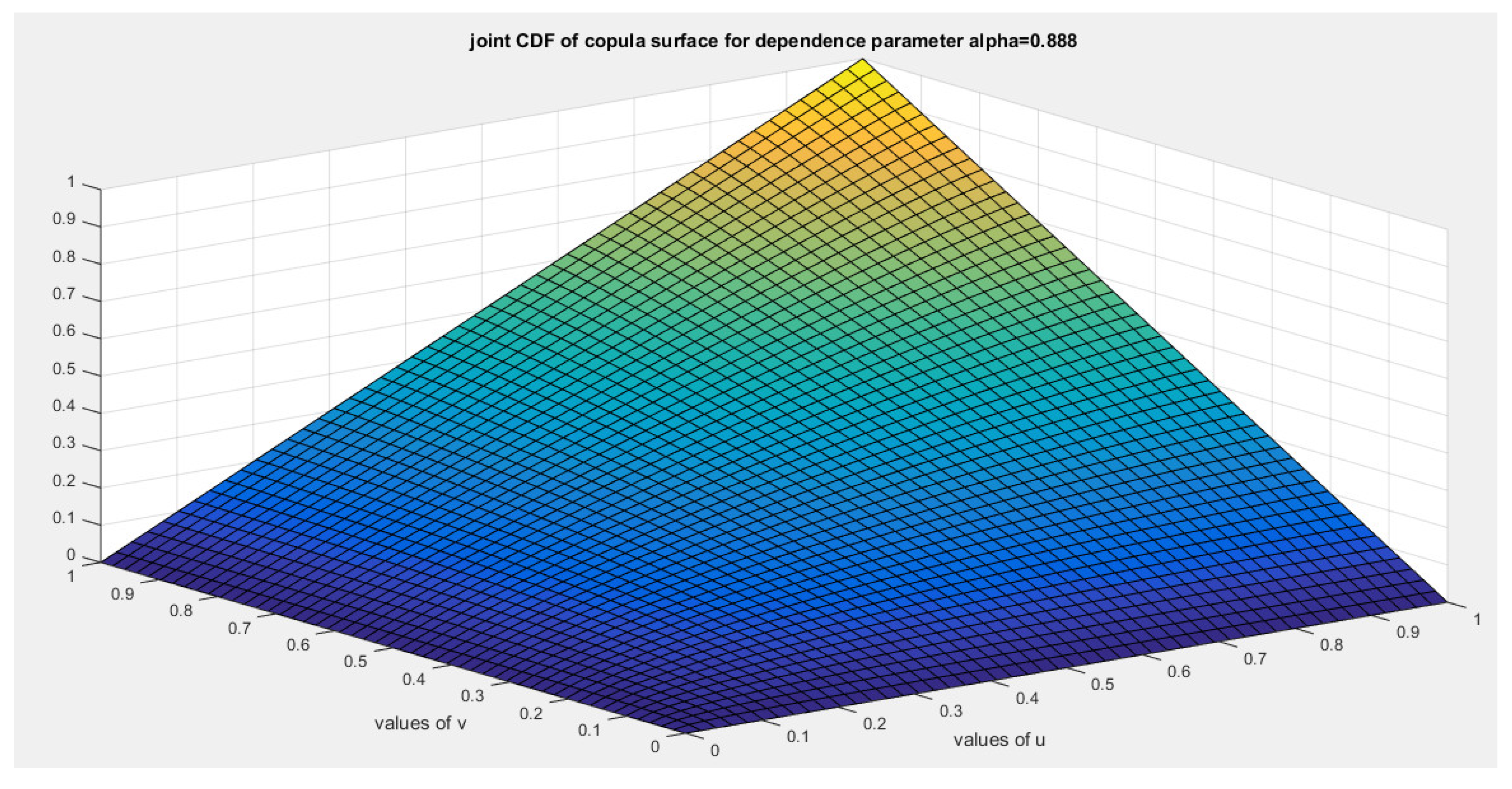
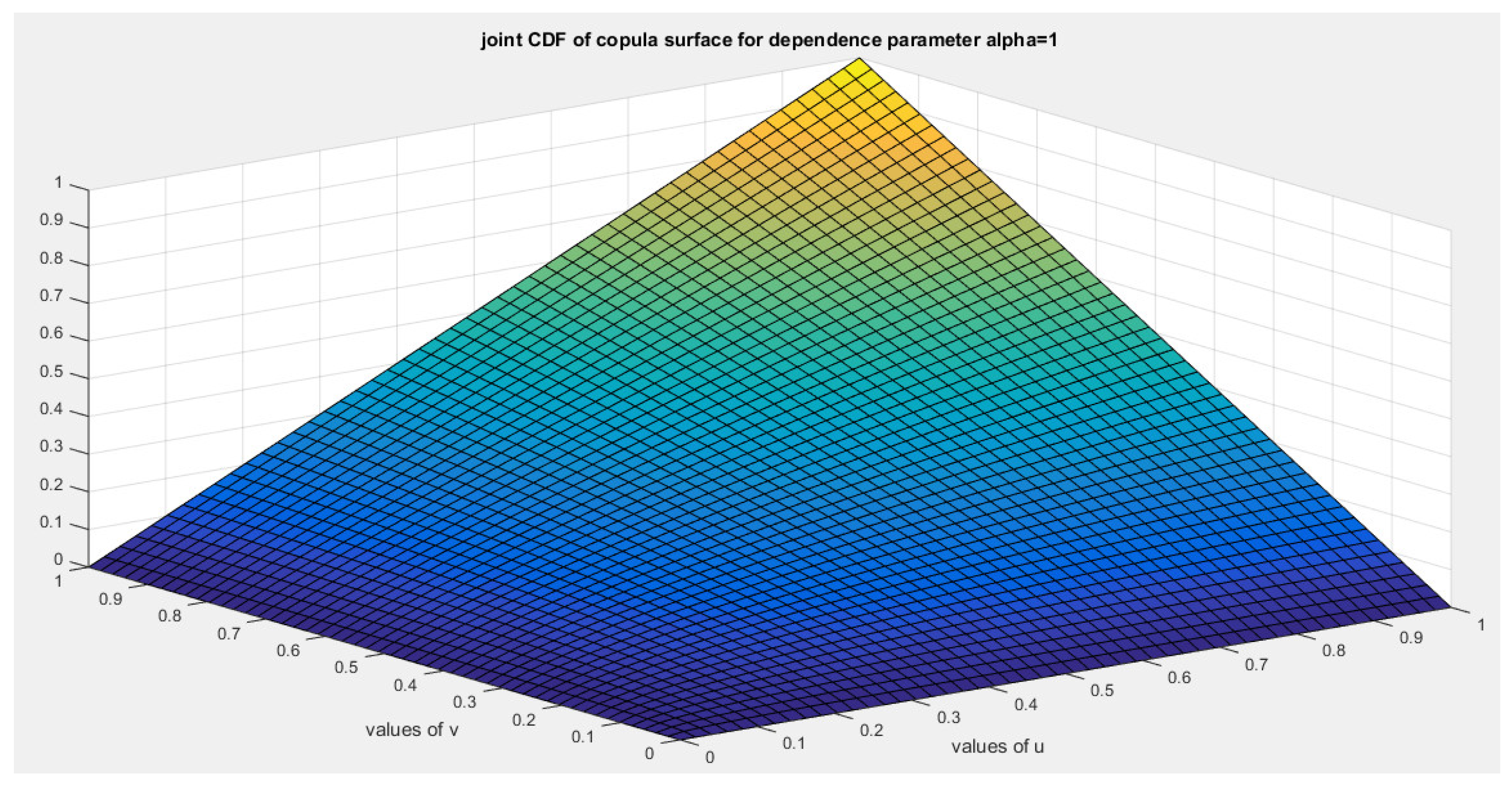
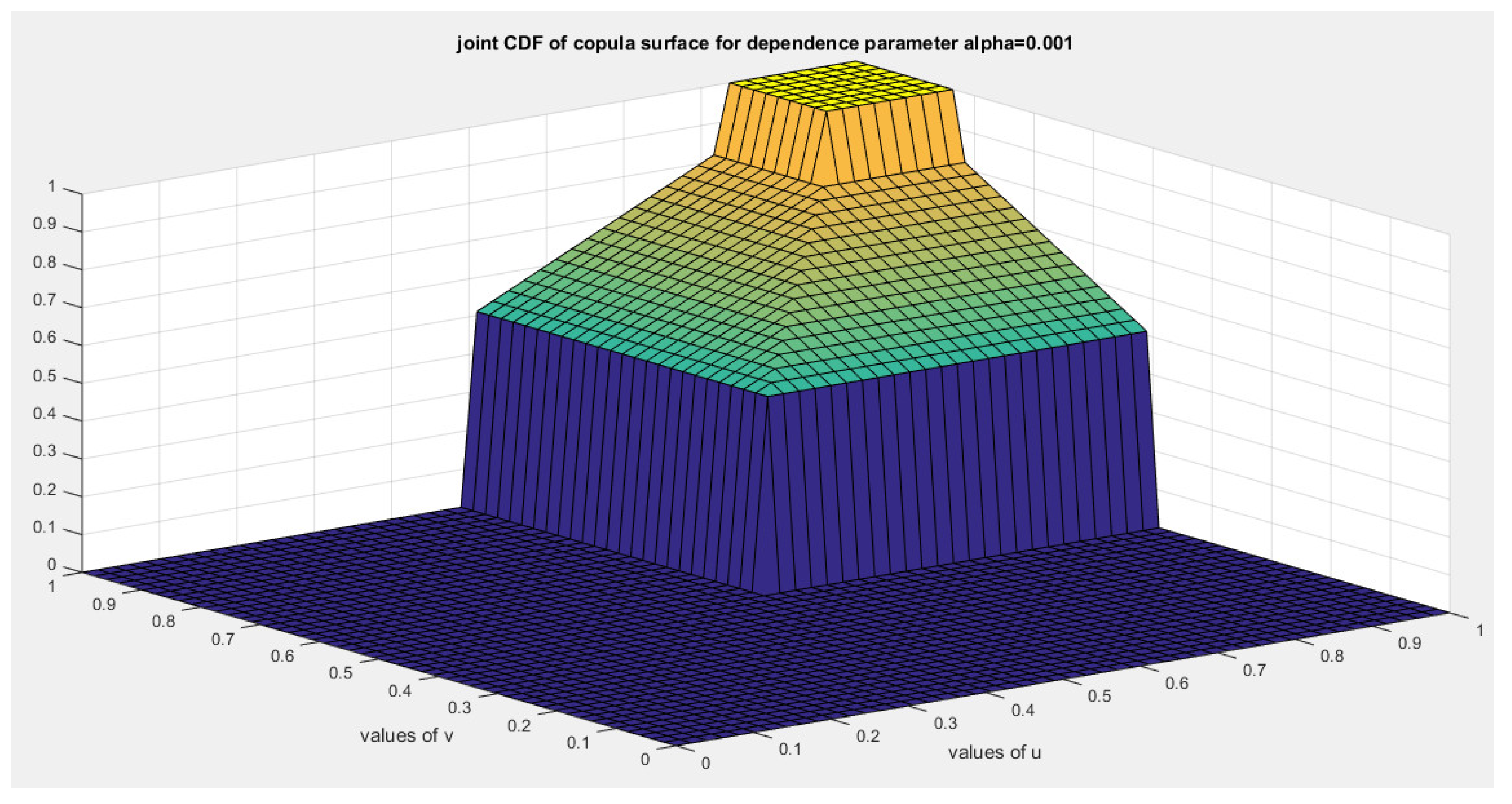
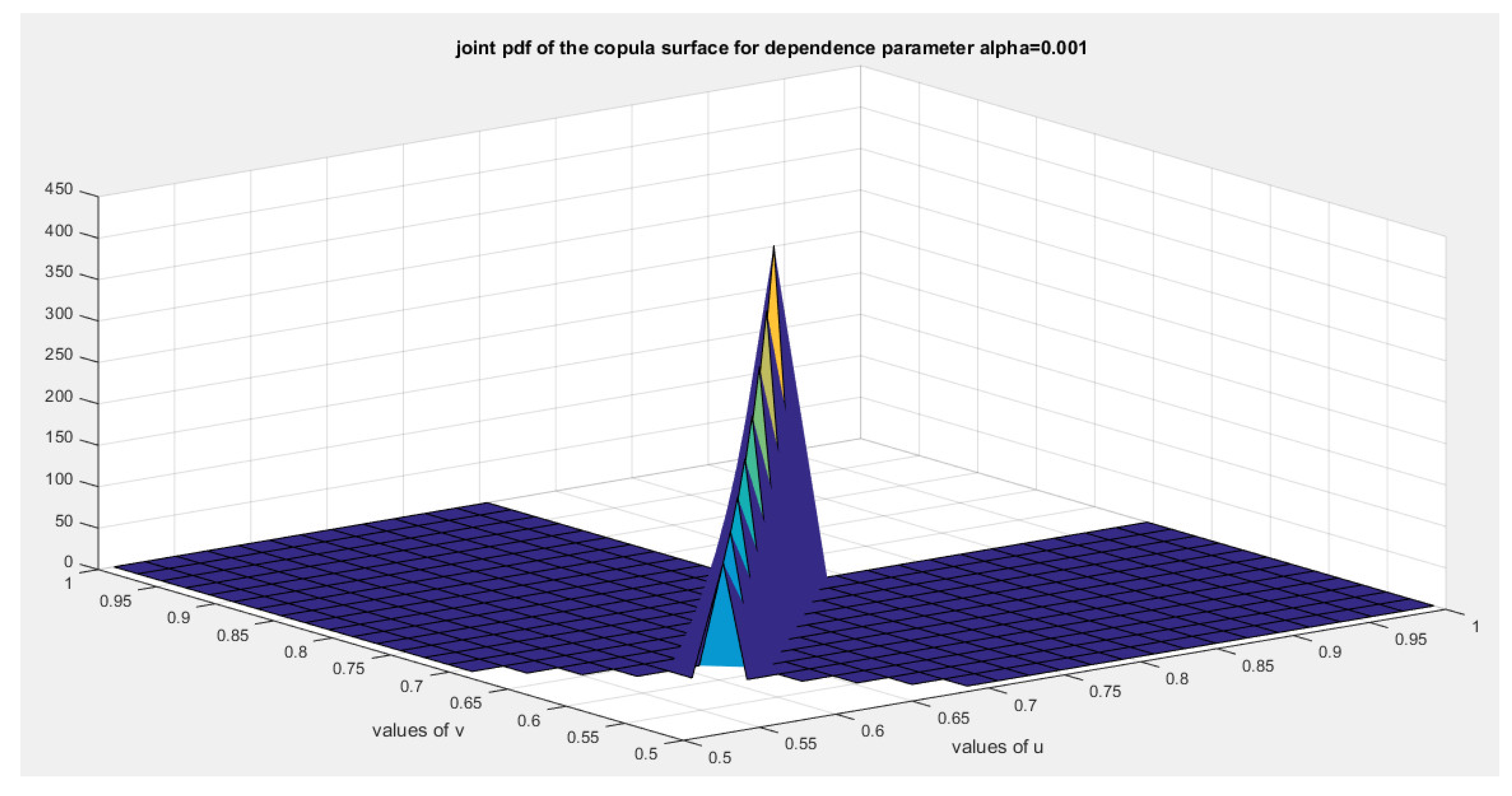
This ensures that the generator is a convex function at $0<\theta \le 1$

For bivariate distribution with uniform marginal CDF (u) and (v), the generators are shown in equations (10-12)

$$\phi \left(u\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}$$

(10)

$$\phi \left(v\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}$$

(11)

$$\begin{gathered} \phi \left(w\right)=\phi \left(u\right)+\phi \left(v\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}+\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\dots ) \\ \phi \left(w\right)=\theta \left\{{\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}+{\left(-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right\} \end{gathered}$$

(12)

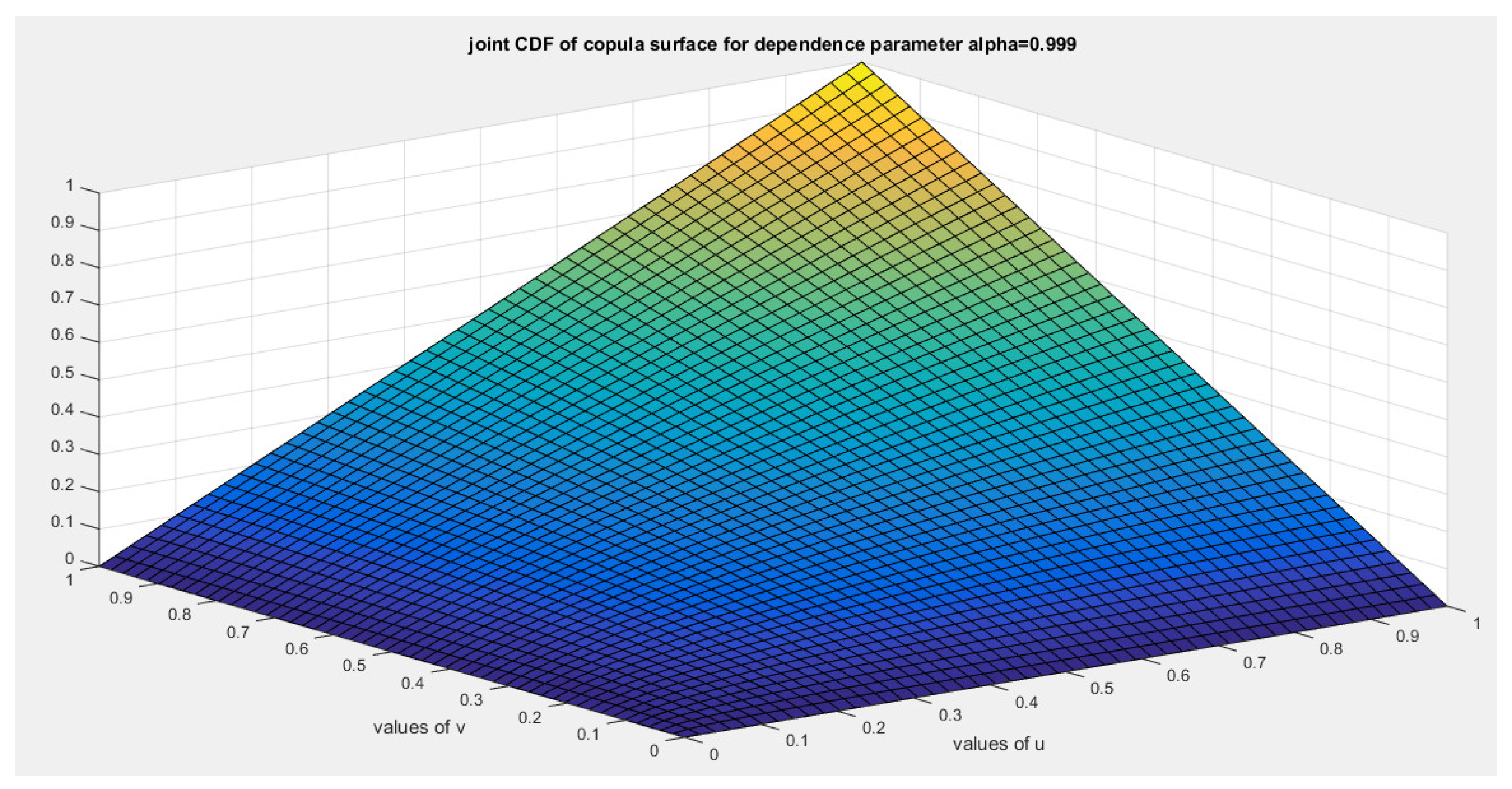
3. The Inverse Generator

To get the inverse generator of this modified generator, the author inverts this (t) as shown in equation (13), as long as t equals:

$$\begin{gathered} t=\phi \left(u\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}},0<\theta \le 1 \\ u={\phi }^{-1}\left(u\right)={\displaystyle \frac{24}{{\left[{\left(\frac{t}{\theta }\right)}^{\theta }+5\right]}^2-1}}=24{\left({\left[{\left({\displaystyle \frac{t}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1},0<\theta \le 1 \end{gathered}$$

(13)

Recall that $C\left(\phi \left(u\right)+\phi \left(v\right)\right)={\phi }^{-1}\left(\phi \left(u\right)+\phi \left(v\right)\right)$

As a valid bivariate Archimedean copula can be expressed as $\mathsf{C}(u,v)=C\left(F_X\right(x),F_Y(y\left)\right)$

Proposition 2

: The copula expressed in equation (13) can be assumed to be a valid copula as it fulfills the boundary conditions, the marginal uniformity and 2- increasing conditions. And this is equivalent to the necessary conditions of the inverse generator to be fulfilled which are the following:

Proof: 

$\mathrm{C}\left(0,v\right)=\mathrm{C}\left(u,0\right)=0$, boundary conditions are fulfilled

$$\mathrm{C}\left(0,v\right)=24{\left({\left[{\left({\displaystyle \frac{\theta \left\{{\left(-5+{\left(1+\frac{24}{0}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}+{\left(-5+{\left(1+\frac{24}{v}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}\right\}}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}=0$$

$\mathrm{C}\left(1,v\right)=vand\mathrm{C}\left(u,1\right)=u$, the marginal uniformity, when u=1

$$\begin{gathered} \mathrm{C}\left(1,v\right)=24{\left({\left[{\left({\displaystyle \frac{\theta \left\{{\left(-5+{\left(1+\frac{24}{1}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}+{\left(-5+{\left(1+\frac{24}{v}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}\right\}}{\theta }}\right)}^{\theta }+5\right]}^2-1\right)}^{-1}=v \\ \mathrm{C}\left(1,v\right)=24{\left({\left[{\left(\left\{{\left(-5+{\left(1+{\displaystyle \frac{24}{1}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}+{\left(-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right\}\right)}^{\theta }+5\right]}^2-1\right)}^{-1} \\ \mathrm{C}\left(1,v\right)=24{\left({\left[{\left({\left(-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2-1\right)}^{-1} \\ \mathrm{C}\left(1,v\right)=24{\left({\left[-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}+5\right]}^2-1\right)}^{-1}=24{\left({\left[{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}}\right]}^2-1\right)}^{-1} \\ C\left(1,v\right)=24{\left(\left(1+{\displaystyle \frac{24}{v}}\right)-1\right)}^{-1}=24{\left({\displaystyle \frac{24}{v}}\right)}^{-1}=v \end{gathered}$$

The same is true for v, if v=1 so $C\left(u,1\right)=24{\left({\displaystyle \frac{24}{v}}\right)}^{-1}=v$

Proposition 3

: This is a valid copula as it is 2-increasing, i.e., ${\displaystyle \frac{{\mathsf{\partial }}^2\mathrm{C}\left(u,v\right)}{\mathsf{\partial }u\mathsf{\partial }v}}\ge 0$ in equation (14)

Proof: 

Let

$$\begin{gathered} p=-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}} and q=-5+{\left(1+{\displaystyle \frac{24}{v}}\right)}^{{\displaystyle \frac{1}{2}}} \\ {\displaystyle \frac{\mathsf{\partial }C\left(u,v\right)}{\mathsf{\partial }u}}= \\ -48{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta -1}\left[p^{{\displaystyle \frac{1}{\theta }}-1}\right]{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{-1}{2}}}\left({\displaystyle \frac{-12}{u^2}}\right) \\ {\displaystyle \frac{\mathsf{\partial }}{\mathsf{\partial }v}}\left({\displaystyle \frac{\mathsf{\partial }C\left(u,v\right)}{\mathsf{\partial }u}}\right)={\displaystyle \frac{{\mathsf{\partial }}^2\mathrm{C}\left(u,v\right)}{\mathsf{\partial }u\mathsf{\partial }v}}= \\ =\left(-48\right)\left({\displaystyle \frac{144}{u^2{v}^2}}\right)\left[{\left(pq\right)}^{{\displaystyle \frac{1}{\theta }}-1}\right]{\left[\left(1+{\displaystyle \frac{24}{u}}\right)\left(1+{\displaystyle \frac{24}{v}}\right)\right]}^{{\displaystyle \frac{-1}{2}}}{\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-2}{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta -2} \\ \times \left\{\left(-4\right){\left[{\left({\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right)}^2-1\right]}^{-1}{\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]}^2{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }+{\left[p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right]}^{\theta }+\left[{\left(p^{{\displaystyle \frac{1}{\theta }}}+q^{{\displaystyle \frac{1}{\theta }}}\right)}^{\theta }+5\right]\left[{\displaystyle \frac{\theta -1}{\theta }}\right]\right\}\ge 0,0<\theta \le 1\dots \end{gathered}$$

(14)

Proposition 4

: This copula is absolutely continuous copula and it has no singular part.

Proof: 

to test for singularity: $\underset{u\to 0}{\lim }{\displaystyle \frac{\phi \left(0\right)}{{\phi }^{\text{'}}\left(0\right)}}=0$ in equation (15). If this limit is zero so the copula has no singular part.

$$\begin{gathered} {\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\text{'}}\left(u\right)}}={\displaystyle \frac{\theta {\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }}}{\theta \left(\frac{1}{\theta }\right){\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}} \\ \underset{u\to 0}{\lim }{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\text{'}}\left(u\right)}}=\left({\displaystyle \frac{-\theta }{12}}\right)\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right){\left(1+{\displaystyle \frac{24}{u}}\right)}^{0.5}{u}^2 \\ \underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{5\theta {\left(\frac{24+u}{u}\right)}^{0.5}{u}^2}{12}}+\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{\theta \left(\frac{24+u}{u}\right)u^2}{-12}} \\ \underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{5\theta {\left(u+24\right)}^{0.5}{u}^{1.5}}{12}}+\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{\theta u\left(24+u\right)}{-12}}=0-0=0 \end{gathered}$$

(15)

As long as this limit is zero at u=0 so the copula has no singular part and it is absolutely continuous copula.

4. Kendall Tau Measure of Dependency

Proposition 5

: Kendall tau for this copula is $\tau =1-0.797\theta$ in equation (16)

Proof: 

$$\begin{gathered} \tau =4{\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\text{'}}\left(u\right)}}du+1 \\ {\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\text{'}}\left(u\right)}}du={\int }_0^1\left({\displaystyle \frac{5\theta {\left(u+24\right)}^{0.5}{u}^{1.5}}{12}}+{\displaystyle \frac{\theta u\left(24+u\right)}{-12}}\right)du= \\ ={\displaystyle \frac{5\theta }{12}}{\int }_0^1{\left(u+24\right)}^{0.5}{u}^{1.5}du+{\displaystyle \frac{-\theta }{12}}{\int }_0^{1}24u+u^{2}du= \\ ={\displaystyle \frac{5\theta }{12}}\left(0.8286\right)-{\displaystyle \frac{\theta }{12}}\left(12+{\displaystyle \frac{1}{3}}\right)=-0.1992\theta \\ \tau =4{\int }_0^1{\displaystyle \frac{\phi \left(u\right)}{{\phi }^{\text{'}}\left(u\right)}}du+1=4\left(-0.1992\theta \right)+1=1-0.797\theta \end{gathered}$$

(16)

For this copula, new one can be created using the following pattern for the generator:

$$t=\phi \left(u\right)=\theta {\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}=\theta {\left(-k+{\left(1+{\displaystyle \frac{h}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}}$$

Let the $\sqrt{1+h}=k$ so other generators can be created and hence related new copulas for each generator such as:

$$\begin{gathered} {t}_1=\phi \left(u\right)=\theta {\left(-\sqrt{2}+{\left(1+{\displaystyle \frac{1}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}} \\ {t}_2=\theta {\left(-6+{\left(1+{\displaystyle \frac{35}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}} \\ {t}_3=\theta {\left(-100+{\left(1+{\displaystyle \frac{9999}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}} \end{gathered}$$

But the Kendall Tau measure of dependency calculation will be

$${\displaystyle \frac{2k\theta }{h}}{\int }_0^1{\left(u+24\right)}^{0.5}{u}^{1.5}du+{\displaystyle \frac{-2\theta }{h}}{\int }_0^{1}24u+u^{2}du=$$

For large values of $h$ the first part of integration will converge to $\left(0.8001\right)$and when added to the second part, the final result will converge to $\left(-0.1999\right)$, when h attains large values so the Kendall tau measure of dependency will be

$\tau =4\left(-0.1999\theta \right)+1=1-0.8\theta$ for large values of $h$

Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23, Figure 24, Figure 25, Figure 26, Figure 27, Figure 28, Figure 29 and Figure 30 illustrate the joint PDF, the joint CDF and the related generator for the copula with different values of dependency parameter.

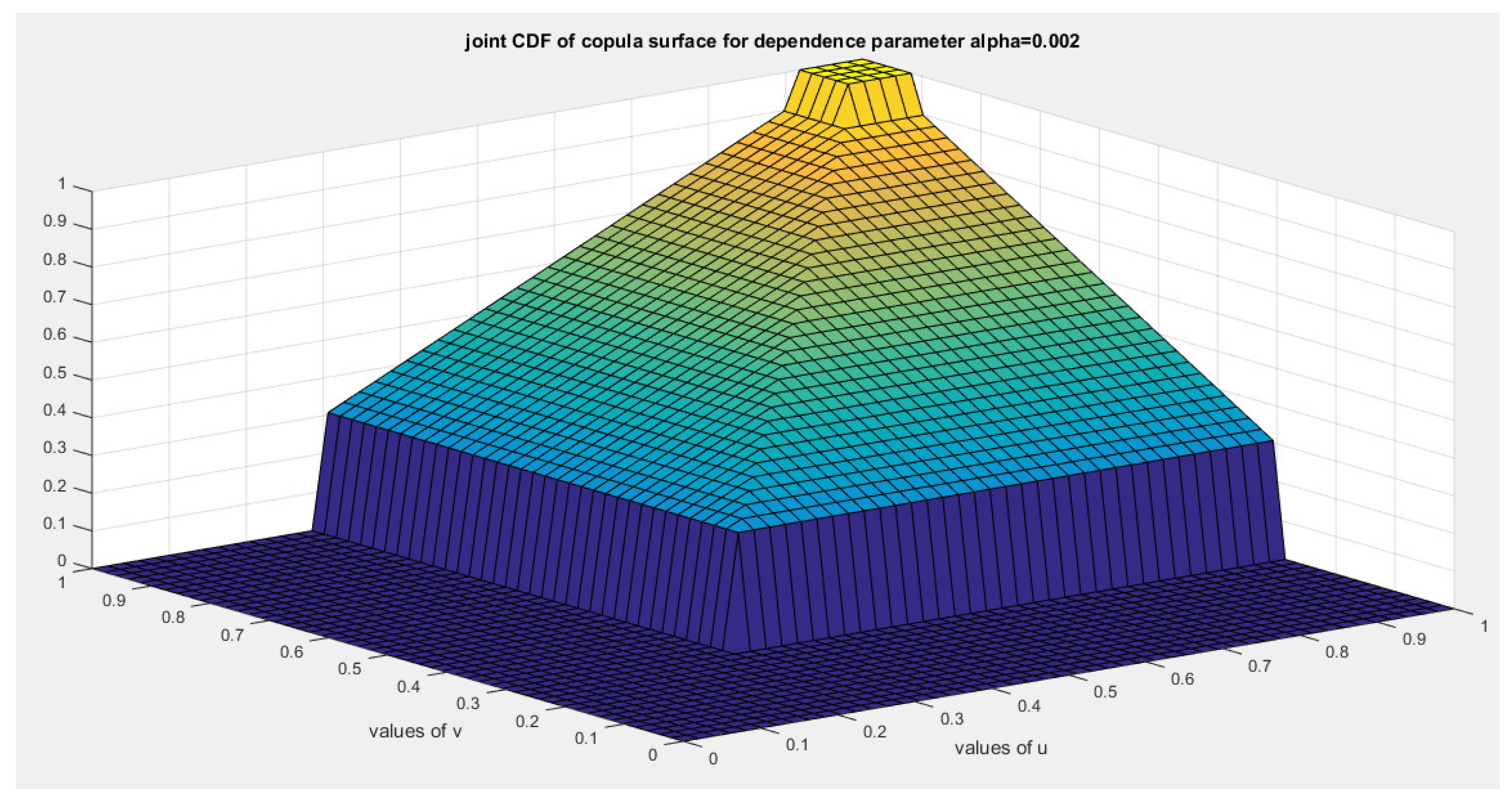
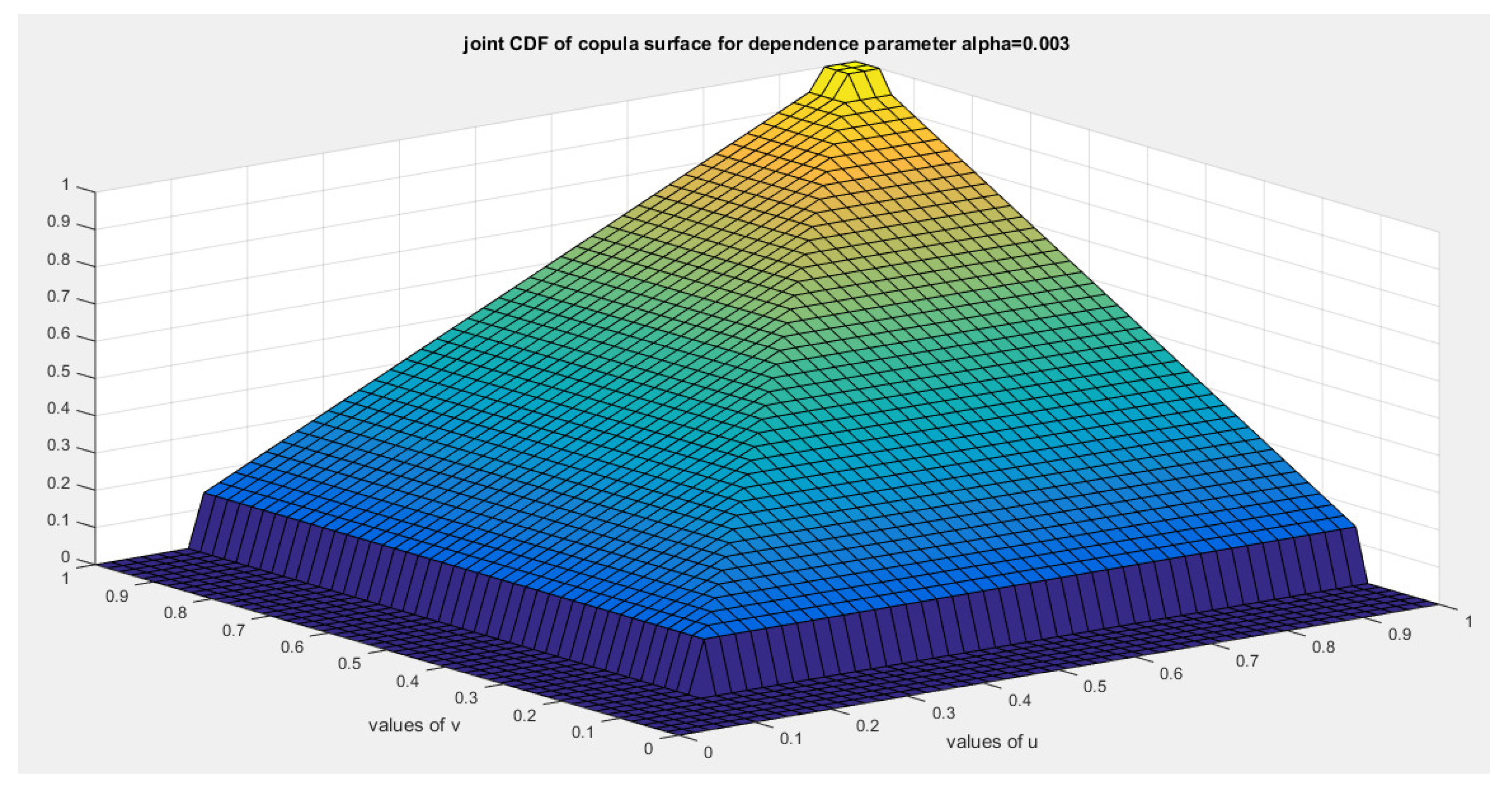
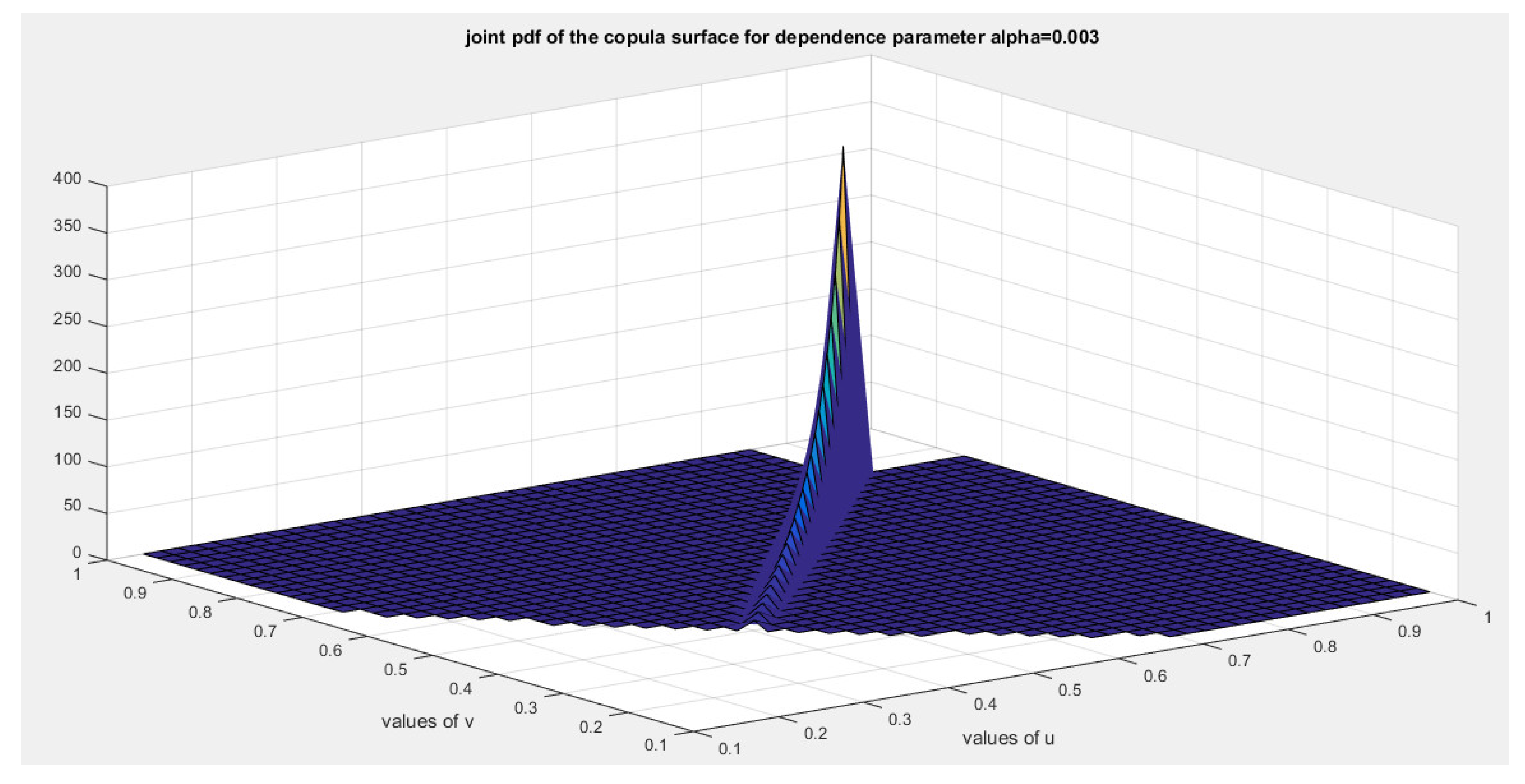
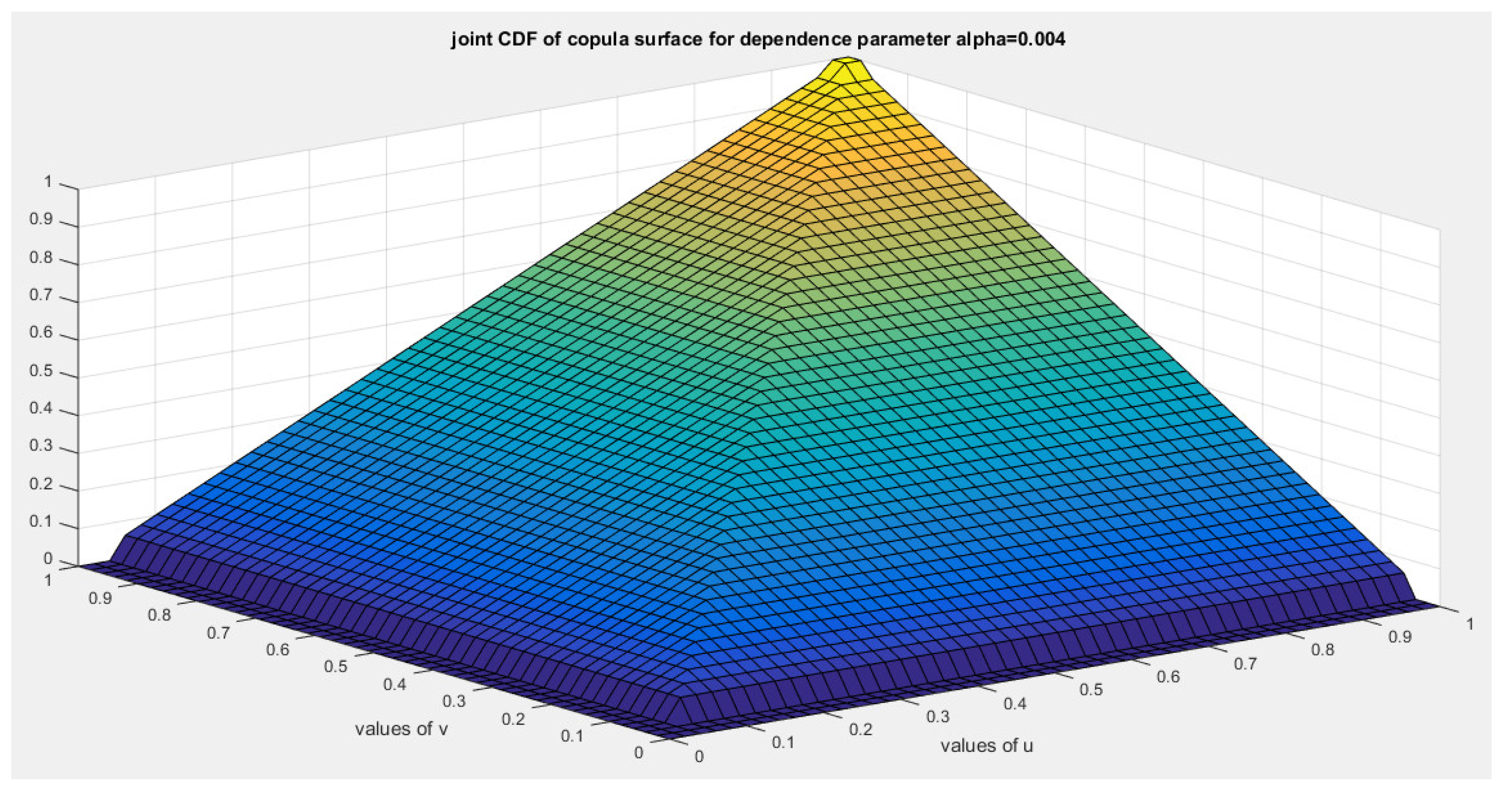
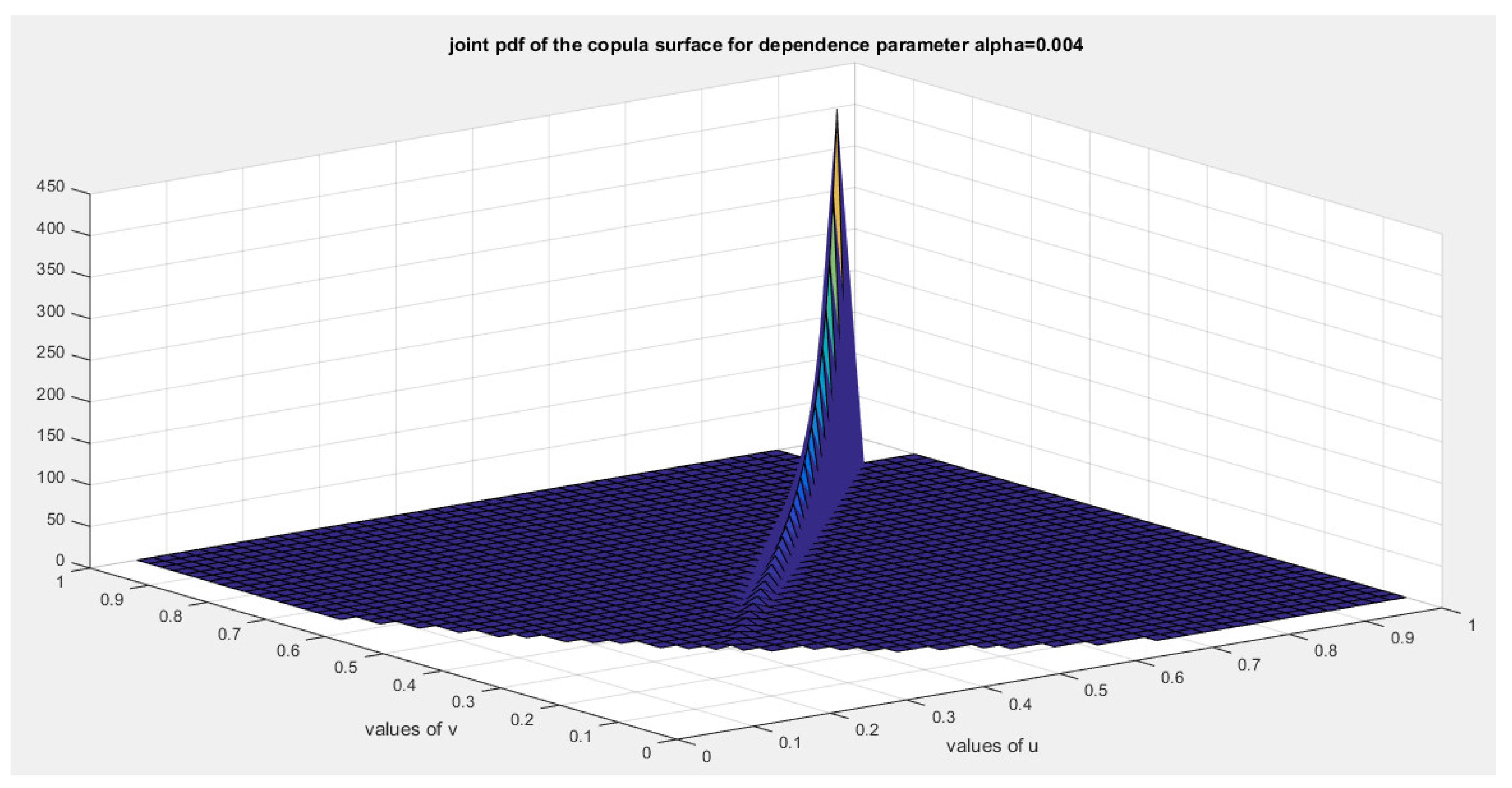
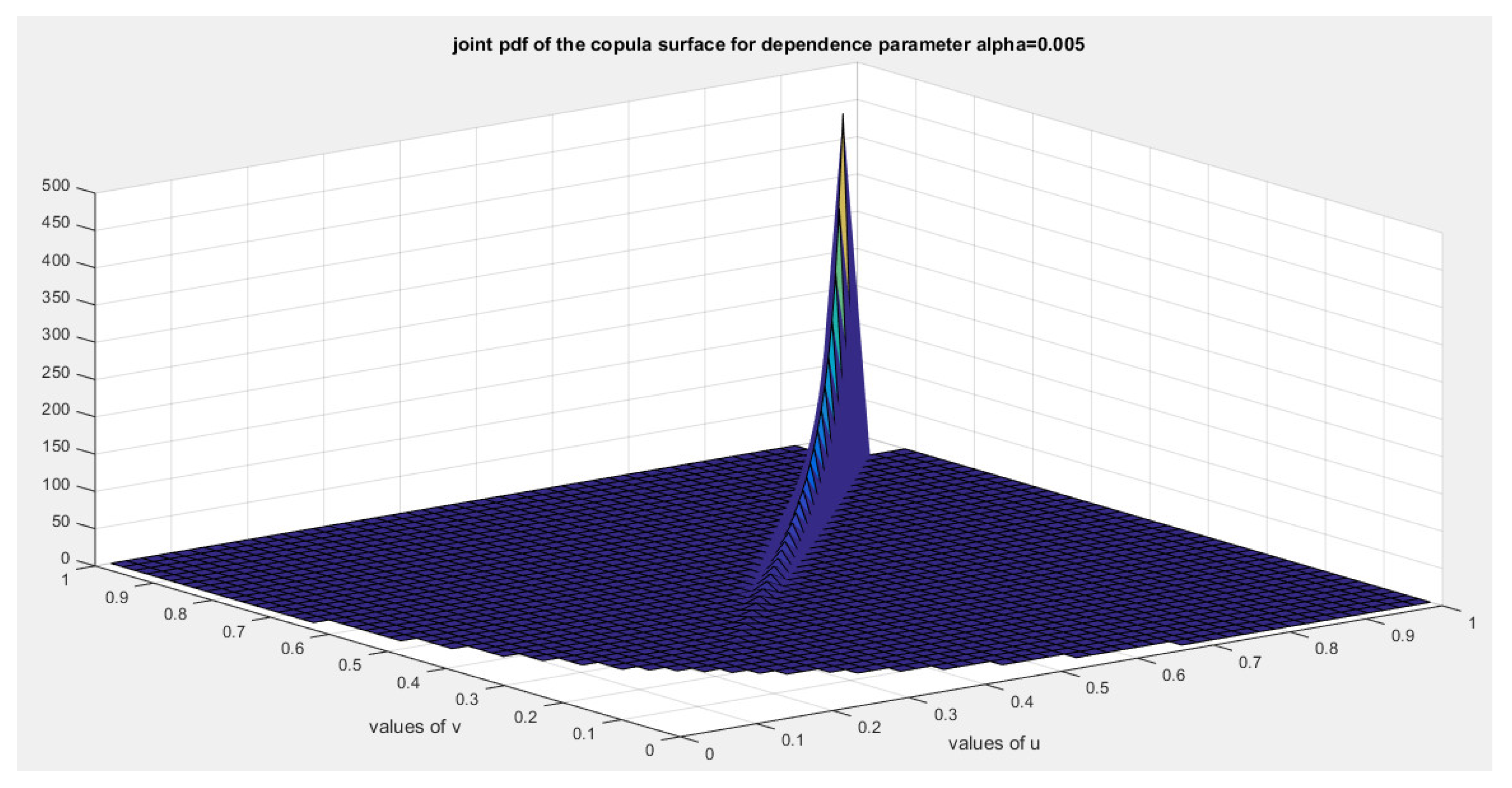
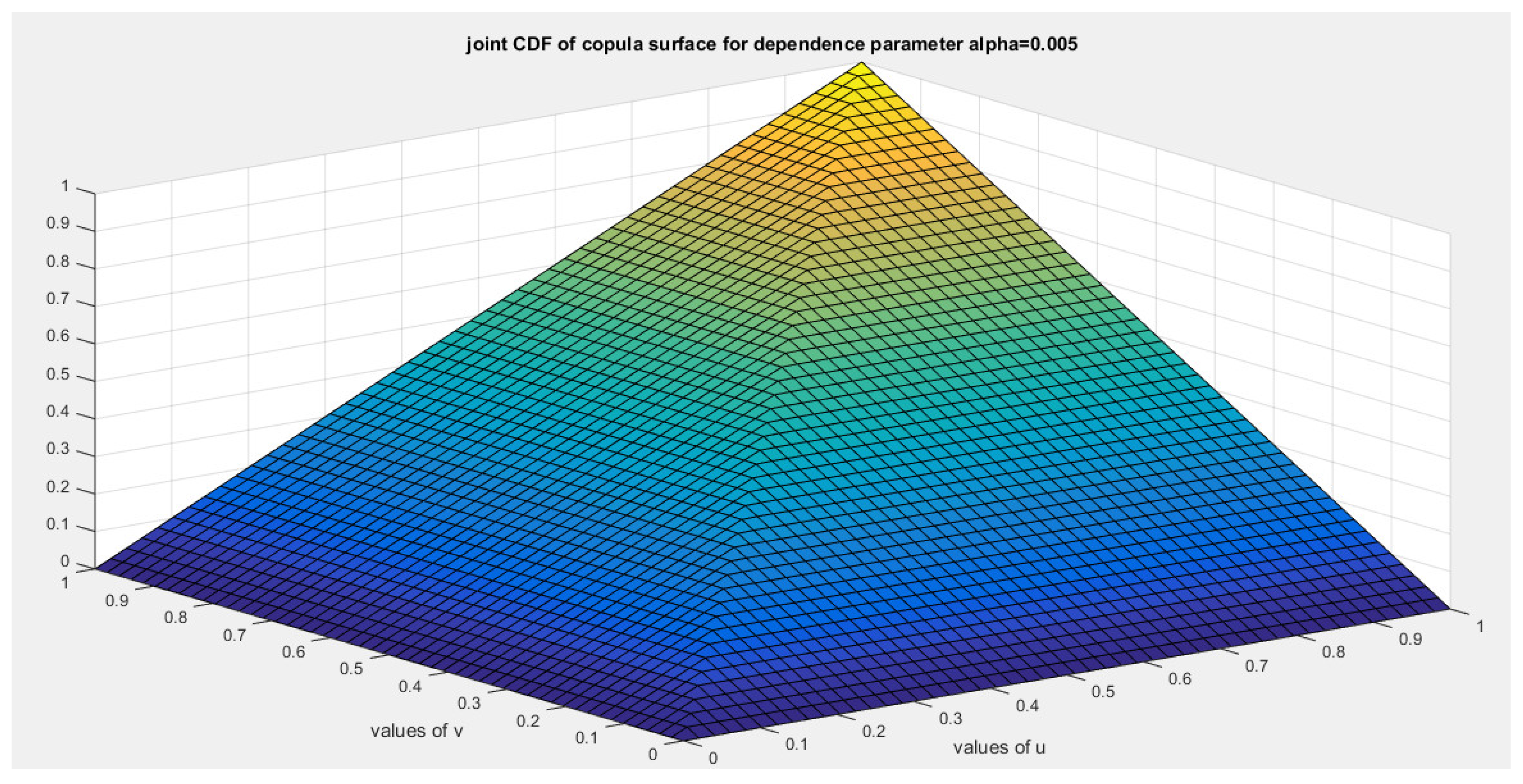
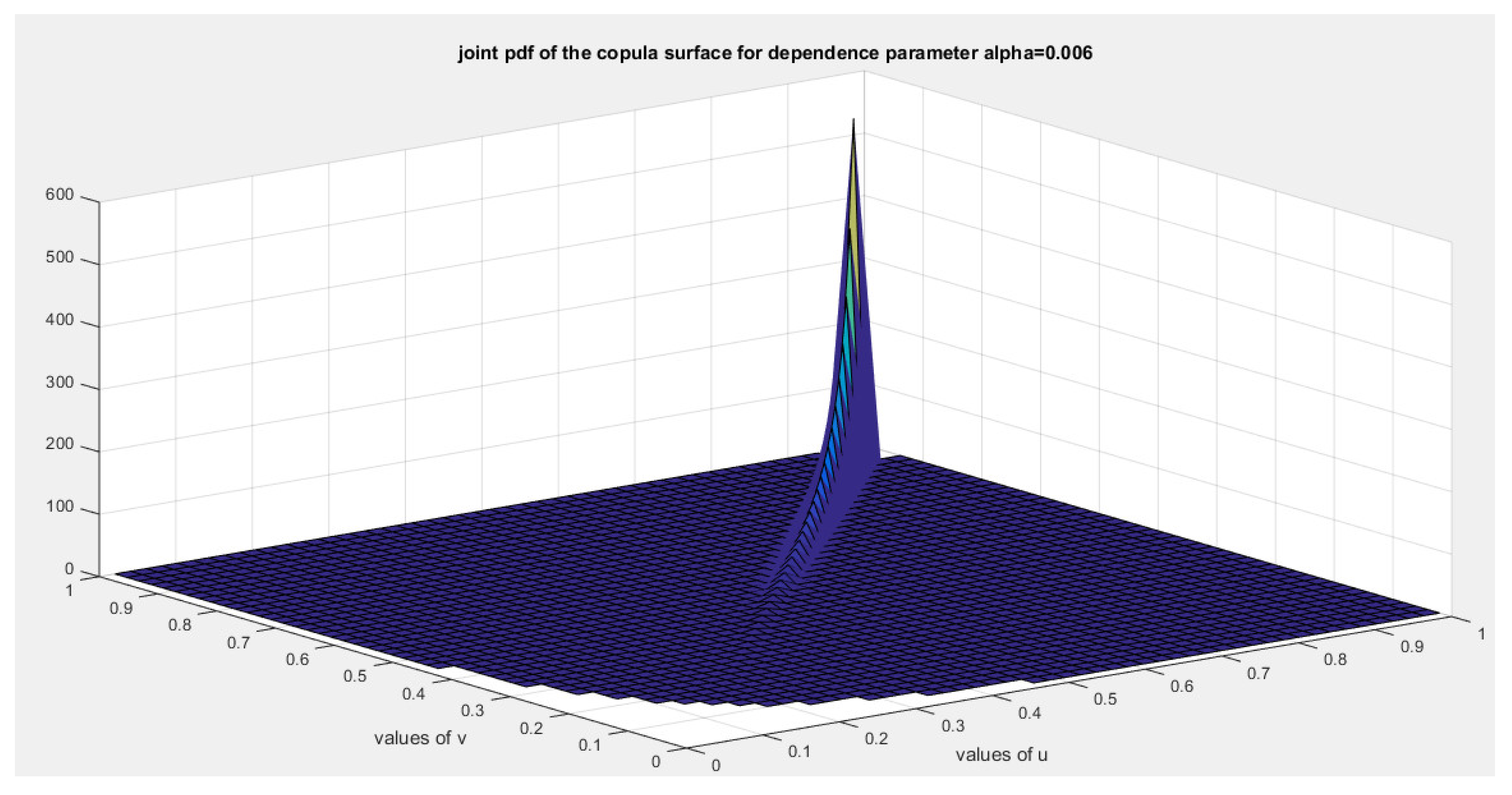
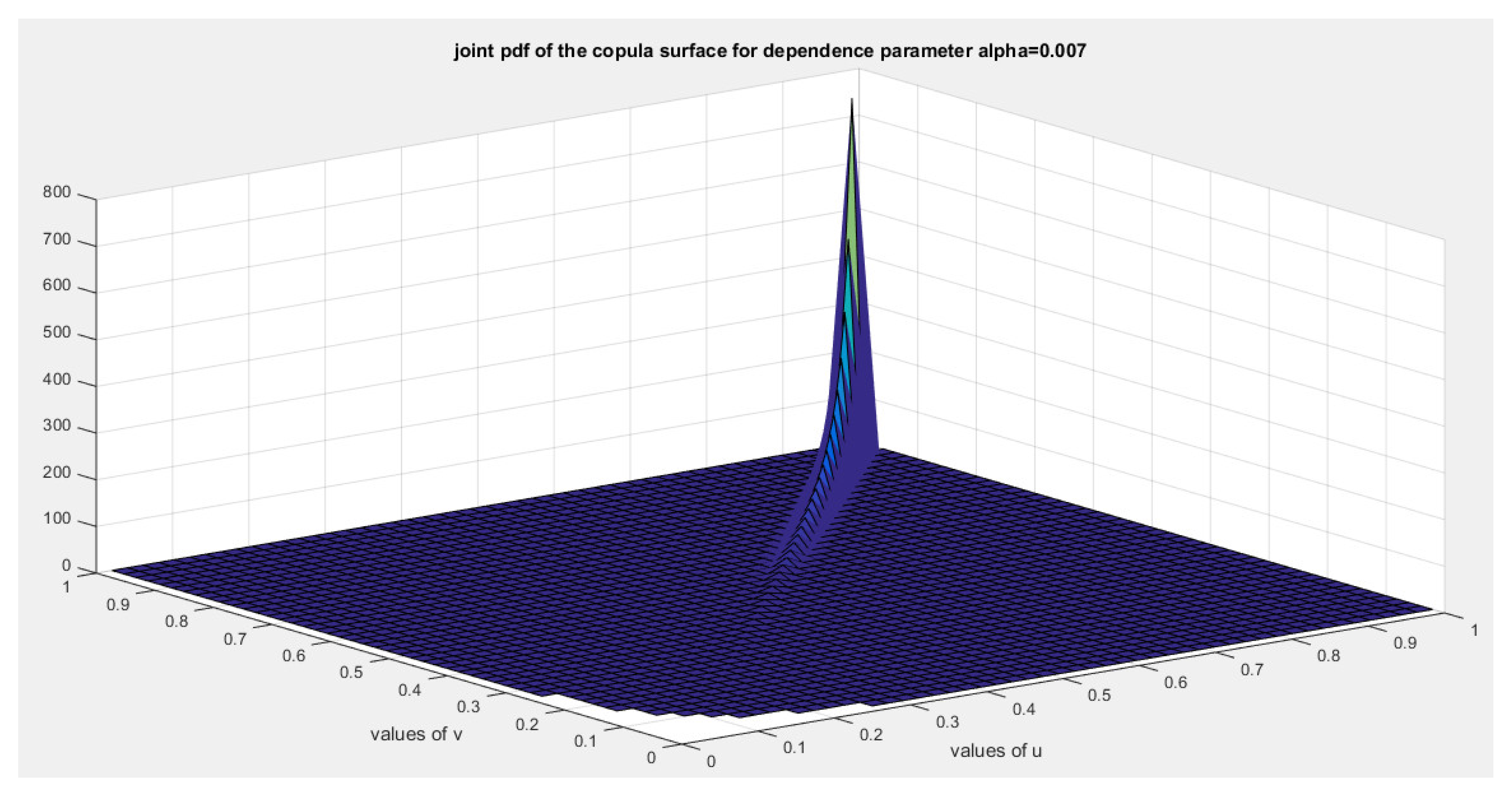
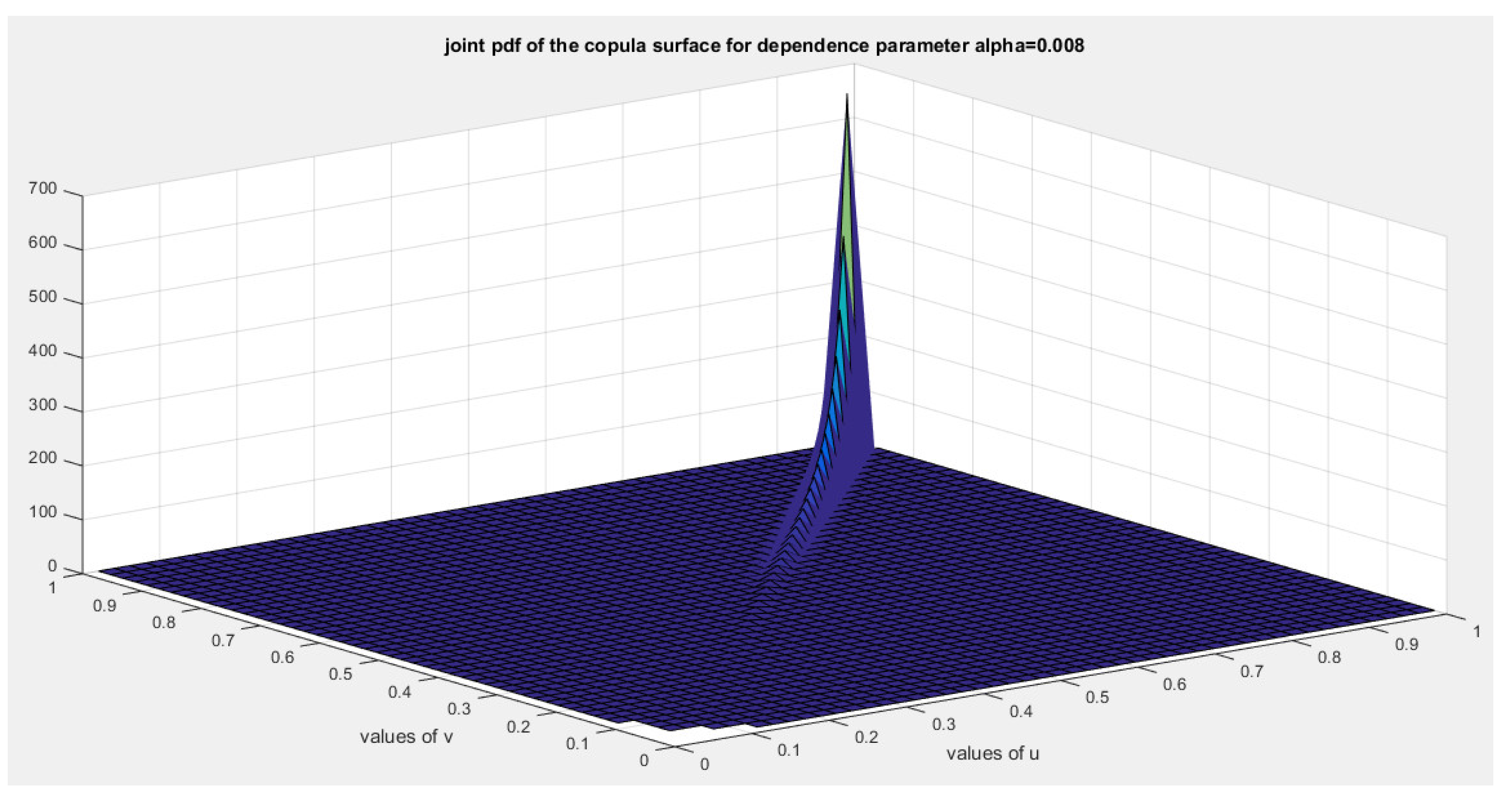
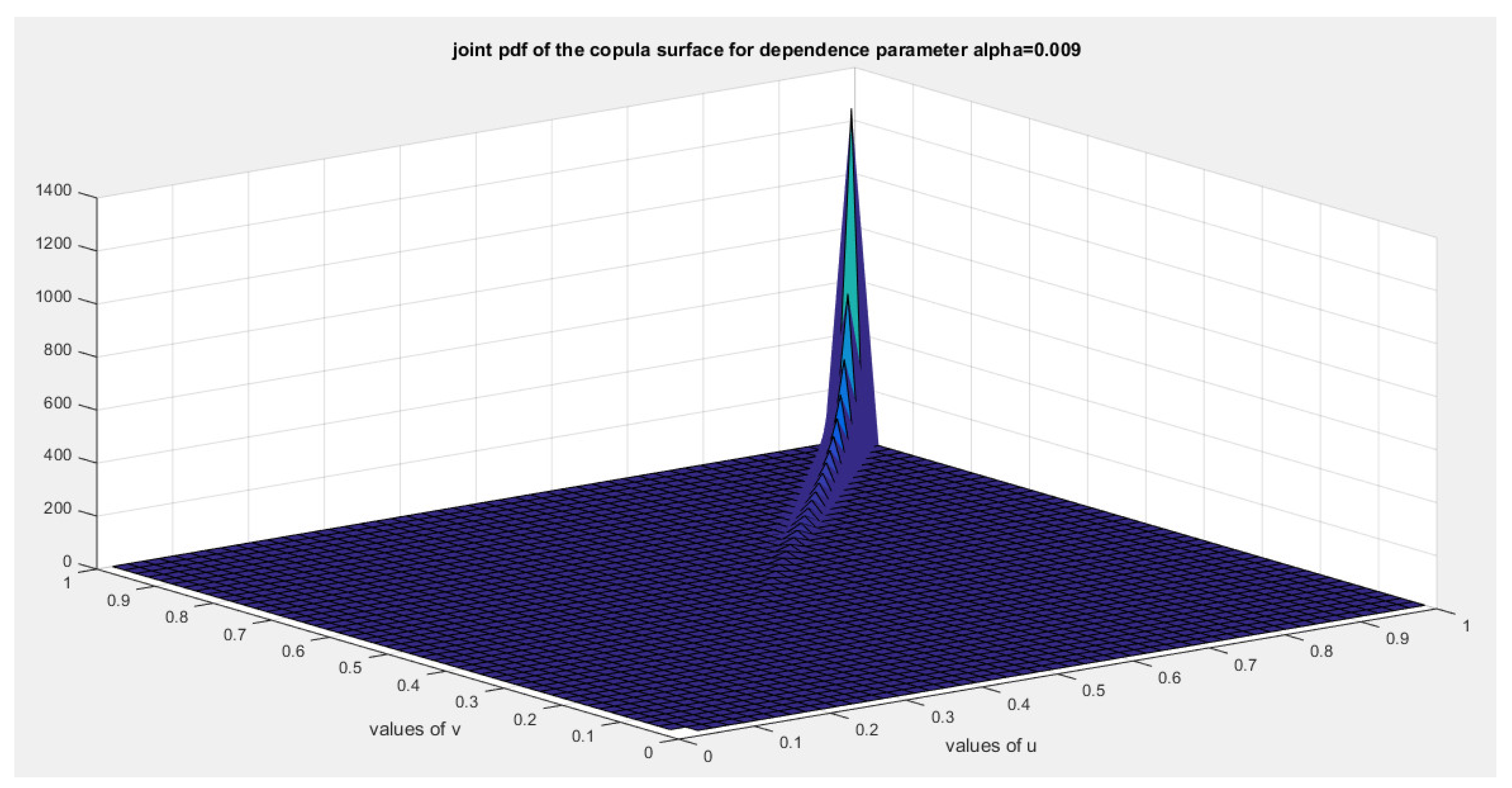
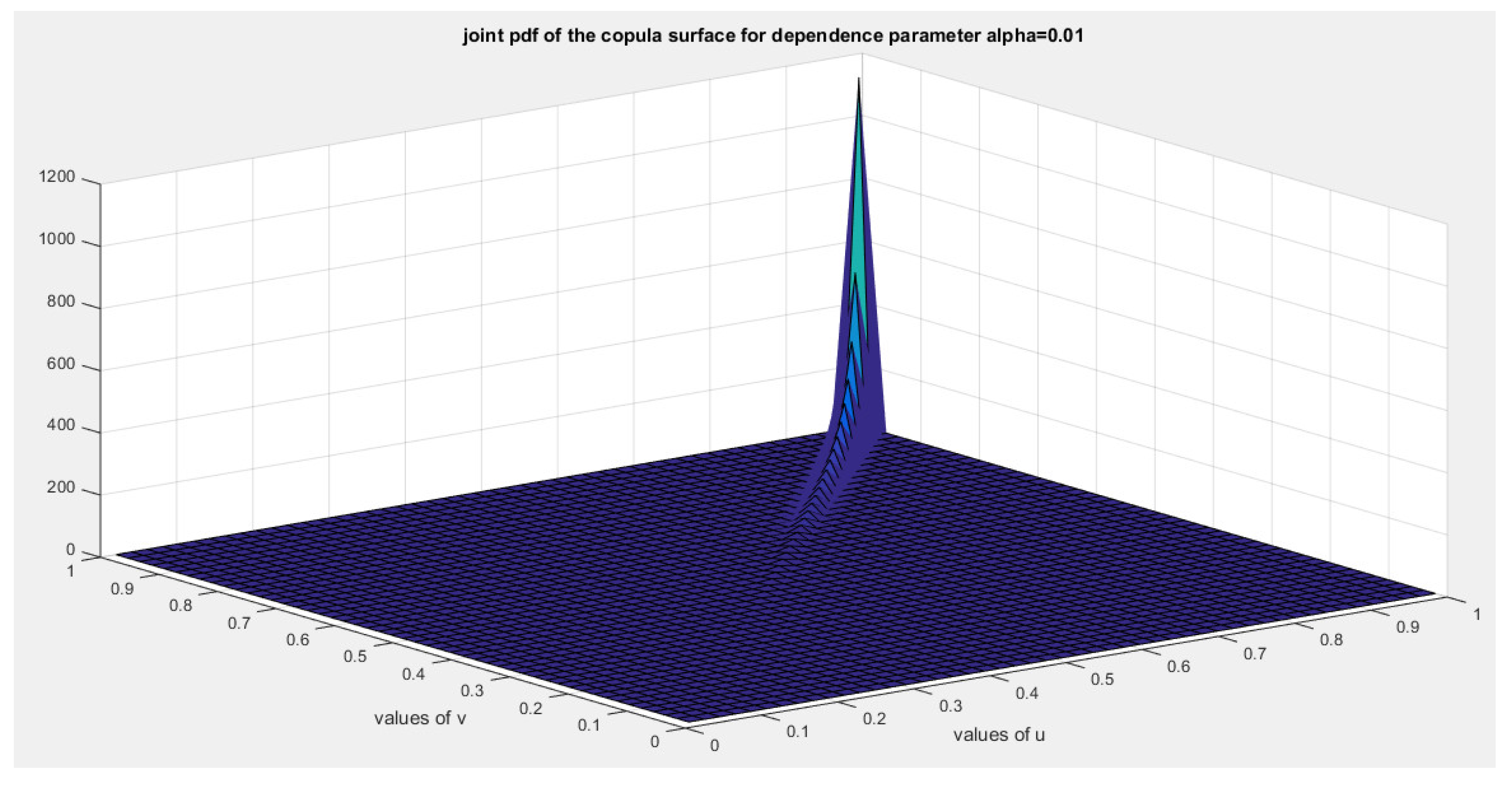
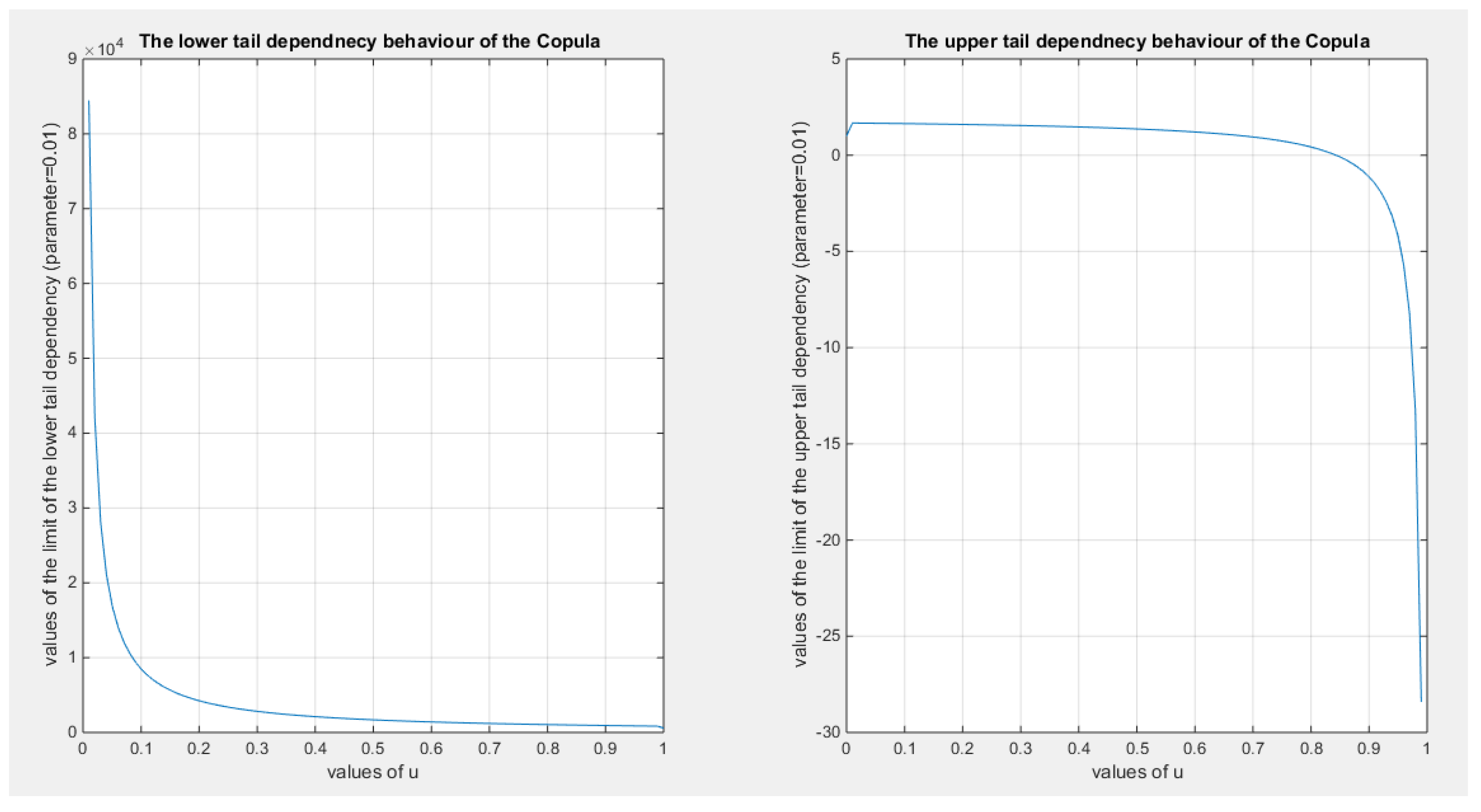
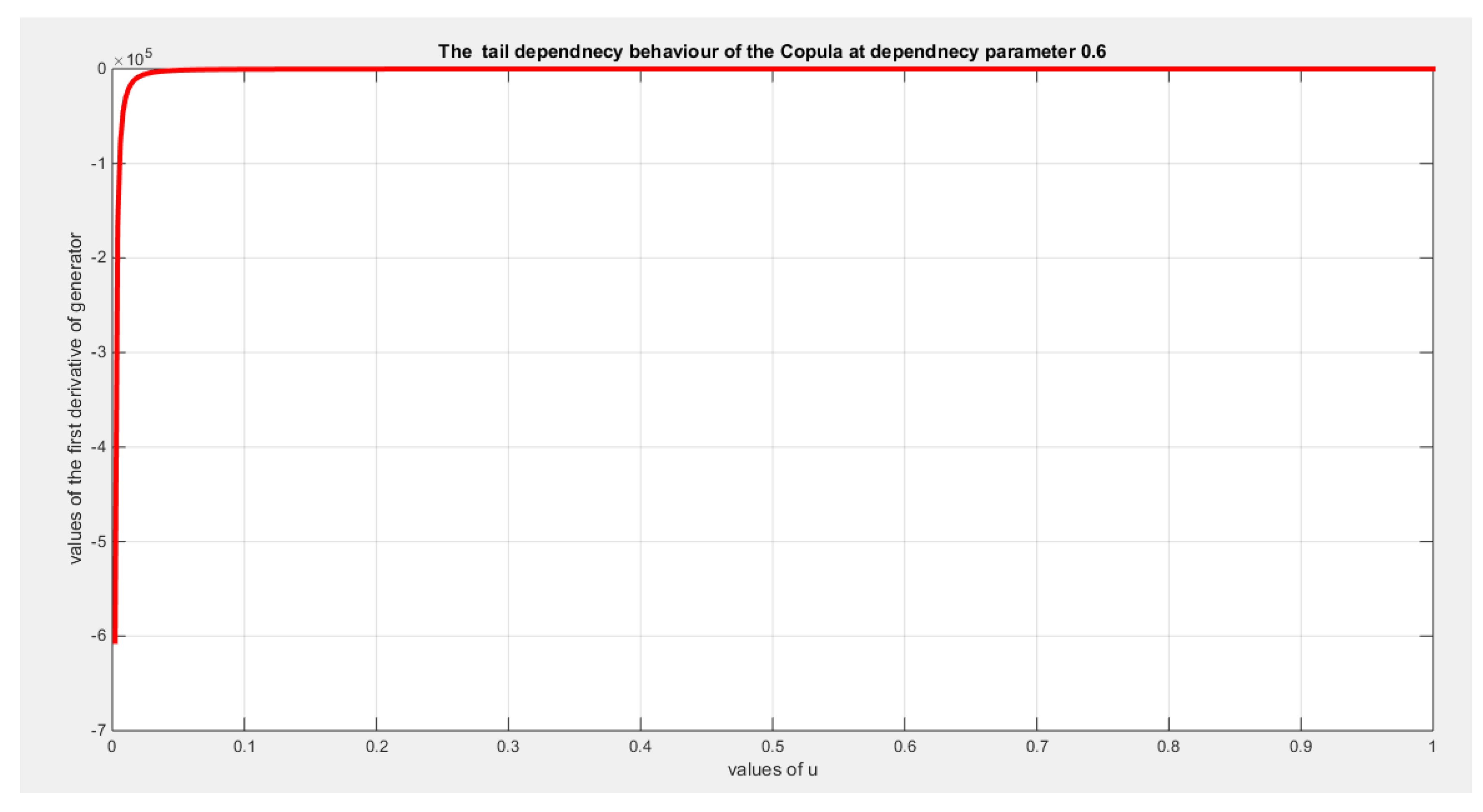
5. Tail Dependency

Preposition 6:

Lower and upper tail dependencies for this copula exist.

Proof: 

$${\lambda }_U=\underset{u\to 1}{\lim }{\displaystyle \frac{1-2u+C\left(u,u\right)}{1-u}}=-\infty$$

(17)

$${\lambda }_U=\underset{u\to 0}{\lim }{\displaystyle \frac{C\left(u,u\right)}{u}}=\infty$$

(18)

$${\phi }^{\text{'}}\left(0\right)={\left(-5+{\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}{\left(1+{\displaystyle \frac{24}{u}}\right)}^{-0.5}\left({\displaystyle \frac{-12}{u^2}}\right)=-\infty$$

(19)

Since both limits in equation (17-18) are infinite and as illustrated in Figure 3) so both lower and upper tail dependencies exist. Moreover, as shown in equation (19) and in Figure 32 the first derivative of the generator approaches $-\infty$ at $u=0$ so the upper tail dependency exists.

Preposition 7

: The values of lower and upper tail dependency can be calculated as shown in equations (20-21)

$${\lambda }_U=2-2.\underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(2u\right)}{{\phi }^{\text{'}}\left(u\right)}}=2-{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+2}\dots$$

(20)

$${\lambda }_L=2-2.\underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(u\right)}{{\phi }^{\text{'}}\left(2u\right)}}=2\left[1-2{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right]\dots$$

(21)

Proof: 

Lower tail dependency:

$$\begin{gathered} \underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(u\right)}{{\phi }^{\text{'}}\left(2u\right)}}=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}{{\left(-5+{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\frac{1}{2}{\left(1+\frac{24}{2u}\right)}^{-0.5}\left(\frac{-24}{2u^2}\right)}} \\ \underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(u\right)}{{\phi }^{\text{'}}\left(2u\right)}}={\displaystyle \frac{{\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}{{\left(-5+{\left(1+\frac{12}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(1+\frac{12}{u}\right)}^{-0.5}\left(\frac{-12}{u^2}\right)}} \\ {\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\cong {\left({\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}foru\in \left(\mathrm{0,1}\right) \\ \underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(u\right)}{{\phi }^{\text{'}}\left(2u\right)}}={\displaystyle \frac{{\left(-5+{\left(\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\frac{\sqrt{u}}{\sqrt{24}}\left(2\right)}{{\left(-5+{\left(\frac{12}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\frac{\sqrt{u}}{\sqrt{12}}}}= \\ \underset{u\to 0}{\lim }2\sqrt{{\displaystyle \frac{12}{24}}}{\left({\displaystyle \frac{\frac{-5\sqrt{u}+\sqrt{24}}{\sqrt{u}}}{\frac{-5\sqrt{u}+\sqrt{12}}{\sqrt{u}}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}=\underset{u\to 0}{\lim }2\sqrt{{\displaystyle \frac{12}{24}}}{\left({\displaystyle \frac{-5\sqrt{0}+\sqrt{24}}{-5\sqrt{0}+\sqrt{12}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}= \\ =2\sqrt{{\displaystyle \frac{1}{2}}}{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-1}={\displaystyle \frac{2}{\sqrt{2}}}{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-1}=2{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2} \\ {\lambda }_L=2-2.\underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(u\right)}{{\phi }^{\text{'}}\left(2u\right)}}=2-2\left(2{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right)=2\left[1-2{\left(\sqrt{2}\right)}^{{\displaystyle \frac{1}{\theta }}-2}\right] \end{gathered}$$

Upper tail dependency

$$\begin{gathered} \underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(2u\right)}{{\phi }^{\text{'}}\left(u\right)}}=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\frac{1}{2}{\left(1+\frac{24}{2u}\right)}^{-0.5}\left(\frac{-24}{2u^2}\right)}{{\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}\left(\frac{1}{2}\right){\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}} \\ \underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(2u\right)}{{\phi }^{\text{'}}\left(u\right)}}=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+{\left(1+\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(1+\frac{12}{u}\right)}^{-0.5}\left(\frac{-12}{u^2}\right)}{{\left(-5+{\left(1+\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(1+\frac{24}{u}\right)}^{-0.5}\left(\frac{-24}{u^2}\right)}} \end{gathered}$$

As long as u is small ${\left(1+{\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}\cong {\left({\displaystyle \frac{24}{u}}\right)}^{{\displaystyle \frac{1}{2}}}foru\in \left(\mathrm{0,1}\right)$

$$\begin{gathered} \underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+{\left(\frac{24}{2u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(\frac{12}{u}\right)}^{-0.5}\left(12\right)}{{\left(-5+{\left(\frac{24}{u}\right)}^{\frac{1}{2}}\right)}^{\frac{1}{\theta }-1}{\left(\frac{24}{u}\right)}^{-0.5}\left(24\right)}}=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\displaystyle \frac{{\left(-5+\frac{\sqrt{12}}{\sqrt{u}}\right)}^{\frac{1}{\theta }-1}\frac{\sqrt{u}}{\sqrt{12}}\left(12\right)}{{\left(-5+\frac{\sqrt{24}}{\sqrt{u}}\right)}^{\frac{1}{\theta }-1}\frac{\sqrt{u}}{\sqrt{24}}\left(24\right)}}= \\ \underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\left({\displaystyle \frac{\frac{-5\sqrt{u}+\sqrt{12}}{\sqrt{u}}}{\frac{-5\sqrt{u}+\sqrt{24}}{\sqrt{u}}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left(\sqrt{2}\right)\left({\displaystyle \frac{1}{2}}\right)=\underset{u\to 0}{\mathrm{l}\mathrm{i}\mathrm{m}}{\left({\displaystyle \frac{-5\sqrt{0}+\sqrt{12}}{-5\sqrt{0}+\sqrt{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left(\sqrt{2}\right)\left({\displaystyle \frac{1}{2}}\right)= \\ {\left({\displaystyle \frac{\sqrt{12}}{\sqrt{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}\left(\sqrt{2}\right)\left({\displaystyle \frac{1}{2}}\right)={\displaystyle \frac{\sqrt{2}}{2}}{\left(\sqrt{{\displaystyle \frac{12}{24}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}={\displaystyle \frac{\sqrt{2}}{2}}{\left(\sqrt{{\displaystyle \frac{1}{2}}}\right)}^{{\displaystyle \frac{1}{\theta }}-1}={\displaystyle \frac{\sqrt{2}}{2}}{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+1}={\displaystyle \frac{{\left(\sqrt{2}\right)}^{\frac{-1}{\theta }+2}}{2}} \\ {\lambda }_U=2-2.\underset{u\to 0}{\lim }{\displaystyle \frac{{\phi }^{\text{'}}\left(2u\right)}{{\phi }^{\text{'}}\left(u\right)}}=2-2\left({\displaystyle \frac{{\left(\sqrt{2}\right)}^{\frac{-1}{\theta }+2}}{2}}\right)=2-{\left(\sqrt{2}\right)}^{{\displaystyle \frac{-1}{\theta }}+2} \end{gathered}$$

6. Conclusions

This copula which is based on frailty model and cox proportional hazard model can only model positive dependency. These types of copula can be used in applications to model the positive dependency between variables. This copula can also model lower and upper tail dependency. This copula has a generator whose derivative is zero when evaluated at zero and this supports modeling upper tail dependency. The definitions of lower and upper tail dependencies that involve the copula equation yielded infinite values and this also supports the tail dependencies.

While the joint distribution function, $H\left(x,y\right)=C\left(F\left(x\right),G\left(y\right)\right)$ for two random variables X and Y, the bivariate density function these 2 variables is shown in equation (22)

$$h_{X,Y}\left(x,y\right)={\displaystyle \frac{\mathsf{\partial }H\left(x,y\right)}{\mathsf{\partial }x\mathsf{\partial }y}}=f_X\left(x\right)f_Y\left(y\right)\mathrm{c}\left(F_X\left(x\right),F_Y\left(y\right)\right)=f_X\left(x\right)f_Y\left(y\right){\displaystyle \frac{{\mathsf{\partial }}^2\mathrm{C}\left(u,v\right)}{\mathsf{\partial }u\mathsf{\partial }v}}$$

(22)