Submitted:
11 April 2025
Posted:
14 April 2025
Read the latest preprint version here
Abstract
A Berry geometrical phase is identified in a strongly metastable system containing dynamically responsive nanoscale clathrate hydrate structures within a crystal-fluid material. High energy degeneracy in the associated chemistry produces local stability and false vacuum conditions that lead to non-extensive and non-additive contributions in the fundamental thermodynamic relation. Application of Ginzburg-Landau theory and the scaling laws reveals a coherence length (3.05 m) and a penetration depth (2.2 m) that characterize a macro-scale dual superconductor. The coherence length describes a magnetic condensate whilst its inverse gives the Higgs mass (0.33 kg) and non-extensive volume changes (± 0.5 l). The penetration depth determines the extent of QCD vacuum suppression whilst its inverse gives an effective vector boson mass (≤ 0.46 kg), resulting in non-additive hyperbolic curvature. Simultaneous emergence of the Ginzburg-Landau superconducting phase transition is consistent with gauge-invariant coupling of the scalar field (≤ 3.6 ks-1) to the Yang-Mills action in QCD. The discovery of an energy gap in the gradient energy term of the system Lagrangian is associated with a critical correlation length (3.05 m) as revealed in the transition from a gapped to a gapless superconducting state. Together with the emergence and reabsorption of the Higgs-like scalar field, a mechanism for describing a renormalized QCD mass gap arises. The phenomena reported are only relevant to a coordinated U(2) Lie symmetry group having scale-invariance across micro- and macro-scale dual superconductivity. Under normal, non-critical conditions the symmetry is broken and separated into condensed matter and QCD elements that are effectively isolated. Energy and momentum cannot thereby be transferred across the QCD mass gap and TeV confinement energies dominate - conservation of energy and momentum are constrained to the individual symmetry groups. It is proposed that where these symmetries are decomposed and synchronized then the QCD mass gap with associated TeV threshold dissipates.
Keywords:
Berry geometrical phase
; dual superconductivity
; scale- and gauge-invariance
; hyperbolic curvature
; renormalization
; magnetic monopole topology
; QCD mass gap
Introduction
The experimental investigation on which the current exposition is based has been previously reported [1]. The data and calculated properties are reproduced in Appendix A. This earlier work identifies the emergence of spontaneous diamagnetism and paramagnetism in the behaviour of nanoscale clathrate hydrate structures (or water ice cages) as critical phenomena responsible for work output in a kinetic system. The accompanying analysis centres upon a superconducting phase transition where the scaling laws reveal the emergence of a critical correlation length ξ (3.05 m). It is shown [1] that relativistic length expansion and time contraction on a Lorentz manifold describe the critical correlation length ξ (calculation reproduced in Appendix B). The Ginzburg-Landau parameter κ (0.65 ≤ κ ≤ 0.707), as defined in Appendix C, is also uncovered together with topological ordering. Additionally, it is noted that the Ginzburg-Landau theory of superconductors invokes gauge-invariant coupling of a scalar field Φ to the Yang-Mills action in QCD. These relativistic and quantum aspects of the findings are examined here in further detail within the context of the Berry geometrical phase, complex energy band gaps and the QCD mass gap.
Situations can arise in thermodynamics whereby a physical system is prevented from attaining its lowest energy and highest entropy state through the existence of an energy barrier. False vacuum conditions can result from such metastability in the extreme so that on short timescales a positive, non-minimum energy density cannot be raised or lowered in response to external interactions. Where an energy barrier is maintained through dynamic inhomogeneities, a system can be isolated from external interactions through local stability conditions, as characterized by a non-concave entropy function [2]. The process of thermodynamic isolation is also described by the characteristic of asymptotic freedom in particle physics [3]. Opposition to dynamical change is established through complex reorganization of individual system components, i.e. degenerate hydrogen bonding in dissipative condensed matter systems [1]; gluon splitting and recombining in the case of colour confinement; and gluon exchange in quark confinement [3,4]. The experimental results reported in [1] reveal that water ice cages under negative pressure can give rise to false vacuum behaviour as a result of which non-extensive and non-additive interactions generate work in a constant energy Hamiltonian oscillator.
The low-energy system reported encompasses both a crystal-fluid material and its embedding vacuum manifold whereby hyperbolic curvature K (- 0.46 ≤ K ≤ - 0.22 m2s-2) and variable volume V (0.005 ≤ V ≤ 0.5 litre), rather than any fluid mechanical response, describe the work performed by the system. The chemical and physical properties associated with water ice cage structures are also shown to elicit magnetic and superconducting behaviours that establish the Berry phase whilst the material maintains almost constant density. This geometric phase results from a cyclic evolution of the system Hamiltonian where the state returns to its origin but gains an additional phase factor.
The crystal-fluid is composed of dissipative, reorganizing, water ice cage structures suspended within a polar dielectric inhibitor solvent. The formulation results in false vacuum behaviour [5] such that the material part of the system is effectively isolated from any external thermodynamic interactions. However, despite the presence of strong local stability conditions, it is possible to perturb the system through an external pressure interaction to induce a ‘rolling’ critical response [6]. This, in turn, exposes a hyperbolic curvature action on the vacuum manifold that combines with a mutually emergent coupling energy to deliver a symmetry-related net energy gain, i.e. an additional source of energy is exposed within the system.
Hyperbolic Gaussian curvature K originates in the negative potential of the false vacuum established by the variable effective radius (i.e. variable inertia) of the highly degenerate system. Conservation of angular momentum requires that a reducing effective radius results from an acceleration whilst an increasing effective radius results from a deceleration. Since the crystal-fluid retains constant energy and density, acceleration acts to reduce the Gaussian radius of hyperbolic curvature Rg of the embedding manifold whilst deceleration increases Rg. Quantum interactions leading to non-additivity can be identified in both instances. The associated changes in swept volume V arising from the condensation of magnetic entities are non-extensive.
During the ‘rolling’ critical response, the magnetic and superconducting behaviours are quantified by a distinctive universality class of critical exponents [1]. Formation of a magnetic condensate induces a phase transition from Type-II superconductivity to a dual of Type-I superconductivity where the spontaneous magnetic field Hs, as an ‘auxiliary’ order parameter, reduces to zero [7]. Following this, ordering is attributed to an emergent complex parameter field, similar to the topological ordering of spin ices as described by Castelnovo et al. [8].
A definitive theory of quark confinement remains elusive despite experimental and lattice gauge theory/ computer simulation successes. The QCD large lattice technique is based upon strong coupling conditions so that perturbative techniques are deemed impractical. From a mathematical perspective, the confinement problem is known as the mass gap problem. A promising solution originally proposed by ‘t Hooft [9] and Mandelstam [10] claims that the ground-state of QCD is a dual superconductor in which quarks are confined by chromoelectric vortices. These vortices are analogous to the Abrikosov vortices seen in Type-II superconductors. In the current exposition these QCD descriptions are also relevant to the macro-scale dual superconductor uncovered.
In a dual superconductor, the roles of the electric and magnetic fields are exchanged so that in this case the electric field is excluded. The significance of dual superconductivity in furthering an understanding of the strong interaction is examined in comprehensive reviews by Ripka [11] and Kondo et al. [12]. The superconducting phase transition established is consistent with Ginzburg-Landau theory suggesting gauge-invariant coupling of a scalar field Φ to the Yang-Mills action in QCD [12]. The emergent gauge field (1.2 ≤ Φ ≤ 3.6 ks-1) is associated with an apparent broken symmetry with gradient energy seemingly determined by the hyperbolic surface of the system as the electric field is excluded. However, gauge symmetry is revealed not to be broken but rather decomposed and synchronized to become more capacious in extent.
A model for the emergent gauge symmetry is presented here to account for the net energy gain enabled by the ‘rolling’ critical behaviour (and subsequent geometrical action of the vacuum manifold) in terms of Noether-conserved quantities, i.e. energy and angular momentum for the case being considered. Since a topological phase factor, or Berry phase, reveals gauge structure in quantum mechanics [13], the existence of a parity-time (PT) symmetry may account for quantum mechanical interactions manifesting as real energy [14] in the gradient energy term of the Lagrangian describing the dual superconducting phase [1].
Emergence of the gauge field corresponds to a critical correlation length ξ that represents long-range ordering of magnetic spins, i.e. a magnetic condensate. This divergence is responsible for an energy gap in the gradient energy term analogous to complex energy band gaps reported in non-Hermitian PT symmetric systems [15]. Also, the existence of a mass gap in QCD is necessary to explain why the strong interaction is strong but only short-ranged. Confirmation of a mass gap would account for the fact that quantum particles have positive masses even though classical waves travel at the speed of light [16]. Evidence of a Berry phase and the Ginzburg-Landau parameter κ [1] thus enables insights into the Yang-Mills action and the mass gap phenomenon in QCD. The current work attempts to elucidate the QCD mass gap problem primarily through the phenomenology of dual superconductivity and magnetic monopole topology.
Experimental Evidence and Background Material
Experimental Setup
The temperature and pressure of the crystal-fluid are measured at five-second intervals with sensors that have direct contact with the crystal-fluid and recorded by a PLC/ PC monitoring system. All values for energy and thermodynamic potentials are derived from the pressure and temperature measurements by the NIST REFPROP program/database [17]. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0) [18]. The piston expander is completely immersed in a heat bath with a temperature of 270K, approx. The schematic arrangement provided in Figure 1 is reproduced from [1].
A negative pressure fluid is established by the Berthelot method [19]. Approx. 3.5 grams of crystal-fluid are transferred into a previously evacuated stainless-steel sample vessel (50ml). A low-energy, negative pressure regime results in the formation of water ice cages hosting methane molecules. The sample vessel is completely immersed in a relatively large heat bath (70 litres) where the temperature of the bath is controlled with an electric element and a refrigeration dip cooler. Once the desired temperature is obtained, the sample is released into the fluid-side of the 0.5 litre retracted piston expander, also completely immersed in the heat bath, which displaces the piston vertically upwards to the fully-extended position. The gas-side of the piston is open to atmospheric pressure during the extension. This action reduces the energy of the system further and is intended to transfer the guest methane molecules from the host water ice cages to similar structures within the inhibitor solvent. An increase in mass of 0.3 kg, approx. is immediately recorded against the first piston extension. Negative and positive piston displacements are then induced through pressurized nitrogen perturbations to produce negative and positive work outputs where displacement ratios are 1:100 and 100:1, approx.
The Phenomena
From completion of the Berthelot mixing process through subsequent positive and negative displacements of the piston expander, REFPROP determines that the crystal-fluid material remains in a subcooled liquid phase, as recorded in Appendix A. It is both astonishing and remarkable that 3.5 grams of material does not transition to a vapour or gas, nor produce any methane outgassing, when contained within the initial sample volume of 50 ml. More remarkable still is that an additional work-generating positive piston displacement of 0.5 litre also has no effect upon the integrity of the subcooled liquid phase. Notwithstanding, a conventional interpretation in terms of fluid mechanics would locate all the crystal-fluid material in the lowest section of stainless-steel tubing connecting the sample vessel to the piston expander (excluding any capillary action) due to ordinary gravity and the generation of work would be inconceivable. Additionally, the mass increase of 0.3 kg, approx. developed during the first piston extension is maintained throughout subsequent piston displacement actions. This perplexing and counterintuitive outcome is examined in more detail below together with supporting mathematical expressions.
In addition to the temperature and pressure measurements, only the piston position and mass of the material components are required to calculate all the thermodynamic properties, critical exponents and scaling relations shown in Appendix A. Whilst validity of the REFPROP calculations may be reasonably challenged, it has been demonstrated successfully that the program/ database is very sensitive to outgassing and re-absorption events associated with phase transitions in similar materials when performing quasi-thermodynamic cycles [5]. In such circumstances methane outgassing accompanies the formation of low-energy, guest-free water ice cages and is consistent with the fluctuation-dissipation theorem. With these phase-change processes, long-range interactions are also established whereby non-additivity in the fundamental thermodynamic relation is revealed.
Figure 2 is reproduced (with some additional annotation) from the recent experimental results reported in [1] where Points 1-4 identify particular stages of the work cycle in a low-energy system; Stage 1-2 corresponds to negative displacement of the 0.5 litre piston expander and Stage 3-4 corresponds to positive displacement.
Changes in negative potential energy and internal energy vary in a 1:1 relationship after discounting the Pv work term associated with the walls of the vessel. Thus, a linear oscillator or constant energy Hamiltonian function is determined. The associated affine non-concave entropy function [1,2] represents local stability conditions achieved through dynamically responsive inhomogeneities, i.e. the complex reorganization of dissipative structures composed of water ice cages, such that energy cannot be minimized and entropy cannot be maximized [2]. Specific volume and internal energy are shown to be highly constrained intensive parameters.
Spontaneous Magnetism and Dual Superconductivity
Evidence for the emergence of spontaneous magnetism and associated superconducting behaviour has been previously reported [1]. The findings are briefly reviewed here with the benefit of additional insights relating to Yang-Mills theory and QCD.
The thermodynamic response functions in Table A4 are calculated by the REFPROP program. These response functions enable a family of critical exponents to be derived. The resulting critical exponents in Table A4 fully satisfy the scaling laws of Fisher, Rushbrooke, Widom and Josephson, to produce a distinctive universality class in 3-dimensional space [20,21].
The response functions and critical exponents of Table A4 allow the magnetic properties of the system to be determined, as recorded in Table A5. The following Maxwell relations then provide for an exchange mechanism to equilibrate frustrated magnetic energy:
and expressing in terms of the interaction energy μN:
The results in Table A6 reveal that PV work is only partially accounted for by relaxation of the constraint on specific volume v and internal energy u, as imposed by inhomogeneities and magnetic frustration. However, calculations based upon extensive parameters and intensive parameters only relate to the material system and do not account for the vacuum occupied by that system [22].
The total energy within the spatial region occupied by the system needs to include the vacuum energy value given by:
where μ0 is the permeability of flat, free space with an historical value of 4π x 10-7 T-m A-1 [22]. However, as detailed in Table A7, the hyperbolic geometry of the system allows for effective values of μ0 which in fact reflect the ratio of Euclidean space to hyperbolic space. From the geometry of the system, the ‘space density’ is then found to be dependent upon the correlation length scale ξ of 3.05, applicable to approximately 3.5 steps of ‘rolling’ critical response, such that;
where μ0f is the final effective value of μ0 and μ0i is the initial effective value of μ0. Variations in effective μ0 require that a spontaneous magnetism Ms with associated spontaneous magnetic field Hs emerges to conserve magnetic charge.
Application of the scaling laws to the experimental results [1] reveals that pressure perturbation induces low susceptibility χ leading to spontaneous magnetism Ms with associated spontaneous magnetic field Hs. For positive Hs, ordering is attributed to the emergence of the complex parameter field Ψ(r) and the topology associated with magnetic frustration and charge fractionalization. Condensation of fractionalized magnetic charges into a gauge monopole condensate [11,12] would act to exclude magnetic current from the embedding vacuum manifold to provide exchange pathways for the spontaneous magnetism Ms that maximally excludes the electric field E to establish dual superconducting behaviour.
Figure A5 in Appendix C describes the emergence of Ms and Hs. Taking Hs as the ‘auxiliary’ order parameter, a phase transition is apparent at Mc2 where Hs = 0. For Ms > 1, Hs takes positive values as the susceptibility χ falls below unity. A new value for the critical magnetism Mc’ is deemed to be established to the right of the plotted values. It then follows that for this region κ < 1/√2 which is consistent with Type I superconducting behaviour. Here, large values of Bs act to exclude the electric field E to establish dual superconducting behaviour [23]. The initial emergence of this spontaneous magnetism is attributed to the anisotropy of the clathrate hydrate structures and is consistent with proton delocalization [24]. A similar situation is described by Purcell and Pound [25] where opposition of the external field to the magnetizing flux arises from the relaxation time for mutual interaction among spins being less than that between spins and the embedding lattice.
Relatively recent advancements in the understanding of spin ice materials provide an explanation for the superconducting phase transition described above, since effective monopole defects act as both divergent sources and convergent sinks of the magnetic field Hs [8]. Local proton ordering in water ice [26] finds a physical equivalent in the frustrated pyrochlore Ising magnet, as originally identified by Anderson [27]. The Ising spin, as the proton spin, possesses only two discrete orientations (up or down) since it is constrained to point along an axis. The centres of the pyrochlore tetrahedra of these spin ice materials identify with the locations of oxygen atoms in water ice. The Ising spin axes are exactly aligned to the water ice oxygen bonding such that residual Pauling entropy can also be precisely demonstrated in spin ices [28].
The high level of degeneracy expected for the tetrahedrally coordinated crystal-lattice being investigated could lead to similar fractionalization of the magnetic moments into effective, irrationally-charged excitations, i.e. fractionalization of the microscopic spin degrees of freedom [29]. This behaviour is widely reported in low-energy, spin ice magnets [30,31], and references therein. Crucially, gauge fields also emerge from the geometrical frustration and defects in these fields lead to further monopole excitations [29].
For a frustrated system with charge fractionalization, ordering is generally characterized by the emergent gauge field; i.e. topological ordering [29,32] that opposes Landau ordering and symmetry breaking. Typically, in an ensemble subjected to constrained disorder, violations of local rules (or topological defects) appear as localized excitations of the low-energy states of the system and these local rule violations control the collective dynamics. In spin ices and other water ice manifolds, the violations manifest as effective magnetic monopoles. Castelnovo et al. [29] describe a mechanism for this fractionalizing process. The monopoles cut off the dipolar correlations (i.e. the interaction potential μ → 0) to allow a correlation length ξ to be defined. As a spin ice approaches a critical point, the spin correlation is not defined by an order parameter. Instead, it is defined by deconfinement of a gauge field which, in this case, is imposed by the quasi-micro-canonical ensemble/ constant energy Hamiltonian function. Such an interpretation is consistent with the convention that superconducting states lack any local order parameter but rather exhibit charge fractionalization whilst remaining sensitive to the global topology of the underlying manifold [33,34].
The discussion below proposes that hyperbolic curvature of the vacuum manifold is derived from the electroweak interchange of gluons and W-bosons to give an effective vector boson mass mV. This action induces a magnetic monopole condensate from the fractionalized charges to establish a macro-scale dual superconductor. The associated Higgs mass mH is then responsible for the non-extensive volume changes in the system. It was previously proposed in [1] that hydrogen bonding-induced curvature on the crystal-fluid lattice initiated the superconducting phase transition. However, the causality is in fact the opposite where electroweak interactions are shown to result in a magnetic condensate with associated Higgs mass mH.
Phase Transitions and Collective Phenomena
Loss of homogeneity is characteristic of phase transitions that give rise to critical phenomena. The discovery of a distinctive universality class of critical exponents that satisfy the scaling laws of Fisher, Rushbrooke, Widom and Josephson [21,22] reveals spontaneous magnetic and superconducting properties for the crystal-fluid material investigated. A phase transition from Type-II superconductivity to dual Type-I superconductivity is identified through the Ginzburg-Landau parameter κ where the spontaneous magnetic field Hs transitions from negative to positive (Appendix C) and a complex order parameter field Ψ(r) emerges. Spontaneous magnetism Ms can either increase or decrease dependent upon the change in direction of hyperbolic curvature K. Positive piston displacement results from a reduction in K to give increasing values of Ms. Negative piston displacement results from an increase in K to give reducing values of Ms.
Derivation of the Gaussian hyperbolic curvature K also gives the Gaussian radius Rg as its inverse, as shown below. This enables the hyperbolic surface area of a hollow, walled sphere having effective radius R to be determined (A = 4πsinh2(R/2)) [1]. The hyperbolic surface area maps almost exactly to the negative inverse of the gradient energy, where topological defects are introduced, in an apparent expression of holographic duality [35]. The external pressure perturbations may be interrupted at any point such that both the swept volume V and the hyperbolic curvature K become fixed and stable. This suggests that the non-equilibrium gradient energy is captured and confined within the hydrogen bonding interactions of the water ice cages and inhibitor solvent as the system relaxes into a non-critical, stable state (refer to equations (1) and (2)).
Inequalities in the associated Maxwell relations together with calculations of the hyperbolic geometry reveal non-additivity and non-extensivity in the fundamental thermodynamic relation. Additivity can be restored through hyperbolic curvature (i.e. surface area A) whilst extensivity can be restored through gradient energy/ coupling energy (i.e. volume V) [22]. The coupling energy is related to the critical correlation length exponent ν in 3-dimensions combined with values of a scalar field Φ as derived from the gradient energy term -½(∇Φ)2 of the Lagrangian such that:
The critical correlation length ξ associated with the universality class is linked to volume V through Lorentz boosts, i.e. relativistic velocity and the reference frames associated with acceleration and deceleration [1]. The critical correlation length ξ is revealed to be a Lorentz length expansion; a relativistic phenomenon coinciding with the formation of a magnetic condensate [12]. The relativistic time contraction conjugate to the critical correlation length is also revealed in Figure 3 where the y-axis representing scalar field values has units of s-1, i.e. the reciprocal of time.
Again, the correlation length ξ is associated with a superconducting phase transition and related to a Lorentz boost in 3-dimensional space (Appendix B). Its value reveals the presence of self-organized criticality responsible for a ‘rolling’ critical response in accordance with:
where T is the system temperature and Tc is the critical temperature. Both temperatures are dynamic under external pressure perturbation to reveal sustained anisotropy in the water ice cage structures in either direction. The magnetic correlation length ξ corresponds to a gap in gradient energy that can be described by a relativistic length expansion having an associated conjugate time contraction [1].
The gradient energy term -½(∇Φ)2 equates with either positive or negative PV work (i.e. it is described by the least action principle of the Lagrangian) whilst the hyperbolic surface area is a function of the Gaussian radius of hyperbolic curvature Rg. Both properties are calculated from experimental results (Appendix A). In order for the surface of the system to be fully expressed in the gradient energy, it is necessary to introduce topological defects at the superconducting phase transition where the spontaneous magnetic field Hs moves from negative to positive through zero.
Analysis and Discussion—New Insights
Gauge Symmetry
The exponential function for the coupling energy e3vΦ (5), as derived from experiment, represents a capturing of the magnetic condensate wavefunction through the interaction energy of the crystal-fluid material such that it becomes real and observable (1,2). Naively, a gauge monopole condensate appears to acquire a temporary critical mass mH through coupling of the Higgs-like gauge field Φ to the magnetization vector field Ms, as represented by the correlation length exponent ν. The exponential function e3vΦ also expresses the scale-invariant and gauge-invariant properties of the critical system. Conservation of angular momentum requires the existence of a sink/ source for the associated changes in inertia (variable effective radius) together with a corresponding symmetry relation.
Scale-invariance is attributed to the hyperbolic curvature of Lorentz boosts that describe a conformal symmetry at the surface of the embedding vacuum manifold [35,36]. Conformal symmetry is able to represent the tetrahedral, hydrogen bonded, 3-dimensional spatial geometry of the crystal-fluid under non-extensive volume changes whilst its variable hyperbolic surface area maps to the gradient energy term of the Lagrangian (see below). Since a universality class of topologically invariant critical exponents has been determined for the continuous (second order) phase transition, the system can be modelled through conformal field theory in 4-spacetime dimensions, i.e. it is describable by a renormalizable quantum field theory in which the non-perturbative conformal bootstrap is irrelevant [37].
Yang-Mills theory represents such a strongly coupled quantum field theory [16], i.e. a gauge theory in which the low-energy dynamics are far removed from any classical description [38]. It is in turn represented through the mathematical structure of Lie symmetry groups that provide for intricate topologies. The compact, simple Lie group SU(3) describes the strong interaction in QCD, i.e. the binding of quarks and gluons through confinement mechanisms. The mechanical action of the piston expander can be described by the emergence of a gauge field Φ (1.2 ≤ Φ ≤ 3.6 ks-1) and the critical length exponent ν (0.593) in 3-dimensions, which maps to the relativistic rapidity angle ±φ (±1.779), as equation (8). In QCD such gauge fields are collectively known as gluon fields. The field strength, or curvature Fμν, takes the general form:
where Aν provides for Lorentz
invariance and Aμ is the gauge connection.
The gauge connection depends upon a complex scaling symmetry that is exact but not directly observable [39]. In the quantum state Ψ → eiθΨ, which could be interpreted as a potential sink/ source for the ‘hidden’ inertia of the false vacuum system (although later this is revealed not to be the case). It also represents the complex order parameter field of the Ginzburg-Landau superconducting phase transition included in equation (10).
Experimental results lead to a relativistic manifestation of length expansion and time contraction arising from false vacuum behaviour in a thermodynamically constrained condensed matter system. The local stability conditions maintained through dynamically responsive inhomogeneities in this soft matter are deemed equivalent to the property of asymptotic freedom, or antiscreening, which accounts for the mechanism of colour confinement in particle physics, i.e. scale-invariance is suggested across the micro- and macro-scales of the system. In micro-scale SU(3) QCD it is the emergence of clouds of virtual gluons that establish the antiscreening phenomenon [3]. In both mechanisms, increasing kinetic/ internal energy is mirrored by an increasing negative energy potential such that total energy remains constant.
Whilst the crystal-fluid material displays high stability in total energy and density, the embedding manifold always remains on the threshold of instability. Small positive or negative pressure perturbations produce divergent critical behaviour manifesting as large variations in swept volume V. However, this is not the specific volume of the material system (density remaining almost constant) but rather the non-extensive volume change associated with the condensation of magnetic entities and simultaneous emergence of a gradient energy term.
The ‘rolling’ critical response enabled through anisotropy in water ice cage structures appears to deliver net energy gains, either positive or negative, in a display of self-organized criticality [40]. The angular momentum of the material is transferred to or from the embedding vacuum manifold through self-organizing behaviour and high energy degeneracy of the water ice cage structures. However, this brief statement does not provide a full description and a more detailed hypothesis follows.
Work derived from the piston expander can be expressed in terms of an electromagnetic pseudo-scalar gauge-invariantly coupled to the gauge field exponent Φ and the critical correlation length exponent in 3-dimensions 3ν (which is equal in magnitude to the rapidity angle ±φ, as described in Appendix B). The relationship is similar in form to the cosmological inflation model proposed by Ratra [41]:
where the covariant vector Fμν and contravariant gradient potential Fμν combine to produce Lorentz invariance for the pseudo-scalar field when rotated on a hyperbolic manifold, i.e. the electromagnetic field pseudo-scalar enables a non-additive energy contribution to enter the non-equilibrium system in the form of hyperbolic curvature. Expressing the exponential function in terms of the rapidity angle ±φ reveals the action of positive and negative spinors that determine the critical correlation length ξ, as (25,26,27), leading to either an increasing or decreasing negative gradient energy.
In the quasi-micro-canonical ensemble [1], the electromagnetic field pseudo-scalar is involved in the coupling mechanism but contributes no work in itself. It expresses the Berry curvature that is indirectly derived from the vacuum manifold whilst hosting the magnetic exchange pathways that facilitate energy transfers either to or from the vacuum manifold. The inner-product of the E and B fields remains the same viewed in all relativistic frames [42] with the pseudo-scalar field remaining Lorentz invariant such that:
where c is the speed of light.
Ginzburg-Landau theory states that the free energy of a superconductor near a phase transition can be expressed in terms of a complex order parameter field [43]:
Then a complex rendering of the coupling energy term maps to a complex wavefunction of the Berry phase:
where the quantity |Ψ(r)|2 reflects the density of superconducting charge carriers; electrons for Type-II and the electroweak monopole counterpart arising from confined fractional magnetic charges for dual Type-I [11]. Appendix C provides a summary of the Ginzburg-Landau theory of superconductors.
In the dual superconductor model of confinement [9,10], the Yang–Mills vacuum is also based on the condensate of a magnetically charged Higgs field. In the current findings, the critical correlation length ξ similarly represents the coherence length ξ’ of a massive macro-scale magnetic monopole condensate [12] that manifests as a divergence in the hyperbolic volume V of the system at the superconducting phase transition [43]. In this case the coherence length ξ' becomes exceptionally large whilst still defining the distance over which the dual superconductor can be represented by a wavefunction.
Since the coherence length ξ’ and maximum value for the Ginzburg-Landau parameter κ for the Type-I dual superconductor are known [1], the London penetration depth λ can be derived (see Appendix C). ξ’ and λ are equal to the inverse Higgs mass mH and inverse vector boson mass mV, respectively [11]. In normal metallic superconductors λ is the distance within which an externally applied magnetic field disappears inside the superconductor. However, for the dual superconductor λ represents a distance beyond the developing flux tubes (confined fractionalized magnetic charges) within which the magnetic current and electric field are expelled as a result of the dual Meissner effect.
So, the Gaussian hyperbolic curvature K of the embedding vacuum manifold derives from mV. Then, the resulting magnetic monopole condensate is responsible for mH, which manifests in the system volume V. Appendix C includes supporting quantitative analysis.
The complex form of the coupling energy term resembles a quantum mechanical wavefunction in which the energy spectrum is made entirely real and observable through dissipative structuring and interaction energy of the crystal-fluid material. Ψ0(r) initially appears to corresponds to the emergence of the gauge field Φ coupled with a magnetization vector field Ms at the Type-II to dual Type-I superconducting phase transition. Dissipation of either the scalar field Φ or the critical correlation length ξ would represent a collapse in the wavefunction.
Application of de Moivre’s formula and isomorphic mapping of the complex field to hyperbolic rotational matrix form gives:
and similarly expressing electromagnetic duality as
rotations in the 2-dimensional hyperbolic plane:
The conjugate transpose of (12) is (13) and the determinant of VVH = 1 suggesting that PV work of the piston expander is contingent upon the decomposition of a Hermitian unitary matrix A into two 2 x 2 non-Hermitian unitary matrices (i.e. two complex matrices V and VH containing both real and imaginary components such that VH ≠ V) [44]. The gauge field and the electromagnetic pseudo-scalar are thereby coupled through a reciprocal interaction in the hyperbolic plane.
Although this interpretation appears at odds with the expression for PV work stated in (8), in fact any 2 x 2 complex symmetric matrix A can be eigendecomposed into a diagonal matrix D sandwiched between two complex unitary matrices, i.e. VDVH in this case. Minkowski spacetime vectors can be represented by 2 x 2 orthogonally diagonalizable matrices and incorporated into the extended physical VDVH decomposition to reveal the coupling energy source.
For:
VDVH can be expressed as the Pauli spin operators acting on a bivector [45]:
and
where ±φ represents the Lorentz rapidity angle (with values of ±1.779) and Φ/2 is the spinor half-angle formulation. Both are incorporated into the Weyl spinors of (25) and (26). Additionally, VVH corresponds to the Pauli identity matrix σ0, also included in the Weyl spinors description. The sign of the rapidity angle φ is associated with either a positive or negative spinor, i.e. an increasing or decreasing negative gradient energy.
The diagonal Hermitian matrices exhibit basic 3-dimensional rotation as well as 4-dimensional Lorentz transformation properties consistent with the relativistic length expansion and time contraction associated with the non-extensive element of PV work, as also revealed through the experimental results [1]. Thus, the 2 x 2 unitary matrix A as a member of the compact U(2) symmetry group is decomposed into factors identifiable as both Hermitian and non-Hermitian.
When represented in terms of gauge symmetry groups [44], the U(1) group of electromagnetism (via its mapping to SO(2) in the 2-dimensional real plane) and the SU(2) group of the complex order parameter Ψ(r), are in fact subgroups of the U(2) group such that:
which describes a mapping to a Yang-Mills electroweak symmetry group [46] where ℤ2 represents the topology associated with a gauge monopole condensate [47]. Formation of the U(2) group is accompanied by critical behaviour and emergence of the gauge field Φ as predicted by the Yang-Mills theory.
The dual superconductor model has several interpretations that require condensation of monopoles, just as normal superconductivity results from the condensation of electric charges (or Cooper pairs – see Appendix C) [11,12]. Theoretical frameworks for the condensation of monopoles have been structured in terms of Abelian projection for the SU(2) gauge symmetry group or non-Abelian gauge-invariance for the SU(3) gauge symmetry group. Recent efforts [12] have sought to extract the Abelian component responsible for gauge-independent quark confinement from the non-Abelian gauge-invariance required for asymptotic freedom, without losing the essential feature of monopole condensation. From the experimental findings [1], an alternative solution emerges where electroweak interactions with fractionalized magnetic charges lead to complex monopole condensation within an overarching U(2) Abelian group, as detailed below.
In the vacuum of a QCD dual superconductor, the dual Meissner effect compresses the chromoelectric flux between a quark and antiquark into a thin flux tube to form the hadronic string [11,48]. As the distance between quark and antiquark increases, the flux tube becomes longer whilst maintaining a minimal thickness. This geometry ensures that the energy increases linearly with length to create a linear confining potential between the quark and antiquark that bears a similarity to the linear oscillating Hamiltonian of the macro-scale system. The flux tube determines the extent of QCD vacuum suppression, i.e. positions where the chromoelectric field is maximally expelled to leave a residual dual superconductivity [49].
Yang-Mills theory requires the existence of both chromomagnetic monopole condensation (given by a coherence length) and the dual Meissner effect (given by a penetration depth) [11,12]. The force carrying gauge bosons of QCD are massless gluons which perform a similar role to photons in electromagnetism. Since the gluon field represents a local expulsion of the QCD vacuum, the (indirect) absorption of gluon emissions into the QCD vacuum would tend to reduce local ‘space density’ and effective magnetic permeability μ0. The net effect is to increase the hyperbolic curvature K of the embedding manifold, i.e. a quantum mechanical process manifests as an effective vector boson mass mv or ‘strong gravity’ [50].
Berry Phase and Parity-Time (PT) Symmetry
The foundations of Berry phase physics lie in the adiabatic theorem of quantum mechanics [51] which provides a formal description for a system coupled to a slowly changing environment. If the system Hamiltonian H(t) varies adiabatically and │Ψ(t)⟩ is an associated eigenstate then, following cyclic evolution of the environmental parameters where H(T) = H(0), the state returns to itself but gains an additional phase factor [51,52]:
where α represents the angular momentum of the wavefunction. For the macro-scale dual superconductor, it originates from the exclusion of momentum resulting from gauge monopole condensation which is effectively stored in the electromagnetic field pseudo-scalar [38].
The adiabatic theorem is based upon a single, non-degenerate eigenstate to which the system ‘clings’ as the environment is slowly changed [53]. However, for the pressure-perturbed system being examined, asymptotic freedom constrains innumerable, degenerate and excited eigenstates to a singular value of total energy in the oscillating Hamiltonian function. External pressure perturbations applied to the crystal-fluid material see changes in kinetic/ internal energy mirrored by changes in negative energy potential such that total energy remains constant. Integration of the scalar potential ∇Φ over a Hamiltonian cycle reveals the gradient energy term -½(∇Φ)2 that becomes observable in the PV work extracted from the piston expander (see equation (29)).
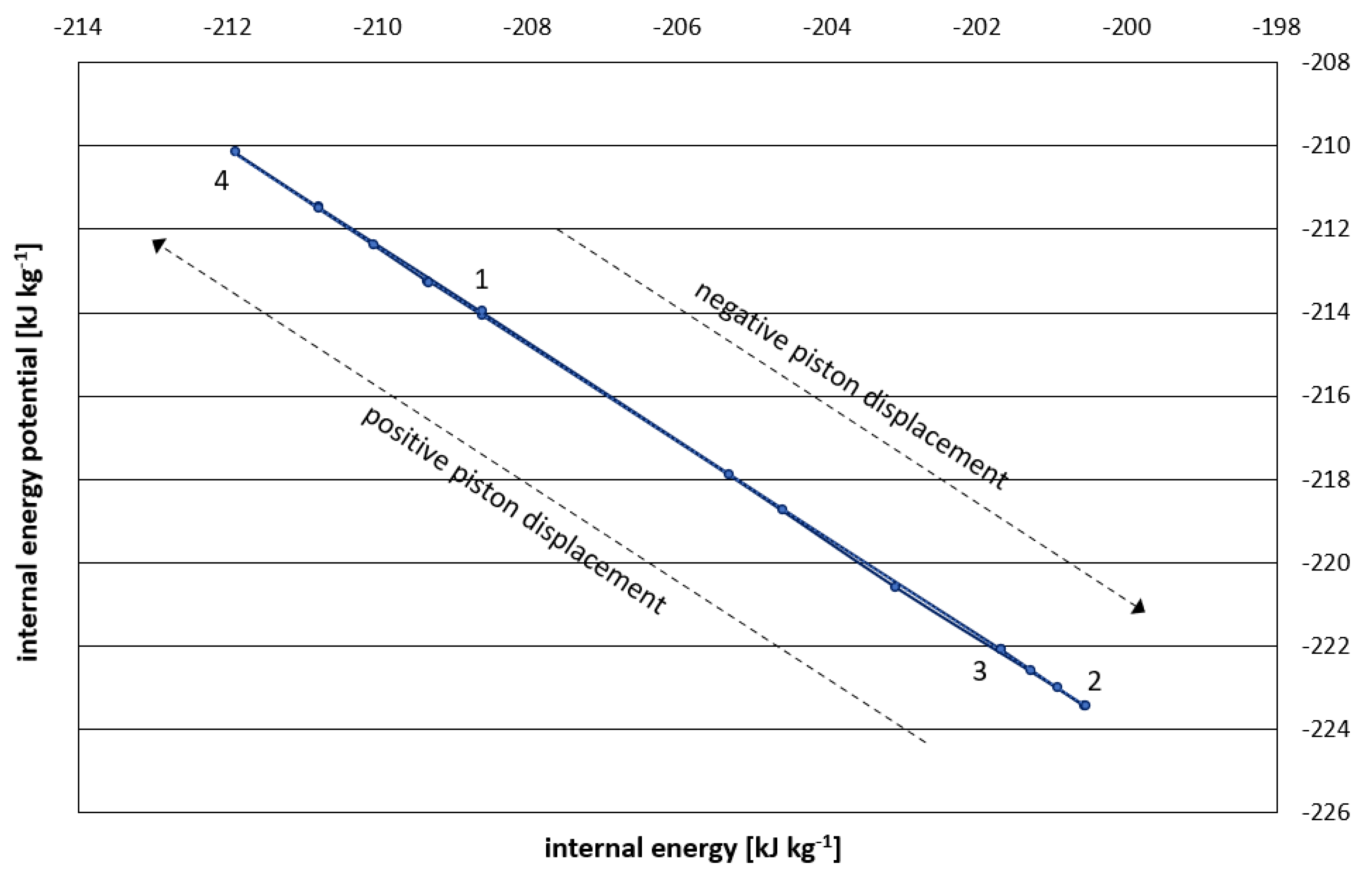
When perturbations cease, the negative energy potential appears to be transferred to the sterically-induced interaction energy of the crystal-fluid, subject to some limited dielectric relaxation. Since hyperbolic geometry is retained in the crystal fluid, there is negligible net loss of mass as the Higgs mass mH and vector boson mass mV dissipate. The phase factor Ψ(T) exists only for the duration of pressure perturbations with the Hamiltonian remaining constant under these perturbations (as Figure 2). The resting values of total energy E are then ‘propped’ and metastabilized through dissipative structuring of water ice cages, subject to limited dielectric relaxation, as quantified by Stage 2-3 and Stage 4-1 (Figure 2). Following metastable decay, which can last several weeks, the mass associated with sterically-induced interaction energy (0.3 kg, approx.) eventually dissipates. For the metastable system, the internal energy potential ue remains approximately constant:
For acceleration (Stage 1-2) the effective radius decreases, and for deceleration (Stage 3-4) the effective radius increases. However, the resulting ‘hidden’ inertia is deemed not to be directly responsible for the Berry curvature term within the geometrical phase (11) since the externally-induced momentum manifests entirely in non-additivity of the hyperbolic curvature K. Instead, the Berry curvature is linked to the condensation of magnetic entities whereby the resulting exclusion of charge momentum manifests in the energy potential of the electromagnetic field pseudo-scalar (9). The Berry curvature is subsequently captured to be made real and observable in the variable hyperbolic volume V of the embedding vacuum manifold. Again, this hyperbolic volume is metastabilized by the dissipative structuring of water ice cages within the crystal-fluid material so that the complex Berry phase is transformed into real work done.
For a classical thermodynamic system, changes in inertia ½mr2 represent changes in kinetic/ internal energy. However, since both internal energy and specific volume are highly constrained parameters within a false vacuum system, the energy of acceleration/ deceleration is prevented from manifesting in the crystal-fluid material. Thus, Pv work is limited to interactions with the walls of the vessel. For the synchronized U(2) symmetry group identified below, conservation of angular momentum may be understood in terms of accelerating/ decelerating quarks that result in the emission/ absorption of gluons, i.e. changes in negative energy potential.
Gluons emitted by quarks are indirectly absorbed by the QCD vacuum manifold whilst the gluons absorbed by quarks indirectly emerge from the QCD manifold, thereby tending to effect local ‘space density’ and effective permeability μ0. A gluon-induced process for gg → W*W* → leptons (where W*W* represents an intermediate W-boson/ vector boson pair) is described in [54]. At some stage in the process, the fine structure constant α (≈ 1/137) appears to play a key role (see Appendix D for analysis).
Lepton decay may therefore result in a chromoelectric confining potential that acts to transform fractionalized microscopic magnetic spin degrees of freedom into SU(2) electroweak monopole entities [31]. A sufficiently large number of SU(2) electroweak monopoles could then generate a Planck mass such that a U(2) magnetic condensate having Higgs mass mH emerges. The associated gauge monopole topology facilitates the spontaneous magnetism Ms that maximally excludes the electric field E and establishes the macro-scale dual superconductor (see for analysis). This phase-change is represented by the Ginzburg-Landau parameter κ with values ≤ 1/√2 that describe the ratio of the Higgs mass mH to the vector boson mass mV.
Pv is insignificant in comparison to PV such that it represents the negative energy potential of the crystal-fluid material only. Therefore, for a constant Hamiltonian oscillator of constant mass m, ½r2 ∝ 1/Pv, as described in Appendix B of [1]. The average 1-dimensional radius rx of the critical system is then found:
The Gaussian curvature K for the 2-dimensional, hyperbolic surface of the critical system for the principal curvature relationship of rx = - ry , can then be determined:
or
Then, the average Gaussian radius of hyperbolic curvature (1/K or Rg) is given by:
Gaussian curvature K has units of m2 s-2 that map directly to the effective vector boson mass mV as the inverse of the penetration depth λ (as described in Appendix C). Through this mechanism, the negative energy potential of gluons is conserved in the associated hyperbolic curvature quantifiable by the non-equilibrium values of pressure P and specific volume v. Thereby, a quantum mechanical action is tuned thermodynamically under false vacuum conditions. Expressed in terms of the holographic principle, or the anti-de Sitter/ Conformal Field Theory (AdS/ CFT) correspondence, this hyperbolic geometry results from a renormalization group flow/ scaling flow. In other words, a scaling flow from the boundary surface (described by a 2-dimensional CFT) to the interior is encoded in the geometrical properties of the hyperbolic manifold (described by a 3-dimensional AdS) in accordance with the Einstein field equations [35] (see Appendix B).
Decomposition of the complex gauge connection (eiΦ)3ν in equations (12) and (13) suggests that complex Berry curvature is necessary for emergence of the coupling energy (5). It also determines the phase of electromagnetic duality, which in the extreme leads to dual superconducting behaviour, i.e. condensation of magnetic entities resulting in the exclusion of fractionalized magnetic current and the electric field. The cyclic evolution of the gauge connection results from the effective adiabatic property of the constrained false vacuum system (as revealed in the constant Hamiltonian oscillator of Figure 2) to establish a novel form of the Berry phase [51], one responsible for topological ordering in the macro-scale dual Type-I superconductor [8]. As with the conventional ground-state Berry phase, this ‘excited-states’ variant exposes the gauge structure in quantum mechanics [13,55].
In addition to describing the emergence of a gauge field Φ, the gradient energy term -½(∇Φ)2 of the Lagrangian also maps to the complex order parameter field Ψ(r) in accordance with Ginzburg-Landau theory. The PV work generated in the piston expander suggests that the associated quantum mechanical wavefunction is made real and observable, a phenomenon recently uncovered by Gu et al. [13]. More precisely, the VDVH decomposition reveals that the wavefunction becomes entirely real as the coupling energy is exposed through the diagonal matrix D in the VDVH decomposition (15).
Since the system can be described through a combination of Hermitian and non-Hermitian matrices, it resembles a PT symmetric system [14]. Such systems are characterized as not being isolated from the environment (i.e. non-adiabatic) but subject to highly constrained interactions. This description is consistent with the false vacuum behaviour of the crystal-fluid material where both specific volume and internal energy are highly constrained. Energy and entropy gains and losses to the environment (including the embedding vacuum manifold in this case) are exactly balanced, i.e. a renormalized, scale-invariant interaction between condensed matter and quantum wavefunction becomes evident in the constant energy Hamiltonian.
PT symmetry requires both space reflection and time reversal symmetries. The upside-down potential of the quartic term as identified by Bender [14] is consistent with the marginal interaction and negative gradient energy term derived from experiment [1]. However, the results presented here reveal the symmetry of Lorentz boosts, i.e. symmetries in the expansion and contraction of both space and time, which may represent a more generalized form of PT symmetry.
Symmetry Synchronization and Conserved Quantities
Quark acceleration produces gluon emissions since a lower binding potential is necessary to maintain the momentum and energy of any given quark colour configuration [56]. This results from a gluon recombination process whereby a quark and antiquark pair are annihilated. The emergence and absorption of gluons signifies a mediated exchange between the non-Abelian gauge symmetry of QCD and the Abelian gauge symmetry of the vacuum manifold, i.e. an electroweak interaction. In other words, the parameter space of the quantum mechanics is the spacetime manifold of an Abelian gauge theory such that the closed cycle of the Berry phase is formally identical to a Wilson loop observable [57], as demonstrated below.
The following non-Abelian Faddeev-Niemi decomposition is considered [58]:
This decomposition is a restricted one since splitting and recombining gluons in SU(3) represents a mediated interaction with a U(2) spacetime manifold rather than full symmetry breaking to SU(2). The requirement for a Higgs-type scalar field is satisfied by the emergent gauge field Φ [12]. So:
Asymptotic freedom is thereby maintained through the dominant SU(3) subgroup. Again, U(2) appears as an electroweak symmetry group [46] with ℤ2 representing an Abelian topology consistent with gauge monopole condensation [47]. For Kondo et al. [12], U(2) is the maximal stability group determined by the fundamental quark group SU(3) where quark confinement is the non-Abelian micro-scale dual superconductivity associated with chromomagnetic monopoles. In the current exposition, this non-Abelian micro-scale dual superconductivity is subsumed into an Abelian gauge monopole condensate, as identified above, under the common U(2) symmetry of macro-scale dual superconductivity.
A U(2) gauge symmetry that provides for a gauge monopole condensate has so far been identified in both the condensed matter system and the underlying QCD particle physics. However, it is also possible to determine a U(2) gauge symmetry for the vacuum manifold of local spacetime through which hyperbolic curvature is enacted. That is, where the splitting and recombining of massless, force-carrying gluons are associated with fictitious forces in non-inertial reference frames, as quantified by the effective vector boson mass (0.22 m2s-2 ≤ mV ≤ 0.46 m2s-2).
The Lorentz group SO(4) provides for the conservation of energy and angular momentum in 4-dimensions (ℝ4) through two continuous symmetries; rotations in 3-dimensional Euclidean space and Lorentz boosts which influence both space and time [59]. The 4 x 4 orthogonal matrix representation of the metric tensor can also be cast in terms of a 2 x 2 unitary matrix operating on a complex 2-component spinor. The complete unitary 2 x 2 transformation matrix for spinor rotations and boosts can be expressed as:
or
where θ is the Lorentz rotation angle, σ is the Pauli spin matrix, and ϕ is the angle associated with the Lorentz boost (or rapidity) [1,60]. Equation (25) represents a ‘right-handed’ spinor ϕR and (26) represents a ‘left-handed’ spinor ϕL, i.e. the Weyl spinors.
For bidirectional Lorentz boost transformations having no rotational components, the Weyl spinors simplify to ϕR = e-σϕ/2 and ϕL = eσϕ/2, which is the half angle formulation given in equations (14) and (15) above. It is observed that the critical correlation length ξ is equal to the average value of the combined rapidity angle exponentials with ±φ. A change in direction of the scalar potential ∇Φ is consistent with a reversal in direction of the rapidity angle exponents such that:
Later insights by Dirac led to the concept of the 4-component spinor which, unlike (25) and (26), preserves parity of the wavefunction under the sign reversal operation Ψ(x,t) → Ψ(-x,t), thereby accommodating changes in scalar potential direction explicitly whilst maintaining a positive gauge field plus positive energy [45] (and also predicting the existence of antimatter). Then, retaining the 2 x 2 unitary matrix whilst acknowledging parity preservation requirements produces the following spacetime group representation [59,61]:
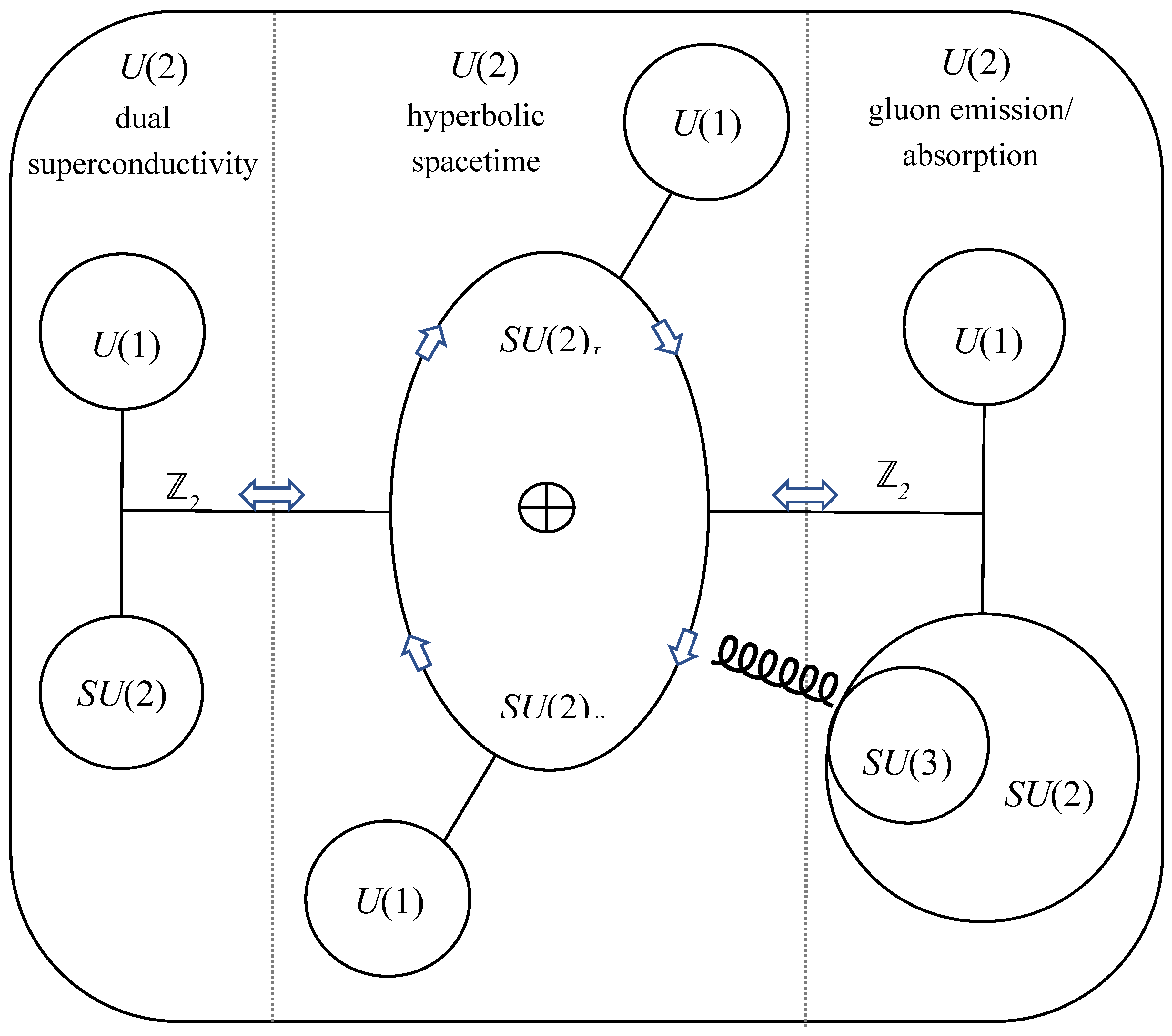
The symmetry group decompositions in (16), (24) and (28) are then amalgamated to describe a consolidated ‘symmetry synchronization’ that establishes common scale- and gauge-invariance in U(2), as shown schematically in Figure 4:
When a symmetry is broken, a corresponding order parameter that diminishes to zero can often be identified. However, in this case the complex order parameter Ψ(r) emerges where symmetry is synchronized.
Both energy and angular momentum are conserved within the common U(2) group to reveal the time and space symmetries of a Lorentz boost in agreement with Noether’s theorem (see below). There is a gluon field for each of the eight colour charges and each gluon field is composed of a time-like component and three space-like components. These components relate to the electric potential and the magnetic potential, respectively, and will interact indirectly with the vacuum manifold to determine the values of effective permittivity ε0 and effective permeability μ0. Additionally, the chromoelectric and chromomagnetic components correspond to the temporal and spatial Wilson loops described below, where the Wilson loop represents an order parameter for quark confinement [4].
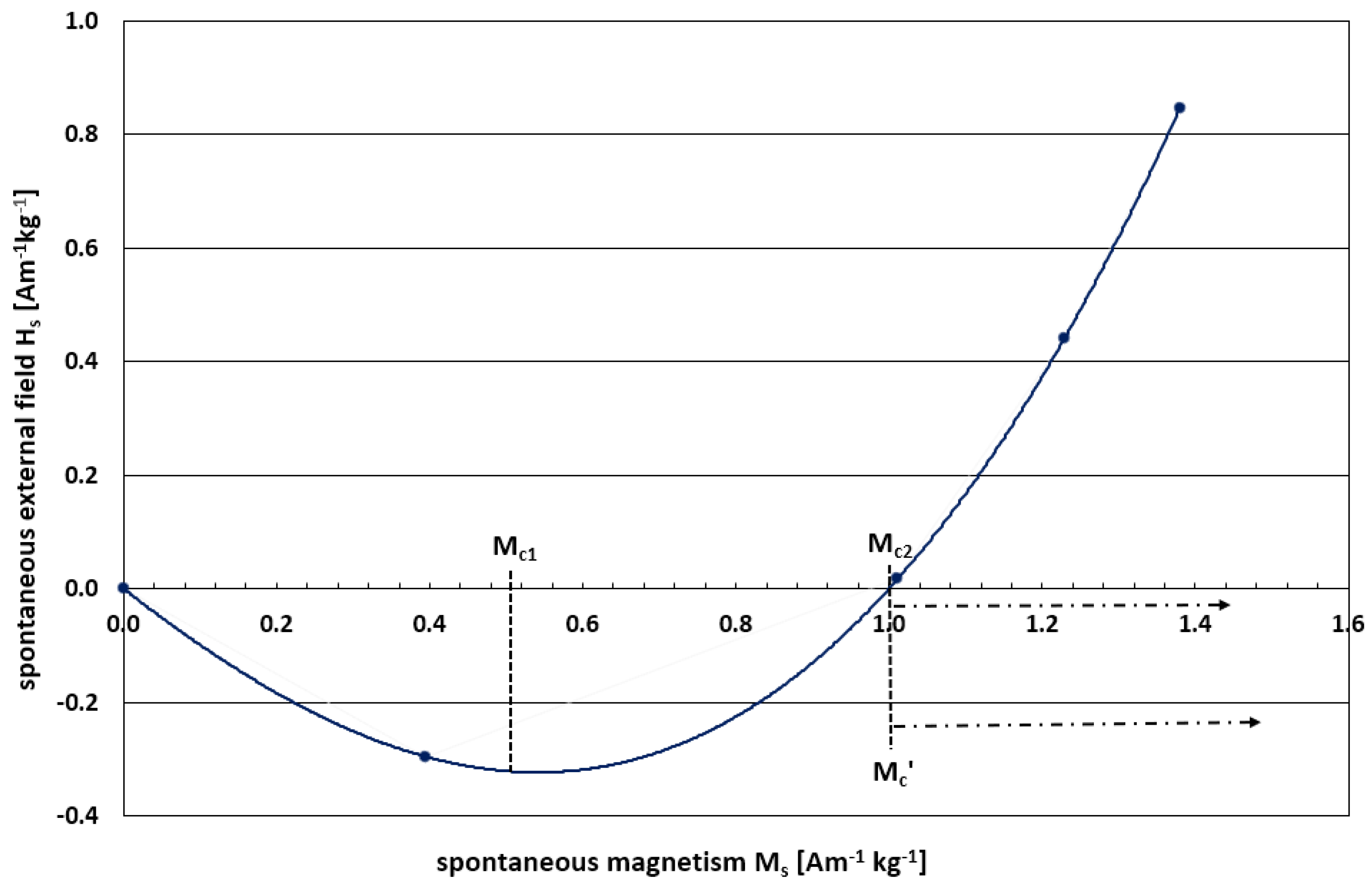
Variations in effective μ0 require that a spontaneous magnetism Ms, with associated spontaneous magnetic field Hs, emerges to conserve magnetic charge. Fractionalized magnetic charges arising from the geometrically frustrated crystal-fluid material appear confined into magnetic entities through lepton decay. These electroweak magnetic monopoles are interpreted as condensing into a gauge monopole topology that excludes magnetic current to leave magnetic exchange pathways available for the spontaneous magnetism Ms. Whilst magnetic exchange interactions are conventionally established through direct and super-exchange mechanisms between metal centres or metal centres and various ligands, exchange can also occur via intermolecular hydrogen bonding interactions [62,63]. Changes in bond lengths and angles along the exchange pathway affect the hopping integrals between magnetic centres, thereby altering the magnetic exchange effect.
The correlation length ξ of the magnetic monopole condensate produces divergent critical behaviour that is shown to have a distinctive universality class of critical exponents. The gauge monopole topological defects act as both convergent sinks (under acceleration) and divergent sources (under deceleration) of the magnetism Ms [8]. The nature of these defects is speculated in .
Similar principles apply to variations in vacuum energy determined by the local ‘space density’ (which determines the embedding manifold curvature). Conservation of energy requires that negative PV work is performed under false vacuum acceleration (energy is transferred to the vacuum manifold) whilst positive PV work is performed under deceleration (energy is transferred from the vacuum manifold). Work is related to the gauge/ scalar field Φ as follows [1]:
The right-side of equation (29) represents the gradient energy term of the Lagrangian function resulting from the scalar potential ∇Φ developed across the gauge monopole topology which is integrated. The Lagrangian action of the left-side, i.e. mechanical work, is also related to the critical response function revealed in the coupling relationship (1) to confirm energy renormalization in the synchronized U(2) group complex parameter field Ψ(r). That is, energy equivalence between the long-range dissipative structuring of water ice cages and the short-range confinement mechanisms of sub-atomic particles, as illustrated in Figure 4. This outcome aligns with Anderson’s speculative prediction [64]:
‘Physics in the 20th century solved the problems of constructing hierarchical levels which obeyed clear-cut generalizations within themselves […]. In the 21st century one revolution which can take place is the construction of generalizations which jump and jumble the hierarchies, or generalizations which allow scale-free or scale transcending phenomena. The paradigm for the first is broken symmetry, for the second self-organized criticality.’
With U(2) scale- and gauge-invariance spanning the asymptotically-free behaviour of both the macro-scale dual superconducting system and the micro-scale quark-gluon system via electroweak interactions with the embedding vacuum manifold, a physical correspondence between non-equilibrium thermodynamics and quantum mechanics is established. Since the superconducting phase transition is represented by Ginzburg-Landau theory (i.e. gauge-invariant coupling of a scalar field to the Yang-Mills action is predicted) it seems reasonable to link the gradient energy gap of Figure 3 to the mass gap problem in QCD.
Gapped and Gapless Topologies
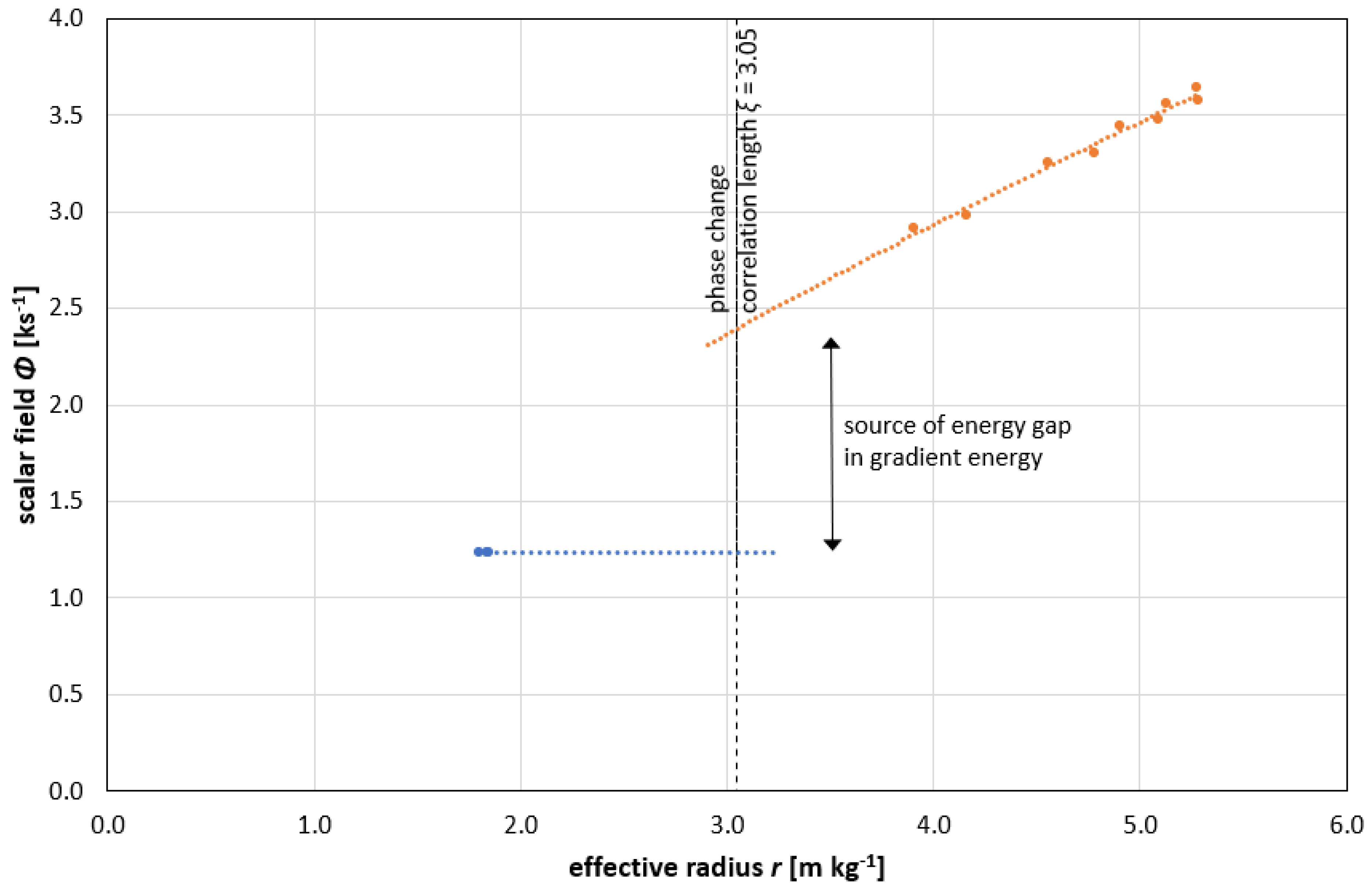
The results in Figure3 show emergence of the gauge field Φ as a gap (∆ 2.4 ks-1) between Type-II superconductivity on the left and dual Type-I superconductivity on the right. This represents a transition between the gapped state of the magnetically ordered Type-II superconductor and gapless state of the topologically ordered dual Type-I superconductor. At this point, the gauge monopole condensate forms to release spontaneous magnetism Ms. The electric field E becomes excluded to be confined on the surface of the system (including the additional surface created through gauge topological defects that form the complex magnetic condensate). That is, a gapless surface is established so that the Berry phase manifests as a non-trivial topological insulator [51].
The gapless surface may be protected from external perturbations tending to re-open the gap through Abelian topology, as represented by the ℤ2 Chern number in the symmetry group decompositions of (16) and (24). In a review of topological superconductors [65], Sato and Ando explore the connection between ℤ2 and time reversal symmetry that is consistent with the symmetry of Lorentz boosts described above. The ℤ2 Chern number can be interpreted as a U(2) group that fibres over a circle as a 3-sphere bundle, i.e. a Hopf fibration results [66].
Typically, a topological insulator is characterized by a non-robust, non-degenerate ground-state in which energy bands coincide and exceptional, or ‘diabolical’, points occur. However, the Berry phase variant identified above displays the following features: asymptotic behaviour (robustness against perturbations); a critical correlation length ξ (long-range entanglement); conformal geometry (describable through quantum field theory); and degeneracy in non-trivial topology on a hyperbolic manifold [66]. Thus, the system also appears to be topologically ordered and so describable by an effective, low-energy topological quantum field theory (TQFT) in which many-body states would typically have topological ground-state degeneracy [67]. In TQFT the critical correlation length ξ is topologically invariant and therefore insensitive to the geometry of the embedding manifold, i.e. the critical exponents within the universality class are background independent under Lorentz boosts.
Within the research field of topological phases of matter, as investigated to date, all the topologically ordered states realized experimentally or investigated theoretically are established through strong electron-electron interactions. The coinciding valence bands of gapless ‘diabolical’ points allow for degenerate electron movements between the bands. In a crystal structure, the electronic band structures are described by Bloch’s theorem as expressed by:
where Ψ is the wavefunction, r is position, u is a periodic function, and k is the crystal momentum vector.
However, the original formulation of the Berry phase was not specifically related to Bloch electrons. Instead, it was based on the general idea that quantum adiabatic transport of particles in slowly varying fields (e.g. electric, magnetic, or strain) could in principle modify the wavefunction by terms other than just the dynamical phase. So, equation (30) is seen to map to the experimentally derived equation (11) where variable electromagnetic duality of the pseudo-scalar field gives the periodic function u(r) and eik.r represents the angular momentum of fractionalized magnetic charges that transfers into the pseudo-scalar field as the gauge monopole condensate forms [38].
Since the degeneracy associated with the crystal-fluid material occurs in metastable excited-states (with non-zero temperatures), the gapless degeneracy of the crystal-fluid material cannot be attributed to Bloch electrons. So, whilst the gapless surface of the dual superconductor is protected through ℤ2 topology, an additional mechanism is necessary to supress excited-state fluctuations such that Bloch-wave behaviour can emerge.
A potential solution is presented in Figure 4 where the synchronized continuous symmetry group U(2) leads to descriptions of asymptotic freedom in both quantum and condensed matter systems. As conservation of angular momentum extends into the microscopic quantum realm, so confinement mechanisms extend out into the macroscopic condensed matter of the dual superconductor under a renormalized Noether symmetry. The non-Abelian SU(3) subgroup of QCD remains dominant so that excited-state fluctuations due to changes in momentum are suppressed through confinement mechanisms and the constant Hamiltonian function is preserved. Topological defects may be created by chromoelectric flux tubes, or penetrating vortices, resulting from electroweak lepton decay, which in turn enable the formation of quark-antiquark pairs together with an inherent confinement mechanism.
In a non-Abelian gauge theory, the expectation value of the confinement phase can be detected by the area law of a Wilson Loop [68]. The Wilson loop average W(C) is related the energy of the interaction of static (i.e. infinitely heavy) quarks. For large loops, the potential energy is a linear function of the distance between quarks since the gluon field contracts to a flux tube that establishes a string tension K.
If Amin(C) is taken to be the hyperbolic area formed by the rapidity angle exponents |±φ| of the Weyl spinors (25) and (26), then - K maps to the reciprocal of the scalar field Φ, i.e. a temporal component with units ks-1 is also represented, as shown in Figure 3. The results in Table A3 and Table A8 reveal that the coupling energy, i.e. the expectation value, is expressed on the surface area of the hyperbolic manifold as topological defects emerge:
The rapidity angle exponents ±φ of the Weyl spinors lead to the same invariant expectation value in both local Lorentz spacetime and the local non-Abelian Wilson loop associated with the critical system (±φ ≡ 3v). Background independence across the entire U(2) symmetry group is thereby demonstrated. Such an interpretation is consistent with the requirements of a TQFT [69].
The Wilson loop operator is comprised of either time-like loops and space-like loops. There is no intrinsic difference between these objects which are related through Lorentz invariance [4] and combined in equations (31) and (32). So, in Yang-Mills theory, the Wilson loop can describe the confined quark potential as a phenomenon that exists autonomous from matter. However, the gauge monopole condensate as identified represents a deconfined Higgs phase which, for the exceptional correlation length ξ established, is expected to satisfy the area law of the ‘t Hooft loop in ℤ2 gauge theory. These two loop operators describe opposite behaviours. Under such circumstances, a mixed phase that is both confined and deconfined is described and the non-Abelian SU(3) can exist as a subgroup within the Abelian U(2) group. Where Wilson loop and ‘t Hooft loop operators exhibit these anti-commutation relations, it is possible to construct a TQFT [70].
Acceleration and deceleration of the crystal-fluid material thereby become confined interactions responsible for the splitting and recombining of gluons. Gluons are either indirectly absorbed by or indirectly emerge from the QCD vacuum manifold [54]. The Higgs-like gauge field Φ also emerges in the transition from gapped Type-II superconductivity to gapless dual Type-I superconductivity to establish a reciprocal gap in the gradient energy, as revealed in Figure 3. For the gapless state, the spin-1 vector gluons are the force-carrying SU(3) gauge bosons that indirectly generate the Bloch-wave description in the U(2) gauge monopole condensate [71]. These indirect gluon interactions with the embedding QCD vacuum manifold enable fictitious forces to emerge in non-inertial reference frames that lead to PV work in the piston expander.
Whilst the massless spin-1 gluons either emitted or absorbed by accelerating or decelerating quarks give rise to gauge particles with effective spin-½ behaviour, gauge invariance is only established where the associated gauge field can emerge under U(2) ‘symmetry synchronization’ at critical correlation length ξ in the low-energy system. That is, a gauge monopole topology [54] is necessary so that the scalar field potential can induce magnetic flux such that ∇. Bs = 0, where Bs is the spontaneous magnetic flux density.
Conclusion
Experimental investigations uncover a macro-scale dual superconductor linked to the emergence of a gauge field and the associated synchronization of a U(2) symmetry group that encompasses dual superconductivity, Minkowski spacetime and quantum interactions. Combining Ginzburg-Landau theory with the scaling laws reveals a penetration depth and a coherence length that characterize the macro-scale dual superconductor. The penetration depth determines the extent of QCD vacuum suppression whilst its inverse gives the effective vector boson mass resulting in hyperbolic curvature. The coherence length describes the gauge monopole condensate whilst its inverse gives the Higgs mass and non-extensive volume changes. The macro-scale dual superconductor signifies long-range entanglement within a magnetic condensate displaying relativistic behaviour, whilst hyperbolic curvature of the vacuum manifold is attributed to additional quantum interactions.
A ‘rolling’ critical response is enabled through structural anisotropy in a crystal-fluid held under false vacuum conditions. Self-organized criticality establishes a U(2) electroweak symmetry that spans both a macro-scale dual superconducting system and a micro-scale quark-gluon system via electroweak interactions with the embedding vacuum manifold. Under external pressure perturbation, dissipative restructuring of the metastable crystal-fluid allows for angular momentum to be transferred to or from the quark-gluon system to establish a gauge monopole condensate with associated dual superconductivity.
The complex reorganization of systems with high energy degeneracy is responsible for asymptotic freedom, as characterized by the emergence of variable negative potential that maintains constant total energy. In these systems, the excess negative potential arises from an effective vector boson mass that imposes variable hyperbolic curvature on the embedding manifold thus creating strong local gravitational effects. This ‘strong gravity’ produces variable effective magnetic permeability, establishing the pre-conditions for spontaneous magnetism with associated spontaneous magnetic field to emerge. Associated electroweak interactions appear responsible for the creation of electroweak monopoles that go on to form a condensate of complex gauge monopoles, thus completing the requirements necessary for spontaneous magnetism to either emerge from or return to the embedding manifold. Changes in the associated Higgs mass are responsible for either positive expansion or negative contraction work in the piston expander.
Conservation of energy and angular momentum across the condensed matter and quantum domains is linked to time and space symmetries in agreement with Noether’s theorem. It has been widely conjectured that gauge monopoles are associated with the U(2) group and ℤ2 topology, which enables a critical correlation length to be established. For the synchronized U(2) group, the effective vector boson mass is attributed to indirect quark emission/ vacuum absorption of gluons from acceleration, and indirect vacuum emission/ quark absorption of gluons from deceleration.
The emergent gauge structure combines with the effective adiabatic property of the constrained false vacuum system to establish an ‘excited-states’, degenerate Berry phase. Since the parameter space of the quantum mechanics is the spacetime manifold of an Abelian gauge theory, the closed cycle of the Berry phase is formally identical to both Wilson loop and ‘t Hooft loop observables describing the negative potential of the gluon field. This geometrical phase is responsible for topological ordering in the dual Type-I superconductor. The excluded electric field represents the gapless surface of a topological insulator that is protected from external perturbations through ℤ2 Abelian topology.
In complex form the gradient energy term of the Lagrangian strongly resembles a quantum mechanical wavefunction in which the energy spectrum becomes entirely real and observable. Such behaviour is also found in PT symmetric systems that are not isolated from the environment (i.e. non-adiabatic) but subject to highly constrained interactions. Conservation of energy and momentum are determined through the symmetry of Lorentz boosts, i.e. symmetries in both time and space, in a system containing both Hermitian and non-Hermitian elements. A net energy gain originates in changing symmetry relations that enable the emergence of the Higgs mass from changes in quantum confinement energies.
The complex parameter field is revealed as the order parameter that emerges to signify a superconducting phase transition from Type-II to a dual of Type-I. The phase transition is consistent with Ginzburg-Landau theory that describes gauge-invariant coupling of a scalar field to the Yang-Mills action in QCD. The Higgs-like gauge field emerges out of the transition from gapped Type-II superconductivity to gapless dual Type-I superconductivity to establish a reciprocal gap in the gradient energy. The gradient energy identifies with the scaling flow of an AdS/ CFT correspondence encoded into the geometrical properties of the hyperbolic manifold. The point at which the critical coherence length and penetration depth emerge in the macro-scale dual superconductor is conjectured as the low-energy, infrared bound of the micro-scale SU(3) QCD mass gap.
Emergence of a Higgs mass displaying a magnitude one hundred times greater than the initial sample mass is consistent with the necessity for electroweak magnetic monopoles in the Standard Model of particle physics. It is proposed that the transient Higgs mass as identified derives from the interaction of the Higgs-like gauge field with the gauge monopole condensate of the Type-I dual superconductor.
The complex parameter field exists only during pressure perturbations, although the Hamiltonian remains constant following the perturbations. The resting values of total energy are then ‘propped’ and metastabilized through dissipative structuring of water ice cages. The magnetic condensate wavefunction is thereby captured through the sterically-induced interaction energy of the crystal-fluid material such that it becomes real and observable.
Appendix A: Recorded Data and Calculated Properties as Reproduced from Reference [1]
Points 1-4 identify particular stages of the work cycle in a low-energy system; Stage 1-2 corresponds to negative displacement of the 0.5 litre piston expander and Stage 3-4 corresponds to positive displacement.
Table A1.
Recorded and calculated thermodynamic properties of a typical piston expander cycle.
|
Temperature T (K) |
Pressure P (MPa) |
specific volume v (m3 kg-1) |
|
| Point 1 | 269.3 | 0.29 | 0.0015 |
| Point 2 | 271.7 | 0.62 | 0.0015 |
| Point 3 | 271.4 | 0.61 | 0.0015 |
| Point 4 | 268.6 | 0.25 | 0.0015 |
|
internal energy u (kJ kg-1) |
entropy s (kJ kg-1 K-1) |
Volume V (m3) |
|
| Point 1 | -209.3 | 0.79 | 0.000505 |
| Point 2 | -200.6 | 0.83 | 0.000005 |
| Point 3 | -201.7 | 0.82 | 0.000005 |
| Point 4 | -211.9 | 0.78 | 0.000505 |
| displacement |
∆Ts heat (kJ kg-1) |
∆Pv work (kJ kg-1) |
∆PV work (kJ kg-1) |
| -ve 1-2 | 1.93 | 0.0015 | 642.9 |
| +ve 3-4 | -2.23 | -0.0015 | -568.6 |
|
enthalpy h (kJ kg-1) |
Gibbs free energy G (kJ kg-1) |
Helmholz free energy F (kJ kg-1) |
|
| Point 1 | -208.9 | -422.5 | -423.0 |
| Point 2 | -199.6 | -424.0 | -424.9 |
| Point 3 | -200.7 | -423.8 | -424.7 |
| Point 4 | -211.5 | -422.1 | -422.4 |
| 1 | 2 | 1 – 2 | |
|
Pvfrom TD potentials (kJ kg−1) |
Pvfrom REFPROP (kJ kg−1) |
ExcessPv (kJ kg−1) |
|
| Point 1 | 0.43 | 0.44 | -0.01 |
| Point 2 | 0.94 | 0.93 | 0.01 |
| Point 3 | 0.92 | 0.92 | 0 |
| Point 4 | 0.37 | 0.38 | -0.01 |
| 1 | 2 | 1 – 2 | |
|
Tsfrom TD potentials (kJ kg−1) |
Tsfrom REFPROP (kJ kg−1) |
excessTs (kJ kg−1) |
|
| Point 1 | -422.1 | 213.7 | -635.8 |
| Point 2 | -423.0 | 224.4 | -647.4 |
| Point 3 | -422.8 | 223.0 | -645.8 |
| Point 4 | -421.7 | 210.5 | -632.2 |
| 1 | 2 | 3 | 1 – 2 + 3 | |
|
excess Ts (kJ kg−1) |
excessPv (kJ kg−1) |
G (kJ kg-1) |
excessu (kJ kg−1) |
|
| Point 1 | -635.8 | -0.01 | -422.5 | -1058.3 |
| Point 2 | -647.4 | 0.01 | -424.0 | -1071.4 |
| Point 3 | -645.8 | 0 | -423.8 | -1069.6 |
| Point 4 | -632.2 | -0.01 | -422.1 | -1054.3 |
Table A2.
Gradient energy where the Gibbs energy is associated with a phase-change process.
| 1 | 2 | 1 - 2 | |
|
u(from TD potentials) - G (kJ kg−1) |
internal energy u (kJ kg-1) |
Excess u (kJ kg−1) |
|
| Point 1 | -422.6 | -209.3 | -213.3 |
| Point 2 | -424.0 | -200.6 | -223.4 |
| Point 3 | -423.8 | -201.7 | -222.1 |
| Point 4 | -422.0 | -211.9 | -210.1 |
| 1 | 2 | 3 | 1 - 2 - 3 | |
|
internal energy u (kJ kg-1) |
excess u (kJ kg−1) |
(kJ kg−1) |
gradient energy § ½(∇Φ)2 (kJ kg−1) |
|
| Point 1 | -209.3 | -213.3 | 651.8 | -647.9 |
| Point 2 | -200.6 | -223.4 | 8.9 | -5.0 |
| Point 3 | -201.7 | -222.1 | 8.3 | -4.4 |
| Point 4 | -211.9 | -210.1 | 576.9 | -578.7 |
§ includes work associated with the walls of the vessel, PV work and gradient energy are associated with the emergent Higgs mass mH.
Table A3.
Calculation of hyperbolic surface area.
| 1 | 2 | 1 - 2 | ||
|
outer radius r1 = 5/(2Pv) (m kg−1) |
inner radius r2 (m kg−1) |
effective radius R= r1 – r2 (m kg−1) |
surface area 4πsinh2(R/2) (m2 kg−1) |
|
| Point 1 | 5.8 | 0.5 | 5.3 | 606.2 |
| Point 2 | 2.7 | 0.8 | 1.8 | 14.0 |
| Point 3 | 2.7 | 1.0 | 1.7 | 11.6 |
| Point 4 | 6.8 | 1.5 | 5.3 | 611.9 |
Hyperbolic surface area is also associated with the emergent Higgs mass mH.
Derivation of the effective system radii is detailed in Appendix B of [1].
Table A4.
Response functions and critical exponent family as calculated by REFPROP [17].
Table A4.
Response functions and critical exponent family as calculated by REFPROP [17].
|
density ρ (kg m-3) |
specific heat capacity Cv (kJ kg-1 K-1) |
specific heat capacity Cp (kJ kg-1 K-1) |
isothermal compressibility KT (kPa-1) |
|
| Point 1 | 665.1 | 2.871 | 3.714 | 0.4557 |
| Point 2 | 663.7 | 2.850 | 3.698 | 0.4484 |
| Point 3 | 663.9 | 2.844 | 3.694 | 0.4462 |
| Point 4 | 665.6 | 2.869 | 3.712 | 0.4547 |
| Critical Exponent | |||
| displacement |
heat capacity α (Cv / Cp) |
order parameter β |
susceptibility ϒ |
|
-ve 1-2 (T – Tcrit) |
0.222 / 0.286 | 0.384 | 0.916 |
|
+ve 3-4 (T – Tcrit) |
0.223 / 0.287 | 0.515 | 0.765 |
| Critical Exponent | |||
| displacement |
equation of state δ |
correlation length ν (Cv / Cp) |
power law decay ρ (Cv / Cp) |
|
- ve 1-2 (T – Tcrit) |
3.385 | 0.593 / 0.571 | 0.455 / 0.396 |
|
+ve 3-4 (T – Tcrit) |
2.485 | 0.592 / 0.571 | 0.708 / 0.660 |
Corresponding scaling laws
ϒ = v(2 – ρ) Fisher law
α + 2β + ϒ = 2 Rushbrooke law
ϒ = β(δ – 1) Widom law
νd = 2 – α Josephson law
where d is the spatial dimension.
Table A5.
Magnetic properties derived from critical exponents.
| reduced volume (V-Vc)/Vc |
spontaneous magnetism Ms (A m-1 kg-1) |
spontaneous magnetic induction Bs (T kg-1) |
spontaneous external field Hs (A m-1 kg-1) |
|
| Point 1* | 0.198 | 1.418 | 3.265 | 1.846 |
| Point 2 | 0.952 | 1.011 | 1.036 | 0.026 |
| Point 3* | 25.0 | 0.394 | 0.099 | -0.295 |
| Point 4 | 0.329 | 1.380 | 1.380 | 0.845 |
* initial value recorded 5s after pressure perturbation.
| 1 | 2 | │2│ +│1│ | │1│ :│2│ | |
| displacement |
(kJ kg-1) |
(kJ kg-1) |
inequality (kJ kg-1) |
ratio |
| -ve 1-2 | 1.23 x 10-3 | -5.52 x 10-3 | 6.75 x 10-3 | 1 : 4.5 |
| +ve 3-4 | 5.07 x 10-4 | -3.17 x 10-3 | 3.68 x 10-3 | 1 : 6.3 |
| 3 | 4 | │3│ +│4│ | │3│ :│4│ | |
| displacement |
(kJ kg-1) |
(kJ kg-1) |
inequality uvac (kJ kg-1) |
ratio |
| -ve 1-2 | -1.23 x 10-3 | 2.75 x 10-4 | 1.51 x 10-3 | 4.5 : 1 |
| +ve 3-4 | -2.74 x 10-3 | 4.39 x 10-4 | 3.18 x 10-3 | 6.3 : 1 |
The difference in the inequalities is attributed to timing inconsistencies when recording the magnetic properties noted in Table A5. Values for vacuum energy contributions would be based upon the following relationship:
Table A7.
Effective Euclidean volume vs. hyperbolic volume.
|
net radius r= r1 – r2 |
Euclidean volume ~ e3r |
Euclidean volume factor (f1) vs. min. at Point 3Ϯ |
|
| Point 1 | 5.3 | 7409663 | 44271 |
| Point 2 | 1.8 | 250 | 1.3 |
| Point 3 Ϯ | 1.7 | 167 | 1.0 |
| Point 4 | 5.3 | 7618473 | 45519 |
ǂ SOC – self-organized criticality – values consistent with the derived correlation length ξ = 3.05, as detailed in Appendix B.
Vacuum permeability μ0 is, historically, a universal constant with a value of 4π x 10-7 T-m A-1 in flat, free space [22]. However, the increase in effective Euclidean volume directly relates to the increase in effective permeability, i.e. the vacuum energy potential increases proportionally with effective Euclidean volume.
| displacement | space density factor (f1) | ln (f1) | ln (f1)/ 3.5 SOC steps |
| -ve 1-2 | 44271 | 10.70 | 3.06 ǂ |
| +ve 3-4 | 45519 | 10.73 | 3.06 ǂ |
Table A8.
Comparison of calculated gradient energy with calculated coupling energy.
|
gradient energy^ ½(∇Φ)2 [kJ kg-1] |
scalar potential^ ∇Φ [km s-1] |
scalar field Φ [ks-1] |
coupling energy e3vΦ [kJ kg-1] |
|
| Point 1 | -651.8 | -36.1 | 3.6 | 651.8 |
| Point 2 | -8.9 | -4.2 | 1.2 | 8.9 |
| Point 3 | -8.3 | 4.1 | 1.2 | 8.3 |
| Point 4 | -576.9 | 34.0 | 3.6 | 576.9 |
^ excludes work associated with the walls of the vessel.
Gradient energy and coupling energy are associated with the emergent Higgs mass mH.
Appendix B: Critical Correlation Length and Lorentz Rotations
Lorentz rotations correspond to changes in hyperbolic surface area. The concept of rapidity [60] is commonly used as a measure of relativistic velocity and simplifies the Lorentz rotational transformation formulae. Rapidity ϕ is defined as the hyperbolic angle that differentiates two frames of reference in relativistic motion with each frame having time and distance coordinates. Since the distance coordinate on a hyperbolic manifold is determined by the critical exponent for correlation length ν, then ν can be taken as the dimensionless group parameter of rapidity, i.e. dν → ϕ.
Since tanh(ϕ) = v/c, the 3-dimensional result is:
The Lorentz transformation for length contraction/ expansion x′ then gives:
such that x′ = correlation length ξ = 3.05 and dV = 28.4.
Since
│T – Tc│ ≈ 0.15K which, in terms of self-organized criticality, represents approximately 3.5 equal steps with an average critical approach temperature of 0.15K.
The calculated overall volume correlation ratio is (3.5 x 28.4 = 99.4) as compared to the experimentally derived value of 100 recorded in Table A1. In Appendix C, the derived Higgs mass mH is also approximately 100 times greater than the initial mass of the crystal-fluid. The result is consistent with predictions from the Standard Model of particle physics where the Higgs mass mH of the unobserved electroweak magnetic monopole is approximately 137 times greater than the W-boson [72]. Discovery of this elementary particle represents the electroweak generalization of the Dirac monopole [73]. Further analysis can be found in Appendices D-E.
Appendix C: Ginzburg-Landau Theory
The Ginzburg-Landau (GL) theory of superconductors is founded upon a general approach to continuous phase transitions that are accompanied by a change in symmetry [20]. Landau proposed that these phase transitions are characterized by an order parameter that is zero in the disordered state above Tc but obtains a non-zero value below Tc. For the relatively simple case of a magnet, its magnetization M(r) provides a suitable order parameter.
For a superconducting system, GL postulates the existence of a complex order parameter Ψ, assumed to be an unspecified physical quantity that characterizes the state of the system. For the normal metallic state above the superconductor Tc it is zero, whilst for the superconducting state below Tc it is non-zero, such that:
However, for the non-metallic dual superconducting state observed experimentally, the system is instead characterized by:
where Ms is the spontaneous magnetism and Ψ represents the complex form of the coupling energy (eiΦ)3v. For 0 < Ms < 1 the system is characterized by an ‘auxiliary’ order parameter Hs, the spontaneous magnetic field.
GL assumes that the real free energy of the superconductor varies smoothly and can only depend upon the complex value of |Ψ| so that the free energy density is given by:
where:
fs(T) and fn(T) are the superconducting state and normal state free energy densities, respectively
and
α(T) and β(T) are generally phenomenological, temperature dependent parameters.
The order parameter Ψ(r) is found by minimizing the free energy of the system which, through further mathematical manipulation, yields an effective non-linear Schrödinger equation:
where:
ℏ is the reduced Planck's constant,
and
m* determines the energy cost associated with gradients in the order parameter Ψ(r) to define an effective mass for the quantum system where m* = 2me and me is the bare electron mass in the normal metallic state.
The non-linearity introduced by the second term in the bracket of (39) ensures that the quantum mechanical principle of superposition does not apply, i.e. it cannot be normalized to zero.
GL theory is developed further to incorporate: inhomogeneous systems introducing a gradient into the order parameter; the effect of external perturbations; and the effect of a magnetic field. The free energy density of the superconductor then takes the form [20]:
where:
2e is the net charge for a Cooper pair of electrons with positive sign convention
and
A is the electromagnetic vector potential
The full GL equations (not included here) are obtained by minimizing the free energy with respect to fluctuations in the order parameter and the vector potential A. These equations predict the existence of two characteristic lengths in a superconductor [20]:
the coherence length ξ’(T):
and the London penetration depth λ(T):
where:
α(T) = ά|T – Tc|
Both lengths diverge as Tc → T.
The ratio κ = λ(T)/ξ’(T) is known as the Ginzburg-Landau parameter where κ > 1/√2 identifies a Type-II superconductor whilst κ < 1/√2 identifies a Type-I superconductor. The ratio is dimensionless and independent of temperature within GL theory.
The transition from Type-II to Type-I and the effect of Abrikosov vortices is related to the experimental results described in [1] from which Figure A5 is updated to reflect the latest findings:
Figure A5.
Critical exponents reveal a magnetic phase transition and superconductor-like behaviour for a negative pressure perturbation. The initial response between 0 < Ms < 0.5 appears as diamagnetism (Hs < 0) and peaks at a lower critical field point Mc1, a result of high susceptibility χ such that Ms >> Bs. Diamagnetism is then completely destroyed at Ms = 1, which represents an upper critical field point Mc2. For Ms > 1 both Mc1 and Mc’ become ‘rolling’ critical values.
Figure A5.
Critical exponents reveal a magnetic phase transition and superconductor-like behaviour for a negative pressure perturbation. The initial response between 0 < Ms < 0.5 appears as diamagnetism (Hs < 0) and peaks at a lower critical field point Mc1, a result of high susceptibility χ such that Ms >> Bs. Diamagnetism is then completely destroyed at Ms = 1, which represents an upper critical field point Mc2. For Ms > 1 both Mc1 and Mc’ become ‘rolling’ critical values.
For Hs < 0, the profile resembles Type-II superconductor behaviour, although it is large rather than negative values of susceptibility χ that are held responsible for the diamagnetic effect. The diamagnetism peaks at Mc1, the lower critical field, corresponding to minimal magnetic flux density Bs. Moving beyond Mc1 towards Mc2 the upper critical field, Bs increases until all superconducting behaviour is destroyed at Ms = 1, Hs = 0. For 0 < Ms < 1, the Ginzburg-Landau parameter κ is determined:
i.e. a Type-II superconductor classification.
For Ms > 1, Hs takes positive values as the susceptibility χ falls below unity. A new value for the critical field Mc’ is deemed to be established at or to the right of the Mc2 value. Both Mc2 and Mc’ become ‘rolling’ critical values such that 0.9 ≤ Mc2/ Mc’ ≤ 1.0 as determined by calculations of κ below. For this region κ < 1/√2 which is consistent with Type-I superconducting behaviour. Here, large values of excluded Bs coincide with exclusion of the electric field E to establish dual superconducting behaviour.
If Mc’ has a minimum value of 1.0 Am-1kg-1 then at the positive displacement phase transition κ = 0.707.
Since ξ’(T) is equal to 3.05 m, the penetration depth λ(T) = 2.2 m
to give the vector boson mass mV (1/ λ(T)) ≤ 0.46 kg
in the constant energy Hamiltonian, kg ∝ m-2s2 as derived through dimensional analysis with E = mc2
so that mV can be expressed in units of Gaussian curvature m2s-2, i.e. the reciprocal
then comparing to the Gaussian curvature calculations using equation (21):
and at Point 1 gives - (290 x 0.0015)/ 2 = - 0.22 m2s-2 [1]
∴ 0.22 m2s-2 ≤ mV ≤ 0.46 m2s-2, i.e. the conjugate transpose
(for unitary group U(2), the conjugate transpose is equal to the reciprocal)
and 0.65 ≤ κ ≤ 0.707
The Higgs mass mH (1/ ξ’(T)) = 0.33 kg
which determines the non-extensive volume V (mH/ ρ)
where ρ is the density of the crystal-fluid material with an approximate value of 664 kg m-3 [1]
to give V = 0.33/ 664 x 10-3 = 0.5 litre, i.e. the swept volume of the piston expander.
Also, mH is approximately 100 times greater than the initial mass of the crystal-fluid (at 3.5 grams, approx.), supporting the hypothesis that mH quantifies changes in quantum confinement energies resulting from the conservation of angular momentum under critical false vacuum conditions.
For spontaneous diamagnetism seen where Hs < 0, and below the critical correlation length ξ in Figure 3, the system appears to be in a gapped superconducting state with Hs acting as an ‘auxiliary’ order parameter. The effects of topological defects in the dual superconductor seem to reflect those of magnetic impurity states that fill-in the energy gap in conventional superconductors. Topological defects may be created by chromoelectric flux tubes, or penetrating vortices, resulting from electroweak lepton decay, which in turn enables the formation of quark-antiquark pairs together with an inherent confinement mechanism. Where Hs > 0, and above the critical correlation length ξ, the system can be described as being in a protected gapless superconducting state with Ψ(r) as the complex order parameter. Similarly, it has been shown [74,75] that the transition between the gapped and gapless superconducting states in the Abrikosov-Gor’kov theory of a superconducting alloy with paramagnetic impurities is of the Lifshitz type, i.e. a topological phase transition where the number of the components of topological connectivity on the Fermi surface undergoes changes under the influence of different factors; pressure, magnetic field, doping, etc.
Appendix D: Electroweak Monopole Analysis
The 3.5 grams of sample comprises 0.22 mol. approx. or: 1.3 x 1023 molecules
Energy of Higgs mass mH (0.33 kg): 1.85 x 1026 GeV/c2
‘t Hooft [76] constructs an electroweak monopole mass of order 137 mV, where mV is the mass of the intermediate W-boson in the Georgi-Glashow model [77]. The stated value of < 53 GeV/c2 in an SO(3) compact Lie group has now been superseded by the experimentally determined value of 80 GeV/c2 from the LHC at CERN.
To give mH of a virtual* condensed complex monopole as (80 x 137)/ √2 : ≥ 7.75 TeV/c2
(NB: compare (137/√2 = 96.9) with the x100 value given in reference [72])
Then, the quantity of complex monopoles (1.85 x 1023/ 7.75) : ≥ 2.39 x 1022
Ratio of (complex monopoles : molecules) : 1 : ≤ 5.4
to deliver a sensible result for the tetrahedrally frustrated crystal-fluid
* total number of monopoles must exceed the Planck mass in order to condense.
Appendix E: Gauge Monopoles and the Planck Mass
From Appendix D:
0.33 kg of Higgs mass (i.e. condensed complex gauge monopole mass): 1.85 x 1026 GeV/c2
Planck mass: 1.22 x 1019 GeV/c2
To give a Planck mass factor: 15.2 x 106
From Appendix A:
Average critical 'space density' or ratio of Euclidean to hyperbolic volume: 7.51 x 106
To give an emergent Planck mass factor per Euclidean volume: 2.02
A similar result is obtained when expressed in terms of the Schwarzschild radius:
Avg. work of the piston expander: 614 kJ kg-1
Avg. work from 0.33 kg Higgs mass mH : 202.7 kJ
With associated power: 8.5 kW
From W = F x d, the force is calculated: 2896 kN
Then F = mH x a gives the acceleration: 8776 x 103 m s-2
Since hyperbolic curvature of the system establishes 'strong gravity', a → G
To give the Schwarzschild radius based upon the Higgs mass rs = 2a mH /c2 :
rs = (2 x 8776 x 103 x 0.33/ c2): 6.44 x 10-11 m
The swept volume of the piston expander is 0.5 litre such that:
Unit vol. of single Planck mass (0.5 litre/ 15.2 x 106): 3.29 x 10-11 m3
where the Planck mass factor has been determined previously above.
Ratio of rs to unit volume: 1.96 : 1
The Schwarzschild radius is thereby equated to the Planck mass, with two Planck masses necessary to establish a dipole pair of gauge monopoles within each emergent Euclidean volume. It then follows that the number of electroweak monopoles required to form a Planck mass, i.e. a U(2) gauge monopole is approximately:
√2 x (2.39 x 1022/ 15.2 x 106) : ≥ 2.22 x 1015
Statements and declarations: There are no competing interests relating to the work.
No funding was received to assist with the preparation of this manuscript.
References
- M. Gibbons, Superconducting phase transition reveals an electromagnetic coupling to a scalar field potential that generates mechanical work, J. Phys. D: Appl. Phys., 56, 054001 (2022). [CrossRef]
- H. Callen, Thermodynamics and an Introduction to Thermostatistics (Wiley, New York, 1985), Chap. 8,10.
- F. Wilczek, Nobel Lecture: Asymptotic freedom: From paradox to paradigm, Rev. Mod. Phys., 77, 3, 857 (2005). [CrossRef]
- J. Greensite, An Introduction to the Confinement Problem (Springer, Cham, 2020), Chap. 1,2,3,4). [CrossRef]
- M. Gibbons, A condensed-matter analogue of the false vacuum, J. Phys. Commun., 5, 065005 (2021). [CrossRef]
- F. Pázmándi, G. Zaránd and G. T. Zimányi, Self-Organized Criticality in the Hysteresis of the Sherrington-Kirkpatrick Model, Phys. Rev. Lett., 83, 1034-1037 (1999). [CrossRef]
- S. V. G. Menon, Renormalization Group Theory of Critical Phenomena (Wiley, New Delhi, 1995), Chap. 1,2,3.
- C. Castelnovo, R. Moessner and S. L. Sondhi, Magnetic monopoles in spin ice, Nature, 451, 42-45, (2008). [CrossRef]
- G. ‘t Hooft, Topology of the gauge condition and new confinement phases in non-abelian gauge theories, Nuclear Physics B, 190, 3, 455-478 (1981). [CrossRef]
- S. Mandelstam, Vortices and quark confinement in non-Abelian gauge theories, Physics Reports, 23, 3, 245-249 (1976). [CrossRef]
- G. Ripka, Dual superconductor models of color confinement, Lecture Notes in Physics (2004), Chap. 1,3,5. [CrossRef]
- K. Kondo, et al., Quark confinement: Dual superconductor picture based on a non-Abelian Stokes theorem and reformulations of Yang–Mills theory, Phys. Rep., 579, 1-266 (2015). [CrossRef]
- Y. Gu, X. Hao and J. Liang, Generalized Gauge Transformation with PT-Symmetric Non-Unitary Operator and Classical Correspondence of Non-Hermitian Hamiltonian for a Periodically Driven System, Ann. Phys., 6, 534, 2200069 (2022). [CrossRef]
- C. M. Bender, PT-symmetric quantum theory, J. Phys.: Conf. Ser., 631, 012002 (2015). [CrossRef]
- Fan, G-Y. Huang and S-D Liang, Complex Berry curvature pair and quantum Hall admittance in non-Hermitian systems, J. Phys. Commun., 4, 115006 (2020). [CrossRef]
- Jaffe, E. Witten, Quantum Yang-Mills Theory. https://www.claymath.org/wp-content/uploads/2022/06/yangmills.pdf.
- E. W. Lemmon, L. H. Huber, M.O. McLinden, and I. Bell, Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) (Boulder, Colorado, 2020).https://www.nist.gov/programs-projects/reference-fluid-thermodynamic-and-transport-properties-database-refprop.
- Kunz and W. Wagner, Journal of Chemical & Engineering Data, 57, 11, 3032-3091 (2012). [CrossRef]
- Imre, K. Martinás and L. P. N. Rebelo, Thermodynamics of negative pressure in liquids, Non-Equilibrium Thermodynamics, 23, 4 (1998). [CrossRef]
- J. A. Annett, Superconductivity, Superfluids and Condensates (Oxford University Press, Oxford, 2004), Chap. 2,3,4.
- Cowan, Topics in Statistical Mechanics (World Scientific, London, 2022), Chap. 4.
- H. Callen, Thermodynamics and an Introduction to Thermostatistics (Wiley, New York, 1985), Chap. 3,7.
- Bonati, G. Cossu, M. D’Elia and A. Di Giacomo, Disorder parameter of dual superconductivity in QCD revisited, Phys. Rev. D, 85, 6, 065001 (2012). [CrossRef]
- Benoit, D. Lauvergnat and Y. Scribano, Does cage quantum delocalisation influence the translation–rotational bound states of molecular hydrogen in clathrate hydrate?, Faraday Discuss., 212, 533-546 (2018). [CrossRef]
- E.M. Purcell and R. V. Pound, A Nuclear Spin System at Negative Temperature, Phys. Rev., 81, 2, 279-280 (1951). [CrossRef]
- L. Pauling, The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement, J. Am. Chem. Soc., 57, 12, 2680-2684 (1935). [CrossRef]
- P. W. Anderson, Ordering and Antiferromagnetism in Ferrites, Phys. Rev., 102, 4, 1008-1013 (1956). [CrossRef]
- Ortiz-Ambriz, Colloquium: Ice rule and emergent frustration in particle ice and beyond, Rev. Mod. Phys., 91, 4, 041003 (2019). [CrossRef]
- Castelnovo, R. Moessner and S. L. Sondhi, Spin Ice, Fractionalization, and Topological Order, Annu. Rev. Condens. Matter Phys., 3, 1, 35-55 (2012). [CrossRef]
- S. T. Bramwell and M. J. Harris, The history of spin ice, J. Phys.: Condens. Matter, 32, 374010 (2020). [CrossRef]
- S. H. Skjærvø, C. H. Marrows, R.L. Stamps and L. J. Heyderman, Advances in artificial spin ice, Nat. Rev. Phys., 2, 13–28 (2020). [CrossRef]
- F.J. Wegner, Duality in Generalized Ising Models and Phase Transitions without Local Order Parameters, J. Math. Phys., 12, 2259 (1971). [CrossRef]
- T. H. Hansson, V. Oganesyan and S. L. Sondhi, Superconductors are topologically ordered, Annals of Physics, 313, 2, 497-538 (2004). [CrossRef]
- X. G. Wen, Topological Orders In Rigid States, Int. J. Mod. Phys. B, 4, 2, 239-271 (1990). [CrossRef]
- J. Zaanen, et al., Holographic Duality in Condensed Matter Physics (Cambridge University Press, Cambridge, 2015), Chap. 1,2.
- P. Herzog, Supersymmetry and Conformal Field Theory (CMMS40), Lecture Notes, Spring Term 2021. https://www.nms.kcl.ac.uk/christopher.herzog/SUSYCFTnotes.pdf.
- W. Zhu et al., Uncovering Conformal Symmetry in the 3D Ising Transition: State-Operator Correspondence from a Quantum Fuzzy Sphere Regularization, Phys. Rev. X, 13, 021009 (2023). [CrossRef]
- Tong, University of Cambridge, Lectures on Gauge Theory, 2018. http://www.damtp.cam.ac.uk/user/tong/gaugetheory/gt.pdf.
- R. Penrose, The Road to Reality (Vintage, London, 2005), Chap. 19.
- P. Bak and K. Chen, The physics of fractals, Physica D, 38, 1-3, 5-12 (1989). [CrossRef]
- B. Ratra, Cosmological 'seed' magnetic field from inflation, ApJL, 391, L1-L4, (1992). https://adsabs.harvard.edu/full/1992ApJ...391L...1R.
- Tong, University of Cambridge, Lectures on Electromagnetism, Chap. 4, 2023. https://www.damtp.cam.ac.uk/user/tong/em/el4.pdf.
- S. Huber, ETH Zürich, Experimental and Theoretical Aspects of Quantum Gases lecture notes, Chapter 7, 2023. https://ethz.ch/content/dam/ethz/special-interest/phys/theoretical-physics/cmtm-dam/documents/qg/Chapter_07.pdf.
- Zee, Group Theory in a Nutshell for Physicists (Princeton University Press, Princeton, 2016), Preface and Parts 1, 2.
- Doran and A. Lazenby, Geometric Algebra for Physicists (Cambridge University Press, Cambridge, 2003), Chap. 1, 2, 8.
- R. Penrose, The Road to Reality (Vintage, London, 2005), Chap. 13, 25.
- I.G. Halliday and A. Schwimmer, Z(2) monopoles in lattice gauge theories, Physics Letters B, 102, 5, 337-340 (1981). [CrossRef]
- Bissey, A. I. Signal, and D. B. Leinweber, Comparison of gluon flux-tube distributions for quark-diquark and quark-antiquark hadrons, Phys. Rev. D, 80, 114506 (2009). [CrossRef]
- H. Suganuma, S. Sasaki and H. Toki, Color confinement, quark pair creation and dynamical chiral-symmetry breaking in the dual Ginzburg-Landau theory, Nuclear Physics B, 435, 1–2, 207-240 (1995). [CrossRef]
- Salam and C. Sivaram, Strong gravity approach to QCD and confinement, Mod. Phys. Lett., 8, 4, 321–326 (1993). [CrossRef]
- Andrei Bernevig, Topological Insulators and Topological Superconductors (Princeton University Press, Princeton, 2013), Chap. 1-4, 9-10.
- J. W. Zwanziger, M. Koenig and A. Pines, Berry’s Phase, Annu. Rev. Phys. Chem., 41, 601-46 (1990). [CrossRef]
- Tong, University of Cambridge, Lectures on the Quantum Hall Effect, Chap. 1, 2016. https://www.damtp.cam.ac.uk/user/tong/qhe/qhe.pdf.
- T. Binoth, et al., Gluon-induced W-boson pair production at the LHC, JHEP, 12, 1126-6708, (2006). [CrossRef]
- M. V. Berry, Quantal phase factors accompanying adiabatic changes, R. Soc. London, 392, 45–57 (1984). [CrossRef]
- L. M. Lederman and C. T. Hill, Symmetry and the Beautiful Universe (Prometheus Books, New York, 2004), Chap. 12.
- B. Lian, C. Vafa, F. Vafa and S-C Zhang, Chern-Simons theory and Wilson loops in the Brillouin zone, Phys. Rev. B, 95, 094512 (2017). [CrossRef]
- J. Evslin, et al., Nonabelian Faddeev-Niemi decomposition of the SU(3) Yang-Mills theory, J. High Energ. Phys. 94 (2011). 2011. [CrossRef]
- M. E. Peskin and D. V. Schroeder, An Introduction to Quantum Field Theory (CRC Press, Boca Raton, 1995), Chap. 3.
- J-M. Lévy-Leblond, J-P. Provost, Additivity, rapidity, relativity, Am. J. Phys., 47, 12, 1045-1049 (1979). [CrossRef]
- N. Mukunda and S. Chaturvedi, Continuous Groups for Physicists (Cambridge University Press, Cambridge, 2022), Chap. 10.
- K. R. O’Neal et al., Pressure-Induced Magnetic Crossover Driven by Hydrogen Bonding in CuF2(H2O)2(3-chloropyridine), Scientific Reports, 4, 6054 (2014). [CrossRef]
- V. Kaiser et al., Emergent electrochemistry in spin ice: Debye-Hückel theory and beyond, Phys. Rev. B, 98, 144413 (2018). [CrossRef]
- P. W. Anderson, More And Different: Notes From A Thoughtful Curmudgeon (World Scientific, New Jersey, 2011), Chap. II.
- M. Sato and Y. Ando, Topological superconductors: a review, Rep. Prog. Phys., 80, 076501 (2017). [CrossRef]
- J. Cayssol and J. N. Fuchs, Topological and geometrical aspects of band theory, J. Phys. Mater., 4, 034007 (2021). [CrossRef]
- X-G. Wen, Colloquium: Zoo of quantum-topological phases of matter, Rev. Mod. Phys., 89, 041004 (2017). [CrossRef]
- Y. Makeenko, Methods of Contemporary Gauge Theory (Cambridge University Press, Cambridge, 2002), Chap. 6.
- Ashtekar, B. K. Berger, J. Isenberg and M. MacCallum, General Relativity And Gravitation: A Centennial Perspective (Cambridge University Press, Cambridge, 2015), Chap. 11.
- Fradkin, Quantum Field Theory: An Integrated Approach (Princeton University Press, Princeton, 2021), Chap. 18, 22.
- S. D. Bass, Emergent gauge symmetries: making symmetry as well as breaking it, Phil. Trans. R. Soc. A, 380, 20210059 (2022). [CrossRef]
- Y. M. Cho, Physical implications of electroweak monopole, Phil. Trans. R. Soc. A, 377, 20190038 (2019). [CrossRef]
- P. A. M. Dirac, The theory of magnetic poles, Phys. Rev. 74, 817–830 (1948). [CrossRef]
- Y. Yerin, C. Petrillo and A. A. Varlamov, The Lifshitz nature of the transition between the gap and gapless states of a superconductor, SciPost Phys, Core 5, 009 (2022). [CrossRef]
- Y. Yerin, A. A. Varlamov and C. Petrillo, Topological nature of the transition between the gap and the gapless superconducting states, EPL, 138, 1 (2022). [CrossRef]
- ‘t Hooft, Magnetic monopoles in unified gauge theories, Nuclear Physics B, 79, 276-284 (1974). [CrossRef]
- M. Georgi and S.L. Glashow, Unified Weak and Electromagnetic Interactions without Neutral Currents, Phys. Rev. Letters, 28, 1494 (1972). [CrossRef]
Figure 1.
Schematic arrangement of the experimental apparatus in which a negative pressure material is formulated and manipulated. Naively, dissipative structuring of the crystal-fluid material is controlled with a view to establishing a power cycle in the piston expander through non-equilibrium, non-extensive volume displacements.
Figure 1.
Schematic arrangement of the experimental apparatus in which a negative pressure material is formulated and manipulated. Naively, dissipative structuring of the crystal-fluid material is controlled with a view to establishing a power cycle in the piston expander through non-equilibrium, non-extensive volume displacements.
Figure 2.
Excess internal energy potential resulting from excess thermodynamic potentials during external pressure perturbations. All values for energy, work and thermodynamic potentials are derived by the NIST REFPROP program/database based only upon temperature, pressure and mass measurements together with the piston position. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0). Each piston displacement is associated with approximately 203 kJ of energy, 8.5 kW of power and 2.9 MN of force.
Figure 2.
Excess internal energy potential resulting from excess thermodynamic potentials during external pressure perturbations. All values for energy, work and thermodynamic potentials are derived by the NIST REFPROP program/database based only upon temperature, pressure and mass measurements together with the piston position. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0). Each piston displacement is associated with approximately 203 kJ of energy, 8.5 kW of power and 2.9 MN of force.
Figure 3.
Effect of the critical correlation length ξ on the magnitude of the scalar field Φ. A gradient energy term -½(∇Φ)2, as derived from the non-equilibrium Lagrangian function, is equivalent in magnitude to the coupling energy. From this, scalar field Φ values associated with the critical response are determined. Changes in negative gradient energy and positive coupling energy are both equivalent in magnitude to PV work done by the piston expander which can be either negative or positive.
Figure 3.
Effect of the critical correlation length ξ on the magnitude of the scalar field Φ. A gradient energy term -½(∇Φ)2, as derived from the non-equilibrium Lagrangian function, is equivalent in magnitude to the coupling energy. From this, scalar field Φ values associated with the critical response are determined. Changes in negative gradient energy and positive coupling energy are both equivalent in magnitude to PV work done by the piston expander which can be either negative or positive.
Figure 4.
Decomposition of symmetry groups to establish common U(2) scale- and gauge-invariance. This model of invariance provides a mechanism through which the pressure-induced ‘rolling’ critical response results in PV work that is either positive or negative. The complex reorganization of water ice cages produces variable inertia which, through the conservation of angular momentum, is responsible for either an acceleration or deceleration of quarks. In the case of acceleration, this leads to the emission of gluons that are indirectly absorbed into the QCD vacuum manifold. A corresponding tendency to reduce local ‘space density’ and effective magnetic permeability μ0 manifests as increased hyperbolic curvature K.
Figure 4.
Decomposition of symmetry groups to establish common U(2) scale- and gauge-invariance. This model of invariance provides a mechanism through which the pressure-induced ‘rolling’ critical response results in PV work that is either positive or negative. The complex reorganization of water ice cages produces variable inertia which, through the conservation of angular momentum, is responsible for either an acceleration or deceleration of quarks. In the case of acceleration, this leads to the emission of gluons that are indirectly absorbed into the QCD vacuum manifold. A corresponding tendency to reduce local ‘space density’ and effective magnetic permeability μ0 manifests as increased hyperbolic curvature K.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
