1. Introduction

2. Evaluating the Evolution of Efforts to Contest the Law of Energy Conservation

3. Breaking the Law of Energy Conservation

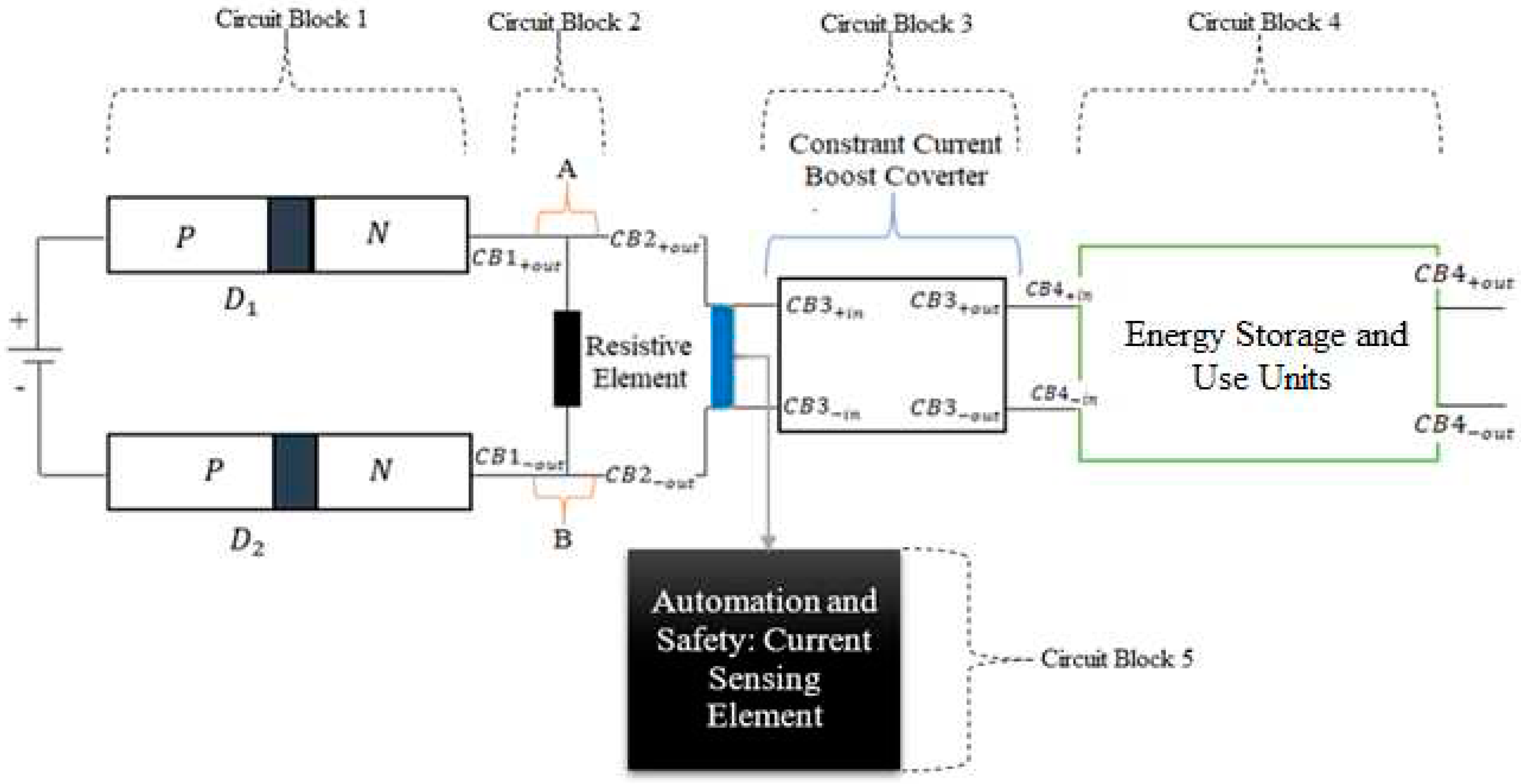
3.2. Design of the Proposed Energy Circuit (The Main Energy Circuit Operational Units)

This section describes the key components and design considerations of the energy circuit. It also offers the specific energy circuit units mathematical framework defining the necessary energy circuit ingredients, and their uses.

Circuit Component 1 (Power Source). The energy circuit begins with a power supply (for safety check, a direct voltage and direct current power source is selected). This power source (variable power supply or using different rating power sources may be considered, as applied in this paper) represents the starting point of the energy conservation challenge. Details on the starting current, the connecting codes (conductors) practical resistance (and conductors material types) will be of importance in working out the input power for the subsequent circuit blocks, modeling the real world scenarios.

Circuit Block 1 (Initial Exploration of Ohm’s Law). This initial section of the energy circuit deviates from the traditional approach of demonstrating standard Ohm’s Law ($V=IR$) that characterizes traditional electrical circuits. Instead, Circuit Block 1 primarily aims to use two identical one-directional current components in a parallel configuration (as shown in Figure 1), to prevent undesired electrical current from flowing back. First, let us set up the mathematical framework for Circuit Block 1 using the diode equation, (equation 1) as applied in [49,50]. Thus, the current-voltage (IV) relationship for a diode is described by the diode equation as follows.

$$I_D=I_s\left(e^{\left(\raisebox{1ex}{$V_D$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)$$

(1)

where:

• $I_D$ is the diode current.
• $I_s$ is the reverse saturation current.
• $V_D$ is the voltage across the diode.
• $n$ is the ideality factor (typically around $1$ for ideal diodes).
• $V_T$ is the thermal voltage, approximately $0.0259V$ at room temperature.

Figure 1. Operational Principle of Circuit Block 1-Diode Configuration. (The diodes ($D_1$ and $D_2$) are configured in parallel with the specific arrangement to prevent undesired backflow of short circuit current from Circuit Block 2. As the short circuit current attempts to flow in reverse, the diodes transition to a reverse-biased mode, widening the depletion region and increasing resistance, acting as a barrier to the reverse flow. The block diagram illustrates the parallel connection of diodes).

Figure 1. Operational Principle of Circuit Block 1-Diode Configuration. (The diodes ($D_1$ and $D_2$) are configured in parallel with the specific arrangement to prevent undesired backflow of short circuit current from Circuit Block 2. As the short circuit current attempts to flow in reverse, the diodes transition to a reverse-biased mode, widening the depletion region and increasing resistance, acting as a barrier to the reverse flow. The block diagram illustrates the parallel connection of diodes).

Since the diodes are in parallel, the total current through Circuit Block 1 ($I_{CB1}$) is the sum of the currents through each diode. Therefore, for two diodes ($D_1$ and $D_2$ as depicted in (Figure 1)) in parallel we have;

$$I_{CB1}=I_{D_1}+I_{D_2}$$

(2)

Substituting the diode equation for this parallel diodes configuration;

$$I_{CB1}=I_s\left(e^{\left(\raisebox{1ex}{$V_{D_1}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)+I_s\left(e^{\left(\raisebox{1ex}{$V_{D_2}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-1\right)$$

(3)

Combining the like terms in Equation (3) and factoring out $I_s$ we get;

$$I_{CB1}=I_s\left[e^{\left(\raisebox{1ex}{$V_{D_1}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}+e^{\left(\raisebox{1ex}{$V_{D_2}$}\!\left/ \!\raisebox{-1ex}{$n{V}_T$}\right.\right)}-2\right]$$

(4)

Equation (4) represents the total current flowing through the diodes in the parallel configuration. Further, the voltage across Circuit Block 1 can be expressed as;

$$V_{CB1}=V_{D_1}+V_{D_2}$$

(5)

To use equation (4); one is required to have the specific voltage values ($V_{D_1}=V_{D_2}$, other options may be carefully explored, beyond this condition which is chosen for demonstrative purpose through the paper), ideality factor ($n$), and reverse saturation current ($I_s$), for the different identical diodes to be applied in the circuit. In this context, the main role for Circuit Block 1 is to inhibit current from returning to the power source, which is vital for ensuring the overall integrity of the following energy circuit stages. The subsequent stage, Circuit Block 2, introduces the concept of an electrical short circuit, a design that relies on the availability of a surplus of electrical current. Allowing the short circuit current to return to the power source could potentially harm the source. The effectiveness of Circuit Block 1 in preventing backflow relies on the initial power supplied from the variable power supply component. Consequently, the selection of the specific one-directional current components used within Circuit Block 1 may vary based on the circuit application’s power requirements. Further, it is important to stress that these one-directional current components are not fixed and can be adapted to the unique characteristics of each application, contributing to the energy circuit’s versatility.

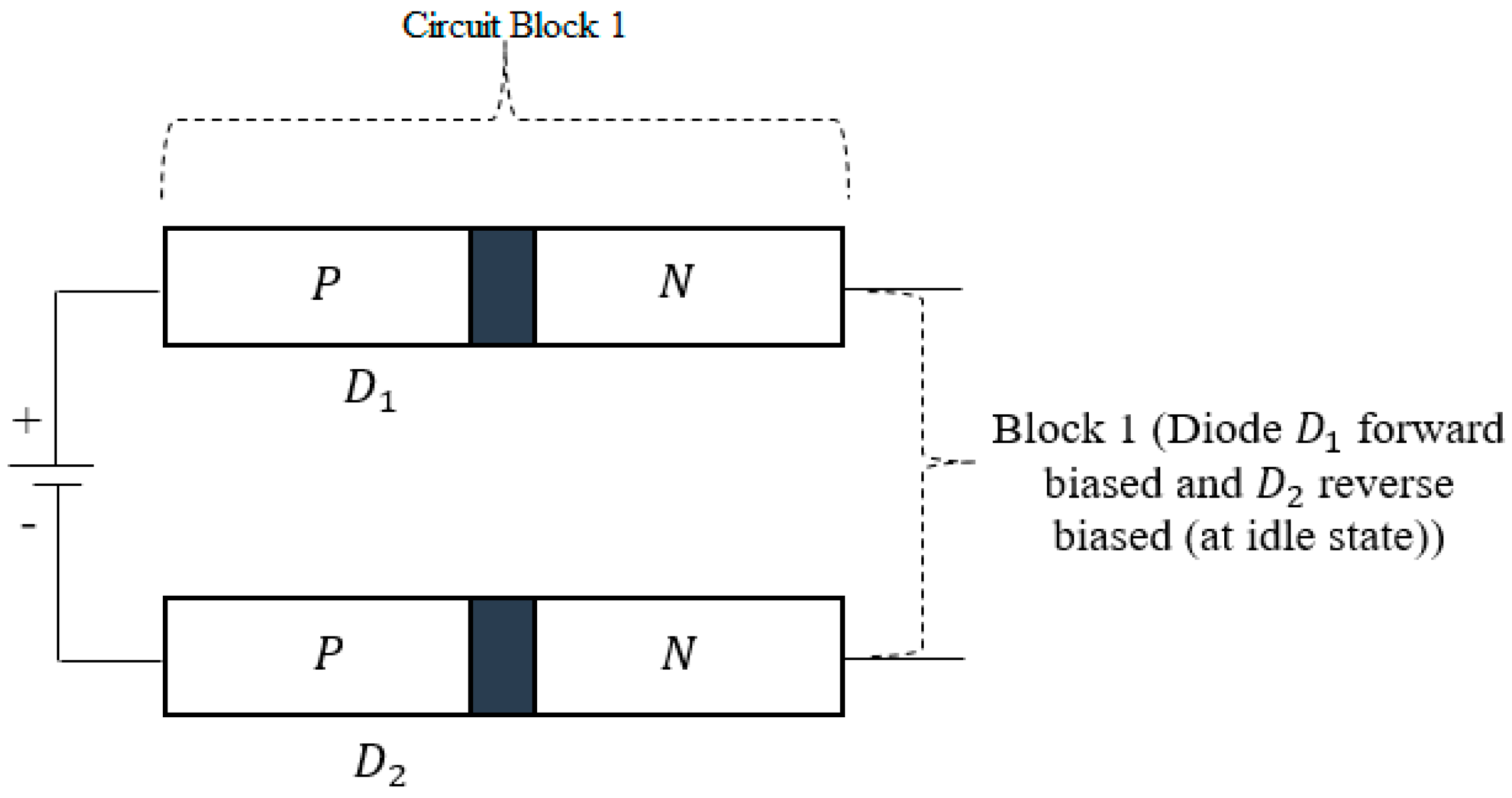
3.2.1. Operation Principles of Circuit Block 1 (Establishing Higher Resistive Circuit Element)

The crucial role of Circuit Block 1 is to prevent the undesired backflow of short circuit current from Circuit Block 2. Its operation involves an uncommon configuration with parallel diodes, hindering the reverse flow of current. When the short circuit current tries to move backward, it forces the diodes into a reverse-biased mode, causing their depletion regions to widen. This widening of the depletion regions increases the resistance in Circuit Block 1, serving as a barrier and limiting the ability of the short circuit current to flow backward through the diodes.

Definition (Diode Idle State or Mode). This definition contextualizes a reverse-biased diode as active but not conducting, and it only conducts in reverse bias mode when an anomalous event occurs within an electric circuit. In Figure 1, $D_2$ is in the idle state or mode, becoming an infinite resistor (theoretically) when the short circuit happens.

Circuit Block 2 (Harnessing the Short Circuit Power). The Circuit Block 2 serves as an extension of the preceding stage, Circuit Block 1, directly receiving the current and voltage output from Circuit Block 1. As shown in Figure 2, a resistive element, which may be symbolized by a high-value resistor, is connected between the positive output terminal (labeled $A$) and the negative output terminal (labeled $B$) of Circuit Block 1. This connection introduces an electrical short circuit, fundamentally altering the energy dynamics within the circuit, facilitating exceptional energy conservation and utilization as demonstrated later.

Figure 2. Circuit Block 2-Short Circuit Power Harnessing. (Circuit Block 2 illustrates the innovative approach to energy conservation and utilization).

Figure 2. Circuit Block 2-Short Circuit Power Harnessing. (Circuit Block 2 illustrates the innovative approach to energy conservation and utilization).

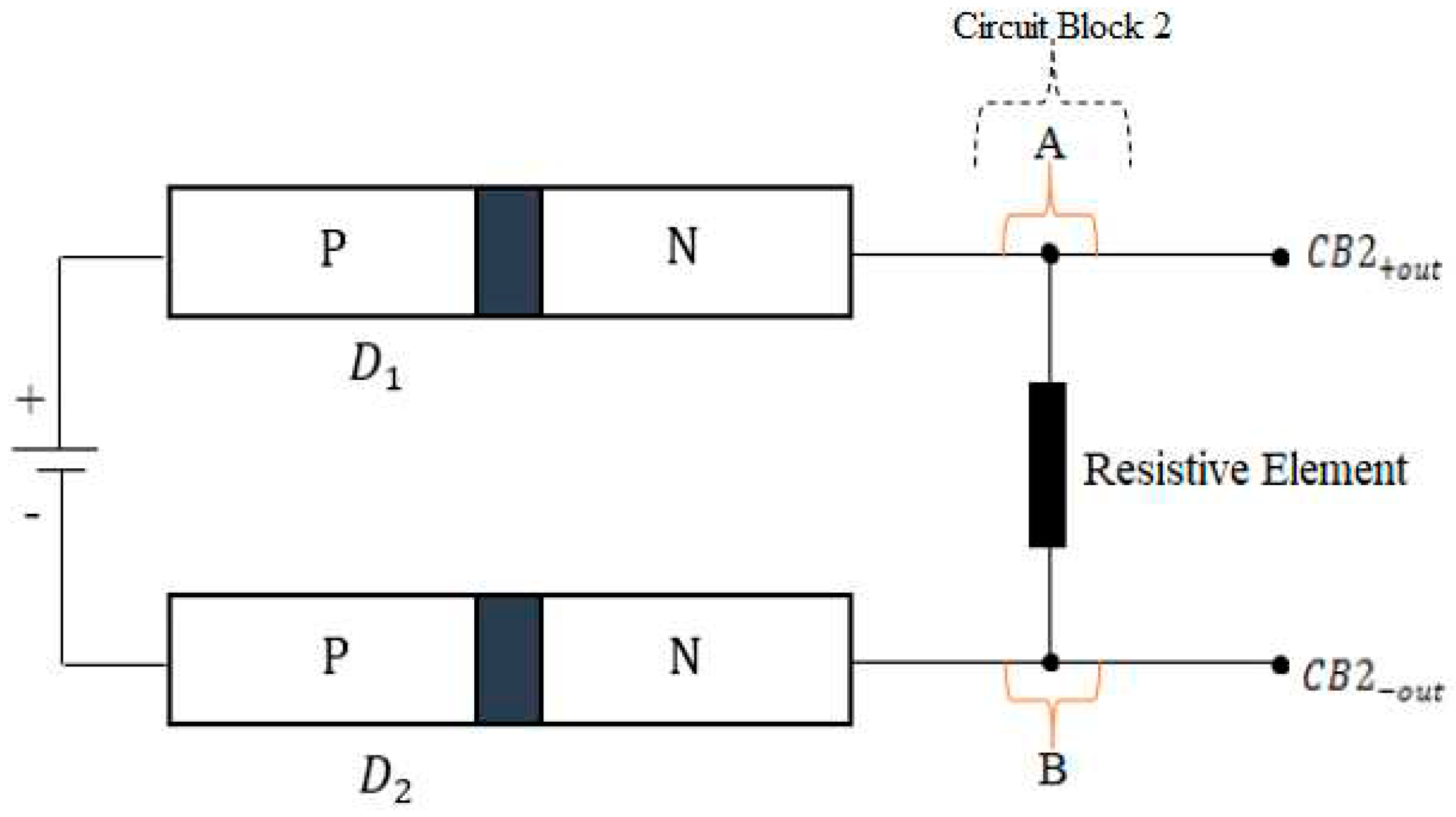
3.2.2. Description of Circuit Block 2 Components

Initial State (Circuit Block 1). Initially, Diode $D_1$ is forward-biased, being connected to the positive terminal of the voltage source. This allows current to flow through $D_1$ from its anode to cathode. Simultaneously, Diode $D_2$ is reverse-biased as it is connected to the negative terminal of the source, preventing significant current flow through it.

Short Circuit (Circuit Block 2)-Current Flow, Voltage Drop and After Short Circuit Event. Upon the creation of a short circuit by connecting points $A$ and $B$, a sudden surge of current traverses the short circuit, causing a momentary voltage drop (the short circuit current and voltage has always been determined, with the short circuit events (current surge and voltage drop) as reported in [51,52]) across both diodes. During this transient phase, $D_1$, initially forward-biased, experiences a reversal of voltage polarity. The voltage at point $A$ becomes lower than that at the cathode, prompting $D_1$ to enter a state of reverse bias. This causes the depletion layer to widen as electrons migrate away from the junction. Concurrently, $D_2$, which was in a state of reverse bias from the outset, continues to be reverse-biased even after the short circuit. The voltage at point $B$ remains higher than at the anode (since the anode is initially connected to the power source negative terminals, with $0V$ (the $0V$ voltage is theoretically assumed here)), sustaining the widened depletion layer in $D_2$. The widened depletion layers in both diodes play a pivotal role in controlling the flow of charge carriers, influencing the circuit’s behavior during transient event.

Remark 2 (Circuit Protection Mechanism). The protective nature of Circuit Block 1 lies in the fact that, post short circuit, both diodes are in a state of reverse bias. This configuration impedes the flow of current in the reverse direction, safeguarding the source from potential damage. The depletion layers in $D_1$ and $D_2$ act as barriers, restricting the movement of charge carriers and effectively isolating the circuit from any adverse effects caused by the short circuit.

The short circuit current here (named as short circuit effect current) is computed using the Ohm’s law modified formula that is designed for use in scenarios including low resistance applications provided in [53], and this current is expressed according to equation (6).

$$I_{short circuit effect current}=a\times e^{\frac{R_{short}}{R_0}}$$

(6)

where:

$a=\frac{V}{{\mathrm{R}}_0}$, is current scaling factor.

$R_0$  is the reference resistance.

$V$ is the source or supply voltage.

$R_{short}$ is the change in resistance from its reference value $\left(R_0\right)$.

In this context, $R_{short}=R\left(x\right)-R_0$, and the details on parameter $x$ have been established at (Appendix A) in [53].

Using equations (5) and (6), the power input to Circuit Block 2 can then be computed as;

$$P_{{input}_{CB2}}=V_{CB1}\times I_{short circuit effect current}$$

(7)

The primary objectives of Circuit Block 2 are two-fold. It focuses on generating excess short circuit current and effectively channeling this high current to the subsequent stages of the circuit. The high-value resistor (the resistive element shown in Figure 2), often termed the resistive element, plays a pivotal role in achieving these goals. It not only establishes the short circuit in tandem with Circuit Block 1 but also ensures the high short circuit current flows forward in the circuit without causing damage. In the essence, this resistive element becomes the first path of low resistance after the electrical short circuit, preventing the excess current from finding its way back. This dual role is crucial, as the resistor, in collaboration with Circuit Block 1, prevents undesired backflow, while its high resistance directs the abundant short circuit current toward the next stages. The resistance of the resistive element can be varied by considering the overall resistance of the subsequent circuits to ensure that it is higher (for practical applications, this resistance can be determined based on the computed $I_{short circuit effect current}$), ensuring a forward flow of current and enhancing the overall efficiency and safety of the energy circuit. Importantly, Circuit Block 1 current and voltage outputs transition to become the inputs for Circuit Block 2, maintaining the uninterrupted flow of power and energy throughout the circuit’s progression.

Further, it is imperative to take into account the effective resistance in the Circuit Block 2. This resistance will include the overall resistance in Circuit Block 1, and it can be computed following equation (8).

$$R_{short effective}=R_{{CB1}_{overall}}$$

(8)

We will then assume that the combined resistance (named subsequently as $R_{forward current}$) between $R_{short effective}$ and the resistance due to the high resistive component facilitating the short circuit also contributes into ensuring the forward current flow, from Circuit Block 2. For practical purposes, we will express this resistance following equation (9).

$$R_{forward current}=R_{short effective}+R_{resistor}(this could be some value)$$

(9)

Here, $R_{resistor}$ is the resistive element resistance. Emphatically, understanding the value ($R_{forward current}$) is important, mainly because of the major role played by the resistive element in the energy circuit (ensuring that the resistive element is not easily damaged by the excess short circuit current, whenever this resistive element becomes the path of low resistance, from Circuit Block 1). There will be solely no other main reasons to compute the ($R_{forward current}$), besides this.

Then, consider that after the short circuit happens (this event should be time depended as described in Circuit Block 5) the input voltage into Circuit Block 2 is expected to drop suddenly (as earlier established), to some value by some factor (let this factor be named $F_{short circuit}$ and for computational and simulation purposes here, it is set to the lowest say $F_{short circuit}=0.8$). The $F_{short circuit}$ means that the voltage drop after the short circuit is $80\%$ of the voltage before the short circuit.

So now the voltage across Circuit Block 2 (referred as $V_{CB2}$) can be computed according to Equation (10).

$$V_{CB2}=F_{short circuit}\times V_{CB1}$$

(10)

To this far, we have all the ingredients to work out the power output form Circuit Block 2. The power output from Circuit Block 2 is then computed as expressed in Equation (11).

$$P_{{output}_{CB2}}=V_{CB2}\times I_{short circuit effect current}$$

(11)

Remark 3. The proposed circuit configuration (Figure 2), while innovative in its application of diode characteristics to create a protective mechanism during short circuits, aligns seamlessly with established principles of semiconductor physics and diode behavior [54–57]. It adheres to the well-established properties of diodes in forward and reverse bias states, demonstrating a clear understanding of their depletion layer dynamics and the consequent influence on current flow.

Circuit Block 3 (Advancing Energy Transformation). Circuit Block 3 continue the process of energy transformation. This phase introduces the concept of “load component_CB3” also named “constant current boost converter”, a component that plays a pivotal role in reshaping the energy circuit, moving it from a non-Ohmic state (Circuit Block 1 and Circuit Block 2 are in the non-Ohmic states) to an Ohmic state while sustaining a high, constant current. In contrast to earlier stages, Circuit Block 3 does not introduce additional resistance through an application resistive element besides its genetic resistance; instead, it concentrates on harnessing the preexisting circuit resistance from Circuit Block 1. The assumed effective resistance (computed earlier as $R_{short effective}$) from these prior stages is now incorporated into the analysis of energy conservation to investigate the outcomes.

Load Component_CB3. To achieve the transition from a non-Ohmic to an Ohmic state while ensuring the consistency of the short circuit current after the resistor junctions, we introduce a load component named as “load component_CB3”. The primary purpose of this component is to boost the voltage to the highest achievable level (one can aim at having the voltage to near the initial power supply voltage) while maintaining a consistent short circuit current. So ideally, “load component_CB3” is a boost converter circuit or element.

3.2.3. Load Component_CB3 (Constant Current Boost Converter) Major Elements

The crucial role of Circuit Block 1 is to prevent the undesired backflow of short circuit current from Circuit Block 2. Its operation involves an uncommon configuration with parallel diodes, hindering the reverse flow of current. When the short circuit current tries to move backward, it forces the diodes into a reverse-biased mode, causing their depletion regions to widen. This widening of the depletion regions increases the resistance in Circuit Block 1, serving as a barrier and limiting the ability of the short circuit current to flow backward through the diodes.

Inductor (L). The inductor value is critical for energy storage and transfer in the boost converter. This value is calculated based on the desired output voltage, input voltage, duty cycle, switching frequency, and the desired ripple current in the inductor [58]. The inductor capable of handling the desired current and suitable for the input voltage range. The inductor value ($L$) may be determined using equation (12), as applied in the later practical simulations.

$$L=\frac{\left(V_{out}-V_{in}\right).D}{f_s.∆I_L}$$

(11)

The equation considers:

• $L$ is the inductor value.
• $V_{out}$ is the desired output voltage.
• $V_{in}$ is the input voltage.
• $D$ is the duty cycle of the converter.
• $f_s$ is the switching frequency.
• $∆I_L$ is the peak-to-peak inductor ripple current.

Switching Element. The objective here is to choose a switching element (such as MOSFET) capable of handling the desired voltage and current while minimizing ON resistance ($R_{dson}$). The procedure involves considering the voltage rating, ensuring the MOSFET in this context can handle maximum current, and selecting a MOSFET with low ON resistance to reduce power losses. The MOSFET is then connected as a switch between the input voltage source and the inductor.

Choose a Diode (D). In this step, a diode (such as Schottky diode) can be selected with a voltage rating higher than the output voltage. The diode is crucial for allowing current flow and maintaining the desired output voltage. The connection involves placing the diode in parallel with the load, with the anode connected to the output and the cathode to the inductor.

Output Capacitor (C). The output capacitor should be capable to handle the output current and maintain the required output voltage. The capacitor can be connected in parallel with the load, with the positive side linked to the output. This component assists in smoothing out voltage variations and ensuring stability in the output.

The selection of a suitable “load component_CB3” (the constant current boost converter in Figure 3) is crucial in this context. The choice for “load component_CB3” contributes to the overall efficiency of the energy circuit and its capacity to challenge the established laws of energy conservation by generating excess energy. In Circuit Block 3, the central objective is to investigate how the inputs derived from Circuit Block 2, can be effectively transformed into an Ohmic format suitable for standard circuit applications. This transformation is a pivotal step towards harnessing the innovative potential of the block and challenging the established laws of energy conservation. Figure 3 is a block diagram depicting the developed energy circuit, so far.

Figure 3. Circuit Block 3-Energy Transformation and “Load Component_CB3”. (The block diagram illustrates the energy transformation process in Circuit Block 3 (constant current boost converter).

Figure 3. Circuit Block 3-Energy Transformation and “Load Component_CB3”. (The block diagram illustrates the energy transformation process in Circuit Block 3 (constant current boost converter).

Remark 4 on Circuit Block 3 (Clarity on Energy Transformation). Circuit Block 3 transforms the energy circuit from a non-Ohmic to an Ohmic state, not aiming for excess power generation. It acts as a bridge to align the circuit with conventional electrical systems, ensuring compatibility. With intentional higher power input than Circuit Block 1, as shown in Table 1, it facilitates smooth integration into existing infrastructure, utilizing excess power for voltage boost. This design emphasizes practicality and adaptability to contemporary electrical and electronic technologies.

Circuit Block 4 (Energy Storage Component). Circuit Block 4 plays a critical role in the energy conservation process by serving as an interface to both capture the output power from Circuit Block 3 and efficiently oversee it for various applications. This part of the system may introduce a power control unit that reduces the output power from Circuit Block 3, optimizing it for different uses. Additionally, Circuit Block 4 may be equipped with an energy storage mechanism designed to capture and store surplus energy for future purposes, including recharging the power supply source (making the energy circuit a self-recharging system) and powering other intended applications. The power control units within Circuit Block 4 should focus on smoothly transitioning from the excess energy proceeding from Circuit Block 3 output to a more manageable voltage level. By precisely adjusting the power, this unit facilitates an efficient distribution of energy throughout the entire system, reducing potential losses and ensuring power quality. The primary goal here is to align the voltage with the power supply voltage (or to some higher desired values), establishing a regenerative loop and enhancing the system’s ability to challenge the laws of energy conservation while providing a consistent power output. Figure 4 depicts a block diagram of Circuit Block 4 configuration.

Figure 4. Circuit Block 4 Configuration-Energy Storage and Potential Recharging System (Circuit Block 4 serves as a crucial interface in the energy conservation process, capturing output power from Circuit Block 3 and overseeing its efficient utilization).

Figure 4. Circuit Block 4 Configuration-Energy Storage and Potential Recharging System (Circuit Block 4 serves as a crucial interface in the energy conservation process, capturing output power from Circuit Block 3 and overseeing its efficient utilization).

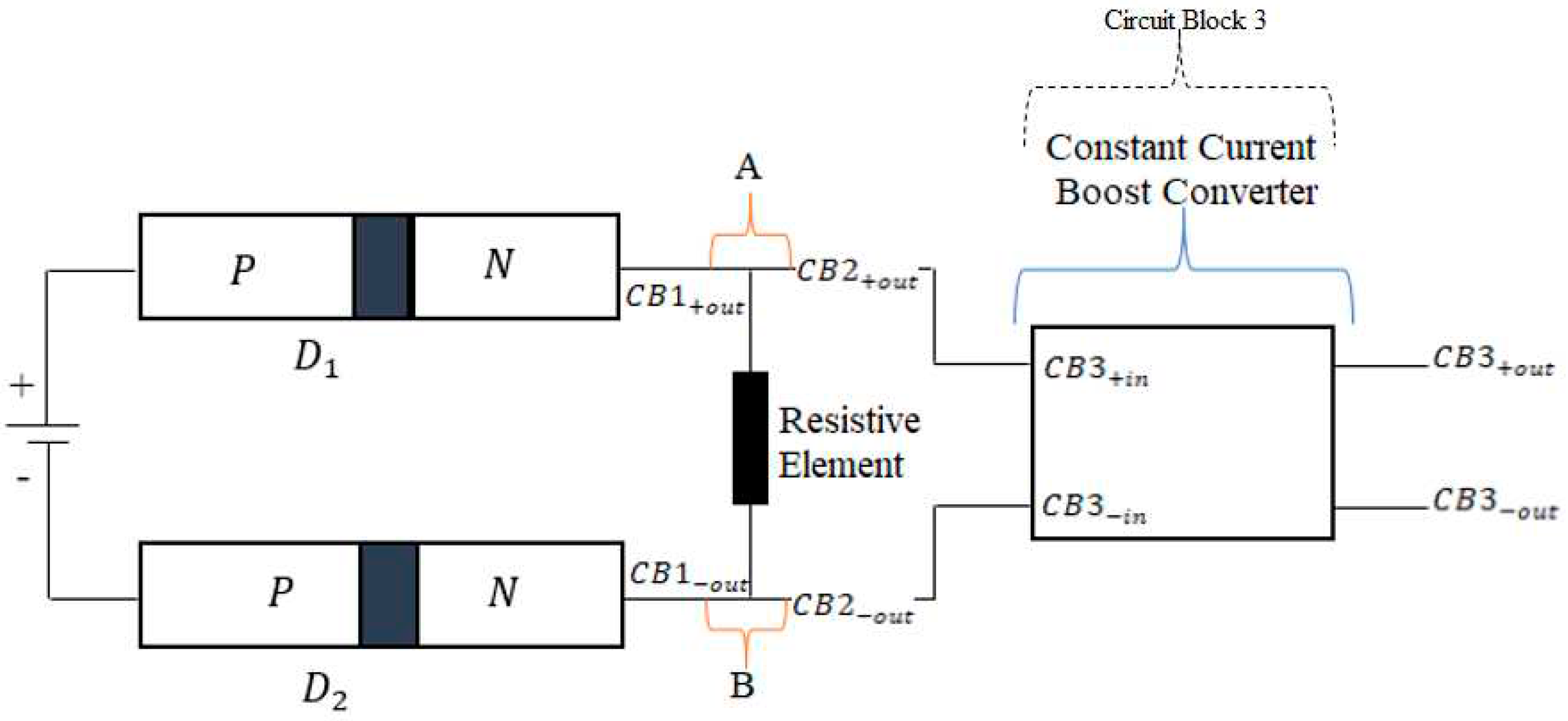
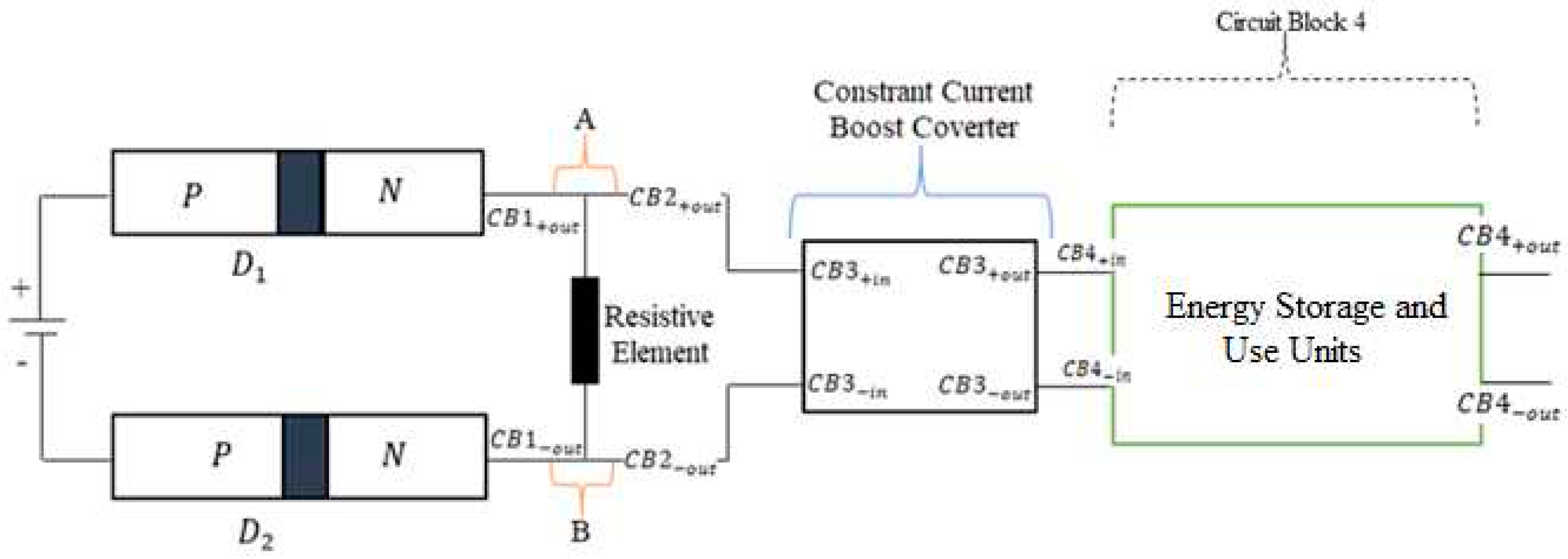
3.2.4. The Choice for Circuit Block 4 Unit

Overall, in Circuit Block 4, the focus shifts to the implementation of an energy storage unit to effectively capture and manage the high power output generated by Circuit Block 3. Among the various energy storage options, this paper suggests a capacitor-based system, because of its unique advantages, and the following discussion elaborates on the circuit, offering alternative considerations as well.

Circuit for Capacitor-Based Storage Unit. The capacitor-based storage unit requires a well-designed circuit to ensure efficient charging and discharging. The charging circuit typically includes a diode to prevent reverse current, a current-limiting resistor, and a voltage regulator to maintain optimal charging levels. On the discharge side, a controlled switch and a load resistor may be employed to regulate the release of stored energy. The choice of a capacitor-based storage unit is grounded in several key advantages. Firstly, capacitors offer rapid charging and discharging capabilities, aligning with the high-power characteristics of Circuit Block 3. Secondly, capacitors boast a longer cycle life compared to batteries, ensuring durability and reliability for repeated charge-discharge cycles. Lastly, their inherent efficiency, owing to low internal resistance, makes capacitors well-suited for applications requiring quick energy transfer [59–62].

Alternative Storage Units. While the capacitor-based system is chosen for its specific merits, alternative energy storage units are worth considering based on application requirements. Traditional batteries [63,64], such as Li-ion or Li-poly, provide higher energy density but may not match capacitors in terms of rapid energy release. Super-capacitors ([62,65–67]) offer a middle ground, combining aspects of both capacitors and batteries. Another alternative, the flywheel energy storage system [68,69], relies on mechanical rotation for energy storage, providing high power but at the cost of space efficiency.

Remark 5 (Recommendation and Considerations). The selection between capacitor-based storage and alternatives hinges on the specific needs of the application. For scenarios demanding quick response times and frequent charge-discharge cycles, the capacitor-based system stands out. Conversely, if higher energy density and longer storage durations are critical, alternatives like batteries or super-capacitors may be more appropriate. It is imperative to carefully evaluate the application’s requirements and constraints to make an informed decision on the most suitable energy storage unit for Circuit Block 4.

Circuit Block 5 (Automation and Safety Control). Circuit Block 5 plays a crucial role within the energy conservation system, aimed at automating and regulating the duration of short circuit events to ensure the safety of the energy circuit’s and the power supply source. To achieve this, a control mechanism, in the form of a sensor, is integrated into the block. The sensing element utilizes a current sensor and a microcontroller to detect variations in the short circuit current. This sensor continuously monitors the operational parameters of the system, specifically the short circuit current in Circuit Block 2. The primary objective of Circuit Block 5 is to prevent extended and potentially harmful short circuit events that could endanger the system’s integrity and the safety of connected devices. By incorporating an automated control system, the block can adjust the duration of the short circuit to strike a balance between maintaining a high short circuit current, necessary for energy generation, and ensuring safety.

3.2.5. Design and Operation of the Sensing Element in Circuit Block 5

The sensing element in Circuit Block 5 serves a critical role in monitoring the short circuit current and ensuring the safety and efficiency of the energy conservation system. The design of the sensing element involves using a current sensor and a microcontroller to detect variations in the short circuit current. Below are the details of the sensing element and its mechanism of operation.

Current Sensor. The choice of a suitable current sensor, such as a Hall-effect sensor or a current transformer, is determined by the specific system requirements. This sensor is positioned in the circuit to measure the short circuit current flowing through Circuit Block 3, specifically sensing the current between points $A$ and $B$, where the short circuit is introduced.

Microcontroller. An appropriate microcontroller, equipped with analog input capabilities, should be selected to process the output signal from the current sensor. The microcontroller serves as the core of the sensing element, interpreting current measurements and making real-time decisions based on predefined threshold settings.

3.2.6. The Sensing Element Operation Mechanism

The mechanism of operation involves continuous monitoring by the current sensor of the short circuit current in Circuit Block 3, detecting the current between points $A$ and $B$. The sensor generates an analog signal proportional to the short circuit current, which is then processed by the microcontroller. Predefined threshold settings are programmed into the microcontroller to establish acceptable limits for the short circuit current, ensuring a safe operating range. The microcontroller compares real-time current measurements with the predefined threshold values, making decisions regarding the duration of the short circuit event. If the short circuit current exceeds or falls below predetermined thresholds, the microcontroller triggers the automation mechanism within Circuit Block 5. The microcontroller control unit adjusts the duration of the short circuit event. If the current exceeds safe limits, the duration may be shortened to prevent damage. Conversely, if the current falls below optimal levels for energy generation, the duration may be extended to improve energy output. Further, Circuit Block 5 establishes a closed feedback loop, facilitating continuous communication between the sensor, microcontroller, and the rest of the energy conservation system. This feedback loop ensures real-time adjustments to maintain both safety and energy efficiency.

Remark 6. The Sensing Element in Circuit Block 5 is designed and operated in a way that it initiates its functionality using an external power source. It is crucial to note that this external power source can be replaced with a recharging circuit, drawing power from the excess energy stored in Circuit Block 4. This deliberate design decision provides the sensing element with adaptability, enabling it to shift from relying on an external power source to a self-sustaining mode powered by the surplus energy generated within Circuit Block 4. This dual-mode functionality improves the overall efficiency and autonomy of the sensing element, aligning it with the innovative and self-recharging characteristics of the broader energy circuit.

3.3. Overall Energy Circuit Representation

The overall representation of the energy circuit, starting from the power supply and extending to the storage unit in Circuit Block 4, is outlined in the block diagram, Figure 5. The Automation block (Circuit Block 5) is connected before Circuit Block 3, forming a cohesive and integrated system. This block diagrammatic illustration encapsulates the innovative design and interconnected functionalities of each circuit block, emphasizing the progression from power input to storage, with the pivotal role of automation and safety control in optimizing energy generation.

Figure 5. Comprehensive Overview of the Energy Conservation Circuit (named energy circuit). (The block diagram provides a comprehensive overview of the circuit’s components and their interconnections, illustrating its novel approach to energy conservation and generation within classical settings).

Figure 5. Comprehensive Overview of the Energy Conservation Circuit (named energy circuit). (The block diagram provides a comprehensive overview of the circuit’s components and their interconnections, illustrating its novel approach to energy conservation and generation within classical settings).

4. Discussion and Implications

5. Conclusions

References

1. P. Bradu et al., “Recent advances in green technology and Industrial Revolution 4.0 for a sustainable future,” Environ. Sci. Pollut. Res., Apr. 2022, . [CrossRef]
2. M. Farghali et al., “Strategies to save energy in the context of the energy crisis: a review,” Environ. Chem. Lett., vol. 21, no. 4, pp. 2003–2039, Aug. 2023, . [CrossRef]
3. Y. Guan et al., “Burden of the global energy price crisis on households,” Nat. Energy, vol. 8, no. 3, Art. no. 3, Mar. 2023, . [CrossRef]
4. Gupta and O. Gupta, “Recent Advancements in the Recovery and Reuse of Organic Solvents Using Novel Nanomaterial-Based Membranes for Renewable Energy Applications,” Membranes, vol. 13, no. 1, p. 108, Jan. 2023, . [CrossRef]
5. J. L. Holechek, H. M. E. Geli, M. N. Sawalhah, and R. Valdez, “A Global Assessment: Can Renewable Energy Replace Fossil Fuels by 2050?,” Sustainability, vol. 14, no. 8, Art. no. 8, Jan. 2022, . [CrossRef]
6. G. Liobikienė, Y. Matiiuk, and R. Krikštolaitis, “The concern about main crises such as the Covid-19 pandemic, the war in Ukraine, and climate change’s impact on energy-saving behavior,” Energy Policy, vol. 180, p. 113678, Sep. 2023, . [CrossRef]
7. S. Singh and J. Ru, “Accessibility, affordability, and efficiency of clean energy: a review and research agenda,” Environ. Sci. Pollut. Res., vol. 29, no. 13, pp. 18333–18347, Mar. 2022, . [CrossRef]
8. J. Woodcock, D. Banister, P. Edwards, A. M. Prentice, and I. Roberts, “Energy and transport,” Lancet Lond. Engl., vol. 370, no. 9592, pp. 1078–1088, Sep. 2007, . [CrossRef]
9. S. S. Akadiri, T. S. Adebayo, M. Nakorji, W. Mwakapwa, E. M. Inusa, and O.-O. Izuchukwu, “Impacts of globalization and energy consumption on environmental degradation: what is the way forward to achieving environmental sustainability targets in Nigeria?,” Environ. Sci. Pollut. Res. Int., vol. 29, no. 40, pp. 60426–60439, 2022, . [CrossRef]
10. M. J. B. Kabeyi and O. A. Olanrewaju, “Sustainable Energy Transition for Renewable and Low Carbon Grid Electricity Generation and Supply,” Front. Energy Res., vol. 9, 2022, Accessed: Nov. 15, 2023. [Online]. Available: https://www.frontiersin.org/articles/10.3389/fenrg.2021.743114.
11. N. Coppedge, “TOP PERPETUAL MOTION MACHINES,” May 2022.
12. P. David, ELECTRO-MAGNETIC INDUCTION: FREE ELECTRICITY GENERATOR. 2017.
13. S. P. C. Mohammad Noor Hidayat, “Design and Analysis of A Perpetual Motion Machine Using Neodymium Magnets as A Prime Mover,” J. Southwest Jiaotong Univ., vol. 56, no. 2, Art. no. 2, May 2021, Accessed: Nov. 15, 2023. [Online]. Available: http://jsju.org/index.php/journal/article/view/844.
14. S. Khatri, “Design and analysis of Free Energy Generator system by balancing of flywheel,” Turk. Online J. Qual. Inq., vol. 13, no. 1, Art. no. 1, Jan. 2022, Accessed: Nov. 15, 2023. [Online]. Available: https://www.tojqi.net/index.php/journal/article/view/8694.
15. J. F. Rodríguez-León, I. Cervantes, E. Castillo-Castañeda, G. Carbone, and D. Cafolla, “Design and Preliminary Testing of a Magnetic Spring as an Energy-Storing System for Reduced Power Consumption of a Humanoid Arm,” Actuators, vol. 10, no. 6, Art. no. 6, Jun. 2021, . [CrossRef]
16. Satellite Research & Development Center/SUPARCO, Lahore 54000, Pakistan, I. Khan, M. Amin, M. I. Masood, and A. Asadullah, “Analysis of ‘free energy’ perpetual motion machine system based on permanent magnets,” Int. J. Smart Grid Clean Energy, 2014, . [CrossRef]
17. B. Mahesh, “Self Flowing Generator,” Int. J. Sci. Res. IJSR, vol. 7, pp. 259–261, Apr. 2018, . [CrossRef]
18. E. Mach, “On the Principle of the Conservation of Energy,” The Monist, vol. 5, no. 1, pp. 22–54, 1894, Accessed: Nov. 15, 2023. [Online]. Available: https://www.jstor.org/stable/27897203.
19. P. Innocenzi, “Perpetuum Mobile,” in The Innovators Behind Leonardo, Cham: Springer International Publishing, 2019, pp. 165–180. [CrossRef]
20. M. Davis, “No Perpetual Motion Machine,” Science, vol. 268, p. 624, May 1995, . [CrossRef]
21. School Adviser of Natural Science Teachers of Ioannina8 Seferi street, Eleoussa, 455 00,Ioannina Hellas and D. Tsaousis, “Perpetual Motion Machine,” J. Eng. Sci. Technol. Rev., vol. 1, no. 1, pp. 53–57, Jun. 2008, . [CrossRef]
22. J. Wisniak, “Conservation of Energy Readings on the Origins of the First Law of Thermodynamics. Part II,” Educ. Quím., vol. 19, no. 3, p. 216, Jun. 2011, . [CrossRef]
23. M. N. Hidayat, S. P. Chairandy, and F. Ronilaya, “Design and Analysis of A Perpetual Motion Machine Using Neodymium Magnets as A Prime Mover,” J. Southwest Jiaotong Univ., vol. 56, no. 2, pp. 211–219, Apr. 2021, . [CrossRef]
24. S. V. Kukhlevsky, “Breaking of Energy Conservation Law: Creating and Destroying of Energy by Subwavelength Nanosystems.” arXiv, Dec. 27, 2006. [CrossRef]
25. S. Abdollahi, “Hypothesis of Nothingness,” vol. 10, pp. 43–49, Jul. 2021, . [CrossRef]
26. B. N. Shanta, “Life and consciousness - The Vedāntic view,” Commun. Integr. Biol., vol. 8, no. 5, p. e1085138, 2015, . [CrossRef]
27. S. Paulson, D. Albert, J. Holt, and N. Turok, “The origins of the universe: why is there something rather than nothing?,” Ann. N. Y. Acad. Sci., vol. 1361, pp. 1–17, Dec. 2015, . [CrossRef]
28. S. Carroll, “Why Is There Something, Rather Than Nothing?,” Feb. 2018.
29. T. R. Mongan, “Origin of the Universe, Dark Energy, and Dark Matter,” J. Mod. Phys., vol. 9, no. 5, Art. no. 5, Apr. 2018, . [CrossRef]
30. M. Lincoln and A. Wasser, “Spontaneous creation of the Universe Ex Nihilo,” Phys. Dark Universe, vol. 2, no. 4, pp. 195–199, Dec. 2013, . [CrossRef]
31. P. Heering, J. Keck, and G. A. Rohlfs, “Laboratory Notes, Laboratory Experiences, and Conceptual Analysis: Understanding the Making of Ohm’s First Law in Electricity,” Berichte Zur Wiss., vol. 43, no. 1, pp. 7–27, Mar. 2020, . [CrossRef]
32. K. M. Tenny and M. Keenaghan, “Ohms Law,” in StatPearls, Treasure Island (FL): StatPearls Publishing, 2023. Accessed: Nov. 15, 2023. [Online]. Available: http://www.ncbi.nlm.nih.gov/books/NBK441875/.
33. Rangel-Abundis, “[Shunt and short circuit],” Cir. Cir., vol. 74, no. 1, pp. 69–70, 2006.
34. D. H. Chen, “Can Law of Conservation of Energy Be Broken?,” Appl. Mech. Mater., vol. 192, pp. 420–424, Jul. 2012, . [CrossRef]
35. T. Kerremans, P. Samuelsson, and P. P. Potts, “Probabilistically Violating the First Law of Thermodynamics in a Quantum Heat Engine,” SciPost Phys., vol. 12, no. 5, p. 168, May 2022, . [CrossRef]
36. J. V. N., “Particle Creation in a Big-bang Universe,” Nature, vol. 246, no. 5433, Art. no. 5433, Dec. 1973, . [CrossRef]
37. R. L. Anjum and S. Mumford, “A Powerful Theory of Causation,” vol. 9780203851289, Jan. 2010, . [CrossRef]
38. Kimuya, Proving the Law of Energy Conservation from Mathematical and Scientific Perspectives. 2022. [CrossRef]
39. H. Lee, W. Chow, and H. Hung, “A Study on Residential Fires due to Electrical Faults in Hong Kong,” 2016. Accessed: Nov. 15, 2023. [Online]. Available: https://www.semanticscholar.org/paper/A-Study-on-Residential-Fires-due-to-Electrical-in-Lee-Chow/05000136e6f2ca0a48bc05b63af08265a218ab7c.
40. H. Lee, W. Chow, and H. Hung, “A Study on Residential Fires due to Electrical Faults in Hong Kong,” 2016. Accessed: Nov. 15, 2023. [Online]. Available: https://www.semanticscholar.org/paper/A-Study-on-Residential-Fires-due-to-Electrical-in-Lee-Chow/05000136e6f2ca0a48bc05b63af08265a218ab7c.
41. J.-H. Kim, B.-K. Park, J.-H. Song, and K.-C. Jung, “A Study on the Possibility of Electrical Fires due to the Short Circuit and Ground Fault of Power Cable Supported by an Iron Fence,” J. Korean Soc. Saf., vol. 22, Jan. 2007.
42. 2022; G. Buica, A. Anca Elena, C. Beiu, M. Risteiu, and D. Pasculescu, “Aspects of the earthing and short-circuit device’s safety quality,” MATEC Web Conf., vol. 373, Dec. 2022, . [CrossRef]
43. L. Salvaraji, M. S. Jeffree, K. Awang Lukman, S. Saupin, and R. Avoi, “Electrical safety in a hospital setting: A narrative review,” Ann. Med. Surg., vol. 78, p. 103781, May 2022, . [CrossRef]
44. S. Szultka, S. Czapp, A. Tomaszewski, and H. Ullah, “Evaluation of Fire Hazard in Electrical Installations Due to Unfavorable Ambient Thermal Conditions,” Fire, vol. 6, no. 2, Art. no. 2, Feb. 2023, . [CrossRef]
45. D. Gao and Q. Liu, “Review of the Research on the Identification of Electrical Fire Trace Evidence,” Procedia Eng., vol. 135, pp. 29–32, Dec. 2016, . [CrossRef]
46. B. B. Pannebakker, A. C. de Waal, and W. G. J. H. M. van Sark, “Photovoltaics in the shade: one bypass diode per solar cell revisited,” Prog. Photovolt. Res. Appl., vol. 25, no. 10, pp. 836–849, 2017, . [CrossRef]
47. F. Fadliondi, H. Isyanto, and B. Budiyanto, “Bypass Diodes for Improving Solar Panel Performance,” Int. J. Electr. Comput. Eng. IJECE, vol. 8, p. 2703, Oct. 2018, . [CrossRef]
48. M. Sofyan, I. Sara, and S. Suriadi, The effect of bypass diode installation on partially covered solar panel output power, vol. 1087. 2021. [CrossRef]
49. J. H. Lee et al., “Characteristics and Electronic Band Alignment of a Transparent p-CuI/n-SiZnSnO Heterojunction Diode with a High Rectification Ratio,” Nanomaterials, vol. 11, no. 5, Art. no. 5, May 2021, . [CrossRef]
50. C. SHARMA, “Solar Panel Mathematical Modeling Using Simulink,” Int. J. Eng. Res. Appl., vol. 4, pp. 67–72, May 2014.
51. Z. Chen, R. Xiong, J. Tian, X. Shang, and J. Lu, “Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles,” Appl. Energy, vol. 184, pp. 365–374, Dec. 2016, . [CrossRef]
52. B. Xia, Z. Chen, C. Mi, and B. Robert, “External short circuit fault diagnosis for lithium-ion batteries,” in 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI: IEEE, Jun. 2014, pp. 1–7. [CrossRef]
53. KIMUYA, A. M. The Modified Ohm’s Law and Its Implications for Electrical Circuit Analysis. Eurasian J. Sci. Eng. Tech. 2023, 4(2), Accepted for publication: 10.11.2023.
54. F. A. Chaves, P. C. Feijoo, and D. Jiménez, “2D pn junctions driven out-of-equilibrium,” Nanoscale Adv., vol. 2, no. 8, p. 3252, Aug. 2020, . [CrossRef]
55. S. K. Tripathi and M. Sharma, “Analysis of the forward and reverse bias I-V and C-V characteristics on Al/PVA:n-PbSe polymer nanocomposites Schottky diode,” J. Appl. Phys., vol. 111, no. 7, p. 074513, Apr. 2012, . [CrossRef]
56. J. R. Sadaf, M. Q. Israr, S. Kishwar, O. Nur, and M. Willander, “Forward- and reverse-biased electroluminescence behavior of chemically fabricated ZnO nanotubes/GaN interface,” Semicond. Sci. Technol., vol. 26, no. 7, p. 075003, Jul. 2011, . [CrossRef]
57. X. Zhang et al., “Near-ideal van der Waals rectifiers based on all-two-dimensional Schottky junctions,” Nat. Commun., vol. 12, p. 1522, Mar. 2021, . [CrossRef]
58. Z. Botao, W. Qi, Z. Min, and H. Huan, “Analytical solution for the inductor current of BOOST converter,” IET Power Electron., vol. 12, no. 9, pp. 2424–2432, 2019, . [CrossRef]
59. Z. Li et al., “Aqueous hybrid electrochemical capacitors with ultra-high energy density approaching for thousand-volts alternating current line filtering,” Nat. Commun., vol. 13, p. 6359, Oct. 2022, . [CrossRef]
60. P. Xia, Z. Zhang, Z. Tang, Y. Xue, J. Li, and G. Yang, “Preparation and Electrochemical Performance of Three-Dimensional Vertically Aligned Graphene by Unidirectional Freezing Method,” Molecules, vol. 27, no. 2, p. 376, Jan. 2022, . [CrossRef]
61. Y. Yuan, C. Wang, K. Lei, H. Li, F. Li, and J. Chen, “Sodium-Ion Hybrid Capacitor of High Power and Energy Density,” ACS Cent. Sci., vol. 4, no. 9, pp. 1261–1265, Sep. 2018, . [CrossRef]
62. N. Kumar, S.-B. Kim, S.-Y. Lee, and S.-J. Park, “Recent Advanced Supercapacitor: A Review of Storage Mechanisms, Electrode Materials, Modification, and Perspectives,” Nanomaterials, vol. 12, no. 20, p. 3708, Oct. 2022, . [CrossRef]
63. Q. Zhu, J. Ma, S. Li, and D. Mao, “Solid-State Electrolyte for Lithium-Air Batteries: A Review,” Polymers, vol. 15, no. 11, p. 2469, May 2023, . [CrossRef]
64. P. Lai et al., “Bifunctional Localized High-Concentration Electrolyte for the Fast Kinetics of Lithium Batteries at Low Temperatures,” ACS Appl. Mater. Interfaces, vol. 15, no. 25, pp. 31020–31031, Jun. 2023, . [CrossRef]
65. J. M. Lim et al., “Advances in high-voltage supercapacitors for energy storage systems: materials and electrolyte tailoring to implementation,” Nanoscale Adv., vol. 5, no. 3, pp. 615–626, . [CrossRef]
66. P. Yang et al., “Ultrafast-Charging Supercapacitors Based on Corn-Like Titanium Nitride Nanostructures,” Adv. Sci., vol. 3, no. 6, p. 1500299, Oct. 2015, . [CrossRef]
67. Y. Xu et al., “High Performance Supercapacitors Based on Mesopore Structured Multiwalled Carbon Nanotubes,” ChemistryOpen, vol. 10, no. 3, pp. 347–351, Feb. 2021, . [CrossRef]
68. Tomczewski, “Operation of a wind turbine-flywheel energy storage system under conditions of stochastic change of wind energy,” ScientificWorldJournal, vol. 2014, p. 643769, 2014, . [CrossRef]
69. S. Wicki and E. G. Hansen, “Clean energy storage technology in the making: An innovation systems perspective on flywheel energy storage,” J. Clean. Prod., vol. 162, pp. 1118–1134, Sep. 2017, . [CrossRef]
70. Mardani, A. Jusoh, E. Zavadskas, F. Cavallaro, and Z. Khalifah, “Sustainable and Renewable Energy: An Overview of the Application of Multiple Criteria Decision Making Techniques and Approaches,” Sustainability, vol. 7, no. 10, pp. 13947–13984, Oct. 2015, . [CrossRef]
71. Zohuri and P. McDaniel, “First Law of Thermodynamics,” in Thermodynamics in Nuclear Power Plant Systems, Cham: Springer International Publishing, 2019, pp. 99–148. [CrossRef]
72. Kutty, R. Al-Jondob, G. Abdella, and T. El-Mekkawy, A Frontier Based Eco-Efficiency Assessment of Electric Vehicles: The Case of European Union Countries Using Mixed and Renewable Sources of Energy. 2021.
73. Costa, J. Barbosa, H. Castro, R. Gonçalves, and S. Lanceros-Méndez, “Electric vehicles: To what extent are environmentally friendly and cost effective? – Comparative study by european countries,” Renew. Sustain. Energy Rev., vol. 151, p. 111548, Nov. 2021, . [CrossRef]
74. J. A. Sanguesa, V. Torres-Sanz, P. Garrido, F. J. Martinez, and J. M. Marquez-Barja, “A Review on Electric Vehicles: Technologies and Challenges,” Smart Cities, vol. 4, no. 1, pp. 372–404, Mar. 2021, . [CrossRef]
75. Sbordone, I. Bertini, B. Di Pietra, M. C. Falvo, A. Genovese, and L. Martirano, “EV fast charging stations and energy storage technologies: A real implementation in the smart micro grid paradigm,” Electr. Power Syst. Res., vol. 120, pp. 96–108, Mar. 2015, . [CrossRef]
76. V. Rajendran Pillai, R. Rajasekharan Nair Valsala, V. Raj, M. Petra, S. Krishnan Nair, and S. Mathew, “Exploring the Potential of Microgrids in the Effective Utilisation of Renewable Energy: A Comprehensive Analysis of Evolving Themes and Future Priorities Using Main Path Analysis,” Designs, vol. 7, no. 3, p. 58, Apr. 2023, . [CrossRef]
77. Hirsch, Y. Parag, and J. Guerrero, “Microgrids: A review of technologies, key drivers, and outstanding issues,” Renew. Sustain. Energy Rev., vol. 90, pp. 402–411, Jul. 2018, . [CrossRef]
78. M. Uddin, H. Mo, D. Dong, S. Elsawah, J. Zhu, and J. M. Guerrero, “Microgrids: A review, outstanding issues and future trends,” Energy Strategy Rev., vol. 49, p. 101127, Sep. 2023, . [CrossRef]
79. M. R. H. Mojumder, F. Ahmed Antara, M. Hasanuzzaman, B. Alamri, and M. Alsharef, “Electric Vehicle-to-Grid (V2G) Technologies: Impact on the Power Grid and Battery,” Sustainability, vol. 14, no. 21, Art. no. 21, Jan. 2022, . [CrossRef]
80. M. Farghali et al., “Social, environmental, and economic consequences of integrating renewable energies in the electricity sector: a review,” Environ. Chem. Lett., vol. 21, no. 3, pp. 1381–1418, Jun. 2023, . [CrossRef]
81. M. Takase, R. Kipkoech, and P. K. Essandoh, “A comprehensive review of energy scenario and sustainable energy in Kenya,” Fuel Commun., vol. 7, p. 100015, Jun. 2021, . [CrossRef]