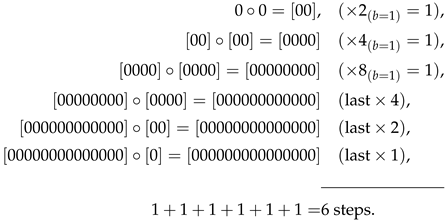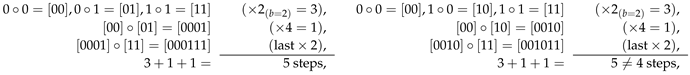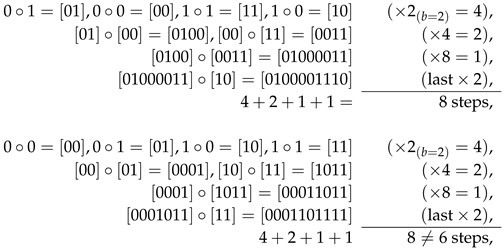2. Results
Theorems 1 and 2 were already stated in our previous study [
9] for
. We restate them here
for clarity.
Theorem 1. A quadruplet is the shortest string that allows for more than one ASI for all b.
Proof.
provides available doublets with unit ASI. provides available triplets with ASI equal to two. Only provides quadruplets that include quadruplets with ASI equal to two, that is b quadruplets and quadruplets , while the ASI of the remaining quadruplets is three. □
For example, to assemble the quadruplet , we need to assemble the doublet and reuse it from the first step ASP , while there is nothing available to reuse, in the case of the quadruplet .
Where the symbol value can be arbitrary, we write * assuming that it is the same within the string. If we allow for the 2nd possibility different from *, we write ★. Thus, , for example, is a placeholder for all b strings, while a placeholder for all strings. Furthermore, we consider the degenerate case of just one basic symbol ().
Theorem 2. The minimum ASI as a function of N corresponds to the shortest addition chain for N (OEIS A003313) for all b.
Proof. Strings
for which
,
can be formed in subsequent steps
s by joining the longest string assembled so far with itself until
is reached. Therefore, if
, then
. Only
strings have such ASI if
, including respectively
b and
strings
and the assembly pathway of each of the strings (
2) is unique. At each assembly step, its length doubles.
An addition chain for having the shortest length (commonly denoted as ) is defined as a sequence of integers such that , for . Thus, an addition chain starts with one, not zero, as zero is the neutral element of addition. For the same reason, two is considered the smallest prime, as one is the neutral element of multiplication. Hence, and the first step in creating an addition chain for N is always ; the ASI of any doublet is one. The second step in creating an addition chain can be , , or . The 1st case does not represent the shortest addition chain, the 2nd one corresponds to assembling a triplet based on the previously assembled doublet, and the 3rd one corresponds to assembling a quadruplet from this doublet. Therefore, four is the smallest number achievable in two ways since and , where the latter case corresponds to assembling a quadruplet by joining a basic symbol to a triplet, which is not the shortest way for assembling a quadruplet having a minimum ASI.
Thus, finding the shortest addition chain for N corresponds to finding the ASI of a string containing basic symbols and/or doublets and/or triplets containing these doublets for since due to Theorem 1 only they provide the same assembly indices . □
The assembly pathways of strings of length are not unique. For example, a string can be assembled in three steps from three working ASPs , , and .
Theorem 3. The strings can contain at most two symbols if . Other minimum ASI strings of length can contain at most three symbols if .
Proof. Minimum ASI strings of length are formed by joining the newly assembled string to itself, where a clear or mixed doublet is created in the first step. Minimum ASI strings of other lengths admit a doublet and a triplet containing this doublet and an additional basic symbol.
To formally prove the first part, we can also use mathematical induction on the assembly step
s. If
, then the minimum ASI strings
are doublets of the form
, where
. If
, the string contains one distinct symbol, and if
, the string contains two distinct symbols. In both cases, the number of distinct symbols does not exceed two. Now assume that for some
, all minimum ASI strings
contain at most two distinct symbols. We must show that
also contains at most two distinct symbols. Consider constructing
by joining two identical minimum ASI strings
with each other. By the inductive hypothesis, each
contains at most two distinct symbols. Therefore, their concatenation also contains at most two distinct symbols. By induction, for all
, the minimum ASI string
contains at most two distinct symbols.
We will now show that other minimum ASI strings of length can contain at most three distinct symbols if . We provide the construction of minimum ASI strings with three symbols. In the first step , we create a doublet where and . Next, we combine the existing doublet with a new symbol where . This forms a triplet , introducing a third distinct symbol and further increasing the ASI by 1. We continue assembling by joining the longest string formed so far with itself or with previously formed strings, maintaining the minimal increase in ASI.
Assume a contrario that there exists a minimum ASI string of length that contains four or more distinct symbols. To incorporate a fourth symbol, at least one additional assembly step is required beyond what is needed for the three symbols. This additional step implies an increase in ASI, which contradicts the minimality of . Thus, Theorem 3 is proven. □
The strings having non-minimum ASI can contain all symbols. For example, the string [
14]
has ASI
and contains all five basic symbols
.
Theorem 4. A string containing the same three doublets has the same ASI as a string containing two pairs of the same doublets, provided that both strings have the same distributions of other repetitions and have the same lengths.
Proof. Without loss of generality (w.l.o.g.), consider the following two strings of the same length
with
and the same distributions of other repetitions (if there are any other repetitions)
where
. Creating a doublet takes one assembly step. Each appending of a doublet to an assembled string counts as another assembly step. Hence, in a general case (i.e., for strings
,
containing also other symbols), the string
requires six additional assembly steps, the same as the string
, which completes the proof. □
Theorem 5. A string containing the same three doublets has the same ASI as a string containing the same two triplets, provided that both strings have the same distributions of other repetitions.
Proof. W.l.o.g. consider the following two strings of the same length
with the same distributions of other repetitions
Creating a triplet takes two assembly steps. Hence, in the general case, the string
requires four additional assembly steps, the same as the string
, which completes the proof. □
Theorem 6. A string containing the same two triplets has the same ASI as a string containing two pairs of the same doublets, provided that both strings have the same distributions of other repetitions and have the same lengths.
Proof. The proof stems from Theorems 4 and 5. □
Theorem 7. A string containing the same two quadruplets of the minimum ASI has the same ASI as a string containing the same three triplets, provided that both strings have the same distributions of other repetitions and have the same lengths.
Proof. W.l.o.g. consider the following two strings of the same length
with the same distributions of other repetitions
Creating such a quadruplet takes two assembly steps. Hence, in a general case, the string
requires five additional assembly steps, the same as the string
, which completes the proof. □
Theorem 8. A string containing the same two quadruplets of the maximum ASI has the same ASI as a string containing a doublet and the same two triplets based on this doublet, provided that both strings have the same distributions of other repetitions.
Proof. W.l.o.g. consider the following two strings of the same length
with the same distributions of other repetitions
Creating such a quadruplet takes three assembly steps. Hence, in a general case, the string requires five additional assembly steps, the same as the string , which completes the proof. □
Theorem 9. A string containing the same two doublets and the same two triplets not based on this doublet has the same ASI as a string containing a doublet and the same two triplets based on this doublet, provided that both strings have the same distributions of other repetitions and have the same lengths.
Proof. W.l.o.g. consider the following two strings of the same length
with the same distributions of other repetitions
where
. In a general case, the string
requires seven additional assembly steps, the same as the string
, which completes the proof. □
In general, Theorems 1-9 show that
k copies of a doublet in a string decrease the ASI of this string at least by ;
k copies of a triplet in a string decrease the ASI of this string at least by ;
k copies of a minimum ASI quadruplet in a string decrease the ASI of this string at least by ;
k copies of a maximum ASI quadruplet in a string decrease the ASI of this string at least by ;
where, the phrase "at least" is meant to indicate that other repetitions, such as e.g. doublets forming multiple quadruplets, etc. can further decrease the ASI of the string. This observation allows us to state the following theorem.
Theorem 10.
Each copies of an -plet contained in a string decrease its ASI at least by . That is
where R is the total number of repeated -plets.
Proof. W.l.o.g. consider the following string
containing two copies of an
n-plet
. The
n-plet
can be assembled in
steps and appended to the assembled string
in one step. Consider that the ASI of the
n-plet
is
, i.e. the
n-plet does not have any repetitions that can be reused. Then one copy of this
n-plet - as expected - does not decrease the ASI of the string
, as
, while more copies
k decrease it by
. On the other hand, if
then even a single copy of this
n-plet will decrease the ASI of
. □
For example, due to the presence of three copies of a 5-plet
, each with
, in a string
its ASI amounts to
. The relation (
10) provides the upper bound on ASI as it does not describe a situation in which
n-plet for
is assembled on a doublet also present in one copy in the string. For example, the string
, while
. We note that the maximum ASI decrease is provided by
-plets of the minimum ASI and amounts to
.
Another quantity quantifying the complexity of a string is the assembly depth (ASD) defined [
15] as
where
, and
and
are the ASDs of two substrings
,
of the string
that were joined in step
s, where for
, and if there are more assembly pathways with different depths
leading to a string, which happens if at least two independent assembly steps are possible, the minimum pathway depth is the ASD of this string. Hence, the ASD captures the notion of an
independent assembly step.
Theorem 11. If a working ASP contains strings having the same ASD they were assembled in independent assembly steps.
Proof. W.l.o.g. assume
a contrario that two strings
,
in the working ASP have the same ASD, i.e.,
, but
was used in the assembly of
along with a basic symbol
c. Then
which contradicts our assumption and completes the proof. □
In other words, if two strings
,
in the working ASP have the same ASD, their assembly pathways are unrelated to each other; by the defining equation (
13) neither of them could have been used in the assembly pathway of the other.
Theorem 12. The ASD of any minimum ASI string is equal to the ASI of this string, .
Proof. We need to show that
. While constructing the minimum ASI string, we start with a doublet and follow the shortest addition chain for
N, joining this doublet with itself or with a basic symbol to form a triplet. At each assembly step, the ASD increases by one, as we join the assembled string with a string or a basic symbol from the working ASP and we cannot perform independent assembly steps. Since, by Theorem 2, the minimum ASI corresponds to the length of the shortest addition chain
, we have
This completes the proof (see
Appendix F for additional comments). □
Theorems 11 and 12 show that
the working ASP of a minimum ASI string cannot contain strings assembled in independent assembly steps,
the working ASP of a non-minimum ASI string must contain at least two such strings, and
the assembly pathway of a maximum ASI string will tend to maximize their number in the working ASP, and hence to minimize the possible ASD, taking into account the saturation of the working ASP, as the number of distinct n-plets in the working ASP cannot exceed .
Theorem 13.
The ASD of any maximum ASI string satisfies
Proof. Let
. For
we have
, as we are joining basic symbols from the initial ASP. This is the base case. In an assembly tree of ASD
, the maximum number of leaves that can be combined is
, because at each assembly step, we join two substrings. Therefore, the maximum length
of a
string that can be assembled with ASD
satisfies:
This implies that
and leads to the relation (
16), since both
and
are natural numbers and the latter does not have to be a power of two. We can also use mathematical induction. For
and for
we have respectively
where
implies that either
or
. Hence,
which completes the proof. □
Theorems 12 and 13 are somehow counterintuitive. For example, the string has the ASI and the ASD , while the string has a smaller ASI but a larger ASD .
For example, the ASD of a string
is
as
even though this string can be assembled with three larger pathway depths
and the ASD of a minimum ASI string
is
Similarly, the ASD of a string
is
as
However, the non-maximum ASI string
has only two doublets that can be assembled in independent steps. Hence, its ASD cannot be decreased to
The seven-bit string is the longest string that can have the maximum ASI
. There are four such bitstrings containing two clear triplets and the starting bit at the end or the ending bit at the start, that is
and their lengths cannot be increased without a repetition of a doublet, which keeps the ASI at the same level
.
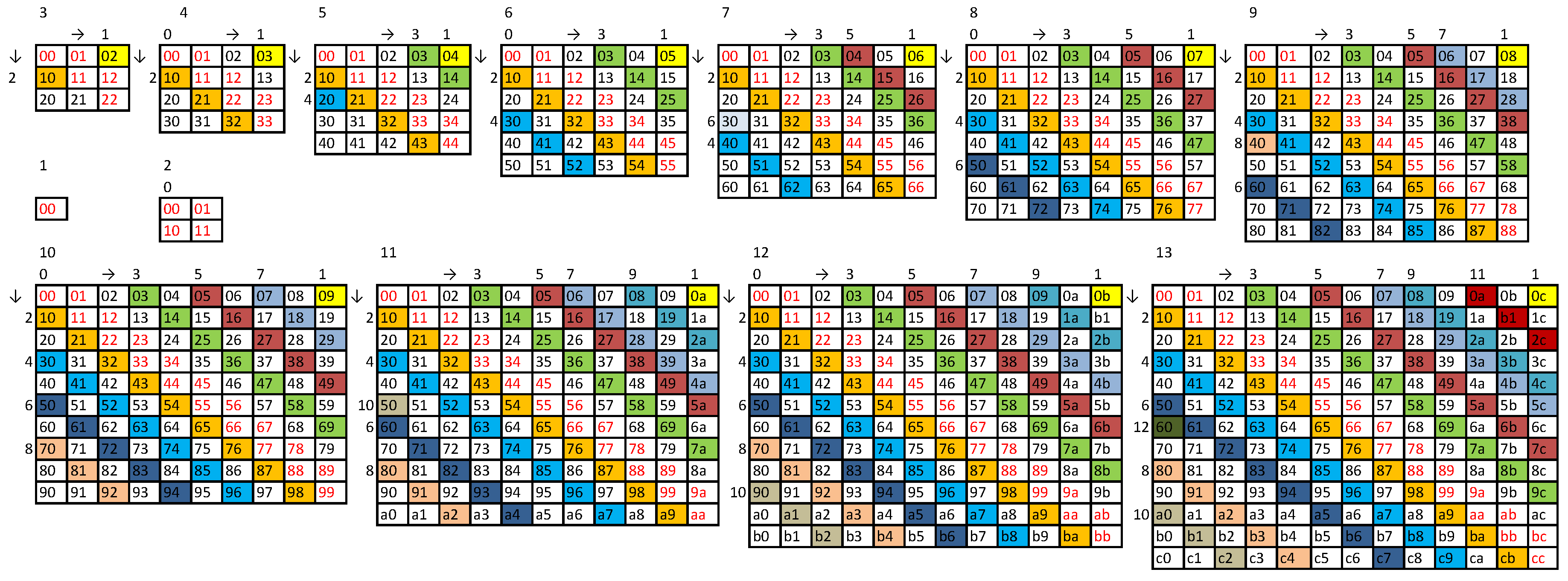
This observation and Theorem 2 motivated us to develop a general method to construct the longest possible string having the ASI , as a function of the radix b. We denote the length of this string by or , and we call this string a string.
After a few groping try-outs, we eventually reached two stable methods (cf. Appendices, Methods
Appendix A and
Appendix B). In both methods, we start with an initial balanced string of length
containing
b clear triplets ordered as
The doublets that can be inserted into the initial string (
26) can be arranged in a
matrix
where the crossed out entries on a diagonal cannot be reused, as they would create repetitions in this string. If we assume that we shall not insert doublets between the clear triplets of the string (
26), we can also cross out the entries in the first superdiagonal of the matrix (
27). The strings of odd lengths generated by these general methods are not only the longest but also the most balanced. This can be stated in the following theorem.
Theorem 14 (
).
The longest length of a string that has the ASI of is given by
(OEIS A353887) and this string is nearly balanced, that is
where is the number of occurrences of all but one symbol within the string, and its Shannon entropy is
The proof of Theorem 14 is given in
Appendix D. A
string must contain all clear triplets and all doublets and if it is generated by Method
Appendix A or
Appendix B it is terminated with 0 and has a form
Although the case for
is degenerate, as no information can be conveyed using only one symbol (
in this case), nothing precludes the assembly of such defunct strings and the formula (
28) yields the correct result; the string
is the longest string with
by Theorem 1, as for
the upper and the lower bound on the ASI are the same,
(OEIS
A003313). This is the only case where the maximum ASI is not a monotonically nondecreasing function of
N.
For
, only two doublets can be introduced without repetitions into the initial string (
26), leading to twelve unique strings of length
Finally, we have to multiply the cardinality of this set by to account for permutations. For example, the first string , is equivalent to five strings , , , , and . Hence, there are seventy-two different strings of length .
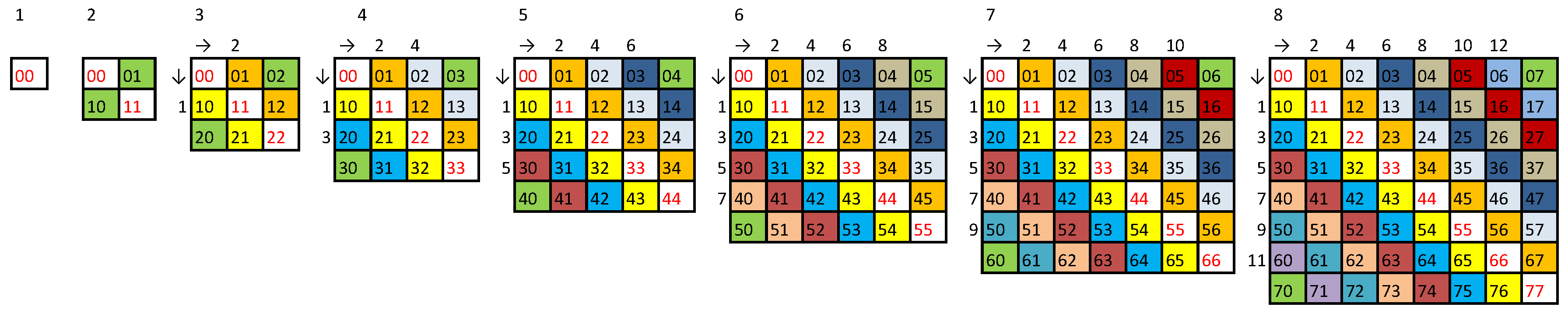
Subsequently, we considered other strings of length with the maximum ASI for .
Theorem 15 (
).
For all and the longest length of a string that has the ASI of is given by
The proof of Theorem 15 is given in
Appendix E. This result disproves our upper bound Conjecture 1 for
stated in our previous study [
9]. If the strings of Theorem 15 are based on strings generated by Method
Appendix A or
Appendix B, for
they owe their properties to the following distributions of symbols
For the strings of the form (
34) the fractions in the Shannon entropy are
where
,
if
and
,
otherwise, as
is inserted into
,
into
and
or
otherwise. This leads to Shannon entropy
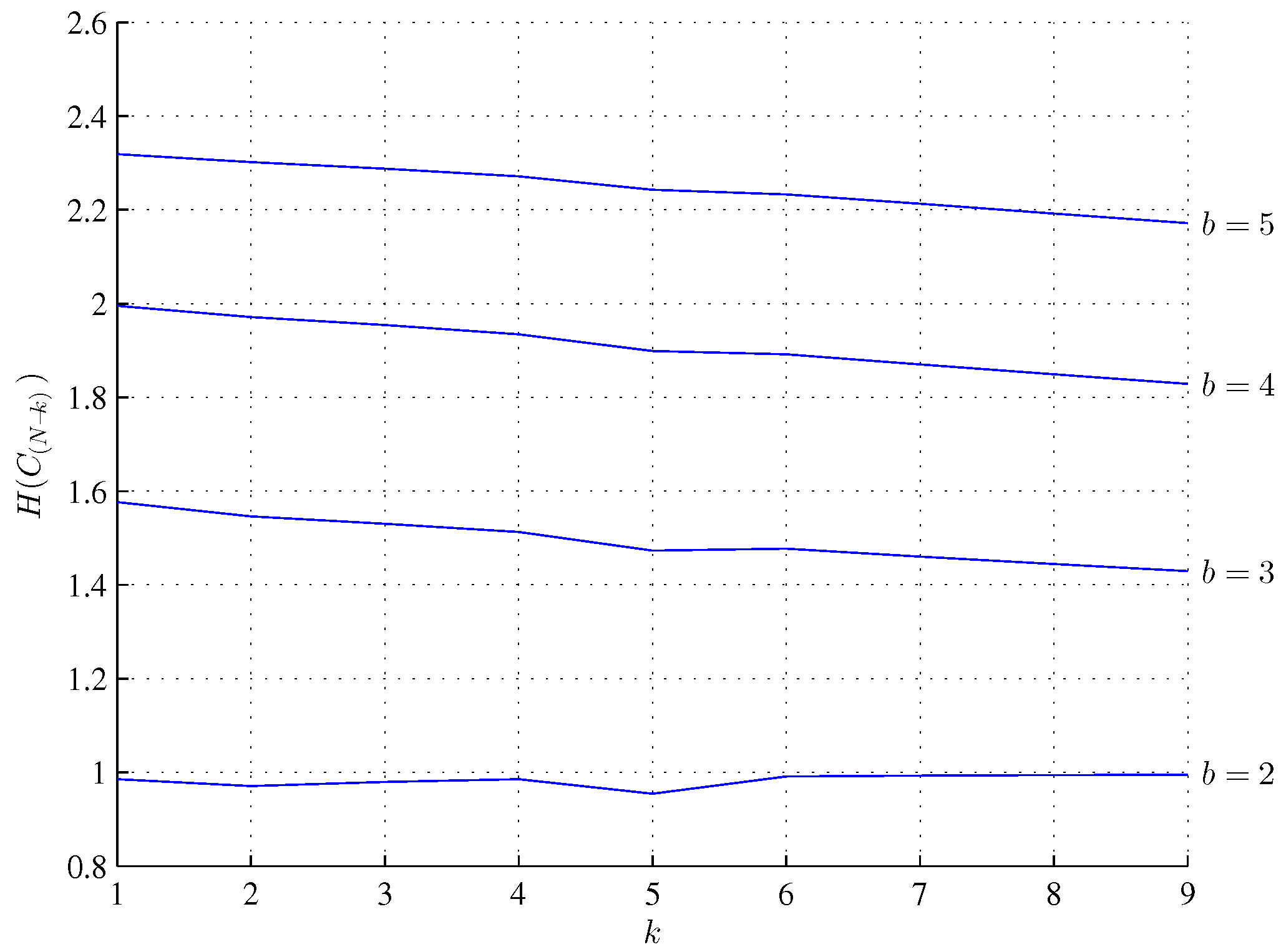
The entropies (
30) and (
36) are shown in
Figure 1. Radix
is the smallest one at which the entropy (
36) is a monotonically decreasing function. For
there is a local entropy minimum for
and for
an additional local entropy minimum for
.
Conjecture 16 (
).
If and then
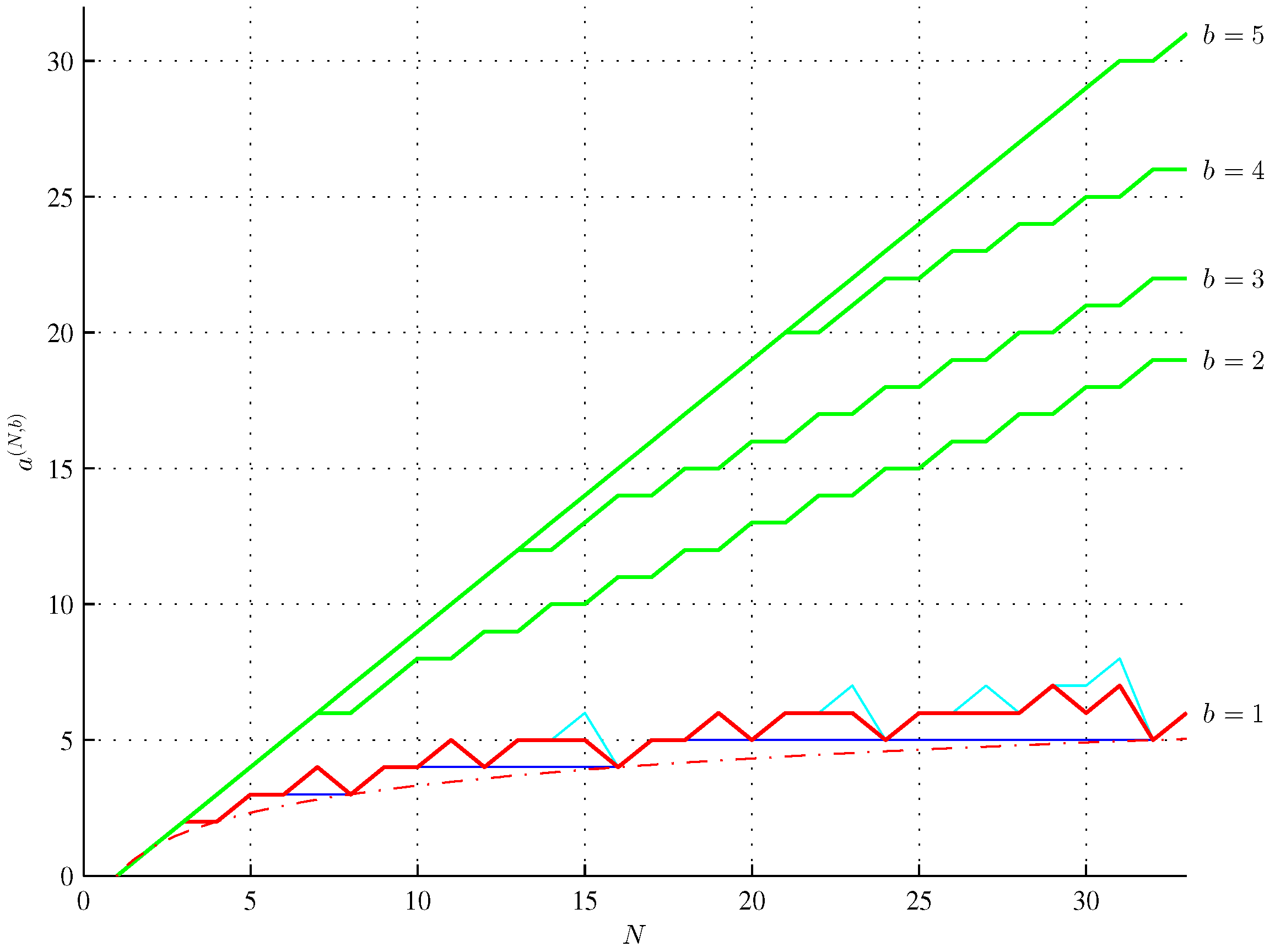
where
In other words, if , then ASI increases by one, where N increases by two ( are triangular numbers, OEIS A000217).
First, we note that maximum ASI must rise. If it were constant for
, then at some even larger
N it would inevitably become lower than the minimum ASI bound 2 which also rises, and this would be a contradiction. W.l.o.g. we aim to prove this conjecture for
. We note that inserting any doublet into a
string (
A19) at any position creates a triplet. Using the equation (
10) of Theorem 10 we have
for any step
s if only
. Now, assume that
,
and
,
. Then
The proof of the Conjecture 16 must show the conditions for the equations (
40) and (
41) to hold. We note that the assumption used in the equation (
41) is valid only for
and
. The bounds of Theorems 14 and 15 and Conjecture 16 are illustrated in
Figure 2.
The results thus far led us to a simple method of determining the ASI of a maximum ASI and a minimum ASD string and strengthened our Conjectures 3 and 4 stated in the previous study [
9]. The method is based on unique
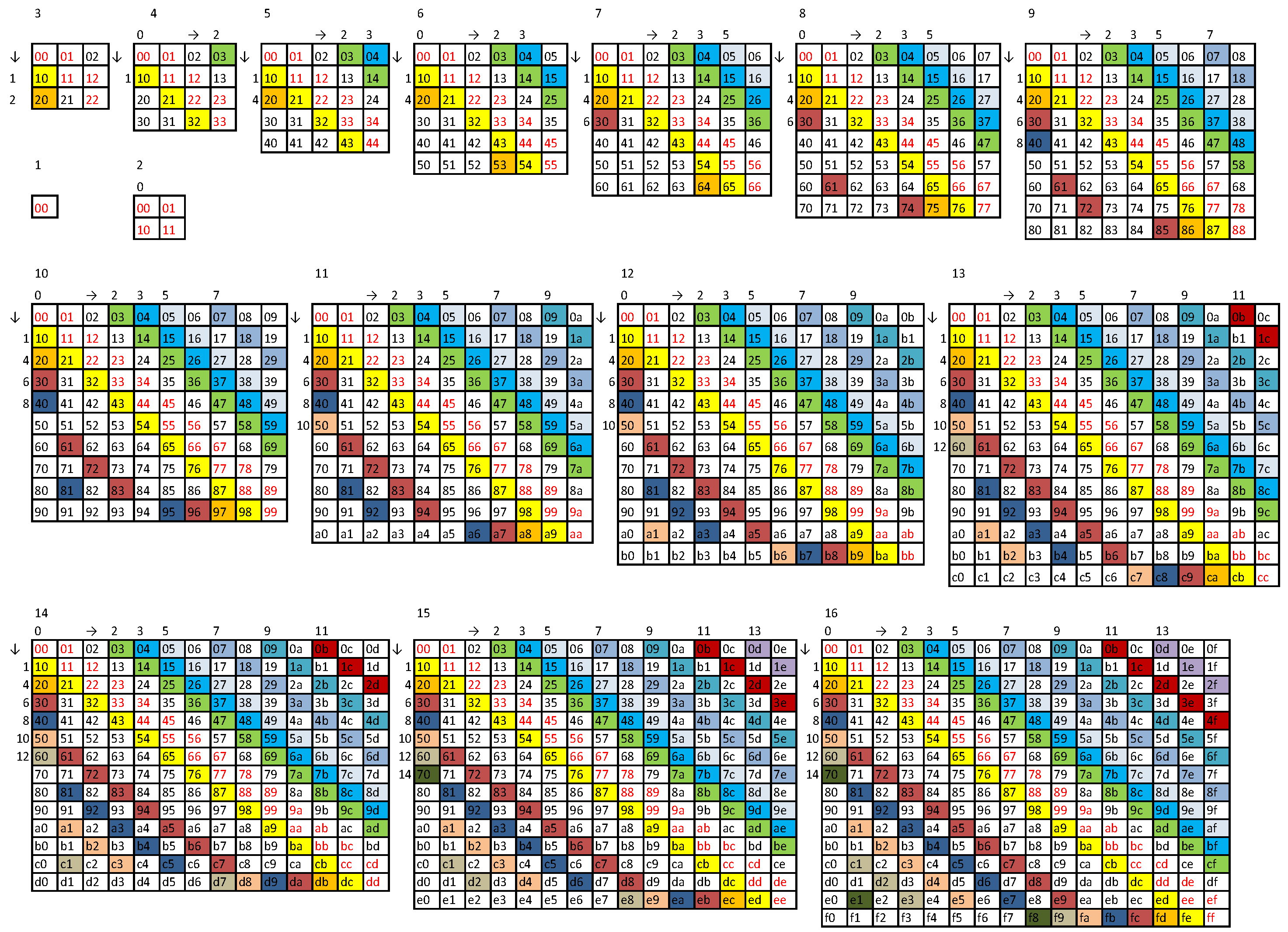
-plets and powers of two, as shown in
Table 1. First, a maximum ASI string is sequenced, every two symbols to find the number
of unique adjoining doublets
. In particular, a
string (
A3) or (
A4) contain the maximum of
unique adjoining doublets, a
string (
A13) contains the maximum of
unique adjoining doublets, and so on. In general, a
string contains the maximum of
unique adjoining doublets, where
is given by the relations (
28) or (
33), which is independent of
k.
Subsequently, these doublets form unique adjoining quadruplets, quadruplets form unique adjoining octuples, and so on depending on the length of the string N and the radix b, as there can be at most unique -plets. The columns "last " indicate if the assembled string should be terminated with a single substring of length in descending order. The empty fields in the respective columns for indicate that a given substring can be interpreted as either a "regular" single substring or a last substring if .
For example, the
string (
A20) of length
for
can be assembled as
Similarly, the
string (
A3) of length
for
can be assembled, as shown in
Table 1 as
For
and for other small
N this combinatorics is valid also for
, where obviously
. For example, the string of length
can be assembled in six steps as
However, this is the 1
st exception for
as the ASI of this string is five if it is assembled using doublet
and triplet
. For
the method produces OEIS
A014701 sequence corresponding to the number of steps to reach 1 starting from
and assigning
if
is odd and
otherwise.
We further note that the method illustrated in
Table 1 cannot be used to construct the maximum ASI string. For example, both the following two distributions of doublets for
satisfy the distributions of
Table 1. However, only the left one correctly reflects the maximum ASI of the assembled string.
as the right one can be assembled in four steps with
. Similarly, only the top distribution of doublets below correctly reflects the maximum ASI of the assembled string for
as the bottom one can be assembled in six steps with
. Furthermore, this method tends to exaggerate the estimated maximum ASI value, that is,
where
is the ASI of a string
determined by the method illustrated in
Table 1. For example, the first six strings below contain four unique doublets instead of the required three. Therefore
Further research should consider researching the formula equivalent to (
28) that captures a quadruplet repetition, similarly as
captures a doublet repetition.