Submitted:
14 April 2025
Posted:
16 April 2025
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
1.1. Koide’s Mass Formula
1.2. Interpretation by Carl A. Brannen
1.3. Brannen’s Neutrino Mass Hypothesis
1.4. Constructing Two Three-Dimensional Mass Models
2. Method
2.1. Construction of the Neutrino Three-Dimensional Mass Models
2.1.1. Case of the Combination
2.1.1.1. Vectors and Dot Products
2.1.1.2. Initial Coordinates
2.1.1.3. Rotation in the -Plane
2.1.1.4. Rotation in the -Plane
2.1.1.5. Rotation in the -Plane
2.1.2. Case of the Combination
2.1.2.1. Vectors and Dot Products
2.1.2.2. Initial Coordinates
2.1.2.3. Rotation in the -Plane
2.1.2.4. Rotation in the -Plane
2.1.2.5. Rotation in the -Plane
3. Result

4. Discussion
4.1. Correspondence to CP Violation
4.2. Product with the Tribimaximal Mixing Matrix
4.3. Neutrino Oscillation
4.3.1. Probability Calculation
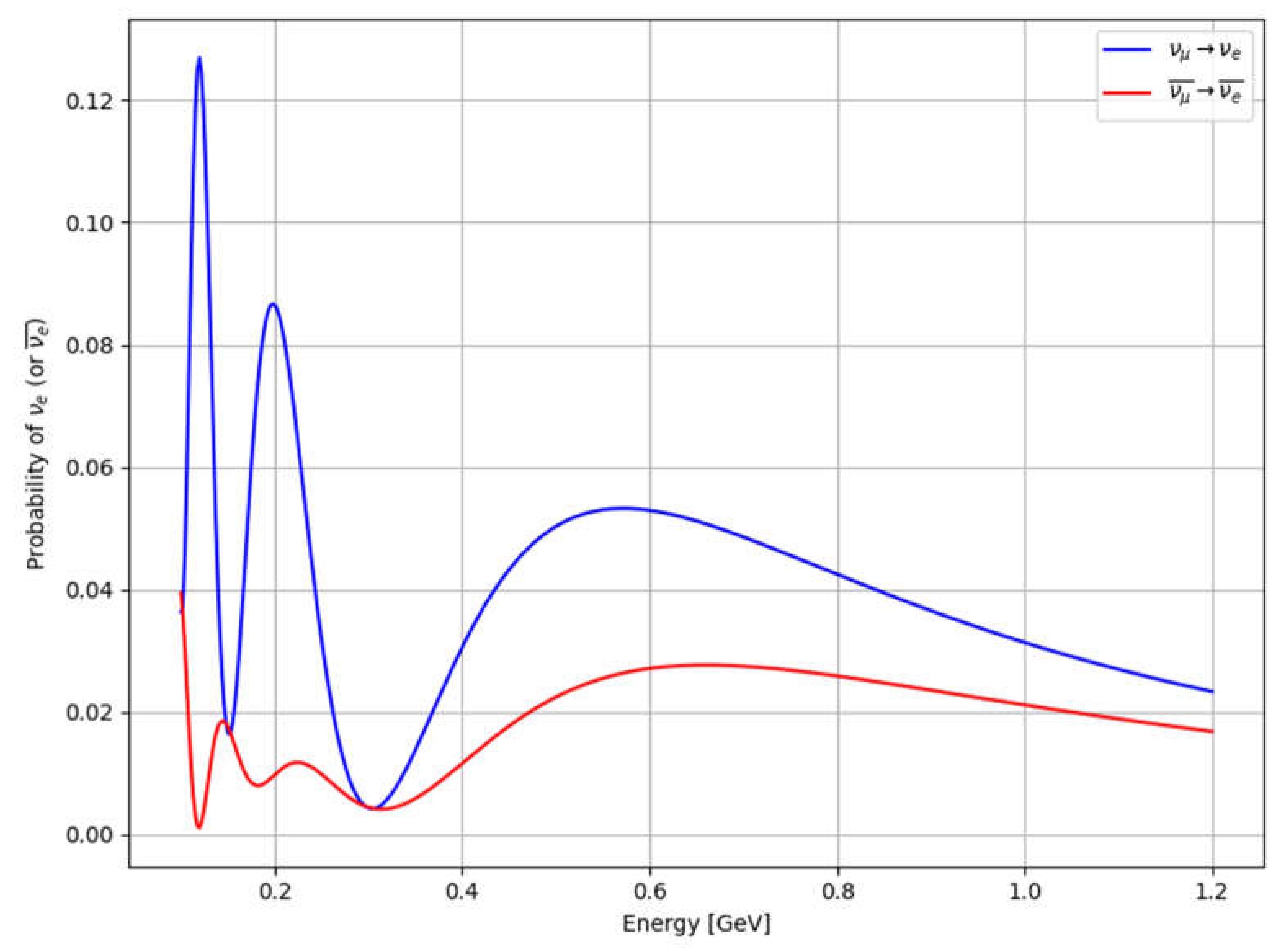
4.3.2. Energy Distribution of the Muon (Anti-)Neutrino Beam
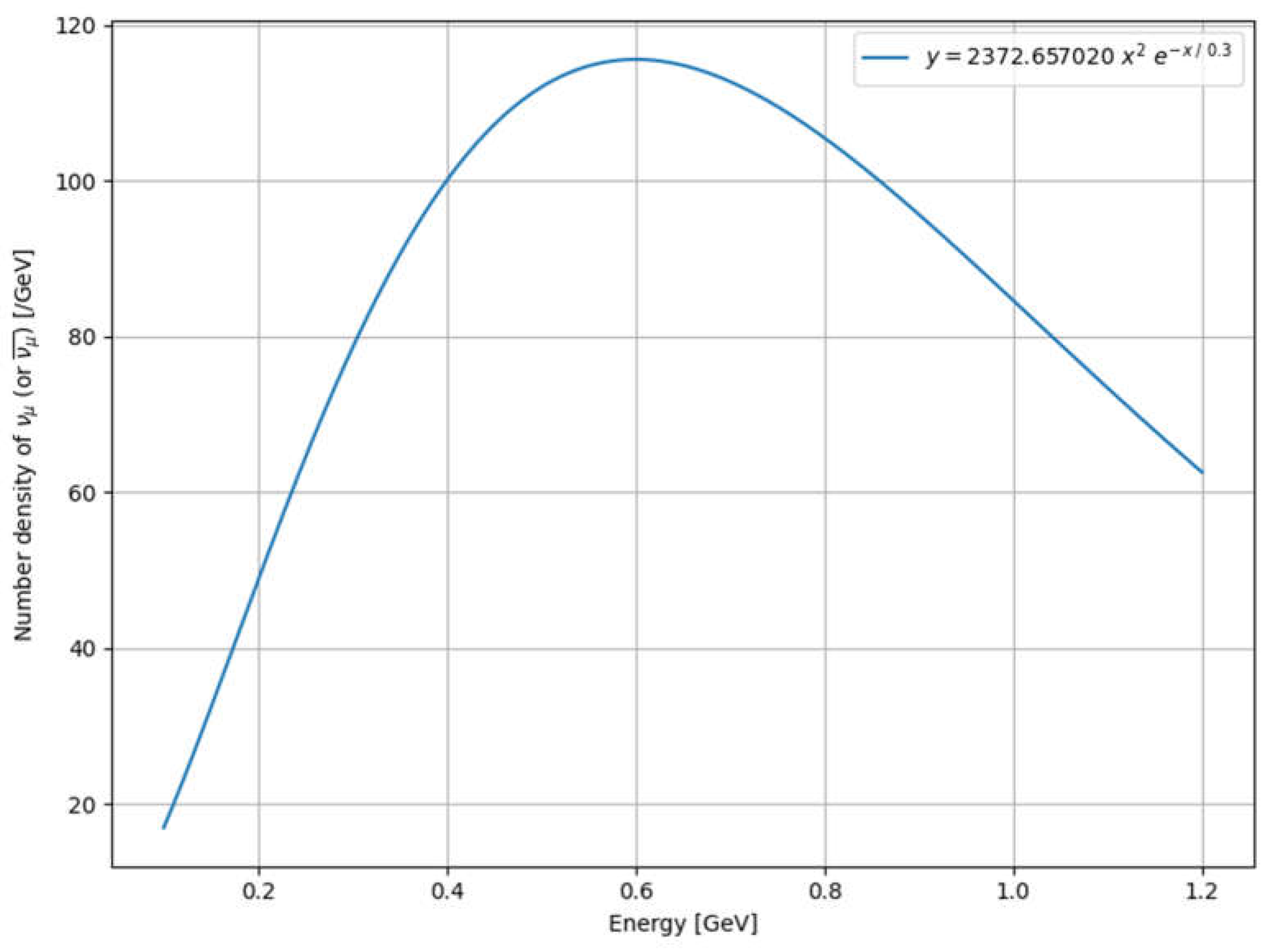
4.3.3. Probability Density and Expected Number of (Anti-)Neutrinos
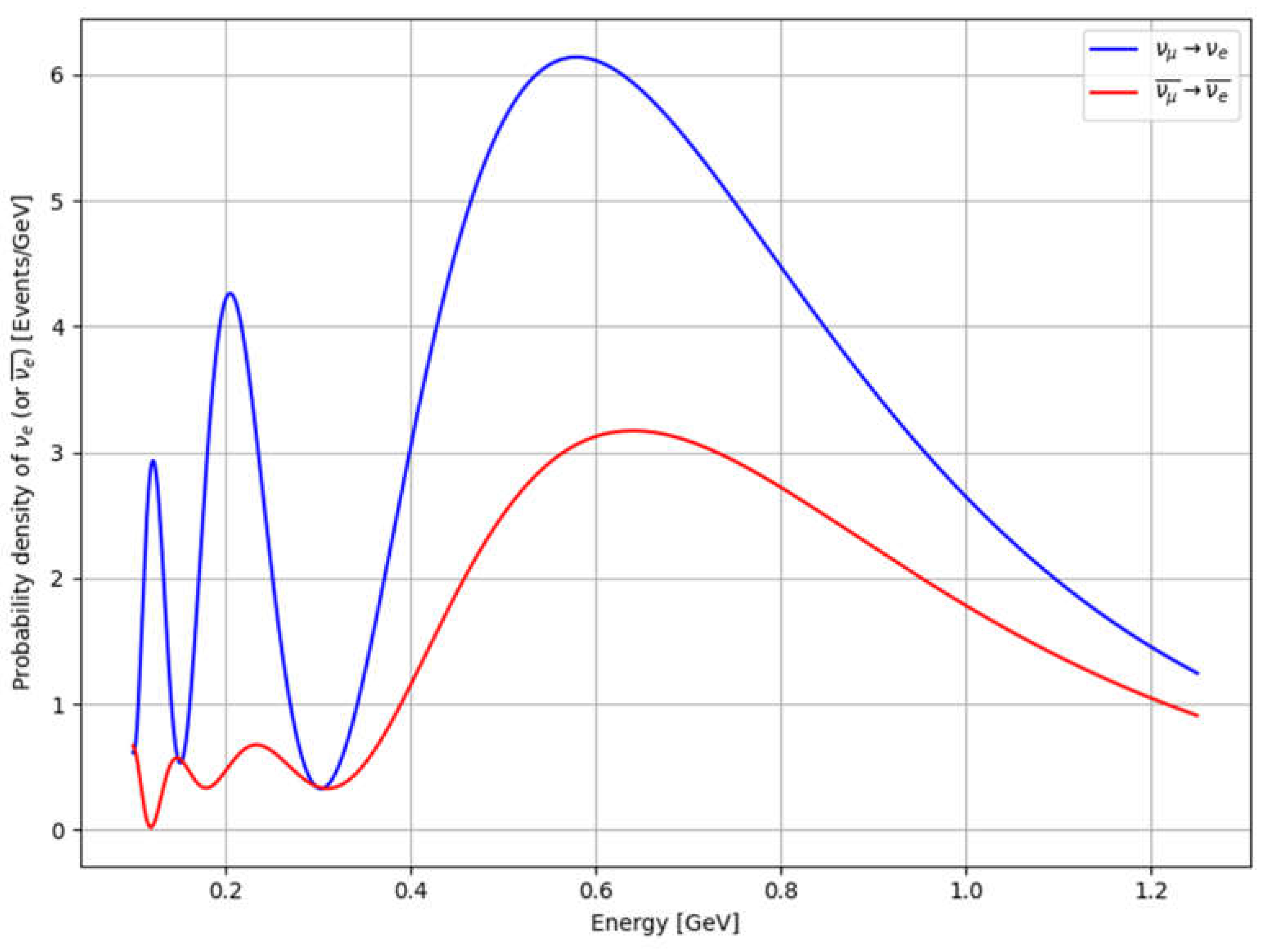
5. Conclusion
Acknowledgements
Revision Note
References
- Koide, Y. “Fermion-Boson Two Body Model of Quarks and Leptons and Cabibbo Mixing. ” Lettere al Nuovo Cimento 1982, 34, 201–206. [Google Scholar] [CrossRef]
- Koide, Y. “A Fermion-Boson Composite Model of Quarks and Leptons. ” Physics Letters B 1983, 120, 161–165. [Google Scholar] [CrossRef]
- Harari, H. , Haut, H. , & Weyers, J. “Quark Masses and Cabibbo Angles.” Physics Letters B 1978, 78, 459–461. [Google Scholar]
- Brannen, C. A. (2006). “The Lepton Masses.” Brannen Works, Retrieved from https://brannenworks.com/MASSES2.pdf.
- Amsler, C. , et al. (Particle Data Group). “Review of Particle Physics.” Physics Letters B 2008, 667, 1–1340. [Google Scholar] [CrossRef]
- Maki, Z. , Nakagawa, M. , & Sakata, S. “Remarks on the Unified Model of Elementary Particles.” Progress of Theoretical Physics 1962, 28, 870–880. [Google Scholar] [CrossRef]
- Christenson, J. H. , Cronin, J. W., Fitch, V. L., & Turlay, R. “Evidence for the 2π Decay of the Meson.” Physical Review Letters 1964, 13, 138–140. [Google Scholar] [CrossRef]
- Kobayashi, M. , & Maskawa, T. “CP-Violation in the Renormalizable Theory of Weak Interaction.” Progress of Theoretical Physics 1973, 49, 652–657. [Google Scholar] [CrossRef]
- Harrison, P. F. , Perkins, D. H., & Scott, W. G. “Tri-Bimaximal Mixing and the Neutrino Oscillation Data.” Physics Letters B 2002, 530, 167–173. [Google Scholar] [CrossRef]
- Esteban, I. , Gonzalez-Garcia, M. C., Maltoni, M., Schwetz, T., & Zhou, A. (2024). “Leptonic Mixing Matrix.” NuFIT 5.3, Retrieved from http://www.nu-fit.org/?q=node/278.
- Pontecorvo, B. (1957). “Inverse Beta Processes and Nonconservation of Lepton Charge.” Zhurnal Éksperimental’noĭ i Teoreticheskoĭ Fiziki 1957, 34, 247–250. Reproduced and translated in Soviet Physics JETP 1958, 7, 172–175. [Google Scholar]
- Abe, K. , et al. (T2K Collaboration) (2017). “Measurement of Neutrino Oscillation Parameters from the T2K Experiment.” Physical Review Letters 2017, 118, 151801. [Google Scholar] [CrossRef]
- T2K Collaboration. (2023). “Search for CP Violation in Neutrino Oscillations.” Preprint available at arXiv:2310.11942v2.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




