| Contents |
| |
|
1. |
Introduction.......................................................................................................................................................................... |
3 |
| |
|
2. |
Theoretical Framework.......................................................................................................................................................... |
4 |
| |
2.1. Glossary of Key Terms.......................................................................................................................... |
4 |
| |
2.2. The Correlationhedron.......................................................................................................................... |
5 |
| |
2.3. Correlationhedron Axioms (A1-A6)............................................................................................................... |
6 |
| |
2.4. The Footballhedron............................................................................................................................. |
7 |
| |
2.5. Footballhedron Axioms (A7-A8).................................................................................................................. |
8 |
| |
2.6. Linking R and ω to Quantum Information Principles............................................................................................. |
9 |
| |
|
3. |
Phenomena................................................................................................................ |
9 |
| |
3.1. Lorentz Symmetry from Correlation Rotation..................................................................................................... |
9 |
| |
3.2. Emergent Gravitational Dynamics................................................................................................................ |
11 |
| |
3.3. Correlation Horizons as Causal Boundaries...................................................................................................... |
12 |
| |
3.4. Ultraviolet Cutoff and Discreteness............................................................................................................ |
13 |
| |
|
4. |
Discussion.................................................................................................................................................................. |
14 |
| |
4.1. Relation to Other Frameworks................................................................................................................... |
15 |
| |
4.2. Predictions and Experimental Tests............................................................................................................. |
15 |
| |
4.3. Future Directions.............................................................................................................................. |
16 |
| |
|
5. |
Conclusion.................................................................................................................................................................. |
17 |
|
A. |
Informational Action and Emergent Einstein Equations................................................................................. |
18 |
|
A.1. Emergent Einstein Equations from Correlation Density................................................................... |
19 |
|
B. |
Lorentz Group from Hyperspherical Rotations................................................................................. |
19 |
|
B.1. Pseudo-Euclidean Embedding and Lorentz Boosts................................................................... |
19 |
|
B.2. Composition of Observer Projections................................................................... |
20 |
|
C. |
UV Cutoff from Finite Granularity................................................................................. |
20 |
|
D. |
References................................................................................. |
21 |
1. Introduction
The search for a quantum theory of gravity remains a central challenge in theoretical physics. Numerous frameworks have been developed, ranging from loop quantum gravity and causal dynamical triangulations [
1,
2] to holographic dualities relating entanglement and geometry [
3,
4] and tensor-network models of emergent spacetime [
5]. A common thread in these modern approaches is that spacetime geometry is not fundamental but emerges from more primitive quantum degrees of freedom. Particularly compelling evidence now links quantum entanglement directly to the fabric of spacetime [
3,
4,
5,
6]. For example, in holographic dualities (AdS/CFT), spatial connectivity and gravitational dynamics are explicitly related to entanglement patterns in a dual quantum theory [
4]. Similarly, tensor network models such as MERA represent spatial geometry through entanglement renormalization [
5]. Such insights have motivated conjectures equating wormhole geometries with entangled states (ER=EPR) and inspired the perspective that spacetime itself is fundamentally constructed from quantum entanglement [
6,
7,
8].
Complementary to these ideas are information-geometric approaches, which define geometry directly on spaces of quantum states or probability distributions [
9,
10]. The Fisher information metric, for instance, provides a natural Riemannian structure on probability manifolds, and analogous constructions apply to quantum state spaces. Such approaches suggest spacetime might naturally emerge as an “information geometry” derived from underlying quantum structures rather than existing as a fundamental manifold.
In this work, we propose a novel framework in which
quantum correlations alone give rise to emergent spacetime and gravity. Extending a recent proposal by Russo [
11], we represent the complete set of correlation functions of a universal quantum state as a single geometric object, the
correlationhedron. Each observer, characterized by their measurement basis or reference frame, perceives different lower-dimensional “slices” of this universal correlation structure, interpreting each slice as their emergent spacetime. In essence, space and time arise observer-dependently from an underlying quantum correlation geometry. Crucially, geometric features of the correlationhedron—such as correlation density and distribution—translate directly into physical phenomena, including spacetime curvature and causal structures.
The initial version of this correlation-based framework introduced core axioms relating correlation structures to emergent geometry [
11]: for example, that the universal state’s correlations are fully embedded within the correlationhedron (akin to a holographic completeness), that observers’ measurements project this structure onto lower-dimensional manifolds, and that local clustering of correlations reproduces locality consistent with area laws for entanglement entropy [
12]. Furthermore, variations in correlation density naturally induce spacetime curvature (reflecting entanglement gradients as gravitational sources [
13]). Additionally, the
entanglement-time duality principle equates temporal ordering and quantum entanglement structure [
14].
However, the static correlationhedron alone did not incorporate dynamical or relativistic features explicitly. Here, we significantly extend this framework by introducing a crucial new assumption: that the correlationhedron has spherical topology and undergoes uniform rotation in correlation space. This structured and rotating correlationhedron, termed the footballhedron due to its spherical geometry and optional discrete tessellation, generates rich emergent phenomena. A universal rotation rate establishes an invariant correlation speed (analogous to the speed of light), yielding Lorentz symmetry for all observers. The rotation defines canonical time evolution of correlations. This enables the construction of an emergent metric whose dynamics directly reproduce Einstein’s gravitational field equations. Moreover, regions devoid of correlations produce intrinsic causal boundaries (“correlation horizons” analogous to black hole horizons, without requiring singularities). Additionally, a finite tessellation (an optional assumption) naturally introduces informational granularity, setting an intrinsic ultraviolet cutoff at the Planck scale and resolving short-distance divergences.
In short, the rotating footballhedron construction proves essential: the static correlationhedron alone cannot produce the relativistic invariances or gravitational dynamics observed in nature.
The paper is structured as follows. In
Section 2, we formalize the footballhedron model and the emergent observer-dependent spacetimes.
Section 3 explicitly demonstrates how key relativistic and gravitational phenomena—including Lorentz symmetry, Einstein equations, correlation horizons, and UV cutoffs—naturally arise from our framework.
Section 4 discusses broader implications, including observer-dependent reality, emergence of the arrow of time, and relations to other quantum gravity frameworks.
Section 5 concludes with a summary and outlines directions for future research.
2. Theoretical Framework
2.1. Glossary of Key Terms
(Quantum-state vector) Normalized pure state in Hilbert space , satisfying .
(Correlationhedron) Convex subset of the correlation space C, consisting of all two-point correlation vectors realizable by .
(Correlation vector) Components given by
for a chosen set of observables
.
(Correlation speed) Invariant correlation speed set by the footballhedron radius R and rotation rate . Analogous to the speed of light in emergent spacetime.
(Observer projection) Smooth map
selecting the subset of correlation components accessible to observer
, yielding their emergent manifold
.
(Emergent spacetime manifold) d-dimensional (typically ) manifold , interpreted as the observer’s effective spacetime.
(Quantum-state density) Density operator on , , with .
(Correlation/clock density) Push-forward scalar density on
, defined by
where
is the uniform volume measure on
.
1
(Emergent metric) Metric on
from the inverse Hessian of
:
MERA (Multiscale Entanglement Renormalization Ansatz) Tensor-network ansatz organizing entanglement across scales, often used to model emergent geometry.
Fisher information metric Riemannian metric on a statistical manifold given by the Hessian of the negative log-density, underpinning the emergent metric construction.
Footballhedron Idealized, discretized correlationhedron of radius
R uniformly rotating at angular frequency
in correlation space, constructed via a normalization to a fixed radius as described in
Sec. 2.4.
2.2. The Correlationhedron
We consider a closed quantum system described by a pure state
in a Hilbert space
. Here we denote the corresponding density operator by
Let
be a basis of observables (Hermitian operators) on
. The
correlation vector of the state
2 is defined as
. Equivalently, one may write
The space of all such correlation vectors (for all possible states) is an abstract high-dimensional
correlation space C. Within
C, the particular subset of correlation vectors that are achievable by the specific state
forms a convex geometric object
, which we call the
correlationhedron:
This represents the set of all correlation vectors consistent with the state. By construction,
is convex, since any probabilistic mixture of states yields correlation vectors that lie between those of the pure states (due to the linearity of expectations). In fact,
can be thought of as a high-dimensional convex polytope (or curved convex body) embedded in
C, much like the set of quantum-mechanically allowed correlation outcomes generalizes the classical Bell polytope of allowed local hidden-variable correlations. (Indeed, the famous Tsirelson bound restricting quantum correlations can be viewed as a facet of such a polytope in suitable settings [
15,
16].) Our correlationhedron concept thus encompasses and extends earlier ideas of convex quantum constraint polytopes.
Geometrically, one can picture as a kind of high-dimensional “shape” encoding all relational information of the state. A priori, this shape can be very complex. However, we will often idealize it as a smooth n-dimensional hypersurface for simplicity.
Observer Projections and Emergent Spacetime
To connect correlation structures explicitly to physical observations, we introduce observer-dependent projections.
Crucially, different
observers correspond to different ways of slicing or projecting
. An observer (characterized by a choice of macroscopic frame or a set of accessible observables) effectively “sees” only a subset of the correlations in
. Each observer’s measurement constraints or choice of reference frame corresponds to selecting a particular subset of correlation components from
. This subset, determined by the observables accessible to the observer, defines their lower-dimensional emergent spacetime manifold
. Formally, we define an observer’s projection as a map
, where
is a four-dimensional (3+1) manifold corresponding to that observer’s emergent spacetime. Here
labels the observer’s parameters (such as their choice of basis, motion, etc.). The map
can be thought of as restricting the full correlation vector
to the components relevant to that observer. For example, an observer might only measure a limited set of commuting observables (defining their local spatial coordinates) and use a particular internal degree of freedom as a clock. This will pick out certain components of
(e.g. spatial correlators and time correlations with the clock subsystem) and ignore others. The result is that the observer perceives an effective “world”
with fewer dimensions. In general,
can be viewed as a foliated manifold (space+time) produced by the projection. Intuitively, the observer’s measurements carve out a slice of the correlationhedron, and this slice is then interpreted by the observer as their physical space and time. Different inertial observers correspond to rotated versions of this projection (see
Appendix B), so their emergent spacetimes are consistently related by Lorentz transformations.
Concrete constructions of for realistic quantum systems beyond simplified toy models remain speculative and require further investigation.
Projection Admissibility
For concreteness, recall from Ref.[
11] that any admissible observer projection
must satisfy:
Positivity preservation: The reduced state on the observer’s subalgebra remains positive semidefinite, so that corresponds only to physical correlation data.
Smoothness: is on , ensuring that all first and second derivatives exist and the emergent metric is well defined.
Full-rank Jacobian: The Jacobian has rank 4 almost everywhere, guaranteeing is locally a smooth 4-manifold.
Since all observers are ultimately looking at the same underlying
(the same state’s correlations), their emergent spacetimes must be related. In fact, one of the original postulates of this framework was that
for any valid quantum state, an observer-dependent projection exists that yields a consistent spacetime (including approximate notions of locality and causality). This
observer-dependent emergence is reminiscent of relational interpretations of quantum mechanics [
17], wherein properties of a system (here, the geometry of spacetime) exist only relative to an observer’s frame.
2.3. Correlationhedron Axioms (A1-A6)
We summarize the key principles (axioms) of the static correlation-to-spacetime correspondence as follows, adapting from Ref. [
11]:
A1. Completeness: All physically realizable correlations of the universal wavefunction are contained in . (This echoes the holographic idea that all information of the state is encoded in its correlations.)
A2. Positivity: All correlation functions derive from a positive semi-definite density operator. This implies is a convex body (through Minkowski sum of extremal correlation outcomes) and ensures consistency with quantum constraints (e.g. no correlator exceeds Tsirelson bounds).
A3. Observer Slicability: Any observer (defined by a set of accessible observables or a reference frame) projects
to a lower-dimensional manifold
. Different choices of
(observer perspective) generally yield different emergent manifolds
, which we interpret as different observers’ spacetimes.
is
on
, ensuring that all first and second derivatives exist so that the Hessian
is well-defined (allowing construction of a valid emergent metric, Eq.
2).
A4. Locality Emergence: In sufficiently small regions of
, clusters of strongly correlated variables give rise to decoupled substructures, allowing an approximate notion of locality in
. This is consistent with the observation of entanglement entropy obeying area-laws in many low-energy states [
12].
A5. Curvature from Correlation Gradients: Variations in the density of correlation points within lead to curvature in the emergent spacetime. Intuitively, where the correlationhedron is “thinner” or less dense, the induced geometry for an observer curves inward analogous to how mass-energy curves spacetime in general relativity. (This principle anticipates that Einstein’s equations will emerge later, linking correlation gradients to the Einstein tensor.)
A6. Entanglement–Time Duality: Quantum entanglement and temporal ordering are two complementary manifestations of the same underlying structure. In particular, if the global state factorizes into a clock subsystem ⊗ a system, the entanglement between them can serve as an emergent time parameter [
14]. More generally, the buildup of entanglement correlates with the forward progression of an emergent time coordinate for each observer.
2.4. The Footballhedron
We now specialize the correlationhedron by adding structure and dynamics through two new axioms (A7-A8), creating the footballhedron, a structured and rotating correlationhedron. These are instrumental to incorporate relativity as well as intrinsic information granularity.
We emphasize that the spherical embedding and uniform rotation assumptions, while simplifying, are motivated by symmetry and periodicity principles common in quantum recurrence scenarios and information geometry frameworks. Although idealized, these assumptions help isolate the essential correlation-to-geometry mechanism clearly.
Spherical Topology
For simplicity and conceptual clarity, we idealize the correlationhedron by embedding it onto an
n-sphere
of fixed radius
R. This embedding is explicitly achieved by normalizing correlation vectors as
where
is an uncorrelated reference point in correlation space, and
denotes the standard Euclidean norm. Thus, all relevant correlation vectors lie at the same radius, ensuring a well-defined spherical geometry. Note that this hyperspherical embedding focuses on the directional structure of
at fixed radius. The actual correlationhedron
remains a convex body in the full correlation space, but here we consider the idealized scenario where all points lie on a common-radius spherical surface for symmetry. This simplification sacrifices strict Euclidean convexity of the surface itself, but preserves a one-to-one mapping to the extremal correlation configurations of the convex set.
Rotation
We start by assuming the hypersphere rotates uniformly around one axis. We subsequently link the rotation frequency and radius explicitly to fundamental quantum information principles. A rotation axis defines a global “timelike” direction through
, providing a universal time parameter for all observers. Importantly, this global timelike axis is unobservable as a preferred frame by any emergent observer, as each observer sees identical local physics due to symmetry. For a rotation with angular frequency
, if we take
R to be the correlation-space radius of
(under the hyperspherical idealization), then this rotation yields a characteristic speed
. We treat
c as a universal constant—indeed it plays the role of the invariant speed of light in the emergent spacetime. All observers, by virtue of observing slices of the same rotating footballhedron, will measure this same
c as the maximum signal velocity. The fixed rotation axis (a preferred direction in
C) corresponds to a global timelike axis (the direction of increasing entanglement) that each observer associates with the flow of time in their projected world. Importantly, because the footballhedron is homogeneous and rotates at a constant rate, no observer’s frame is singled out; the situation is fully analogous to the relativity of inertial frames, with
c providing the conversion between space and time coordinates for all observers. In other words, the uniform rotation ensure that all inertial frames share the same invariant
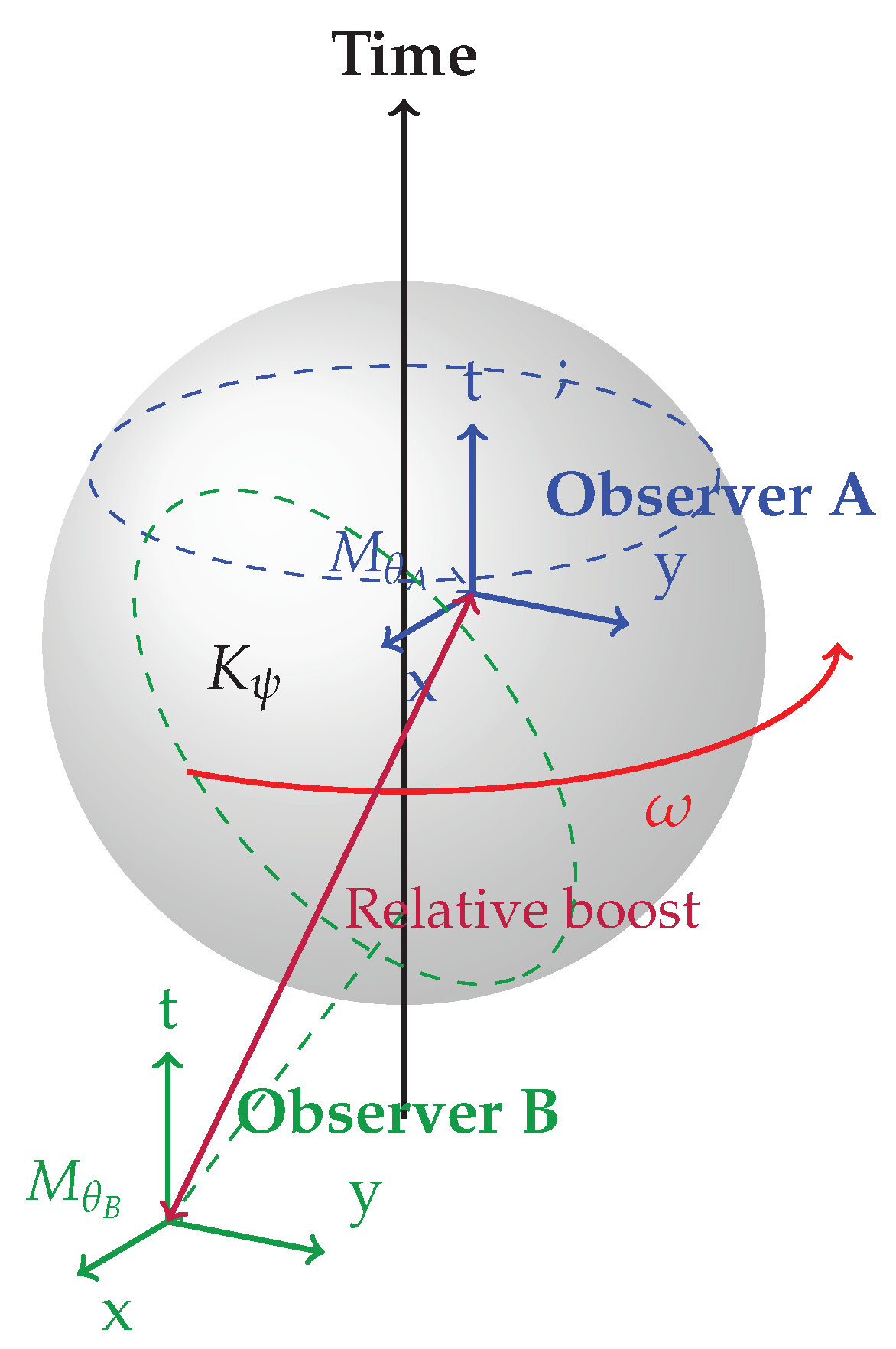
c (enforcing Lorentz symmetry in the emergent spacetime). See
Figure 1 for illustration.
For an intuition, consider a simplified analogy of a sphere rotating in 3D space. Different observers, analogous to taking slices at different angles, perceive different time and spatial projections, naturally generating Lorentz transformations.
To preserve the simplicity of this rotation model, we assume that retains its shape (apart from small perturbations corresponding to interactions, addressed later) and only its orientation in C changes with time.
Finite Tessellation
Finally, adding finite discretization, an intrinsic ultraviolet cutoff (on the order of the Planck length) is built into the emergent physics. A similar finite-information assumption underlies many approaches to quantum gravity that invoke a minimal length or a discrete spacetime structure. The finite granularity assumption is motivated by information-theoretic limits (Bekenstein bound) [
18], holographic principles, and analogies from discrete quantum gravity frameworks (loop quantum gravity, causal sets). These suggest fundamental limits on information content and resolution, naturally introducing a Planck-scale granularity.
2.5. Footballhedron Axioms (A7-A8)
The following two axioms define the footballhedron as a rotating, multi-faceted correlationhedron of spherical topology, reminiscent of a football:
A7. Shape and Rotation: The correlationhedron maintains a fixed spherical topology and undergoes uniform rotation at a constant angular frequency in correlation space C. This rotation introduces a universal correlation speed , analogous to the speed of light.
A8. Finite Tessellation (Optional) has a finite angular resolution or a discrete tessellation into a large but finite number of elementary patches or “facets”. This finite subdivision introduces an intrinsic informational granularity (reflecting a fundamental limit on how finely correlations can be distinguished), setting a fundamental ultraviolet cutoff at the Planck-scale in the emergent spacetime.
Smoothness (Axiom A7) is understood as an idealized continuum limit, while finite tessellation (Axiom A8) introduces intrinsic granularity at short scales. Reconciling these limits explicitly involves a coarse-graining procedure discussed further in
Appendix C.
2.6. Linking R and to Quantum Information Principles
Initially, rotation is introduced as a simplifying assumption to clearly illustrate the correlation-to-geometry mechanism. However, we conjecture this rotation emerges intrinsically from quantum recurrence. A rigorous derivation remains open and is an important direction for future work.
Crucially, while we initially introduce the footballhedron as rotating with an angular frequency , this rotation is not an external or arbitrary input. Instead, it emerges naturally and necessarily from the intrinsic quantum dynamics of the universal wavefunction itself. The periodic recurrence of quantum probabilities and correlations sets a fundamental cycle, intrinsically determining the angular frequency .
This profound connection implies that the rotation period of the footballhedron, and therefore the invariant speed , is fully fixed by the underlying quantum structure. Thus, is removed as an independent degree of freedom.
The state undergoes cyclical evolution in a larger state space such that its correlation properties periodically revisit the same configuration (up to symmetry transformations). The periodic recurrence assumption is an idealization useful for conceptual clarity. Realistic quantum systems might exhibit only approximate recurrence patterns. From a fundamental perspective, this ensures a stationary (time-symmetric and unitary) evolution. Yet, from the perspective of an observer projecting onto , there naturally emerges an apparent passage of time and dynamical evolution of fields.
We interpret as the intrinsic angular frequency associated with this fundamental quantum recurrence—effectively a universal quantum clock frequency. Consequently, the combination emerges as a fundamental limit on correlation propagation speed, analogous to a no-signaling constraint from quantum information theory.
Similarly, the correlation-space radius R is not merely an arbitrary geometric scale. Instead, it directly encodes the total information content of the universal quantum state. By normalizing correlation vectors, we embed the correlationhedron onto a sphere of radius R, ensuring all correlation states lie at equal “informational distance” from an uncorrelated reference point. Thus, the radius R represents the maximum achievable correlation strength or, equivalently, the total informational capacity of the universal quantum state.
This identification remains conceptual; a rigorous quantitative relationship between R and entropy or Hilbert-space dimension is a topic for future research.
3. Phenomena
3.1. Lorentz Symmetry from Correlation Rotation
We now explicitly demonstrate how uniform rotation of the correlationhedron naturally leads to Lorentz symmetry.
A key consequence of Axiom 7 is that the rotating correlationhedron on
endows every inertial observer with the same invariant correlation speed:
Two observers whose emergent spacetimes move at relative velocity
v (with
) correspond to projections
and
related by a rotation of
. In their local coordinates this rotation induces the standard Lorentz boost in the
x-direction:
with y’ = y, z’ = z.
Theorem 1 (Lorentz Transformations Induced by Correlationhedron Rotations).
For any two inertial observers differing by relative velocity , there exists a rotation by rapidity φ in a two-plane of (one timelike, one spacelike) such that:
and the induced map on emergent coordinates is exactly the Lorentz boost .
Intuitively, this theorem shows that a simple geometric rotation in correlation space precisely recovers Lorentz transformations. This establishes a direct equivalence between symmetry in correlation structure and relativistic invariance in emergent spacetime, reinforcing the physical plausibility of our correlation-based approach.
Proof. A rotation by rapidity in the correlation space -plane corresponds precisely to a Lorentz boost, aligning one observer’s time-axis with that of the other. Setting reproduces the Lorentz transformations, while leaving unchanged. Closure and inversions follow naturally from the group properties of rotations on . □
Theorem 2 (Lorentz Invariance from Invariant Correlation Speed). All observer projections preserving the invariant speed yield emergent spacetimes related by transformations, thereby ensuring complete Lorentz symmetry.
Hence, the uniform rotation of the correlationhedron directly generates the Lorentz group on the emergent spacetimes, explicitly deriving special relativity purely from quantum correlation structure.
In effect, the emergent metric is Lorentzian with one timelike and three spacelike dimensions (Minkowski signature ), the single rotation axis providing the universal time direction.
Worked Example: Correlation Circle
As the simplest nontrivial illustration, consider the case
. Idealizing
as a circle:
rotating at constant angular frequency
:
Defining emergent coordinates:
a relative rotation by angle
between two observers gives:
Writing
with
, and using
,
, exactly yields the standard Lorentz boost:
This concrete example transparently demonstrates how the invariant speed c, enforced by a fixed rotation rate , naturally induces special relativity within the footballhedron geometry.
3.2. Emergent Gravitational Dynamics
We now show explicitly how gravitational dynamics, specifically Einstein’s equations, emerge from the underlying correlation structure.
Each observer’s projected spacetime
inherits a scalar density
from the correlationhedron
, quantifying the local abundance of correlation information at event
x. We define the emergent metric
3 This inverse-Hessian form parallels an information-geometry metric: if
is uniform the Hessian vanishes (yielding locally flat spacetime), whereas spatial variations in
produce curvature. In regions of smooth variation,
has Lorentzian signature with one timelike direction (aligned with correlation rotation) and three spacelike directions (tangential to the observer’s projection).
The dynamics of
arise from the fundamental consistency requirement that deformations in the correlation structure respect the contracted Bianchi identity,
This forces the introduction of a conserved stress-energy tensor built purely from
. A full derivation is given in
Appendix A.1, but the upshot is that the emergent metric satisfies
with
arising informationally from the correlation density itself, rather than from an independent matter sector, and
a coupling constant analogous to Einstein’s gravitational constant.
As demonstrated in
Appendix A.1, the single ansatz (
2), together with the contracted Bianchi identity
, suffices to reproduce the full Einstein field equations as a self-consistency condition on
.
Theorem 3 (Emergent Einstein Equations).
Let be given by Eq. (2). Then its Einstein tensor satisfies
where the stress-energy tensor emerges purely informationally as the variation of an effective action encoding correlation structure :
Proof. Detailed variational derivation provided in
Appendix A.
The effective informational action
is explicitly defined as:
where
R is the Ricci scalar,
is the gravitational coupling constant (matched to Newton’s constant), and
is a correlation-dependent informational Lagrangian. In the limit of smoothly varying correlation density (
), this precisely recovers standard Einstein gravity
. Continuum validity applies for length scales significantly larger than the intrinsic ultraviolet cutoff
.
Corollary 1 (Informational Origin of Stress-Energy Conservation). Since is invariant under reparametrizations of , it follows naturally that . Hence, the conservation of emergent stress-energy arises directly from diffeomorphism invariance of the underlying correlation structure.
All mathematical and physical consistency checks align precisely with standard general relativity:
The tensorial structure and symmetry of Einstein’s equations are preserved.
Covariant conservation emerges naturally from variational symmetry.
Newtonian and relativistic gravitational limits are consistently recovered.
Remark: Although we speak of a spherical correlationhedron (of radius
R) in the Euclidean correlation space, this same structure can be viewed in a
-dimensional pseudo-Euclidean embedding as a hyperboloid surface satisfying
. This formal embedding (
Appendix B) does not change the intrinsic spherical geometry, but introduces a timelike coordinate
such that a rotation about the
-axis corresponds to a Lorentz boost. In short, the footballhedron’s “sphere” in Euclidean space is equivalent to a hyperboloid in Minkowski space, which is how Lorentz transformations emerge from correlation rotations.
This demonstrates that Einstein’s equations arise naturally and necessarily as a projection consistency condition on the higher-dimensional, finite-resolution quantum correlation structure.
Thus, the familiar dualism—“spacetime tells matter how to move; matter tells spacetime how to curve”—is replaced by a unified informational principle: Both curvature and matter fields emerge simultaneously from the geometry and structure of quantum correlations.
As a concrete intuition, imagine a slight localized increase (“bump”) in correlation density . According to our emergent metric definition, this would manifest as curvature—much like how mass-energy induces curvature in general relativity. On the footballhedron, such a correlation “bump” corresponds geometrically to a small deformation on its otherwise spherical surface, illustrating the direct geometric interpretation of gravitational phenomena.
3.3. Correlation Horizons as Causal Boundaries
We now demonstrate how horizons—causal boundaries analogous to black hole horizons—arise purely from vanishing quantum correlations in our framework.
Let
represent the local correlation density on an observer’s emergent spacetime
. If in some region
, this correlation density vanishes smoothly:
then points within
H become completely uncorrelated with the exterior. Since physical interactions and signals are fundamentally carried by correlations, a region devoid of correlations (
) becomes causally disconnected. Consequently, no timelike or null trajectories can cross the boundary into or out of this region. We term such a boundary a
correlation horizon.
Theorem 4 (Emergent Correlation Horizons).
If as x approaches an open region , then the emergent metric’s temporal component diverges, causing proper time to “freeze” at the boundary. Explicitly:
Consequently, no timelike or null geodesics can penetrate H, making it a purely informational causal boundary arising solely from vanishing correlations.
In this derivation,
is not treated as an independent dynamical variable; instead, because
is defined in terms of
, the field equations arise purely from consistency conditions on
. In other words, we recover
without varying the metric independently of
, by enforcing
(see
Appendix A) for the detailed variation with
only).
For instance, if the global state factorizes into sectors A and B, and sector B is entirely uncorrelated from the observer’s perspective, then sector B resides beyond a correlation horizon in that observer’s emergent spacetime . Such horizons naturally admit a thermodynamic interpretation, as one can associate an “entanglement entropy” proportional to the missing correlation modes beyond the boundary, analogous to the Bekenstein-Hawking entropy for black hole horizons.
Remarkably, these correlation horizons differ fundamentally from traditional black hole horizons: they arise purely informationally without requiring mass-energy singularities or infinite curvature. Indeed, curvature invariants remain finite since correlation density can vanish smoothly.
Thus, correlation horizons generalize the concept of causal boundaries to purely informational structures, demonstrating that horizons fundamentally arise from patterns of quantum entanglement—or its absence—rather than solely from classical curvature singularities.
The exact relationship between vanishing correlation density and divergent metric components depends on model-specific details of how approaches zero.
3.4. Ultraviolet Cutoff and Discreteness
In ordinary continuum quantum field theory, arbitrarily high-energy modes lead to ultraviolet divergences. In the footballhedron framework, the emergent manifold
inherits a built-in discreteness from its underlying correlationhedron
. The correlationhedron
has finite angular resolution
so that only
degrees of freedom reside on the hypersphere of radius
R. This enforces a maximal physical momentum
below which no modes exist. This corresponds to a smallest meaningful length (or time) scale
. Beyond this scale, the notion of distinct spacetime points ceases to exist, and all ultraviolet divergences are tamed.
Because the discretization is uniform on the footballhedron, every inertial observer sees an identical band-limit, preserving Lorentz invariance even at the cutoff scale.
Moreover, just as a black-hole horizon forms in general relativity when (equivalently ), freezing the flow of external time, in our emergent model an observer encounters a horizon-like region whenever the local correlation density , since no further points can be resolved.
Theorem 5 (UV Completion by Hyperspherical Projection).
All projected fields on are band-limited by the finite angular resolution with cutoff . In momentum space, the effective propagator is
which ensures ultraviolet finiteness.
Proof sketch. See
Appendix C for details of the finite-granularity cutoff.
Corollary 2 (Non-Local Effective Action).
Field dynamics are governed by the non-local action
where . The exponential operator smooths high-frequency modes, regularizing short-distance fluctuations.
Corollary 3 (Planck Scale from Mode Resolution).
Identifying yields
so that the smallest resolvable angular feature on the hypersphere corresponds to one Planck length in the emergent spacetime.
Here we assume R and are expressed in the same length units. More precisely, for an n-dimensional spherical correlationhedron with N patches, one finds . Setting gives . In our simplified estimate we take (effectively considering the linear angular resolution along one great circle) to obtain the order-of-magnitude relation . For a 3+1 dimensional emergent spacetime, one might expect or 4, but the exact numerical factor will depend on how one distributes N across angular degrees of freedom.
Although discretization typically breaks Lorentz invariance, our hyperspherical embedding and uniform discretization scheme suggest an invariant cutoff scale shared by all inertial observers. Establishing rigorous proof of exact Lorentz invariance at the cutoff scale requires further detailed investigation.
Exact Lorentz invariance at the cutoff scale is assumed here for simplicity; detailed verification through rigorous group-theoretic analysis remains to be done.
4. Discussion
Our results support a fundamentally relational view, in which spacetime and matter emerge purely as observer-dependent projections of quantum correlations. In this picture, an observer’s universe is an emergent “information shadow” cast by the underlying universal quantum state. In this view, there is no objective, observer-independent spacetime—rather, observers experience consistent spacetimes because their projections are related through fundamental symmetries, notably the footballhedron rotations generating Lorentz transformations and general coordinate invariance. This resonates deeply with the philosophical perspective of relational quantum mechanics [
17], in which properties of physical systems—here, spacetime geometry—exist only in relation to the observer’s chosen correlations.
An intriguing consequence of our framework is the natural emergence of the arrow of time. Although the rotation of itself is fundamentally reversible, each observer perceives an irreversible evolution and a clear distinction between past and future. This arises from the observer’s inherently limited perspective: their projection onto a lower-dimensional spacetime necessarily discards detailed information about correlations. Such coarse-graining, as familiar from statistical mechanics, introduces an entropy gradient and a perceived directionality—thus creating the observer’s arrow of time. The global choice of rotation direction (clockwise vs. counterclockwise in correlation space) consistently aligns this emergent arrow of time across all observers by convention.
Intuitively, an observer initially sensitive to fine-grained correlations gradually loses track of detailed patterns as the correlationhedron rotates, effectively perceiving an increasing number of microstates consistent with their measurements. This irreversible increase in apparent entropy mirrors classical entropy growth and defines their arrow of time.
A key strength of our framework is its inherent unification of geometry (spacetime) and matter. Unlike standard theories—where geometry and matter fields are distinct—in our approach, both emerge simultaneously from the single quantum correlation structure . The apparent separation into curvature (gravity) and matter-energy content () is observer-dependent rather than fundamental. Einstein’s equations thus reflect two facets of the same underlying quantum informational structure.
Below, we briefly discuss how our framework relates to existing approaches, outline potential experimental predictions, and highlight important directions for future research.
4.1. Relation to Other Frameworks
Here we clarify how the footballhedron framework relates to—and differs from—other prominent quantum gravity paradigms.
Our approach complements Van Raamsdonk’s demonstration that entanglement patterns reconstruct AdS bulk geometry [
6]. However, unlike holographic dualities, our emergent geometry arises directly from the complete set of quantum correlations without requiring a boundary dual. Similarly, unlike Jacobson’s thermodynamic derivation of Einstein’s equations, which relies explicitly on local Rindler horizons and equilibrium thermodynamics [
13], our emergent Einstein equations follow directly from global projection consistency of the correlation structure.
In holographic scenarios like AdS/CFT, spacetime emerges from the entanglement structure of a boundary conformal field theory [
4,
6]. Our proposal shares the fundamental insight that entanglement builds geometry; however, it entirely removes the need for a separate boundary system. The spacetime geometry emerges directly from the internal correlations of the universal quantum state, independently accessible to all observers. Similarly, tensor network models of holography [
5] view geometry as a structured code encoding degrees of freedom, whereas the footballhedron generalizes this concept by using the full continuous spectrum of correlations rather than relying on a predetermined network ansatz.
Approaches like loop quantum gravity [
1] and causal set theory aim to discretize spacetime itself as a fundamental assumption. In contrast, our framework discretizes quantum correlations at a fundamental informational level, from which spacetime itself emerges naturally. Thus, our intrinsic Planck-scale cutoff arises automatically from correlation granularity, without needing an a priori discretization of spacetime geometry.
Our use of an information-based metric connects conceptually with the field of
geometric quantum mechanics, which views quantum states as points on a projective Hilbert space manifold equipped with metrics like the Fubini-Study metric [
10]. However, rather than endowing the state space itself with a metric structure, we focus directly on the manifold of correlation configurations of a given quantum state. This emphasizes operationally meaningful observables—quantum correlations—rather than the states themselves, resulting in an emergent geometry more explicitly tied to measurable, relational quantities.
4.2. Predictions and Experimental Tests
Our correlation-based framework makes distinct, testable predictions that, while speculative, offer concrete pathways for empirical investigation. Potential empirical tests include subtle entanglement-induced gravitational effects measurable in proposed laboratory experiments (such as those by Bose et al.) and small deviations in astrophysical observations consistent with a fundamental ultraviolet (UV) cutoff. Specific predictions include:
UV-Protected Propagators: Emergent quantum field propagators acquire exponential suppression factors (e.g., ), naturally regulating ultraviolet divergences. Direct Planck-scale observation remains challenging, yet subtle signatures could manifest as deviations in ultra-high-energy cosmic-ray spectra or precision short-distance experiments. For instance, such exponential suppression might cause the intergalactic medium to become unexpectedly transparent to photons above , modifying the predicted GZK cutoff.
Fundamental Planck-scale Discreteness: Finite angular resolution of the footballhedron predicts an absolute minimal length scale , beyond which no additional physical degrees of freedom exist. This discretization should indirectly appear as intrinsic limits on spatial resolution and potentially as the absence of expected Lorentz-violating dispersions in high-energy astrophysical observations.
Correlation Horizons: The model predicts horizons formed purely by quantum entanglement patterns, without requiring mass-energy concentrations. Observable signatures—such as anomalous gravitational lensing or unique radiation patterns—may appear in scenarios where quantum correlations vanish abruptly, particularly during the early universe or in controlled quantum experiments.
Dark Matter from Quantum Correlations: Dark matter phenomena might emerge purely from correlations between visible matter and unobservable sectors beyond an observer’s correlation horizon. In this scenario, gravitational signatures attributed to dark matter represent entanglement with inaccessible degrees of freedom, not additional particle species. Precision cosmological surveys and galaxy rotation measurements could test this scenario, especially where quantum coherence effects become significant.
Emergent Dark Energy and Cosmological Expansion: Cosmic acceleration and inflationary phenomena could emerge purely from internal rearrangements and projections of correlations within the intrinsically fixed correlationhedron structure, appearing as effective time-dependence to local observers.
Entanglement-Induced Geometry: Quantum entanglement alone could generate gravitational curvature without classical matter-energy. Laboratory tests involving quantum simulators—such as cold-atom arrays or trapped-ion experiments—might measure entanglement-dependent effective metrics or gravitational effects, providing direct evidence supporting the framework’s foundational assumptions.
Non-Local Quantum Dynamics: Non-local modifications to quantum field actions (e.g., terms like ) could induce subtle, frequency-dependent dispersion effects near the Planck scale. Astrophysical observations, particularly high-energy signals from pulsars or gamma-ray bursts, might detect such dispersive delays, serving as indirect evidence for non-local effective dynamics.
These distinctive predictions provide clear, experimentally testable avenues that can help empirically validate or falsify the footballhedron framework as observational precision and laboratory capabilities continue to advance.
Though speculative, potential tests could look for subtle deviations in high-energy dispersion relations or minute quantum-induced corrections to gravitational phenomena, which this finite-resolution framework might predict.
4.3. Future Directions
The footballhedron framework opens numerous avenues for further theoretical exploration and empirical investigation.
This perspective, where gravity emerges purely from information encoded in a single scalar density, offers new pathways for exploring the statistical origins of other geometric identities (e.g. topological constraints, higher-curvature invariants). In particular, the derivation of Einstein’s equations presented in
Appendix A.1 suggests that similar consistency conditions on correlation functions might underlie more general gauge-gravity dualities.
To promote these kinematic insights to full dynamics, we must develop a unified variational principle for both the emergent metric
and the correlation density
. In particular, one seeks an effective action, which we denote
on the space of correlation operators
associated with the underlying quantum state
. Varying
should yield coupled equations of motion for
and
, ensuring fully consistent back-reaction between geometry and matter in the emergent spacetime. Such a formalism would not only specify the dynamics of the “correlationhedron” but also elucidate how perturbations—interpreted as particle- or wave-like excitations—propagate, and how quantum fluctuations in
manifest as geometric and field fluctuations in the emergent gravitational background.
Several other promising extensions and open questions naturally emerge from our current framework:
Holography and Entropy–Area Scaling: Explore explicit relationships between correlation boundary structures, entropic bounds, and holographic principles, clarifying how entropy–area scaling emerges naturally in this framework.
Cosmological Evolution: Investigate how local observers might perceive cosmological evolution—including expansion, inflation, and redshift—arising purely from internal rearrangements and coarse-graining of correlation structures within a fundamentally fixed correlationhedron. Clarify how observed dynamical behaviors, often modeled as variations in effective parameters like and , can emerge without introducing new fundamental degrees of freedom.
Topological Transitions: Analyze the implications of nontrivial topologies or phase transitions within the correlationhedron, and identify potential observational consequences.
Gauge Fields as Fiber Structures: Investigate whether internal symmetries associated with subsystems within the correlationhedron project onto emergent gauge fields, potentially corresponding to Standard Model interactions via fiber-bundle structures over the emergent spacetime manifold.
Experimental Signatures and Tests: Further refine and develop phenomenological predictions, exploring strategies to test the theory through cosmological surveys, quantum-optical setups, and analogue gravity experiments.
These open questions and research directions highlight the substantial potential of the footballhedron framework to yield novel theoretical insights and empirically testable predictions, guiding future research in quantum gravity and emergent spacetime physics.
5. Conclusion
We have introduced and explored a new conceptual framework in which spacetime and gravity emerge entirely from quantum correlations encoded in a universal quantum wavefunction. By introducing additional constraints (spherical topology, finite tessellation, and uniform rotation) into a “footballhedron” structure, we derived Lorentz symmetry, Einstein’s gravitational dynamics, causal horizons, and an intrinsic UV cutoff—all from a unified quantum-informational model. This provides a unified framework where geometry (spacetime) and matter-energy content are not fundamentally distinct entities but arise simultaneously as different projections of the same underlying quantum-informational structure.
The strengths of this approach lie in its conceptual clarity and its compatibility with core principles of quantum mechanics and relativity. The framework is intrinsically background-free, assuming no pre-existing spacetime—only a universal quantum state from which all structure emerges. Additionally, the finite information assumption naturally resolves divergences that traditionally plague quantum field theories.
However, significant open questions remain. The current model has a phenomenological aspect: we have not yet derived the footballhedron’s rotation mechanism from first principles, nor identified uniquely the global quantum state describing our universe. Moreover, it remains to be seen how fully the complexities of the Standard Model might be incorporated, or whether fundamental modifications will be suggested. Nevertheless, the results here indicate a tantalizing possibility: that spacetime, with all its complexity, might ultimately be nothing more than an emergent manifestation of quantum entanglement.
In summary, the footballhedron paradigm invites a profound reconsideration of the ontological status of space and time, positing a radically relational cosmos in which reality itself is emergent and observer-dependent. Should key elements of this picture prove correct, it would mean that at the deepest level, John Wheeler’s famous dictum—“it from bit” (or indeed “it from qubit”)—is not merely metaphorical but precisely describes the quantum-informational code that weaves the tapestry of the universe.
This approach adopts an explicitly relational ontology, viewing spacetime not as a fundamental entity but as a robust emergent structure arising purely from quantum correlations.
Perhaps we have finally uncovered physics’ true holy grail, the ultimate “theory of everything”: the elegant unification of football and fundamental physics.
Appendix A. Informational Action and Emergent Einstein Equations
In this appendix we derive Einstein’s equations from a variational principle based on an emergent informational action. We write the effective action as
where
and:
is the Ricci scalar of the emergent metric .
is the emergent gravitational coupling.
is the correlation density on , inherited from the global state .
is a constant (phenomenological for now) and stabilizes .
Parameters and V should be derivable from first principles in future work.
Variation w.r.t.. Holding
fixed, one finds
Hence
where
and
Setting
for arbitrary
yields
Diffeomorphism invariance of
implies
, and hence
ensuring self-consistent emergent gravity.
Newtonian limit. Writing
in harmonic gauge and linearizing, one obtains
where
, recovering the Poisson equation for weak fields.
Assumptions and boundary conditions.
is smooth with signature .
so that and remain finite.
Boundary terms vanish (or are fixed) under standard asymptotic fall-off conditions on .
Appendix A.1. Emergent Einstein Equations from Correlation Density
Recalling the inverse-Hessian ansatz of Eq. (
2),
and imposing the contracted Bianchi identity
, one immediately recovers the full Einstein field equations as a self-consistency condition on
. The five-step derivation is as follows:
Define , so that .
Compute and set .
Use (Levi-Civita connection of g) to obtain the Bianchi/-constraint.
Identify , which is automatically conserved.
(Optional) Vary the pure-
action
to see that its equation of motion is equivalent to
.
Thus one arrives at
showing that Einstein’s equations emerge without ever varying the metric independently.
Appendix B. Lorentz Group from Hyperspherical Rotations
Here we explicitly demonstrate how Lorentz symmetry emerges naturally from rotations of the correlationhedron embedded in a pseudo-Euclidean ambient space.
Appendix B.1. Pseudo-Euclidean Embedding and Lorentz Boosts
Here we embed the n-dimensional hyperspherical correlationhedron into a -dimensional pseudo-Euclidean space . This formal step does not alter the earlier Euclidean geometry of the n-sphere; it simply introduces a timelike dimension so that a rotation about this axis corresponds to a Lorentz boost.
We embed the correlationhedron
as an
n-dimensional hypersurface in the pseudo-Euclidean space
, equipped with the metric
Idealizing
as an
n-dimensional surface of fixed radius
R, we impose the hypersurface constraint
where
denote ambient coordinates.
Consider a rotation (boost) by rapidity
in the timelike plane
:
Defining emergent coordinates by
the rotation (
A5) induces the standard Lorentz boost:
with the usual relativistic relations
Thus, boosts in the ambient pseudo-Euclidean space directly correspond to Lorentz transformations in emergent spacetime.
Appendix B.2. Composition of Observer Projections
Each inertial observer
corresponds to a projection map selecting a four-dimensional emergent spacetime from
:
A change of inertial observer, represented by an ambient-space rotation
, generates a new observer projection
Because successive rotations compose associatively within
, the family of projections naturally inherits a group action structure:
This ensures a rigorous implementation of the relativity principle, guaranteeing consistency across different inertial observers’ emergent spacetimes. Specifically, for rotations confined to the timelike plane , the induced transformations precisely recover the standard Lorentz group structure .
Appendix C. UV Cutoff from Finite Granularity
Here we explicitly show how finite granularity in the correlationhedron naturally implies an intrinsic ultraviolet (UV) cutoff in the emergent spacetime.
Suppose the correlationhedron
consists of
N elementary correlation patches distributed evenly over an
n-sphere
. Each patch thus subtends an angular size scaling as
The total number of distinguishable correlation directions on the sphere scales linearly with
N. Consequently, the maximal distinguishable momentum scale
in emergent spacetime is related inversely to this minimal angular resolution:
This yields a minimal emergent length scale (UV cutoff):
which represents an intrinsic resolution limit—no finer spatial structure can emerge below this length scale.
To recover continuum general relativity accurately up to a maximal energy scale
, we require
As a concrete example, consider our observable universe radius
, and suppose we seek consistency with continuum physics up to the grand unified theory (GUT) energy scale
. For
, this gives
Thus, ensures a granularity consistent with observed physics down to extremely high energies. Even if we push this requirement closer to the Planck scale, the resulting large N remains consistent with a natural Planck-scale discretization of spacetime.
References
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Loll, R. Quantum gravity from causal dynamical triangulations: A review. Class. Quantum Grav. 2019, 37, 013002. [Google Scholar] [CrossRef]
- Maldacena, J. The large-N limit of superconformal field theories and supergravity. Adv. Theor. Math. Phys. 1998, 2, 231–252. [Google Scholar] [CrossRef]
- Ryu, S.; Takayanagi, T. Holographic derivation of entanglement entropy from the anti-de Sitter space/conformal field theory correspondence. Phys. Rev. Lett. 2006, 96, 181602. [Google Scholar] [CrossRef] [PubMed]
- Swingle, B. Entanglement renormalization and holography. Phys. Rev. D 2012, 86, 065007. [Google Scholar] [CrossRef]
- Van Raamsdonk, M. Building up spacetime with quantum entanglement. Gen. Relativ. Gravit. 2010, 42, 2323–2329. [Google Scholar] [CrossRef]
- Maldacena, J.; Susskind, L. Cool horizons for entangled black holes. Fortschr. Phys. 2013, 61, 781–811. [Google Scholar] [CrossRef]
- Susskind, L. Dear Qubitzers, GR=EQM. Fortschr. Phys. 2016, 64, 551–564. [Google Scholar] [CrossRef]
- Amari, S. Information Geometry and Its Applications; Springer: Tokyo, Japan, 2016. [Google Scholar]
- Brody, D.C.; Hughston, L.P. Geometric quantum mechanics. J. Geom. Phys. 2001, 38, 19–53. [Google Scholar] [CrossRef]
- Russo, A. The Correlationhedron: Spacetime as Projections of Quantum Correlations. Preprint. [CrossRef]
- Eisert, J.; Cramer, M.; Plenio, M.B. Colloquium: Area laws for the entanglement entropy. Rev. Mod. Phys. 2010, 82, 277–306. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of spacetime: The Einstein equation of state. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Page, D.N.; Wootters, W.K. Evolution without evolution: Dynamics described by stationary observables. Phys. Rev. D 1983, 27, 2885–2892. [Google Scholar] [CrossRef]
- Pitowsky, I. Quantum Probability—Quantum Logic; Springer: Berlin, 1991. [Google Scholar]
- Tsirelson, B.S. Quantum generalizations of Bell’s inequality. Lett. Math. Phys. 1980, 4, 93–100. [Google Scholar] [CrossRef]
- Rovelli, C. Relational Quantum Mechanics. International Journal of Theoretical Physics 1996, 35, 1637–1678. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Universal upper bound on the entropy-to-energy ratio for bounded systems. Phys. Rev. D 1981, 23, 287–298. [Google Scholar] [CrossRef]
| 1 |
Note: The correlation density defined here is distinct from the density operator used in quantum mechanics; here, it represents a local density of quantum correlation information projected onto the emergent spacetime. |
| 2 |
More generally, one could include higher-point correlations and temporal correlation functions, but for clarity we focus on equal-time two-point correlations here |
| 3 |
In standard information geometry, the Hessian of defines a Riemannian metric (the Fisher information metric). Here we take the matrix inverse of to define . This inverse-Hessian metric can still be positive-definite locally, but we impose a universal correlation rotation and embed the correlationhedron in a -dimensional pseudo-Euclidean space ( Appendix B) to endow with a Lorentzian signature (one timelike eigen-direction). |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).